A Digital Twin-Assisted VEC Intelligent Task Offloading Approach

Abstract

Vehicular edge computing (VEC) represents a concrete application of mobile edge computing (MEC) in the field of intelligent transportation, with task offloading serving as one of its core components. The design of efficient task offloading strategies poses significant challenges due to the dynamic network topology, stringent low-latency requirements, and massive data processing demands. This paper proposes a digital twin (DT)-assisted intelligent task offloading approach, which establishes a dynamic interaction and mapping between the virtual and physical worlds to enable real-time monitoring of VEC network states, thereby optimizing offloading decisions. First, to meet diverse user service requirements, an optimization model is formulated with the objective of minimizing task processing latency and energy consumption. Next, a gravity model-based vehicle clustering algorithm is integrated with digital twin technology to find the optimal offloading space and ensure link stability among vehicles within aggregated clusters. Furthermore, to minimize overall system costs, the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm is utilized to train the offloading policy, enabling automatic optimization of both latency and energy consumption. consumption. Finally, a feedback mechanism is introduced to dynamically adjust parameters and enhance the robustness of the clustering process. Simulation results demonstrate that the proposed approach significantly outperforms baseline methods in terms of task completion cost, energy consumption, delay, and success rate, thereby validating its potential and superior performance in dynamic vehicular network environments.

1. Introduction

The widespread adoption of 5G and the continuous advancement of 6G technologies are driving the swift advancement of the Internet of Vehicles (IoV) [1]. As a representative scenario of the Internet of Things (IoT) [1] in transportation systems, IoV is showing unprecedented growth potential. Diverse vehicular applications have become deeply integrated into everyday life, ranging from driving safety and in-vehicle entertainment to mobility services [2]. However, vehicles with constrained computational resources may face significant challenges in processing these tasks efficiently. Cloud servers are typically located far from end users [3]. Transmitting the exponentially growing vehicular application data to centralized cloud servers imposes a substantial burden [4] on the network and leads to unpredictable latency, making it unsuitable for IoV scenarios with strict real-time requirements. Mobile edge computing (MEC) [5] addresses this issue by relocating data processing from remote cloud centers to edge nodes closer to the data source, significantly lowering communication delay and enhancing response times [6]. Vehicle edge computing (VEC), an emerging paradigm integrating MEC with IoV, enables the offloading of computationally intensive and latency-sensitive tasks to VEC servers or roadside units, thereby reducing latency and improving service quality for users [7]. However, the increasing number of service-requesting vehicles intensifies competition for limited edge resources, resulting in excessive load pressure on edge servers (ES). With advancements in vehicle intelligence, smart vehicles now possess certain levels of computational and caching capabilities. Aggregating and utilizing the idle resources [4] of these vehicles can both expand the computational capacity of the VEC system and alleviate the burden on edge servers. Nonetheless, the high mobility of vehicles and the dynamic environment often cause existing task offloading approaches to perform poorly in such unpredictable and rapidly changing systems.

Edge intelligence, which integrates edge computing with artificial intelligence, is a promising emerging technology. Deep reinforcement learning (DRL), a subfield of artificial intelligence, fuses the powerful perceptual abilities of deep learning with the decision-making capabilities of reinforcement learning. It is increasingly used to tackle decision-making problems in dynamic and complex environments, offering an effective solution for tasks such as offloading and resource allocation. Compared with heuristic algorithms, DRL offers greater robustness and more stable convergence, enabling instant and dynamic decision-making. Digital twin (DT) is an emerging technology that creates digital replicas of physical entities based on real-time status and historical data. Until 2025, DT technology has been widely adopted in a large variety of domains [8], such as smart community, healthcare and intelligent transportation systems. By ensuring reliable communication between the physical and digital domains, DT bridges the gap [2] between physical space and its digital representation, enhancing real-time interaction and enabling close monitoring [9]. The mapping between virtual models and physical entities provides comprehensive insights into the VEC network, enabling feature extraction and predictive analysis of physical vehicles and dynamic environments [10,11].

In recent years, some studies have started to explore the integration of DT technology with DRL to solve complex problems in practical applications. The role of DT varies across different use cases. For instance, one study [12] utilizes DT to predict the arrival capabilities of future tasks and then applies DRL algorithms to optimize offloading strategies, determining whether tasks should be offloaded to cloud centers, edge servers, or local computing resources. Another study [13] leverages DT’s ability to sense global and historical information, assisting in vehicle clustering, and then employ DRL algorithms to identify the optimal offloading location for tasks. Additionally, a further study [14] uses DRL to make resource allocation [15] and task offloading decisions, while DT simulates the real-world environment of autonomous vehicles to gather global information and optimize resource distribution. The combination of these technologies provides theoretical support for efficient vehicle management and demonstrates high quality and feasibility in practical applications.

Research on DT-based solutions for VEC networks is still in its early stages. First, most existing DT-assisted vehicular task offloading approaches rely on full offloading, whereas partial offloading strategies have shown greater potential in reducing latency. Second, the majority of current studies focus on single-objective optimization, typically minimizing latency. However, user requirements can vary, and single-objective approaches may not adequately address the diverse needs of all users. Furthermore, few studies have investigated the integration of DT technology with DRL approaches in the context of VEC networks. To deeply explore the performance of the combination of these two technologies in VEC, this paper proposes a novel digital twin-assisted intelligent task offloading (DTAITO) approach for VEC networks to support efficient offloading decision-making. The primary contributions of this paper can be outlined as follows:

(1) The partial task offloading optimization model is proposed to jointly minimize latency and energy consumption. This model balances computational performance with energy efficiency while accommodating the diverse requirements of IoV users.

(2) The digital twin network is used to capture real-time, system-wide information on vehicles and network conditions. A Gravity-Inspired Vehicle Clustering (GIVC) algorithm is applied to dynamically form highly resource-compatible clusters, ensuring reliable and stable communication links among vehicles within each cluster. This approach significantly lowers the complexity of task offloading, increases task scheduling success rates, and improves overall system performance under highly dynamic IoV environments.

(3) The TD3 algorithm is introduced to make real-time task offloading decisions in complex and dynamic vehicular networks, improving both the efficiency and stability of decision-making.

(4) A feedback mechanism is incorporated to dynamically tune the parameters of the GIVC algorithm according to task offloading outcomes. This enhances the adaptability and robustness of the clustering process across varying scenarios, further increasing offloading success rates and improving network performance.

The organization of this paper is outlined as follows: Section 2 reviews related work, Section 3 describes the system model and optimization problems, Section 4 describes the DTAITO approach in detail, Section 5 analyzes the experimental evaluation, and Section 6 concludes the study.

2. Related Work

In this section, a comprehensive review of the task offloading literature in V2V scenarios is reviewed. Additionally, methods that leverage DRL and DT technologies to assist task offloading are also discussed. Moreover, the limitations of existing studies are summarized, and the innovative contributions of this work are emphasized.

2.1. Task Offloading in V2V

VEC has emerged as a highly promising computing paradigm, offering a feasible solution to the limitations of on-board computational capabilities that hinder the efficient execution of computation-intensive applications. Consequently, it has attracted significant attention from both academia and industry in recent years. Considering offloading scenarios, the majority of existing studies have primarily focused on V2I environments [16,17]. However, when the number of ES near the vehicle is limited or the load on the edge servers is high, the offloading and execution of vehicle tasks can be significantly affected. To address this issue, several studies have explored task offloading in V2V scenarios, leveraging the idle resources of nearby vehicles to execute tasks. Wu et al. [18] propose a V2V-based secure computation offloading algorithm, R-MDDQN, for video analysis. It ensures data security through Wyner’s wiretap coding approach, dynamically adjusts multi-objective weights using a Radial Basis Function (RBF) network, and optimizes the offloading strategy with a Double Deep Q-Network (DDQN). Chen et al. [19] regard nearby vehicles with idle resources as a resource pool and propose a distributed computation offloading strategy based on the DQN algorithm to minimize the execution time of composite tasks in V2V scenarios. In another work, Chen et al. [5] formulate the problem of offloading as a generalized allocation model with constraints which is solved by the discrete bat algorithm and greedy algorithm, respectively. However, although the above studies utilize the idle computing resources of vehicles, they focus solely on minimizing latency without jointly considering energy consumption.

2.2. Task Offloading with DRL

Numerous studies have proposed a variety of solutions to solve the task offloading problem in VEC. To effectively address the complexity and vast search space associated with task offloading in IoV scenarios, some studies have adopted swarm intelligence-based heuristic approaches. Cong et al. [20] propose a two-stage heuristic task offloading strategy to address the issue of inefficient resource allocation resulting from offloading decisions in multi-vehicle, multi-server IoV scenarios. The strategy integrates an improved artificial fish swarm algorithm with an improved hybrid genetic algorithm, using iterative optimization to allocate resources efficiently in task offloading, thereby achieving joint optimization of average cost, energy consumption and latency. Chen et al. [21] propose an enhanced heuristic task offloading strategy to improve offloading and resource allocation in IoV environments. They employ an improved dual-population immune genetic algorithm, which retains elite populations while introducing an adaptive migration operator. The approach considers constraints such as the maximum tolerable delay of vehicles and the allocatable resources of the roadside units to optimize system energy consumption and latency. However, the scenarios addressed by the aforementioned approaches are overly idealized. In contrast, real-time vehicular network scenarios are dynamic and complex, making it difficult for these solutions to effectively adapt to practical environments.

Recently, DRL has been regarded as an effective technique for addressing task offloading problems in dynamic vehicular network scenarios. Among the studies employing DRL for task offloading, some have adopted binary offloading strategies. Shi et al. [22] propose a blockchain-enabled VEC framework and develop a computation offloading approach based on the soft actor–critic (SAC) algorithm. Several studies have focused on partial task offloading, under the premise that it offers greater potential and flexibility than full offloading. Yao et al. [23] formulate the dynamic computation offloading problem as a Markov Decision Process and applied the TD3 algorithm in an IoV context to support real-time decision-making and prediction for optimal offloading strategies. Some studies have focused on partial task offloading. Huang et al. [24] consider a cloud-edge-end architecture in a dynamic network environment and introduced the CORA algorithm to minimize system costs under task latency and transmission power constraints, jointly optimizing resource allocation and task offloading. Gao et al. [25] propose a federated learning-assisted DRL approach that allows tasks to be partially offloaded to the ES, enabling concurrent execution on both the local device and ES to reduce task completion time. However, the aforementioned studies have not taken into account that, as the number of edge servers and vehicles increases, the size of the decision space also expands, thereby affecting the real-time capability of obtaining the optimal offloading strategy.

2.3. Task Offloading with DT

Digital twin is a technology that enables real-time mapping and interaction between virtual models and their corresponding physical entities, processes, systems, and environments. It has been widely applied in various fields such as manufacturing, transportation, and smart cities [26,27]. Dai et al. [28] propose a DRL-based resource allocation approach for digital twin-enabled VEC networks. They jointly optimize computational resource allocation and task offloading to minimize overall system offloading latency and enhance network performance and computational efficiency. Cao et al. [29] apply digital twin technology to vehicular task offloading scenarios, addressing vehicle mobility challenges through the formulation of a multi-objective joint optimization problem. Sun et al. [30] introduce a mobility-aware offloading approach for digital twin-enhanced networks. By constraining service migration costs, the approach aims to minimize offloading waiting time. They employ Lyapunov optimization to convert long-term migration cost constraints into a multi-objective dynamic optimization problem, which is then solved using a DRL algorithm. In addition, several other notable studies have explored the role of DT in various scenarios. For instance, some studies use DT to predict the arrival rate of tasks [12] at future edge servers, simulate resource allocation [13], or monitor global information and acquire historical data [14] through DT. Subsequently, these studies integrate DRL algorithms to make decisions regarding task offloading locations or resource allocation. The aforementioned studies employ DT technology as an auxiliary approach to address task offloading in vehicular networks. Although this represents an innovative attempt, other aspects of the proposed approaches still suffer from limitations such as relying on a single optimization objective or neglecting the reduction of the decision space.

2.4. Summary

By analyzing prior studies, the related work is summarized as follows. First, leveraging the idle computing resources [31] of vehicles can alleviate the load pressure on edge servers in V2I scenarios. Second, DRL algorithms have proven effective in addressing task offloading problems in dynamic and heterogeneous environments. Third, DT technology provides valuable support for tackling high-risk or challenging tasks in real-world scenarios. Nevertheless, the core challenge of vehicular task offloading remains how to deliver efficient real-time services in highly dynamic vehicular environments. To this end, this paper integrates DRL and DT technologies and proposes the DTAITO approach, which optimizes task offloading decisions in VEC scenarios and enables efficient real-time services in dynamic vehicular networks while simultaneously improving overall system performance.

3. System Model

3.1. Network Model

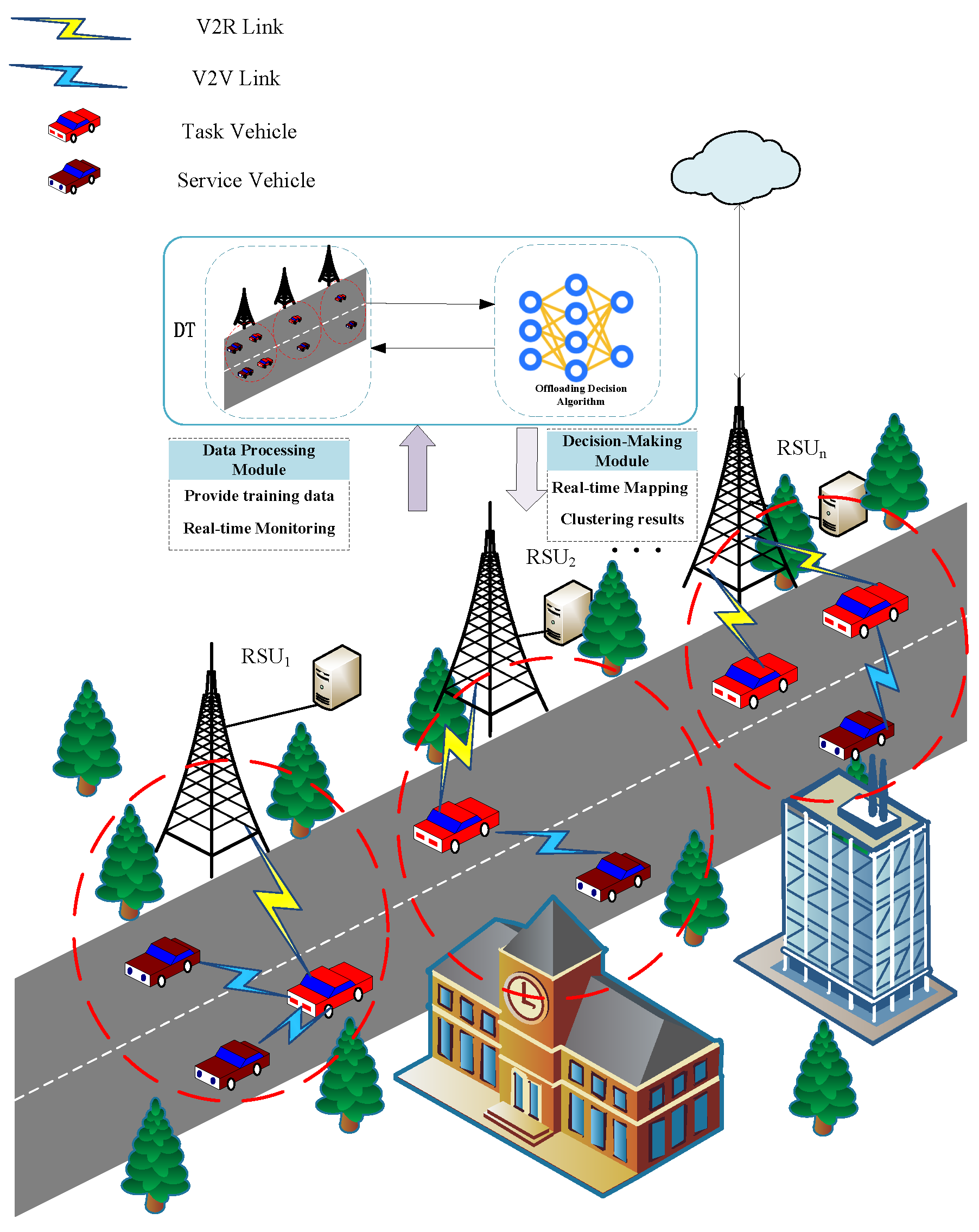
The digital twin-assisted VEC architecture is illustrated in Figure 1. The digital twin network (DTN) is structured into two parts: a digital twin layer and a physical entity layer. Meanwhile, the vehicular edge computing system is organized into three tiers, namely the cloud, edge, and user layers. Vehicles in the user layer are responsible for collecting and analyzing data, and they offload tasks to other vehicles when computational resources are insufficient, thereby reducing the burden on roadside units (RSUs). RSUs in the edge layer communicate wirelessly with surrounding vehicles, acquiring real-time vehicle information and generating digital twin models to reflect and predict the physical state of vehicles in real time. The cloud layer consists of high-performance servers responsible for efficiently managing the edge servers. The architecture of the DTN comprises three fundamental modules: model mapping, data storage and digital twin management. These modules are intended to facilitate real-time updates and sustain synchronization across the physical and digital layers.

By utilizing a clustering algorithm assisted by the DTN deployed on RSUs, the comprehensive information of all vehicles on the road can be acquired, enabling the dynamic grouping of vehicles into distinct aggregation clusters. Each aggregation group consists of an RSU connected to an edge server and K vehicles, denoted by the set $V=\{1,2,\dots ,V\}$. All vehicles in the cluster have access to the RSU. When a vehicle lacks sufficient resources to execute a task locally, it initiates constrained offloading within the group, thereby narrowing the candidate offloading targets in advance. Vehicles within the group that lack the computational capacity to handle intensive tasks [32] send task requests to the RSU. The RSU then makes optimal offloading decisions based on factors such as the available resources and load of the connected ES, as well as the idle resources of other vehicles, thereby reducing both task execution energy consumption and delay.

Based on their roles in requesting or providing computational resources, vehicles within an aggregation group are categorized as service vehicles (SVs) and task vehicles (TVs). Assume there are K vehicles on the road. Among them, i vehicles request task offloading during a given period and are represented by $TV=\{T{V}_1,T{V}_2,\dots ,T{V}_I\}$, while j vehicles provide computational resources and are represented by $SV=\{S{V}_1,S{V}_2,\dots ,S{V}_J\}$. We let $H_i=\{D_i,C_i,T_i^{tolerate}\}$ express the task of vehicle, where $C_i$ represents the number of CPU cycles required to complete task $H_i$, $D_i$ represents the size of the input data and $T_i^{tolerate}$ represents the maximum tolerable latency of task $H_i$. This work adopts a partial offloading approach, whereby the task of $T{V}_i$ can be offloaded to either the RSU or an SV according to an optimal offloading ratio. We let ${\theta }_i$ represent the proportion of the task offloaded, and $1-{\theta }_i$ represent the proportion executed locally, with ${\theta }_i\in [0,1]$. ${\theta }_i=1$ means that it will be fully offloaded, ${\theta }_i=0$ denotes that the task will be executed entirely locally. $0<L<1$ represents partial task offloading, in which the task is partially executed locally and partially at the ES, enabling collaborative processing between the local device and the ES.

3.2. Social Relationship Model

Considering the highly dynamic properties of VEC networks, unstable communication links can significantly increase both energy consumption and latency. Therefore, ensuring the stability of inter-vehicle communication links is critical. To address this, the DTAITO approach introduces a social relationship model that integrates multi-scale factors within the VEC network. It constructs social trust values from raw data and represents them as a social trust matrix, which serves as a quantitative indicator of inter-vehicle social relationships. This matrix is used to describe the stability of communication links between vehicles, thereby mitigating the challenges posed by vehicular mobility. The core idea of the social trust value is to assess the level of trust between two vehicles based on their proximity, evaluated using two key parameters: directional similarity and velocity similarity.

(1) Directional Similarity: $o_{i,j}^d$ is used to indicate whether the directions of vehicles $T{V}_i$ and $S{V}_j$ are aligned. It is defined by the following expression:

$$o_{i,j}^d=\{\begin{array}{cc}0,& \mathrm{if}i\mathrm{has}\mathrm{the}\mathrm{same}\mathrm{direction}\mathrm{as}j\\ 1,& \mathrm{if}i\mathrm{has}\mathrm{no}\mathrm{same}\mathrm{direction}\mathrm{as}j\end{array}$$

(1)

(2) Velocity Similarity: Let $v_i$ and $v_j$ represent the speeds of vehicle i and j, respectively. The velocity similarity between the two vehicles is denoted by $o_{i,j}^v$, and it is defined by the following expression:

$$o_{i,j}^v=\{\begin{array}{cc}0,\hfill & \mathrm{if}{v}_i=0\mathrm{or}{v}_j=0\hfill \\ {\displaystyle \frac{v_j}{v_i}},\hfill & \mathrm{if}{v}_j<v_i\hfill \\ {\displaystyle \frac{v_i}{v_j}},\hfill & \mathrm{if}{v}_i<v_j\hfill \\ 1,\hfill & \mathrm{if}{v}_i=v_j\hfill \end{array}$$

(2)

Based on directional similarity and velocity similarity, the social trust value between vehicle i and j is expressed as:

$$o_{i,j}={\eta }_1{o}_{i,j}^d+{\eta }_2{o}_{i,j}^v$$

(3)

where ${\eta }_1$ and ${\eta }_2$ are the weighting coefficients for directional and velocity similarity, respectively. A higher value of $o_{i,j}$ indicates a stronger trust level between vehicle i and j. For ease of representation, $U=[o_{i,j}{]}_{M\times M}$ is introduced to describe the trust relationships among vehicles within a given region.

By clustering vehicles according to the social relationship model, communication links within each aggregation group are stabilized, thereby mitigating the latency and energy overhead caused by link instability or disconnection. When applying the DRL algorithm for offloading decisions, this approach significantly reduces the decision space and improves the efficiency of V2V task offloading.

3.3. Communication Model

When the task of $T{V}_i$ is offloaded to the ES, data transmission is required. The communication model we adopt is similar to that presented in [33]. Let $R_i$ represent the data transmission rate from $T{V}_i$ to RSU or $S{V}_j$, and it is calculated as follows:

$$R_i=W_i{log}_2\left(1+{\displaystyle \frac{P_i{d}_i^{-\beta }{\left|h_i\right|}^2}{N_0+I_n}}\right)$$

(4)

where $W_i$ represents the bandwidth of the wireless channel, $d_i$ indicates the distance between $T{V}_i$, $P_i$ represents the transmission power used by the vehicle to upload data. $\beta$ is the exponent of path loss, $d_i$ indicates the distance between $T{V}_i$ and ES or another vehicle $S{V}_j$, $h_i$ denotes the wireless channel gain, $I_i$ indicates the inter-cell interference of the uplink [34], and $N_0$ refers to the Gaussian noise power in the channel. Given that the delay in returning the results is minimal and can be disregarded, the transmission rate for result delivery is not considered in this study.

Offloading an excessive number of tasks to the SVs can cause significant interference, impacting communication efficiency. Additionally, interference in the communication link may result in fluctuations in the V2V communication range. The instant V2V communication, denoted as $\mathcal{D}$, is given by the following expression:

$$\mathcal{D}={\mathcal{D}}_0\times \ell \left(1+{\displaystyle \frac{P_i{d}_i^{-\beta }{\left|h_i\right|}^2}{N_0+I_n}}\right)$$

(5)

where ℓ is the adjustment coefficient and ${\mathcal{D}}_0$ is the initial communication distance.

3.4. Task Offloading Model

3.4.1. Local Computing Model

When a vehicle has sufficient computational resources to process its own tasks, it does not need to rely on the ES or other vehicles. Under this circumstance, the local computation of the task involves both latency and energy consumption, denoted as $T_i^{local}$ and $E_i^{local}$, respectively. The corresponding formulas are given as follows:

$$T_i^{local}={\displaystyle \frac{(1-{\theta }_i)C_i}{f_i}}$$

(6)

$$E_i^{local}=\kappa {\left(f_i\right)}^2(1-{\theta }_i)C_i$$

(7)

where $f_i$ represents the computational capability of $T{V}_i$, and $\kappa$ denotes the power consumption coefficient of the vehicle.

3.4.2. Edge Computing Model

When the task of $T{V}_i$ is offloaded, and the RSU has sufficient computational resources with low load, the DTAITO approach allows the requesting vehicle to offload its task to the edge server associated to the RSU for processing. In this case, the total delay is primarily composed of the transmission delay from the vehicle to the RSU and the computation delay at the ES. The energy consumption includes both the transmission energy to the RSU and the execution energy at the ES. The transmission and computation delays for tasks offloaded to the ES are expressed as follows:

$$T_i^{trans,es}={\displaystyle \frac{{\theta }_i{D}_i}{R_i^{v2r}}}$$

(8)

$$T_i^{exe,es}={\displaystyle \frac{{\theta }_i{C}_i}{f_i^{es}}}$$

(9)

The total delay for task processing at the ES can be expressed as:

$$T_i^{total,es}=T_i^{trans,es}+T_i^{exe,es}$$

(10)

where $f_i^{es}$ represents the computational resources allocated by the ES to task $H_i$, which must be less than $f^{es}$. $f^{es}$ denotes the computational capacity of the ES, measured in CPU cycles per second. As the output data size after task execution is much smaller than the input data size, the result return delay in the DTAITO approach will be reasonably ignored. The transmission energy to the RSU and the execution energy at the ES are expressed as follows:

$$E_i^{trans,es}=P_i^{trans}{T}_i^{trans,es}$$

(11)

$$E_i^{exe,es}=P_i^{exe}{T}_i^{exe,es}$$

(12)

The total energy consumption for task execution at the ES is displayed by:

$$E_i^{total,es}=E_i^{trans,es}+E_i^{exe,es}$$

(13)

When the RSU lacks sufficient computational resources or is heavily loaded, the task is offloaded to a service vehicle with available computing capacity for execution. Under this circumstance, the total delay $T_{i,j}^{total,sv}$ for completing the task comprises the transmission delay $T_{i,j}^{trans,sv}$ for sending $H_i$ to $S{V}_j$, and the computation delay $T_{i,j}^{exe,sv}$ for executing it on $S{V}_j$. The corresponding expressions are given as follows:

$$T_{i,j}^{trans,sv}={\displaystyle \frac{{\theta }_i{D}_i}{R_i^{v2v}}}$$

(14)

$$T_{i,j}^{exe,es}={\displaystyle \frac{{\theta }_i{C}_i}{f_{i,j}^{sv}}}$$

(15)

where $f_{i,j}^{sv}$ represents the computational resources allocated by $S{V}_j$ to $T{V}_i$, and $f_{i,j}^{sv}$ must be less than $f_j^{sv}$. $f_j^{sv}$ denotes the computational capability of $S{V}_j$, measured in CPU cycles per second. Therefore, the total delay for executing task $H_i$ offloaded to $S{V}_j$ is given by:

$$T_{i,j}^{total,sv}=T_{i,j}^{trans,sv}+T_{i,j}^{exe,sv}$$

(16)

Under the assistance of $S{V}_j$, the total energy consumption $E_{i,j}^{total,sv}$ for completing the task includes the transmission energy from $T{V}_i$ to $S{V}_j$ and the computation energy consumed by $H_i$ when processing the task on $S{V}_j$. The respective expressions are given as follows:

$$E_{i,j}^{trans,sv}=P_i^{trans}{T}_{i,j}^{trans,sv}$$

(17)

$$E_{i,j}^{exe,sv}=P_j^{exe}{T}_{i,j}^{exe,sv}$$

(18)

Therefore, the total energy consumption $E_{i,j}^{total,sv}$ for task $H_i$ offloaded to $S{V}_j$ for processing is expressed as:

$$E_{i,j}^{total,sv}=E_{i,j}^{trans,sv}+E_{i,j}^{exe,sv}$$

(19)

Therefore, when task $H_i$ of $T{V}_i$ is offloaded, the delay $T_i^{off}$ and energy consumption $E_i^{off}$ for the offloaded portion are given by the following expressions:

$$T_i^{off}=\{\begin{array}{cc}{T}_i^{total,es},& \mathrm{if}\mathrm{the}\mathrm{task}\mathrm{is}\mathrm{offloaded}\mathrm{to}ES\hfill \\ T_{i,j}^{total,sv},& \mathrm{if}\mathrm{the}\mathrm{task}\mathrm{is}\mathrm{offloaded}\mathrm{to}S{V}_j\hfill \end{array}$$

(20)

$$E_i^{off}=\{\begin{array}{cc}{E}_i^{total,es},& \mathrm{if}\mathrm{the}\mathrm{task}\mathrm{is}\mathrm{offloaded}\mathrm{to}ES\hfill \\ E_{i,j}^{total,sv},& \mathrm{if}\mathrm{the}\mathrm{task}\mathrm{is}\mathrm{offloaded}\mathrm{to}S{V}_j\hfill \end{array}$$

(21)

Since partial offloading allows local and offloaded computations to be executed in parallel, the execution delay and energy consumption for task $H_i$ can be formulated based on the above equations as follows:

$$T_i=max\{T_i^{local},T_i^{off}\}$$

(22)

$$E_i=E_i^{local}+E_i^{off}$$

(23)

3.5. Problem Formulation

In line with most existing studies, this paper adopts energy consumption and delay as the key performance metrics for evaluating system efficiency. Two weighting parameters are introduced to transform the multi-objective optimization problem of energy consumption and delay into a single-objective one. By adjusting these weights, the model can accommodate varying user [35] preferences. The total cost incurred by all vehicles within a cluster can be formulated as Equation (24):

$$minZ=\sum _{i=1}^I({\alpha }_1{T}_i+{\alpha }_2{E}_i)$$

(24)

$$\mathrm{s}.\mathrm{t}.I\cup J=K,$$

(25)

$$T_i\le T_i^{tolera},\forall i\in I,$$

(26)

$${\theta }_i\in [0,1],\forall i\in I,$$

(27)

$$0\le \left(f_{i,j}^{sv}\right|{\theta }_i\ne 0)\le f_j^{sv},\forall i\in I,\forall j\in J,$$

(28)

$$0\le \left(f_i^{es}\right|{\theta }_i\ne 0)\le f^{es},\forall i\in I,$$

(29)

$$\sum _{i=1}^I\left(f_i^{es}\right|{\theta }_i\ne 0)\le f^{es},\forall i\in I,$$

(30)

$${\alpha }_1+{\alpha }_2=1,{\alpha }_1\in [0,1],{\alpha }_2\in [0,1],\forall i\in I,$$

(31)

where constraint (25) requires that $T{V}_i$ must select $S{V}_j$ within the aggregation group to provide computational services. Constraint (26) ensures that the execution time of task $H_i$ does not surpass its maximum tolerable latency. Constraint (27) stipulates that the offloading ratio of task $H_i$ must not exceed 1, allowing any proportion of the task to be processed locally or offloaded. Constraints (28) and (29) ensure that the computing resources allocated to $T{V}_i$ by $S{V}_j$ and ES do not exceed their respective maximum computational capacities. Constraint (30) requires that the total computing resources allocated by the RSU to task $H_i$ do not exceed its available computational capacity. Constraint (31) defines ${\alpha }_1$ and ${\alpha }_2$ as the relative weights of delay and energy consumption, which can be adjusted according to different users’ service requirements.

When ${\theta }_i=0/1$, the time complexity of obtaining the optimal solution increases exponentially with the number of $TV$. This problem has been proven to be NP-hard [36]. With the introduction of the partial offloading problem, where ${\theta }_i\in (0, 1)$, the problem becomes more complex. Therefore, this study employs a DRL algorithm to solve it.

4. Proposed Approach

The DTAITO approach proposed in this study addresses the aforementioned problems through the GIVC algorithm and TD3 algorithm. First, the approach uses the GIVC algorithm assisted by DT for vehicle clustering, ensuring the stability of the links between vehicles within the aggregation group. Then, the TD3 algorithm is employed to obtain the optimal offloading decision, with the design of the action space, state space, and reward function for the partial offloading problem. By training a neural network, the optimal solution for the task offloading problem is obtained. In the end, a feedback mechanism is introduced to adjust the parameters of clustering according to the offloading results, enhancing the robustness of the GIVC algorithm in various environments.

4.1. Gravity-Inspired Vehicle Clustering (GIVC) Algorithm

Given the high vehicle density, direct large-scale scheduling is impractical. Aggregation groups are formed based on the availability and demand for computational resources, using the DT and GIVC algorithms to determine the optimal offloading space, thereby effectively reducing the complexity of task scheduling. A DT node for the VEC is established in each RSU, where each RSU collects the topology of vehicles and computational capabilities in the surrounding environment. Data is transmitted through wired communication, constructing the overall DT network of the VEC. For clarity, the DTAITO approach in this paper defines the elements of the DT network as $\{\Lambda ,\Theta ,\Psi \}$, where $\Lambda$ represents the digital model of the vehicle, consisting of the task set $\left\{{\mathrm{H}}_i\right\}$, the social trust value set ${\{\mathrm{o}}_i^j\}$, the computational resource set $\left\{f_i\right\}$ and the transmission rate set $\left\{R_i\right\}$. $\Theta =\{{\Theta }_1,{\Theta }_2,{\Theta }_3\}$ denotes the correlation coefficient between computational resources, social trust values, and transmission rates in the DT network. $\Psi$ is the cyclic sequence number, which assists in parameter updates.

The GIVC algorithm used for clustering in the DTAITO approach is an improvement based on the K-Means algorithm, inspired by Newton’s law of gravitation. This paper uses the algorithm to generate optimal aggregation groups, each consisting of one RSU and V vehicles. In this study, the “mass” of a vehicle i is defined as:

$$M_i={\displaystyle \frac{C_i}{f_i}}$$

(32)

where $C_i$ denotes the number of CPU cycles required by vehicle i to complete task $H_i$ and $f_i$ represents the computational capability of each vehicle. This variable is used to estimate the computational demand of vehicle i, which is supplemented by offloading tasks to address resource deficiencies. When vehicle i acts as the service vehicle, its “mass” becomes $M_i^{-1}$. Next, according to Equation (32), the gravitational force between vehicle i and vehicle j can be expressed as:

$$F_{i,j}={\displaystyle \frac{{\Theta }_{1}max(M_i/M_j,M_j/M_i)}{{({\Theta }_2/{\omega }_{i,j}+{\Theta }_3/R_{i,j})}^2}}$$

(33)

where the numerator of Equation (33) primarily represents the supply–demand relationship strength between vehicle i and vehicle j, reflecting their relative strength in terms of computational resource requirements. The proposed method modifies the K-Means algorithm by replacing its distance metric in the denominator with social trust values and communication rates. Through the incorporation of the gravitational formula (33) in place of the distance element, enhanced clustering performance for vehicles is achieved.

Let the ensemble of vehicles in the region excluding the cluster centers be denoted as $\overline{X}=\{v_1,v_2,\dots ,v_n\}$, and the set of vehicles serving as the cluster centers be denoted as $\overline{Y}=\{v_1^{\prime },v_2^{\prime },\dots ,v_m^{\prime }\}$. Ultimately, the aggregation groups produced by the algorithm are collectively denoted as $\overline{\Gamma }=\{{\overline{\Gamma }}_1,{\overline{\Gamma }}_2,\dots ,{\overline{\Gamma }}_m\}$. The specific procedure of Algorithm 1 is as follows.

Algorithm 1 GIVC Algorithm

Input:  Desired number of aggregation groups; number of vehicles Output:  A set of m aggregation groups $\overline{\Gamma }=\{{\overline{\Gamma }}_1,{\overline{\Gamma }}_2,\dots ,{\overline{\Gamma }}_m\}$  1: Initialize model parameters ${\Theta }_1$, ${\Theta }_2$, ${\Theta }_3$, and the value of the number of aggregation groups m;  2: Initialize the aggregation group set $\overline{\Gamma }=\varnothing$;  3: Randomly select m vehicles as cluster centers $\overline{Y}=\{v_1^{\prime },v_2^{\prime },\dots ,v_m^{\prime }\}$;  4: for  $k=[1,2,\dots ,m]$  do  5:    Update ${\overline{\Gamma }}_k$ to ${\overline{\Gamma }}_k=\left\{v_k^{\prime }\right\}$;  6: end for  7: for  $p=[1,2,\dots ,n]$  do  8:    Calculate the gravitational set $\{F_{v_i,v_j}\},\forall v_j\in \overline{Y}$ using Equation (33);  9:    Select the vehicles $v_j$ that make $\left\{F_{v_i,v_j}\}=\max \{F_{v_i,v_j}\right\}$; 10:    Update ${\overline{\Gamma }}_j$ to ${\overline{\Gamma }}_j={\overline{\Gamma }}_j\cup \left\{v_i\right\}$; 11: end for 12: return $\overline{\Gamma }=\{{\overline{\Gamma }}_1,{\overline{\Gamma }}_2,\dots ,{\overline{\Gamma }}_m\}$.

4.2. Task Offloading Decision Approach

The Markov Decision Process (MDP) is formulated as a mathematical model to capture sequential decision-making in stochastic environments. First, the DTAITO approach models the above optimization problem as an MDP, and then uses the TD3 to make task offloading decisions.

4.2.1. Markov Decision Process

The MDP model is typically represented by a four-tuple (S, A, T, R), where S denotes the state space, A represents the action space, T is the state transition probability function (which is unknown in this paper), and R is the immediate reward obtained by performing action A in state S. Based on the above definitions, the problem under study is modeled as the following MDP model.

(1) State Space: The state space of the entire system is obtained through the DT-assisted clustering process, which includes the vehicles number in the aggregation group, the task information of TV, the related information between SV and TV, and the information of ES. Therefore, the system state is expressed as:

$$S=\{S_{H_i},S_i,S_j,S_{es}\}$$

(34)

where $S_{H_i}$ can further be expressed as $(D_i,C_i,T_i^{tolera})$, which includes the task size, the required computational resources, and the maximum tolerable delay. $S_i$ denotes the information of task vehicle $T{V}_i$, including its transmission power $P_i^{trans}$, computation power $P_i^{exe}$, and remaining computational resources $f_i^{remain}$. $S_j$ represents the information of service vehicle $S{V}_j$, including its computation power $P_j^{exe}$ and remaining computational resources $f_j^{remain}$. $S_{es}$ denotes the information of the ES connected to the RSU, including its computation capacity $f^{es}$ and remaining computational resources $f_{es}^{remain}$.

(2) Action Space: To determine the offloading ratio and offloading target for each vehicle, ${\theta }_i\in [0,1]$ can represent three scenarios: full local execution, partial task offloading, and complete offloading. $x_i^j$ denotes the task offloading location for $T{V}_i$, where $j\in \{0,1,\dots ,J\}$ indicates offloading to the ES connected to the RSU or to an eligible $S{V}_S$. Therefore, the action space is expressed as:

$$A=\{{\theta }_i,x_i^j\}$$

(35)

(3) Reward: After executing action A in state S, the agent receives the corresponding reward $R(S,A)$. The goal of the DRL algorithm is to maximize cumulative rewards. To align the objective function with the goal of the algorithm, this study designs the following reward function:

$$R(S,A)=\{\begin{array}{c}-{\displaystyle \sum _{i=1}^I}({\alpha }_1{T}_i+{\alpha }_2{E}_i)\\ \vartheta \end{array}$$

(36)

In this case, when the agent successfully completes the task as required, it receives reward $-{\displaystyle \sum _{i=1}^I}({\alpha }_1{T}_i+{\alpha }_2{E}_i)$. If the agent fails to complete the task as required, it incurs a corresponding penalty $\vartheta$. Under this setup, the larger the reward value, the smaller the offloading cost Z that is focused on, thus achieving effective optimization of the system’s performance.

4.2.2. Vehicle Partial Task Offloading with TD3

Given that the DQN [37] method is not well-suited for continuous action control problems and that the Deep Deterministic Policy Gradient (DDPG [38]) algorithm exhibits poor robustness in hyperparameter selection and tuning, the DTAITO approach chooses the TD3 algorithm to make partial offloading task decisions for vehicles. TD3 addresses issues such as value function overestimation bias, training instability, and slow convergence speed that exist in DDPG during policy optimization. Several improvements have been proposed to enhance the performance and stability of algorithm: First, a dual Q-network architecture is used, with two independent critic networks learning two Q-functions in parallel. When calculating target values, the smaller of the two Q-function estimates is chosen to effectively suppress the overestimation problem caused by value function approximation errors. Secondly, a target policy smoothing mechanism is introduced during the target policy calculation process. By adding truncated Gaussian noise to the target action, the tendency of the policy function to overfit in the steep regions of the Q-value function is reduced, thus improving the stability and robustness of the learning process. Finally, a delayed policy update mechanism is introduced, where the actor network is updated once for every several updates to the critic network. Consequently, the policy network benefits from more reliable value estimates, leading to reduced variance and improved training efficiency.

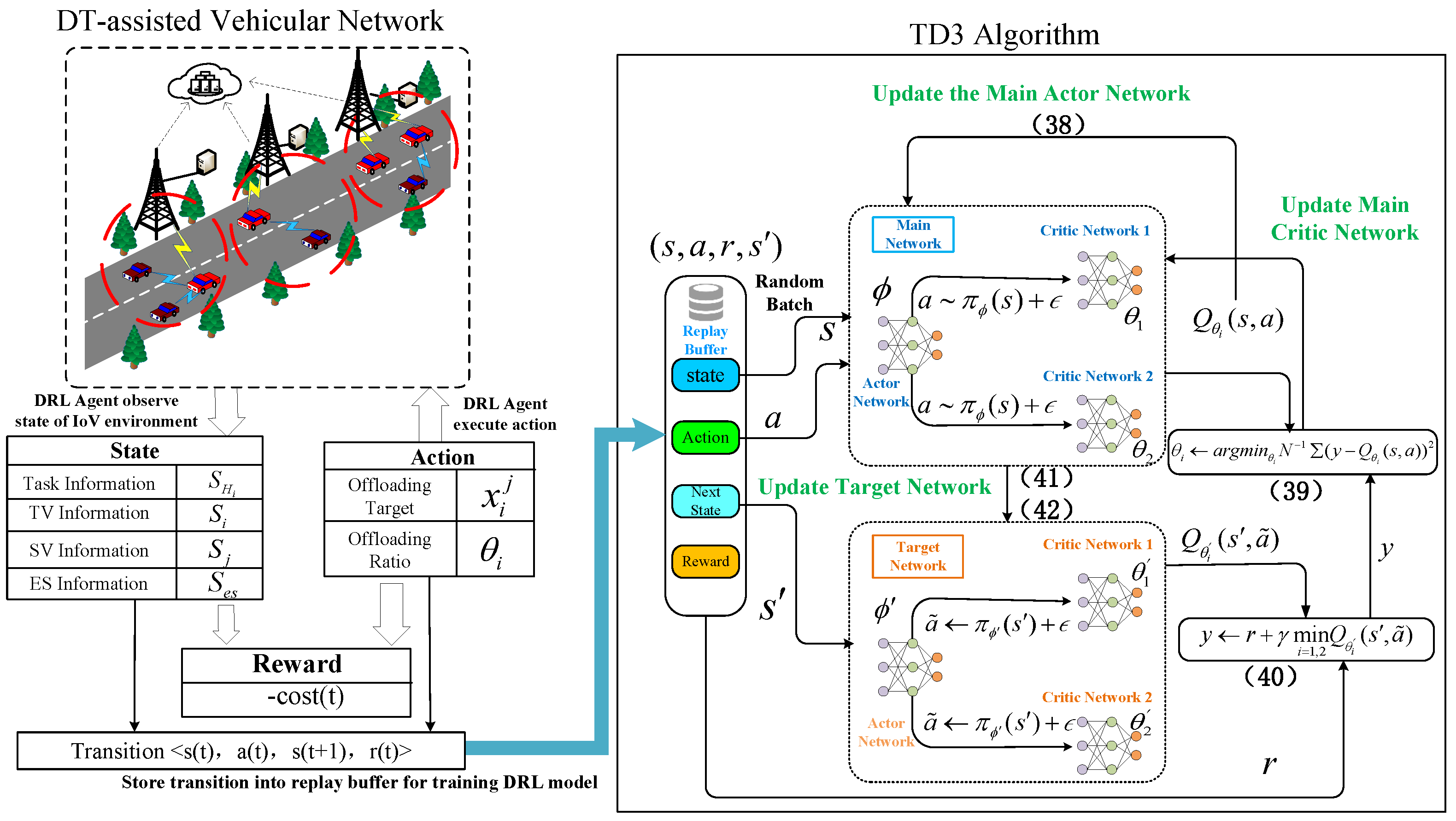
The flowchart of the TD3 algorithm is shown in Figure 2. First, the TD3 algorithm employs a DRL model composed of a main and a target network. Each network is composed of two critic networks and an actor network, which are used to approximate the policy function and the value function, respectively. At the same time, the parameters of the critic and actor networks in the target network are denoted as ${\theta }_1^{\prime }$, ${\theta }_2^{\prime }$ and ${\varphi }^{\prime }$. The role of the actor network ${\pi }_{\varphi }$ is to generate action $a\left(t\right)$, that is:

$$a\left(t\right)={\pi }_{\varphi }\left(s\right)+\epsilon ,\epsilon \sim N(0,\mu )$$

(37)

where $\epsilon$ represents the noise, which plays a crucial role in promoting exploration within the DRL model. It follows a normal distribution, characterized by a mean of 0 and a variance of $\mu$.

The actor network receives its input from the state space, which is derived from the data provided by the DT. The actor network selects action $a\left(t\right)$ based on the present state $s\left(t\right)$, then engages with the environment, leading to the next state $s(t+1)$ and producing the reward $r\left(t\right)$ associated with performing that action in the given state. The resulting four-tuple $<s\left(t\right),a\left(t\right),r\left(t\right),s(t+1)>$ is then stored in the experience replay buffer for updating the TD3 network parameters. To update the parameters of the main actor network, the TD3 algorithm utilizes the deterministic policy gradient. The expression for the deterministic policy gradient is as follows:

$${\nabla }_{\varphi }J\left(\varphi \right)=N^{-1}\sum {\nabla }_a{Q}_{{\theta }_1}(s,a){|}_{a={\pi }_{\varphi }\left(s\right)}{\nabla }_{\varphi }{\pi }_{\varphi }\left(s\right)$$

(38)

where $Q_{{\theta }_1}$ represents the first critic network of the main network, and ${\pi }_{\varphi }$ represents the actor network of the main network, which is used to approximate the optimal policy.

The parameter update formula for the main network is as follows:

$${\theta }_i=arg\underset{{\theta }_i}{min}{N}^{-1}\sum {(y-Q_{{\theta }_1}(s,a))}^2$$

(39)

where $Q_{{\theta }_1}(s,a)$ represents the actual value of the Q-function, and $\mathrm{y}$ represents the target Q-value of the target critic network. The calculation formula for y is as follows:

$$\mathrm{y}=r+\gamma \underset{i=1,2}{min}{Q}_{{\theta }_i^{\prime }}(s^{\prime },\tilde{a})$$

(40)

where $\gamma$ represents the discount factor, which lies within the range $[0,1]$. r represents the immediate reward. $\tilde{a}$ is the action generated by ${\pi }_{{\varphi }^1}$ based on state $s^{\prime }$.

The parameters of the target network will be updated using soft updates, ensuring smoother and more stable parameter updates. The update formula is as follows:

$${\theta }_i^{\prime }\leftarrow \tau {\theta }_i+(1-\tau ){\theta }_i^{\prime }$$

(41)

$${\varphi }^{\prime }\leftarrow \tau \varphi +(1-\tau ){\varphi }^{\prime }$$

(42)

where $\tau$ represents the soft update rate of the target network, which is typically set to a small value, such as 0.01 in this study. The specific details are shown in Algorithm 2.

The computational complexity of the TD3 algorithm for partial offloading based on VEC can be analyzed by considering the operations performed at each step. The initialization of networks and the replay buffer has a complexity of $O\left(1\right)$. For each episode, initializing the exploration process and the environment is a constant time operation, giving a complexity of $O\left(1\right)$. Within each episode, there are T timesteps. Each timestep involves action selection, execution, observation, storing transitions, sampling mini-batches, target action calculation, target Q-value computation, and critic network update, each contributing $O\left(1\right)$ or $O\left(N\right)$, where N is the mini-batch size. Every d timesteps, the policy is updated, involving the actor network update and target network soft update, contributing complexities of $O\left(N\right)$ and $O\left(1\right)$. Summing up the complexities, the overall complexity is $O\left(1\right)$ + $M\times \left(O\right(1)+T\times O(N\left)\right)$ + $M\times (T/d)\times O\left(N\right)$. Upon simplification, the dominant term is $M\times T\times O\left(N\right)$, indicating that the computational complexity of TD3 algorithm is $O(M\times T\times N)$, showing that the complexity scales linearly with the number of episodes M, the number of timesteps per episode T, and the mini-batch size N.

Algorithm 2 TD3 Algorithm for Partial Offloading Based on VEC

Input:  Task information and resource information Output:  Optimal task offloading strategy  1: Initialize the actor network ${\pi }_{\varphi }$ and critic network $Q_{{\theta }_1}$, $Q_{{\theta }_2}$ using random parameters $\varphi ,{\theta }_1,{\theta }_2$;  2: Initialize the target network parameters ${\theta }_1^{\prime }\leftarrow {\theta }_1$, ${\theta }_2^{\prime }\leftarrow {\theta }_2$, ${\varphi }^{\prime }\leftarrow \varphi$;  3: Initialize the mini-batch S and the experience replay buffer B;  4: Initialize the soft update factor $\tau$ and the discount factor $\gamma$;  5: for  $episode\leftarrow 1$to  M  do  6:    Reset simulation environment of VEC and obtain clustering results;  7:    Get initial state $s_0$;  8:    for $t\leftarrow 1$ to T do  9:       Obtain action $a\left(t\right)$ using Equation (37); 10:      Execute action $a\left(t\right)$, obtaining reward $r\left(t\right)$ and the next state $s(t+1)$; 11:      if B is not full then 12:         Store $<s\left(t\right),a\left(t\right),r\left(t\right),s(t+1)>$ into B for training the network; 13:      else 14:         Randomly replace $<s\left(t\right),a\left(t\right),r\left(t\right),s(t+1)>$ in B; 15:      end if 16:      Randomly sample mini-batch of N transitions from replay memory B; 17:      Update $\varphi$ with Equation (38); 18:      Update ${\theta }_1$ and ${\theta }_2$ with Equation (39); 19:      if $tmodd=0$ then 20:         Update the target network parameters ${\theta }_1^{\prime },{\theta }_2^{\prime },{\varphi }^{\prime }$ using soft updates based on Equations (41) and (42); 21:      end if 22:    end for 23: end for

4.2.3. Feedback Mechanism

To further improve the robustness of the GIVC algorithm in dynamic and complex scenarios, a feedback mechanism is introduced, dynamically adjusting the parameters of the next cycle based on the offloading results from the previous cycle. Let ${\Theta }_T=\{{\Theta }_{1,T},{\Theta }_{2,T},{\Theta }_{3,T}\}$ denote the set of gravitational parameters within cycle T, which is updated according to the comparison results of the adjacent cycles.

First, the update formula for ${\Theta }_{1,T}$ is as follows:

$${\Theta }_{1,T}={\Theta }_{1,T-1}·{\displaystyle \frac{{\sum }_{i=1}^{m·M}{C}_i}{{\sum }_{{\Gamma }_m\in \overline{\Gamma }}·{\sum }_{n=1}^N{C}_n^{\prime }}}$$

(43)

where Equation (43) demonstrates the role of resource factors in the gravitational model. In the formula, the coefficient denotes the ratio of computational resources of the current DT network to those of the final DT network within cycle T. If this ratio is above 1, it implies that the average resource requirement of the aggregation group has increased during the new mapping cycle. Therefore, ${\Theta }_{1,T}$ must be adjusted upward to strengthen the sensitivity of resource alignment in clustering.

${\Theta }_{2,T}$ is used to measure the role of social trust values in the gravitational model. The update expression is given by:

$${\Theta }_{2,T}={\Theta }_{2,T-1}·{\displaystyle \frac{{\sum }_{{\Gamma }_m\in \overline{\Gamma }}{\sum }_{m=1}^M{\sum }_{n=1}^N{o}_{m,n}^{\prime }}{{\sum }_{i=1}^{k·K}·{\sum }_{j=1}^{k·K}{o}_{i,j}}}$$

(44)

where $o_{m,n}^{\prime }$ and $o_{i,j}$ denote the social trust values between the two vehicles during cycles $T-1$ and T, respectively. When the coefficient in the formula is less than 1, it indicates that the social trust level within the aggregation group has increased in the new cycle. Therefore, ${\Theta }_{2,T}$ can be reduced to enhance the role of social trust values in the clustering process.

${\Theta }_{3,T}$ denotes the impact of data transmission capability in the gravitational model. The update formula can be expressed as follows:

$${\Theta }_{3,T}={\Theta }_{3,T-1}{\displaystyle \frac{{\sum }_{{\Gamma }_m\in \overline{\Gamma }}{\sum }_{m=1}^M{\sum }_{n=1}^N{r}_n^{\prime }{T}_{n,m}^{\prime }}{{\sum }_{i=1}^{k·K}{D}_i}}$$

(45)

where the coefficient in the formula represents the ratio of data transmission capability between the current cycle and the previous cycle. $T_{n,m}^{\prime }$ represents the transmission time between vehicle m and n in cycle $T-1$. If this value is below 1, reducing ${\Theta }_{3,T}$ can increase the relative importance of data transmission capability during the clustering process.

Dynamically adjusting the parameters of the gravitational model can better reflect computational resource demands, social trust values, and data transmission capabilities, thereby effectively improving the accuracy of clustering and further optimizing the performance of the VEC network.

5. Simulation and Evaluation

5.1. Simulation Environment Setup

All experiments were performed on a machine with a GTX 1050 Ti (4 GB VRAM) graphics card and an Intel Core(TM) i7-8750H processor. The code and training weights of the tested algorithm did not use the official pre-trained version. Instead, a customized version of the code was employed to construct the base network architecture of the corresponding algorithm and implement the optimization functionalities. The experimental environment simulates a 2000 m long two-way road, with a total of 25 vehicles in the area, including task vehicles and service vehicles. Each aggregation group contains 15 vehicles. In the experiment, the RSUs are uniformly distributed, with a distance of 500 m between two RSUs, and each RSU has a coverage radius of 250 m. The noise power density is set to −174 dBm/Hz, the transmission bandwidth is 10 MHz, the channel gain range is (10⁻⁸, 10⁻⁷), and the vehicle’s upload power is 0.1 W. For offloading tasks, the maximum tolerable delay is 1.5 s, the data size ranges from 0.8 MB to 1.2 MB, and the required CPU cycles for task execution range from 0.1 G to 1.0 G. The CPU frequencies of the ES and vehicles are 2.0 GHz to 2.8 GHz and 0.5 GHz, respectively. The algorithm implementation uses Python 3.8, PyTorch 1.11.0, as well as libraries such as NumPy 1.22.4 and pandas 1.4.2. The Adam optimizer is used for training the deep reinforcement learning model. Some experimental simulation parameters are shown in

Table 1. Environmental simulation parameters.

Parameters	Value	Parameters	Value
$N_0$	−174 dBm/Hz	$C_i$	(0.1, 1.0) G
$W_i$	10 MHz	$D_i$	(0.8, 1.2) MB
$W_i$	0.1 W	$f_i$	0.5 GHz
$T_i^{tolerate}$	1.5 s	$f_{rsu}$	(2.0, 2.8) GHz

.

For the TD3 network structure shown in Figure 2, key parameters have been carefully designed to ensure the algorithm’s stability and efficiency. The discount factor $\gamma$ is set to 0.99 to achieve a reasonable trade-off between long-term and short-term returns, and to control the range of noise through the discount factor, thereby enhancing the robustness of the policy. The soft update coefficient $\tau$ is also set to 0.01 in the experiments to ensure the smooth updating of the target network parameters and avoid policy instability caused by too rapid parameter changes. Furthermore, to suppress noise interference during the policy optimization process, the noise clipping parameter is set to 0.5, which limits the range of random noise and ensures the rationality of the exploration behavior. The policy update delay is set to 2, which delays the update frequency of the actor network, allowing the critic network enough time to learn, thereby improving the accuracy of the Q-function. To improve the performance of the TD3 algorithm, some experiments are conducted to select the optimal values for several key parameters.

The experimental results in this study are presented through bar charts and line charts. The data source for these result graphs is explained as follows: Since the different approaches used in this experiment all include DRL algorithms, the rewards obtained in each round after training the DRL algorithm typically form a fluctuating curve. To evaluate the performance of the tested approaches, it is crucial to observe the overall trend of this curve. Therefore, we choose to average the results every 100 episodes to smooth the fluctuations and present them as a line chart. This method clearly demonstrates the trends of different approaches, making it easier to visually compare their performance. Additionally, the experimental results also include bar charts, where each value in the bar chart represents the average reward of each approach over the last 100 episodes.

5.1.1. Selection of Experience Replay Buffer Size

In Figure 3a, the total cost is compared for different experience replay buffer sizes (1600, 3200, 6400, 8400). Experimental results demonstrate that the total cost is minimized when the experience replay buffer size is 6400. Therefore, the buffer capacity is fixed at 6400 to optimize network performance, as it provides sufficient storage for diverse samples and alleviates excessive sample correlation during training.

5.1.2. Selection of Batch Size

In Figure 3b, the total cost is compared for different batch sizes (32, 64, 128, 256). The results show that the total cost is minimal when the batch size is 64. Therefore, the batch size is set to 64, which helps strike a balance between computational efficiency and the stability of gradient estimation.

5.1.3. Selection of Learning Rate Size

In Figure 3c compares the effect of varying learning rates on the total cost. The results indicate that assigning learning rates of 0.001 to the critic network and 0.0001 to the actor network leads to the minimum total cost. This helps balance the training speed of the network with convergence performance, reducing the likelihood of divergence due to an overly high learning rate or inefficiency from a low one.

5.2. Approach Evaluation

5.2.1. Comparison Approaches

The proposed GIVC-TD3 algorithm is compared with the following algorithms: No Clustering + TD3 (NC-TD3), K-Means + TD3 (K-TD3), Gravitational Model-based Clustering + DDPG (GIVC-DDPG), Gravitational Model-based Clustering + PPO (GIVC-PPO), Gravitational Model-based Clustering without feedback mechanism + TD3 (GIVC-NF-TD3), and Gravitational Model-based Clustering + Local Computation (GIVC-LOCAL). Except for the GIVC-NF-TD3 method, all other methods using the GIVC algorithm default to employing a feedback mechanism. The specific details are as follows:

(1) NC-TD3: This algorithm does not consider the use of clustering algorithms by DT to find the optimal decision space before offloading. The comparison demonstrates the benefit of pre-determining the optimal decision space using clustering algorithms.

(2) K-TD3: Leveraging DT assistance, this approach integrates K-Means clustering with TD3-based offloading decisions. Comparative analysis confirms the effectiveness and benefits of the GIVC algorithm.

(3) GIVC-DDPG: The vehicle clustering algorithm uses the GIVC algorithm, and the DRL algorithm for offloading decisions uses DDPG. The comparison with the TD3 algorithm in this study reflects whether the TD3 algorithm yields better results.

(4) GIVC-PPO: The GIVC algorithm is used for clustering, and the PPO algorithm is used for task offloading decisions.

(5) GIVC-NF-TD3: This method employs a clustering algorithm for clustering but does not use the feedback mechanism to dynamically adjust the parameters within the clustering algorithm. Instead, it utilizes the TD3 algorithm for offloading decisions.

(6) GIVC-LOCAL: In this approach, the task is executed only locally on the task vehicle. When computational resources are inadequate or the task surpasses the delay threshold, task execution will fail. This highlights the importance of task offloading technology.

5.2.2. Evaluation Metrics

(a) Total Cost (TC): This is the optimization objective of the system, representing the weighted sum of energy consumption and delay during the task offloading process. The value of TC reflects the quality of the offloading approach.

(b) Total Completion Delay (TCD): This refers to the sum of the computation delays for all vehicle tasks within the aggregation group, reflecting the performance of the task offloading approach in terms of delay.

(c) Total Energy Consumption (TEC): This is the total energy consumption for task execution within the aggregation group, reflecting the effectiveness of this approach in energy saving.

(d) Success Rate (SR): This is the ratio of tasks completed within the delay constraint to the total number of tasks requested, reflecting the stability of the approach.

5.3. Performance Evaluation

This section compares the proposed approach in this study with the aforementioned comparison approaches. The analysis is conducted by providing the average results of 10 independent runs under the same configuration.

5.3.1. Approach Optimization Performance Analysis

(1).

Optimization Effect of Different Approaches on Total Cost

As shown in Figure 4a, different algorithms exhibit significant differences in optimizing total cost, with the GIVC-TD3 approach showing a distinct advantage. First, in the initial stage of the algorithm (0–200 episodes), GIVC-TD3 and GIVC-DDPG optimize significantly faster than the other approaches, with their total cost decreasing the most, demonstrating strong initial convergence ability. This is because the gravitational model-based vehicle clustering algorithm comprehensively considers factors such as communication, resources and social aspects, allowing it to obtain a reasonable aggregation group in advance. This reduces the decision space range, effectively lowering the complexity of the state space and reducing high system overhead costs caused by erroneous decisions to some extent. Secondly, in the mid-stage (200–600 episodes), the approaches using TD3 continue to optimize, while the GIVC-DDPG approach stabilizes around episode 400. Finally, in the later stage (600–1000 episodes), GIVC-TD3 shows the best convergence performance, with the total cost stabilizing around 56. Compared to K-TD3, NC-TD3, GIVC-DDPG, GIVC-NF-TD3 and GIVC-PPO, it reduces the total cost by 7.35%, 19.21%, 22.85%, 11.28% and 27.83%, respectively. The GIVC-NF-TD3 approach, due to the absence of a feedback mechanism, exhibits suboptimal performance in comparison to the GIVC-TD3 approach in terms of optimization effectiveness. In conclusion, the GIVC-TD3 approach demonstrates significant advantages both in terms of initial convergence speed and later-stage stability.

(2).

Optimization Effect of Different Approaches on Total Completion Delay

Figure 4b compares the impact of different approaches on the total completion delay. In the figure, the number of episodes is shown on the x-axis, and the total completion delay is shown on the y-axis. As the number of episodes increases, the delay of the NC-TD3, K-TD3, and GIVC-TD3 approaches decreases, while the GIVC-DDPG approach shows limited improvement. The total completion delay of the GIVC-TD3 approach is reduced by 21.10%, 23.02%, 27.05%, 18.74% and 31.34% compared to the GIVC-DDPG, K-TD3, NC-TD3, GIVC-NF-TD3 and GIVC-PPO approach, respectively. In contrast, the GIVC-TD3 approach proposed in this study achieves the lowest total completion delay. The reason for this is that the proposed approach uses the GIVC algorithm to obtain the most reasonable aggregation group, reducing the decision space, and applies the TD3 algorithm to make optimal offloading decisions. This allows tasks to be offloaded at the best ratio to the most suitable service vehicles or edge servers for computation. The results show that the GIVC-TD3 approach maximizes the utilization of computational resources and minimizes the total completion delay.

(3).

Optimization Effect of Different Approaches on Total Energy Consumption

Figure 4c compares the energy consumption of the GIVC-TD3, K-TD3, NC-TD3 and GIVC-DDPG approaches. The results show that the proposed approach in our study effectively decreases the energy consumption of task computation. Specifically, the GIVC-TD3 approach reduces energy consumption by 31.81%, 39.64%, 42.76% and 73.07% compared to the K-TD3, NC-TD3, GIVC-NF-TD3 and GIVC-PPO approach, respectively. This can be attributed to the clustering algorithm employed in this study, which determines the optimal aggregation group by taking into account factors such as resources and speed, thus significantly reducing the high energy consumption caused by task failures resulting from unstable vehicle links. At the same time, compared to the GIVC-DDPG approach, the proposed approach in this study reduces energy consumption by 54.62%. This effect arises from the introduction of a dual Q-network in the TD3 algorithm, which effectively mitigates the overestimation bias and improves the stability and accuracy of the policy.

(4).

Optimization Effect of Different Approaches on Offloading Success Rate

Figure 4d shows the impact of different approaches on the offloading success rate. In terms of success rate comparison, the average values of different methods are utilized to ensure the credibility of the proposed approaches. From the experimental analysis, the GIVC-TD3 method in this study demonstrates the highest offloading success rate. Compared to the NC-TD3 and K-TD3 methods, the success rate after convergence improves by approximately 23.58% and 33.77%, respectively. The improvement can be attributed to the adoption of the clustering algorithm based on the gravitational model. This algorithm, with the assistance of DT, efficiently aggregates the optimal task vehicles, service vehicles, and edge servers into a group, thereby reducing the decision space and mitigating task failures caused by unstable links. When compared to the GIVC-DDPG method, the proposed GIVC-TD3 method yields a success rate improvement of about 16.58%. This enhancement is due to the introduction of the TD3 algorithm, which decreases overestimation of Q-values through dual-value networks, thereby improving the stability and accuracy of decision-making. In comparison to the GIVC-NF-TD3 method, the success rate of GIVC-TD3 increases by 9.95%, which can be attributed to the incorporation of a feedback mechanism in this study, ensuring robust performance in the dynamic and complex vehicular network environment. Furthermore, compared to the GIVC-PPO method, the success rate of GIVC-TD3 improves by 27.89%, confirming that the use of the TD3 algorithm as the decision-making approach is highly suitable for the experimental environment in this study.

5.3.2. Approach Adaptability Analysis

(1).

Adaptability of the approach under different task sizes

Figure 5a compares the total computation cost of four approaches under different task sizes. The x-axis represents task size, and the y-axis represents total cost. As the task size increases, the total cost of all approaches rises. However, among the four approaches, the proposed GIVC-TD3 approach has the lowest total cost, while the GIVC-LOCAL approach has the highest total cost. The reason for this is that, as the task size increases, the GIVC-TD3 approach, with limited computational resources at the edge layer, first employs the GIVC algorithm to obtain the optimal aggregation group and then utilizes the TD3 algorithm to make optimal offloading decisions, including whether to offload, the best offloading ratio and the optimal offloading location. It is really worth noting that for the GIVC-LOCAL approach, the total task cost remains almost unchanged when the task size is greater than or equal to 1 Mbits. This is because the delay in local task computation exceeds the maximum tolerable delay, causing the penalty to reach its maximum, thereby keeping the total cost constant.

(2).

Adaptability of the approach under different vehicle computational capacities

Figure 5b analyzes the impact of vehicle computational capacity on computation cost. The results show that as vehicle computational resources increase, the total computation cost of all approaches gradually decreases. This is because, with increased vehicle computational capacity, more task vehicles can obtain sufficient computational resources, which reduces both the energy consumption and transmission delay when offloading tasks to SVs or ES, as well as the high delay and energy losses caused by offloading failures. At the same time, among the four approaches, the proposed approach in this study consistently achieves the lowest total computation cost, followed by the K-TD3 approach and the GIVC-DDPG approach. This can be attributed to the fact that the algorithm in this study combines vehicle clustering algorithms with the TD3 deep reinforcement learning algorithm and ensures the robustness of the clustering algorithm through a feedback mechanism. In terms of performance, the approach introduced in this study surpasses the others.

(3).

Adaptability of the approach under different RSU computational capacities

Figure 5c shows the impact of RSU computational capacity on the total computation cost of the four approaches. The results show that as the RSU computational capacity increases, the total computation cost of the approaches gradually decreases, indicating that an increase in RSU computational capacity enhances the overall system performance. It is worth noting that the proposed approach in this study consistently incurs the lowest total computation cost under different RSU computational capacities, while the local computation approach incurs the highest total computation cost. The main reason is that the proposed approach in this study makes full use of idle computational resources, combines an improved clustering algorithm to obtain the optimal aggregation group, and uses the TD3 algorithm to determine the best offloading location and task offloading ratio. Therefore, the final offloading decision minimizes the total computation cost.

(4).

Adaptability of the approach under different vehicle counts

Figure 5d examines the impact of the number of vehicles on total computation cost. The experimental results show that as the number of vehicles increases, the total computation cost of the various approaches continues to rise. Among them, the proposed approach in this study has the lowest total computation cost. The main reason is that, first, this study uses the GIVC algorithm, which takes into account the distance, computational resources, and social trust values between vehicles. Even with an increase in the number of vehicles, the algorithm still achieves excellent aggregation groups, significantly reducing the size of the decision space. At the same time, the link quality between vehicles within the aggregation group is good, avoiding high delays and energy consumption caused by link interruptions. Furthermore, the feedback mechanism in this study enhances the robustness of the clustering algorithm as the number of vehicles increases. Meanwhile, the TD3 algorithm can quickly obtain optimal offloading decisions in complex environments with a large number of vehicles. The proposed approach in this study performs well in continuous action spaces, and as the number of vehicles increases, it still maintains the lowest total computation cost, demonstrating the good scalability of the approach.

6. Conclusions

This paper proposes a DTAITO task offloading approach for VEC systems, which comprehensively considers both delay and energy consumption, and defines it as a combinatorial optimization problem. The approach aims to provide an efficient and intelligent task offloading solution for dynamic and heterogeneous vehicular network environments, ensuring the smooth execution of user tasks. First, DT technology and the GIVC algorithm are used to cluster the vehicles on the road, obtaining the optimal decision space and ensuring the stability of vehicle links within the same aggregation group. Next, a partial task offloading method based on the TD3 algorithm is proposed. This method trains the offloading policy through the TD3 algorithm to obtain the best offloading decision. Finally, to ensure the stability of the clustering algorithm in different scenarios, a feedback mechanism is employed to adaptively tune the parameters of the GIVC algorithm according to offloading outcomes, thereby improving clustering performance in the subsequent round. Simulation results show that the proposed DTAITO approach outperforms other offloading approaches in terms of total delay, total cost, total energy consumption, and success rate. Although this study has made notable progress in both methodology and experimentation, several limitations remain to be addressed. First, in terms of digital twin technology, only a simplified version of the core functionalities was implemented, without constructing a comprehensive digital twin system that encompasses modeling, real-time interaction, and feedback mechanisms. This limitation may restrict the generalizability and applicability of this work. Second, due to space constraints, privacy preservation and secure communication during data transmission among vehicles were not sufficiently considered, which could pose potential risks in real vehicular networks.

Future work can be carried out in several directions. (1) Integrating resource allocation with task offloading to achieve more efficient system scheduling in multi-user competitive environments, thereby reducing resource wastage and improving overall performance; (2) developing advanced privacy-preserving mechanisms, such as differential privacy, to ensure data security while maintaining offloading efficiency; (3) exploring the feasibility of coordinating multiple edge servers within aggregation groups, aiming to enhance system adaptability and robustness in dynamic and complex scenarios; and (4) deploying a full-scale digital twin system and validating it in representative smart transportation scenarios, in order to assess its feasibility and practical value. By pursuing these directions, future studies are expected to better align with real-world requirements and provide both theoretical insights and practical support for the deep integration of edge computing and digital twin technologies.