Abstract
Rapid data growth in large systems has introduced significant challenges in real-time monitoring and analysis. One of these challenges is detecting anomalies in time series data with high-dimensional inputs that contain complex inter-correlations between them. In addition, the lack of labeled data leads to the use of unsupervised learning that relies on daily system data to train models, which can contain noise that affects feature extraction. To address these challenges, we propose PCA-AAE, a novel anomaly detection model for time series data using an Adversarial Autoencoder integrated with Principal Component Analysis (PCA). PCA contributes to analyzing the latent space by transforming it into uncorrelated components to extract important features and reduce noise within the latent space. We tested the integration of PCA into the model’s phases and studied its efficiency in each phase. The tests show that the best practice is to apply PCA to the latent code during the adversarial training phase of the AAE model. We used two public datasets, the SWaT and SMAP datasets, to compare our model with state-of-the-art models. The results indicate that our model achieves an average F1 score of 0.90, which is competitive with state-of-the-art models, and an average of 58.5% faster detection speed compared to similar state-of-the-art models. This makes PCA-AAE a candidate solution to enhance real-time anomaly detection in high-dimensional datasets.
1. Introduction
In the era of artificial intelligence (AI) and the Internet of Things (IoT), systems have been accompanied by a huge increase in the amount of data. This comes because of the interconnected devices of these systems and their networks. Such data, known as big data, are stored and displayed in various forms. One form of big data is time series data, which record data from its source over a specific period []. These data can record one variable at a time, which is then called univariate time series data, or it can record multiple interconnected variables at the same time, which is known as multivariate time series data. Multivariate time series data is known by the relationships between its variables. Provides a new dimension for understanding and analyzing data. These relationships vary in complexity across systems, which make them difficult to discover using traditional methods such as expert analysis and statistical tools.
Real-time anomaly detection is a critical tool for time series analysis []. This importance returns to its ability to identify irregular patterns early in the system. Such early detection will help in indicating system failures, cyberattacks, and the prediction of disasters in the environmental monitoring and finance sectors. However, anomaly detection in multivariate time series data faces many challenges, specifically the number of features in the time series data and the complex interdependencies between them, especially in systems with numerous interconnected devices and sensors. To address this challenge, classic dimensionality reduction techniques like Principal Component Analysis (PCA) and distance-based algorithms such as k-NN have been used for anomaly detection. While PCA can be effective in capturing linear correlations, it struggles to capture non-linear interdependencies and often fails to retain informative structures when dimensionality increases. In the same way, distance-based algorithms can identify points that deviate from local or global structures, but their distance measures can lose contrast with the increase in dimensionality. This is known as the “curse of dimensionality,” where higher dimensionality increases data spread, making it difficult to generalize and leading to lower quality results, thus limiting the applicability of these classical methods in complex, high-dimensional systems [].
In recent years, methods based on AI and deep learning have gained popularity for anomaly detection, especially with the lack of labeled anomaly data that is required for supervised learning. This drives recent research to use unsupervised learning techniques, which depend on unlabeled data to train models []. The encoder-decoder structure is an unsupervised framework that is widely used to reduce dimensions. It extracts key features and then reconstructs data to its original form [,]. This structure relies on the model’s ability to distinguish key features in the input data based on learned features to identify unseen features as anomalies []. Recent research based on encoder-decoder structure provided promising results in identifying anomalies across various domains.
The Autoencoder is an encoder-decoder application that is used widely in time-series research. It has been used widely by combining it with other deep learning methods to handle multiple challenges such as long-term and short-term dependencies, temporary anomalies, and noise. However, this combination increases the complexity of the model and the time required to detect anomalies. This returns to the model’s need for many layers and long training periods. This could limit the usability for real-time applications, especially in applications with strict latency requirements, due to the increased model complexity and longer inference time.
To solve the previous problems, we propose an anomaly detection system for time series data. We use an Adversarial Autoencoder (AAE) integrated with Principal Component Analysis (PCA) and unsupervised training. Instead of treating PCA as a preprocessing step as in traditional methods, we integrate PCA directly into the latent space of the AAE. The integration allows PCA to analyze features in the latent space in uncorrelated components. Each component contains related features only. This makes the model identify key features represented in high components and eliminate noise in low components. Then, we use adversarial training to approach latent space to real data distributions and enhance the model’s effectiveness. Our proposed model focuses on detecting anomalies effectively while preserving rapid processing, which makes it outperform existing methods while being fast enough for real-time applications. We evaluate the model on both SWaT and SMAP datasets demonstrate its generalization across domains.The contributions of this paper are as follows.
- Development of a hybrid anomaly detection system for time series data, using an unsupervised deep learning AAE combined with PCA for real-time application.
- Proposal of a novel latent code representation that incorporates PCA directly into the latent space of the AAE, enhancing feature extraction, reducing noise, and improving model robustness.
- Validation of the model on two publicly available datasets, synthetic and real-world data, demonstrating superior detection speed and generalization to different types of anomalies compared to state-of-the-art systems.
The rest of the paper is organized as follows. The related work to deep learning anomaly detection is in Section 2, the proposed method is detailed in Section 3, the experiment description and the results are presented in Section 4. A discussion of the characteristics and limitations of the proposed model are presented in Section 5. Finally, the conclusion and future work are shown in Section 6.
2. Related Work
Anomaly detection in time series datasets using deep learning has witnessed a significant effort in recent years. Many unsupervised learning approaches, such as recurrent neural networks (RNNs), convolutional neural networks (CNNs), and reconstruction-based architectures, have been extensively explored for their ability to train on unlabeled data. However, each method presents unique advantages and challenges.
2.1. RNN-Based Approaches
Recurrent neural networks (RNNs) are commonly used in a forecasting-based approach. RNNs rely on internal memory to store sequence values and pass them as input to the next point to capture temporal dependencies []. However, early RNNs faced issues like vanishing gradients that resulted from a too large or a too small value of gradient as the model went deeper in early RNNs. Long short-term memory (LSTM) [] and its variant gated recurrent units (GRU) [] addressed these limitations by introducing advanced memory that can store longer sequences to allow capturing long-term temporal dependencies [].
Hundman et al. [] improved model performance by using LSTM with two hidden layers, using a single-channel model for each telemetry in the input data. This enables the model to predict multidimensional input more accurately and provide more granular control. In a similar way, Ding et al. [] enhanced LSTM performance with the probabilistic Gaussian mixture model (GMM) that addresses low-dimensional data in real-time anomaly detection. In general, RNN-based methods achieve high accuracy as more layers are added to the model. However, stacking deeper layers significantly increases computational costs, making them less suitable for real-time applications.
2.2. CNN-Based Approaches
Convolutional neural networks (CNNs) started by processing images, where they were designed to take 2-dimensional data as input [], and recently, they have been investigated for anomaly detection in time series data []. CNNs capture hierarchical patterns in input data by learning features progressively through convolutional layers []. CNNs are commonly used in supervised learning, but they can be used in unsupervised learning too. Ren et al. [] proposed CNNs combined with spectral residual (SR) techniques to allow better unsupervised learning through the model and improve accuracy. However, CNNs struggle with long sequences of data due to their inherent structures [], leading to the development of Temporal Convolutional Networks (TCNs) [] that can take longer sequences just as RNNs without data leakage. Nonetheless, forecasting-based methods like CNNs are more effective in predicting only short-term anomalies, as the sudden and continual change in sequences of time series data increases the prediction errors over longer horizons [].
2.3. Reconstruction-Based Approaches
Reconstruction-based methods, such as Autoencoder (AE) and generative adversarial networks (GANs), are known for capturing correlations between variables of time series sequences. Unlike forecasting-based approaches, reconstruction-based methods focus on reconstructing the current data instead of past data by mapping it to a latent space. The latent space is decoded back to the original form using the decoder. After training the model, anomalies can be defined by comparing reconstructed values of training and test phases to obtain the reconstruction error that can be used later to identify anomalies [,].
Reconstruction-based methods have witnessed a significant effort in recent research by integrating them with other deep learning approaches. Zhao et al. [] proposed an Autoencoder with normalized flows and a shuffling mechanism of channels to isolate anomalies in the latent space and improve accuracy in anomaly detection. Backhus et al. [] proposed bandpass filtering for noise reduction with an autoencoder and leveraged its ability to capture non-linear temporal relationships by using a functional neural network within the autoencoder. Variational Autoencoder (VAE) [] is problematic-based AE that encodes input data as a distribution instead of single points in regular AE. In addition, VAE regularizes the latent space using Kullback–Leibler divergence to match it to the normal distribution as possible []. Li et al. [] proposed a sequential VAE with a smoothness-inducing prior to improve reconstruction regularization. Yokkampon et al. [] proposed a multi-scale convolutional VAE to capture both temporal dependences and inter-correlations between features.
Much recent research used Adversarial Autoencoder (AAE) [] as a cost-effective alternative to regular AE and VAE, offering both generative-based networks and latent space regularization. Recent work by Audibert et al. [] proposed an adversely trained Autoencoder with one encoder and two decoders to increase the training speed while maintaining high performance. Ning et al. [] used an AAE with memory augmented and multi-scale convolution fusion to address the complex anomalies in time-series anomaly detection.
Despite the advancements in previous work, several limitations persist across existing methods. RNN-based approaches, while accurate, are computationally intensive and unsuitable for real-time applications. CNN models struggle with long sequences and are limited to short-term anomaly predictions. Reconstruction-based methods excel at feature extraction but often require complex models to maintain performance, which impacts their ability to meet the real-time detection demands of modern systems. To address these challenges, the proposed model PCA-AAE leverages a reconstruction-based Adversarial Autoencoder (AAE) and reduces complexity by integrating PCA directly into the latent representation. PCA has been widely adopted in anomaly detection tasks. Hyndman et al. [] applied PCA to find unusual time series in a large collection of data by selecting the first two principal components and then using multiple outlier detection methods. Jin et al. [] used Robust PCA (RPCA) to prevent confidential information leakage in monitoring high-frequency data of computer application systems. Similarly, Wang et al. [] proposed a new version of RPCA using Hankel-structured tensor to detect anomalies in traffic time series.
In the context of deep learning, Quilodrán-Casas et al. [] applied PCA as a preprocessing step on the input of AAE, which was later integrated with adversarial Long short-term memory (LSTM) networks to improve the forecast of computational fluid dynamics (CFD). Pham et al. [] were the first to introduce the integration of PCA in the latent code of AE to disentangle the latent space for image data in generative networks.
To the best of our knowledge, the proposed model is the first to apply PCA within the latent code of AAE in the domain of anomaly detection in time series data. This approach dynamically balancing simplicity with strong performance, enhancing latent representations while mitigating the curse of dimensionality typically encountered when PCA is applied directly to complex high-dimensional input.
3. Materials and Methods
3.1. Problem Formulation
We can describe the univariate time series data as a set of observations T that describe a single variable, where T contains multiple points x, and each point represents a single observation of the variable at a specific time from 1 to t:
where . In multivariate data, we have multiple variables m instead of a single variable. Since x now observes m variables simultaneously, we can describe x as a vector of m dimensions, where . Each x now represents the correlation of features at a specific time t.
To handle the temporal correlation between each data point and the points before it, we use a time window that contains the data point x and its k previous points where:
The result sequence will represent both feature correlations of each point and temporal correlations between data points.
In this paper, we intend to detect anomalies in multivariate time series data in an unsupervised manner. For unsupervised learning training, we use T as input to the model assuming T contains a sequence of regular data distribution windows . To detect anomalies, we need to calculate the difference between unseen sample and its reconstruction value. The resulting amount is the anomaly score which can be compared to a threshold to label anomaly samples.
The goal of our anomaly detection model is to give each unseen sample a label value y where that indicates either anomaly (where ) or normal (where ) based on the anomaly score.
3.2. The Proposed Model: PCA-AAE
The Adversarial Autoencoder model consists of an encoder, a decoder, and a discriminator, which encourage the latent code from the encoder to match the prior distribution. AAE performs two phases to train the model. First is the reconstruction phase. This phase is similar to AE when training the model to minimize the reconstruction error of the input [].
Consider x is the input to the encoder, the encoder maps x to a latent code z:
where is the encoder, and is the parameters of the encoder network. This encoder will define a new distribution based on the hidden code called the aggregated posterior :
where is the data distribution. The second phase of training AAE is Regularization, where the discriminator updates its parameters to distinguish between samples generated from the encoder and samples of the prior distribution. After that, the encoder that is used as a generator for the discriminator updates its parameters to confuse the discriminative network and map aggregated posterior to prior distribution , which is the main goal of the discriminator.
The latent representation that results from the reconstructing phase contains the main features and explains the temporal dependencies between point samples. As AAE is an unsupervised model where the encoder is trained using daily data, if the input data contains some noise or a small amount of anomaly as in the case of real datasets, the encoder will treat it as a part of the main features. This reflects on the smoothness of the latent space and makes it difficult to align well with the prior distribution , resulting in overfitting or inefficient reconstruction of the input. To overcome these problems, we propose an additional latent representation of the latent space by applying PCA to the latent z. The goal of PCA is to transform the input data matrix X to a new representation matrix Y by finding related linear transformation matrix P where its rows represent new basis vectors to transform X into Y [] as follows:
To find the best basis vectors, PCA calculates the covariance matrix that represents relationships between all features in X as follows:
where is the inverse matrix of X. After that, PCA calculates the eigenvalues and eigenvectors from the covariance matrix decomposition as follows:
where columns in P is the eigenvectors of , D is a diagonal matrix containing eigenvalues sorted in descending order where:
After selecting , which are the desired k components of P with the highest eigenvalues, the data is projected onto the new principal components:
where Z is the transformed data, is the projection matrix containing the first k eigenvectors. When applying PCA to the latent representation, we get:
While PCA is a preprocessing technique used for dimensionality reduction, we use it here to extract the components of maximum variance from the latent space. Then, the latent space is projected onto these uncorrelated and orthogonal components. This new alignment of latent space, which appears as a linear transformation, allows for a better understanding and potentially facilitates mapping it to the prior distribution we want to impose, thus enhancing the model’s generative capacity and overall performance.
A structure of the model is illustrated in Figure 1. It consists of encoder, latent representation, PCA representation, decoder, and discriminator. The encoder reduces the input window into a latent representation, which is then transformed using PCA to emphasize significant features and reduce noise. The decoder reconstructs back the latent representation into the input data, ensuring accurate regeneration of features. The discriminator aligns the latent representation with a prior distribution to enhance the model’s generative capabilities.
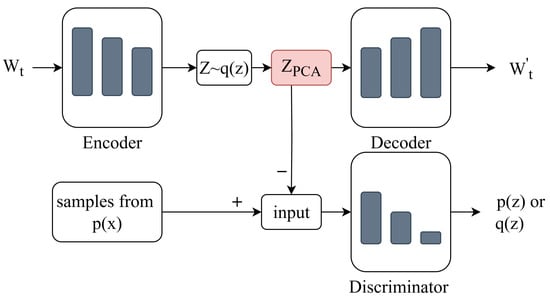
Figure 1.
Overall Architecture of the PCA-AAE Model.
PCA can be applied to the latent code at multiple points within the AAE architecture, where the latent code is utilized in the reconstruction, adversarial, and generation networks. Each phase is briefly described below with the impact of PCA on it.
3.2.1. Reconstruction Network
The reconstruction network identifies the main features of the input and serves as the basis for its regeneration, making it important for preserving the system’s characteristics. Applying PCA within this network helps in reducing overfitting by standardizing the latent input, especially in medium-to-high dimensional data. But in low-dimensional data, it could introduce new difficulties in decoding the latent code, where some subtle features might be distorted.
3.2.2. Adversarial Network
The adversarial network helps the encoder learn the prior data distribution and align the latent representation accordingly. To achieve this, the discriminator is trained on both encoded latent vectors (labeled as fake samples) and data from prior distribution (labeled as true samples). Then the resulting feedback is used to update the encoder. When applying PCA during discriminator training, it helps identify key features in the latent, enabling the discriminator to better distinguish between encoded and prior samples. This will strengthen the adversarial training and help in generalizing the model. In addition, the prior distribution must also be PCA-transformed to avoid false confidence in the discriminator, where it may identify latent code due to representation mismatch, leading to poor performance in real testing.
3.2.3. Generator Network
While the AAE does not have an explicit generator like in traditional GANs, it uses the latent code produced by the encoder to fool the discriminator into labeling the latent data as real samples. The resulting feedback is used to update the encoder parameters. This helps the encoder not only learn how to extract features from data but also it will learn how to match it to prior distribution. The application of PCA in the generator network helps the encoder align key features without affecting the reconstruction or losing subtle information. This helps in reducing noise, where the encoder learns from PCA-projected latent space. On the other hand, if the discriminator is not trained using PCA transformed latent representation, the encoder may receive mismatched feedback, risking instability during training. Hence, it is recommended to apply PCA in both adversarial and generation networks. More practical experiments are conducted in Section 4.5. Based on this experiments, we selected the application of PCA to the adversarial training network, as it demonstrated the most efficient performance. Therefore, this configuration is used in all subsequent experiments, evaluations, and results presented in this paper.
3.3. Implementation
The anomaly detection method we proposed consists of three stages: Data preprocessing, offline training, and online detection. Each stage is explained in this section.
3.3.1. Data Preprocessing
Time series datasets often require normalization before being used in training and detection. We apply min-max scale to normalize the data within the range of 0 to 1, facilitating faster model training. Considering the long time-series, we employ a sliding window technique by dividing the dataset into overlapping windows, where each window contains k consecutive time-points starting from to incrementally. The value of k directly impacts the type of anomalies detected and the speed of detection. Larger k values can capture long anomaly sequences but may overlook short anomaly sequences, while smaller k values enable faster training and detection. After testing various values of and observing their effects, we selected for the SWaT dataset and for the SMAP dataset to effectively detect short anomalies while maintaining efficient training and detection speeds.
3.3.2. Offline Training
As discussed earlier in Section 3.2, the model operates in two training phases. In the first phase, the input data is transformed into a latent space by the encoder, which consists of three linear layers, each followed by batch normalization and ReLU activation. We applied batch normalization to accelerate training and converge faster using higher learning rates []. The resulting latent space is then processed by the PCA function, which analyzes and rearranges it to produce the final representation. After applying PCA to the latent code, is obtained, and the reconstruction loss is calculated as follows.
where is the decoder and its parameters, which shares a similar structure with the encoder, and denotes the squared L2 norm corresponding to the sum of squared errors (MSE loss). In the second training phase, the adversarial loss is computed using a discriminator, which consists of three linear layers. The first and second layers are followed by ReLU activation functions, while the final layer uses a sigmoid activation function. The discriminator d takes the final latent representation after applying PCA, , as input and outputs a single value, distinguishing fake samples generated by the encoder and real samples from the prior distribution . The loss was calculated using the binary cross-entropy (BCE):
where is the aggregated posterior distribution, denotes the expectation over Z latent samples generated from the posterior distribution. Finally, the model’s total loss will be calculated to match q(z) to p(z):
where is a hyperparameter controlling the trade-off between reconstruction and adversarial objectives. We study the effect of different values of during the training as shown in Figure 2. We can notice that has a limited effect on the total loss when the value is smaller than 1. On the other hand, multiplying its value decreased the F1 score of the model. Based on this result, we choose to give reconstruction loss more dominant over adversarial training and maintain model consistency.
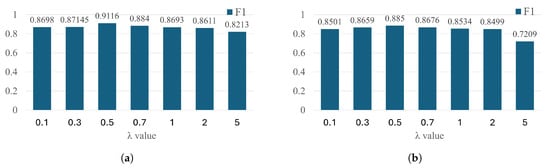
Figure 2.
Effect of the adversarial loss parameter on the F1 score; (a) SWaT dataset; (b) SMAP dataset.
One of the objectives of the proposed model is to detect real-time anomalies without delaying or interrupting the main functions of the application. To achieve this, the model was designed with the simplest structure possible without decreasing the performance by using three linear layers in the encoder, decoder, and discriminator. The resulting latent code from the encoder feeds to the PCA that transforms it to the final latent representation. This structure allows both efficiency in analyzing inter-correlations between elements and feature extraction.
3.3.3. Online Detecting
In this phase, the trained model is used to identify anomalies in real-time. After training the model on time series windows, it evaluates incoming windows sequentially by calculating an anomaly score A:
where is the input window, is the decoder and its parameters, and z is the reconstruction of .
The system processes each window as it arrives, without access to future data, to simulate online behavior and imitate real-time data flow. The resulting anomaly score is compared to a predefined threshold, and the window is labeled as an anomaly if the score exceeds the threshold. We evaluate the model’s processing speed and detection latency in Section 4.4 to ensure its feasibility under streaming data conditions.
4. Results
In this section, we present the experiments we conducted to evaluate the properties of the proposed model. The section begins with an explanation of the SWaT and SMAP datasets we used to evaluate the model. Then, a comparison between PCA-AAE and state-of-the-art unsupervised models is conducted to assess the model’s effectiveness. Then, we explain the effect of hyperparameter on the system’s performance and study the model training and detection time compared with state-of-the-art models. Finally, we apply an Ablation study to illustrate the effectiveness of adding PCA to different training phases of AAE.
We implemented these experiments using Google Colab, a cloud-based machine learning environment. We configured the model in Python 3.10, using NVIDIA Tesla T4, a 12 GB virtual RAM, and the PyTorch version 2.6.0 library.
4.1. Dataset
We use two publicly available datasets, Secure Water Treatment (SWaT) and Soil Moisture Active Passive (SMAP), to evaluate our model against state-of-the-art approaches. The SWaT dataset was created by Singapore’s Public Utility Board using a virtual testbed that produces filtered water created for research purposes. The dataset consists of time series data collected over 11 days, 7 days in normal operations, and 4 days under attack []. This dataset simulates real-world industrial systems and has been widely used in recent research to evaluate machine-learning methods for detecting anomalies in multivariate data. The dataset specification is summarized in Table 1.

Table 1.
SWaT and SMAP datasets specification.
The plant testbed operates across six filtration process stages, each equipped with multiple sensors and actuators, resulting in a total of 51 data points collected at each point in time. The attacks were implemented in four distinct manners, varying by the number of process stages involved and the points targeted. Table 2 provides an overview of the attack types and their corresponding counts.

Table 2.
Types of attack in SWaT dataset.
SMAP is a spacecraft telemetry dataset that was collected by Nase. It contains information of 55 entities, where each entity is monitored by 25 features. The anomalies in the SMAP dataset experts-labeled and contain both point and contextual anomalies. Dataset specifications in Table 1.
4.2. Comparison Experiments with State-of-the-Art Models
We selected multiple reconstruction-based models to evaluate PCA-AAE model. All selected models use unsupervised learning to detect anomalies in multivariate time series datasets. the description of each model is as follows.
- PCA: We applied PCA by fitting it to the training data, then transformed the test data by reducing each window’s dimensionality to the latent size and projecting it back to the original space. The anomaly score was calculated as the reconstruction error between the original data and the reconstructed data.
- AE: We implemented an autoencoder consisting of an encoder and a decoder with the same hyperparameter as our proposed model to ensure a fair comparison. The hyperparameter specifications are presented in Table 3.
 Table 3. Model hyperparameter.
Table 3. Model hyperparameter. - PCA-AE: We implemented an autoencoder model in which PCA is applied to the latent space during training.
- LSTM-AE: We implemented an autoencoder model based on two LSTM layers and one linear layer in both the encoder and the decoder.
- AAE: We implemented an Adversarial Autoencoder similar to our proposed model but without PCA. The hyperparameter specifications are presented in Table 3.
- OmniAnomaly []: An anomaly detection model designed to capture normal patterns in time series data using GRU and VAE, along with planar normalizing flow and stochastic variable connection techniques.
- USAD []: An adversarially trained Autoencoder with one encoder and two decoders to allow fast training while maintaining high performance in the industrial domain.
- TranAD []: A transformer-based anomaly detection model that uses attention-based sequence encoders and adversarial training.
- MCFMAAE []: An AAE with Multi-scale convolution fusion module and multi-head attention mechanism to discover complex and subtle anomalies.
We compared models in terms of standard evaluation metrics: recall (R), precision (P), and F1 score (). The computation of each metric is as follows:
where : True Positives, : False Positives, and : False Negatives.
The result of the experiments is shown in Table 4. The results demonstrate the effectiveness of the proposed model, PCA-AAE, across both datasets. On the SWaT dataset, PCA-AAE significantly outperforms all models with an F1 score of 0.9116, showing a strong balance between precision and recall. We can notice that PCA-AAE achieves the highest recall among the adversarially trained models such as plain AAE (0.6759), TranAd (0.6997), and MCFMAAE (0.6879). This highlights the impact of integrating PCA into the latent space during adversarial training on medium- to high-dimensional datasets, by improving the latent representation and enhancing feature separability in the latent space. On the SMAP dataset, PCA-AAE performs competitively, with F1 score of 0.889, close to state-of-the-art models such as TranAD (0.8915) and MCFMAAE (0.9067), indicating a strong balance between precision and recall. The F1 score provides a better view of the model’s performance when both false positives and false negatives are critical. Models with higher precision are likely to produce fewer false positives, which means more conservative detection. Models with higher recall are likely to make fewer false negatives, which means more sensitive detection. Typically, increasing precision comes at the cost of recall, and vice versa. Therefore, it is generally preferable to balance both metrics in most applications.

Table 4.
Evaluation metrics of state-of-the-art models and PCA-AAE on SWaT and SMAP datasets.
The adversarially trained models with different structures, such as USAD, TranAD and MCFMAAE, are strong performers. However, PCA-AAE achieves similar or better performance without the added complexity of multiple encoders, transformer-based or multi-branch models, which makes it a lightweight alternative with strong generalization capability. This improvement is due to PCA-AAE’s effect on the latent space, reorganizing it based on informative versus noisy directions, which leads to easier discriminator learning, smoother training and better reconstruction in AAE model. While PCA-AAE performs better in high-dimensional datasets such as SWaT, it shows slightly lower performance on low-dimensional, short-sequences datasets such as SMAP. This suggests potential improvements could focus on filtering false positives to increase precision.
4.3. Effect of Hyperparameter
We perform an exhaustive search on the model’s parameters and hyperparameter to choose the best fit with our objective and fine-tune the model. A summary of the model’s parameters is presented in Table 3. The number of components in the PCA defines how many of the components we want to include in the latent space. After experimenting with different values of components, we found that including all components in the latent space allows for capturing more features, in addition to isolating each inter-correlated features in one component. This improves the reconstruction of the latent space and enhances interoperability between encoder and decoder. However, extracting components from latent space introduces another challenge where PCA requires two-dimensional input (matrix) to produce components. The smaller dimension of the matrix will be treated as the features of the model, while the larger one will represent the raw data. We use the batch size as the second dimension of the input matrix, but this requires selecting a batch size greater than or equal to the size of latent space. We balanced the selection of latent space size and batch size to ensure both effective dimensionality reduction and efficient model training. However, in real-time applications, this trade-off is less critical, as increasing the batch size can accelerate the model’s speed to better synchronize with data flow.
4.4. Detecting Time
To test the speed of the proposed model compared to state-of-the-art models, we chose AE, LSTM-AE, AAE, and the USAD model, one of the recently proposed methods that focuses on industrial applications using a novel generative adversarial network, in terms of detection time for both SWaT and SMAP datasets. We used the official architecture and implementation of USAD from its original paper [] and GitHub repository (manigalati/usad, commit e25af45). To ensure fairness, all models were tested under identical conditions and using the same batch size across all models (250 for SWaT and 512 for SMAP). Other state-of-the-art models were excluded from this timing comparison due to time limitations.
Table 5 shows the experimental results, where the detection time is reported both per batch and per window, which provides a realistic view of performance under stream conditions. While PCA-AE has similar detection time to AE and AAE, it outperforms LSTM-AE and the USAD model in detection speed by an average of 44% for USAD and 73% for LSTM-AE. Where PCA-AAE achieved the fastest detection time on both datasets, outperforming USAD by 40.7% on SWaT and 46.7% on SMAP, and LSTM-AE by 87.2% on SWaT and 59.5% on SMAP. This makes our model suitable for real-time anomaly detection scenarios, where high-speed inference is achieved using a standard autoencoder without requiring additional phases or complex calculations.

Table 5.
Average processing time per batch and per window on SWaT and SMAP datasets.
On the other hand, PCA-AAE requires longer time in the offline training, as PCA is applied to every batch during training, adding computational overhead. However, since training is performed offline and represents a one-time cost, it does not affect real-time detection performance and is acceptable in most practical applications.
We implemented these experiments using Google Colab, a cloud-based machine learning environment. We configured the model in Python 3.10, using NVIDIA Tesla T4, a 15 GB virtual RAM, and the PyTorch library. We acknowledge that the performance of the experiment may be limited compared to industrial-grade hardware. Therefore, the reported results are intended to highlight the relative differences in time between the proposed model and state-of-the-art models rather than serve as absolute deployment benchmarks. In real-world applications, more powerful hardware could further reduce latency.
4.5. Ablation Study
To illustrate the effectiveness of PCA in adversarial training, we conduct extensive studies by applying PCA in different stages of the AAE. The study includes the following models:
- Applying PCA to the reconstruction network.
- Applying PCA to the adversarial network.
- Applying PCA to the generator network.
- Applying PCA to both reconstruction and adversarial network.
- Applying PCA to all networks.
- AAE without PCA.
Precision, recall, and F1 score results on the SWaT and SMAP datasets are shown in Figure 3. When applying PCA to the reconstruction network only (PCA-rec-AAE) on the SWaT dataset, it improves recall (0.7759) compared to AAE and strengthens the F1 score (0.8582). This indicates that PCA can enhance the model’s sensitivity to anomalies. However, on the SMAP dataset, this configuration significantly reduces precision (0.396) and leads to a low F1 (0.5107). We also observe that variants involving applying PCA to the reconstruction network, such as PCA-rec-adv-AAE and PCA-All-AAE, either have no noticeable effect on the SWaT dataset or negatively impact performance on the SMAP dataset. This suggests that applying PCA to the reconstruction network may increase false positives in more complex datasets that contains subtler anomalies and diverse entity behaviors.
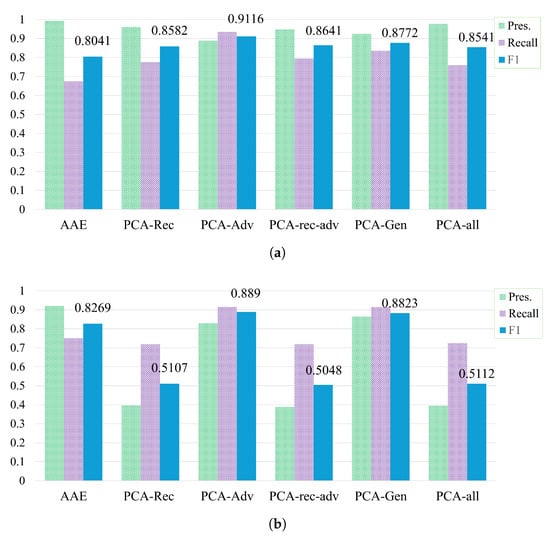
Figure 3.
Impact of PCA placement in different parts of the AAE model on the (a) SWaT dataset and (b) SMAP dataset. AAE: no PCA; PCA-Rec: PCA applied on the reconstruction network; PCA-Adv: PCA applied on the adversarial network; PCA-Rec-Adv: PCA applied on both reconstruction and adversarial networks; PCA-Gen: PCA applied on the generator network; PCA-All: PCA applied on all networks.
In contrast, applying PCA to the adversarial network (PCA-adv-AAE) achieves the best overall performance on both datasets, where it achieves an F1 score of 0.9116 on SWaT and 0.889 on SMAP. This indicates that applying PCA to the latent space learned via adversarial training strengthens the structure of the feature distribution, which enhances the model’s ability to distinguish between normal and anomalous behavior effectively. Notably, this variant includes applying PCA to the samples drawn from the prior distribution used to train the adversarial network, where excluding it destabilizes training.
Applying PCA to the generation network (PCA-gen-AAE) also performs well, particularly on the SMAP dataset, where it achieves similar results compared to PCA-adv-AAE. We believe this configuration is especially beneficial for data with high noise, where PCA helps reduce noise in the final reconstruction representation.
In conclusion, integrating PCA into AAE enhances anomaly detection performance when applied to the adversarial or generator networks. The effectiveness of PCA varies based on the dataset characteristics, such as the number of entities, the distribution of anomalies, and the presence of noise.
5. Discussion
In this paper, we proposed a novel anomaly detection model for multivariate time series data by integrating Principal Component Analysis (PCA) with an Adversarial Autoencoder (AAE). The proposed model achieved notable improvements over traditional reconstruction-based methods, particularly in terms of F1 score and detection speed, both of which are crucial for real-time anomaly detection. The results highlight the model’s ability to enhance feature representation through PCA integration, which plays a key role in its superior performance. The integration of PCA directly in the latent space allows better feature extraction and noise isolation by grouping features into uncorrelated components, where each component contains inter-correlated features. In this way, the latent space arranges components with high variance at the beginning and components with low variance at the end, which often represent noise or less relevant information. This enhances its ability to discriminate between normal and anomalous patterns. When compared with related studies that employ AEs or adversarial training, our model achieves a notable improvement in generalization and stability during training. This is likely due to the noise reduction provided by PCA.
In addition to improving feature extraction, PCA enhances anomaly detection and speeds up computation. As PCA is applied only during training, the model tests new samples without extra overhead beyond the autoencoder’s processing. This efficiency makes the proposed model well-suited for real-time applications like industrial and critical infrastructure monitoring, as confirmed by the low processing time per data window.
Despite the model’s promising results, there are some challenges facing it. One of the challenges is the application of PCA, which is designed to apply to a two-dimensional input with rows and columns. However, In the proposed model, the data is represented in batches, and each batch contains a latent space representation. This requires applying PCA across batches by treating them as the second dimension and the latent space as a first dimension. We need to ensure that batch size is larger than or equal to latent space, which is one of the requirements for applying the PCA function, in addition to balancing between batch size and training speed, which contributes significantly to the proposed model’s overall efficiency.
Another challenge is the representation of components, which requires careful consideration. PCA can return all components, a subset of components, or the projection of the data onto a subset of components. Each approach has its own advantages and drawbacks. Although PCA is typically used for dimensionality reduction, in our approach we retain all components without reducing dimensionality. We analyzed the effects of each method separately to understand their impact on performance and computational efficiency. Using all components was the most suitable to the evaluated datasets. This is due to the difficulty of taking an equal subset for each batch when batches vary in representations and cover only a short time interval compared to the entire time series.
Moreover, while the models were evaluated on two datasets that both simulate real-world systems and real satellite dataset. They can be generalized to other domains or datasets. Additionally, data with low dimensions and short sequences show high sensitivity to PCA application. Future studies could apply the proposed model to additional datasets and enhance the feature extraction technique for data with low dimensions.
6. Conclusions
In this paper, we proposed a novel anomaly detection model for multivariate time series data that integrates PCA with an Adversarial Autoencoder. This integration improves feature representation and isolates noise in the latent space, resulting in faster anomaly detection and enhanced system performance. Our proposed model proved its effectiveness by outperforming similar systems in the average F1 score and achieving faster detection times. In conclusion, our system is suitable for anomaly detection in real-time applications and online detection. For future work, we plan to test the model on a wider range of anomaly detection datasets for more generalization. In addition, we plan to improve feature extraction capability by experimenting with different dimensionality reduction techniques, such as Linear Discriminant Analysis (LDA), to enhance our deep learning model.
Author Contributions
Conceptualization, A.H.A., H.A. and E.A.; methodology, A.H.A., H.A. and E.A.; software, A.H.A.; validation, A.H.A., H.A. and E.A.; formal analysis, A.H.A., H.A. and E.A.; investigation, A.H.A., H.A. and E.A.; resources, A.H.A.; data curation, A.H.A.; writing—original draft preparation, A.H.A.; writing—review and editing, H.A., E.A. and A.A.; visualization, A.H.A.; supervision, H.A. and E.A.; project administration, H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PCA | Principal Component Analysis |
| SWaT | Secure Water Treatment |
| AAE | Adversarial Autoencoder |
| AI | artificial intelligence |
| IoT | Internet of Things |
| RNNs | convolutional neural networks |
| CNNs | recurrent neural networks |
| LSTM | Long short-term memory |
| GRU | gated recurrent units |
| GMM | Gaussian mixture model |
| SR | spectral residual |
| TCNs | Temporal Convolutional Networks |
| GANs | generative adversarial networks |
| VAE | Variational Autoencoder |
| BCE | binary cross-entropy |
| AE | Autoencoder |
References
- Chalapathy, R.; Chawla, S. Deep learning for anomaly detection: A survey. arXiv 2019. [Google Scholar] [CrossRef]
- Blázquez-García, A.; Conde, A.; Mori, U.; Lozano, J.A. A review on outlier/anomaly detection in time series data. ACM Comput. Surv. (CSUR) 2021, 54, 1–33. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Hinneburg, A.; Keim, D.A. On the surprising behavior of distance metrics in high dimensional space. In Proceedings of the International Conference on Database Theory, London, UK, 4–6 January 2001; Springer: Berlin/Heidelberg, Germany, 2001; pp. 420–434. [Google Scholar]
- Mejri, N.; Lopez-Fuentes, L.; Roy, K.; Chernakov, P.; Ghorbel, E.; Aouada, D. Unsupervised anomaly detection in time-series: An extensive evaluation and analysis of state-of-the-art methods. Expert Syst. Appl. 2024, 256, 124922. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Bahdanau, D.; Bengio, Y. On the properties of neural machine translation: Encoder-decoder approaches. arXiv 2014. [Google Scholar] [CrossRef]
- Zamanzadeh Darban, Z.; Webb, G.I.; Pan, S.; Aggarwal, C.; Salehi, M. Deep learning for time series anomaly detection: A survey. ACM Comput. Surv. 2024, 57, 1–42. [Google Scholar] [CrossRef]
- Schmidl, S.; Wenig, P.; Papenbrock, T. Anomaly detection in time series: A comprehensive evaluation. Proc. VLDB Endow. 2022, 15, 1779–1797. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014. [Google Scholar] [CrossRef]
- Choi, K.; Yi, J.; Park, C.; Yoon, S. Deep learning for anomaly detection in time-series data: Review, analysis, and guidelines. IEEE Access 2021, 9, 120043–120065. [Google Scholar] [CrossRef]
- Hundman, K.; Constantinou, V.; Laporte, C.; Colwell, I.; Soderstrom, T. Detecting spacecraft anomalies using lstms and nonparametric dynamic thresholding. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 387–395. [Google Scholar]
- Ding, N.; Ma, H.; Gao, H.; Ma, Y.; Tan, G. Real-time anomaly detection based on long short-Term memory and Gaussian Mixture Model. Comput. Electr. Eng. 2019, 79, 106458. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Wen, T.; Keyes, R. Time series anomaly detection using convolutional neural networks and transfer learning. arXiv 2019. [Google Scholar] [CrossRef]
- Ren, H.; Xu, B.; Wang, Y.; Yi, C.; Huang, C.; Kou, X.; Xing, T.; Yang, M.; Tong, J.; Zhang, Q. Time-series anomaly detection service at microsoft. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 3009–3017. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, P.; Mahmoudi, S.; Garg, S.; Kaddoum, G.; Hassan, M.M. DDANF: Deep denoising autoencoder normalizing flow for unsupervised multivariate time series anomaly detection. Alex. Eng. J. 2024, 108, 436–444. [Google Scholar] [CrossRef]
- Backhus, J.; Rao, A.R.; Venkatraman, C.; Gupta, C. Time Series Anomaly Detection Using Signal Processing and Deep Learning. Appl. Sci. 2025, 15, 6254. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Li, L.; Yan, J.; Wang, H.; Jin, Y. Anomaly detection of time series with smoothness-inducing sequential variational auto-encoder. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 1177–1191. [Google Scholar] [CrossRef]
- Yokkampon, U.; Mowshowitz, A.; Chumkamon, S.; Hayashi, E. Robust unsupervised anomaly detection with variational autoencoder in multivariate time series data. IEEE Access 2022, 10, 57835–57849. [Google Scholar] [CrossRef]
- Makhzani, A.; Shlens, J.; Jaitly, N.; Goodfellow, I.; Frey, B. Adversarial autoencoders. arXiv 2015, arXiv:1511.05644. [Google Scholar]
- Audibert, J.; Michiardi, P.; Guyard, F.; Marti, S.; Zuluaga, M.A. Usad: Unsupervised anomaly detection on multivariate time series. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Online, 23–27 August 2020; pp. 3395–3404. [Google Scholar]
- Ning, Z.; Miao, H.; Jiang, Z.; Wang, L. Using Multi-Scale Convolution Fusion and Memory-Augmented Adversarial Autoencoder to Detect Diverse Anomalies in Multivariate Time Series. Tsinghua Sci. Technol. 2024, 30, 234–246. [Google Scholar] [CrossRef]
- Hyndman, R.J.; Wang, E.; Laptev, N. Large-scale unusual time series detection. In Proceedings of the 2015 IEEE International Conference on Data Mining Workshop (ICDMW), Atlantic City, NJ, USA, 14–17 November 2015; IEEE: New York, NY, USA, 2015; pp. 1616–1619. [Google Scholar]
- Jin, Y.; Qiu, C.; Sun, L.; Peng, X.; Zhou, J. Anomaly detection in time series via robust PCA. In Proceedings of the 2017 2nd IEEE International Conference on Intelligent Transportation Engineering (ICITE), Singapore, 1–3 September 2017; IEEE: New York, NY, USA, 2017; pp. 352–355. [Google Scholar]
- Wang, X.; Miranda-Moreno, L.; Sun, L. Hankel-structured tensor robust PCA for multivariate traffic time series anomaly detection. arXiv 2021. [Google Scholar] [CrossRef]
- Quilodrán-Casas, C.; Arcucci, R.; Mottet, L.; Guo, Y.; Pain, C. Adversarial autoencoders and adversarial LSTM for improved forecasts of urban air pollution simulations. arXiv 2021. [Google Scholar] [CrossRef]
- Pham, C.H.; Ladjal, S.; Newson, A. PCA-AE: Principal component analysis autoencoder for organising the latent space of generative networks. J. Math. Imaging Vis. 2022, 64, 569–585. [Google Scholar] [CrossRef]
- Shlens, J. A tutorial on principal component analysis. arXiv 2014. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 7–9 July 2015; PMLR: Cambridge, MA, USA, 2015; pp. 448–456. [Google Scholar]
- Goh, J.; Adepu, S.; Junejo, K.N.; Mathur, A. A dataset to support research in the design of secure water treatment systems. In Proceedings of the Critical Information Infrastructures Security: 11th International Conference, CRITIS 2016, Paris, France, 10–12 October 2016; Revised Selected Papers 11. Springer: Berlin/Heidelberg, Germany, 2017; pp. 88–99. [Google Scholar]
- Su, Y.; Zhao, Y.; Niu, C.; Liu, R.; Sun, W.; Pei, D. Robust anomaly detection for multivariate time series through stochastic recurrent neural network. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2828–2837. [Google Scholar]
- Tuli, S.; Casale, G.; Jennings, N.R. Tranad: Deep transformer networks for anomaly detection in multivariate time series data. arXiv 2022, arXiv:2201.07284. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).