You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Electronics
Download PDF
  • Article
  • Open Access

6 August 2025

Decision Tree Pruning with Privacy-Preserving Strategies

,
,
and
1
Faculty of Information Science and Technology, Multimedia University, Jalan Ayer Keroh Lama, Melaka 75450, Malaysia
2
Centre for Advanced Analytics (CAA), COE for Artificial Intelligence, Multimedia University, Jalan Ayer Keroh Lama, Melaka 75450, Malaysia
*
Authors to whom correspondence should be addressed.
Electronics2025, 14(15), 3139;https://doi.org/10.3390/electronics14153139
This article belongs to the Special Issue Digital Security and Privacy Protection: Trends and Applications, 2nd Edition
Version Notes
Order Reprints

Abstract

Machine learning techniques, particularly decision trees, have been extensively utilized in Network-based Intrusion Detection Systems (NIDSs) due to their transparent, rule-based structures that enable straightforward interpretation. However, this transparency presents privacy risks, as decision trees may inadvertently expose sensitive information such as network configurations or IP addresses. In our previous work, we introduced a sensitive pruning-based decision tree to mitigate these risks within a limited dataset and basic pruning framework. In this extended study, three privacy-preserving pruning strategies are proposed: standard sensitive pruning, which conceals specific sensitive attribute values; optimistic sensitive pruning, which further simplifies the decision tree when the sensitive splits are minimal; and pessimistic sensitive pruning, which aggressively removes entire subtrees to maximize privacy protection. The methods are implemented using the J48 (Weka C4.5 package) decision tree algorithm and are rigorously validated across three full-scale NIDS datasets: GureKDDCup, UNSW-NB15, and CIDDS-001. To ensure a realistic evaluation of time-dependent intrusion patterns, a rolling-origin resampling scheme is employed in place of conventional cross-validation. Additionally, IP address truncation and port bilateral classification are incorporated to further enhance privacy preservation. Experimental results demonstrate that the proposed pruning strategies effectively reduce the exposure of sensitive information, significantly simplify decision tree structures, and incur only minimal reductions in classification accuracy. These findings reaffirm that privacy protection can be successfully integrated into decision tree models without severely compromising detection performance. To further support the proposed pruning strategies, this study also includes a comprehensive review of decision tree post-pruning techniques.

1. Introduction

In data classification, machine learning algorithms have been successfully applied to resolve many predictive tasks in various domains. By providing sets of instances (dataset) to a machine classifier, it is able to learn the importance of each bit of data according to the heuristics underneath a classifier and subsequently gain the ability to predict new instances. The field of privacy began to gain huge attention in recent years due to the explosion of artificial intelligence and the advancement of data storage technology. Privacy concerns have led the statistical research communities to propose a distinct set of data privacy algorithms for concealing the sensitive information found in the dataset (privacy-preserving data publishing [1,2]). On the other side of the coin, researchers have also fine-tuned many machine learning algorithms to consider the importance of privacy (privacy-preserving machine learning [3,4,5]).
Privacy-preserving data publishing intends to safeguard the privacy of data by sanitizing or anonymizing the information before performing any classification tasks, while privacy-preserving machine learning aims to prevent sensitive information from being inferred by the machine learning models. Unlike most of the works proposed, we have utilized the decision tree pruning approach for concealing the sensitive values appearing in the decision tree model by removing the particular nodes containing the sensitive data.
A white box model, the decision tree, is selected in this paper because of its ability to generate straightforward, simple, and understandable classification rules. Although the tree model is able to perform at a satisfactory level in various domains, it is also susceptible to various privacy issues. As the model of a tree classifier provides the class distributions of each node, Li et al. [6] describe the possibility of deidentification for a particular individual by illustrating the scenario using a decision tree model. Unlike the privacy pruning designed by Li et al. [6], our approach focuses on the splitting values of a decision tree model. From a fully built decision tree model, the proposed pruning approach will remove the particular nodes whenever a predetermined sensitive value is detected on each iteration of the pruning procedure. The merit of this approach is the unaltered decision tree induction for generating the tree model. In other words, the entire procedure for inducing the tree follows the original statistical heuristics (e.g., information gain [7], information gain ratio [8], or Gini index [9]).
Our work is motivated by the application of decision trees on Network Intrusion Detection Systems (NIDSs), and the privacy concerns are described in Section 4. This study is an extended version of our previous work [10], where we initially proposed a sensitive pruning-based decision tree for privacy protection in Network-based Intrusion Detection Systems. The earlier work introduced the concept of pruning sensitive nodes to mitigate privacy risks associated with decision tree visibility. However, the prior study was limited to a single NIDS dataset (6% GureKDDCup) and employed only the standard sensitive pruning strategy. In this paper, we further develop and enhance the sensitive pruning framework by introducing two additional pruning strategies: optimistic and pessimistic sensitive pruning. Moreover, the current study significantly expands the experimental validation by testing on multiple large-scale NIDS datasets and integrating additional privacy-preserving techniques such as IP address truncation and port bilateral classification. The extended experiments, improved algorithms, and detailed complexity analysis provide a more comprehensive view of the practical applicability and scalability of the proposed approach in diverse NIDS environments. In this paper, the proposed privacy pruning approach is enhanced based on the C4.8 decision tree algorithm (better known as J48 in the Weka package).
Related work on post-pruning algorithms is reviewed in Section 2. Section 3 described our proposed privacy post-pruning in detail. Application and motivation of the designed algorithm are explained in Section 4. Section 5 provides the experimental settings and empirical results tested against three NIDS datasets. Lastly, Section 6 concludes our work along with some future works and challenges.

3. Proposed Model

As depicted by Li and Sarkar [6], confidential information can be inferred from a fully built decision tree by linking attacks. In our studies, we proposed a distinct way to protect the sensitive information in a decision tree. The proposed pruning algorithm is extended from the original J48 (Weka C4.5 package) for considering the importance of privacy.

3.1. Sensitive Pruning

Figure 1 presents a simple unpruned decision tree. A decision tree starts from a root and splits by selecting the best attribute (e.g., A, B, C, and D) iteratively until it is able to achieve a pure leaf node. The splitting attribute value is represented as A1, A2, A3, B1, etc., while the nodes are represented by #1, #11, #12, #2, #3, etc.
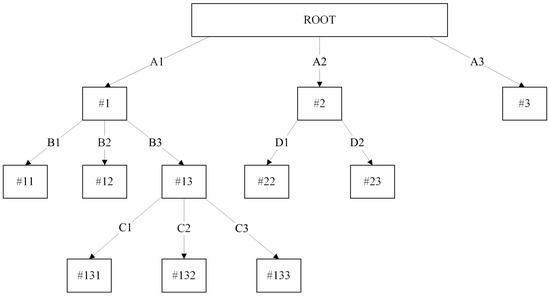
Figure 1. Example of an unpruned decision tree. Numbered labels (e.g., #1, #11, #13, #131) refer to nodes, while alphabetical labels (e.g., A1, B2, C3) indicate attribute splits at each branch.
To illustrate the concepts of our proposed algorithm, let us assume that attribute value B3 is a confidential value. Following the standard bottom–up post-pruning strategy, our proposed method will compare each of the attribute values with the value of B3. If its value is equivalent to B3, we will prune the related node #13 to a leaf and modify the attribute value of B3 to “SENSITIVE”. Since node #13 consists of three children, #131, #132, and #133, all of its children will be removed as it is no longer significant in the classification process. Although node #13 is no longer useful in classification, the strength of the decision tree allows each of the nodes in the model to perform classification tasks. In this case, node #1 will handle the classification duty on behalf of node #13, as the testing instance is not able to traverse to the leaf of the decision tree. Additionally, retaining the sensitive node #13 might also give a better insight to the decision tree user. It is also worth mentioning that the removal of the class label for node #13 or even the entire node #13 can be performed without affecting the current classification ability of the entire model. Figure 2 shows the decision tree model after the sensitive pruning procedure.
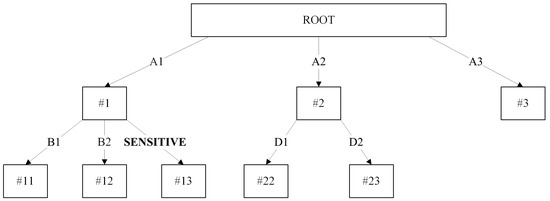
Figure 2. Sensitive pruning decision tree. Numbered labels (e.g., #1, #11, #13, #131) refer to nodes, while alphabetical labels (e.g., A1, B2, C3) indicate attribute splits at each branch.
The sensitive pruning algorithm can be summarized as follows in Algorithm 1:
Algorithm 1: Sensitive Pruning Algorithm
Input:
    Tmax, Unpruned Decision Tree
    Sensitive Attribute Value, AS
Output:
    Pruned Sensitive Decision Tree
Procedure:
Learning Procedure I:
1.  for all split in node t, do
2.      Let node ts be the child node of t
3.      Let Attribute Value A equals to current split attribute value
4.      if (A == AS):
5.       Replace A value with “SENSITIVE”
6.       if (ts contains any child node):
7.        Replace ts with a leave node
8.       endif
9.      endif
10.  Endfor
Learning Procedure II:
11. Let T = Tmax
12. if T is not “leave node”:
13.   for all node t ∈ T, starting from leaf nodes towards the root node, do
14.        Repeat step 1–10
15.   endfor
16. endif

3.2. Optimistic Sensitive Pruning

Assuming attribute value D2 is denoted as the confidential value, succeeding the sensitive pruning in Section 3.1 would result in the tree illustrated in Figure 3 and Figure 4. If the decision tree only splits based on two values, it is basically absurd to follow the sensitive pruning because a single split in the decision tree does not provide any significant benefit to the current tree. Therefore, we proposed to prune all of the descendants (subtree) of node #2 when the number of splits is equivalent to two, converting node #2 into a leaf node.
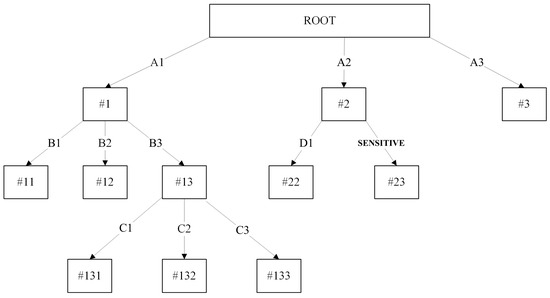
Figure 3. Limitation of sensitive pruning decision tree. Numbered labels (e.g., #1, #11, #13, #131) refer to nodes, while alphabetical labels (e.g., A1, B2, C3) indicate attribute splits at each branch.
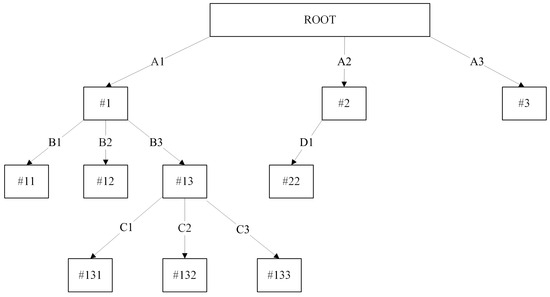
Figure 4. Limitation of sensitive pruning decision tree. Once node #23 is pruned, node #22 becomes insignificant. Numbered labels (e.g., #1, #11, #13, #131) refer to nodes, while alphabetical labels (e.g., A1, B2, C3) indicate attribute splits at each branch.
The optimistic sensitive pruning algorithm can be summarized as follows in Algorithm 2:
Algorithm 2: Optimistic Sensitive Pruning Algorithm
Input:
    Tmax, Unpruned Decision Tree
    Sensitive Attribute Value, AS
Output:
    Pruned Sensitive Decision Tree
Procedure:
Learning Procedure I:
1.  for all split in node t, do
2.  Let node ts be the child node of t
3.  Let Attribute Value A equals to current split attribute value
4.  if (A == AS):
5.      Replace A value with “SENSITIVE”
6.      if (ts contains any child node):
7.           Replace ts with a leave node
8.      endif
9.      if (number of split == 2):
10.       Replace t with a leave node
11.    endif
12.   endif
13. endfor
Learning Procedure II:
14. Let T = Tmax
15. if T is not “leave node”:
16.     for all node t ∈ T, starting from leaf nodes towards the root node, do
17.          Repeat step 1–13
18.     endfor
19. endif

3.3. Pessimistic Sensitive Pruning

In the scenario whereby privacy is given the highest priority, we would remove the entire same-level subtree when the sensitive value is detected. For example, Figure 2, consisting of the confidential attribute value B3, will result in Figure 5 by using the pessimistic sensitive pruning. The essential benefit from this pruning approach is the privacy is preserved, as the attribute does not even exist in the decision tree. The primary inspiration of this pruning approach is the ideology of guessing theory, assuming that attribute values B1 and B2 are equal to ‘low’ and ‘medium’. One can easily predict the value of B3 to be equivalent to ‘high’. Therefore, each of the suggested pruning algorithms is able to provide different privacy requirements depending on the user’s preference.
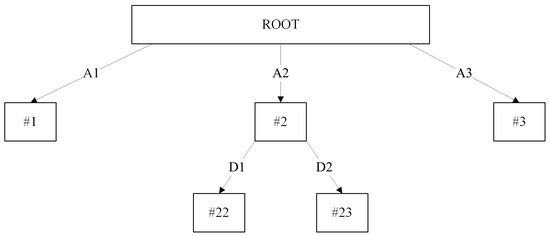
Figure 5. Pessimistic sensitive pruning decision tree. Numbered labels (e.g., #1, #11, #13, #131) refer to nodes, while alphabetical labels (e.g., A1, B2, C3) indicate attribute splits at each branch.
Pessimistic sensitive pruning algorithm is summarized as follows in Algorithm 3:
Algorithm 3: Pessimistic Sensitive Pruning Algorithm
Input:
    Tmax, Unpruned Decision Tree
    Sensitive Attribute Value, AS
Output:
    Pruned Sensitive Decision Tree
Procedure:
Learning Procedure I:
1.  for all split in node t, do
2.      Let node ts be the child node of t
3.      Let Attribute Value A equals to current split attribute value
4.      if (A == AS):
5.       Replace t with a leave node
6.      endif
7.  endfor
Learning Procedure II:
8.  Let T = Tmax
9.  if T is not “leave node”:
10.   for all node t ∈ T, starting from leaf nodes towards the root node, do
11.        Repeat step 1–7
12.   endfor
13. endif

3.4. Sensitive Values Considerations

Sensitive attributes and values can vary significantly across different domains; therefore, domain knowledge or the input of domain experts is typically required to determine which attributes should be considered sensitive. In this work, sensitive attributes and values were identified based on established knowledge in the field of NIDSs (for example, private IP addresses and host-specific identifiers). Although no domain experts were directly consulted, these attributes reflect widely accepted sensitivity indicators reported in prior NIDS research. The same principle can be extended to other domains, such as finance or healthcare, by tailoring the sensitivity list to domain-specific requirements (for example, account numbers or patient identifiers).

3.5. Privacy Risk Metrics Considerations

The primary goal of the sensitive pruning algorithm is to minimize the exposure of sensitive attribute values within the decision tree nodes. However, the publicly available NIDS datasets used in this study do not provide ground-truth annotations indicating which attributes are sensitive. Consequently, widely adopted privacy risk metrics such as k-anonymity or differential privacy could not be applied. Instead, we approximate privacy preservation by evaluating structural simplification of the decision tree, specifically through the number of sensitive nodes removed and the overall reduction in tree complexity. This approach aligns with the objective of concealing sensitive splits while maintaining classification utility.

3.6. GDPR-Compliant Model Sharing

The General Data Protection Regulation (GDPR) emphasizes data minimization and pseudonymization to support safer sharing of machine learning models in critical domains such as healthcare, finance, and network security. The proposed sensitive pruning strategies align with these principles by concealing sensitive attribute values within decision tree models. Through the replacement or removal of sensitive nodes, the resulting pruned trees reduce the risk of exposing personally identifiable information, such as private IP addresses. While our experiments focus on publicly available NIDS datasets, these strategies can be readily applied to other privacy-critical domains to facilitate GDPR-compliant model sharing during collaborative research and deployment.

4. Application and Motivation

To demonstrate the capability of our proposed pruning algorithm, we adopted the post-pruning method in the domain of NIDS. Traditionally, NIDS relies on the signature database in Snort for detecting malicious traffic. With the explosion of machine learning, many techniques involving the use of artificial intelligence have been widely proposed by researchers for detecting malicious packets [60,61,62]. It is necessary to supply huge and quality-labeled training data for building a machine classifier with high performance. In NIDS, the training data generally refers to the network traces information extracted from the packets. Some of the common information found in packets includes IP addresses, port numbers, TCP flags, transport protocol, etc.
While both the independent field of privacy-preserving decision trees [6,63,64] and privacy solutions [65,66] in the domain of NIDS have been explored for quite some time, none of the literature has yet to study the combination of them. At a glance, a decision tree model built upon sets of network traces data might appear to be non-intrusive. To illustrate the concepts of privacy leakage for decision trees in NIDS, Figure 6 is generated for portraying the described scenario.
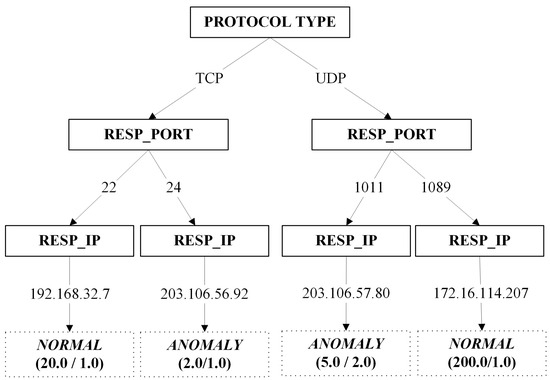
Figure 6. A sample decision tree model built using IDS data. The root node (PROTOCOL TYPE) represents the network protocol (e.g., TCP or UDP). The internal nodes (RESP_PORT and RESP_IP) denote the response port and response IP address used in the connections. Leaf nodes indicate the predicted class (NORMAL or ANOMALY) with two numbers in parentheses: the total number of instances and the number of misclassified instances.
Referring to Figure 6, several pieces of inductive information can be inferred. For instance, there is a high possibility of opened TCP port 22 for the IP address of 192.168.32.7. Further analysis by a domain expert might reveal that secure shell services are made available for the host with the unique IP address of 192.168.32.7 [67]. Zhang et al. [68] and Coull et al. [69] state that services operating on a specific host can be uncovered by utilizing mappings of port numbers to services. Subsequently, adversaries can then launch an attack on an individual or organization by exploiting the information discovered [70]. Although researchers have proposed various approaches for concealing the IP addresses [66,71,72,73] while retaining their unique characteristics for network analysis purposes along with a decent level of privacy protection, some of the methods suffer from re-identification attacks [74]. Moreover, it is also not an easy task to maintain the consistency of IP address anonymization (pseudonymization) across various network trace datasets over a period of time. On top of that, the utility of the anonymization solution is questionable when tested against the traditional Snort IDS [65,66]. Hence, we proposed to take a different approach in safeguarding the privacy by adopting the proposed pruning algorithms described in Section 3.
Before conducting the experiments, it is important to first define the confidential attribute values as required by our pruning algorithms. Due to the lack of domain experts, we proposed the confidential values to encompass all private IP addresses because the range can resemble a group of IP addresses for an organization. The full list of private IP addresses is tabulated in Table 1.
Table 1. Range of private IP addresses.

5. Experiment

5.1. Datasets and Experimental Settings

To evaluate the effect of our proposed pruning algorithms, several experiments have been conducted against 3 publicly available NIDS datasets: GureKDDCup [75,76], UNSW-NB15 [77], and CIDDS-001 [78]. The three mentioned datasets are utilized in our work because they contain the missing pair of IP attributes from the benchmark NIDS datasets (KDDCup 99′ [79] and NSL-KDD [80]). It is not plausible for us to perform any experiments utilizing the proposed privacy pruning without the pairs of IP addresses. Several recent reviews of the NIDS datasets are published in [62,81,82]. Datasets adopted in our studies are summarized and tabulated in Table 2.
Table 2. Summary of experimental datasets.
To fairly judge the performance of each machine learner, no (minimal) data cleansing and pre-processing are performed against the datasets employed for conforming the classifiers data requirements. Each of the description and pre-processing steps for the datasets are thoroughly explained in Section 5.1.1, Section 5.1.2 and Section 5.1.3. Since the standard tenfold cross validation [83] is not suitable to be adopted due to temporal dependencies and data leakage risks, we utilized a rolling-origin resampling scheme for training and testing distribution, following the methodology presented in our previous benchmarking study [84]. Rolling-origin, widely used in time-series forecasting, progressively expands the training set while moving the testing window forward, providing a more realistic and unbiased evaluation for NIDS datasets. The detailed train-test splits using this approach are illustrated in the subsequent subsection.

5.1.1. GureKDDCup Dataset and Pre-Processing

GureKDDCup [75,76] was released in 2008 to complement the drawback of the KDDCup 99′ [80] NIDS datasets. As KDDCup 99′ is more than several decades old, researchers have deemed the datasets to be obsolete in reflecting the present network traffics [85,86]. GureKDDCup was generated by imitating the similar procedure of creating the KDDCup 99′. Additionally, payloads, IP addresses, and port numbers, which are missing from the KDDCup 99′, are incorporated into the dataset. On top of that, the creators of GureKDDCup have also included several new attacks that are absent in KDDCup 99′. The full version of the GureKDDCup dataset is compressed into a 9.3 GB file (gureKddcup.tar.gz). The file size is tremendously huge due to the added payloads data to each of the network traffics. However, we only used the daily logs found in each gureKddcup-matched.list for the experiment conducted. Each of the daily logs are concatenated and merged into a single file containing a week of network traffic. Table 3 shows the total number of instances available in each week, while Table 4 presents the distribution of training and testing data in accordance with the number of weeks. No data cleansing, feature extraction, or attribute reduction is necessary to be performed against the GureKDDCup dataset.
Table 3. Full GureKDDCup #instances.
Table 4. Full GureKDDCup distribution.

5.1.2. UNSW-NB15 Dataset and Pre-Processing

Moustafa et al. [77] released the UNSW-NB15 dataset in 2015 to complement the lack of footprint attacks [81] in KDDCup 99′ [79]. Although the documentation stated a total number of instances equivalent to 2,540,044, we have verified that an additional instance is found in each week (weeks 1, 2, and 3), leading to a total of 2,540,047 instances. As shown in Table 5, some data cleansing is unavoidable; it is necessary to be conducted against the dataset before we are able to build the machine learner. The label attribute, which consists of a binary class {normal, attack}, was discarded as we employ the attack_cat containing 10 different classes as our class label. Table 6 tabulated the number of instances contained in each week, while Table 7 provides the partition of training and testing data distribution. It is also worth mentioning that although UNSW-NB15 has provided a small version of the dataset, the absence of IP addresses in the small version prohibits us from performing our experiment against it.
Table 5. UNSW-NB15 dataset cleaning.
Table 6. Full UNSW-NB15 #instances.
Table 7. Full UNSW-NB15 distribution.

5.1.3. CIDDS-001 Dataset and Pre-Processing

The CIDDS-001 NIDS [78] dataset has been publicly available since 2017. The dataset contains a total of 32 million flows, whereby 31 million are from the emulated internal environment (Openstack software); and 0.7 million are from the external traffic consisting of real traffic from the internet. We have excluded the external traffic from our experiment due to inaccurate labels and the absence of some attacks. The full CIDDS-001 Openstack internal traffic is employed in the experimental procedure. Table 8 shows some of the data cleansing necessary to be performed against the dataset. The entire flows attribute was removed from the dataset, as it contains only a single constant value for all instances [81]. In the case of flags, we have split the single-attribute flags into five distinct flags in accordance with their value. The IP addresses are modified in such a way that they will not collide with other IP addresses and match the dot separator of IP addresses. The total number of instances for each week are tabulated in Table 9. while the training and testing data distribution is presented as shown in Table 10. A significant reason for excluding the week 3 and 4 data from the experimental procedure is because it only encompassed normal traffic.
Table 8. CIDDS-001 Openstack dataset cleaning.
Table 9. CIDDS-001 Openstack #instances.
Table 10. CIDDS-001 Openstack distribution.

5.2. Types of Pruning, Evaluation Metrics, and Experimental Setup

As discussed in Section 3.1, three variants of sensitive pruning are proposed in this paper. To compare the performance of the designed algorithm, the experimental results of J48 with and without the default pruning are compared empirically. Additionally, three hybrid pruning algorithms incorporating the default J48 pruning and the proposed sensitive pruning algorithms are also implemented. It should be noted that our program will perform the default J48 pruning algorithm ahead of the proposed sensitive pruning. Table 11 summarizes all of the pruning procedures employed in this paper.
Table 11. Summary of technical implementation for all pruning algorithms.
Three performance evaluation metrics are used in comparing the empirical results, including (i) classification accuracy, (ii) number of pruned nodes, and (iii) number of final nodes. The number of pruned nodes is calculated by accumulating the number of nodes pruned by the sensitive pruning (inclusive of the sensitive nodes as depicted in Figure 2 in Section 3.1) as well as the J48 pruning. For the number of final nodes, the final model of the decision tree nodes will exclude the nodes splitting with the value of “SENSITIVE”. This is because the nodes are no longer significant in the classification process.
All of the aforementioned pruning algorithms in Table 11 are performed on the same computing environment with the hardware specification of an eight-core 3.64 GHz AMD Ryzen CPU and 64 GB RAM on Windows 10. The Weka J48 package (stable version 3.8) is employed for extending the default pruning algorithm throughout the entire experiment.

5.3. Experimental Results

5.3.1. Performance Comparison of All Pruning Algorithms

Experimental results based on the pruning described in Section 5.2 are tabulated in Table 12 and Table 13. All of the performed experiments follow the aforementioned dataset distribution as explained in Section 5.1. From both Table 12 and Table 13, the performance of the proposed pruning algorithm is very encouraging, as most of the proposed model only suffers a slight loss in terms of accuracy as compared to the unpruned tree (J48U-NO). Although the classification accuracy has slightly decreased, the number of nodes removed by the sensitive pruning escalates substantially. Additionally, the hybrid version of pruning, consisting of the default J48 pruning and sensitive pruning, further reduced the number of nodes available in the final model. In the case of a decision tree, a smaller tree with a satisfactory classification accuracy is much preferred over a highly complex tree that overfits the training data. This is because a smaller tree improves the readability and interpretability of a decision tree.
Table 12. Classification accuracies for four pruning algorithms in three experimental datasets.
Table 13. Classification accuracies for four hybrid pruning algorithms in three experimental datasets.
To illustrate the relationship between the pruning algorithm, classification accuracy, and the number of pruned nodes, Figure 7, Figure 8 and Figure 9 are generated in accordance with each dataset. The number of pruned nodes can be clearly seen to escalate when J48 default pruning is applied with sensitive pruning for the GureKDDCup (Figure 7) and UNSW-SB15 (Figure 8) datasets. However, we observed a constant number of pruned nodes and classification accuracy when either one of the sensitive pruning methods was applied against the CIDDS-001 dataset. This can be explained by the ratio of the number of unique IP addresses against the number of unique private IP addresses in the dataset. As shown in Table 14, 34 out of 38 source IP addresses and 785 out of 790 destination IP addresses in CIDDS-001 are comprised of private IP addresses. Referring to the three figures, we observe that the number of pruned nodes and classification accuracy remain constant for both J48U-SP and J48U-OSP. After analyzing the decision rules in the model, the scenario can be justified, as all of the IP addresses in the decision tree always split into more than 2 branches. Thus, leading the J48U-OSP to have the same effects as J48U-SP. The hybrid pruning J48P-SP and J48P-OSP are observed to be having the similar effects as they are built upon the identical sensitive pruning (J48U-SP, J48U-OSP). From the empirical results attained in this section, we proved that the privacy of attribute values can be preserved in a decision tree in exchange for a small loss of classification accuracy.
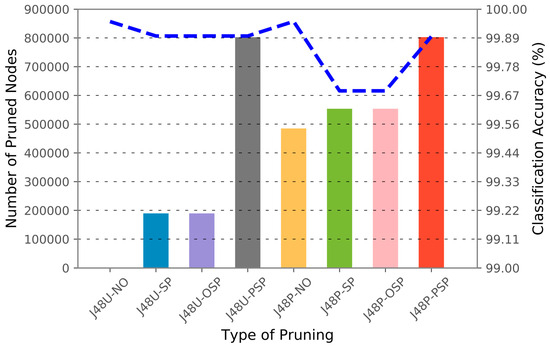
Figure 7. Number of pruned nodes (Y1-axis) (represented by bars) and classification accuracy (Y2-axis) (represented by blue dotted lines) according to each of the pruning algorithms (X-axis) in GureKDDCup [Train: 1~6; Test: 7].
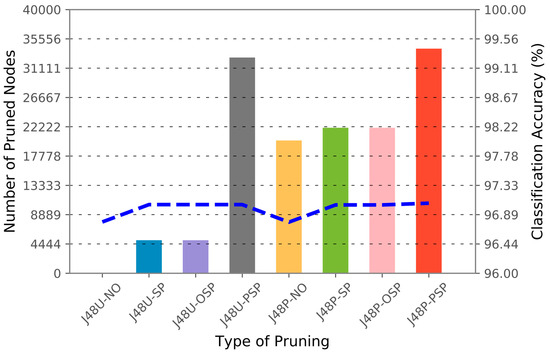
Figure 8. Number of pruned nodes (Y1-axis) (represented by bars) and classification accuracy (Y2-axis) (represented by blue dotted lines) according to each of the pruning algorithms (X-axis) in UNSW-NB15 [Train: 1~3; Test: 4].
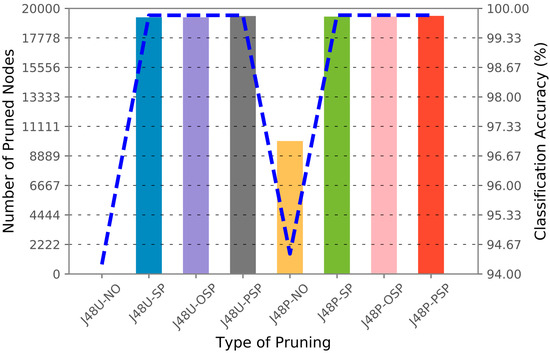
Figure 9. Number of pruned nodes (Y1-axis) (represented by bars) and classification accuracy (Y2-axis) (represented by blue dotted lines) according to each of the pruning algorithms (X-axis) in CIDDS-001 [Train: 1; Test: 2].
Table 14. Number of unique IP addresses for each IDS dataset.

5.3.2. Visibility of Sensitive Information in Decision Tree

Sensitive pruning, optimistic sensitive pruning, and pessimistic sensitive pruning are sensitive pruning extensions established upon the default J48 Weka decision tree package. Adopting the similar properties from a decision tree, the tree-like structure of a model remains. Thus, the classification information and splitting values, except the predefined sensitive values, in the final model of the proposed pruning are made visible. The availability of this information will allow the domain expert (e.g., system administrator) to interpret and have a better understanding regarding the current situation of the network. For the sake of simplicity, a partial of the ASCII J48U-SP tree model built against the CIDDS-001 dataset is shown in Figure 10. The results obtained are based on the train-test data distribution as tabulated in Table 10.
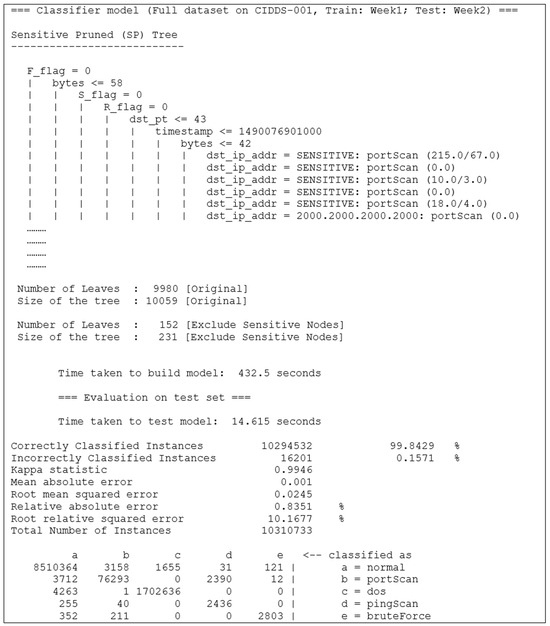
Figure 10. ASCII-sensitive pruned tree model (partial), performance result, and confusion matrix on CIDDS-001.
As mentioned earlier in Section 3.1, retaining or removing the sensitive nodes would not directly affect the classification performance of the decision tree model. Therefore, several options are provided to the users for flexibility in displaying the classification information on the sensitive nodes. Depending on the requirement, the resulting decision tree model can (i) show the label (class) and distribution of the sensitive nodes as shown in Figure 10, (ii) show only an attribute value containing “SENSITIVE”, or (iii) directly remove the entire sensitive nodes from the model.

5.3.3. Computational Complexity Comparison Against All Pruning Algorithms

As described in Section 5.3.1, the advantages of a small tree over a complex tree include the simplicity in interpreting and understanding the decision rules. On top of that, a smaller tree with fewer nodes would probably require less time for the model to evaluate the test instances. This is because when the test instances traverse from the root node to the decision (leaf) node, a lesser node would be necessary for the test instances to move in a smaller tree.
To substantiate our hypothesis, the computation time for evaluating the test instances with each of the proposed pruning algorithms is tabulated in Table 15. Referring to Table 15, most of the proposed sensitive pruning algorithms required less time as compared to the tree without pruning (J48U-NO). The most noticeable dataset that benefitted from the smaller size of the tree is CIDDS-001. Although the proposed pruning algorithms are able to decrease the model evaluation time, most of them require a little extra time in building the proposed model. As shown in Table 16, almost all of the proposed pruning algorithms consume more time in contrast to the unpruned model (J48U-NO) and standard J48 pruned model (J48P-NO). This scenario is entirely justifiable, as all of the pruning algorithms are mandatory in building the full decision tree model before removing any insignificant nodes. Although there is a slight increase in time required for building the decision tree model, the additional time is still acceptable because the privacy of information is able to be preserved in exchange for some computational resources.
Table 15. Computation time for evaluating the test instances with each pruning algorithm.
Table 16. Computation time for building the decision tree with each pruning algorithm.
While sensitive pruning effectively reduces tree size and slightly decreases evaluation time, it introduces additional computational steps during tree construction. Each sensitive attribute check requires a full traversal of the decision tree, resulting in computational overhead proportional to both the number of sensitive attributes and the number of nodes (approximately O k · n , where k is the number of sensitive attributes and n is the node count). In our experiments, this overhead is negligible even for the largest dataset (CIDDS-001, with approximately 18 million records) due to the pruning being performed offline during model training. In real-time intrusion detection, inference speed is critical, and the reduced tree size from pruning directly benefits detection latency.

5.3.4. Application of Anonymization Algorithm: Truncation and Bilateral Classification

In principle, anonymization solution would definitely destroy or degrade the original dataset to a certain extent. From the experimental results obtained by Mivule et al. [87,88], the Iris dataset that is applied with data privacy solutions (noise) always results in higher classification errors when compared against the original dataset. However, the scenarios observed are not always true based on the empirical results acquired in our previous work.
Motivated by our previous studies [89,90] related to the various anonymization techniques on network traces data, we have proven that some of the anonymization techniques are suitable to be adopted for improving the performance of classifiers. For instance, our first studies [89] convince us of the suitability and possibility of an anonymization solution (e.g., bilateral classification performed against port numbers) for raising the classification accuracy of the J48 decision tree model. Inspired by our first studies, we subsequently performed IP address truncation [90] with 10 different machine learning classifiers against the 6 percent GureKDDCup [75] NIDS dataset. The empirical results obtained are very encouraging because the classification accuracy for 4 out of the 10 classifiers has actually improved, and the time taken for building the model for 7 out of the 10 classifiers is reduced significantly. Additionally, the results attained also verified the capability of the IP anonymization solution (IP address truncation) as a dimensionality reduction technique in the domain of machine learning.
With the strength and advantages of the data privacy algorithms discussed in our previous works, we have applied the similar anonymization solutions with our proposed pruning algorithms against all of the NIDS datasets in this paper to safeguard a higher level of privacy. For simplicity, the experimental results shown only include the combination of bilateral classification on both source and destination port numbers as well as 24-bit (3-octet) IP address truncation against both source and destination IP addresses. To provide a fair comparison between the experiments conducted in Section 5.3.1, similar datasets and experimental procedures are employed. The empirical results adopting both the anonymization solution and all of the proposed pruning algorithms are tabulated in Table 17 and Table 18. The total number of unique IP addresses after applying the 24-bit IP address truncation is also shown in Table 14.
Table 17. Classification accuracies for four pruning algorithms in three experimental datasets with 24-bit (3-octet) IP address truncation and port bilateral classification.
Table 18. Classification accuracies for four hybrid pruning algorithms in three experimental datasets with 24-bit (3-octet) IP address truncation and port bilateral classification.
To scrutinize the difference in performance, Table 19 is generated by measuring the mathematical difference in empirical results in Section 5.3.1 and Section 5.3.4. Referring to Table 19, interesting results are observed when J48U-NO is applied against the GureKDDCup week 1 and 1~2 training data, whereby the accuracy is increased by 47.61% and 51.45% when the privacy solution is applied. As shown in Table 19, we noticed that the number of final nodes is significantly reduced for most of our proposed algorithms in all datasets. At the same time, our proposed algorithm suffers a small loss (approximately less than ~1%) in classification accuracy when tested against all the datasets. The trade-off is obviously worth it because we are able to secure a higher level of privacy in a smaller tree by sacrificing a small loss of accuracy. As mentioned earlier, a smaller tree would undoubtedly benefit the users in interpreting a decision tree model. The experimental results obtained further substantiate our claims that not all data privacy algorithms would degrade the quality of data; some of the anonymization solutions are suitable to be utilized as a grouping mechanism or dimensionality reduction in the domain of machine learning for improving the performance of a classifier.
Table 19. Classification accuracies and performance comparison of eight pruning algorithms in three experimental datasets with 24-bit (3-octet) IP address truncation and port bilateral classification.

5.3.5. Benchmarking Against Other Machine Learning Models

To compare the performance of the proposed sensitive pruning algorithms, we conducted benchmark testing against ten widely used machine learning classifiers available in the Weka package: ZeroR, Random Tree, REPtree, Decision Stump, AdaBoost, BayesNet, Naïve Bayes, Random Forest, and Support Vector Machine (SMO). Due to limited prior experiments on the adopted datasets, results for these classifiers were taken from our previous work [84]. For comparability, only the results corresponding to the largest training–testing splits are considered: GureKDDCup (Train: 1–6; Test: 7), UNSW-NB15 (Train: 1–3; Test: 4), and CIDDS-001 (Train: 1; Test: 2). Results for the proposed pruning algorithms are taken from Table 12 and Table 13.
Table 20 presents the classification accuracies for all baseline models and pruning strategies across the three datasets, while Figure 11 illustrates the comparative results. As shown in Figure 11, the proposed sensitive pruning algorithms (J48U-SP, J48U-OSP, J48U-PSP, and their hybrid counterparts) achieved classification accuracies comparable to, and in some cases exceeding, those of strong baselines such as Random Forest. Notably, the pruned models consistently maintained high performance while simultaneously reducing tree complexity and concealing sensitive attributes, thereby offering both interpretability and privacy advantages. This demonstrates that privacy-preserving decision tree pruning can achieve competitive utility while fulfilling stricter privacy requirements in critical domains.
Table 20. Classification accuracies of ten benchmark machine learning models and proposed sensitive pruning algorithms in three experimental datasets.
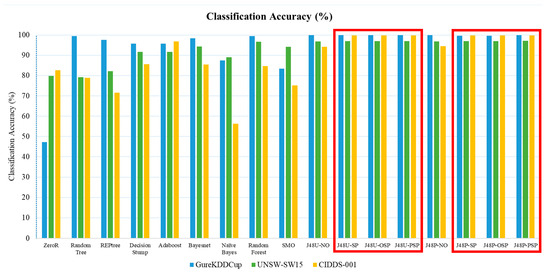
Figure 11. Comparison of classification accuracy (%) (Y-axis) according to each classifier (X-axis) in three experimental datasets: GureKDDCup [Train: 1~6; Test: 7], UNSW-SW15 [Train: 1~3; Test: 4], and CIDDS-001 [Train: 1; Test: 2]. The classifiers enclosed in the red box (J48U-SP, J48U-OSP, J48U-PSP, J48P-SP, J48P-OSP, J48P-PSP) represent the proposed pruning algorithms.

6. Conclusions

In this paper, pruning approaches with privacy considerations are proposed, namely Sensitive Pruning (SP), Optimistic Sensitive Pruning (OSP) and Pessimistic Sensitive Pruning (PSP). All three of the proposed algorithms are enhanced based on the Weka J48 (C4.8) model. The designed solutions removed (“pruned”) nodes containing sensitive information from the final decision tree model. Additionally, we also integrated the proposed algorithms with the default J48 pruning algorithm. Based on the promising evaluation results tested against the three publicly available NIDS datasets, the proposed privacy pruning spells the following four advantages: (1) preserving privacy by discarding sensitive IP addresses from the tree model with a small sacrificial loss in terms of accuracy; (2) visibility of classification rules except rules containing sensitive information; (3) a smaller tree with fewer nodes that leads to lower computational time necessary for evaluating the test instances; and (4) suitability of the network traces privacy solution algorithm (port number bilateral classification and IP address truncation) in safeguarding the sensitive information and improving the performance of a model.
For future works, we plan to extend our work so that (1) it is flexible enough to be applied across various domains, (2) it resolves the instability when sensitive values are detected at the higher level of the decision tree, (3) it incorporates formal privacy risk metrics such as k-anonymity or differential privacy to measure privacy leakage and (4) it explores optimizations, including incremental pruning, streaming-based updates, and GPU or multi-core parallelism, to ensure scalability in high-throughput or real-time environments.

Author Contributions

Conceptualization, Y.J.C.; methodology, Y.J.C. and S.Y.O.; formal analysis, Y.J.C. and S.Y.O.; investigation, Y.J.C.; visualization, Y.J.C. and Z.Y.L.; writing—original draft, Y.J.C.; funding acquisition, S.Y.O.; resources, S.Y.O.; project administration, S.Y.O.; supervision, S.Y.O. and Y.H.P.; writing—review and editing, S.Y.O., Y.H.P. and Z.Y.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research work was supported by a Fundamental Research Grant Scheme (FRGS) under the Ministry of Education and Multimedia University, Malaysia (Project ID: MMUE/160029).

Data Availability Statement

The original datasets presented in the study are openly available in [76] GureKDDCup at https://aldapa.eus/res/gureKddcup/ (accessed on 3 August 2025), [77] UNSW-NB15 at https://research.unsw.edu.au/projects/unsw-nb15-dataset, (accessed on 3 August 2025), and [78] CIDDS-001 at https://www.hs-coburg.de/forschen/cidds-coburg-intrusion-detection-data-sets/. (accessed on 3 August 2025).

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
AAAdaptive Apriori
AAAoP-DTAdaptive Apriori post-pruned Decision Tree
CARTsClassification and Regression Trees
CCPCost–Complexity Pruning
CSPCost-Sensitive Pruning
CVPCritical Value Pruning
DIDepth–Impurity
EBPerror-based pruning
IEEPImproved Expected Error Pruning
IQNImpurity Quality Node
KLKullback–Leibler
MEPMinimum Error Pruning
NIDSNetwork Intrusion Detection System
OPTOptimal Pruning Algorithm
PEPPessimistic Error Pruning
PSOParticle Swarm Optimization
REPReduced Error Pruning
ROCReceiver Operating Characteristics
BMRBayes Minimum Risk

References

  1. Fung, B.C.M.; Wang, K.; Chen, R.; Yu, P.S. Privacy-Preserving Data Publishing. ACM Comput. Surv. 2010, 42, 1–53. [Google Scholar] [CrossRef]
  2. Nettleton, D. Chapter 18: Data Privacy and Privacy-Preserving Data Publishing. In Commercial Data Mining: Processing, Analysis and Modeling for Predictive Analytics Projects; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2014; pp. 217–228. ISBN 0124166024/9780124166028. [Google Scholar]
  3. Aggarwal, C.C.; Yu, P.S.-L. A General Survey of Privacy-Preserving Data Mining Models and Algorithms. In Privacy-Preserving Data Mining: Models and Algorithms; Springer: Boston, MA, USA, 2008; Volume 34, pp. 11–52. [Google Scholar] [CrossRef]
  4. Aldeen, Y.A.A.S.; Salleh, M.; Razzaque, M.A. A Comprehensive Review on Privacy Preserving Data Mining. Springerplus 2015, 4, 694. [Google Scholar] [CrossRef] [PubMed]
  5. Dhivakar, K.; Mohana, S. A Survey on Privacy Preservation Recent Approaches and Techniques. Int. J. Innov. Res. Comput. Commun. Eng. 2014, 2, 6559–6566. [Google Scholar]
  6. Li, X.-B.; Sarkar, S. Against Classification Attacks: A Decision Tree Pruning Approach to Privacy Protection in Data Mining. Oper. Res. 2009, 57, 1496–1509. [Google Scholar] [CrossRef]
  7. Quinlan, J.R. Induction of Decision Trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
  8. Quinlan, J.R. C4.5: Program for Machine Learning; Morgan Kaufmann Publishers Inc.: San Mateo, CA, USA, 1993; ISBN 1-55860-238-0. [Google Scholar]
  9. Breiman, L.; Friedman, J.; Stone, C.J.; Olshen, R.A. Classification and Regression Trees; Taylor & Francis: Oxfordshire, UK, 1984. [Google Scholar]
  10. Chew, Y.J.; Ooi, S.Y.; Wong, K.-S.; Pang, Y.H. Decision Tree with Sensitive Pruning in Network-Based Intrusion Detection System BT—Computational Science and Technology; Alfred, R., Lim, Y., Haviluddin, H., On, C.K., Eds.; Springer: Singapore, 2020; pp. 1–10. [Google Scholar]
  11. Martin, J.K. An Exact Probability Metric for Decision Tree Splitting and Stopping. Mach. Learn. 1997, 28, 257–291. [Google Scholar] [CrossRef]
  12. Breslow, L.A.; Aha, D.W. Simplifying Decision Trees: A Survey. Knowl. Eng. Rev. 1997, 12, 1–40. [Google Scholar] [CrossRef]
  13. Frank, E.; Witten, I.H. Reduced-Error Pruning with Significance Tests; Department of Computer Science, University of Waikato: Hamilton, New Zealand, 1999. [Google Scholar]
  14. Quinlan, J.R. Simplifying Decision Trees. Int. J. Man. Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
  15. Mingers, J. An Empirical Comparison of Selection Measures for Decision Tree Induction. Mach. Learn. 1989, 3, 319–342. [Google Scholar] [CrossRef]
  16. Esposito, F.; Malerba, D.; Semeraro, G.; Kay, J. A Comparative Analysis of Methods for Pruning Decision Trees. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 476–491. [Google Scholar] [CrossRef]
  17. Costa, V.G.; Pedreira, C.E. Recent Advances in Decision Trees: An Updated Survey. Artif. Intell. Rev. 2023, 56, 4765–4800. [Google Scholar] [CrossRef]
  18. Harviainen, J.; Sommer, F.; Sorge, M.; Szeider, S. Optimal Decision Tree Pruning Revisited: Algorithms and Complexity. arXiv 2025, arXiv:2503.03576. [Google Scholar]
  19. Esposito, F.; Malerba, D.; Semeraro, G. Simplifying decision trees by pruning and grafting: New results (Extended abstract). In Machine Learning: ECML-95. ECML 1995, Lecture Notes in Computer Science; Lavrac, N., Wrobel, S., Eds.; Springer: Berlin/Heidelberg, Germany, 1995; Volume 912. [Google Scholar] [CrossRef]
  20. Witten, I.H.; Frank, E.; Hall, M.A.; Christopher, J.P. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 9780128042915. [Google Scholar] [CrossRef]
  21. Jensen, D.; Schmill, M.D. Adjusting for Multiple Comparisons in Decision Tree Pruning. In Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mining, Newport Beach, CA, USA, 14–17 August 1997; pp. 195–198. [Google Scholar] [CrossRef]
  22. Cestnik, B.; Bratko, I. On Estimating Probabilities in Tree Pruning. In Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1991; Volume 482, pp. 138–150. [Google Scholar] [CrossRef]
  23. Watkins, C.J.C.H. Combining Cross-Validation and Search. In Proceedings of the 2nd European Conference on European Working Session on Learning, Bled, Yugoslavia, 1 May 1987; Sigma Press: Rawalpindi, Pakistan, 1987; pp. 79–87. [Google Scholar]
  24. Zhang, Y.; Chi, Z.X.; Wang, D.G. Decision Tree’s Pruning Algorithm Based on Deficient Data Sets. In Proceedings of the Sixth International Conference on Parallel and Distributed Computing Applications and Technologies (PDCAT’05), Dalian, China, 5–8 December 2005; Volume 2025, pp. 1030–1032. [Google Scholar] [CrossRef]
  25. Mitu, M.M.; Arefin, S.; Saurav, Z.; Hasan, M.A.; Farid, D.M. Pruning-Based Ensemble Tree for Multi-Class Classification. In Proceedings of the 2024 6th International Conference on Electrical Engineering and Information & Communication Technology (ICEEICT), Mirpur, Dhaka, 2–4 May 2024; IEEE: Dhaka, Bangladesh, 2024; pp. 481–486. [Google Scholar]
  26. Gelfand, S.B.; Ravishankar, C.S.; Delp, E.J. An Iterative Growing and Pruning Algorithm for Classification Tree Design. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 163–174. [Google Scholar] [CrossRef]
  27. Bohanec, M.; Bratko, I. Trading Accuracy for Simplicity in Decision Trees. Mach. Learn. 1994, 15, 223–250. [Google Scholar] [CrossRef]
  28. Almuallim, H. An Efficient Algorithm for Optimal Pruning of Decision Trees. Artif. Intell. 1996, 83, 347–362. [Google Scholar] [CrossRef]
  29. Lazebnik, T.; Bunimovich-Mendrazitsky, S. Decision Tree Post-Pruning without Loss of Accuracy Using the SAT-PP Algorithm with an Empirical Evaluation on Clinical Data. Data Knowl. Eng. 2023, 145, 102173. [Google Scholar] [CrossRef]
  30. Bagriacik, M.; Otero, F. Fairness-Guided Pruning of Decision Trees. In Proceedings of the 2025 ACM Conference on Fairness, Accountability, and Transparency, Athens, Greece, 23–26 June 2025; Association for Computing Machinery: New York, NY, USA, 2025; pp. 1745–1756. [Google Scholar]
  31. Osei-Bryson, K.-M. Post-Pruning in Decision Tree Induction Using Multiple Performance Measures. Comput. Oper. Res. 2007, 34, 3331–3345. [Google Scholar] [CrossRef]
  32. Fournier, D.; Crémilleux, B. A Quality Index for Decision Tree Pruning. Knowl.-Based Syst. 2002, 15, 37–43. [Google Scholar] [CrossRef][Green Version]
  33. Barrientos, F.; Sainz, G. Knowledge-Based Systems Interpretable Knowledge Extraction from Emergency Call Data Based on Fuzzy Unsupervised Decision Tree. Knowl.-Based Syst. 2012, 25, 77–87. [Google Scholar] [CrossRef]
  34. Wei, J.M.; Wang, S.Q.; You, J.P.; Wang, G.Y. RST in Decision Tree Pruning. In Proceedings of the Fourth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2007), Haikou, China, 24–27 August 2007; Volume 3, pp. 213–217. [Google Scholar] [CrossRef]
  35. Pawlak, Z. Rough Sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
  36. Wei, J.-M.; Wang, S.-Q.; Yu, G.; Gu, L.; Wang, G.-Y.; Yuan, X.-J. A Novel Method for Pruning Decision Trees. In Proceedings of the 2009 International Conference on Machine Learning and Cybernetics, Baoding, China, 12–15 July 2009; Volume 1, pp. 339–343. [Google Scholar]
  37. Osei-Bryson, K.-M. Post-Pruning in Regression Tree Induction: An Integrated Approach. Expert Syst. Appl. 2008, 34, 1481–1490. [Google Scholar] [CrossRef]
  38. Wang, H.; Chen, B. Intrusion Detection System Based on Multi-Strategy Pruning Algorithm of the Decision Tree. In Proceedings of the 2013 IEEE International Conference on Grey Systems and Intelligent Services (GSIS), Macao, China, 15–17 November 2013; pp. 445–447. [Google Scholar] [CrossRef]
  39. Knoll, U.; Nakhaeizadeh, G.; Tausend, B. Cost-Sensitive Pruning of Decision Trees. In Proceedings of the European Conference on Machine Learning, Catania, Italy, 6–8 April 1994; pp. 383–386. [Google Scholar]
  40. Bradley, A.; Lovell, B. Cost-Sensitive Decision Tree Pruning: Use of the ROC Curve. In Proceedings of the Eighth Australian Joint Conference on Artificial Intelligence, Canberra, Australia, 13–17 November 1995; pp. 1–8. [Google Scholar]
  41. Ting, K.M. Inducing Cost-Sensitive Trees via Instance Weighting. In Proceedings of the European Symposium on Principles of Data Mining and Knowledge Discovery, Nantes, France, 23–26 September 1998; pp. 139–147. [Google Scholar] [CrossRef]
  42. Bradford, J.P.; Kunz, C.; Kohavi, R.; Brunk, C.; Brodley, C.E. Pruning Decision Trees with Misclassification Costs. In Machine Learning ECML-98, Proceedings of the 10th European Conference on Machine Learning, Chemnitz, Germany, 21–23 April 1998; Springer: Berlin/Heidelberg, Germany, 1998; Volume 1398, pp. 131–136. [Google Scholar] [CrossRef]
  43. Chen, J.; Wang, X.; Zhai, J. Pruning Decision Tree Using Genetic Algorithms. In Proceedings of the 2009 International Conference on Artificial Intelligence and Computational Intelligence, Shanghai, China, 7–8 November 2009; Volume 3, pp. 244–248. [Google Scholar] [CrossRef]
  44. Zhang, W.; Li, Y. A Post-Pruning Decision Tree Algorithm Based on Bayesian. In Proceedings of the 2013 International Conference on Computational and Information Sciences, Shiyang, China, 21–23 June 2013; pp. 988–991. [Google Scholar] [CrossRef]
  45. Mehta, S.; Shukla, D. Optimization of C5.0 Classifier Using Bayesian Theory. In Proceedings of the 2015 International Conference on Computer, Communication and Control (IC4), Indore, India, 10–12 September 2015. [Google Scholar] [CrossRef]
  46. Malik, A.J.; Khan, F.A. A Hybrid Technique Using Binary Particle Swarm Optimization and Decision Tree Pruning for Network Intrusion Detection. Clust. Comput. 2017, 21, 667–680. [Google Scholar] [CrossRef]
  47. Sim, D.Y.Y.; Teh, C.S.; Ismail, A.I. Improved Boosted Decision Tree Algorithms by Adaptive Apriori and Post-Pruning for Predicting Obstructive Sleep Apnea. Adv. Sci. Lett. 2011, 4, 400–407. [Google Scholar] [CrossRef]
  48. Ahmed, A.M.; Rizaner, A.; Ulusoy, A.H. A Novel Decision Tree Classification Based on Post-Pruning with Bayes Minimum Risk. PLoS ONE 2018, 13, e0194168. [Google Scholar] [CrossRef]
  49. Bahnsen, A.C.; Stojanovic, A.; Aouada, D. Cost Sensitive Credit Card Fraud Detection Using Bayes Minimum Risk. In Proceedings of the 2013 12th International Conference on Machine Learning and Applications, Miami, FL, USA, 4–7 December 2013; Volume 1, pp. 333–338. [Google Scholar] [CrossRef]
  50. Frank, E.; Witten, I.H. Using a Permutation Test for Attribute Selection in Decision Trees. In Proceedings of the the 15th International Conference on Machine Learning, Madison, WI, USA, 24–27 July 1998; pp. 152–160. [Google Scholar]
  51. Crawford, S.L. Extensions to the CART Algorithm. Int. J. Man. Mach. Stud. 1989, 31, 197–217. [Google Scholar] [CrossRef]
  52. Efron, B.; Tibshirani, R. Improvements on Cross-Validation: The.632+ Bootstrap Method. J. Am. Stat. Assoc. 1997, 92, 548–560. [Google Scholar] [CrossRef]
  53. Scott, C. Tree Pruning with Subadditive Penalties. IEEE Trans. Signal Process. 2005, 53, 4518–4525. [Google Scholar] [CrossRef]
  54. García-Moratilla, S.; Martínez-Muñoz, G.; Suárez, A. Evaluation of Decision Tree Pruning with Subadditive Penalties. In Intelligent Data Engineering and Automated Learning—IDEAL 2006, Proceedings of International Conference on Intelligent Data Engineering and Automated Learning, Burgos, Spain, 20–23 September 2006; Sringer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
  55. Rissanen, J. Modeling by Shortest Data Description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
  56. Mehta, M.; Rissanen, J.; Agrawal, R. MDL-Based Decision Tree Pruning. In Proceedings of the First International Conference on Knowledge Discovery and Data Mining, Montreal, QC, Canada, 20–21 August 1995; AAAI Press: Washington, DC, USA, 1995; pp. 216–221. [Google Scholar]
  57. Sweeney, L. K-ANONYMITY: A MODEL FOR PROTECTING PRIVACY. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 2002, 10, 557–570. [Google Scholar] [CrossRef]
  58. Pantoja, D.; Rodríguez, I.; Rubio, F.; Segura, C. Complexity Analysis and Practical Resolution of the Data Classification Problem with Private Characteristics. Complex. Intell. Syst. 2025, 11, 274. [Google Scholar] [CrossRef]
  59. Patil, D.D.; Wadhai, V.M.; Gokhale, J.A. Evaluation of Decision Tree Pruning Algorithms for Complexity and Classification Accuracy. Int. J. Comput. Appl. 2010, 11, 975–8887. [Google Scholar] [CrossRef]
  60. Tsai, C.F.; Hsu, Y.F.; Lin, C.Y.; Lin, W.Y. Intrusion Detection by Machine Learning: A Review. Expert. Syst. Appl. 2009, 36, 11994–12000. [Google Scholar] [CrossRef]
  61. Buczak, A.; Guven, E. A Survey of Data Mining and Machine Learning Methods for Cyber Security Intrusion Detection. IEEE Commun. Surv. Tutor. 2016, 18, 1153–1176. [Google Scholar] [CrossRef]
  62. Mishra, P.; Varadharajan, V.; Tupakula, U.; Pilli, E.S. A Detailed Investigation and Analysis of Using Machine Learning Techniques for Intrusion Detection. IEEE Commun. Surv. Tutor. 2018, 21, 686–728. [Google Scholar] [CrossRef]
  63. Sharkey, P.; Tian, H.W.; Zhang, W.N.; Xu, S.H. Privacy-Preserving Data Mining through Knowledge Model Sharing. In Proceedings of the International Workshop on Privacy, Security, and Trust in KDD, San Jose, CA, USA, 12 August 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 97–115. [Google Scholar]
  64. Prasser, F.; Kohlmayer, F.; Kuhn, K.A. Efficient and Effective Pruning Strategies for Health Data De-Identification. BMC Med. Inform. Decis. Mak. 2016, 16, 49. [Google Scholar] [CrossRef][Green Version]
  65. Yurcik, W.; Woolam, C.; Hellings, G.; Khan, L.; Thuraisingham, B. Privacy/Analysis Tradeoffs in Sharing Anonymized Packet Traces: Single-Field Case. In Proceedings of the 2008 Third International Conference on Availability, Reliability and Security, Barcelona, Spain, 4–7 March 2008; pp. 237–244. [Google Scholar] [CrossRef]
  66. Lakkaraju, K.; Slagell, A. Evaluating the Utility of Anonymized Network Traces for Intrusion Detection. In Proceedings of the the 4th International Conference on Security and Privacy in Communication Netowrks, Istanbul, Turkey, 22–25 September 2008; ACM: New York, NY, USA, 2008; p. 17. [Google Scholar]
  67. SSH Port|SSH.COM. Available online: https://www.ssh.com/ssh/port (accessed on 8 September 2018).
  68. Zhang, J.; Borisov, N.; Yurcik, W. Outsourcing Security Analysis with Anonymized Logs. In Proceedings of the 2006 Securecomm and Workshops, Baltimore, MD, USA, 28 August–1 September 2006. [Google Scholar] [CrossRef]
  69. Coull, S.E.; Wright, C.V.; Monrose, F.; Collins, M.P.; Reiter, M.K. Inferring Sensitive Information from Anonymized Network Traces. Ndss 2007, 7, 35–47. [Google Scholar]
  70. Riboni, D.; Villani, A.; Vitali, D.; Bettini, C.; Mancini, L. V Obfuscation of Sensitive Data for Increamental Release of Network Flows. IEEE/ACM Trans. Netw. 2015, 23, 2372–2380. [Google Scholar] [CrossRef]
  71. Yurcik, W.; Woolam, C.; Hellings, G.; Khan, L.; Thuraisingham, B. SCRUB-Tcpdump: A Multi-Level Packet Anonymizer Demonstrating Privacy/Analysis Tradeoffs. In Proceedings of the 2007 Third International Conference on Security and Privacy in Communications Networks and the Workshops—SecureComm 2007, Nice, France, 17–21 September 2007; pp. 49–56. [Google Scholar] [CrossRef]
  72. Qardaji, W.; Li, N. Anonymizing Network Traces with Temporal Pseudonym Consistency. In Proceedings of the 2012 32nd International Conference on Distributed Computing Systems Workshops, Macau, China, 18–21 June 2012. [Google Scholar] [CrossRef]
  73. Xu, J.; Fan, J.; Ammar, M.H.; Moon, S.B. Prefix-Preserving IP Address Anonymization: Measurement-Based Security Evaluation and a New Cryptography-Based Scheme. In Proceedings of the 10th IEEE International Conference on Network Protocols, Paris, France, 12–15 November 2002; Volume 46, pp. 280–289. [Google Scholar] [CrossRef]
  74. Coull, S.E.; Wright, C.V.; Keromytis, A.D.; Monrose, F.; Reiter, M.K. Taming the Devil: Techniques for Evaluating Anonymized Network Data. In Proceedings of the Network and Distributed System Security Symposium, NDSS 2008, San Diego, CA, USA, 10–13 February 2008; pp. 125–135. [Google Scholar]
  75. Perona, I.; Arbelaitz, O.; Gurrutxaga, I.; Martin, J.I.; Muguerza, J.; Perez, J.M. Generation of the Database Gurekddcup. 2016. Available online: http://hdl.handle.net/10810/20608 (accessed on 3 August 2025).
  76. Perona, I.; Gurrutxaga, I.; Arbelaitz, O.; Martín, J.I.; Muguerza, J.; Ma Pérez, J. Service-Independent Payload Analysis to Improve Intrusion Detection in Network Traffic. In Proceedings of the 7th Australasian Data Mining Conference, Glenelg/Adelaide, SA, Australia, 27–28 November 2008; Volume 87, pp. 171–178. [Google Scholar]
  77. Moustafa, N.; Slay, J. UNSW-NB15: A Comprehensive Data Set for Network Intrusion Detection Systems. In Proceedings of the 2015 Military Communications and Information Systems Conference (MilCIS), Canberra, Australia, 10–12 November 2015; pp. 1–6. [Google Scholar]
  78. Ring, M.; Wunderlich, S.; Grüdl, D.; Landes, D.; Hotho, A. Flow-Based Benchmark Data Sets for Intrusion Detection. In Proceedings of the 16th European Conference on Cyber Warfare and Security, Dublin, Ireland, 29–30 June 2017; pp. 361–369. [Google Scholar]
  79. Stolfo, S.J.; Fan, W.; Lee, W.; Prodromidis, A.; Chan, P.K. Cost-Based Modeling for Fraud and Intrusion Detection: Results from the JAM Project. In Proceedings of the DARPA Information Survivability Conference and Exposition DISCEX’00, Hilton Head, SC, USA, 25–27 January 2000; IEEE Computer Society: Los Alamitos, CA, USA, 2000; Volume 2, pp. 130–144. [Google Scholar]
  80. Tavallaee, M.; Bagheri, E.; Lu, W.; Ghorbani, A.A. A Detailed Analysis of the KDD CUP 99 Data Set. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence for Security and Defense Applications, Ottawa, ON, Canada, 8–10 July 2009; pp. 1–6. [Google Scholar]
  81. Nicholas, L.; Ooi, S.Y.; Pang, Y.H.; Hwang, S.O.; Tan, S.-Y. Study of Long Short-Term Memory in Flow-Based Network Intrusion Detection System. J. Intell. Fuzzy Syst. 2018, 35, 5947–5957. [Google Scholar] [CrossRef]
  82. Bhuyan, M.H.; Bhattacharyya, D.K.; Kalita, J.K. Network Anomaly Detection: Methods, Systems and Tools. IEEE Commun. Surv. Tutor. 2014, 16, 303–336. [Google Scholar] [CrossRef]
  83. Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, QC, Canada, 20–25 August 1995; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1995; Volume 2, pp. 1137–1143. [Google Scholar]
  84. Chew, Y.J.; Lee, N.; Ooi, S.Y.; Wong, K.-S.; Pang, Y.H. Benchmarking Full Version of GureKDDCup, UNSW-NB15, and CIDDS-001 NIDS Datasets Using Rolling-Origin Resampling. Inf. Secur. J. A Glob. Perspect. 2021, 31, 544–565. [Google Scholar] [CrossRef]
  85. Ahmed, M.; Mahmood, A.N.; Hu, J. A Survey of Network Anomaly Detection Techniques. J. Netw. Comput. Appl. 2016, 60, 19–31. [Google Scholar] [CrossRef]
  86. Catania, C.A.; Garino, C.G. Automatic Network Intrusion Detection: Current Techniques and Open Issues. Comput. Electr. Eng. 2012, 38, 1062–1072. [Google Scholar] [CrossRef]
  87. Mivule, K. An Investigation Of Data Privacy And Utility Using Machine Learning As A Gauge. In Proceedings of the Doctoral Consortium, Richard Tapia Celebration of Diversity in Computing Conference, TAPIA, Seattle, WA, USA, 5–8 February 2014; Volume 3619387, pp. 17–33. [Google Scholar] [CrossRef]
  88. Mivule, K.; Turner, C. A Comparative Analysis of Data Privacy and Utility Parameter Adjustment, Using Machine Learning Classification as a Gauge. Procedia Comput. Sci. 2013, 20, 414–419. [Google Scholar] [CrossRef]
  89. Chew, Y.J.; Ooi, S.Y.; Wong, K.; Pang, Y.H.; Hwang, S.O. Evaluation of Black-Marker and Bilateral Classification with J48 Decision Tree in Anomaly Based Intrusion Detection System. J. Intell. Fuzzy Syst. 2018, 35, 5927–5937. [Google Scholar] [CrossRef]
  90. Chew, Y.J.; Ooi, S.Y.; Wong, K.; Pang, Y.H. Privacy Preserving of IP Address Through Truncation Method in Network-Based Intrusion Detection System. In Proceedings of the 2019 8th International Conference on Software and Computer Application, Penang, Malaysia, 19–21 February 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Analogical Reasoning with Multimodal Knowledge Graphs: Fine-Tuning Model Performance Based on LoRA
Previous
Enhancing Real-Time Anomaly Detection of Multivariate Time Series Data via Adversarial Autoencoder and Principal Components Analysis
Next