Abstract
Modern electronic information system software is becoming increasingly complex, making manual debugging prohibitively expensive and necessitating automated fault localization (FL) methods to prioritize suspicious code segments. While Single-Fault Localization (SFL) methods, such as spectrum-based fault localization (SBFL) and Deep Learning-Based Fault Localization (DLFL), have demonstrated promising results in localizing individual faults, extending these methods to multiple-fault scenarios remains challenging. Deep Learning–Based Fault Localization (DLFL) methods combine metamorphic testing and clustering to locate multiple faults without relying on test oracles. However, these approaches suffer from a severe class imbalance problem: the number of failed cases (the minority class) is far smaller than that of passed cases (the majority class). To address this issue, we propose MetaGAN: Metamorphic GAN-based Augmentation for Improving Deep Learning-based Multiple-Fault Localization Without Test Oracles. MetaGAN is a novel method that integrates Metamorphic Testing (MT), clustering-based fault isolation, and Generative Adversarial Networks (GANs). The method first utilizes MT to gather information from failed Metamorphic Test Groups (MTGs) and extracts metamorphic features that capture the underlying failure causes to represent each failed MTG; then, these features are used to cluster the failed MTGs into several groups, with each group forming an independent single-fault debugging session; finally, in each session, data augmentation is performed by combining MT with a GAN model to generate failed test cases (the minority class) until their number matches that of passed test cases (the majority class), thereby balancing the dataset for precise DLFL-based fault localization and enabling parallel debugging of multiple faults. Extensive experimental validation on an expanded open-source benchmark shows that, compared with the baseline MetaMDFL, MetaGAN significantly improves fault localization accuracy, particularly in parallel multiple-fault scenarios. Specifically, MetaGAN achieves significant improvements in both the EXAM and the rank metrics, with EXAM showing the highest improvement of , the rank showing the highest improvement of , and the top- showing the highest improvement of . This method, through coordinated dynamic feature extraction, adaptive data augmentation, and distributed collaborative debugging, provides a scalable solution for complex systems where test oracles are unavailable, thereby advancing state-of-the-art methods.
1. Introduction
With the rapid evolution and widespread adoption of electronic information systems, coupled with continuous technological innovations and the deepening digital transformation, the scale and functional integration of modern software systems are growing exponentially. Modern systems now exhibit significantly higher complexity and interactivity compared to earlier generations. In the context of digital transformation and information-driven modernization, traditional manual debugging methods, which require substantial time and effort, impose a considerable human resource burden during development and maintenance [1,2,3,4]. Moreover, these labor-intensive methods are prone to human errors, potentially triggering secondary faults, and are increasingly inadequate for the rapid iterative demands of contemporary software engineering. To address these challenges, an effective method is the adoption of automated fault localization methods. These methods conduct a detailed suspiciousness assessment of each erroneous statement to swiftly pinpoint potential fault locations, thereby guiding developers to prioritize the inspection of code regions most likely to harbor faults, resulting in more efficient debugging. Additionally, this method not only streamlines the error detection process and reduces redundant labor but also provides robust support for overall software quality enhancement, significantly improving system stability and reliability.
In the field of Single-Fault Localization (SFL) [5], the academic community has established a comprehensive theoretical method and technical infrastructure. Classical studies focus on the benchmark problem of faults caused by a single program entity. In this context, Spectrum-Based Fault Localization (SBFL) methods [6,7,8] devise probabilistic association models between statement coverage and test outcomes, whereas emerging Deep Learning-based Fault Localization (DLFL) [9,10,11] methods leverage neural network architectures such as LSTM and Transformer to extract deep semantic features from execution traces. These SFL methods primarily rely on collected runtime data (e.g., code coverage) and test results (passed/fail) to explore the correlation between statement execution and program failures. Fundamentally, both methodologies are rooted in dynamic program analysis. By constructing a coverage matrix that shows whether a statement is executed or not executed and combining it with a Boolean vector of test outcomes, they compute a suspiciousness score for each statement using statistical learning or deep representation methods. Particularly, if the coverage status of a statement is perfectly correlated with test outcomes, i.e., it is always executed when tests fail and not executed when tests pass, it is assigned a high fault suspiciousness score, which forms the formal theoretical basis for fault localization methods.
In complex systems containing multiple faults, Multiple-Fault Localization (MFL) faces significant technical challenges due to fault interaction effects. When there are multiple coupled faults, traditional sequential localization methods exhibit high time complexity [12]. In contrast, MFL methods based on parallel debugging paradigms effectively reduce this complexity by leveraging the orthogonal decomposition of test cases [13,14,15]. The core innovation lies in the development of a fault cluster identification model: first, a spectral clustering algorithm partitions failed test cases into mutually exclusive subsets, each corresponding to an independent fault mode; subsequently, distributed SFL computations enable development teams to concurrently process multiple fault suspiciousness ranking lists.
This collaborative mechanism offers dual advantages. First, by decoupling the fault space, it minimizes interference during the localization process. Empirical data demonstrate a significant reduction in false positive rates within projects [16]. Second, by employing a dynamic priority scheduling algorithm that assigns high-frequency covered code entities to experienced developers, the average fault repair time is substantially shortened. Moreover, this method not only enhances the efficiency of debugging but also improves overall system reliability and maintainability by optimizing resource allocation and reducing redundant iterations. In benchmark tests, traditional sequential methods often require more than ten iterations of SFL to achieve comparable coverage, while the parallel method completes the complete fault localization in just a few iterations [17]. These advancements underscore the potential of parallel MFL methods to revolutionize fault localization in complex, multiple fault environments, paving the way for more robust and efficient software maintenance practices.
Since clustering methods play a pivotal role in this method [13], this study adopts a multiple-fault localization method that supports parallel debugging, which we refer to as Cluster-Based Multiple-Fault Localization (CBMFL), the primary focus of our research. It is important to note that the term CBMFL specifically denotes this concrete implementation of MFL, while MFL, in a broader sense, describes the overall task or process of locating multiple faults. By leveraging clustering, our method efficiently partitions failed test cases into distinct fault clusters, thereby decomposing the complex multiple-fault localization challenge into several independent subtasks, enabling both parallelization and automation in the debugging process.
Based on the analysis above, it is evident that both the Cluster-Based Multiple-Fault Localization (CBMFL) and Single-Fault Localization (SFL) methods fundamentally rely on test outcome information, specifically, distinguishing between success and failure based on test case execution results. In practice, a test case is considered to have passed only when the program executes correctly and its output meets the predefined expected criteria (i.e., the test oracle); otherwise, it is marked as a failure. Thus, the test oracle serves as a critical prerequisite for the proper functioning of both CBMFL and SFL methods. However, the test oracle problem is pervasive in real-world applications, which means that in many cases, an appropriate test oracle is either unavailable or prohibitively expensive to construct [15]. This reality not only significantly hinders the adoption of conventional SFL and CBMFL methods but also adversely affects the efficiency and accuracy of fault localization in practical software engineering contexts [16,17]. Consequently, the development of novel methods that reduce dependence on traditional test oracles has emerged as a key research direction to improve fault localization performance.
Interestingly, we can adopt an innovative method known as Metamorphic Testing (MT) [18] to tackle the challenges posed by the test oracle problem in software testing. The essence of MT lies in abandoning traditional value comparison methods and instead evaluating program correctness by verifying logical expressions. For example, with the trigonometric function sin(x), one can ingeniously validate its implementation by confirming that sin(3) + sin(−3) equals zero, rather than comparing the output of sin(3) to a specific numerical value (e.g., 0.141120008059). This novel method offers a completely new testing paradigm that enables effective program evaluation even in the absence of a traditional test oracle by identifying invariant properties of the program and formulating the corresponding propositional expressions. Extensive empirical evidence has demonstrated the outstanding capability of MT in addressing the oracle problem, and it has been successfully applied across various related fields, including Single-Fault Localization (SFL). These successful implementations provide valuable insights, suggesting that similar methods can be employed to further extend and enhance Cluster-Based Multiple-Fault Localization (CBMFL), e.g., the current best performance method for CBMFL is MetaMDFL [11], which stands for Metamorphic Multiple Deep Learning-based Fault Localization. This localization method utilizes transformational testing to extend CBMFL to scenarios without test oracles. Specifically, MetaMDFL uses metamorphic test groups (MTGs) as the minimum unit for testing. It defines the transformational characteristics that represent the violation of transformational relationships. In this way, CBMFL can perform clustering to support parallel debugging, thereby achieving MetaMDFL without the need to test oracles.
However, during practical deployment, MetaMDFL [11] has encountered significant challenges due to severe class imbalance. Specifically, the number of passed test cases far exceeds that of failed ones, resulting in an imbalanced dataset. This disparity leads the deep learning model to favor predicting the ”passed” category, thereby diminishing the accuracy of statement suspiciousness evaluations. Metamorphic Testing (MT) categorizes test cases into two groups based on whether they satisfy the metamorphic relations (MRs). In real-world testing environments, test cases that meet the MRs overwhelmingly outnumber those that do not, creating a highly skewed data distribution. This imbalance causes the MetaMDFL model to lean toward the majority class (i.e., MR satisfying samples), ultimately reducing both the precision and reliability of fault localization. To address this issue, researchers have explored various data augmentation methods [19,20,21] aimed at mitigating class imbalance by generating synthetic samples. Nevertheless, another challenge lies in producing a sufficient number of ”failed” samples to balance the distribution, as failed test cases are typically scarce and irregularly distributed. Therefore, developing effective solutions to tackle dataset imbalance is crucial for enhancing the overall efficacy of the MetaMDFL method.
To address this issue, we introduce Generative Adversarial Networks (GANs) as an innovative data augmentation method to mitigate the scarcity of failed test cases. By employing an adversarial training mechanism, GANs establish a competitive method between a generator and a discriminator, learning the distribution characteristics from the original failed test cases and producing a large number of synthetic samples that closely resemble them. This process effectively increases the proportion of failed labels within the dataset, thereby balancing the class distribution. Adopting this method not only alleviates the negative impact of data imbalance on the performance evaluation of MetaMDFL—significantly enhancing fault localization accuracy and robustness—but also enriches the diversity of training data, bolstering the deep learning model’s ability to detect anomalous patterns. Moreover, the incorporation of GANs offers new insights into our research, inspiring further exploration of generative models to optimize software testing and fault-localization methods.
Therefore, we propose MetaGAN: Metamorphic GAN-based Augmentation for Improving Multiple Deep Learning-based Fault Localization Without Test Oracles. The core idea behind MetaGAN is to leverage a powerful and widely adopted GAN model [22] to generate additional failed samples, thereby constructing a balanced dataset that enhances the efficiency of MetaMDFL fault localization. This novel method integrates metamorphic testing, clustering algorithms, and GAN to extend multiple-fault localization to scenarios where test oracles are unavailable. Specifically, failed Metamorphic Test Groups (MTGs) are first obtained via metamorphic testing, from which metamorphic features that capture the underlying fault causes are extracted. These features are then used to cluster the MTGs into several groups, with each cluster representing an independent single-fault debugging activity. Finally, within each debugging activity, data augmentation is performed by combining Metamorphic Testing (MT) with the GAN model to generate additional failed test cases (i.e., the minority class) until their number matches that of the non-failed test cases (i.e., the majority class). This balanced dataset enables accurate fault localization and facilitates the parallel debugging of multiple faults.
To evaluate our method, we expanded the original MT dataset [23] by generating multiple fault versions from the seed faults in all seven subject programs. We then compared the multiple-fault localization performance of MetaGAN with that of MetaMDFL, and the experimental results demonstrate that MetaGAN significantly improves the performance of MetaMDFL (i.e., MDFL without test oracles).
The main contributions of this study are as follows:
(1) We propose a general method, MetaGAN, which integrates metamorphic testing, clustering, and GAN to extend multiple-fault localization to scenarios where test oracles are unavailable.
(2) We introduce a novel hybrid method in the multiple-fault localization domain to address the class imbalance issue in fault data.
(3) We design and implement a concrete method based on this method and conduct experiments on a dataset comprising seven programs to evaluate its effectiveness in mitigating class imbalance, thereby enabling more efficient application environments without test oracles.
(4) We open-sourced the relevant self-constructed benchmark (https://drive.google.com/drive/folders/16nVOebeoJNe-xC1Txy-tLINnOlo4PsOF (accessed on 6 May 2025)) to enable subsequent researchers to build upon this work for further research endeavors.
The remainder of this paper is organized as follows: Section 2 presents the background and related work, including clustering-based multiple-fault localization, metamorphic testing, and generative adversarial networks. Section 3 details the core components and workflow of the MetaGAN method. In Section 4, we describe the experimental design, covering the research questions, datasets, independent variables, evaluation metrics, and the experimental environment and tools. Section 5 analyzes and discusses the experimental results, comparing them with the original MetaMDFL. Section 6 discusses issues such as internal and external threats, generation strategies, and defect data during the research process. Finally, Section 7 concludes the study.
Through this work, we aim to offer a novel solution for fault localization, particularly in multiple-fault scenarios characterized by the absence of test oracles and data imbalance that significantly enhances the efficiency and accuracy of fault localization.
2. Background and Related Works
2.1. Clustering-Based Multiple-Fault Localization
To support a parallel debugging paradigm for multiple developer collaboration, CBMFL achieves distributed fault localization by clustering failed test cases [13]. The core mechanism of this method lies in the intelligent clustering of failed test cases to form fault clusters that share semantic consistency. Theoretically, each cluster should comprise failed test cases triggered by the same fault, while different clusters correspond to independent faults. Under ideal conditions, each developer is assigned a composite test suite that combines a specific fault cluster with all passed test cases , allowing them to focus on diagnosing and repairing the unique fault within that cluster. This optimized configuration is theoretically capable of linear acceleration in fault repair, significantly enhancing parallel debugging efficiency (see Figure 1).
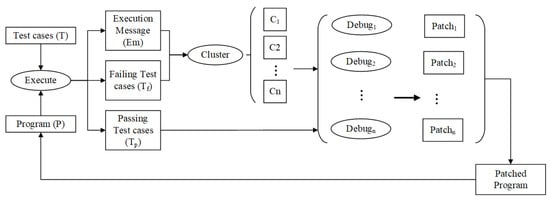
Figure 1.
Workflow of clustering-based multiple-fault localization.
The innovation of CBMFL is evident in its ability to localize all faults in a single iteration. By isolating interference from unrelated tests, it dramatically boosts developer diagnostic efficiency. The implementation process can be divided into four stages:
- Test Execution Stage: Execute the complete test suite on the program P to generate the passed test cases set and the failed test cases set , while recording execution traces (e.g., branch coverage or method call graphs).
- Intelligent Clustering Stage: Based on the execution characteristics of failed test cases, apply a specific clustering algorithm to generate fault-centric clusters .
- Test Suite Construction Stage: Combine each cluster with the passed test cases to construct a targeted diagnostic suite .
- Parallel Repair Stage: Developers perform concurrent debugging using the tailored suite , generating the corresponding patches .
As illustrated in the accompanying diagram, this hierarchical processing mechanism effectively decouples the fault space and enables parallel repair, significantly improving overall debugging efficiency.
In the following sections, we outline several key aspects of CBMFL: the representation of failed test cases, clustering, and parallel debugging.
In the task of clustering failed test cases, the choice of the representation model directly impacts the effectiveness of the distance metric between samples. Two technical methods are available: one can either adopt conventional geometric distance metrics (e.g., Euclidean distance), which requires numerically encoding the test cases (e.g., via vector space mapping), or develop a domain-specific similarity measurement algorithm. Regardless of the chosen method, an ideal representation model should exhibit fault-sensitive properties, that is, it must accurately capture the fundamental causes of test case failures. This property ensures that failed test cases triggered by the same fault cluster closely in the feature space, thus increasing the probability that the clustering algorithm will group test cases with similar fault origins into the same cluster. Empirical studies using program coverage features have validated this theory: When employing coverage information vectors along with Euclidean distance metrics, the model’s effectiveness derives from its ability to capture the coverage characteristics of fault-related code paths [13]. The underlying assumption of this representation method is that test cases triggering the same fault will inherently share similar code execution trajectories, which are effectively mapped into a vector space through coverage feature encoding. Within this method, the discriminative power of the representation model directly determines how well the clustering results align with the true distribution of faults.
In a fault localization method, the clustering engine based on a representation model partitions failed test cases into clusters that exhibit semantic consistency by mapping to a feature space. Ideally, such clusters should satisfy the single-fault isolation criterion, meaning that all test cases within each cluster are triggered by the same fault, while different clusters correspond to distinct fault origins; hence, these clusters are often defined as fault-centric clusters. Theoretically, any clustering architecture based on distance metrics can achieve this function. However, for algorithms that require prior parameter input (such as key parameter configuration methods), it is necessary to develop auxiliary statistical inference methods to estimate the number of faults in a multiple-fault program. Taking K-means clustering as an example, the initialization of its core parameter K can be informed by analyzing the characteristics of the fault distribution [24]. By constructing a Bayesian estimation model using indicators such as the test failure rate, one can infer the potential number of faults that will serve as the basis for parameter initialization. This method transforms empirical parameter selection into a statistical inference process based on runtime characteristics, thereby significantly enhancing the alignment between the clustering results and the actual distribution of faults.
After the fault clusters are established, the system implements a developer resource allocation method that generates a diagnostic isolated test suite for each developer. This suite is composed of a fault-associated cluster (comprising failed test cases of common origin) combined with the complete set of passed test cases, thereby creating a customized diagnostic environment. Based on this allocation mechanism, the development team can initiate a multi-threaded, parallel debugging workflow. Specifically, within their dedicated diagnostic environment, developers perform the following steps: (1) Feature Spectrum Analysis: Using SFL methods, conduct a feature spectrum analysis on the targeted test suite to generate quantifiable suspiciousness metrics for program entities. (2) Causal Validation: Rank code statements in descending order by suspiciousness and carry out step-by-step causal verification. (3) Patch Generation: Upon isolating the faulty code segment, generate a targeted repair patch. Once all concurrent diagnostic tasks are completed, the system integrates individual repair solutions into a unified code base through a patch fusion engine. In the final phase, a comprehensive regression test is executed by rerunning the entire test suite on the refactored version of the program. If all test cases are passed, the debugging cycle is considered complete; if any faults persist, a new iteration is triggered. This closed-loop verification mechanism effectively ensures the integrity and consistency of multiple fault repairs, with its technical advantages demonstrated in two key aspects: (1) isolating diagnostic environments prevents interference among parallel repairs; and (2) employing full regression testing as a convergence criterion guarantees the completeness of the iterative process.
2.2. Metamorphic Testing
Metamorphic Testing (MT) was originally developed to address the urgent need to overcome the test oracle problem in software verification. With the establishment of a theoretical method for method transferability, researchers discovered that its core mechanisms exhibit remarkable cross-domain adaptability. This insight has driven the successful adoption and integration of MT in heterogeneous fields, as demonstrated in [10,25,26]. Building on the foundational discussions from the previous section, this part establishes a multidimensional analytical method by formally defining key components, including metamorphic relations, source test case generators, and derived constraints, and by developing a standardized terminology system (e.g., metamorphic coverage). This rigorous mathematical foundation supports the subsequent construction of the fault localization model. Such systematic deconstruction not only deepens the theoretical underpinnings of MT but also enhances its engineering applicability in intelligent software engineering through a standardized conceptual method.
Metamorphic Testing (MT) is a complementary testing methodology whose core objective aligns with that of conventional testing, namely, to verify the functional correctness of the target program over a specified input space. The essential difference lies in the validation mechanism: traditional methods rely on explicit test oracles to determine output correctness, whereas MT employs Metamorphic Relations (MRs) to achieve implicit verification. An MR, which represents an invariant property of the program’s functional specification, can be formalized as a logical expression that involves both input and output variables. Each instance of an MR forms an ordered testing tuple, where test cases are causally linked according to their roles within the relation. Specifically, when certain test slots (i.e., input parameter domains) are populated by existing test cases referred to as source test cases, the remaining slots can be parameterized through constraint propagation and degrees-of-freedom analysis to generate follow-up test cases. The complete MT execution process comprises three phases: (1) Formalization Phase: Extract a key set of MRs through program specification analysis. (2) Generation Phase: Generate follow-up test cases based on the source test cases by applying constraint solving or symbolic execution methods. (3) Verification Phase: Construct Metamorphic Test Groups (MTGs) and verify that the MRs are upheld in the program’s execution traces. The theoretical advantages of this method are twofold: (1) it circumvents the difficulties of directly constructing test oracles by relying on invariant verification, and (2) it leverages the intrinsic interrelations among test cases to enable combinatorial error detection, thereby significantly enhancing test coverage.
In this article, the minimum testing granularity is the Transformation Test Group (MTG). For any line of statements, as long as at least one test case in the MTG covers it, it is considered to be covered. Therefore, = [there is a test case in the i-th MTG that covers the j-th line of the statement]. The correctness of the program is recorded by violating vectors. This article uses 1 to represent a violation and 0 to represent a non-violation. The violation status of all m MTGs constitutes the violation vector y, where = [the i-th MTG violates its metamorphosis relationship], as shown in Figure 2.

Figure 2.
Coverage matrix (training samples) and violation vector (training labels).
Within an empirical software verification method, this study targets the numerical computation function and addresses a typical scenario in which the expected result for is difficult to verify directly due to floating point precision limitations. We propose a Metamorphic Relation (MR)-based testing method with the following implementation path: First, we construct an MR grounded in the algebraic homomorphism property of the square root function, formalized as the invariant . Next, a ternary test group is formed by selecting as the baseline input (a), using a pseudo-random sampling method to choose , and determining the subsequent input c via the product constraint . Executing the test group yields the output vector . We then indirectly validate the outputs by verifying the numerical equivalence of and . This results in a metamorphic test group (MTG) consisting of three test cases that are executed using the program, with the outputs substituted into the MR to check whether equals . If the expression holds, the program passes the test; otherwise, it fails. This method effectively circumvents the conventional oracle problem. Experimental results demonstrate that the proposed method can detect typical faults, such as floating point truncation errors and errors in iterative convergence conditions [10].
2.3. Generative Adversarial Network
Generative Adversarial Networks (GANs) [22] are deep learning architectures based on adversarial training with two core components, namely, a generator (G) and a discriminator (D), as illustrated in Figure 3. The generator produces synthetic data from a latent variable z, while the discriminator assesses the probability that a given input originates from the true data distribution rather than from G. These two networks are jointly optimized through a min–max game: the generator aims to minimize the distinguishability between its outputs and real data, whereas the discriminator strives to maximize its accuracy in differentiating the two. During training, a significant drop in the generator’s loss indicates that the synthetic data is converging towards the real distribution, while an increase in the discriminator’s loss reflects greater confusion between the generated and real data in the feature space. Ultimately, this adversarial mechanism drives the generated data to statistically align with the true distribution. Figure 4 is a detailed architecture diagram of the generator and discriminator of GAN, showing the size of each layer and clearly illustrating the process of the coverage matrix changing from input to output.
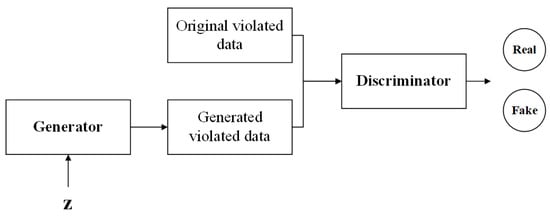
Figure 3.
Architecture of a GAN.
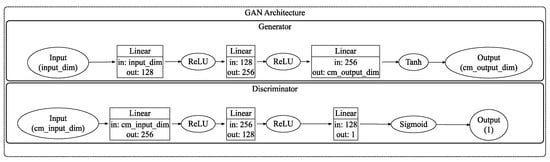
Figure 4.
The generator and discriminator architecture of a GAN.
In the adversarial training mechanism of GANs, the discriminator D performs the binary classification task by optimizing the value function V(G, D). This function is constructed based on the following principle: for real data samples, D(x) should output values close to 1, whereas for synthetic samples produced by the generator G(z), D(G(z)) should approach 0—a behavior enforced by the log(1 − D(G(z))) term in the loss function. In contrast, the generator G adjusts its parameters via backpropagation to compel D(G(z)) to converge toward 1. This bidirectional optimization creates a classic min–max game: D strives to maximize V(G, D) to strengthen its discrimination capability, while G minimizes the same function to enhance the quality of its generated outputs. Ultimately, this dynamic interplay in the parameter space converges to a Nash equilibrium, where the generated data distribution becomes statistically indistinguishable from the real data distribution.
Existing research [27,28,29] has demonstrated that class imbalance in datasets adversely affects the effectiveness of Fault Localization (FL), making it imperative to address this issue. One of the key advantages of Generative Adversarial Networks (GANs) is their ability to generate data that closely mimics real-world distributions. This capability has led to numerous applications in practice, such as image, text, and audio synthesis. Drawing on this strength, our study leverages GANs to synthesize the minority class of failed test cases, thereby creating a balanced dataset that mitigates the impact of class imbalance on FL.
2.4. Related Works
In this section, we have listed some relevant studies on MFL and provided references for readers interested in more details.
In terms of clustering methods, this article adopts the Jones2 algorithm, which is a distance-based clustering method. In addition, attention has also been paid to some clustering methods, such as FATOC [30], which is a density-based clustering algorithm, and MSeer [31], which is a parallel multiple-fault locator. Due to the fact that MSeer and FATOC have an oracle scenario design, while our MetaGAN and MetaMDFL do not have an oracle scenario design, they are two different types of problems. Furthermore, clustering methods are not the focus of this article’s discussion. Therefore, currently, MSeer and FATOC tools have not been added to the comparison. However, in future research, we will take this into consideration.
3. Materials and Methods
In this study, we introduce the MetaGAN method, which extends multiple-fault localization to complex scenarios lacking test oracles by establishing a semantically constrained dynamic verification mechanism. The method features a modular architecture with a core workflow comprising three coordinated stages: first, a metamorphic relation-driven test case evolution model is developed to generate fault sensitive follow up test sets via input transformation rules; second, a latent semantic analysis based fault decoupling module is constructed to automatically partition fault clusters and prioritize them; and finally, an adaptive scheduling method is integrated to dynamically optimize the fault localization process. Additionally, the method includes specially designed pluggable components, such as a metamorphic relation generator, clustering algorithm interfaces, and a suspiciousness calculation engine that support the configuration of various technical baselines to form specific implementation solutions for our experiments.
3.1. Components
In Figure 5, the interchangeable components within the method include EXTRACT, DIST, CLUSTER, and MetaDLFL. Any component that conforms to the required interface can be integrated into the MetaGAN method. For EXTRACT, DIST, and CLUSTER, this paper opts to reuse existing methods from the naive CBMFL method. In the following, we describe the basic configuration of these components as used in our experiments.
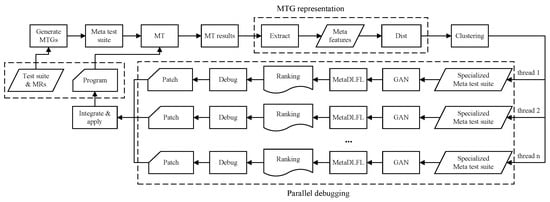
Figure 5.
Workflow of MetaGAN.
In this study, coverage information is employed as the metamorphic feature, thereby allowing the reuse of the coverage-based distance metric commonly used in naive CBMFL. The current coverage-based distance metric represents an individual failed test case as a coverage vector , where indicates whether covers . We define the EXTRACT process as collecting coverage information from each test case within an MTG and then aggregating them via a union operation to obtain a single coverage vector, which serves as the metamorphic feature of the MTG.
Regarding DIST and CLUSTER, this paper reuses the methods proposed by James A. Jones et al. in [13]. In that study, DIST comprises the numerical distance metric and a numerical encoding algorithm, ENCODE. To capture the cause of failure, for any failure unit, whether a test case in conventional testing or an MTG in metamorphic testing, ENCODE applies a single-fault localization tool to its coverage vector and then selects the most suspicious set of statements from the resulting ranking as the encoding for that failure unit. Thereafter, uses the Jaccard similarity measure to compute the distance between any two sets, thereby quantifying the differences between failure units. Finally, CLUSTER connects those failure units that are sufficiently similar in terms of Jaccard similarity, forming several connected components. Each connected component comprises fault units that are interconnected, and these components collectively form the clustering results.
The MetaDLFL component is responsible for performing single-fault localization on the metamorphic test suite. As illustrated in Figure 5, the underlying fault localization tasks within this method are ultimately executed by DLFL.
3.2. Workflow
As depicted in Figure 5, the MetaGAN workflow is designed as an iterative process. We begin with a program that contains multiple faults and, by applying clustering and failure data augmentation, we repeatedly localize and repair a set of faults until the program ultimately passes metamorphic testing. In the following, we decompose this workflow into several stages and provide a formal description of each phase. It is important to note that this subsection focuses solely on the overall MetaGAN method, while the specific methods used for each variable component are detailed in Section 4 of our experiments.
(1) Construction of the Metamorphic Test Case Suite: The data inputs provided consist of a subject program containing multiple faults, a set of test cases without a test oracle, and several metamorphic relations defined according to the program’s functionality. However, for the sake of simplicity, we will assume that only a single default metamorphic relation exists.
The program under test consists of lines of code, denoted as . Initially, the program contains faults, represented as , where the i-th fault is associated with statement . The original test suite T is composed of test cases, defined as .
The primary task during the preparation phase is to construct a metamorphic test case suite for subsequent metamorphic testing. In this phase, we first select test cases from T based on the definition of metamorphic relations to form partial metamorphic test groups (MTGs) that contain only source test cases. Next, follow-up test cases are generated for these partial MTGs to complete them into full MTGs. Consequently, we obtain a metamorphic test case suite composed of MTGs, where and each MTG consists of a set of source test cases and follow-up test cases, i.e., .
(2) Metamorphic Testing: In scenarios where test oracles are available, every test case is paired with a corresponding expected outcome. Thus, after conventional testing, each test case produces a test result that indicates whether the program’s output meets the expected outcome, i.e., , where signifies that the program fails on the test case .
In scenarios where test cases are insufficient, metamorphic testing is employed to obtain equivalent test outcomes. For each metamorphic test group (MTG) , the process begins by executing all the test cases contained in on the program under test and collecting their outputs. These inputs and outputs are then substituted into the metamorphic relation to verify its validity. If the metamorphic relation holds, the test outcome for is recorded as satisfying the relation; otherwise, it is noted as violating the metamorphic relation. Consequently, metamorphic testing produces a set of test results , where indicates that violates its corresponding metamorphic relation.
(3) Failure MTG characterization: Metamorphic testing results merely indicate which test cases require clustering. To effectively cluster failed Metamorphic Test Groups (MTGs), it is essential to obtain information regarding the causes of these failures. Therefore, specific processing is necessary to extract features from each MTG that contain such information. Hereafter, we will refer to this processing as EXTRACT, and the features extracted from MTGs as metamorphic features .
In order to effectively cluster failed Metamorphic Test Groups (MTGs), it is necessary to obtain information regarding the causes of their failures in addition to the metamorphic test results that indicate which test cases require clustering. Therefore, a specific process, referred to as EXTRACT, is implemented to extract features containing such information from each MTG. These extracted features are termed metamorphic features . To perform clustering using these metamorphic features, an algorithm, DIST, must be defined to quantify the differences between them. For any pair of metamorphic features (, ), this algorithm calculates the distance d between them, reflecting the extent of their differences in terms of failure causes.
In addition to designing a custom distance algorithm for metamorphic features, an alternative method is to leverage an existing numerical distance metric, , in conjunction with an encoding algorithm, ENCODE, which converts metamorphic features into numerical form.
The encoding algorithm, ENCODE, must transform metamorphic features into a standard numerical format that meets the parameter requirements of , while preserving the failure cause information inherent in these features. Conversely, the numerical distance metric, , should extract the stored failure cause information from the encoded data and use it to quantify the differences between two MTGs.
(4) Failure MTG Clustering: Next, leveraging the previously defined distance metric, the clustering algorithm CLUSTER groups the failed MTGs (i.e., ) based on their metamorphic features, yielding clusters, denoted as , such that each cluster contains only MTGs with similar failure causes.
(5) Violation of Dataset Augmentation Using the GAN Model: Subsequently, for each cluster , an adversarial network is integrated within the GAN model to augment the failed metamorphic test data. Specifically, the generator G produces synthetic data for failed MTGs by sampling from a latent variable z, while the discriminator D evaluates the probability that the input data originates from the true distribution of failed data rather than from the generated output. Figure 6 shows the loss curves of the generator and discriminator during GAN training on some datasets. This curve is used as a criterion for stopping training when it is relatively stable and smooth, that is, reaching the Nash equilibrium state. A low loss for the generator indicates that the synthesized fault data is nearly identical to the real fault data. The original failed MTGs, the generated failed MTGs, and all passed MTGs are then merged to form an independent metamorphic test suite . Finally, these independent metamorphic test suites are distributed to developers to initiate parallel debugging.
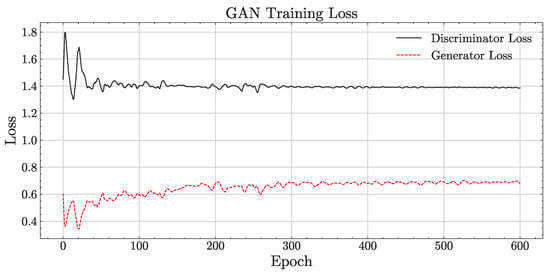
Figure 6.
GAN training loss.
(6) Parallel Debugging: In the parallel debugging phase, clustering is first performed and then divided into clusters, with each cluster having a type of fault. Then, multiple developers can each be responsible for debugging a type of fault simultaneously. In this way, each developer will only be responsible for one fault and will only locate and fix that fault. At the onset of each single-fault localization and repair process, the developer employs the metamorphic testing-based single-fault localization tool, METASFL, on the given independent test suite to perform fault localization and compute a suspiciousness ranking of program statements.
In this ranking, the statements most likely to contain faults are prioritized at the top. Consequently, developers sequentially inspect the statements according to their suspiciousness scores, and upon identifying a fault, they debug the program and develop a patch to rectify it.
Parallel debugging can demonstrate its highest efficiency, as all faults can be located in just one iteration, and the debugging efficiency of each developer is also improved by not being affected by other irrelevant faults. Sequential debugging is inefficient, as each developer arranges debugging in order.
(7) Fix Patch Integration: Finally, these patches are uniformly applied to the source code of the program under test. After this round of parallel debugging iterations, the total number of faults localized and fixed, denoted as , will lie within the range . A lower bound of 1 is achieved when all developers fix the same fault, while an upper bound of is reached when a sufficient number of developers address different faults. If the program still fails certain MTGs during regression metamorphic testing after these fixes, a new round of parallel debugging iterations will be initiated to repair the remaining faults, i.e., . Thus, the number of iterations required to fix all faults is at least 1 and at most .
4. Experimental Design
In this section, we first clearly define the core research problem. Subsequently, we provide an in-depth description of the benchmark datasets that underpin our experiments, serving as the foundation for ensuring both reproducibility and comparability. Next, we systematically enumerate all the independent variables involved in the controlled experiments, thereby establishing a clear method for our experimental design. Concurrently, we present a diverse array of metrics for evaluating the experimental outcomes to guarantee a comprehensive and accurate assessment. Furthermore, we detail the specific implementations of the various artifacts involved in the experiments, as well as the environmental conditions required for their execution. Finally, we discuss potential threats from multiple dimensions and conduct rigorous empirical studies on the validity of the experiments, thereby ensuring the reliability and scientific rigor of our research conclusions.
4.1. Research Questions
For this study, we investigate the following research questions.
(1) RQ1: How effective is our method, MetaGAN, in mitigating the oracle problem?
(2) RQ2: How effective is our method, MetaGAN, in addressing imbalanced violations of data categories?
(3) RQ3: How effective is MetaGAN on different fault programs?
4.2. Benchmark
To rigorously evaluate the effectiveness of fault localization methods and validate their efficacy, it is crucial to conduct experiments on specific fault datasets. In fault localization research, publicly available datasets such as SIR [32] (mainly for C/C++ programs) are widely adopted due to their comprehensiveness and standardization. These datasets not only include the subject programs’ source code, fault variants, and test suites, but they also sometimes provide auxiliary tools and scripts, significantly facilitating research efforts. However, since our study employs metamorphic testing as a specialized method, it is necessary to carefully define metamorphic relations for each subject program based on these datasets. Unfortunately, current public datasets do not encompass this critical element; therefore, as is common in metamorphic testing research, constructing our own dataset becomes an inevitable choice to ensure the accuracy and effectiveness of our experiments.
We adopt the method outlined in MetaDLFL [10] to construct the MT dataset, which comprises seven subject programs, each featuring three Metamorphic Relations (MRs) and various single-line faults. Table 1 presents the number of executable Lines Of Code (eLOC), fault versions, MRs, and test cases for each program. For most programs, previously published studies have defined the metamorphic relations, which we directly reuse; for the remaining programs, we follow standard practices in metamorphic testing research by analyzing the program functionalities and selecting several testable properties as the metamorphic relations. Ultimately, for each subject program, we select three metamorphic relations, as detailed in Table 2. These metamorphic relations generate follow-up test cases by transforming the inputs of source test cases, and the transformations, along with the corresponding outputs, are used to assess whether the metamorphic relations are violated. Specifically, for programs such as grep and sed, our focus is on testing their common regular expression functionalities, hence the chosen metamorphic relations are related to regular expressions; for string matching programs like SeqMap, the metamorphic relations primarily concern string transformations; for algorithm implementations such as ShortestPath and PrimeCount, we extract inherent algorithmic properties as the metamorphic relations; and for calculator programs like clac and quich, we select the equivalence of mathematical expressions as the metamorphic relation.

Table 1.
Subject programs.

Table 2.
Metamorphic Relations (MRs) for different programs.
Another crucial aspect is the generation of fault mutants. Our method involves first using a mutation tool to generate single-fault mutants and then randomly selecting and combining these mutants to produce multiple fault mutants. The generation of single-fault mutants is automated using the Mutate++ [11] tool, which produces compilable and executable mutants. As shown in Table 3, our study utilizes 11 mutation operators.

Table 3.
List of mutation types.
For multiple fault mutant generation, we follow the experimental methodology established in related multiple-fault localization research [11]. In this study, we limit the number of mutants of faults to contain at most four faults. This constraint ensures that a sufficient number of multiple fault mutants with the maximum fault count can be generated during the experiments, while also keeping the experiment duration within reasonable limits. When multiple fault mutants with a specific fault count are abundant, the experimental outcomes are stable and credible. In summary, after setting the maximum fault limit to four, we generate at least 60 multiple fault mutants for each subject program, and each fault counts at least twice the volume used in related research to ensure comparable persuasiveness. Subsequently, it is necessary to derive multiple fault mutants with fewer faults from existing multiple fault mutants to ensure that all potential mutants arising during the multiple-fault localization process are represented in the dataset. If the number of mutants for a specific fault count remains insufficient, additional mutants are generated for that fault count using the aforementioned random sampling method for four fault mutants. In essence, employing these two methods, we have generated a sufficient number of multiple fault mutants for each subject program and each fault count, as detailed in Table 1.
4.3. Independent Variables
Below, we list all the independent variables involved in our study. In terms of algorithms, we investigate three aspects: the single-fault localization method embedded within the MDFL method, the clustering algorithm used to isolate faults, and the GAN-based method for augmenting fault data; in terms of data, we examine three dimensions: the localization scenario, the subject program, and the number of faults in the multiple fault version. We now describe each of these variables, how they are integrated into the relevant research questions (RQs), and their respective value ranges.
(1) Single Deep Learning-based Fault Localization Methods: Utilizing deep neural networks with multiple hidden layers, we develop a localization model capable of identifying the statements potentially responsible for program faults, thereby generating a suspiciousness ranking of program statements. To assess the effectiveness of MetaGAN in mitigating the oracle problem (RQ1), we comparatively study various DLFL methods as addressed in RQ1 and RQ3. Specifically, we apply MetaGAN to three state-of-the-art MetaMDFL methods, namely, MetaGAN-CNN, MetaGAN-MLP, and MetaGAN-RNN which respectively employ convolutional neural networks (CNN), multilayer perceptrons (MLP), and recurrent neural networks (RNN).
(2) Generative Adversarial Networks (GAN): We conduct an in-depth analysis for RQ2, innovatively applying GANs to augment failure data within software fault datasets. Through an adversarial training mechanism, GANs generate synthetic samples that capture latent fault features. The generator network models the distribution of real fault data to produce diverse fault samples, while the discriminator network continuously refines the quality of these samples to better approximate the real fault characteristics. This adversarial generation method alleviates data scarcity and class imbalance issues in fault detection, thereby enhancing the generalization capability of deep learning fault localization models.
(3) Number of Faults: For subject programs containing multiple faults, where the number of faults ranges from 2 to 4, we explore the performance of MetaGAN under both multiple-fault and single-fault scenarios in RQ3. This analysis systematically evaluates the effectiveness and stability of MetaGAN under varying fault complexities, providing robust support for further optimization of multiple-fault localization methods in the absence of test oracles.
4.4. Measurements
In the field of fault localization, commonly used evaluation metrics can be divided into two categories. The first category consists of individual evaluation metrics, such as EXAM and Rank, that quantitatively describe localization performance. The second category comprises pairwise evaluation metrics, including relative improvement and the Wilcoxon signed rank test, which statistically compare the differences in localization effectiveness between two groups, yielding either quantitative or qualitative results. To assess our experimental outcomes, we employ three categories of metrics to quantify the effectiveness of MDFL, along with three summary statistics to aggregate the pairwise comparison results, as these are the most widely used metrics in MDFL research [12]. Below, we introduce these metrics in detail.
(1) Rank and A-Rank: Rank [33] is a metric used to evaluate single-fault localization performance. It is defined as the suspiciousness ranking of the faulty statement, that is, the position of the faulty statement in a list of statements sorted in descending order based on their suspiciousness values. For multiple-fault localization, several single-fault localization processes performed iteratively yield individual Rank scores, and aggregating these scores can quantitatively describe the overall localization effectiveness. When using the average as the aggregation method, the resulting metric is called the Average Rank (A-Rank), formally defined in Equation (7).
For both the Rank and A-Rank metrics, lower values indicate more effective fault localization. The optimal value is 1, while the worst case scenario equals the number of executable lines in the subject program.
(2) EXAM, T-EXAM, A-EXAM, and C-EXAM: EXAM [13,30] is a metric used to evaluate single-fault localization effectiveness. It is defined as the percentage of code that must be examined before the fault is found, essentially representing a normalized version of Rank, where eLOC denotes the number of executable lines. This normalization ensures that EXAM is independent of the program size.
For multiple-fault localization, each single-fault localization conducted during the iterative process produces an EXAM score, and aggregating these scores provides a quantitative measure of the overall multiple-fault localization effectiveness. When the arithmetic sum is used for aggregation, the result is the Total EXAM metric (T-EXAM) [13,31], which is formally defined in Equation (9).
Alternatively, using the arithmetic mean yields the Average EXAM metric (A-EXAM) [30], where represents the number of single-fault localization instances.
Critical EXAM (C-EXAM): C-EXAM is a metric specifically designed to assess the effectiveness of the CBMFL method. It is defined as the sum of the EXAM scores for the single-fault localizations along the critical path, meaning that in each iteration, it refers to the single-fault localization with the highest EXAM score. C-EXAM is formally defined in Equation (11), where “iteration” refers to a single cycle of the process.
(3) Top-: The Top- [30] metric is defined as the number of faults that can be localized when only the top of statements in the suspiciousness ranking are examined. A higher Top- value indicates that fewer statements need to be reviewed to identify faults, reflecting superior fault localization performance. The optimal value equals the total number of faults, while the worst case value is zero.
(4) Relative Improvement: The Relative Improvement (RImp) [34] metric is defined as the overall ratio between two sets of measurements. It is used to compare the performance differences between two fault localization methods across various individual evaluation metrics. A relative improvement value of less than 1 indicates that the first method is superior to the second overall.
(5) Wilcoxon Signed-Rank Test: The Wilcoxon signed-rank test [35] is used to assess the risk associated with drawing specific conclusions from two sets of measurements. Specifically, for any given comparative outcome (e.g., better, similar, or worse), the Wilcoxon signed-rank test quantitatively evaluates the risk in the form of a p-value.
4.5. Implementation
(1) Environment: The experiments were performed on a system equipped with an Intel Core i9-13900K CPU, 64GB of memory, and an NVIDIA RTX4080 GPU with 16GB VRAM. The software environment included Windows and Python 3.10.14.
(2) Tools: Visual Studio Code (version 1.95), PyCharm (version 2024.1.7).
(3) Key hyper-parameters: Regarding the key hyper-parameters of the GAN component, the batch size is 128, the optimizer is Adam, the generator learning rate is 0.00025, and the discriminator learning rate is 0.000025. In this scenario, the learning rates of the two are 10 times related. In addition, pattern collapse can be avoided by increasing the training frequency of the discriminator and adding noise. The entire dataset contains 7 types of datasets, and the training time for different matrices in each dataset ranges from several tens of minutes to several hours.
5. Results
5.1. RQ1 More Effective Mitigation of Oracle Problem
To investigate how MetaGAN more effectively mitigates the oracle problem compared to MetaMDFL, we executed the MFL process under various localization scenarios. Since the normalized EXAM metric is independent of the program’s executable lines (eLOC), it is more appropriate to evaluate performance using EXAM-based metrics, namely, T-EXAM, A-EXAM, and C-EXAM, as shown in Figure 7. Each subplot displays the EXAM distribution for MetaGAN relative to MetaMDFL. In these plots, the horizontal axis represents the percentage of code examined, while the vertical axis represents the percentage of mutants (or faults) that have been fixed. Each point on the curve indicates the proportion of mutants that can be fixed when a portion of code is inspected in descending order of suspiciousness. Consequently, the performance curve of MetaGAN consistently lies above those of the three original MetaMDFL methods (namely, MetaGAN-CNN, MetaGAN-RNN, and MetaGAN-CNN). Experimental results indicate that MetaGAN outperforms two out of these three methods, demonstrating that generating class-balanced datasets with MetaGAN significantly enhances the effectiveness of MetaMDFL.
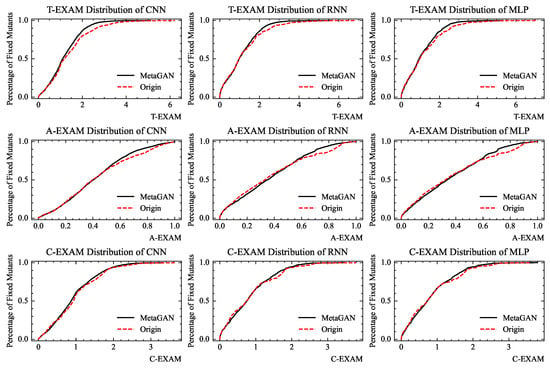
Figure 7.
EXAM distribution.
Specifically, on T-EXAM, our MetaGAN method detects faults approximately higher than the original method when detecting – of code lines using CNN, RNN, and MLP methods; on A-EXAM, when CNN detects approximately of code lines, our MetaGAN method detects faults approximately higher than the original method; on C-EXAM, our MetaGAN method detected faults approximately higher than the original method when detecting approximately of code lines using CNN, RNN, and MLP methods.
To quantify the performance differences between MetaGAN and MetaMDFL, we aggregated paired comparison results. As shown in Table 4, we employed the relative improvement metric to compare the performance of MetaGAN relative to MetaMDFL. It is evident that MetaGAN outperforms the original MetaMDFL in terms of T-EXAM, A-EXAM, C-EXAM, and A-Rank.

Table 4.
RImp of different metrics.
5.2. RQ2 Using Different DLFL Methods
Table 5 presents the performance of MetaGAN relative to MetaMDFL when employing different DLFL methods. For each DLFL method, we conducted an RImp Score analysis comparing the MetaGAN results with those of MetaMDFL, and we evaluated their performance using various metrics. As evidenced by the A-Rank, T-EXAM, A-EXAM, C-EXAM, Top-, Top-, and Top- metrics, MetaGAN, when combined with each of the three different DLFL methods, consistently outperforms MetaMDFL. Table 6 presents the qualitative results of MetaGAN relative to MetaMDFL on the WSR metric, indicating that T-EXAM, A-EXAM, C-EXAM, A-Rank, and Top- all achieved better results.

Table 5.
RImp score of MetaGAN with different localizers.

Table 6.
WSR performance comparison.
5.3. RQ3 the Effectiveness of Different Fault Programs
Figure 8, titled “RANK Distribution,” illustrates the performance of MetaGAN relative to MetaMDFL across different fault programs using various DLFL methods. The A-Rank distribution for all subject programs and scenarios is presented in the form of box plots. The numbers on the vertical axis in Figure 8, ranging from 0 to 200, 300, 600, 1000, 2000, and 3000, indicate the purpose of identifying faults. The average number of lines of code that need to be checked for a statement is 200, 300, 600, etc., which is sometimes referred to as the average localization cost in academia. In each box plot, the red horizontal line at the center of the rectangle represents the average rank, while the upper and lower boundaries of the rectangle correspond to the upper and lower quartiles, respectively. The short horizontal lines extending beyond the rectangle denote the maximum and minimum values after excluding outliers (which are indicated by dots in the figure). It is evident that the three DLFL methods integrated with MetaGAN outperform MetaMDFL on the grep, sed, seqMap, clac, and quich programs.
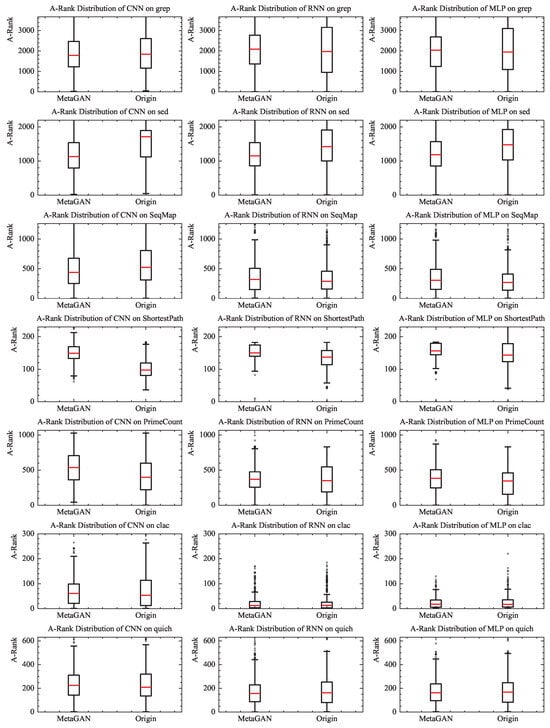
Figure 8.
RANK distribution.
5.4. Ablation Experiments
(1) The result of “no GAN” is the result of MetaMDFL, and MetaGAN is the result of applying GAN. Rank, EXAM, Rimp, WSR and other indicators in the paper all reflect the comparison results between MetaGAN and MetaMDFL methods, that is, the ablation experiment results of “with GAN” and “no GAN”.
(2) Firstly, many multiple-fault localization methods generally use clustering, and few do not use clustering. Therefore, based on the experience of previous researchers, our experiment directly adopted clustering methods. Secondly, clustering methods are not the focus of this article’s discussion. Therefore, we did not consider the case of no clustering, we will consider this aspect in our future research.
(3) We used the previous clustering method [11] to set the optimal value, so we did not consider other thresholds.
6. Discussion
In this study, we introduce MetaGAN, a metamorphic GAN-based augmentation framework designed to enhance Deep Learning-based Multiple-Fault Localization (DLFL) in environments lacking test oracles. MetaGAN synergistically combines Metamorphic Testing (MT), clustering-based fault isolation, and generative adversarial networks (GANs) to address the challenges of class imbalance and parallel debugging in multi-fault scenarios.
The method operates through a three-phase process:
(1) Metamorphic Feature Extraction: MetaGAN begins by applying MT to identify failed Metamorphic Test Groups (MTGs). It then extracts metamorphic features that encapsulate the underlying causes of these failures, effectively characterizing each failed MTG.
(2) Clustering-Based Fault Isolation: Utilizing the extracted features, MetaGAN clusters the failed MTGs into distinct groups. Each cluster represents an independent single-fault debugging session, facilitating targeted analysis.
(3) GAN-Driven Data Augmentation: Within each debugging session, MetaGAN employs a GAN model to generate synthetic failing test cases (minority class). This augmentation continues until the number of failing test cases matches that of the passing ones (majority class), resulting in a balanced dataset. The balanced data is then used for precise DLFL, enabling effective parallel debugging of multiple faults.
By integrating MT, clustering, and GAN-based augmentation, MetaGAN addresses the limitations of existing DLFL methods in handling multiple faults without relying on test oracles. The experimental results demonstrate that MetaGAN outperforms existing MetaMDFL methods across multiple evaluation metrics, particularly in addressing class imbalance challenges. Specifically, MetaGAN achieves significant improvements in both the EXAM and the rank metrics, with EXAM showing the highest improvement of , the rank showing the highest improvement of , and the top- showing the highest improvement of . These results validate the effectiveness of MetaGAN in performing fault localization without relying on test oracles and mitigating class imbalance through GAN-generated violation samples. This approach not only mitigates the class imbalance issue but also enhances the accuracy and efficiency of fault localization in complex software systems.
Our method, MetaGAN, solves the problem of class imbalance and improves the effectiveness of multiple-fault localization in oracle-free scenarios. However, due to certain independent internal and external factors, there are some threats to the effectiveness of fault localization. There are mainly two types of threats:
(1) Internal Threats: MetaGAN builds upon a CBMFL approach enhanced with both metamorphic testing and GAN-based augmentation. CBMFL methods [12,13,14,36] assume that faults occur independently. In real-world software, however, multiple faults often interact in complex, non-independent ways. Therefore, our results cannot be generalized to scenarios involving tightly coupled faults. Decoupling interdependent faults in such logical interactions remains a significant and challenging direction for future research. Nevertheless, our empirical findings clearly demonstrate that MetaGAN can successfully extend the CBMFL method to situations lacking an oracle and outperforms the MetaMDLFL baseline.
(2) External Threats: We leverage an open-source dataset from a recent MT study [10] and apply GAN-based augmentation. Consequently, we inherit several external threats, such as a limited selection of subject programs, unverified effectiveness of the adopted MRs, and the possibility that the GAN may overfit—producing synthetic data that does not accurately reflect real-world conditions. However, our work remains valuable, as we have demonstrated in some cases that our approach effectively addresses the issue of oracle deficiency and outperforms MetaMDFL.
There is still a threat of fault interaction, as most multiple faults can be separated and transformed into multiple single faults acting independently to generate failures. Currently, most methods (including our method) use clustering methods to solve this problem, converting multiple faults into a single fault. However, a small portion requires two or more factors to work together to generate a failure. Due to the mutual interference of faults, it is very difficult to handle, and most methods cannot solve this scenario.
Selecting four faults is a common strategy adopted by many researchers [11,37], and to date, no studies have examined scenarios involving more than four faults. Investigating fault scenarios beyond this threshold presents significant challenges; therefore, we intend to extend our work to include more than four faults in future research.
Regarding the generation strategy, this article adopts Generative Adversarial Networks (GANs) for data augmentation of test case coverage matrices, solving the problem of imbalanced matrix vector categories and achieving good multiple-fault localization results. In this study, we also introduced other generation strategies to address the issue of class imbalance in matrix vectors, such as the SMOTE [38] method.
Table 7 compares the WSR performance of our state-of-the-art MetaGAN with MetaSMOTE (i.e., the MetaMDFL method enhanced with SMOTE as the generation strategy). The results demonstrate that MetaGAN outperforms MetaSMOTE.

Table 7.
WSR performance comparison (MetaGAN vs. MetaSMOTE).
7. Conclusions
MetaGAN presents a pioneering framework for multiple-fault localization by seamlessly integrating Generative Adversarial Networks (GANs), Metamorphic Testing (MT), and clustering-based fault isolation. By leveraging MT to extract failure-specific features from Metamorphic Test Groups (MTGs) and then clustering those MTGs into independent single-fault sessions, MetaGAN establishes a scalable, parallelizable debugging pipeline. Within each session, GAN-driven augmentation synthesizes additional violation samples—balancing the minority class until it matches the majority of non-violation cases. This design successfully eliminates the reliance on traditional test oracles and addresses the pervasive class imbalance challenge in multi-fault scenarios, all while maintaining computational efficiency comparable to state-of-the-art baselines.
Extensive empirical evaluation confirms MetaGAN’s superiority over existing approaches. Across multiple benchmarks, MetaGAN consistently achieves higher localization accuracy—reflected in metrics such as Average Rank (A-Rank) and Total EXAM (T-EXAM)—by virtue of its balanced training dataset. The synthetic violation samples generated by the GAN effectively populate sparse regions of the feature space, enabling deep learning–based fault localizers to distinguish faulty statements with greater precision. Nevertheless, class imbalance remains a critical obstacle: in oracle-less contexts with few real failure cases, even robust augmentation cannot fully eliminate the disparity between failing and passing samples. This limitation underscores the continued need for innovative data synthesis and resampling techniques.
Looking ahead, we plan to broaden MetaGAN’s applicability through several key extensions. First, we will incorporate additional generative strategies—such as transformer-based syntheses—to capture more diverse fault distributions. Second, we aim to integrate density-based fault localizers (e.g., FATOC [30]) and parallel localization techniques (e.g., MSeer [31]) into the MetaGAN pipeline, forming a hybrid system that combines multiple paradigms. Finally, we will undertake comprehensive ablation and sensitivity studies—examining cases without clustering, varying thresholds, and experimenting with alternative metamorphic relations—to quantify the contribution of each component. These future directions promise to enhance MetaGAN’s robustness, scalability, and overall effectiveness in complex, oracle-free software systems.
Author Contributions
Conceptualization, A.H. and W.F.; methodology, A.H.; software, X.Z. and J.W.; validation, X.Z., Y.A. and H.F.; formal analysis, A.H.; investigation, A.H.; resources, A.H.; data curation, A.H. and X.Z.; writing original draft preparation, A.H. and X.Z.; writing review and editing, A.H. and X.Z.; visualization, A.H. and Y.A.; supervision, W.F. and H.F.; project administration, A.H. and J.W.; funding acquisition, W.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the General Project of Chongqing Natural Science Foundation (Grant Number: CSTB2024NSCQ-MSX0812).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest. Moreover, it is explicitly stated that the funders exerted no influence on the study’s design, the gathering and analysis of data, the interpretation of results, the drafting of the manuscript, or the determination to disseminate the findings.
Abbreviations
The following abbreviations are used in this manuscript:
| SFL | Single-Fault Localization |
| MFL | Multiple-Fault Localization |
| DLFL | Deep Learning-based Fault Localization |
| SBFL | Spectrum-Based Fault Localization |
| MT | Metamorphic Testing |
| MR | Metamorphic Relations |
| MTG | Metamorphic Test Group |
| CBMFL | Cluster-Based Multiple-Fault Localization |
| GAN | Generative Adversarial Networks |
| MDFL | Multiple Deep learning-based Fault Localization |
| MetaDLFL | Metamorphic Deep Learning-based Fault Localization |
| MetaMDFL | Metamorphic Multiple Deep learning-based Fault Localization |
| MetaGAN | Metamorphic GAN-based Augmentation for Improving Multiple Deep |
| Learning-based Fault Localization Without Test Oracles |
References
- Wong, W.E.; Li, X.; Laplante, P.A. Be more familiar with our enemies and pave the way forward: A review of the roles bugs played in software failures. J. Syst. Softw. 2017, 133, 68–94. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z.; Liu, Y.; Chen, X.; Paul, D.; Cai, Y.; Fan, L. Can higher-order mutants improve the performance of mutation-based fault localization. IEEE Trans. Reliab. 2022, 71, 1157–1173. [Google Scholar] [CrossRef]
- Dutta, A.; Manral, R.; Mitra, P.; Mall, R. Hierarchically Localizing Software Faults Using DNN. IEEE Trans. Reliab. 2020, 69, 1267–1292. [Google Scholar] [CrossRef]
- Gou, X.; Zhang, A.; Wang, C.; Liu, Y.; Zhao, X.; Yang, S. Software Fault Localization Based on Network Spectrum and Graph Neural Network. IEEE Trans. Reliab. 2024, 73, 1819–1833. [Google Scholar] [CrossRef]
- Wong, W.E.; Gao, R.; Li, Y.; Abreu, R.; Wotawa, F. A Survey on Software Fault Localization. IEEE Trans. Softw. Eng. 2016, 42, 707–740. [Google Scholar] [CrossRef]
- Wong, W.E.; Debroy, V.; Gao, R.; Li, Y. The DStar Method for Effective Software Fault Localization. IEEE Trans. Reliab. 2014, 63, 290–308. [Google Scholar] [CrossRef]
- Zhang, L.; Li, Z.; Feng, Y.; Zhang, Z.; Chan, W.K.; Zhang, J.; Zhou, Y. Improving Fault-Localization Accuracy by Referencing Debugging History to Alleviate Structure Bias in Code Suspiciousness. IEEE Trans. Reliab. 2020, 69, 1021–1049. [Google Scholar] [CrossRef]
- Tang, C.M.; Chan, W.K.; Yu, Y.T.; Zhang, Z. Accuracy Graphs of Spectrum-Based Fault Localization Formulas. IEEE Trans. Reliab. 2017, 66, 403–424. [Google Scholar] [CrossRef]
- Zhang, Z.; Lei, Y.; Mao, X.; Yan, M.; Xu, L.; Zhang, X. A study of effectiveness of deep learning in locating real faults. Inf. Softw. Technol. 2021, 131, 106486. [Google Scholar] [CrossRef]
- Fu, L.; Lei, Y.; Yan, M.; Xu, L.; Xu, Z.; Zhang, X. MetaFL: Metamorphic fault localization using weakly supervised deep learning. IET Softw. 2023, 17, 137–153. [Google Scholar] [CrossRef]
- Fu, L.; Wu, Z.; Lei, Y.; Yan, M. MetaMFL: Metamorphic Multiple Fault Localization without Test Oracles. IEEE Trans. Reliab. 2024, 1–15. [Google Scholar] [CrossRef]
- Zakari, A.; Lee, S.P.; Abreu, R.; Ahmed, B.H.; Rasheed, R.A. Multiple fault localization of software programs: A systematic literature review. Inf. Softw. Technol. 2020, 124, 106312. [Google Scholar] [CrossRef]
- Jones, J.A.; Bowring, J.F.; Harrold, M.J. Debugging in Parallel. In Proceedings of the 2007 International Symposium on Software Testing and Analysis, New York, NY, USA, 9–12 July 2007; ISSTA ’07. pp. 16–26. [Google Scholar]
- Wu, Y.; Liu, Y.; Wang, W.; Li, Z.; Chen, X.; Doyle, P. Theoretical Analysis and Empirical Study on the Impact of Coincidental Correct Test Cases in Multiple Fault Localization. IEEE Trans. Reliab. 2022, 71, 830–849. [Google Scholar] [CrossRef]
- Barr, E.T.; Harman, M.; McMinn, P.; Shahbaz, M.; Yoo, S. The Oracle Problem in Software Testing: A Survey. IEEE Trans. Softw. Eng. 2015, 41, 507–525. [Google Scholar] [CrossRef]
- Xie, X.; Ho, J.; Murphy, C.; Kaiser, G.; Xu, B.; Chen, T.Y. Application of Metamorphic Testing to Supervised Classifiers. In Proceedings of the 2009 Ninth International Conference on Quality Software, Jeju, Republic of Korea, 24–25 August 2009; pp. 135–144. [Google Scholar]
- Xie, X.; Ho, J.W.; Murphy, C.; Kaiser, G.; Xu, B.; Chen, T.Y. Testing and validating machine learning classifiers by metamorphic testing. J. Syst. Softw. 2011, 84, 544–558. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.Y.; Cheung, S.C.; Yiu, S.M. Metamorphic Testing: A New Approach for Generating Next Test Cases. arXiv 2020, arXiv:2002.12543. [Google Scholar]
- Xie, H.; Lei, Y.; Yan, M.; Yu, Y.; Xia, X.; Mao, X. A universal data augmentation approach for fault localization. In Proceedings of the 44th International Conference on Software Engineering, New York, NY, USA, 21–29 May 2022; ICSE ’22. pp. 48–60. [Google Scholar]
- Lei, Y.; Liu, C.; Xie, H.; Huang, S.; Yan, M.; Xu, Z. BCL-FL: A Data Augmentation Approach with Between-Class Learning for Fault Localization. In Proceedings of the 2022 IEEE International Conference on Software Analysis, Evolution and Reengineering (SANER), Honolulu, HI, USA, 15–18 March 2022; pp. 289–300. [Google Scholar]
- Zhuo, Z.; Donghui, L.; Lei, X.; Ya, L.; Xiankai, M. A Data Augmentation Method for Fault Localization with Fault Propagation Context and VAE. IEICE Trans. Inf. 2024, E107-D, 234–238. [Google Scholar]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Lei, F. Metafl Dataset. 2024. Available online: https://github.com/YanLei-Team/MetaFL_dataset (accessed on 1 December 2024).
- MacQueen, J. Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics, Berkeley, CA, USA, 21 June–18 July 1965 and 27 December 1965–7 January 1966; University of California Press: Berkeley, CA, USA, 1967; Volume 5, pp. 281–298. Available online: https://www.cs.cmu.edu/~bhiksha/courses/mlsp.fall2010/class14/macqueen.pdf (accessed on 1 December 2024).
- Chen, T.; Tse, T.; Zhou, Z.Q. Semi-Proving: An Integrated Method for Program Proving, Testing, and Debugging. IEEE Trans. Softw. Eng. 2011, 37, 109–125. [Google Scholar] [CrossRef]
- Jiang, M.; Chen, T.Y.; Kuo, F.C.; Towey, D.; Ding, Z. A metamorphic testing approach for supporting program repair without the need for a test oracle. J. Syst. Softw. 2017, 126, 127–140. [Google Scholar] [CrossRef]
- Gong, C.; Zheng, Z.; Li, W.; Hao, P. Effects of Class Imbalance in Test Suites: An Empirical Study of Spectrum-Based Fault Localization. In Proceedings of the 2012 IEEE 36th Annual Computer Software and Applications Conference Workshops, Izmir, Turkey, 16–20 July 2012; pp. 470–475. [Google Scholar]
- Zhang, L.; Yan, L.; Zhang, Z.; Zhang, J.; Chan, W.; Zheng, Z. A theoretical analysis on cloning the failed test cases to improve spectrum-based fault localization. J. Syst. Softw. 2017, 129, 35–57. [Google Scholar] [CrossRef]
- Zhang, Z.; Lei, Y.; Mao, X.; Yan, M.; Xu, L.; Wen, J. Improving deep-learning-based fault localization with resampling. J. Softw. Evol. Process 2021, 33, e2312. [Google Scholar] [CrossRef]
- Wu, Y.H.; Li, Z.; Liu, Y.; Chen, X. Fatoc: Bug isolation based multi-fault localization by using optics clustering. J. Comput. Sci. Technol. 2020, 35, 979–998. [Google Scholar] [CrossRef]
- Gao, R.; Wong, W.E. MSeer: An advanced technique for locating multiple bugs in parallel. In Proceedings of the 40th International Conference on Software Engineering, New York, NY, USA, 27 May–3 June 2018; ICSE ’18. p. 1064. [Google Scholar]
- Do, H.; Elbaum, S.; Rothermel, G. Supporting controlled experimentation with testing techniques: An infrastructure and its potential impact. Empir. Softw. Eng. 2005, 10, 405–435. [Google Scholar] [CrossRef]
- Parnin, C.; Orso, A. Are automated debugging techniques actually helping programmers? In Proceedings of the 2011 International Symposium on Software Testing and Analysis, New York, NY, USA, 17–21 July 2011; ISSTA ’11. pp. 199–209. [Google Scholar]
- Debroy, V.; Wong, W.E.; Xu, X.; Choi, B. A Grouping-Based Strategy to Improve the Effectiveness of Fault Localization Techniques. In Proceedings of the 2010 10th International Conference on Quality Software, Zhangjiajie, China, 14–15 July 2010; pp. 13–22. [Google Scholar]
- Richardson, A. Nonparametric statistics for non-statisticians: A step-by-step approach by Gregory W. Corder, dale I. foreman. Int. Stat. Rev. 2010, 78, 451–452. [Google Scholar] [CrossRef]
- Wong, W.E.; Debroy, V.; Golden, R.; Xu, X.; Thuraisingham, B. Effective Software Fault Localization Using an RBF Neural Network. IEEE Trans. Reliab. 2012, 61, 149–169. [Google Scholar] [CrossRef]
- Li, Y.; Liu, P. A preliminary investigation on the performance of SBFL techniques and distance metrics in parallel fault localization. IEEE Trans. Reliab. 2022, 71, 803–817. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).