Abstract
This work presents a comprehensive technological study of dielectric resonator-based microstrip filters (DRMFs), encompassing the design, fabrication, and rigorous characterization of the mode. Through systematic coupling analysis, we demonstrate filters featuring novel input–output coupling techniques and innovative implementations of both transmission zeros (4-2-0 configuration) and equalization zeros (4-0-2 configuration), specifically designed for demanding space and radar receiver applications, while the loaded quality factor () and insertion loss do not match those of dielectric resonator cavity filters (DRCFs), our solution significantly surpasses conventional microstrip filters (MFs), achieving > 3000 compared to typical ≈ 200 for coupled-line MFs in X-band. The fabricated filters exhibit exceptional performance as follows: input reflection () below −18 dB (4-2-0) and −16.5 dB (4-0-2), flat transmission response (), and out-of-band rejection exceeding −30 dB. Mechanical tuning enables precise control of input–output coupling, inter-resonator coupling, cross-coupling, and frequency synthesis, while equalization zeros provide tailored group delay characteristics. This study positions DRMFs as a viable intermediate technology for high-performance RF systems, bridging the gap between conventional solutions.
Keywords:
aspect ratio (AR); band-pass filter (BPF); coupling matrix (CM); curved transmission line (C-TL); dielectric resonator (DR); dielectric resonator based-microstrip filter (DRMF); equalization zeros (EZ); input multiplexer (IMUX); input–output coupling; inter-resonator coupling; group delay; quality factor (Q); TE01δ; transmission zeros (TZ) 1. Introduction
In modern satellite communication systems, particularly for X-band and higher frequencies, signal filtering represents a critical component to ensure optimal performance in increasingly congested spectral environments [1].The requirement for extremely narrowband filters in filter banks— typically characterized by fractional bandwidth (FBW)—commonly implemented as Input Multiplexers (IMUX) [2] becomes essential to maintain signal integrity and selectivity in multi-frequency coexistence scenarios.
The quality factor (Q) of these filters assumes particular importance, as high-Q implementations enable enhanced near-band selectivity while minimizing insertion loss—both critical parameters for receiver chain performance. These characteristics directly impact key system metrics, including Noise Figure (NF) and the gain-to-noise temperature ratio (G/T) [3].
Figure 1 shows a receiver chain with a filter bank, further detailed in Figure 2, where an IMUX consists of two filters representing separate receiver channels for downlink transmission [2,4]. The IMUX isolates closely spaced bands while pre-filtering signals before High Power Amplifiers (HPAs) to prevent intermodulation near compression regions.
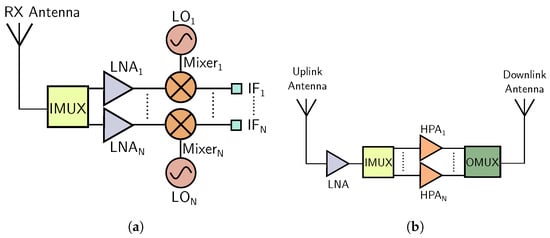
Figure 1.
Block diagram in communications systems. (a) Receiver chain with an IMUX integrated. (b) Payload of communications satellite [5].
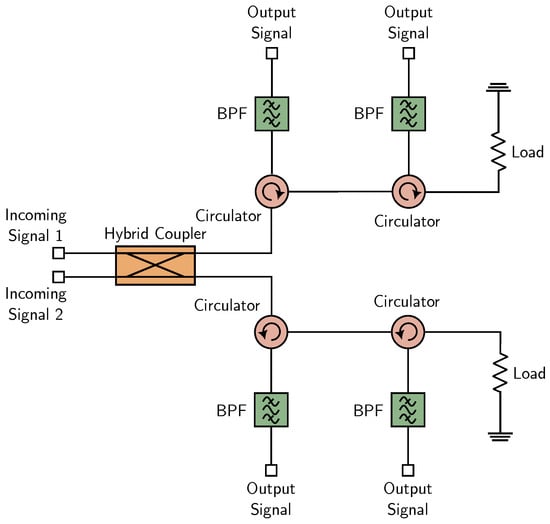
Figure 2.
Example of 2-stage IMUX used as a filter bank [2].
Figure 2 presents an IMUX where each filter isolates a dedicated frequency band with low insertion loss and high adjacent-channel rejection. Each branch uses an RF circulator to route signals through the corresponding filter, terminating out-of-band energy in matched loads. The 90-degree hybrid coupler enables the following critical functions: dual-polarized operation (e.g., orthogonal linear polarizations), system redundancy, and band separation. Additionally, it supports sub-band filtering when configured to isolate signals at the Incoming Signal 2 port. This architecture reduces the number of required RF channels, optimizing power efficiency and form factor by minimizing bulky components.
To meet stringent performance requirements, filters must implement sophisticated responses, as demonstrated in [6], incorporating high-order designs [7], transmission zeros (TZs), and/or equalization zeros (EZs) [8]. Transmission zeros—specific frequencies where the filter achieves deep attenuation through cross-coupling mechanisms [9]—are essential for rejecting interference and enhancing selectivity. Conversely, equalization zeros compensate for phase and amplitude distortions, yielding flatter frequency responses and more consistent group delay (GD) characteristics [6,10]. These features prove indispensable in multi-band systems where frequency-dependent delays and distortions could otherwise cause signal desynchronization or performance degradation [10].
While microstrip technology initially seems appealing for its integration simplicity, weight advantages, and manufacturing ease, it remains inadequate for high-performance applications [11]. Fundamental constraints—particularly low quality factor (Q) [12], excessive insertion loss, and unreliable TZ/EZ implementation (especially in mass production)—render it incompatible with systems demanding exacting performance criteria [6,13].
A widely adopted solution for these demanding specifications employs dielectric resonator-based cavity filters (DRCFs) [14,15]. These filters provide exceptionally high Q-factors, delivering superior selectivity and stability against temperature variations and mechanical vibrations [16,17]. Furthermore, high-order DRCF implementations enable steeper band-edge transitions and enhanced bandwidth-critical characteristics for high-precision applications requiring bandwidth expansion.
However, DRCFs introduce substantial design and fabrication challenges stemming from their mechanical complexity. Precise input–output probe positioning, strict X/Y/Z-axis resonator alignment, and tight manufacturing tolerances necessitate extensive laboratory characterization. These requirements often lead to reprocessing cycles, even when incorporating discrete mechanical adjustment elements to compensate for anticipated design tolerances.
This context drives the development of an innovative intermediate approach—the dielectric resonator-based microstrip filter (DRMF) [18]. The proposed architecture simultaneously addresses multiple challenges as follows: simplifying fabrication, enhancing microwave circuit integration, and enabling mechanical tunability. Most critically, the DRMF must maintain cavity-like performance—including precise alignment and advanced filtering features (high Q-factor, transmission/equalization zeros)—while preserving microstrip technology’s inherent advantages.
Figure 3 shows an X-band dielectric resonator cavity filter developed by Thales Alenia Space España (TASE). The design integrates isolators at both input and output ports to suppress reflected waves caused by impedance mismatches.

Figure 3.
X-Band DRCF, courtesy of Thales Alenia Space España (TASE).
Paper Organization
The paper structure progresses as follows: Section 2 provides a detailed state-of-the-art comparison between DRCF and microstrip filter technologies, thoroughly analyzing their respective advantages and drawbacks for space applications. Section 3 describes the characterization algorithms developed for input–output coupling, inter-resonator coupling optimization, mechanical adjustment procedures, and transmission/equalization zeros’ analysis. Building on these foundations, Section 4 presents the complete design methodology for two filter topologies (4-2-0 and 4-0-2), covering theoretical principles, simulation approaches, and performance trade-offs. Section 5 then documents the full manufacturing process and experimental validation, including measurement techniques, simulation-to-hardware correlation, and performance verification against specifications. Finally, Section 6 concludes with key findings and recommendations for space-grade filter design.
2. State-of-the-Art
This section examines current dielectric resonator cavity filter (DRCF) technology, analyzing operating principles, advantages, and limitations while comparing them with alternative solutions such as microstrip filters.
Dielectric resonator cavity filters are widely used in satellite communication systems due to their high performance characteristics. These filters are particularly effective at increasing near-band selectivity as the roll-off factor increases, which directly translates to an improvement in the quality factor. This enhanced performance stems from the filters’ ability to maintain steep rejection slopes while preserving excellent passband characteristics. These filters feature a high dielectric constant () typically ranging from 10 to 30 [19,20], combined with low insertion loss (IL) enabled by low loss tangent values (). They achieve high intrinsic quality factors, e.g., > 10,000 [19,20,21], while maintaining a low coefficient of thermal expansion (CTE) below 10 ppm/°C [20,21] and excellent mechanical stability under extreme vibration conditions.
Common dielectric resonator materials are employed, such as alumina (Al2O3), lead zirconate titanate (PZT), barium titanate (BaTiO3), calcium zirconate (CaZrO3), and silicon dioxide (SiO2) [19,20,21]. These high-permittivity materials enable significant size reduction while providing intrinsic quality factors ranging from 5000 to 20,000 [19,20,21]. The resonators are typically housed in silver-plated aluminum cavities with alodine or bonderite surface treatments [22], achieving low insertion loss and high external quality factors suitable for satellite communication systems.
The performance of dielectric resonators depends critically on their resonant mode, which may be transverse electric (TE), transverse magnetic (TM), or hybrid electromagnetic (HE). Hybrid modes are less common in practical applications due to their combined longitudinal electric and magnetic field components, which complicate both theoretical analysis and performance predictability.
In contrast, TE and TM modes exhibit greater stability as they maintain purely transverse field components relative to the propagation direction. This results in more predictable field distributions and reduced sensitivity to manufacturing tolerances, material variations, and environmental conditions. The combination of this modal stability with the inherent high permittivity and low-loss characteristics of ceramic materials makes TE and TM modes preferable for high-performance applications.
Figure 4 shows the electric field distribution for the primary modes in a cylindrical DR: TE01δ (the dominant low-frequency mode) and HE11.
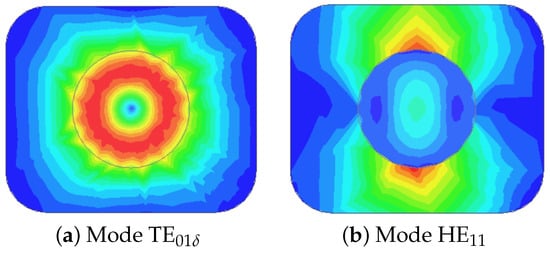
Figure 4.
Primary modes in a cylindrical DR.
Figure 5 shows a third-order dielectric resonator cavity filter implementation. The excitation modes are mainly determined by the resonator’s geometry and aspect ratio (thickness-to-diameter relationship) [23].
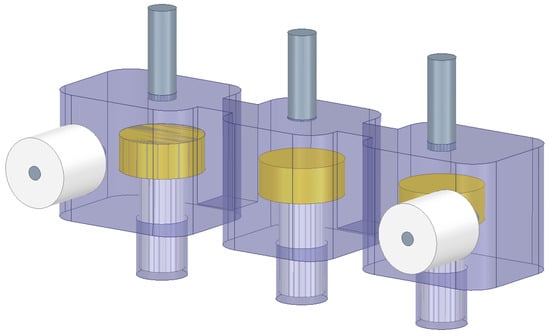
Figure 5.
Third-order dielectric resonator-based cavity filter (DRCF).
The design uses mechanical tuning elements for individual dielectric resonator frequency adjustment. Inter-resonator coupling combines iris-coupled cavities with precisely controlled spacing. The resonators are mounted on dedicated pedestals to maintain exact vertical positioning.
However, as previously discussed, flexible filter solutions demand not only higher-order designs but also the implementation of both transmission zeros and equalization zeros, especially when operating with highly constrained fractional bandwidths.
In DRCF implementations, these zeros can be realized using either probe- or iris-based cross-coupling techniques that extract a portion of the energy from the main transmission path [16,24], as demonstrated in Figure 6a,b. This approach generates a coupling matrix where element M41 retains identical magnitude but opposite polarity. Consequently, the field distribution in resonator DR3 undergoes orientation reversal, causing the cross-coupling mechanism to alternate between electric and magnetic coupling in the equivalent circuit representation (corresponding to capacitive and inductive coupling, respectively).
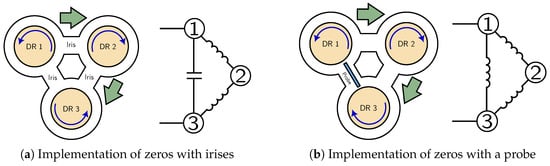
Figure 6.
Implementation of zeros in a third-order DRCF [16].
In contrast, microstrip filters exhibit significantly lower quality factors (typically in the range of tens to hundreds) [21], rendering them unsuitable for demanding applications. Furthermore, when implementing designs requiring high attenuation through transmission zeros, the resulting responses often display asymmetry. This asymmetric behavior stems from several factors as follows: parasitic effects (as microstrip resonators operate in quasi-TEM mode rather than pure TEM mode, leading to increased dispersion at higher frequencies) [25], manufacturing misalignments, and geometric variations between resonators.
These asymmetries particularly affect transmission zeros, which may demonstrate unequal attenuation levels and slight frequency shifts. Conventional microstrip cross-coupling implementations typically use stubs [26]—asymmetric distributed elements with carefully designed lengths and positions relative to the center frequency.
Common microstrip filter implementations include various coupled-line structures, such as Hairpin, parallel-coupled line, and directly coupled filters [27].
Key observations highlight the following three fundamental trade-offs: First, DRCFs provide superior frequency stability through high-Q ceramic resonators with low insertion loss. Second, microstrip designs benefit from simpler planar workflows but suffer from substrate tolerances that need correction, either by multiplying circuit variants through tolerance sweeps or implementing electronic tunability. Third, DRCF manufacturing requires precision machining versus automated PCB production for microstrip alternatives.
The DRCF assembly process requires significant characterization time, and in production, this reduces yield in terms of electrical performance consistency between final circuits. While high-Q resonators demonstrate better temperature stability, they come with larger size (volume) and higher design complexity, requiring more time to properly match experimental results with simulation predictions.
These factors collectively justify the need for an intermediate technology to bridge the existing gaps between DRCFs and microstrip filters for space applications, as summarized in Table 1.

Table 1.
DRCF vs. microstrip filter comparison for space applications.
3. Algorithms
The design characterization is performed based on the resonator geometry and dimensional scaling, as well as through the coupling matrix (CM). The input–output coupling factors and inter-resonator coupling coefficients are derived from the external quality factor expression and even–odd mode analysis, respectively.
3.1. Dielectric Resonator Aspect Ratio
The dimensional scaling of the pill is determined using the aspect ratio (AR), which relates the resonator thickness to its diameter , as defined in (1). This relationship is critical for characterizing the quality factor as follows:
3.2. Quality Factor and Bandwidth Formulation
The 3 dB bandwidth in [2,28] relates to the center frequency through the generalized quality factor Q or the dimensionless coupling coefficient k, expressed in (2) as follows:
This generalized Q specifically corresponds to the loaded quality factor for coupled resonator systems, which combines the following three principal contributions: the unloaded quality factor of the resonators, the external quality factor of the feed structure, and the parasitic quality factors from tuning elements and bonding materials. The complete relationship is expressed in (3), as discussed in [2,28], including the following parasitic contribution:
where comprises individual loss contributions from conductors (), dielectrics (), and radiation (). Given that the cavity design incorporates multiple screws to ensure hermetic sealing, the system operates in a loss-dominant regime where radiative losses become negligible (). Consequently, (4) reduces to the following:
3.3. Coupling Matrix
The Coupling Matrix (CM) in (5) is employed to characterize the normalized coupling level through the coupling coefficients .
where S indicates the Source port, L represents the Load port, accounts for self-resonance effects, and quantifies the inter-resonator coupling between elements i and j.
This coupling matrix describes a fourth-order filter network comprising four internal resonators, with the non-zero parameter specifically characterizing the cross-coupling mechanism that generates either transmission zeros or equalization zeros, determined by the sign of the matrix element.
For this passive, symmetric two-port network, where and , the reciprocity condition implies , under ideal circuit assumptions, as described in (5).
3.4. Group Delay and Phase Delay Formulation
The group delay and the phase delay are computed from the unwrapped phase shift , as given in (6) and (7), according to [2,28], as follows:
The physical interpretation of (6) establishes that group delay represents the negative frequency derivative of the phase response. This formulation ensures that positive group delay values correspond to physically realizable signal delays, as the negative phase slope versus frequency in (7) combines with the negative sign in (6) to produce this causal behavior.
3.5. Input and Output Coupling Formulation
The Q-factor extraction method described in [2] can be applied via maximum reflection group delay , which is derived in [5] and expressed in (8). The external quality factor is obtained from evaluated at the center frequency .
with = 2 at .
3.6. Inter-Resonator Coupling Formulation
The Q-factor method can be applied from full-wave or eigen-mode solutions [16]. The inter-resonator coupling coefficient can be determined through the full-wave simulation of two identical resonators in a shared housing, as specified in (9). For isolated resonators with identical natural frequencies , coupling produces frequency splitting into two distinct eigen-frequencies, and . The coupling coefficient is then derived from this characteristic frequency separation.
This work implements an alternative symmetric approach for determining inter-resonator coupling using identical resonator pairs with the Q-factor method. Leveraging structural symmetry, only half the geometry requires simulation, substantially reducing computational cost. Perfect Electric Conductor (PEC) and Perfect Magnetic Conductor (PMC) boundary conditions are applied at the symmetry plane to extract the odd-mode and even-mode resonant frequencies, respectively. These characteristic frequencies enable the computation of the coupling coefficient through the relationship given in (10), derived from [5,16].
Figure 7 shows the equivalent circuit representation used for analyzing even–odd modes with respect to (10).
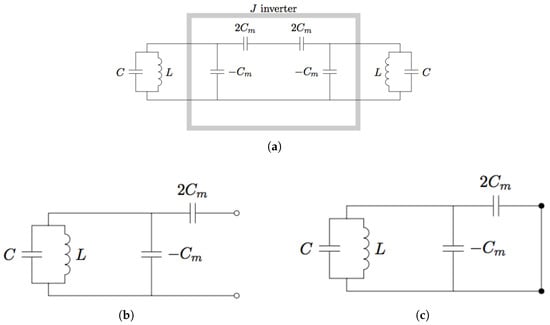
Figure 7.
Even–odd analysis. (a) Circuit model for inter-resonator coupling between two identical resonators. (b) Even-mode analysis. (c) Odd-mode analysis.
Section 4 incorporates all presented algorithms to fully characterize and validate the filter designs, including the determination of the unloaded quality factor, input–output coupling coefficients, and inter-resonator coupling values through even–odd mode analysis, along with group delay evaluation and complete frequency response modeling. The Generalized Chebyshev Matrix (GCM) approach [29] provides the theoretical foundation for this validation process, with its effectiveness demonstrated throughout the design methodology and experimentally confirmed in Section 5.
4. Design and Electrical Performance Characterization
This section outlines the design procedure and intermediate analyses required to accurately characterize the dielectric resonator, the input and output coupling (including quality factor and bandwidth), and the inter-resonator coupling, which arise when studying the behavior of both direct and cross-coupled configurations for a given resonant mode.
4.1. Design Procedure
The filter design procedure was implemented through five sequential steps, each validated by full-wave simulations of the Device Under Simulation (DUS) as follows:
- Eigen-mode frequency and intrinsic quality factor analyses:An eigen-mode frequency analysis and external quality factor () evaluation of the selected resonator were performed in a representative environment incorporating specific boundary conditions. To distinguish between the resonator’s eigen-modes and those of the cavity, the conductivity of the cavity housing was deliberately reduced by four orders of magnitude relative to silver . Specifically, the lateral boundaries were assigned a conductivity of = 1000 S/m, while the top and bottom faces maintained infinite conductivity to preserve a high-quality ground plane and accommodate Z-axis variations in the circular dielectric resonator modes.
- Resonant mode selection:The cylindrical resonator geometry was chosen to enable the excitation of non-hybrid modes, consistent with typical satellite application requirements [23]. To optimize the operational bandwidth while avoiding unwanted mode interactions, the design employs the resonator’s fundamental mode. This mode selection specifically maximizes the fundamental mode’s single-mode bandwidth, ensuring a spurious-free frequency response.
- Parametric analysis of the dielectric resonator aspect ratio and boundary conditions:A parametric study of the resonator’s aspect ratio (AR) was conducted to evaluate its behavior and identify the optimal design point for maximizing the quality factor when implemented on Rogers-family substrates. Additionally, the minimum distance between the resonator and lateral boundaries was systematically varied to ensure a robust design with minimal sensitivity to boundary effects. This methodology maintains consistent resonant frequency and performance characteristics while preventing unwanted cavity-mode excitation. The cavity height was fixed to allow for manual frequency tuning.
- Input–output coupling and inter-resonator coupling characterization:Various feeding methods for exciting the target mode (input–output coupling) were evaluated. After identifying the optimal configurations, their performance was thoroughly characterized across multiple parameters. In parallel, inter-resonator coupling techniques were investigated and parametrically analyzed to determine the nominal operating point (NOP).
- Cross-coupling characterization:The final design stage involves analyzing cross-coupling mechanisms to synthesize complex filter responses, incorporating transmission zeros and/or frequency response equalization techniques.
4.2. Configuration Set-Up, and Identification of Materials and Their Electrical Performance
This section presents the materials used along with their electrical properties, as well as the experimental setup for characterizing resonator behavior via design charts.
4.2.1. Setup of Analysis
The resonator is housed within a cavity on a perforated substrate, with the hole diameter ensuring proper centering and alignment while minimizing mechanical design complexity. Both dielectric and conductor losses have been incorporated in the simulation setup. The eigen-mode analysis was initialized at 4 GHz—a frequency sufficiently separated from the X-band lower boundary to avoid influencing potential nearby modes.
The Device Under Simulation (DUS) is shown in Figure 8, depicting both lateral and cross-sectional views.
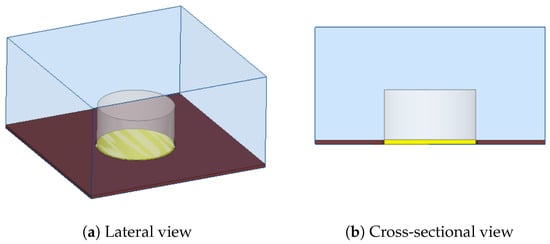
Figure 8.
Device under simulation views.
4.2.2. Identification of Materials and Electrical Performance
The materials employed during characterization and design include the following:
- A ceramic cylindrical dielectric resonator [30] with a dielectric constant = 24, loss tangent = 10−4, initial aspect ratio AR = 0.5, and radius constraint = 3 mm [31].
- A Rogers RO6002 substrate (relative permittivity = 2.94 ± 0.04, = 0.0012 at 10 GHz [32]) with thickness t = 0.254 mm (10 mils).
- Dielectric adhesive Ablebond 8360 with nominal thickness 0.15 mm and ≈ 3–6, and = 0.005–0.01 (1–10 GHz)—electrical properties not specified in the datasheets. The Q-factor method (detailed in Section 3.5 and Section 3.6) enables characterization via comparison between standalone and bonded DR configurations, though variations occur due to manual application preventing substrate overflow.
- A cavity with height h = 7 mm (arbitrary lateral dimensions), featuring lateral boundaries of conductivity = 1000 S/m and Perfect Electric Conductor (PEC) conditions for both bottom and top boundaries.
4.3. Mode Selection
This section evaluates multiple characterization charts to establish an optimal design compromise between the quality factor, frequency stability, and mode separation.
The eigen-mode analysis conducted in Ansoft HFSS (Table 2) yields resonant frequencies and the corresponding unloaded quality factors . Lower values associated with eigen-modes 1, 2, 3, and 9 are excluded from the analysis, as these modes are not dominated by the dielectric resonator’s characteristic behavior. The fourth mode, designated as TE01δ in cylindrical coordinates (r,,z), represents the fundamental mode of the dielectric resonator, fully determined by its geometric dimensions and aspect ratio. Conversely, as evidenced by Table 2, higher-order modes are undesirable as their closer spacing reduces the Spurious Free Dynamic Range (SFDR) of the system.

Table 2.
First ten eigen-modes.
This mode exhibits no radial variation, but features azimuthal and axial z variations. This mode in dielectric resonators exhibits a horizontal magnetic dipole behavior [33], which is essential for achieving high unloaded Q and stable coupling in microwave filter applications [34]. Figure 9 illustrates both the electric and magnetic field distributions.
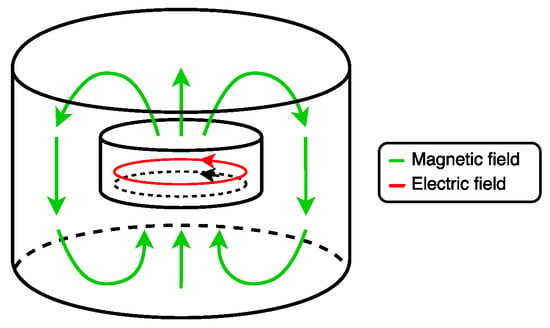
Figure 9.
Electric and magnetic field— mode.
The effectively corresponds to the intrinsic quality factor in this setup, comprising the following three principal loss components:
- Dielectric losses from the resonator substrate.
- Losses originating from the bonding material.
- Non-radiative contributions independent of external loading.
Quality Factor Enhancement
Following the operating mode selection, the stand-alone DR design optimization under representative conditions focuses on maximizing the unloaded quality factor while minimizing the physical housing dimensions to ensure stable resonant frequency behavior under extreme conditions, including temperature drifts and fabrication tolerances. A parametric study evaluated the following two key variables: the DR aspect ratio ranging from 0.4 to 0.55 (achieved through height variation at fixed diameter) and the housing dimensions where cavity height remains constant while lateral (X-Y) dimensions scale proportionally from an initial 0.89 × 0.89 baseline.
As shown in Figure 10a,b, the resonance frequency stabilizes when the enclosure size increases by 40% relative to the initial dimensions, with corresponding stabilization in . The maximum occurs at AR = 0.55 (Figure 10b), which was selected as the optimal point despite the continuing upward trend in quality factor. This conservative choice prevents the excitation of adjacent modes near the target frequency while meeting the design constraints. The optimal configuration combines an aspect ratio of 0.55 with 40% increased lateral enclosure dimensions (1.25 × 1.25 ), achieving optimal balance between robustness and performance.
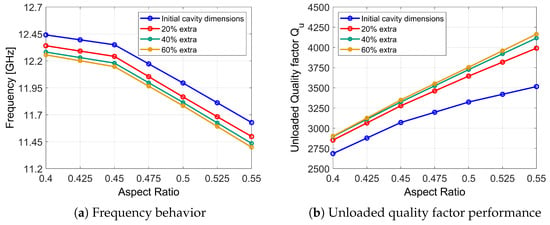
Figure 10.
Aspect ratio variation for TE01δ mode.
4.4. Input, Inter-Resonator, and Output Coupling Characterization
This section presents the characterization charts for both input–output couplings and inter-resonator coupling behavior.
4.4.1. Input and Output Coupling
The generation of the TE01δ has been studied through various feeding techniques [16,35,36]. In this work, two established coupling methods are investigated as follows:
The first approach, illustrated in Figure 11a, employs parallel transmission line coupling similar to classic microstrip coupled-line configurations as presented in [26]. However, this method exhibits limited coupling enhancement with increasing line length due to diminishing interaction with the resonator’s induced currents.
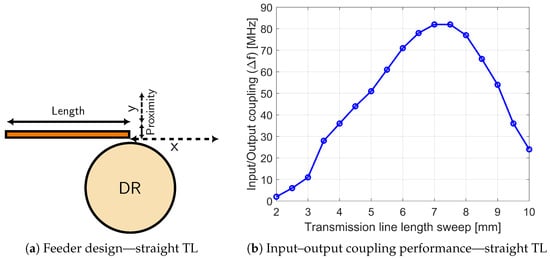
Figure 11.
feeding methods—straight transmission line.
The second approach, shown in Figure 12a, implements a contour-following parallel transmission line or curved transmission line (C-TL), building upon prior coaxial implementations [36] but adapted to planar technology. Here, the rotation angle corresponds to the physical arc length along the DR circumference (top view). In Figure 12a, serves as an example, while this work also analyzes the angle in terms of wavelength to characterize the C-TL’s EM behavior.
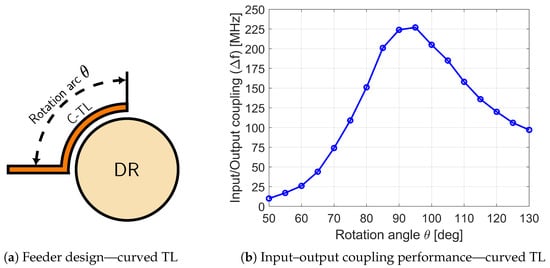
Figure 12.
feeding methods—curved transmission lines (C-TL).
The analysis results shown in Figure 11b and Figure 12b—expressed using the notation in (2)—validate the bandwidth-limiting constraints of the first coupling approach. While the second method exhibits more favorable characteristics, it displays an unexpected behavior, as follows: the coupling factor k (inversely proportional to quality factor) initially grows with increasing arc-shaped C-TL length (), reaches a maximum, and then decreases to complete cancellation (Figure 13). This phenomenon occurs when the induced current vectors along the coupled line transition from constructive to destructive interference with respect to the resonator mode. Coupling restoration occurs only when the currents re-establish phase coherence for the desired mode.
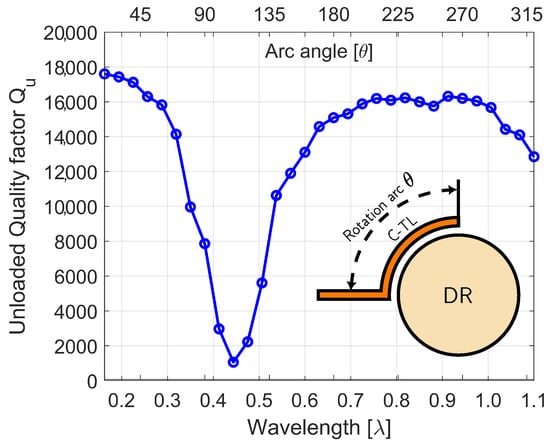
Figure 13.
Unloaded quality factor performance—curved TL.
This behavior, intrinsic to both the mode excitation mechanism and the mode characteristics, reveals inherent bandwidth limitations for -based implementations while simultaneously suggesting potential approaches for innovative bandwidth extension techniques.
The maximum achievable bandwidth coupling, calculated using expression (2), is presented in Figure 12b. This configuration demonstrates a coupling exceeding 200 MHz with gradual variation, representing a significant improvement over the rectangular transmission line results shown in Figure 11b. The smoother response characteristic enables reliable filter tuning through mechanical adjustments while providing enhanced absolute input coupling compared to conventional methods.
The simulation results in Figure 13 demonstrate that although the transmission line C-TL terminates in an open circuit, the majority of the electromagnetic field transfers from the transmission line to the DR, exciting the TE01δ mode. The simulations reveal anomalous behavior where the resonator response varies with the excitation’s electrical length. Under certain conditions, the transmission line mode couples efficiently to the resonator, while at other lengths the coupling coefficient becomes negative, with periodic re-coupling occurring at specific intervals. This undesirable effect limits resonator capabilities and introduces heightened design sensitivity.
The peak coupling condition coincides with the minimum . The electrical spacing between consecutive minima remains constant at , while the maxima spacing follows an irregular pattern. Specifically, subsequent maxima occur at approximately intervals.
To elucidate this coupling mechanism and explain the periodicity disruption, a mathematical model characterizes the dependence on wavelength. Figure 14 presents the comparison between simulated results and model predictions.
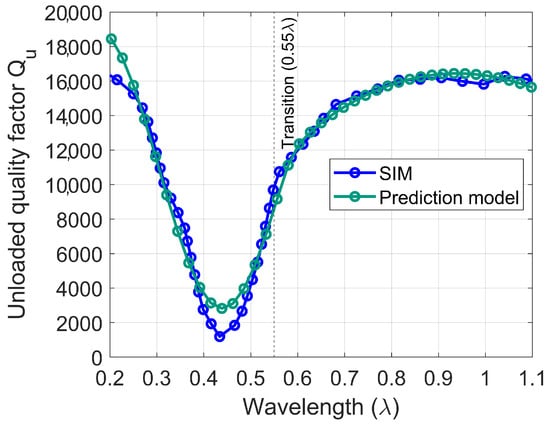
Figure 14.
Comparison of simulated and modeled behavior, w/o stub configuration.
The analysis reveals a periodic behavior (though not identical between maxima and minima) in the simulated results, from which we extract the unloaded quality factor characteristics showing distinct properties in two separate regions, as mathematically represented by the piecewise model in (11).
where represents the transition point between regions. The short-range coupling ()—low-region—is described by the following:
The key parameters in (12) have the following physical interpretations:
- : Spatial frequency of coupling variation (related to the effective propagation constant).
- , : Linear and quadratic attenuation coefficients accounting for radiation and dielectric losses.
- , , n: Coefficients which characterize near-field reactive coupling.
For the long-range upper region (), the model is expressed as follows:
where the following hold:
- , , and describe the periodic re-coupling effects, as shown in Figure 14.
- and model the dominant loss mechanism in this region.
- represents the asymptotic unloaded quality factor at large values
The model characterization confirms the phase-dependent nature of the coupling mechanism for achieving maxima and minima, as previously established. While the maximum and minimum coupling points maintain the theoretical /4 spacing, the initial coupling phase depends critically on both the phase distribution along the curved transmission line (C-TL) and its summation with the dielectric resonator’s phase profile. This phase-sensitive behavior makes the method particularly susceptible to manufacturing tolerances, thermal variations, and alignment inaccuracies, evidenced by the abrupt transitions and the need for complex two-region modeling to match simulation results with theoretical predictions (Figure 14). These limitations fundamentally constrain both the maximum achievable coupling factor and the system’s operational bandwidth.
To address these challenges, a shunt open-ended stub with intentionally mismatched high characteristic impedance and optimized electrical length (°) has been implemented, as shown in Figure 15a. This design prevents equal power splitting that would cancel the resonator fields by directing most current through the primary transmission line, while the carefully tuned stub length provides strategic mode perturbation at specific phase intervals. The configuration effectively eliminates sudden cancellations of the electric field while promoting constructive interference to enhance coupling efficiency.
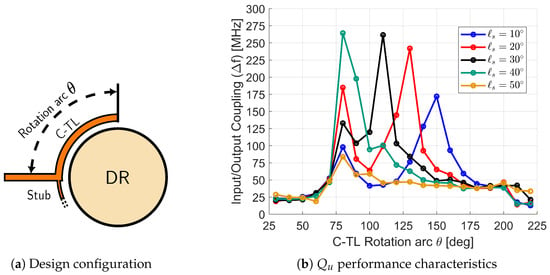
Figure 15.
Input–output coupling characterization.
As shown in Figure 15b, the coupling factor varies significantly as the C-TL extends along the DR contour (rotation angle ) with stub lengths ranging from 10° to 50°. Initial simulations at ° revealed maximum coupling at a secondary peak, which is undesirable as it would require impractically long transmission lines for proper coupling. Furthermore, increasing the stub length introduced operational challenges by bringing transmission line resonances into the near-band region.
On the other hand, progressive stub extension showed the secondary peak merging with the primary coupling peak at °, beyond which coupling efficiency degraded rapidly. This merged condition represents the optimal operating point, combining the original local maxima observed at 80° and 150° in shorter and stub-less configurations while effectively suppressing unwanted C-TL resonances.
A key advantage of this configuration lies in the differential phase variation between the main C-TL and the open-ended stub. For equivalent electrical length changes, the stub characteristics vary more rapidly, facilitating fine-tuning, while the main line responds more gradually to coarse adjustments. The optimized = 40° configuration achieves an ideal balance between coupling efficiency and bandwidth preservation, resulting in direct improvements to input–output port performance.
The optimized system employing a higher-impedance open-circuit stub demonstrates improved coupling behavior, as described by the expressions below, which were obtained from a predicted behavior model derived through genetic algorithm optimizations of simulation data as follows:
where the low-region—rising edge ()—follows a modified logistic growth as follows:
with representing the coupling growth rate (dependent on stub tuning), indicating the position of maximum coupling gradient, and denoting the linear coupling coefficient from the main line.
The upper-region—falling edge ()—exhibits a dual-exponential decay as follows:
characterized by (dominant energy decay rate), (coupling resonance width), and (background coupling level).
In Figure 16, the correlation between the model and the simulated behavior is shown.
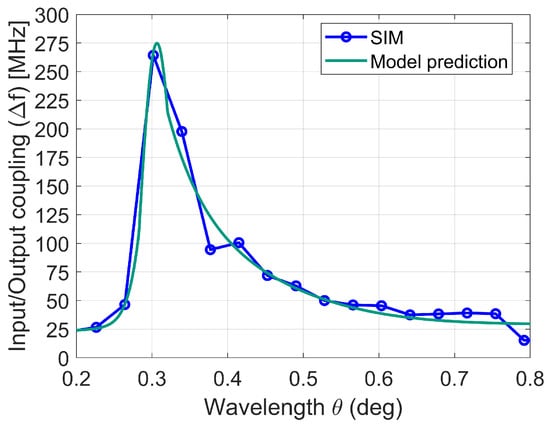
Figure 16.
Comparison of simulated and modeled behavior, w/stub.
The stub implementation delivers three primary performance enhancements. First, it maintains phase synchronization and constructive interference up to through precise impedance matching. Second, it effectively combines the primary (around ) and secondary (approximately ) coupling peaks—case with stub length °, via optimized stub length . Finally, the design achieves substantial bandwidth enhancement.
4.4.2. Inter-Resonator Coupling
Two distinct inter-resonator coupling methods have been analyzed as fikkiws: conventional distance-based coupling (Figure 17a) and C-TL coupling (Figure 17b).
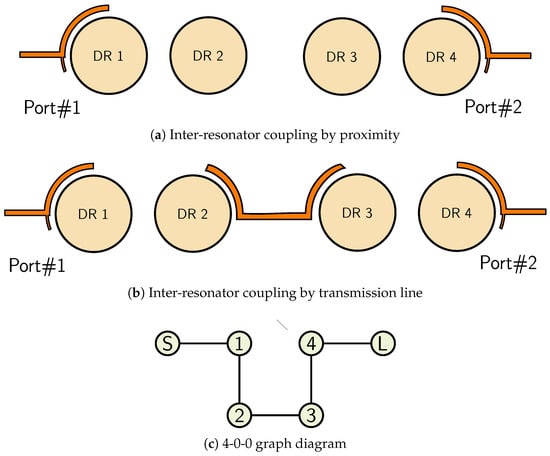
Figure 17.
Even–odd analysis.
The C-TL coupling approach exhibits both advantages and disadvantages compared to distance-based coupling. While enabling larger physical separation between resonators reduces unwanted cross-coupling parasitics, it simultaneously increases those from the C-TL extension.
This method also facilitates more compact layouts through meandered line geometries. However, this approach suffers from three key limitations. First, the maximum achievable coupling factor remains lower than with distance-based coupling. Second, the C-TL configuration excites quasi-TEM mode resonances within the cavity that can interfere with the desired passband response. Third, as characterized in Figure 13, the curved transmission line exhibits an inherent length limitation where coupling reaches a maximum before decreasing as the coupling coefficient changes sign beyond a certain electrical length.
Figure 17 compares both coupling configurations between DR2 and DR3 using even–odd mode analysis. The full filter structure is considered to ensure representative characterization due to housing size, and to define minimum distance to minimize parasitic inter-resonator coupling non desired.
For the distance-based coupling setup (Figure 17a), the minimum center-to-center spacing is 6 mm (DR radius = 3 mm), corresponding to tangential resonator contact—an impractical scenario due to required tuning mechanisms. Nevertheless, the results confirm that increasing coupling with reduced resonator separation (Figure 18a) follows an exponential coupling behavior as distance increase.
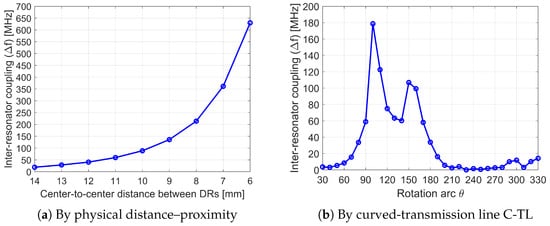
Figure 18.
Inter-resonator coupling characterization.
The expected behavior is observed in Figure 13 through quality factor analysis. The key distinction lies in the coupling mechanisms as follows: Figure 13 demonstrates input–output coupling via (8), while Figure 18b shows inter-resonator coupling through (9) and (10). This results in different coupling rate dynamics due to the interactions between two dielectric resonators.
Figure 18b reveals that the transmission line limits maximum coupling, as modeled in (11)–(13). Peak coupling occurs at °, beyond which coupling decreases—an effect amplified by adjacent resonator field interactions. The secondary peak remains a local maximum, never reaching the principal peak’s magnitude.
Based on the advantages and drawbacks outlined in Table 3, distance-based coupling emerges as the preferred approach for inter-resonator coupling.

Table 3.
Comparison of inter-resonator coupling methods.
4.4.3. Transmission and Equalization Zeros’ Characterization
This section presents a comprehensive analysis of a novel cross-coupling implementation, beginning with a baseline fourth-order filter employing only direct couplings, designed using the characterization charts previously discussed in Section 4.4.2. The study includes complete coupling matrix analysis and its progressive refinement to achieve enhanced transmission zero control and response equalization.
Two distinct approaches were investigated. The first method, well-established in dielectric resonator filter design (particularly in DRCFs), utilizes an iris configuration [16] (Figure 6a), where the aperture functions as a controlled energy window to generate the required cross-coupling. The second approach employs C-TL coupling, which—while limited for direct path coupling as shown in Figure 18b—proves entirely suitable for cross-coupling applications.
Regarding potential Q-TEM mode excitation at specific transmission line lengths, the substantially lower coupling factor compared to cross-coupling paths inherently reduces resonant mode impact. For robust operation, the C-TL electrical length is carefully optimized to prevent interference between TE01δ and Q-TEM modes in both near-band and out-of-band regions.
As established earlier, the coupling factor of C-TL along dielectric resonators exhibits phase dependence. To investigate cross-coupling behavior, we systematically varied transmission line lengths while maintaining a constant curvature angle , thereby creating different phase relationships between resonator couplings.
Figure 19 illustrates the progressive extension of transmission line length for fixed . The characterization results (Figure 20) validate the predicted behavior as follows: the coupling factor varies with phase relationship and, due to the unique properties of this coupling method, undergoes sign reversal (transitioning between inductive and capacitive effects) at /4 intervals. This characteristic enables the selective implementation of either transmission zeros or equalization zeros.
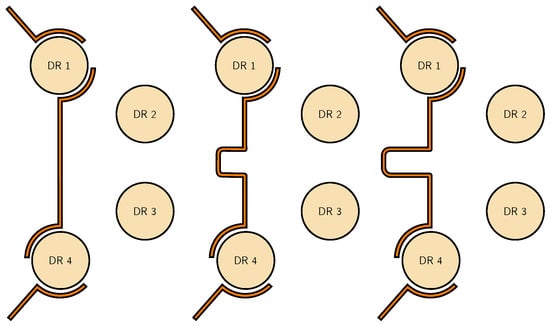
Figure 19.
Cross-coupling transmission-line length sweep.
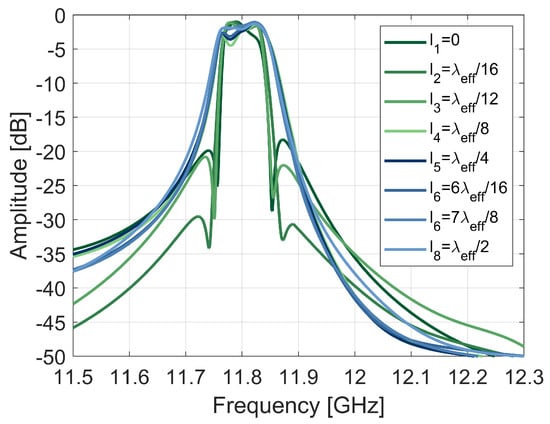
Figure 20.
Frequency response variation versus stub length —simulation results.
To complete the characterization of transmission and equalization zero behavior, Figure 21 shows their variation as the arc length in C-TL increases, confirming control of both TZs and EZs through this novel coupling method.
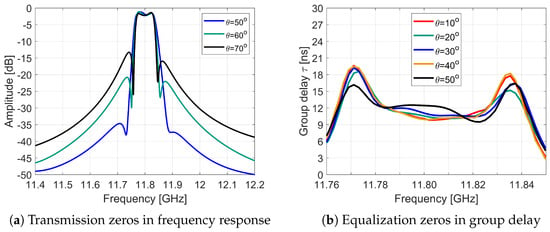
Figure 21.
Cross-coupling variation versus C-TL rotation angle —simulation results.
The simulation results are presented in Figure 22 for the case without additional transmission line length (Figure 22a) and with extra line length = /4 in Figure 22b.
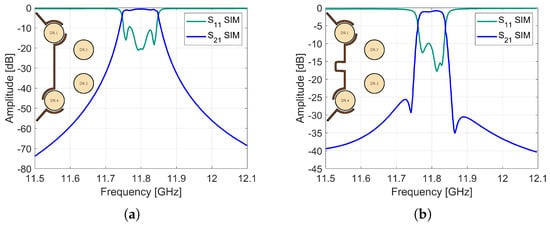
Figure 22.
Electromagnetic cross-coupling characterization. (a) Response of the negative sign in the coupling matrix in coefficient M41. (b) Response of the positive sign in the coupling matrix in coefficient M41.
This behavior is summarized for relevant cases in Figure 23 using the generalized Chebychev matrix approach, where each /4 multiple forces a sign reversal, enabling the implementation of both equalization and transmission zeros as required by the design specifications.
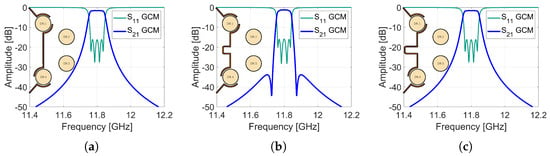
Figure 23.
Generalized Chebychev matrix, cross-coupling model. (a) Negative sign in M41—cross-coupling w/o offset. (b) Positive sign in M41—cross-coupling with offset = . (c) Negative sign in M41—cross-coupling with offset = .
While this effect is undoubtedly valuable for enabling the straightforward introduction of transmission and reflection zeros, it remains susceptible to near-band Q-TEM mode excitation. Consequently, despite its conceptual interest, each design requires ad hoc optimization to suppress Q-TEM resonant behavior. Given the established understanding of C-TL characteristics, an evolution method has been implemented to achieve sign reversal without physically extending the transmission line length—by reversing the arc direction, clockwise to counter-clockwise and vice versa—which directly introduces a sign change in the coupling matrix. Notably, the model exhibits symmetry, making the behavior equivalent, regardless of rotation direction, as long as the relative rotation or phase relationship between resonators is maintained.
To cross-validate this behavior, a cross-coupling between DR1 and DR3 has been forced, as this configuration introduces circuit asymmetry, generating an upper-band transmission zero when the phase relationship is positive, by convention, or a lower-band transmission zero when negative.
Figure 24 presents the validation filters demonstrating coupling matrix sign change through asymmetric coupling generation in Figure 25. The directional reversal of arc successfully converts the response between transmission-zero and equalization-zero behavior.
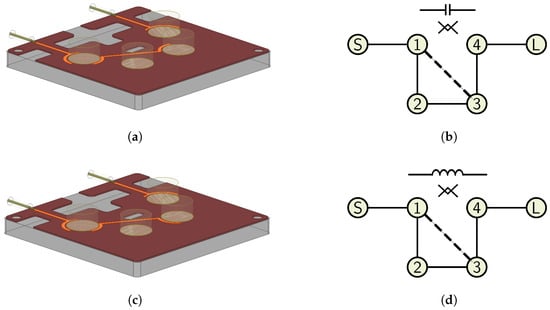
Figure 24.
Cross-coupling characterization design. (a) Negative sign in the coupling matrix in coefficient . (b) Negative sign in the coupling matrix in coefficient . (c) Positive sign in the coupling matrix in coefficient . (d) Positive sign in the coupling matrix in coefficient .
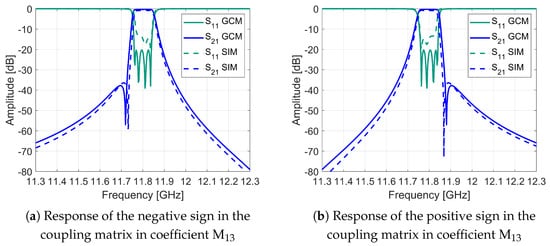
Figure 25.
Electromagnetic cross-coupling characterization.
Figure 25 presents the frequency responses of both electromagnetically simulated filters and their comparison with the ideal coupling matrix obtained from generalized coupling matrix synthesis. The results demonstrate the sign inversion behavior in the coupling matrix achieved through a simple rotation that reverses the TE01δ mode’s electric field distribution, as described by the CM in (17). The key difference between both coupling matrices lies in the cross-coupling factor M13 (sign reversal), which verifies the effectiveness of the proposed coupling method. Furthermore, the results highlight common parameter values between both matrices, where self-resonance terms Mii are also adjusted to compensate for matrix asymmetry, and consequently, the frequency response asymmetry.
The coupling matrix elements that vary between the two frequency responses are as follows: M31 = M13 = 0.32, M11 = −0.02, M22 = 0.21, and M33 = −0.04.
The results demonstrate that the principal design limitation for filters combining both transmission zeros and equalization zeros—namely the increased physical length requirement—has been successfully addressed through a simpler, more easily implemented solution.
Leveraging the established sign-dependent behavior of the coupling matrix, this work proposes a novel cross-coupling evolution technique as follows: maintaining identical transmission-line lengths while physically reversing the arc orientation (clockwise to counter-clockwise or vice versa). This straightforward PCB-level modification effectively inverts the matrix sign while preserving the filter response, offering significant advantages from a manufacturability perspective.
4.4.4. Mechanical Adjustment
Mechanical tuning elements have been implemented to compensate for measurement–simulation discrepancies, manufacturing tolerances, and temperature/vibration effects, necessitating adjustable components for both frequency and coupling optimization. A thorough characterization of these mechanical tuning elements was conducted, encompassing resonant frequency control, input–output coupling optimization, inter-resonator coupling management, and cross-coupling effect mitigation.
For this purpose, a basic microstrip line () was designed (Figure 26a) and fabricated to validate field distribution modifications through tuning screw insertion. A bridge-shaped structure was incorporated to enable precise screw positioning and depth control. The characterization included the following three test configurations: no tuning element, screw positioned 0.3 mm from the transmission line, and screw at 0.15 mm proximity.
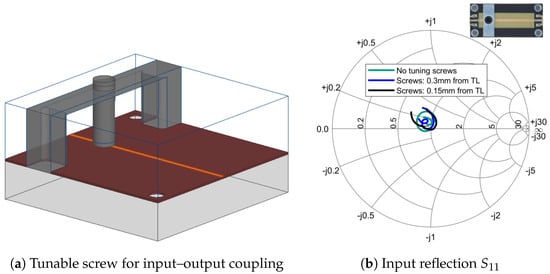
Figure 26.
Mechanical adjustment characterization.
Figure 27a,b presents the measured transmission and reflection responses, respectively. The results reveal resonant frequency shifts, evidenced by rotation of the imaginary component within a constant-radius circle on the Smith chart, with decreasing screw-to-line distance. This behavior, apparent in both Figure 26b and Figure 27b, results from direct field distribution manipulation (affecting both amplitude and phase). The tuning screws exhibit limited , which directly impacts final filter performance. However, as Figure 27a demonstrates, improper embedding structure design can induce in-band screw resonance when penetration depth exceeds , observed in both 0.3 mm and 0.15 mm proximity cases through response analysis (resonance at 11.15 GHz).
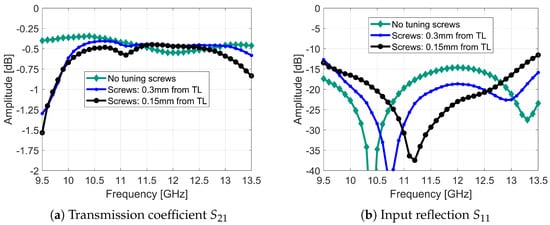
Figure 27.
Screw depth variation versus frequency response.
5. Filter Design, Simulation, and Experimental Results
This section presents the performance characteristics of the implemented designs, which were previously simulated and subjected to minimum specifications to validate the core technology. The key requirements include the following:
- Center frequency = 11.8 GHz.
- Bandwidth BW = 60 MHz.
- Filter topologies implementing either of the following:
- –
- Transmission zeros (4-2-0 configuration).
- –
- Equalization zeros (4-0-2 configuration).
Using standard P-T-E notation (poles—transmission zeros—equalization zeros), Figure 28a shows the direct-coupled filter design (4-0-0 configuration), while Figure 28b demonstrates its physical implementation with a stepped mechanical housing for tuning. The fundamental difference between 4 and 2-0 and 4-0-0 configurations lies solely in the cross-coupling transmission line geometry—specifically, the clockwise or counter-clockwise arc orientation () that determines whether transmission zeros or equalization zeros are implemented, as previously explained.
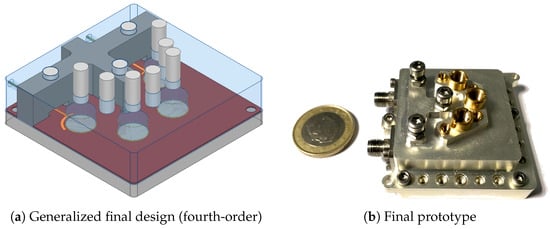
Figure 28.
Filter design and filter prototype.
The filter designs were developed under stringent manufacturing constraints, with the aspect ratio reduced to AR = 0.48 due to material stock limitations from suppliers, resulting in a lower measured than simulated values. The implementation accounts for adhesive material uncertainties, including frequency-dependent electrical property variations and thickness tolerances, while accommodating for low-Q tuning elements that degrade the loaded quality factor (). A specialized cross-head assembly was developed to address both mechanical resonance in tuning elements and cavity resonance challenges. This integrated component controls enclosure resonances while providing secure screw fixation, effectively suppressing parasitic modes from both the housing structure and internal tuning components.
Manufacturing imperfections were carefully considered, particularly hand-filing tolerances during dielectric resonator fabrication and assembly, along with the use of unfinished aluminum cavity surfaces. As a proof-of-concept (PoC), this implementation deliberately excluded surface treatments such as silver plating to focus exclusively on electrical performance validation, though at the expense of reduced quality factor and increased insertion loss.
5.1. Filter Design, 4-2-0 Topology
The design of a transmission-zero filter implementation has been successfully developed and is presented in Figure 29a, with the corresponding graph diagram shown in Figure 29b.
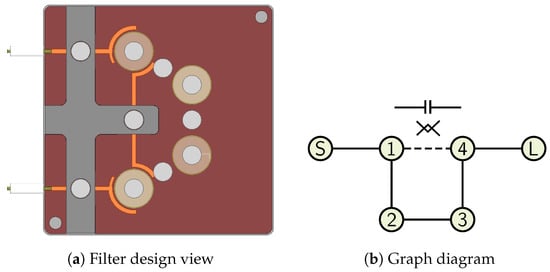
Figure 29.
Filter design, 4-2-0 topology.
The electromagnetic simulation results are presented in Figure 30a, with the corresponding experimental measurements shown in Figure 30b. The near-band frequency response demonstrates strong correlation between simulation and measurement.
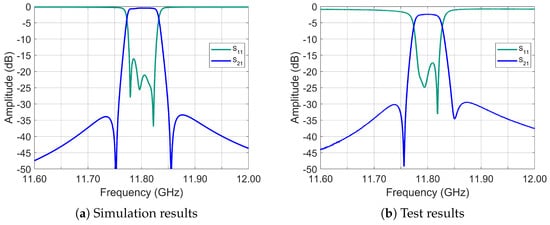
Figure 30.
Frequency response, 4-2-0 topology.
The reflection coefficient performs better than −20 dB across 90% of the passband (worst-case −18 dB), with symmetrically adjustable transmission zeros achieving over 35 dB rejection in simulation and 30 dB in measurement. The transmission response demonstrates successful implementation and precise control of transmission zeros, marking a significant advancement in dielectric resonator microstrip filter (DRMF) technology for demanding applications.
A measurable degradation occurs in both insertion loss and loaded quality factor . The insertion loss increases from 0.7 dB (simulated) to 2.4 dB (measured), corresponding to a reduction to approximately 3000. Despite this, the measured S-parameters validate the simulated behavior, showing excellent in-band symmetry and flatness—particularly when accounting for bandwidth and insertion loss limitations imposed by input–output coupling constraints.
This performance degradation stems from multiple factors: the finite conductivity of uncoated aluminum cavity surfaces, dielectric losses, the reduced resonator aspect ratio (including ±0.1 mm hand-filing tolerances), adhesive uncertainties at operational frequencies (including parasitic effects from adhesive overflow and ground plane voids [29]), deep penetration of tuning screws near resonators and transmission lines, and PCB bonding losses to the carrier. Additional considerations include the test setup measurement error (±0.15 dB) and phase deviations between the C-TL and stub relative to dielectric resonator energy coupling. These factors collectively degrade the overall quality factor.
The group delay results (Figure 31a for simulation and Figure 31b for measurement) show both total variation and absolute value. The measured filter, affected by the aforementioned factors, exhibits a degraded ground plane (reduced ) and limited input–output coupling, resulting in slightly narrower bandwidth than simulated. Crucially, it confirms proper and controlled transmission-zero operation.
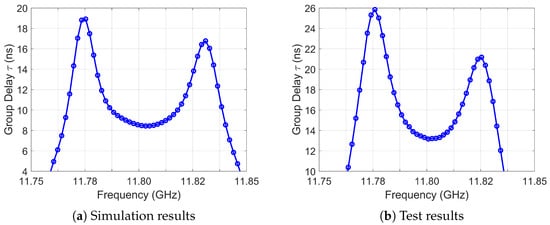
Figure 31.
Group delay response, 4-2-0 topology.
Finally, both in-band (Figure 32a) and out-of-band behaviors are examined in Figure 32b. For frequencies above the passband, the response remains spurious-free over a 1 GHz span. Below the passband, a controlled peak below −40 dB appears at 11.15 GHz—eleven times the filter bandwidth. This frequency, which corresponds to the response shown in Figure 27a, verifies the quality factor of the weakly excited resonant mode—specifically, the over-penetration mode of a tuning screw within the housing structure for mechanical adjustment.
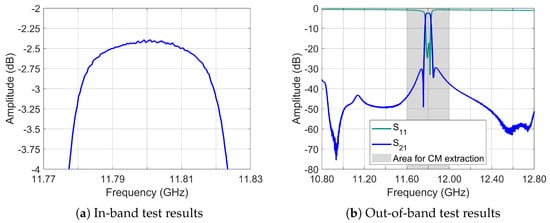
Figure 32.
Frequency response in specific regions, 4-2-0 topology.
The measured coupling matrix in (18) demonstrates a negative coefficient, verifying the standard-compliant cross-coupling behavior for the transmission-zero implementation.
5.2. Filter Design, 4-0-2 Topology
The design of an equalization-zero filter implementation has been successfully developed and is presented in Figure 33a, with the corresponding graph diagram shown in Figure 33b.
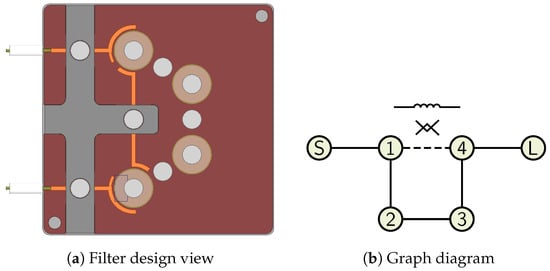
Figure 33.
Filter design, 4-0-2 topology.
The electromagnetic simulation results from ANSYS HFSS® 2024 R1 appear in Figure 34a, with corresponding experimental measurements in Figure 34b. The frequency response demonstrates a reflection coefficient dB across 82% of the passband (minimum −16.5 dB), featuring symmetric adjustable equalization zeros that achieve 0.28 dB peak-to-peak insertion loss variation across the operational bandwidth.
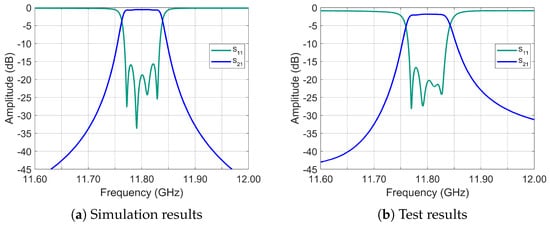
Figure 34.
Frequency response, 4-0-2 topology.
Measured insertion loss increases from 0.7 dB (simulated) to 1.9 dB while maintaining 1 GHz spurious-free operation from band edges. This configuration’s quality factor (approximately 4000) exceeds that of the transmission-zero-based topology, underscoring the importance of characterizing dominant quality factor degradation mechanisms as previously analyzed.
As shown in Figure 35, the equalization zeros behave as expected, maintaining a flatter in-band response, particularly at the band edges.
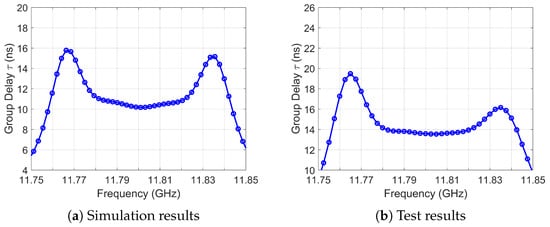
Figure 35.
Group delay response, 4-0-2 topology.
The in-band and out-of-band performance are characterized in Figure 36a,b. Notably, the slope at the lower band edge (Figure 36a) results from the equalization zero position, which aligns with the group delay response shown in Figure 35b, at lower frequencies within the passband.
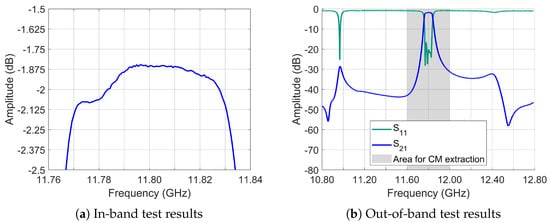
Figure 36.
Frequency response in specific regions—4-0-2 topology.
Regarding far-band behavior, a resonant mode appears at 11 GHz (twelve times the filter bandwidth), sufficiently distant from the passband. Above the passband, another mode emerges at 12.40 GHz (ten times the bandwidth, centered at 11.8 GHz), maintaining −32 dB suppression in transmission with low quality factor.
The measured coupling matrix in (19) exhibits a positive M41 coefficient, confirming successful implementation and control of equalization zero pairs.
Finally, the summary of the experimental results obtained for both filter designs are shown in Table 4 and Table 5.

Table 4.
4-2-0 Topology with Transmission Zeros (TZs).

Table 5.
4-0-2 Topology with Equalization Zeros (EZs).
In addition, a comparative analysis of the three technologies is presented in Table 6. The results demonstrate successful positioning of DRMFs as an intermediate solution between conventional microstrip filters and DRCFs. The proposed DRMF technology achieves balanced electrical performance, making it a viable candidate for space system applications.

Table 6.
DRCF vs. MF vs. DRMF Comparison for Space Applications.
6. Conclusions
Two innovative lateral-space-independent dielectric resonator-based microstrip filters (DRMFs) have been successfully developed and experimentally validated as follows: one incorporating transmission zeros (TZs) and another utilizing equalization zeros (EZs). The designs differ exclusively in the rotation direction of their curved cross-coupling transmission lines. Both were originally designed for 60 MHz bandwidth in X-band, though the 4-2-0 configuration could only be adjusted to 45 MHz, while the equalization-based 4-0-2 version achieved the full 60 MHz bandwidth without compromise.
These solutions demonstrate precise control of zero positioning, input–output coupling, inter-resonator coupling, and frequency tuning. While prior literature has extensively studied dielectric resonator cavity filters (DRCFs) [14,15], and the mode, no microstrip-based multi-resonator dielectric filters had been implemented previously—with research limited to standalone DR characterization, alternative resonance modes, or stopband applications [37], primarily due to their high quality factor requirements.
This work advances the state-of-the-art by establishing an intermediate technology between DRCFs and conventional microstrip filters (MFs) through the following three key innovations: novel transmission/equalization zero implementations, an innovative input coupling topology, and the first comprehensive characterization of the mode in this configuration. The characterization methodology optimizes dielectric resonator geometry and aspect ratio to maximize the intrinsic quality factor via efficient energy confinement when coupled to the microstrip curved transmission line (C-TL).
A novel input–output coupling technique employing open-ended high-impedance stubs enhances maximum coupling while compensating for the mode’s characteristic behavior, where coupling strength oscillates between constructive maxima (phase-aligned transmission-line/resonator fields) and destructive minima (phase-opposed fields) as a function of electrical length. This length-dependent coupling mechanism has been thoroughly analyzed, physically interpreted, and mathematically modeled to enable efficient filter design.
The measured results demonstrate strong correlation with simulations when using adjustment screws, achieving RL exceeding 18 dB (TZ filter) and 16.5 dB (EZ filter), with maximum insertion losses of 2.4 dB and 1.9 dB, respectively. This represents a significant improvement over conventional microstrip filters. The loaded quality factors reach approximately 3000 for the TZ configuration and exceed 4000 for the EZ implementation, with the EZ filter showing superior group delay ripple reduction as theoretically predicted. Group delay measurements confirm in-band ripple performance, where the EZ design effectively minimizes peak-to-peak variation. Testing verified the absence of spurious resonances within ±650 MHz of the center frequency (worst-case scenario).
The achieved values remained below simulated predictions due to several factors: the reduced aspect ratio (AR = 0.48), adhesive-related inconsistencies (including excess adhesive and conductive material degradation—particularly in the PCB ground plane bonded to the metallic carrier), and conductive losses in tuning screws. These losses primarily affect input–output and cross-coupling paths, along with resonator interactions during frequency tuning. These findings highlight the need for more comprehensive laboratory characterization to improve manufacturing repeatability and reduce performance variations.
This initial characterization phase establishes the foundation for DRMF technology, contributing several key advancements, including novel input–output coupling techniques, enhanced understanding of TE01δ mode behavior, and controlled generation of cross-coupling for precise transmission zero and equalization zero placement. This research represents a significant advancement in microwave filter technology, effectively bridging the performance gap between microstrip and cavity-based implementations.
7. Future Lines
The measured degradation relative to simulations—attributed to the reduced aspect ratio (AR = 0.48), adhesive inconsistencies in PCB ground plane bonding, and tuning screw losses—dictates the following three critical research thrusts: refined bonding processes to mitigate coupling deviations, extension of DRMF designs from 4th to 12th order to meet space qualification standards while preserving transmission zero flexibility and equalization capabilities, and development of bandwidth enhancement techniques for TE01δ modes. These efforts collectively address the observed limitations in manufacturing repeatability and high-order filter implementation.
Author Contributions
Conceptualization, D.E.-A., V.G.-P. and J.L.J.-M.; Methodology, D.E.-A., S.L.-R., V.G.-P. and J.L.J.-M.; Software, D.E.-A. and S.L.-R.; Validation, D.E.-A. and J.L.J.-M.; Formal analysis, D.E.-A. and J.L.J.-M.; Investigation, D.E.-A.; Writing—original draft, D.E.-A.; Writing—review & editing, D.E.-A. and D.S.-V.; Supervision, S.L.-R., V.G.-P., J.L.J.-M. and D.S.-V.; Project administration, S.L.-R.; Funding acquisition, D.S.-V. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by a Research and Development (R&D) project between Thales Alenia Space España and University Carlos III of Madrid.
Data Availability Statement
Data are contained within the article.
Acknowledgments
This work was supported by Thales Alenia Space España, Tres Cantos (Madrid), Spain. The authors acknowledge the fabrication and assembly of the passband filters, as well as the use of company facilities for prototype characterization, which were made possible during the period in which one of the authors was affiliated with the company.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pellaco, L.; Singh, N.; Jaldén, J. Spectrum Prediction and Interference Detection for Satellite Communications. arXiv 2019, arXiv:1912.04716. [Google Scholar]
- Latif, M.; Salfi, A.U. Design of 5-channel C-band input multiplexer for communication satellites. J. Space Technol. 2015, 5, 40–46. Available online: https://www.researchgate.net/publication/328812628_Design_of_5-Channel_C-Band_Input_Multiplexer_for_Communication_Satellites (accessed on 6 April 2025).
- Monzello, R.C. Unifying G/T and noise figure metrics for receiver systems. In Proceedings of the 2020 Antenna Measurement Techniques Association Symposium (AMTA), Newport, RI, USA, 2–5 November 2020; pp. 1–4. [Google Scholar]
- Lucix Corporation. Space-Qualified Multiplexers. Available online: https://lucix.com/space-passive/multiplexers/ (accessed on 6 April 2025).
- Cameron, R.J.; Kudsia, C.M.; Mansour, R.R. Microwave Filters for Communication Systems: Fundamentals, Design and Applications; Wiley-Interscience: Hoboken, NJ, USA, 2007. [Google Scholar]
- Yu, M.; Tang, W.-C.; Malarky, A.; Dokas, V.; Cameron, R.; Wang, Y. Predistortion technique for cross-coupled filters and its application to satellite communication systems. IEEE Trans. Microw. Theory Tech. 2003, 51, 2505–2515. [Google Scholar] [CrossRef]
- Galaz, J.S.; del Pino, A.P.; Iglesias, P.M. High Order RF Filters for Communications Satellite Systems. In Proceedings of the 6th CNES/ESA International Workshop on Microwave Filters, Toulouse, France, 23–25 March 2015. [Google Scholar]
- Steffè, W.; Vitulli, F. Multilayer Metallic Filters for Q/V Band IMUX. Int. J. Microw. Wirel. Technol. 2022, 14, 362–368. [Google Scholar] [CrossRef]
- Hsieh, L.-H.; Chang, K. Tunable microstrip bandpass filters with two transmission zeros. IEEE Trans. Microw. Theory Tech. 2003, 51, 520–525. [Google Scholar] [CrossRef]
- Huang, X.; Caron, M. Type-based group delay equalization technique. IEEE Trans. Circuits Syst. I Reg. Pap. 2011, 58, 1661–1670. [Google Scholar] [CrossRef]
- Zrigui, N.; Majdy, L.; Zenkouar, L. Regulations Solution of Planar Superconductive Resonators Used in the IMUX Filters of a Communications Satellite Payload in Band C. Power 2014, 4, 6. [Google Scholar]
- Le, T.-H.; Zhu, X.-W.; Ge, C.; Duong, T.-V. A novel diplexer integrated with a shielding case using high Q-factor hybrid resonator bandpass filters. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 215–217. [Google Scholar] [CrossRef]
- Karimzadeh-Jazi, R.; Honarvar, M.A.; Khajeh-Khalili, F. High Q-factor narrow-band bandpass filter using cylindrical dielectric resonators for X-band applications. Prog. Electromagn. Res. Lett. 2018, 77, 65–71. [Google Scholar] [CrossRef]
- Chu, Q.-X.; Ouyang, X.; Wang, H.; Chen, F.-C. TE01δ-mode dielectric-resonator filters with controllable transmission zeros. IEEE Trans. Microw. Theory Tech. 2013, 61, 1086–1094. [Google Scholar] [CrossRef]
- Chen, J.-X.; Zhan, Y.; Qin, W.; Bao, Z.-H. Design of high-performance filtering balun based on TE01δ-mode dielectric resonator. IEEE Trans. Ind. Electron. 2017, 64, 451–458. [Google Scholar] [CrossRef]
- Wang, C.; Zaki, K.A. Dielectric Resonators and Filters, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2001. [Google Scholar]
- Sparagna, S.M. L-band dielectric resonator filters and oscillators with low vibration sensitivity and ultra low noise. In Proceedings of the 43rd Annual Symposium on Frequency Control, Denver, CO, USA, 31 May–2 June 1989; pp. 94–106. [Google Scholar] [CrossRef]
- Ain, M.F.; Ahmad, Z.A.; Othman, M.A.; Zubir, I.A.; Hutagalung, S.D.; Sulaiman, A.A.; Othman, A. X-band dielectric resonator bandpass filter. In Proceedings of the 2010 International Conference on Computer Applications and Industrial Electronics, Kuala Lumpur, Malaysia, 15–17 June 2010; pp. 406–410. [Google Scholar]
- Liang, E.C. An Overview of High Q TE Mode Dielectric Resonators and Applications. Ph.D. Thesis, Department of Electronic Engineering, University of California, Los Angeles, CA, USA, 2015. [Google Scholar]
- Fiedziuszko, S.J.; Holmes, S. Dielectric resonators raise your high-Q. IEEE Microw. Mag. 2001, 2, 50–60. [Google Scholar] [CrossRef]
- Mansour, R.R. High-Q tunable dielectric resonator filters. IEEE Microw. Mag. 2009, 10, 84–98. [Google Scholar] [CrossRef]
- Norman, A.; Das, S.; Rohr, T.; Ghidini, T. Advanced manufacturing for space applications. CEAS Space J. 2023, 15, 1–6. [Google Scholar] [CrossRef]
- Liu, Y.; Tomassoni, C.; Jiang, S. Dual-band dielectric resonator filters employing TE01δ mode and degenerate HEH11 modes. IEEE J. Microw. 2023, 3, 1212–1221. [Google Scholar] [CrossRef]
- Xue, Q.; Jin, J.-Y. Bandpass filters designed by transmission zero resonator pairs with proximity coupling. IEEE Trans. Microw. Theory Tech. 2017, 65, 4103–4110. [Google Scholar] [CrossRef]
- Getsinger, W.J. Microstrip dispersion model. IEEE Trans. Microw. Theory Tech. 1973, 21, 34–39. [Google Scholar] [CrossRef]
- Massoni, E.; Bozzi, M.; Perregrini, L.; Tamburini, U.A.; Tomassoni, C. A novel class of high dielectric resonator filters in microstrip line technology. In Proceedings of the 2017 IEEE MTT-S International Microwave Workshop Series on Advanced Materials and Processes for RF and THz Applications (IMWS-AMP), Pavia, Italy, 20–22 September 2017; pp. 1–3. [Google Scholar] [CrossRef]
- Bohra, H.; Prajapati, G. Microstrip filters: A review of different filter designs used in ultrawide band technology. Makara J. Technol. 2020, 24, 5. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering, 4th ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Cameron, R.J. General coupling matrix synthesis methods for Chebyshev filtering functions. IEEE Trans. Microw. Theory Tech. 1999, 47, 433–442. [Google Scholar] [CrossRef]
- Maruwa Co. Microwave Dielectric Ceramics. 2025. Available online: https://www.maruwa-g.com/e/products/ceramic/powdery-molding-goods-1.html (accessed on 4 April 2025).
- Pospieszalski, M.W. Cylindrical dielectric resonators and their applications in TEM line microwave circuits. IEEE Trans. Microw. Theory Tech. 1979, 27, 233–238. [Google Scholar] [CrossRef]
- Rogers Corporation. RT/Duroid 6002 Laminates. Available online: https://www.rogerscorp.com/advanced-electronics-solutions/rt-duroid-laminates/rt-duroid-6002-laminates (accessed on 6 April 2025).
- Khan, U.M. Dual Polarized Dielectric Resonator Antennas; Chalmers University of Technology: Göteborg, Sweden, 2010. [Google Scholar]
- Kajfez, D.; Guillon, P. Dielectric Resonators; Artech House: Norwood, MA, USA, 1990. [Google Scholar]
- Wu, Y.; Gajaweera, R.; Everard, J. Dual-band bandpass filter using TE01δ mode quarter cylindrical dielectric resonators. In Proceedings of the 2016 Asia-Pacific Microwave Conference (APMC), New Delhi, India, 5–9 December 2016; pp. 1–4. [Google Scholar]
- Ouyang, X.; Wang, B.-Y. Inline TE01δ-mode dielectric-resonator filters with controllable transmission zero for wireless base stations. Prog. Electromagn. Res. Lett. 2013, 38, 101–110. [Google Scholar] [CrossRef]
- Awasthi, S.; Biswas, A.; Akhtar, M.J. Dual-band dielectric resonator bandstop filters. Int. J. RF Microw. Comput.-Aided Eng. 2015, 25, 282–288. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).