Abstract
This study addresses the challenge of ride height control in linear motor-based active suspension systems by proposing a control strategy based on linear active disturbance rejection control (LADRC). The effectiveness of the proposed approach is experimentally validated using a high-precision test platform built on the NI cRIO-9014 real-time controller. The platform integrates a permanent magnet synchronous linear motor, a motor driver, acceleration sensors, and a vibration control system to realize closed-loop control of vehicle body height. Experimental results demonstrate that, compared with conventional PID control, LADRC achieves superior performance in height regulation accuracy, dynamic responsiveness, vertical acceleration suppression, and steady-state stability. In step response experiments, LADRC reduces the regulation time by 53.8% (from 1.3 s to 0.6 s) and lowers the steady-state error from 0.502 mm to 0.05 mm. In sinusoidal trajectory tracking tests, the LADRC approach reduces peak and RMS tracking errors by 81.5% and 80.3%, respectively. Moreover, under random road excitation, LADRC effectively attenuates high-frequency body vibrations, with reductions of 29.58% in peak vertical acceleration and 12.23% in RMS acceleration.
1. Introduction
With the continuous advancement of vehicle speed and ride comfort requirements, active suspension systems are playing an increasingly critical role in suppressing body vibrations and improving handling stability and ride quality. Although traditional active suspensions based on pneumatic or hydraulic actuators have demonstrated certain improvements in vehicle dynamics, they are often constrained by limited response speed, insufficient control precision, and low energy efficiency [1,2], making it difficult to meet the dual demands of precise posture regulation and fast response under complex driving conditions. In recent years, electromechanical active suspensions driven by linear motors have emerged as a promising solution, offering millisecond-level response time and micron-level positioning accuracy—thus overcoming key performance limitations of conventional systems [3,4].
Several studies have explored various aspects of linear motor-driven active suspension systems. For instance, Papagiannis et al. [5] proposed fault-tolerant control strategies under actuator and sensor failures to improve ride comfort and system reliability. A combined torque and suspension force control scheme based on active disturbance rejection control was presented for bearing less induction motors in [6]. Ye et al. [7] conducted a comparative study on semi-active suspension using LQR and H2/H∞ multi-objective control, revealing that both methods significantly enhance ride comfort and handling, with H2/H∞ performing better across multiple metrics. Mohamed et al. [8] compared passive suspensions with active suspensions controlled by PID and fuzzy logic within a quarter-car model, concluding that active systems markedly outperform passive ones, with fuzzy controllers showing the best performance. Zhang et al. [9] proposed an adaptive neural network backstepping controller based on an extended state observer (ESO) to improve stability and comfort. Tan et al. [10] developed a novel vertical active damping system based on electromagnetic interaction between traction and damping coils, demonstrating effective suppression of vertical and pitch motions in superconducting electrodynamic suspension systems. Shao et al. [11] introduced a robust fuzzy H∞ controller for hub motor-driven electric vehicle suspensions, achieving both vibration suppression and improved system robustness. Feng et al. [12] designed and studied a linear motor actuator tailored for active suspensions in electric vehicles, with simulation results confirming its effectiveness in enhancing comfort and stability. Sun et al. [13] employed model predictive control for accurate thrust control of linear motors and proposed a novel constrained control strategy that significantly improved thrust tracking and suspension performance. Sande et al. [14] designed a robust electromagnetic suspension controller, validated through both simulation and bench tests. Luo et al. [15] design a cascaded control strategy that combines active disturbance rejection control (ADRC) with a PID controller. A quarter-car model considering system uncertainties and the electrical characteristics of the VCM is established. Both simulation and experimental results demonstrate that the proposed method significantly outperforms passive suspension in terms of vibration suppression, dynamic tire load reduction, and suspension travel control. However, the study also highlights that using a VCM as the sole actuator results in high energy consumption. Moreover, recent works have also focused on energy recovery technologies using linear motor-based actuators, where electromechanical coupling models and regenerative control strategies have been developed to convert vibration energy into electrical energy, thereby improving energy efficiency [16,17].
However, most existing research on linear motor-based active suspensions has focused primarily on ride comfort enhancement and energy recovery. Studies and experimental investigations on dynamic ride height regulation remain limited. In addition, many of the control strategies mentioned above rely heavily on accurate suspension models, which are difficult to obtain under real-world uncertainties. Moreover, the complexity of these advanced control algorithms poses challenges for real-time implementation, given the stringent time and stability requirements of suspension systems.
To address these issues, this paper proposes a linear active disturbance rejection control (LADRC) strategy [18] for vehicle body height regulation in active suspension systems. LADRC employs a Linear Extended State Observer (LESO) to estimate and compensate for internal and external disturbances in real time, significantly reducing the dependence on model accuracy and simplifying parameter tuning compared to traditional ADRC.
To validate the proposed method, a two-degree-of-freedom active suspension model with a linear motor actuator was first built in MATLAB/Simulink. Simulation results verified the effectiveness of the control strategy in ride height regulation. Subsequently, a high-precision experimental platform was constructed using the NI cRIO embedded system, integrating a permanent magnet synchronous linear motor, high-dynamic driver, draw-wire encoder, and acceleration sensors. Motor control and synchronized multi-source data acquisition were implemented using LabVIEW FPGA [19,20]. Control performance was evaluated under both sinusoidal tracking and random road excitations to assess tracking accuracy and disturbance rejection capabilities.
2. Establishment of Linear Motor Active Suspension Model
2.1. Dynamic Model of the Active Suspension System
The two-degree-of-freedom (2-DOF) quarter-car model effectively captures the vertical dynamics of a vehicle and is widely used for analyzing ride comfort and suspension performance. The corresponding dynamic model is illustrated in Figure 1.
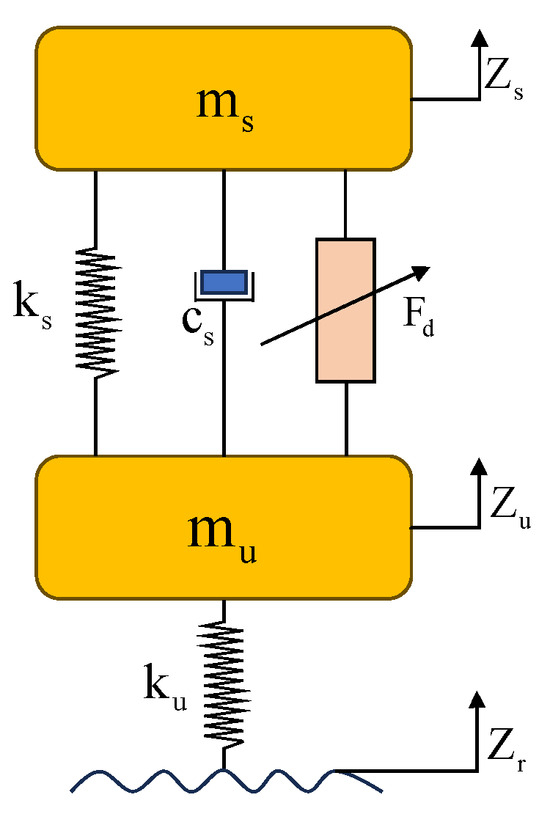
Figure 1.
Quarter-car suspension model.
Based on Newton’s laws of motion, the dynamic behavior of the vehicle suspension system can be described by the following set of differential equations:
In the simplified model shown in Figure 1, represents the sprung mass (vehicle body), and denotes the unsprung mass (wheel assembly). and correspond to the suspension stiffness and tire stiffness, respectively. denotes the vertical displacements of the sprung and unsprung masses, while represents the road excitation input. The term denotes the actuation force generated by the linear motor actuator.
The road excitation input is modeled using a filtered white noise approach, which effectively captures the stochastic characteristics of real road surfaces in the time domain: , where represents the vertical road displacement, is the vehicle forward speed, is a zero-mean Gaussian white noise process, and is a constant that characterizes the spatial frequency content of the road profile.
2.2. Mathematical Model of Linear Motor
The linear motor is derived from the traditional rotary motor by unwrapping its radial structure and reshaping it into a linear configuration. Specifically, when a rotary motor is radially cut and laid out along the circumference, it forms a tubular linear motor. In this transformation, the stator of the rotary motor becomes the primary part (stator) of the linear motor, and the rotor becomes the secondary part (mover). Through the relative motion between the primary and secondary, the linear motor enables bidirectional conversion between electrical and mechanical energy. Compared to other types of actuators used in active suspension systems, linear motors offer notable advantages such as simple structure, high energy conversion efficiency, and excellent control precision.
Under the assumptions of negligible harmonics, magnetic saturation, and end effects, the voltage and flux linkage equations of the linear motor in the rotating d–q coordinate frame can be expressed as [21,22]
In these equations, and represent the d- and q-axis stator voltages, and are the corresponding stator currents, and and denote the d- and q-axis inductances. and are the d- and q-axis components of the stator flux linkage. is the linear velocity of the mover, is the pole pitch of the motor, denotes the stator resistance, and is the permanent magnet flux linkage.
The electromagnetic thrust generated by the linear motor can be expressed as
Under the vector control strategy, the electromagnetic thrust equation simplifies to
The mechanical equilibrium of the mover is governed by the following equation:
In this equation, denotes the thrust constant of the linear motor, is the mass of the mover, is the viscous friction coefficient, and represents the external load force acting on the mover.
3. Ride Height Regulation Based on Linear Active Disturbance Rejection Control
When a vehicle is in motion, the active suspension system experiences forced vertical vibrations due to road surface excitations, which significantly reduce ride comfort. Therefore, the active suspension must achieve two simultaneous objectives: suppressing body vibrations and regulating ride height.
The Linear Active Disturbance Rejection Controller (LADRC) consists of three main components: a Linear Extended State Observer (LESO), a linear feedback control law, and a disturbance compensation unit. Among these, the LESO is the most critical component. It enables real-time estimation of the total disturbance acting on the system, which includes both internal disturbances due to model inaccuracies and external disturbances caused by road irregularities [23]. The structure of the LADRC is illustrated in Figure 2.
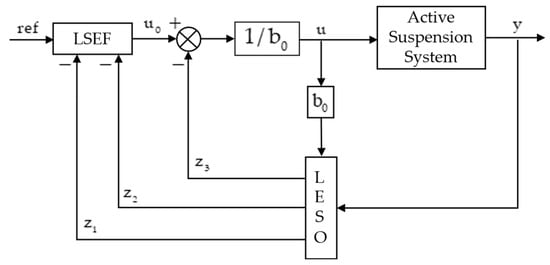
Figure 2.
Control structure of LADRC.
The goal of the control system is to minimize body vibration while maintaining the desired ride height. Accordingly, the vertical displacement of the sprung mass is selected as the system output. Since the active suspension force is generated by the linear motor, the motor thrust is selected as the control input.
The second-order system described in Equation (7) can be rewritten as
In this equation, and are system parameters, and represent the system output and control input, respectively, and denotes the external disturbance acting on the system.
Equation (1) can be reformulated as
In this expression, is the estimated value of the system parameter , and represents the total disturbance of the system, which includes both internal and external disturbances.
Let , , and ; the system equation can then be expressed as
In this equation, and are the system state variables, and is the extended state representing the total disturbance.
Equation (9) can be transformed into the extended state-space form as follows:
where , , , and .
The Linear Extended State Observer (LESO) is constructed as follows:
In this observer, , , and denote the estimates of the system states and and the total disturbance , respectively. is the measured system output, and , , and are the observer gain coefficients that determine the convergence rate of the estimates. Since the total disturbance is unknown but can be estimated through the correction term, its derivative is not required. Therefore, the LESO can be reformulated as
In this formulation, represents the composite input, and is the observer output. Through the use of a pole placement approach, the observer gains are determined by assigning the poles of the LESO to specific locations at :
The observer gains can be selected to be , , and , where denotes the observer bandwidth.
When the state error feedback controller is able to accurately estimate the total disturbance, i.e., , the LADRC control law can be defined as . Under this condition, the closed-loop system can be simplified into a cascaded integrator structure:
The linear error feedback control law is implemented in the form of a proportional–derivative (PD) controller:
where is the desired ride height, and and are the controller gains. Through the substitution of Equation (15) into Equation (14), the closed-loop transfer function of the system can be obtained as
Let and , where denotes the controller bandwidth. Through the selection of an appropriate value of , the system can be ensured to be bounded-input bounded-output (BIBO)-stable.
The working principle of the ride height controller is illustrated in Figure 3. A cascaded position–current dual-loop control strategy is adopted. The outer position loop employs a Linear Active Disturbance Rejection Controller (LADRC), which calculates the force required to move the active suspension to the desired ride height based on the reference height and the measured body displacement.
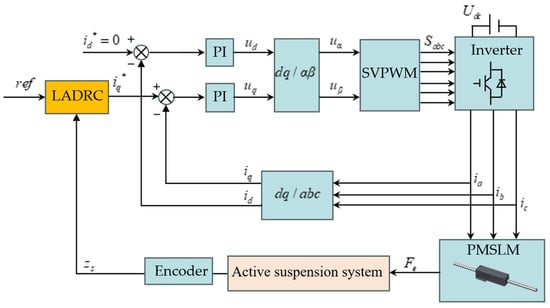
Figure 3.
Schematic diagram of the ride height control system.
The inner current loop utilizes a PI controller. The desired force output from the position loop is converted into a reference q-axis current via the thrust constant. This current reference is then used to generate three-phase voltage inputs through space vector pulse-width modulation (SVPWM), which are applied to the servo control system of the permanent magnet synchronous linear motor (PMSLM), thereby realizing precise vehicle body height adjustment.
4. Simulation and Experimental Validation
To validate the effectiveness of the linear active disturbance rejection control (LADRC) strategy for ride height regulation, a MATLAB/Simulink R2024a-based simulation model of a linear motor-driven active suspension system was developed. The model integrates the vehicle dynamics, linear motor actuator, and the dual-loop LADRC–PI control structure. The parameters of the vehicle model are as follows: = 29 kg, = 5.88 kg, = 1880 , = 19,000 , and = 174 . The parameters of the linear motor are listed in Table 1. The sprung mass, unsprung mass, suspension stiffness, and other vehicle-related parameters are based on the bench test platform design, while the linear motor parameters are obtained from the manufacturer’s datasheet. To ensure sufficient thrust margin during the initial design of the test bench, a relatively large linear motor was selected. The primary (mover) coil has a length of 330 mm with a base cross-section of 60 mm × 60 mm, while the secondary (stator) permanent magnet assembly measures 560 mm in length with a base diameter of 32 mm.

Table 1.
Specifications of PMSLM.
In order to ensure a fair and meaningful comparison with the proposed LADRC, a systematic tuning approach was adopted for the PID controller in both the simulation and experimental stages.
In the simulation phase, the PID parameters were designed using the Control System Designer toolbox in MATLAB/Simulink. The Bode plot-based pole–zero adjustment method was applied to improve system characteristics, followed by step response tests to validate the performance. After fine-tuning, a satisfactory set of parameters was obtained: , , and .
For the hardware-in-the-loop experiments, a discrete incremental-form PID controller was implemented on the LabVIEW FPGA platform. Based on the gain-tuning results from simulation, further step response tests were conducted to balance rise time and overshoot under real-world constraints. After multiple iterations, a well-optimized set of parameters was determined: , , and .
This two-stage tuning process ensures that the PID controller used in the comparison represents a realistically optimized benchmark, thereby lending credibility and reference value to the comparative evaluation with LADRC.
To verify the effectiveness of the proposed ride height control strategy, a sinusoidal road excitation with a frequency of 2 Hz and an amplitude of 0.01 m was applied as the input. The desired ride height was set to 0.03 m. The simulation results are presented in Figure 4, Figure 5 and Figure 6.
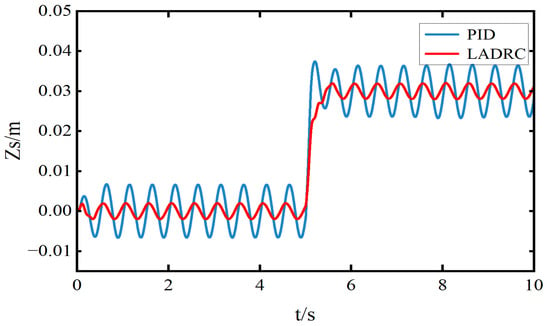
Figure 4.
Sprung mass displacement with 0.03 m ride height increase.
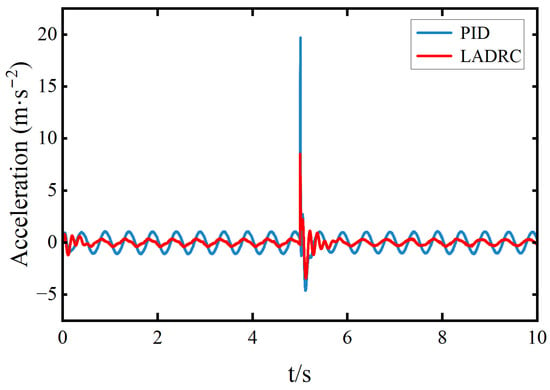
Figure 5.
Electromagnetic thrust during a 0.03 m ride height increase in the sprung mass.
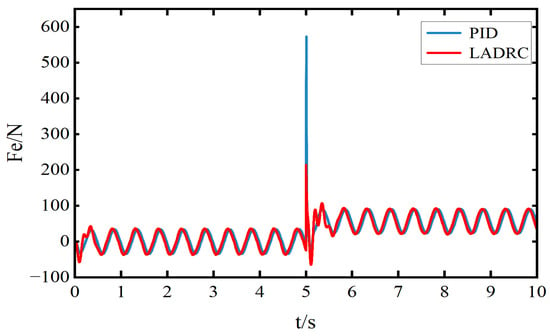
Figure 6.
Sprung mass acceleration during a 0.03 m ride height increase.
Figure 4 shows the ride height displacement response under sinusoidal road excitation. It can be observed that the LADRC significantly reduces the steady-state error. The root mean square (RMS) value of the steady-state error under LADRC is 0.00274 m, which represents a 49.35% reduction compared to the PID controller (0.0054 m). Figure 5 illustrates the acceleration of the sprung mass. Under the same excitation, the RMS value of the vertical acceleration with LADRC is 0.4397 m/s2, showing a 54% reduction compared to the PID controller (0.9573 m/s2), indicating improved ride comfort. Figure 6 presents the electromagnetic thrust response. It can be seen that the average thrust produced by both controllers is nearly the same. However, the PID controller exhibits a large thrust spike in the rising phase around 5 s, while the LADRC maintains a smoother and more controlled thrust profile.
To further verify the effectiveness of the proposed ride height control strategy, an active suspension system was constructed by mechanically paralleling a permanent magnet synchronous linear motor (PMSLM) with a suspension spring. The electrical parameters of the linear motor are listed in Table 1, and the control workflow of the experimental platform is illustrated in Figure 7.
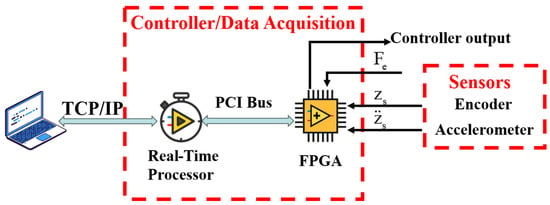
Figure 7.
Software control architecture.
The experimental platform is shown in Figure 8. The primary coil of the linear motor is rigidly connected to the sprung mass, while the secondary permanent magnet part is fixed to the unsprung mass. The linear motor is equipped with a built-in encoder that measures the relative displacement between the vehicle body and the wheel. The sprung and unsprung masses are connected via four guide rods and linear bearings, allowing smooth vertical sliding. An external draw-wire displacement encoder is used to measure the absolute body displacement, and an acceleration sensor is mounted on the sprung mass to capture vertical acceleration.

Figure 8.
Experimental platform structure.
The control and data acquisition system consists of a host PC, an NI cRIO controller, NI data acquisition modules, various sensors, and a motor driver. The motor driver is configured to operate in current control mode, and all necessary power and signal wiring is completed to enable control of the linear motor and its driver. The motor control and data acquisition programs are developed on the LabVIEW FPGA platform. The control voltage signal is generated via the NI-9263 module and sent to the linear motor driver to achieve real-time control of the linear motor system, including ride height tracking. Meanwhile, the NI-9411 module is used to acquire encoder signals, and the NI-9234 module is used to acquire acceleration signals. All collected data is transmitted from the real-time (RT) controller to the host PC via a network stream. On the host side, various physical signals can be visualized, analyzed, and stored for further evaluation.
Based on the ride height regulation strategy proposed in Section 3, the linear active disturbance rejection control (LADRC) algorithm was first implemented and discretized using the zero-order hold (ZOH) method. The discrete controller was then deployed to the LabVIEW FPGA platform. According to the physical parameters of the suspension system, the high-frequency gain was set to 0.04, the controller bandwidth to 16 rad/s, and the observer bandwidth to 96 rad/s. The control sampling period was configured to 200 μs. The external excitation signal was generated by a DG1022 arbitrary waveform generator and applied to the vibration platform. Under external excitation, the active suspension system responded dynamically. The absolute displacement of the vehicle body, measured by the displacement sensor, was used as the feedback signal. A target ride height was set via the host PC. The LADRC running on the LabVIEW FPGA computed the required active control force, which was then converted into an analog voltage signal. This voltage signal was output to the motor driver through the NI-9263 module, enabling the linear motor actuator to generate the corresponding control force to track the desired ride height.
Test Condition 1: Step Response Evaluation. The step input signal represents a sudden change in the desired vehicle body height, simulating scenarios such as abrupt road obstacles or active ride height adjustment. Figure 9 and Figure 10 and Table 1 illustrate the displacement tracking performance and tracking error of the LADRC and PID controllers under the given step input.
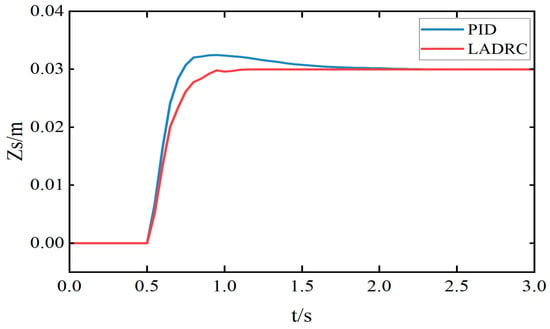
Figure 9.
Sprung mass displacement under step input.
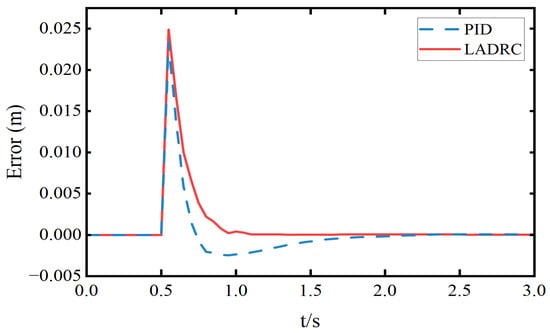
Figure 10.
Tracking error of sprung mass displacement.
As shown in Figure 9 and Figure 10 and Table 2, under the given height command, the traditional PID controller exhibits a settling time of 1.3 s, an overshoot of 7.87%, and a steady-state error of 0.502 mm. In contrast, the LADRC achieves a faster settling time of 0.6 s with a significantly lower steady-state error of 0.05 mm. Moreover, the response of the LADRC is smoother and free from overshoot, demonstrating superior transient and steady-state performance.

Table 2.
Step response test performance evaluation indicators.
Under this test condition, the LADRC parameters and the current-loop PI controller parameters were kept identical in both the simulation and the experimental setup. The resulting sprung mass displacement curves for a 0.03 m upward step in body height are shown in Figure 11. As illustrated, the vehicle body reaches the target height in a short time in both cases. Specifically, the adjustment time in the simulation is approximately 0.4 s, while in the experiment, it is around 0.6 s. The slightly longer adjustment time observed in the experiment is mainly due to practical factors such as unmodeled friction, actuator delay, and sensor noise. Nevertheless, the strong agreement between simulation and experimental results confirms the effectiveness and robustness of the proposed control strategy in real-world applications.
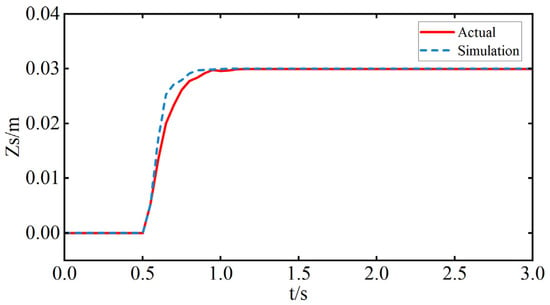
Figure 11.
Sprung displacement from simulation and experiment.
Test Condition 2: Ride Height Control under Random Road Excitation. In this test, the equilibrium position is set to 0 m and the target ride height is set to 0.03 m. The vehicle speed is 30 m/s, and the road excitation corresponds to a Class B road profile. The experimental results are presented in Figure 12, Figure 13 and Figure 14 and Table 3.
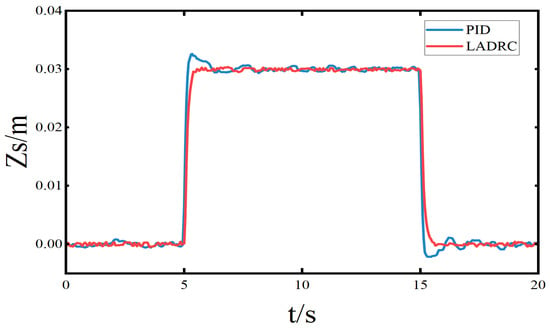
Figure 12.
Tracking error of sprung mass displacement (B, 30 m/s).
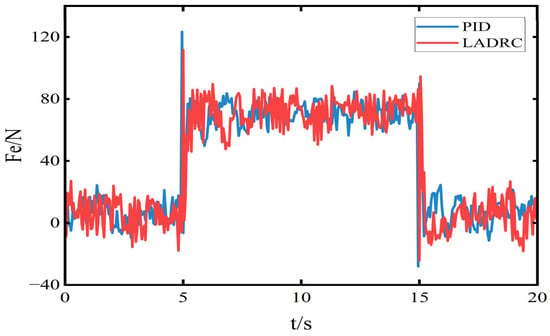
Figure 13.
Electromagnetic thrust during a 0.03 m upward movement.
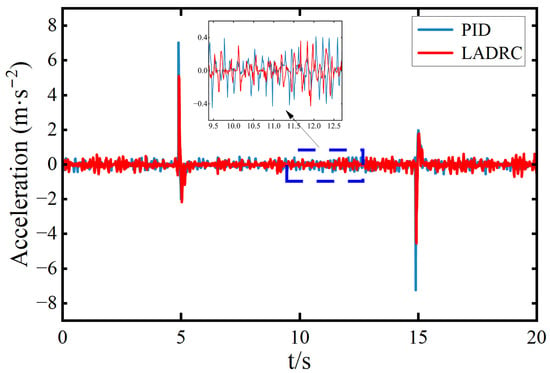
Figure 14.
Sprung mass acceleration during a 0.03 m upward movement.

Table 3.
Comparison of control performance between PID and LADRC.
Figure 12, Figure 13 and Figure 14 illustrate the time-domain performance differences between PID control and LADRC in terms of body displacement, electromagnetic thrust, and body acceleration. At 5 s, an upward control action is applied. The LADRC achieves a settling time of 0.55 s, whereas the PID controller requires 1.15 s. At 15 s, a downward control action returns the vehicle body to the equilibrium position, where LADRC settles within 0.65 s, while PID takes 1.05 s. Moreover, by comparison, the tracking error of LADRC is only about 38.4% of that of the PID controller, representing a 61.6% reduction in RMS error, further confirming the superior transient and steady-state performance of LADRC.
During the 5–15 s interval, the root mean square (RMS) value of the electromagnetic thrust under LADRC is 72.69 N, while that under PID control is 70.67 N, indicating a comparable average thrust level. The thrust output under PID control appears more stable. This is because LADRC continuously estimates and compensates for disturbances in real time to maintain ride height stability, which leads to larger thrust fluctuations during rapid adjustments.
Figure 14 shows the time-domain response of body acceleration throughout the entire ride height adjustment process. As shown in Table 2, the RMS value of body acceleration under LADRC is 0.33 m/s2, compared to 0.376 m/s2 under PID control, representing a 12.23% reduction. At the moments of upward and downward movement, both control strategies exhibit transient spikes in acceleration. The maximum body acceleration under LADRC is 5.095 m/s2, while that under PID reaches 7.235 m/s2, reflecting a 29.58% decrease with LADRC.
Figure 15 shows the power spectral density (PSD) of the body acceleration. It can be observed that the PID-controlled system exhibits higher PSD peaks across the entire frequency range, indicating a stronger response to disturbances, particularly under random road excitation or external inputs in the low- and mid-frequency bands. Although PID is effective in attenuating low-frequency disturbances, its performance in suppressing high-frequency noise is limited, which may lead to high-frequency oscillations and potential instability. In contrast, the PSD of the LADRC-controlled system remains consistently lower than that of PID across all frequencies, especially in the high-frequency range (>30 Hz), demonstrating its superior ability to suppress high-frequency disturbances. This indicates that LADRC offers better acceleration attenuation performance under random road excitation compared to PID control.
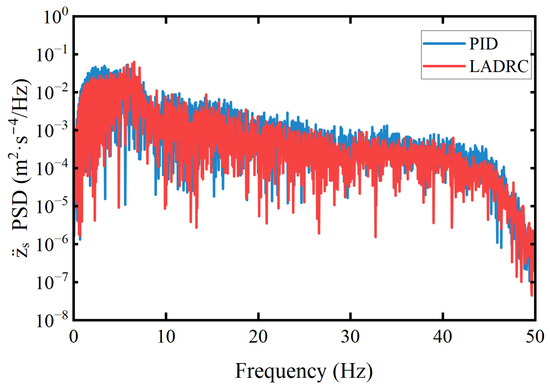
Figure 15.
Sprung mass acceleration PSD.
Test Condition 3: Sinusoidal Trajectory Tracking Test. A sinusoidal signal with a frequency of 0.2 Hz and an amplitude of 0.03 m is applied as the reference displacement trajectory for the sprung mass, in order to compare the tracking performance of the two controllers. The resulting sprung mass trajectory, tracking error, and acceleration response are shown in Figure 16, Figure 17 and Figure 18, and the corresponding performance metrics are summarized in Table 3.
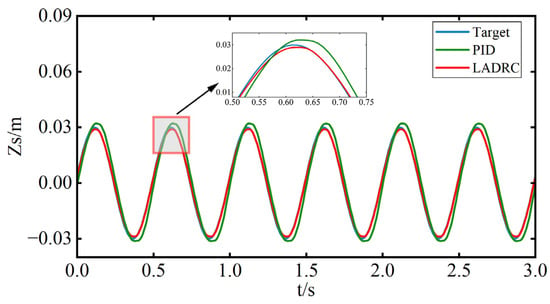
Figure 16.
Sprung mass displacement tracking (sinusoidal signal).
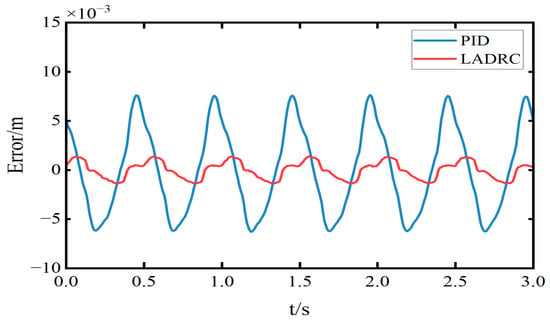
Figure 17.
Sprung mass displacement tracking error.
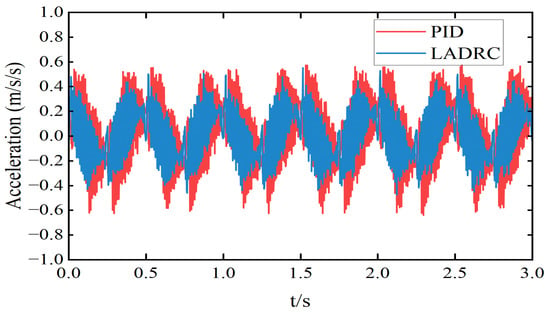
Figure 18.
Sprung mass displacement acceleration.
As shown in the figure, both control strategies exhibit phase delay in the tracking curves, but the LADRC shows no noticeable overshoot and exhibits a smaller phase lag compared to PID. According to Table 4, the LADRC demonstrates superior performance in sinusoidal trajectory tracking. Specifically, it reduces the peak tracking error by 81.5% and the RMS tracking error by 80.3% compared to PID. Additionally, the peak acceleration is reduced by 16.74%, and the RMS acceleration is reduced by 26.61%. These results indicate that LADRC outperforms PID in terms of both accuracy and stability, particularly during dynamic transitions, where it significantly reduces tracking error.

Table 4.
Comparison of sinusoidal trajectory tracking performance metrics.
The actual and estimated data of the sprung mass position and velocity obtained by the LESO used in the LADRC are shown in the figures. Figure 19 illustrates the position and its estimation, where the estimated curve closely overlaps with the actual position curve, indicating high estimation accuracy. Figure 20 presents the velocity and its corresponding estimation. The estimated velocity generally follows the actual velocity well. However, there is a noticeable estimation error when the velocity undergoes sudden changes. This discrepancy may be attributed to a slight lag in the LESO’s response to abrupt disturbances. Nevertheless, overall, the LESO is capable of accurately tracking velocity variations, with estimation errors primarily occurring during transient moments. These errors have minimal impact on overall system stability.
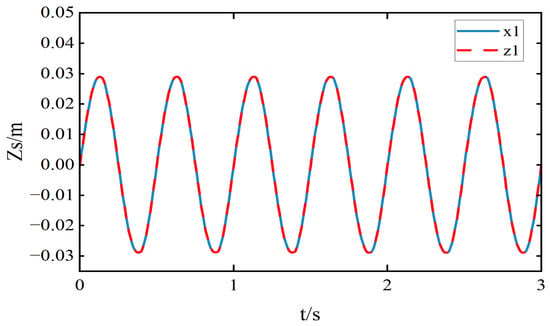
Figure 19.
Sprung mass position and position estimation.
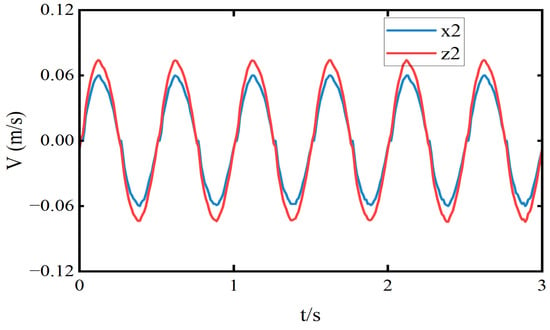
Figure 20.
Sprung mass velocity and velocity estimation.
5. Discussion and Conclusions
This study focuses on an active suspension system driven by a linear motor and proposes a linear active disturbance rejection control (LADRC) algorithm tailored for such actuators. A height control strategy based on LADRC is developed to address the problem of fast and accurate vehicle body height adjustment. Through the construction of a two-degree-of-freedom active suspension model that incorporates a permanent magnet synchronous linear motor (PMSLM), an LADRC with real-time disturbance estimation and compensation capability is designed and implemented, significantly improving the system’s dynamic response and robustness.
In contrast to Luo et al. [15] who investigated the vertical dynamics of a voice coil motor (VCM)-based active suspension system under sinusoidal road profiles, this study focuses on random road excitations. Their simulation and experimental results demonstrated that the VCM active suspension, controlled by an ADRC algorithm, can significantly enhance suspension performance. However, their research primarily targeted disturbance rejection under large, periodic excitations. In comparison, our study emphasizes the effective suppression of continuous small-scale disturbances caused by random road inputs, further demonstrating that the proposed LADRC-based control strategy enhances the overall stability and robustness of the suspension system in more complex and realistic driving scenarios.
In the simulation phase, the performance of the proposed LADRC strategy under sinusoidal road excitation was analyzed. The results demonstrate that the LADRC achieves smaller steady-state error and overshoot in height regulation, and effectively suppresses vertical acceleration induced by road disturbances, outperforming traditional PID control. Building on this, an active suspension test platform based on the NI cRIO platform was developed. The LADRC algorithm was discretized and deployed on LabVIEW FPGA, enabling microsecond-level control cycle operation. The experimental results further verify that the proposed control method achieves fast response, high precision, and good stability in height regulation for linear motor-driven active suspension systems.
Author Contributions
Conceptualization, J.Y. and C.J.; methodology, J.Y. and C.J.; software, J.Y. and C.J.; validation, J.Y. and C.J.; formal analysis, J.Y. and C.J.; investigation, J.Y. and C.J.; resources, J.Y.; data curation, J.Y. and C.J.; writing—original draft preparation, C.J.; writing—review and editing, J.Y.; visualization, J.Y. and C.J.; supervision, J.Y. and C.J.; project administration, J.Y. and C.J.; funding acquisition, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Natural Science Foundation of China (Grant number 51975299) and the Key Research and Development Project of Yangzhou City (No. YZ2023009).
Data Availability Statement
The data are not publicly available due to privacy or ethical restrictions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ding, R.; Wang, R.; Meng, X.; Chen, L. Study on Coordinated Control of the Energy Regeneration and the Vibration Isolation in a Hybrid Electromagnetic Suspension. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2017, 231, 1530–1539. [Google Scholar] [CrossRef]
- Abdelkareem, M.A.A.; Xu, L.; Guo, X.; Ali, M.K.A.; Elagouz, A.; Hassan, M.A.; Essa, F.A.; Zou, J. Energy Harvesting Sensitivity Analysis and Assessment of the Potential Power and Full Car Dynamics for Different Road Modes. Mech. Syst. Signal Process. 2018, 110, 307–332. [Google Scholar] [CrossRef]
- Shi, D.; Chen, L.; Wang, R.; Jiang, H.; Shen, Y. Design and Experiment Study of a Semi-Active Energy-Regenerative Suspension System. Smart Mater. Struct. 2014, 24, 015001. [Google Scholar] [CrossRef]
- Shi, D.; Pisu, P.; Chen, L.; Wang, S.; Wang, R. Control Design and Fuel Economy Investigation of Power Split HEV with Energy Regeneration of Suspension. Appl. Energy 2016, 182, 576–589. [Google Scholar] [CrossRef]
- Papagiannis, D.; Tsioumas, E.; Jabbour, N.; Koseoglou, M.; Mademlis, C. Fault Tolerance in an Active Suspension System with a Linear Permanent Magnet Actuator for Automotive Applications. In Proceedings of the 2019 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Athens, Greece, 22–23 April 2019; Volume 1, pp. 203–208. [Google Scholar]
- Li, K.; Cheng, G.; Sun, X.; Zhao, D.; Yang, Z. Direct Torque and Suspension Force Control for Bearingless Induction Motors Based on Active Disturbance Rejection Control Scheme. IEEE Access 2019, 7, 86989–87001. [Google Scholar] [CrossRef]
- Ye, H.; Zheng, L. Comparative Study of Semi-Active Suspension Based on LQR Control and H2/H∞ Multi-Objective Control. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 3901–3906. [Google Scholar]
- Soudani, M.S.; Aouiche, A.; Chafaa, K.; Aouiche, E.; Taleb, M.; Fares, Z. Comparison between a Passive and Active Suspension Vehicle Using PID and Fuzzy Controllers with Two Entries Applied on Quarter Vehicle Model. In Proceedings of the 2019 1st International Conference on Sustainable Renewable Energy Systems and Applications (ICSRESA), Tébessa, Algeria, 4–5 December 2019; pp. 1–6. [Google Scholar]
- Chang, L.; Wang, H.; Tian, Y. Extended State Observer Based Backstepping Control for Active Suspension System Ride Comfort. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 5718–5723. [Google Scholar]
- Tan, Y.; Zhou, D.; Qu, M.; Li, J.; Chen, Q.; Jia, Z.; Leng, P.; Liu, M. A Novel Vertical Active Damping System for the Superconducting Electrodynamic Suspension. IEEE Trans. Intell. Transp. Syst. 2024, 25, 17702–17717. [Google Scholar] [CrossRef]
- Shao, X.; Naghdy, F.; Du, H. Reliable Fuzzy H∞ Control for Active Suspension of in-Wheel Motor Driven Electric Vehicles with Dynamic Damping. Mech. Syst. Signal Process. 2017, 87, 365–383. [Google Scholar] [CrossRef]
- Feng, Y.; Lu, Q.; Li, Y. Design and Research of a Linear Actuator for Electric Vehicle Active Suspension. In Proceedings of the 2023 26th International Conference on Electrical Machines and Systems (ICEMS), Zhuhai, China, 5–8 November 2023; pp. 136–141. [Google Scholar]
- Sun, X.; Wu, M.; Yin, C.; Wang, S. Model Predictive Thrust Force Control for Linear Motor Actuator Used in Active Suspension. IEEE Trans. Energy Convers. 2021, 36, 3063–3072. [Google Scholar] [CrossRef]
- van der Sande, T.P.J.; Gysen, B.L.J.; Besselink, I.J.M.; Paulides, J.J.H.; Lomonova, E.A.; Nijmeijer, H. Robust Control of an Electromagnetic Active Suspension System: Simulations and Measurements. Mechatronics 2013, 23, 204–212. [Google Scholar] [CrossRef]
- Luo, J.; Wu, W.; Ge, L. Vertical Dynamics of Voice Coil Motor Active Suspension with Active Disturbance Rejection Control. In Proceedings of the 2019 IEEE International Conference on Mechatronics and Automation (ICMA), Tianjin, China, 4–7 August 2019; pp. 1919–1924. [Google Scholar]
- Kou, F.; Chen, L.; Zhang, D. Energy Management Strategy for Active Suspension with Linear Motor. In Proceedings of the 2016 IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 3–5 October 2016; pp. 419–423. [Google Scholar]
- Silveira, M.; Wahi, P.; Fernandes, J.C.M. Exact and Approximate Analytical Solutions of Oscillator with Piecewise Linear Asymmetrical Damping. Int. J. Non-Linear Mech. 2019, 110, 115–122. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and Bandwidth-Parameterization Based Controller Tuning. In Proceedings of the 2003 American Control Conference, Denver, CO, USA, 4–6 June 2003; Volume 6, pp. 4989–4996. [Google Scholar]
- Ortiz, A.; Mendez, E.; Balderas, D.; Ponce, P.; Macias, I.; Molina, A. Hardware Implementation of Metaheuristics through LabVIEW FPGA. Appl. Soft Comput. 2021, 113, 107908. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Zhang, W.; Zhao, F. IC-GLI: A Real-Time, INS-Centric GNSS-LiDAR-IMU Localization System for Intelligent Vehicles. Meas. Sci. Technol. 2025, 36, 026314. [Google Scholar] [CrossRef]
- Wang, J.; Li, D. Application of Fuzzy PID Control in PMLSM Servo Drive System. In Proceedings of the 2015 IEEE International Conference on Mechatronics and Automation (ICMA), Beijing, China, 2–5 August 2015; pp. 6–10. [Google Scholar]
- Xu, W.; Liao, K.; Ge, J.; Qu, G.; Cheng, S.; Wang, A.; Boldea, I. Improved Position Sensorless Control for PMLSM via an Active Disturbance Rejection Controller and an Adaptive Full-Order Observer. IEEE Trans. Ind. Appl. 2023, 59, 1742–1753. [Google Scholar] [CrossRef]
- Lin, P.; Wu, Z.; Fei, Z.; Sun, X.-M. A Generalized PID Interpretation for High-Order LADRC and Cascade LADRC for Servo Systems. IEEE Trans. Ind. Electron. 2022, 69, 5207–5214. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).