Abstract
As an essential platform for aggregating and coordinating distributed energy resources (DERs), the virtual power plant (VPP) has attracted widespread attention in recent years. With the increasing scale of VPPs, energy interaction and sharing among VPP clusters (VPPCs) have become key approaches to improving energy utilization efficiency and reducing operational costs. Therefore, studying the coordinated operation mechanism of VPPCs is of great significance. This paper proposes a two-stage coordinated operation model for VPPCs based on energy interaction to enhance the overall economic performance and coordination of the cluster. In the day-ahead stage, a cooperative operation model based on Nash bargaining theory is constructed. The inherently non-convex and nonlinear problem is decomposed into a cluster-level benefit maximization subproblem and a benefit allocation subproblem. The Alternating Direction Method of Multipliers (ADMM) is employed to achieve distributed optimization, ensuring both the efficiency of coordination and the privacy and decision independence of each VPP. In the intra-day stage, to address the uncertainty in renewable generation and load demand, a real-time pricing mechanism based on the supply–demand ratio is designed. Each VPP performs short-term energy forecasting and submits real-time supply–demand information to the coordination center, which dynamically determines the price for the next trading interval according to the reported imbalance. This pricing mechanism facilitates real-time electricity sharing among VPPs. Finally, numerical case studies validate the effectiveness and practical value of the proposed model in improving both operational efficiency and fairness.
1. Introduction
With the rapid advancement of electricity market reforms and the increasing penetration of distributed energy resources (DERs), virtual power plants (VPPs)—as a key means of aggregating and managing distributed resources—have attracted widespread attention and extensive research [1]. Within a given region, multiple VPPs can form a virtual power plant cluster (VPPC), where energy interaction and sharing among VPPs can significantly enhance energy utilization efficiency and reduce individual operating costs [2]. However, the coordinated operation of a VPPC involves multiple stakeholders with complex competitive and cooperative relationships, making the study of VPPC coordination mechanisms of great significance [3].
The existing research on VPPC coordination mechanisms can generally be categorized into two approaches: centralized scheduling [4,5,6,7] and distributed trading [8,9,10,11]. In the centralized scheduling approach, the coordinated operation of the VPPC is managed by a central computing unit, which collects operational parameters from all VPPs and solves the global optimization problem in a centralized manner. In contrast, the distributed trading approach does not rely on a central coordinator; instead, each participant independently engages in sequential iterative optimization through distributed algorithms. Due to challenges such as data privacy concerns, high computational complexity, and dimensional scalability, centralized models are often unsuitable for multi-stakeholder applications. By comparison, the distributed trading approach allows each VPP to solve its own optimization problem independently, better aligning with the needs for privacy protection and decision-making autonomy among stakeholders.
Similarly, transaction-solving algorithms for VPPC systems can also be broadly classified into two categories. The first category includes distributed optimization algorithms such as ADMM and Lagrangian relaxation methods. These algorithms coordinate trading decisions by iteratively updating transaction strategies through limited information exchange among VPPs, ultimately forming a global trading solution. References [12,13,14] have proposed multi-agent economic dispatch models for VPPCs based on ADMM, objective cascading, and other distributed approaches. These methods offer strong privacy guarantees, as convergence can be achieved through minimal data exchange between entities. However, these studies do not address the issue of benefit allocation following distributed optimization. To address this, some works [15,16,17] incorporate cooperative profit allocation using the Shapley value method within a distributed trading framework. Nonetheless, the Shapley value suffers from high computational complexity and scalability issues, especially as the number of participants increases, which limits its applicability in large-scale scenarios. In contrast, the Nash bargaining model does not experience significant computational burden growth with more participants. Accordingly, references [18,19,20] adopt Nash bargaining theory combined with ADMM to achieve fair benefit allocation among VPPs, offering better computational efficiency than the Shapley-based approach. From the above literature, it is evident that the primary characteristic of this first category of algorithms lies in the relatively long iteration time required, making them more suitable for day-ahead planning and transaction scheduling.
The second category of algorithms includes economic mechanism design-based approaches such as continuous double auction (CDA) algorithms and bill-sharing mechanisms. References [21,22,23,24] implement multi-agent electricity trading through continuous double auctions, enabling dynamic power matching among market participants. Building on this, references [25,26] introduce the Vickrey–Clarke–Groves (VCG) auction mechanism to incentivize truthful bidding behavior among agents during the market-clearing process. Reference [27] presents a comparative analysis of three representative market mechanisms: bill-sharing, intermediate market rate, and auction-based mechanisms. This second category of algorithms is characterized by fewer iterations and shorter computation times, making it more suitable for real-time operation in the intra-day stage.
In summary, this paper proposes a two-stage energy sharing mechanism for VPPC, covering both the day-ahead and intra-day stages. In the day-ahead stage, a cooperative operation model for the VPPC is established based on Nash bargaining theory. The model is solved in a distributed manner using the ADMM algorithm, ensuring privacy preservation and decision-making autonomy for each participant during the iterative trading process. In the intra-day stage, a real-time energy sharing mechanism is developed based on the supply–demand ratio. Each VPP performs short-term energy forecasting to obtain its real-time supply and demand estimates, which are then submitted to the coordination center. The coordination center dynamically generates the real-time transaction price for the next interval based on the supply–demand ratio pricing mechanism.
2. Coordinated Operation Architecture of VPPC
A VPP aggregates various types of DERs and externally exhibits a dual nature of both generation and load. In this study, the distributed resources within each VPP are assumed to include controllable generators (CGs), wind turbines (WTs), photovoltaic units (PVs), energy storage systems (ESSs), translational loads (TLs), and interruptible loads (ILs).
The coordinated operation architecture of VPPC is shown in Figure 1. In the day-ahead stage, with a temporal resolution of 1 h, the VPPC conducts distributed energy trading based on a Nash bargaining model combined with the ADMM. The non-convex and nonlinear bargaining problem is decomposed into a cluster-wide profit maximization subproblem and a revenue allocation subproblem, both of which are solved in a distributed manner using the ADMM algorithm. This approach ensures that the optimization process maintains the privacy and decision autonomy of each VPP participant while achieving global economic efficiency.
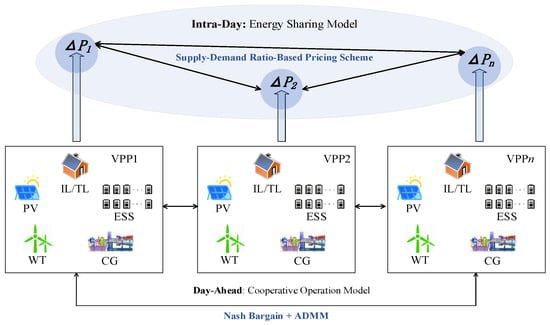
Figure 1.
Coordinated Operation Architecture of VPPC.
In the intra-day stage, to address the real-time fluctuations of renewable generation and load demand, a dynamic pricing mechanism based on the supply–demand ratio is proposed. Each VPP performs short-term energy forecasting to determine its 15 min interval supply and demand values, and calculates the deviation from the day-ahead schedule. These deviations are submitted to the coordination center. Considering the responsiveness required for real-time dispatch, the coordination center automatically generates and announces the real-time electricity price for the upcoming trading interval based on the reported deviations, thereby guiding energy sharing adjustments within the cluster in a timely and efficient manner.
3. Day-Ahead Cooperative Operation Model of VPPC
3.1. Single VPP Independent Operation Mode
The operation goal of a single VPP is to minimize its own operating costs based on the transaction costs with the power grid. Its objective function can be expressed as follows:
where represents the cost of VPPi in independent operation mode; represents the power generation cost of the unit; represents the charging and discharging cost of ESS; represents the call cost of interruptible load; represents the call cost of transferable load; represents the transaction cost with the power grid.
The above costs are specifically as follows:
where represents the output of the unit; represent the power generation cost coefficient of the unit; and respectively represent the charging and discharging power of the energy storage; represents the ESS charging and discharging cost coefficient; and respectively represent the ESS charging and discharging efficiency; represents the load interruption of IL users; represent the load transfer of TL users; and respectively represent the unit compensation costs of IL users and TL users; and respectively represent the electricity purchased and sold to the power grid; and respectively represent the purchase and sale prices of electricity of the power grid.
The specific constraints are as follows:
- (1)
- CG operation constraints
- (2)
- ESS operation constraints
- (3)
- TL and IL operation constraint
- (4)
- Interactive power constraint
- (5)
- Power balance constraint
3.2. VPPC Cooperative Operation Model
3.2.1. Nash Bargaining-Based Cooperative Operation Model for VPPC
In the previous subsection, a mathematical model for the independent operation of a single VPP was introduced. Under the independent operation mode, each VPP only interacts with the external power grid for electricity exchange. In contrast, under the cooperative operation mode within a VPP cluster, VPPs are allowed to engage in peer-to-peer (P2P) energy transactions. Through such P2P energy interactions, VPPs can achieve mutual energy support and complementary advantages.
In this case, the objective function of each VPP is modified accordingly:
where represents the cost of VPPi in cooperative operation mode; represents the transaction cost with other VPPs. Its specific expression and the constraints that should be satisfied are as follows:
where represents the electricity trade between VPPi and VPPj; represents the trade prices between VPPi and VPPj; represents the upper limit of the amount of electricity traded between the VPPs.
Under the cooperative operation mode of VPPC, it should be ensured that the cooperative benefits of each VPP can be distributed fairly and reasonably. As an important branch of cooperative game theory, the Nash bargaining model is usually used to describe the cooperative and competitive relationship between multiple subjects in the interactive process, which is consistent with the cooperative operation mode of VPPC. According to the definition of the standard Nash bargaining model, the cooperative operation model of VPPC is as follows:
In the above formula, represents the negotiation breakdown point, which is the operating cost in the independent operation mode. If a VPP incurs higher costs under the cooperative operation compared to operating independently, it will choose to withdraw from the cooperative framework. Therefore, it is necessary to ensure that all VPPs benefit from participating in the cooperative operation model.
By solving the above model, it can be ensured that each VPP obtains Pareto optimality. However, due to the non-convex and nonlinear nature of the original problem, it is difficult to solve directly. Therefore, an equivalent transformation is required. After transformation, the Nash bargaining model is reformulated into two tractable convex subproblems: the cluster-level profit maximization problem and the benefit allocation problem.
- (1)
- Subproblem 1: Cluster-Level Profit Maximization
Subproblem 1 focuses on maximizing the overall profit of VPPC. The decision variables include the internal energy dispatch within each VPP and the amount of electricity traded with other VPPs in the cluster:
In this subproblem, the transaction costs between VPPs are neglected. This is because, under the cooperative operation framework, electricity is traded at a uniform price between buyers and sellers, resulting in the offsetting of purchasing costs and selling revenues.
- (1)
- Subproblem 2: Benefit Allocation Problem
Subproblem 2 aims to ensure a fair and reasonable allocation of the cooperative benefits among VPPs. The decision variable is the transaction price between VPPs:
The multiplicative objective function in the above formulation is difficult to solve directly. Therefore, it is transformed into a logarithmic form for easier computation:
3.2.2. ADMM-Based Distributed Solution Framework
As a large-scale distributed optimization algorithm, ADMM offers favorable convergence performance while preserving the privacy of each participant during the optimization process. Based on ADMM, the solution procedure for Subproblem 1 and Subproblem 2 is as follows.
- (1)
- Solution process of Subproblem 1
In Subproblem 1, the distributed optimization model for VPPi is formulated as:
where represents the Lagrange multiplier in Subproblem 1; represents the penalty parameter of Subproblem 1.
Each VPP independently determines its own scheduling plan and trading strategy. Through limited information exchange among VPPs, Subproblem 1 is solved in a distributed and iterative manner. In each iteration, the optimization variables of each VPP are as follows:
where k represents iteration round.
The update formula for the dual variables is given as follows:
The convergence criterion of the algorithm is that both the primal residual and the dual residual are less than their respective convergence thresholds. The primal and dual residuals are defined as follows:
where and respectively represent the primal residual and dual residual at the (k + 1)-th iteration.
The convergence condition of the algorithm is as follows:
where and respectively represent the convergence tolerances for the primal and dual residuals of Subproblem 1.
- (2)
- Solution process of Subproblem 2
In Subproblem 2, the distributed optimization model for VPPi is formulated as follows:
where represents the Lagrange multiplier in Subproblem 2; represents the penalty parameter of Subproblem 2.
In each iteration, the optimization variables of each VPP are as follows:
The update formula for the dual variables is given as follows:
The convergence criterion of the algorithm is also that both the primal residual and the dual residual are less than their respective convergence thresholds. The primal and dual residuals are defined as follows:
where and respectively represent the primal residual and dual residual at the (k + 1)-th iteration.
The convergence condition of the algorithm is as follows:
where and respectively represent the convergence tolerances for the primal and dual residuals of Subproblem 2.
In the proposed ADMM-based framework, the choice of the penalty parameter plays a critical role in determining the convergence behavior. To enhance convergence stability and adaptability of VPPC, this study adopts an adaptive adjustment strategy for the penalty factor, thereby improving the robustness of the distributed coordination process.
where , , and respectively represent the penalty parameter, the primal residual, and dual residual of Subproblems 1 and 2 at the k-th iteration.
4. Intra-Day Energy Sharing Model for VPPC
While the day-ahead stage provides an optimized baseline for cooperative scheduling, it is inherently limited by the forecast uncertainties associated with renewable energy outputs and load demands. In real-world operations, these uncertainties often result in significant deviations from the planned schedules, which can lead to power imbalances within the VPPC. To address this challenge, an intra-day adjustment mechanism is introduced as the second stage of the proposed framework.
This intra-day model serves as a real-time adaptive layer, complementing the day-ahead decisions by dynamically rebalancing power within the VPPC in response to forecast deviations. It ensures that the overall operation remains both economically efficient and physically feasible, even under fluctuating system conditions.
In contrast to the day-ahead stage—where iterative algorithms such as ADMM can be employed to reach near-optimal agreements through sufficient computation and communication—the intra-day stage prioritizes responsiveness and speed. Sequential iterative methods are thus ill-suited for intra-day operations, where time constraints demand lightweight and decentralized decision-making.
During the intra-day stage, each VPP performs short-term forecasting based on updated information, yielding relatively accurate estimates of its renewable generation and load demand. However, due to forecast errors, some VPPs may experience surplus generation while others face shortfalls in the same time period. This supply–demand mismatch creates an opportunity for intra-cluster energy sharing, where surpluses can be reallocated to compensate for deficits among peers, thereby maintaining internal balance within the VPPC.
4.1. Supply–Demand Ratio-Based Pricing Scheme
Based on the above analysis, this paper proposes a supply–demand ratio-based pricing scheme for the intra-day stage. Under this scheme, each VPP is required to submit its trading information only once per interval, enabling the determination of the trading price and facilitating energy sharing within the VPPC.
Assume that in a given intra-day time period, the internal power demand or power supply of VPPi is known. VPPi is required to report its trading role and trading quantity within the designated time window. The coordination center collects the overall supply and demand information from all VPPs within the VPPC and calculates the intra-cluster supply–demand ratio as follows:
where and respectively represent the total energy supply and total energy demand within the VPPC; represents the energy supply–demand ratio.
In the intra-day trading stage, it is assumed that all VPPs within the same time interval trade electricity at a uniform buy/selling price: and . When the total internal energy supply within the VPPC is zero, or when the total energy demand is zero, the transaction price among VPPs naturally defaults to the grid electricity price. The following discussion focuses on the pricing scheme when both supply and demand are non-zero.
Furthermore, the intra-day purchase/sale price is designed to satisfy the following three principles:
- Revenue neutrality for VPPC;
- The electricity purchase price is no less than the electricity sale price;
- When the supply–demand ratio is equal to 1, the purchase and sale prices should be the same.
Based on the above principles, the transaction price among VPPs is discussed under the following classified scenarios.
- (1)
In this scenario, the VPPC system is experiencing a supply shortage, where the total energy supply is less than the total energy demand . Based on the inverse relationship between the transaction price and the supply–demand ratio, the internal electricity selling price can be expressed as follows:
where a and b are the unknown variables to be determined.
At this point, according to Principle 2 and the boundary conditions, the following equation holds:
- When supply and demand are balanced, the electricity purchase price should equal the electricity selling price, and both should be set to the midpoint of the grid electricity prices;
- When R = 0, i.e., when the total energy supply is zero, and the demand side can only trade with the external grid.
By solving the above two equations, the unknown variables a and b can be determined. Substituting them into the expression gives the following:
The energy demand side still needs to purchase electricity from the external grid. Therefore, according to Principle 1, which requires revenue neutrality for VPP, the following equation can be established:
The internal electricity purchase price can be expressed as follows:
- (2)
In this scenario, the VPPC system is now in a state of energy surplus, where the total energy supply exceeds the total energy demand . At this point, the ratio of demand to supply, denoted , is defined as follows:
Similarly, the internal electricity purchase price can be expressed as follows:
where c and d are the unknown variables to be determined.
By also considering Principle 2 and the relevant boundary conditions, the following equation holds:
- When supply and demand are balanced, the result is consistent with Scenario 1, and the price is set to the midpoint of the grid electricity prices;
- When X = 0, i.e., when the total energy demand is zero, the supply side can only trade with the external grid.
By solving the above equations, the internal purchase and selling prices within the VPPC can be obtained as follows:
4.2. Penalty Mechanism for Forecast Deviations
While the intra-day pricing model enables real-time coordination among VPPs based on dynamic supply–demand conditions, its effectiveness hinges on the accuracy of short-term forecasts provided by individual VPPs. In practice, however, some VPPs may consistently under- or over-estimate their expected net power due to limited forecasting capabilities or even intentional strategic misreporting. If left unaddressed, such deviations can disrupt intra-cluster fairness, weaken pricing efficiency, and reduce the stability of energy sharing within the VPPC.
To mitigate these risks, we introduce a penalty mechanism that imposes price-based corrections or monetary penalties on VPPs exhibiting significant forecast deviations. This mechanism is designed to align individual incentives with system-wide performance, encouraging truthful reporting and more accurate forecasting.
The penalty mechanism is implemented in a differentiated manner based on each VPP’s supply–demand status:
- (1)
- For VPPs in a power purchase position (i.e., ), if their actual intra-day net load (defined as the difference between real-time load and renewable generation) exceeds 110% of the day-ahead forecast, the excess portion is charged at a 10% premium over the internal purchase price, capped at the grid purchase price.
- (2)
- For VPPs in a power selling position (i.e., ), if the actual intra-day net generation—the difference between renewable generation and load—exceeds 110% of the day-ahead forecast, the excess portion of the sale will be priced 10% lower than the intra-cluster sale price, but not lower than the grid sale price. Conversely, if the actual net generation drops below 90% of the forecasted value, the VPP will be penalized at 20% of the internal purchase price for the shortfall.
All penalty revenues will be redistributed among VPPs whose forecast deviations remain within acceptable bounds, thus creating positive incentives for honest participation in intra-day energy sharing. Moreover, VPPs that attempt to strategically misreport their forecasted capacity may face even more severe penalties or financial assessments from the external grid during the final real-time balancing stage.
By explicitly addressing large forecast deviations, this mechanism reinforces pricing fairness, discourages opportunistic behavior, and enhances the overall stability and credibility of intra-day coordination under the proposed two-stage VPPC operation framework.
5. Practical Considerations
The two-stage coordinated operation mechanism proposed in this study demonstrates sound theoretical coordination and economic performance. However, several technical and regulatory challenges remain for its real-world deployment.
To emphasize algorithmic performance, the proposed model assumes an ideal communication environment, where information exchange is reliable, delay-free, and bandwidth-sufficient. In large-scale VPPC scenarios, however, actual communication networks may experience latency, bandwidth constraints, or asynchronous interactions among nodes, all of which could impair the convergence and synchronization performance of the ADMM algorithm. Nevertheless, as the number of participants increases, communication overhead and computational burden could grow rapidly. Practical application projects should focus on asynchronous or delay-tolerant variants to improve scalability in ultra-large VPPC systems.
During the intra-day trading stage, this paper adopts a unified pricing mechanism based on the supply–demand ratio to ensure real-time feasibility and computational simplicity. However, this uniform pricing may overlook differences in marginal operating costs across VPPs, potentially impacting allocation efficiency and fairness. To address this, future work may explore zonal or lightweight differentiated pricing strategies that incorporate geographic location, grid topology, or VPP operating status—enhancing economic incentives and resource matching without significantly increasing computational complexity.
The implementation of peer-to-peer energy trading hinges not only on distributed coordination algorithms but also on practical constraints such as regulations, market rules, and cybersecurity. Several pilot projects have explored P2P energy trading worldwide. For instance, the PowerMatching City project in the Netherlands, the Piclo platform in the UK, and multiple local energy internet demonstration projects in China have tested blockchain- or smart contract-based energy exchange mechanisms at small scales—verifying the technical feasibility of P2P trading in localized grids.
Nonetheless, such demonstrations have yet to scale in broader electricity markets, and key market processes—such as energy metering, transaction settlement, and user accountability—must be further clarified. Specifically, P2P trading requires advanced metering infrastructure capable of real-time bidirectional monitoring and data reporting within each trading interval. The settlement mechanism should support flexible clearing cycles and a transparent, auditable accounting structure.
In addition, ensuring secure and trustworthy energy exchanges demands robust authentication and access control. Although this study does not implement a specific cybersecurity model, future research may integrate blockchain technologies for tamper-proof transaction records or apply digital signatures and identity verification to prevent false reporting of power availability, thereby enhancing the system’s resilience in practical deployments.
In summary, while the two-stage framework offers promising coordination and operational feasibility in theory, its large-scale application will require deeper integration with communication systems, regulatory environments, and market infrastructure. These practical challenges will be further investigated in future work.
6. Case Study
6.1. Parameter Settings
In this study, a case analysis is conducted involving four VPPs. The parameters of the devices within each VPP, as well as the electricity price information of the grid, are detailed in Table 1, Table 2 and Table 3. The unit compensation fees for IL and TL users are set at 0.3 CNY/kWh and 0.1 CNY/kWh, respectively [28]. In the day-ahead stage, the forecasted renewable generation outputs and load demands for each VPP are illustrated in Figure 2.

Table 1.
CG parameters.

Table 2.
ESS parameters.

Table 3.
Grid purchase and sale price.
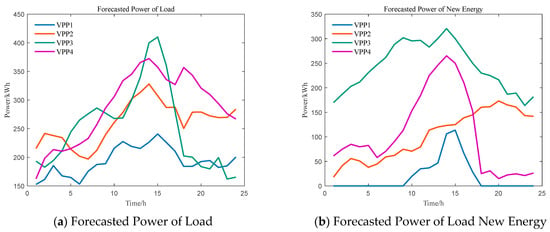
Figure 2.
Forecasted power of VPPs.
6.2. Analysis of Day-Ahead Cooperative Operation Results
The proposed model is solved in a distributed manner using both the standard ADMM and the improved adaptive ADMM algorithms. The convergence behavior of the primal and dual residuals is illustrated in Figure 3. The convergence threshold for both Subproblems 1 and 2 is set to 10−2. As shown in the figure, under the adaptive ADMM, Subproblem 1 converges in 39 iterations and Subproblem 2 in 25 iterations. In contrast, under the standard ADMM, Subproblem 1 and Subproblem 2 require 54 and 47 iterations, respectively. These results demonstrate that the adaptive ADMM significantly improves convergence performance.
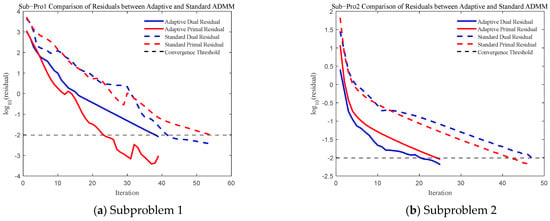
Figure 3.
Comparison of residuals between adaptive and standard ADMM.
To further evaluate the convergence performance of the proposed model under varying VPPC scales, the number of participating VPPs is increased from 4 to 8, and the convergence trajectories of primal and dual residuals are compared in Figure 4. Results show that the model converges within 39 iterations in the four-VPP scenario, while the iteration count increases to 73 with eight VPPs. This indicates that as the cluster size grows, the convergence speed of the ADMM algorithm is affected. Nevertheless, the enhanced ADMM still demonstrates stable and efficient convergence in small- to medium-scale VPPCs. For larger clusters involving over 100 VPPs, however, the algorithm may face greater challenges in terms of convergence speed and communication burden.
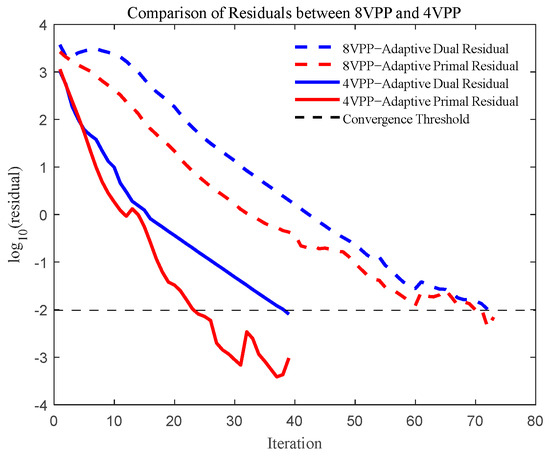
Figure 4.
Comparison of residuals between 8VPP and 4VPP.
Following the analysis of convergence behavior under varying cluster sizes, the proposed algorithm is further tested for adaptability and stability across different operational scenarios. Based on a four-VPP system, three cases are constructed: Scenario 1 serves as the baseline, Scenario 2 simulates changes in market pricing conditions, and Scenario 3 adopts a different load dataset to reflect an alternative load scenario. The convergence of primal and dual residuals under each case is presented in Figure 5. By comparing the convergence behavior of Subproblem 2 between Scenarios 1 and 2, and Subproblem 1 between Scenarios 1 and 3, the results show minimal differences in iteration counts across all scenarios, confirming that the proposed algorithm maintains stable convergence and strong robustness under diverse market and load configurations.
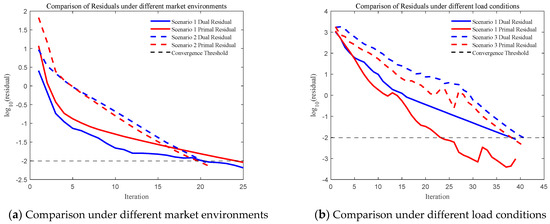
Figure 5.
Comparison under different scenarios.
Figure 6 and Figure 7 illustrate the day-ahead optimal scheduling results of each VPP and the corresponding energy transactions within the VPPC, respectively. As shown in Figure, VPP1 primarily relies on photovoltaic generation, and due to its limited installed capacity, it acts predominantly as a power consumer in intra-cluster transactions. Similarly, although VPP2 integrates wind power, the limited capacity of its controllable generators results in it also functioning mainly as a power consumer within the VPPC. VPP3 benefits from a combination of wind and solar resources and maintains a relatively low net load throughout the day. Consequently, it is able to provide surplus electricity to other VPPs during cooperative operation. VPP4, in contrast, exhibits time-varying roles across different scheduling intervals. From 00:00 to 17:00, it serves as a net supplier to the VPPC, whereas from 18:00 to 24:00, it transitions into a net electricity consumer. This role shift is determined by the internal characteristics of its renewable resources. Although VPP4 includes both wind and photovoltaic generation, its wind capacity is relatively limited and its overall load demand is high. As a result, between 12:00 and 16:00, VPP4 not only supplies electricity to the VPPC but also exports surplus power to the external grid. However, after 18:00, as solar output drops significantly, VPP4 increasingly shifts to a demand-dominant role within the cluster.
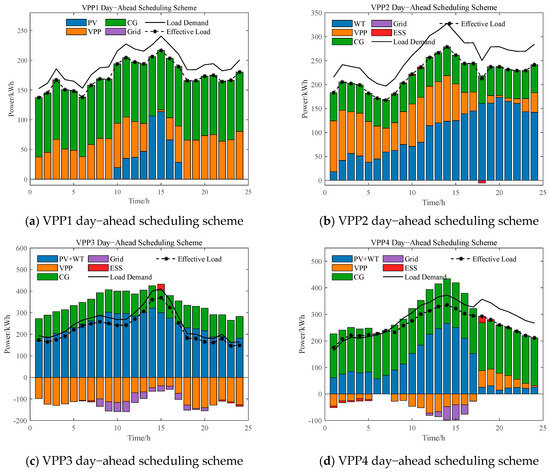
Figure 6.
Day-ahead scheduling scheme.
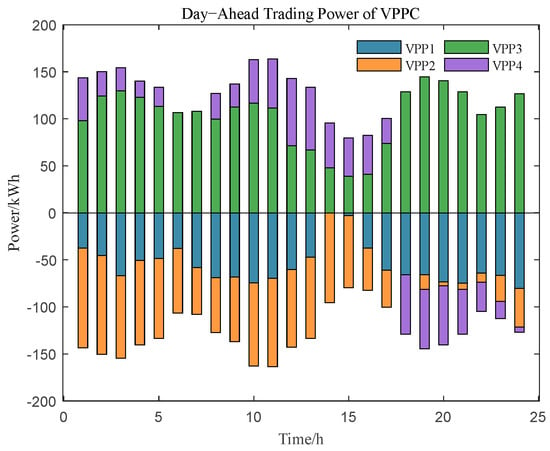
Figure 7.
Day−ahead trading power of VPPC.
Figure 8 shows the day-ahead trading prices within the VPPC obtained through distributed iterative optimization. It can be observed that the transaction prices of all VPPs lie between the grid purchase and selling prices, indicating that each VPP benefits economically from the Nash bargaining process and that mutually advantageous trading outcomes are achieved.
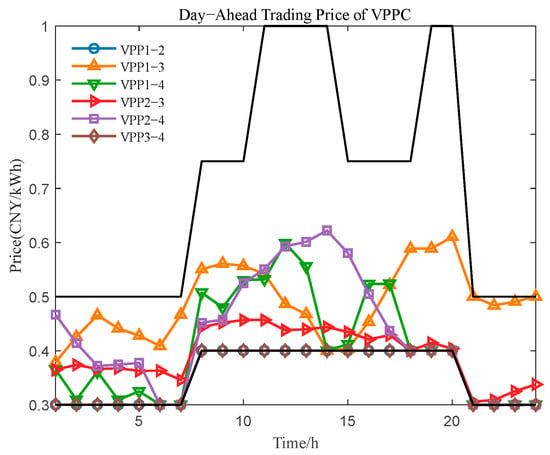
Figure 8.
Day−ahead trading price of VPPC.
Table 4 presents the cost analysis of each VPP before and after the Nash bargaining process. Under independent operation, the operating costs of VPP1, VPP2, VPP3, and VPP4 are CNY 1455.87, CNY 1227.89, CNY –358.46, and CNY 1033.62, respectively. After energy sharing is conducted based on the objective function of Subproblem 1, their operating costs are reduced to CNY 640.47, CNY 467.66, CNY 595.20, and CNY 1085.82, respectively.

Table 4.
Nash bargaining cost analysis.
While VPP1 and VPP2 experience significant cost reductions, VPP3 and VPP4 incur increased costs. This is because the optimization in the energy-sharing stage aims to minimize the total cost of the VPPC, without considering compensation mechanisms for inter-VPP energy transactions. As VPP1 and VPP2 are primarily energy consumers, cooperation allows them to reduce reliance on the external grid, thereby lowering costs.
Conversely, VPP3 and VPP4 act as energy providers to support overall system efficiency, which causes them to lose potential revenue from selling electricity to the grid, resulting in increased costs.
After applying the bargaining mechanism in Subproblem 2, the net benefits of all VPPs are adjusted to a similar level—approximately CNY 142—ensuring both overall system efficiency and individual fairness are achieved.
To further validate the rationality of the benefit-allocation scheme, we compared the revenues allocated to the four VPPs under the same coordinated schedule using the Nash-bargaining model and the Shapley value method. The detailed results and the associated Gini coefficients are listed in Table 5.

Table 5.
Comparison of Nash bargaining and Shapley value methods.
Under Nash bargaining, the revenues are highly balanced: all four VPPs receive between CNY 141.77 and CNY 142.75, with minimal variation, giving a Gini coefficient of just 0.0014—indicative of strong fairness. By contrast, the Shapley allocation shows pronounced disparities: VPP1 earns CNY 234.68 while VPP2 receives only CNY 65.52, yielding a Gini coefficient of 0.2580 and markedly lower fairness.
From a computational-complexity perspective, the Nash solution can be solved in a distributed manner via ADMM, achieving fast convergence with moderate communication overhead—well suited to multi-agent coordination inside a VPPC. The Shapley method, however, requires enumerating every possible coalition; its complexity grows factorially with the number of participants. In our simulations, this combinatorial explosion made Shapley’s runtime far longer than that of the Nash model, so execution times are not reported here.
Overall, the Nash-bargaining approach strikes a better balance between economic efficiency, fairness, and implementability, making it more appropriate for the two-stage VPPC coordination framework proposed in this work.
6.3. Analysis of Intra-Day Energy Sharing Results
In the intra-day stage, each VPP obtains relatively accurate forecasts of renewable generation and load demand through short-term energy prediction. At this point, the deviation between the short-term forecast and the day-ahead forecast represents the net load of each VPP during the intra-day period—that is, the amount of energy that must be additionally balanced in real time. Based on a 15 min forecasting interval, resulting in 96 dispatch periods per day, the short-term forecasted power profiles of each VPP are illustrated in Figure 9 and Figure 10.
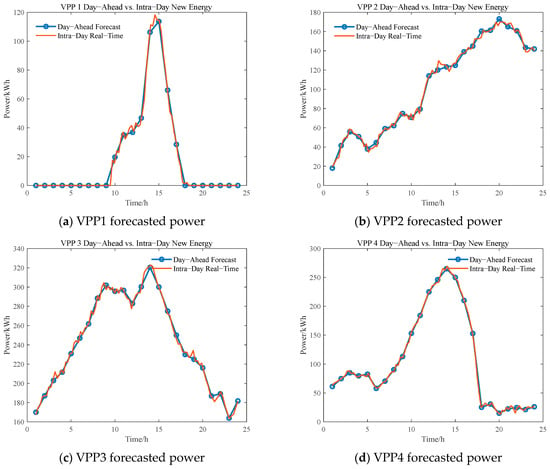
Figure 9.
Intra-day short-term forecasted renewable power.
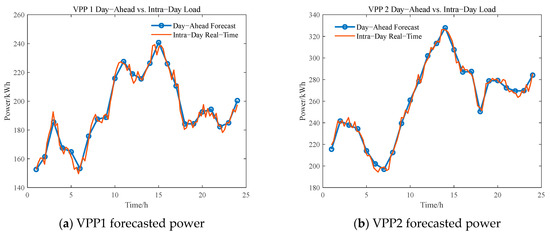
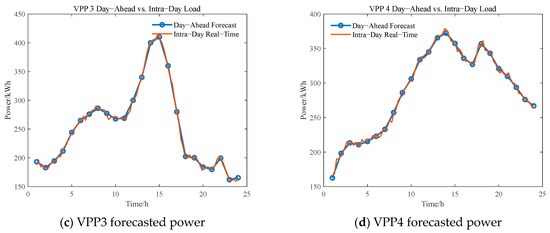
Figure 10.
Intra-day short-term forecasted load power.
Using the intra-day net load of each VPP, as shown in Figure 9 and Figure 10, as the basis for energy transactions, the intra-day transaction prices within the VPPC are determined according to the supply–demand ratio-based pricing mechanism. As illustrated in Figure 11, all transaction prices between VPPs fall within the range defined by the grid’s purchase and selling prices: VPPs experiencing energy shortages are able to purchase electricity at prices lower than the grid purchase price, while VPPs with surplus electricity can sell at prices higher than the grid selling price. This energy-sharing mechanism within the VPPC effectively enhances the actual economic returns of all participating entities, achieving a balance between overall system coordination and individual profitability.
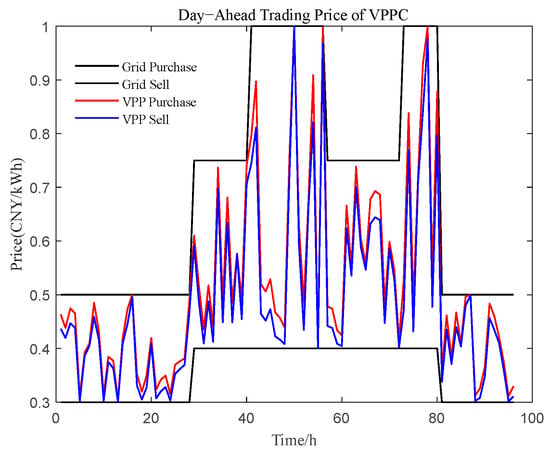
Figure 11.
Intra-day short-term forecasted load power.
To compare different intra-day operation strategies, two modes are considered: independent operation and energy sharing among VPPs. Under the independent operation mode, intra-day deviation energy must be traded directly with the external grid. In contrast, the energy sharing mode allows VPPs to mutually balance their deviations through a supply–demand ratio-based pricing mechanism.
As shown in Table 6, the energy sharing mode significantly outperforms the independent operation mode in terms of both electricity purchase costs and selling returns. For VPP1, the purchase cost drops from CNY 193.55 to CNY 128.65, while the selling revenue improves from CNY 90.17 to CNY 141.32. Similar patterns are observed in VPP2 through VPP4, demonstrating that the proposed energy sharing scheme effectively enhances the economic performance of all participating VPPs.

Table 6.
Intra-day cost analysis.
Figure 12 illustrates the variation in purchase and selling prices under ±15% fluctuations of renewable generation, based on the output of VPP2 at 11:00. This analysis is conducted to evaluate the impact of forecasting deviations on the proposed pricing mechanism. The results show that the overall price trends are consistent with economic principles: as renewable output increases and the supply–demand ratio rises, both purchase and selling prices decrease; conversely, when renewable output decreases, prices increase accordingly. These outcomes confirm that the proposed supply–demand-ratio-based pricing mechanism responds effectively to fluctuations and exhibits strong responsiveness, stability, and economic rationality under forecasting uncertainty.
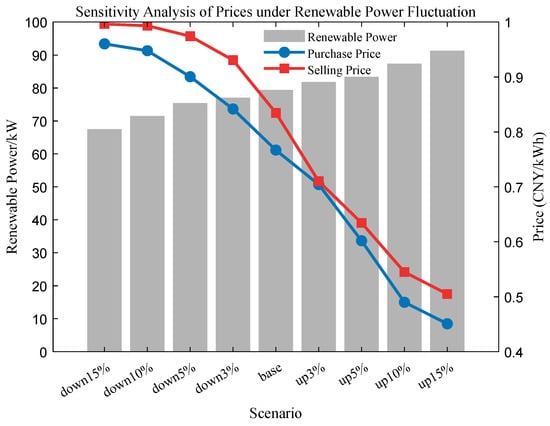
Figure 12.
Sensitivity Analysis of Prices under Renewable Power Fluctuation.
7. Conclusions
This paper proposes a two-stage coordinated operation model for a VPPC, incorporating a Nash bargaining framework in the day-ahead stage and a supply–demand ratio-based pricing mechanism in the intra-day stage. The effectiveness of the proposed model is validated through case studies.
- (1)
- In the day-ahead stage, a cooperative operation model is established based on Nash bargaining theory. This model improves both individual and system-level benefits and is solved in a distributed manner using the ADMM algorithm, ensuring the privacy and decision-making autonomy of each VPP.
- (2)
- In the intra-day stage, an energy sharing model is established based on a supply–demand ratio pricing mechanism, which effectively smooths the fluctuations of renewable generation and load power. This approach not only enhances the economic benefits of individual VPPs but also ensures fast and responsive real-time transactions.
- (3)
- The proposed two-stage model, covering both day-ahead and intra-day coordination, facilitates energy interaction within the VPPC, alleviates grid peak regulation pressure, and enhances the economic performance of individual VPPs.
Author Contributions
Conceptualization, X.Y. and L.Q.; Data curation, X.Y.; Formal analysis, L.Q.; Funding acquisition, Q.A.; Investigation, X.Y.; Methodology, L.Q.; Project administration, Q.A.; Resources, L.Q.; Software, X.Y.; Supervision, Q.A.; Validation, X.Y., L.Q. and D.W.; Visualization, X.Y.; Writing—original draft, L.Q.; Writing—review and editing, X.Y. and D.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Project of State Grid Corporation of China (520940230038).
Data Availability Statement
Relevant data have been shared in the paper.
Conflicts of Interest
Xingang Yang was employed by the State Grid Shanghai Electric Power Research Institute. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be constructed as a potential conflict of interest. The State Grid Shanghai Electric Power Research Institute had no role in the design of the study, in the collection, analysis, or interpretation of data, in the writing of the manuscript, or in the decision to publish the results.
References
- Gao, H.; Wang, Y.; Zhang, H.; Wang, Y. Review of virtual power plant operations: Resource coordination and multidimensional interaction. Appl. Energy 2024, 357, 122284. [Google Scholar] [CrossRef]
- Ju, L.; Chen, Y.; Wang, X.; Zhang, L.; Zhang, L. Two-stage scheduling optimization model and benefit allocation strategy for virtual power plant clusters aggregated by multidimensional information indicators. Renew. Energy 2025, 240, 122245. [Google Scholar] [CrossRef]
- Wen, J.; Chen, M.; Liu, Z.; Zhang, H.; Chen, C. Multi-source shared operation optimization strategy for multi-virtual power plants based on distributionally robust chance constraint. Energy 2025, 322, 135761. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, Y.; Wang, M.; Liu, R.; Zhao, X. Synergistic Operation Framework for the Energy Hub Merging Stochastic Distributionally Robust Chance-Constrained Optimization and Stackelberg Game. IEEE Trans. Smart Grid 2025, 16, 1037–1050. [Google Scholar] [CrossRef]
- Liu, Y.; Ai, X.; Hu, P.; Pan, X. Economic scheduling of multiple microgrids considering power interaction and demand response. Mod. Electr. Power 2020, 37, 605–612. [Google Scholar]
- Hu, J.; Yan, Z.; Wang, H. Optimal scheduling of community power day-ahead considering clean power sharing. Grid Technol. 2020, 44, 61–70. [Google Scholar]
- Wang, S.; Wu, Z.; Zhang, J. Optimal scheduling model of regional multi-microgrids of combined cooling, heating and power type considering inter-microgrid power interaction and micro-source output coordination. Chin. J. Electr. Eng. 2017, 37, 7185–7194+7432. [Google Scholar]
- Zhu, Z.; Liu, B.; Guo, L. Distributed optimal scheduling of integrated energy multi-microgrid system considering dynamic hydrogen pricing mechanism. Grid Technol. 2023, 47, 5036–5054. [Google Scholar]
- Li, X.; Ji, H.; Zhang, R.; Jiang, T.; Chen, H.; Ning, R. Distributed optimal scheduling of urban distribution systems taking into account the response characteristics of multi-type microgrids. Power Syst. Autom. 2022, 46, 74–82. [Google Scholar]
- Li, Y.; Peng, M. Distributed optimal scheduling of integrated energy microgrid considering carbon capture and methanation. Power Autom. Equip. 2023, 43, 46–53. [Google Scholar]
- Shi, J.; Hu, H.; Zhang, J. Distributed low-carbon economic dispatch of integrated energy systems accounting for multiple independent operators. Grid Technol. 2019, 43, 127–136. [Google Scholar]
- Li, J.; Shao, Y.; Zhu, X.; Guo, Q.; Qi, J. Distributed low-carbon economic dispatch of multiregional interconnected power systems taking into account carbon emission constraints. J. Electrotechnol. 2023, 38, 4715–4728. [Google Scholar]
- Chen, J.; Jia, Y.; Han, X.; Ren, H.; Ge, H. Distributed cooperative optimal scheduling of multiple micro-energy networks considering demand-side carbon trading mechanism. Grid Technol. 2023, 47, 2196–2207. [Google Scholar]
- Zhao, H.; Wang, X.; Li, B.; Zhao, M.; Wang, Y. Distributed robust optimal scheduling of multi-community optical storage systems considering energy sharing. Power Syst. Autom. 2022, 46, 21–31. [Google Scholar]
- Hu, R.; Wei, Z.; Huang, Y.; Du, C.; Lu, B.; Fang, T. Joint economic dispatch of multiple microgrids based on alternating multiplier method and Shapley allocation method. Electr. Power Constr. 2021, 42, 28–38. [Google Scholar]
- Tian, X.; Chen, L.; Li, X.; Yuan, W. Optimal operation strategy of distributed photovoltaic community shared energy storage based on master-slave game and improved Shapley value. Grid Technol. 2023, 47, 2252–2261. [Google Scholar]
- Song, X.; Chen, J.; Shi, Q. Optimal scheduling of integrated energy microgrids under the background of multi-subject game. High Volt. Technol. 2023, 49, 3163–3178. [Google Scholar]
- Li, X.; Yang, Z.; Li, F.; Cheng, S. Optimized scheduling strategy for joint operation of wind-water alliance and regional power grid based on ladder hydropower regulation. Chin. J. Electr. Eng. 2023, 43, 2234–2248. [Google Scholar]
- Gu, X.; Wang, Q.; Hu, Y.; Zhu, Y.; Ge, Z. Distributed low-carbon optimal operation strategy for multi-microgrid integrated energy system based on Nash bargaining. Grid Technol. 2022, 46, 1464–1482. [Google Scholar]
- Ma, T.; Pei, W.; Xiao, H.; Li, D.; Lv, X.; Hou, K. Cooperative operation method of wind-photo-hydrogen multi-subject energy system based on Nash negotiation theory. Chin. J. Electr. Eng. 2021, 41, 25–39+395. [Google Scholar]
- Bandara, K.Y.; Thakur, S.; Breslin, J. Flocking-based decentralised double auction for P2P energy trading within neighbourhoods. Int. J. Electr. Power Energy Syst. 2021, 129, 106766. [Google Scholar] [CrossRef]
- Singh, K.; Gadh, R.; Singh, A.; Dewangan, C.L. Design of an optimal P2P energy trading market model using bilevel stochastic optimization. Appl. Energy 2022, 328, 120193. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, F.; Liu, J.; Liu, Y.; Wang, X.; Yang, Z.; Fa, D.; Ge, X.; Sun, J.; Cai, J.; et al. Design of P2P transaction mechanism for community microgrid system considering differentiated characteristics of prolific consumers. Chin. J. Electr. Eng. 2022, 42, 1455–1470. [Google Scholar]
- Wang, J.; Zhou, N.; Wang, Q.; Wang, P. Microgrid direct trading model and strategy based on blockchain and continuous two-way auction mechanism. Chin. J. Electr. Eng. 2018, 38, 5072–5084+5304. [Google Scholar]
- Shan, J.J.; Dong, Z.M.; Hu, J.J.; Huang, Q.R.; Wang, F. Blockchain technology-based P2P electricity smart transaction contract for producers and consumers. Grid Technol. 2021, 45, 3830–3839. [Google Scholar]
- Ping, J.; Chen, S.; Zhang, N.; Yan, Z.; Yao, Z. A decentralized transaction mechanism for distribution networks based on smart contracts. Chin. J. Electr. Eng. 2017, 37, 3682–3690. [Google Scholar]
- Long, C.; Wu, J.; Zhang, C.; Thomas, L.; Cheng, M.; Jenkins, N. Peer-to-peer energy trading in a community microgrid. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017; IEEE: Chicago, IL, USA, 2017; pp. 1–5. [Google Scholar]
- Wang, H.; Gao, H.; Wang, R. Day-Ahead Market Trading Strategy of Virtual Power Plants Considering Demand Response. Smart Power 2024, 52, 64–71. (In Chinese) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).