Selective Combining for HARQ-Employed MIMO Systems with Spatial Correlations

Abstract

In this paper, the selective combining scheme is proposed for hybrid automatic repeat request (HARQ)-employed multiple-input multiple-output (MIMO) systems with spatial correlations at the receiver. To reduce the computational complexity load during the reception procedure, through using only a part of the total receive antennas, the proposed scheme generates the subsets of receive antennas, and the receive antennas in each subset are utilized for selective combining. For a given number of selected receive antennas, each subset is generated to minimize the summation of the spatial correlations between the receive antennas in the subset. During the subset generation, the proposed scheme utilizes only spatial correlation information (i.e., the receiver correlation matrix) and does not require the instantaneous channel state information (CSI). Thus, the calculated subsets in the proposed scheme can be utilized for the selective combining as long as the receiver spatial correlation remains unchanged. Simulation results verify that the proposed scheme can outperform the norm-based selective combining scheme that requires an additional calculation for every new instantaneous CSI.

1. Introduction

Wireless communication systems have been rapidly developed in recent decades by exploiting techniques and algorithms to adapt to wireless communication channels. To correct the errors caused by the impairment of wireless communication channels, forward error correction (FEC) schemes can be employed for error detection and correction by encoding and decoding procedures [1]. However, because of various reasons, such as link adaptation failures, there can be some remaining errors after the decoding procedure, and using only the FEC scheme is insufficient to overcome the characteristics of wireless communication channels. Consequently, hybrid automatic repeat request (HARQ) schemes, which allow for the retransmissions of FEC-encoded packets by acknowledgment/non-acknowledgment (ACK/NACK) feedback from the receiver [2,3], have been employed in various commercial wireless communication systems [4,5,6,7].

To fully utilize the benefit from retransmissions, HARQ schemes can enable additional performance improvement by combining the retransmitted signals with the previously transmitted signals. Specifically, in multiple-input multiple-output (MIMO) systems, the combining scheme can greatly impact the system performance, receiver complexity, and flexibility. Bit-level combining (BLC) [8,9], also known as log-likelihood ratio (LLR) combining, calculates the LLRs of each HARQ round separately before combining. Although this BLC scheme has high flexibility that can be applied for HARQ-employed MIMO systems, regardless of the HARQ retransmission strategy (e.g., Chase combining and incremental redundancy) and number of simultaneous HARQ processes, it can experience degraded error performance. Thus, several combining schemes have been studied and investigated for HARQ-employed MIMO systems [10,11,12,13,14].

Meanwhile, for performance improvement, MIMO systems can employ many inputs and outputs, e.g., massive MIMO systems [15,16]. However, as the number of receive antennas increases, e.g., uplink massive MIMO with a massive number of antennas at base station (BS), the computational complexity load for the HARQ combining schemes can be significantly increased [13]. In addition, as the number of receive antennas increases, spatial correlation can be easily introduced to MIMO systems [17,18]. Because of spatial correlation, the channel for a specific antenna can provide a certain amount of information about the channels for different antennas, that is, by carefully selecting the receive antennas to be used for the reception procedures among all receive antennas, the complexity load for the HARQ combining procedure can be maintained at the practical level while reducing the potential performance loss by the selection.

Therefore, in this paper, the selective combining scheme for HARQ-employed MIMO systems with receiver spatial correlations is proposed. Before the beginning of the reception procedure with the employed HARQ combining scheme, the proposed scheme determines the receive antennas to be used for the reception procedures among all receive antennas, and the reception procedure is performed with the selected receive antennas. In addition, the proposed scheme utilizes the receiver correlation matrix instead of instantaneous channel state information (CSI), which enables the effective selection of receive antennas without performing the determination procedure for every transmission with new instantaneous CSI.

This paper is organized as follows. Section 2 describes the HARQ-employed MIMO system model. Section 3 describes the operations of the proposed scheme in detail, and Section 4 presents numerical results to verify the performance of the proposed scheme. Finally, Section 5 provides the conclusions.

1.1. Literature Review

For HARQ-employed MIMO systems, there have been several approaches for signal combining at the receiver to improve system performance. In [10], the pre-combing and post-combining schemes for linear detection, e.g., linear zero-forcing (LZF) and linear minimum mean-squared-error (LMMSE), were investigated for Chase combining-based HARQ-employed MIMO systems. Further, in [11], symbol-level combining (SLC) schemes that directly optimize LLR values instead of the signal-to-interference-plus-noise ratio (SINR) were developed, and, in [12], fast-decodable MIMO-HARQ systems were developed to reduce the decoding complexity when space–time block codes (STBCs) are considered. In [9], the performance of SLC and BLC in HARQ-employed MIMO systems was analyzed for the case of multiple HARQ processes. In addition, in [13], the Kalman combining (KC) scheme was developed to enable the LMMSE-based SLC regardless of the HARQ retransmission strategy and number of simultaneous HARQ processes, and, in [14], the KC scheme was extended to perform iterative detection and decoding (IDD) for better system performance. However, in the existing approaches for combining in HARQ-employed MIMO systems (e.g., [10,11,12,13,14]), the selective combining concept, e.g., utilizing a subset of the receiver antennas for combining, or utilization of spatial correlation has not yet been considered.

Meanwhile, the conventional receive antenna selection schemes for MIMO systems can be utilized for the selective combining in HARQ-employed MIMO systems. In [19], the suboptimum antenna selection scheme with the success elimination of the receive antennas for a minimum capacity loss was developed, and in [20], the antenna selection algorithm with the near-identical performance to [19] at the reduced complexity was investigated. Further, in [21], the correlation-based method was proposed to select the receive antennas such that the rows of the effective channel matrix, including only the selected antennas, were maximally uncorrelated and had maximum powers. Meanwhile, the global-searching-based antenna selection scheme was developed in [22], which can be employed when the number of selected receive antennas is equal to the number of transmit antennas. For massive MIMO, as studied in [23], the asymptotic upper capacity bounds with antenna selection according to the switching architecture were derived in a large-scale limit, and antenna selection algorithms based on branch-and-bound were developed. Further, for multiuser massive MIMO uplink, a receive antenna selection scheme assuming an MMSE detection scheme was developed in [24]. In [25], a joint receive antenna selection and beamforming was developed for reconfigurable intelligent surfaces (RIS)-aided MIMO systems.

Although these conventional antenna selection schemes for MIMO systems can achieve suboptimum performance, because of utilizing instantaneous CSI, the selection procedure needs to be performed for new instantaneous CSI. Furthermore, because of the computational complexity load to find a suboptimum solution, utilizing these schemes for the selective combining in HARQ-employed MIMO systems can require more computational complexity than a full combining approach, i.e., utilizing all receive antennas for a HARQ combining procedure without the selection procedure.

1.2. Contributions

The contributions of this study can be summarized as follows.

• Because the proposed scheme selects the receive antennas that will be used for HARQ combining, the proposed scheme is independent of the HARQ combining scheme employed at the receiver, that is, there are basically no restrictions on the HARQ combining scheme, e.g., the proposed scheme can be used with any of HARQ combining schemes in [10,11,12,13,14]. Therefore, if the combining scheme is employed that supports any numbers of HARQ processes and HARQ retransmission strategies (i.e., BLC and KC), the proposed scheme can also support any numbers of HARQ processes and HARQ retransmission strategies.
• In the proposed scheme, the selection of the receive antennas is performed using the receiver correlation matrix only, that is, unlike [19,20,21,22,23,24,25], the proposed scheme does not require instantaneous CSI. Thus, unless the receiver correlation matrix is changed or the estimated receiver correlation matrix is updated, the receiver with the proposed scheme can maintain the existing selection without additional complexity load for selection in each transmission time interval (TTI), i.e., the time interval used for packet transmission.
• In the proposed scheme, the receive antennas for each receive signal vector are selected to minimize the sum of the receive spatial correlation, i.e., the maximum uncorrelation in terms of the effective receiver correlation matrix (including only the selected antennas). Further, when a high temporal correlation is considered, e.g., a quasi-static fading channel, to provide the diversity effect for the selective combining, the selected receive antennas can be changed for a different receive signal vector to utilize each receive antenna as evenly as possible during each TTI. Consequently, as verified by numerical simulations, the proposed scheme can outperform the instantaneous channel-gain-based selective combining scheme, which utilizes the instantaneous CSI and thus requires the additional complexity load for every TTI with new instantaneous CSI.

The following Table 1 summarizes the characteristics of the conventional receive antenna selection schemes (e.g., [19,20,21,22,23,24,25]) and proposed selective combining scheme.

Table 1. Characteristics of the conventional receive antenna selection schemes and proposed scheme.

Conventional Receive Antenna Selection Schemes	Proposed Scheme
• Designed for MIMO systems without considering HARQ employment	• Designed for HARQ-employed MIMO systems for complexity reduction
• Requiring instantaneous CSI → Needs to be performed again for the new instantaneous CSI	• Requiring receiver correlation matrix → Needs to be performed again for the new receiver correlation matrix
• Approaching suboptimum performance comparable to the exhaustive search	• Not optimum, but additional performance improvement is possible for MIMO channels with a high temporal correlation

1.3. Notations

Matrices and vectors are denoted by upper-case and lower-case boldface letters, respectively. The superscripts T, H, and $-1$ represent the transpose, conjugate-and-transpose, and inverse operations for a matrix, respectively. Furthermore, ${\mathbf{I}}_j$ is the $j\times j$ identity matrix; $\mathsf{E}$ is the expectation operation; $\mathsf{V}$ is the variance operation; $\left|a\right|$ is the norm of scalar a; $\left|\mathbb{A}\right|$ is the number of elements in the set $\mathbb{A}$; $\mathbf{A}(\mathbb{B},\mathbb{C})$ is the $\left|\mathbb{B}\right|\times \left|\mathbb{C}\right|$ matrix, including the elements of matrix $\mathbf{A}$ in the $b(\in \mathbb{B})$th rows and and $c(\in \mathbb{C})$th columns; ${\left[\mathbf{A}\right]}_i$ is the ith row of the matrix $\mathbf{A}$; ${\left[\mathbf{A}\right]}_{i,n}$ is the element of $\mathbf{A}$ at the ith row and nth column; and the operator ⊗ represents the Kronecker product.

2. System Model

The spatially multiplexed MIMO system with total N transmit antennas (e.g., N single-antenna users or one user with N antennas) and M receive antennas (e.g., M BS antennas) is considered throughout this paper, as shown in Figure 1. For the transmission in each transmit antenna, a modulated symbol is selected from a Q-ary constellation set $\mathbb{S}$, satisfying ${\sum }_{s\in \mathbb{S}}s=0$ and ${\sum }_{s\in \mathbb{S}}{s}^2=Q$. Let L denote the number of transmit signal vectors for each TTI. Then, the input–output relationship for the $l(1\le l\le L)$th transmit and receive signal vectors in each TTI can be written for MIMO systems with spatial correlations [26] as

$${\mathbf{y}}_l={\mathbf{H}}_l{\mathbf{x}}_l+{\mathbf{n}}_l={\mathbf{R}}^{0.5}{\mathbf{G}}_l{\mathbf{x}}_l+{\mathbf{n}}_l.$$

(1)

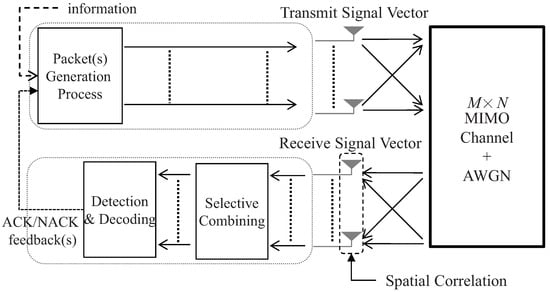
Figure 1. The spatially multiplexed MIMO system model.

In (1), ${\mathbf{y}}_l$ is the $M\times 1$ receive signal vector, ${\mathbf{x}}_l$ is the $N\times 1$ transmit signal vector, and ${\mathbf{n}}_l$ is the $M\times 1$ additive white Gaussian noise (AWGN) vector with zero mean and variance ${\sigma }^2$ in watts, i.e., $\mathsf{E}\left[{\mathbf{n}}_l{\mathbf{n}}_l^H\right]={\sigma }^2{\mathbf{I}}_M$. In addition, ${\mathbf{H}}_l={\mathbf{R}}^{0.5}{\mathbf{G}}_l$ is the $M\times N$ MIMO channel matrix for the lth transmit and receive signal vectors in the given TTI. Additionally, $\mathbf{R}=\mathsf{E}\left[{\mathbf{H}}_l{\mathbf{H}}_l^H\right]$ is the $M\times M$ receiver correlation matrix, and ${\mathbf{G}}_l$ is the $M\times N$ complex Gaussian matrix with zero mean and unit variance, i.e., $\mathsf{E}\left[{\mathbf{G}}_l{\mathbf{G}}_l^H\right]={\mathbf{I}}_M$. The full CSI at the receiver is assumed for simplicity, i.e., ${\mathbf{H}}_l$, $\mathbf{R}$, and ${\sigma }^2$ are known at the receiver. If the quasi-static fading channel is considered, i.e., the channel matrix remains static during a given TTI and is changed for the next TTI, then ${\mathbf{H}}_l={\mathbf{H}}_{l^{\prime }}$ and ${\mathbf{G}}_l={\mathbf{G}}_{l^{\prime }}$ applies for any two l and $l^{\prime }$ with $1\le l,l^{\prime }\le L$ in the given TTI.

At the receiver, selective combining is employed to reduce the complexity load for the HARQ combining and corresponding reception procedure, as illustrated in Figure 2. Let S denote the number of receive antennas selected for each receive signal vector, and let ${\mathbb{M}}_l$ denote the subset of $\mathbb{M}=\{1,2,\dots ,M\}$ selected for ${\mathbf{y}}_l$ with $|{\mathbb{M}}_l|=S$. Then, after the selection, (1) can be rewritten as

$${\mathbf{y}}_{l,{\mathbb{M}}_l}={\mathbf{H}}_{l,{\mathbb{M}}_l}{\mathbf{x}}_l+{\mathbf{n}}_{l,{\mathbb{M}}_l}.$$

(2)

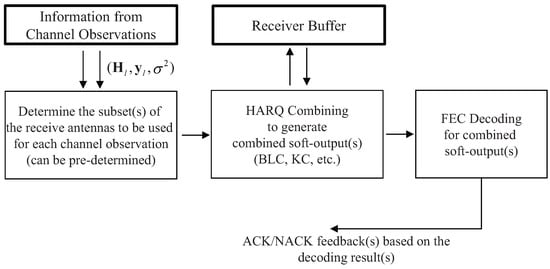
Figure 2. The overall procedure of the selective combining at the receiver of HARQ-employed MIMO systems.

In (2), ${\mathbf{y}}_{l,{\mathbb{M}}_l}$ and ${\mathbf{n}}_{l,{\mathbb{M}}_l}$ are, respectively, the $S\times 1$ receive signal and AWGN vectors, including the elements of $\mathbf{y}$ and $\mathbf{n}$ corresponding to ${\mathbb{M}}_l$, and ${\mathbf{H}}_{l,{\mathbb{M}}_l}$ is the $S\times N$ effective MIMO channel matrix, including the rows of ${\mathbf{H}}_l$ corresponding to ${\mathbb{M}}_l$.

After the selection, the reception procedure for HARQ combining and detection, e.g., LLR calculation and combining, and decoding is performed based on (2). The decoding result is informed by ACK/NACK message(s) from the receiver to the transmitter(s). Based on the informed decoding result, the transmitter decides the retransmission of the previous packet or the transmission of the new packet.

Let P denote the number of packets with different HARQ processes, e.g., $P=1$ when all the transmit symbols in ${\mathbf{x}}_l$ are included in the same HARQ process (i.e., transmitted for the same packet) and $P=N$ when each transmit symbol in ${\mathbf{x}}_l$ has an independent HARQ process (i.e., transmitted for different packets). Further, let $a\left(p\right)$ with $1\le a\left(p\right)\le A$ and $1\le p\le P$ denote the HARQ round of the pth packet at the given TTI, where A is the maximum HARQ round of each packet, i.e., ($A-1$) is the maximum number of retransmissions for each packet. If the ACK message is received at the transmitter or a packet reaches the maximum HARQ round A (e.g., $a\left(p\right)=A$), the packet is terminated, and the transmitter sends a new packet from the next TTI. Otherwise, if the NACK message is received at the transmitter and the corresponding packet does not reach A (i.e., $a\left(p\right)<A$), the transmitter retransmits the packet at the next TTI. In this way, by enabling retransmission of FEC-encoded packets via ACK/NACK feedback messages, HARQ-employed MIMO systems can greatly improve the error performance from the MIMO systems without employing HARQ.

3. Proposed Selective Combining Scheme

In the proposed selective combining scheme, the receive antennas are selected based on the receiver spatial correlation matrix $\mathbf{R}$ instead of the instantaneous CSI ${\mathbf{H}}_l$. For that, first the proposed scheme finds the set ${\mathbb{M}}^m$ for $1\le m\le M$, where ${\mathbb{M}}^m$ is defined as the subset of $\mathbb{M}=\{1,2,\dots ,M\}$ with $|{\mathbb{M}}^m|=S$ and $m\in {\mathbb{M}}^m$. Clearly, there are many subsets of $\mathbb{M}$ satisfying these conditions. It is known that the performance of MIMO systems degrades as the spatial correlation becomes significant [18,27,28]. Let ${\mathbf{R}}_{{\mathbb{M}}_l}$ denote the $S\times S$ effective receiver correlation matrix by considering the selection by ${\mathbb{M}}_l$, i.e., ${\mathbf{R}}_{{\mathbb{M}}_l}=\mathsf{E}\left[{\mathbf{H}}_{l,{\mathbb{M}}_l}{\mathbf{H}}_{l,{\mathbb{M}}_l}^H\right]$. Then, to find the ${\mathbb{M}}^m$ that reduces the performance loss by selective combining, the proposed scheme finds ${\mathbb{M}}^m$ such that the overall receiver spatial correlation through using ${\mathbb{M}}^m$ can be reduced, i.e., finding ${\mathbb{M}}^m$ with the minimum ${\sum }_{n=1}^S{\sum }_{i=1}^S|{\left[{\mathbf{R}}_{{\mathbb{M}}_l}\right]}_{i,n}|$ for maximum uncorrelation. To avoid an exhaustive search requiring $\mathcal{O}\left(C\right(M-1,S-1)$ to find each ${\mathbb{M}}^m$ for $1\le m\le M$, the proposed scheme employs the greedy algorithm to find the suboptimum solution.

As the initialization to find ${\mathbb{M}}^m$ for a given m, the proposed scheme sets ${\mathbb{M}}^m=\left\{m\right\}$. Let ${\mathbb{M}}_1^m$ denote the initial ${\mathbb{M}}^m(=\left\{m\right\})$, and let ${\mathbb{M}}_s^m$ for $2\le s\le S$ denote the updated set with $|{\mathbb{M}}_s^m|=s$ during the selection procedure for s. Then, from $2\le s\le S$, the proposed scheme selects the additional antenna index $m^{*}\in \mathbb{M}-{\mathbb{M}}_{s-1}^m$ that minimizes the overall receiver spatial correlation when $m^{*}$ is selected instead of different remaining antennas in $\mathbb{M}-{\mathbb{M}}_{s-1}^m$. Thus, the overall receiver spatial correlation in the case of selecting $m^{\prime }$ is calculated for every element $m^{\prime }\in \mathbb{M}-{\mathbb{M}}_{s-1}^m$ as

$$c\left(m^{\prime }\right)={\sum }_{n=1}^s{\sum }_{i=1}^s\left|{\left[\mathbf{R}({\mathbb{M}}_{s-1}^m\cup \left\{m^{\prime }\right\},{\mathbb{M}}_{s-1}^m\cup \left\{m^{\prime }\right\})\right]}_{i,n}\right|.$$

(3)

In (3), $c\left(m^{\prime }\right)$ for $m^{\prime }\in \mathbb{M}-{\mathbb{M}}_{s-1}^m$ denotes the sum of the norms of the receiver spatial correlations when the elements ${\mathbb{M}}_{s-1}^m\cup \left\{m^{\prime }\right\}$ are selected, i.e., the sum of all $|{\left[{\mathbf{R}}_{{\mathbb{M}}_{s-1}^m\cup \left\{m^{\prime }\right\}}\right]}_{i,n}|$. Then, $m^{*}$ for ${\mathbb{M}}_s^m$ can be decided as

$$m^{*}=arg\underset{m^{\prime }}{min}c\left(m^{\prime }\right),$$

(4)

and ${\mathbb{M}}_s^m$ can be determined by

$${\mathbb{M}}_s^m={\mathbb{M}}_{s-1}^m\cup \left\{m^{*}\right\}.$$

(5)

This is repeated for $2\le s\le S$ to find the set of the S receive antennas, including the mth antenna. After the procedure for $s=S$, ${\mathbb{M}}^m$ is set to ${\mathbb{M}}_S^m$ and the procedure to find ${\mathbb{M}}^m$ for a given m is terminated.

Based on the procedure in (3)–(5), the proposed scheme finds the subsets ${\mathbb{M}}^m$ for $1\le m\le M$. Let K denote the number of the subsets that are decided to be used in each TTI. Further, let $\mathcal{K}$ denote the group of K subsets (i.e., ${\mathbb{M}}^m$), where $\mathcal{K}\left(k\right)$ for $1\le k\le K$ is the kth subset selected in $\mathcal{K}$. If $K=1$, i.e., only one of ${\mathbb{M}}^m$ for $1\le m\le M$ is used for each TTI, then the proposed scheme finds the subset with the minimum overall receiver correlation among all ${\mathbb{M}}^m$ for $1\le m\le M$, i.e.,

$$\mathcal{K}=arg\underset{m}{min}{\sum }_{n=1}^S{\sum }_{i=1}^S\left|{\left[\mathbf{R}({\mathbb{M}}^m,{\mathbb{M}}^m)\right]}_{i,n}\right|.$$

(6)

In this case, ${\mathbb{M}}_l=\mathcal{K}\left(1\right)$ such that ${\mathbf{H}}_{l,{\mathbb{M}}_l}={\mathbf{H}}_{l,\mathcal{K}\left(1\right)}$ for $1\le l\le L$.

When a temporal correlation is sufficiently low, e.g., no temporal correlation such that ${\mathbf{G}}_l$ and ${\mathbf{G}}_{l^{\prime }}$ are independent for different l and $l^{\prime }$, $K=1$ will be sufficient because the transmitted packet(s) experienced the different effective channel ${\mathbf{H}}_{l,{\mathbb{M}}_l}$ for each receive signal vector in a given TTI (e.g., $\mathsf{E}\left[{\left[{\mathbf{H}}_{l,{\mathbb{M}}_l}\right]}_{i,n}{\left[{\mathbf{H}}_{l^{\prime },{\mathbb{M}}_{l\prime }}\right]}_{i,n}^H\right]\approx 0$). However, when a temporal correlation is high, e.g., the quasi-static Rayleigh fading such that ${\mathbf{G}}_l={\mathbf{G}}_{l^{\prime }}$ regardless of l and $l^{\prime }$, then setting $K=1$ can limit the information about the transmitted packet(s) because ${\mathbf{H}}_{l,{\mathbb{M}}_l}$ and ${\mathbf{H}}_{l^{\prime },{\mathbb{M}}_{l^{\prime }}}$ becomes similar (e.g., $\mathsf{E}\left[{\left[{\mathbf{H}}_{l,{\mathbb{M}}_l}\right]}_{i,n}{\left[{\mathbf{H}}_{l^{\prime },{\mathbb{M}}_{l^{\prime }}}\right]}_{i,n}^H\right]\approx 1$), that is, under the quasi-static fading channel for (1), the proposed scheme with $K=1$ will also results in the quasi-static fading for (2), which can limit the error performance by the lack of diversity.

Thus, for the cases of a high temporal correlation, multiple ${\mathbb{M}}^m$ can be used for each TTI, i.e., $K>1$, to provide the diversity effect by the selection. For that, let $\mathbf{d}\left({\mathbb{M}}^m\right)$ denote the $M\times 1$ vector, where the $m^{\prime }(1\le m^{\prime }\le M)$th element of $\mathbf{d}\left({\mathbb{M}}^m\right)$ is 1 when $m^{\prime }\in {\mathbb{M}}^m$ and 0 otherwise. Then, when $K\ge 2$, the first two ${\mathbb{M}}^{m^{\prime }}$ and ${\mathbb{M}}^{m^{″}}$ are selected for $\mathcal{K}\left(1\right)$ and $\mathcal{K}\left(2\right)$ as

$$\{\mathcal{K}\left(1\right),\mathcal{K}\left(2\right)\}=\{{\mathbb{M}}^{m^{\prime }},{\mathbb{M}}^{m^{″}}\}\mathrm{with}arg\underset{m^{\prime },m^{″}}{min}\mathsf{V}[\mathbf{d}\left({\mathbb{M}}^{m^{\prime }}\right)+\mathbf{d}\left({\mathbb{M}}^{m^{″}}\right)],$$

(7)

where $m^{\prime }$ and $m^{″}$ are interchangeable, i.e., $\{\mathcal{K}\left(1\right),\mathcal{K}\left(2\right)\}=\{{\mathbb{M}}^{m^{″}},{\mathbb{M}}^{m^{\prime }}\}$ is also possible. Then, if $K\ge 3$, for $\mathcal{K}\left(k\right)$ with $3\le k\le K$, the additional subset ${\mathbb{M}}^{m^{*}}$ is selected among the remaining ${\mathbb{M}}^m$ except the previously selected subsets (i.e., $\mathcal{K}\left(1\right),\dots \mathcal{K}(k-1)$) as

$$\mathcal{K}\left(k\right)={\mathbb{M}}^{m^{*}}\mathrm{with}arg\underset{m^{*}}{min}\mathsf{V}[{\sum }_{i=1}^{k-1}\mathbf{d}\left(\mathcal{K}\right(i\left)\right)+\mathbf{d}\left({\mathbb{M}}^{m^{*}}\right)].$$

(8)

After the determination of $\left\{\mathcal{K}\right(1),\dots \mathcal{K}(K\left)\right\}$, they can be used for (2) in a round-robin manner, i.e.,

$${\mathbb{M}}_l=\mathcal{K}(((l-1)modK)+1).$$

(9)

In this way, the proposed selective combining can provide the diversity effect when a temporal correlation is high, which can additionally improve the error performance.

To sum up, the proposed scheme selects the receive antennas to minimize the overall receiver spatial correlation after the selection. During this procedure, the receiver spatial correlation matrix $\mathbf{R}=\mathsf{E}\left[{\mathbf{H}}_l{\mathbf{H}}_l^H\right]$ is used instead of the instantaneous spatial correlation obtained by ${\mathbf{H}}_l{\mathbf{H}}_l^H$. Thus, unless $\mathbf{R}$ is changed, the subset selection procedure of the proposed scheme does not need to be performed again for every receive signal vector or every TTI, which is a great advantage over the selection based on the instantaneous CSI ${\mathbf{H}}_l$. In addition, for a high temporal correlation environment such as the quasi-static fading channel, the proposed scheme can provide the diversity effect by switching the subset of the receiver antennas utilized for receive signal vectors, where the subsets used for the switching also do not need to be obtained again as long as $\mathbf{R}$ remains unchanged.

Next, the complexity order of the proposed scheme to obtain $\left\{\mathcal{K}\right(1),\dots \mathcal{K}(K\left)\right\}$ is derived. To find each ${\mathbb{M}}^m$ for $1\le m\le M$, the procedure in (3)–(5) needs to be repeated $(S-1)$ times, where the procedure for $s(2\le s\le S)$ requires the complexity of $\mathcal{O}\left((M-s+1)s^2\right)$ by the summation of $s\times s$ matrix for $(M-s+1)$ times. Therefore, considering the highest-order terms, finding all ${\mathbb{M}}^m$ for $1\le m\le M$ requires the complexity of $\mathcal{O}(M^2{S}^3-M{S}^4)$. Meanwhile, the procedure in (6)–(9) requires the complexity of $\mathcal{O}\left(M^3\right)$ when $K\ge 2$. Thus, the overall complexity load of the proposed scheme is $\mathcal{O}(M^2{S}^3-M{S}^4+M^3)$. If $K=1$, then the procedure in (6)–(9) does not need to be performed and the complexity of the proposed scheme becomes $\mathcal{O}(M^2{S}^3-M{S}^4)$.

Figure 3 shows the complexity of the proposed scheme when $K=1$ (i.e., $M^2{S}^3-M{S}^4$), according to M and S. It is shown that the complexity, according to S, became the largest when $S/M$ was around 0.7, regardless of M. Further, the complexity required for the proposed scheme was able to be significantly increased with M. However, the actual operations required in the proposed scheme were norm, addition, and comparison. Thus, if the norm of the elements in $\mathbf{R}$ is pre-calculated, i.e., calculating $\left|\mathbf{R}\right|$ during the estimation of $\mathbf{R}$, the proposed scheme requires only addition and comparison operations, which are much simpler than the matrix-based operations [29] usually required in the conventional antenna selection schemes and HARQ combining schemes. In addition, because of utilizing the receiver correlation matrix $\mathbf{R}$, the proposed scheme does not need to be performed again unless $\mathbf{R}$ has changed, where $\mathbf{R}$ changes significantly slowly compared to the instantaneous CSI, e.g., ${\mathbf{H}}_l$ and ${\mathbf{G}}_l$ [30].

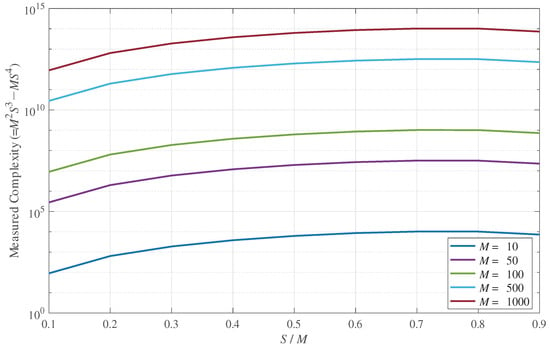
Figure 3. The complexity of the proposed scheme for different M and S.

Furthermore, the following approaches can be additionally used to accelerate the proposed scheme for a larger M. Because the calculation of each ${\mathbb{M}}^m$ is independent, the parallel processing can be employed for (3)–(5). Also, when there are existing ${\mathbb{M}}^m$ obtained from the previous $\mathbf{R}$, the stopping criterion can be employed to terminate the calculation of new ${\mathbb{M}}^m$ if the new ${\mathbb{M}}^m$ is expected be identical to the existing ${\mathbb{M}}^m$.

4. Simulation Results

In this Section 4, the average packet error rate (PER) is evaluated to verify the performance of the proposed scheme by numerical simulations using MATLAB R2020a without built-in functions. The average PER is defined as the average decoding failure probability of the packet until the last HARQ round, and the numerical simulations for each point of the figures are performed until at least 200 packet errors (i.e., decoding failure at the lastAth HARQ round) are observed and at least 1000 TTIs are passed. In addition to the proposed scheme, the round-robin scheme (i.e., when the receive antennas are sequentially selected for each TTI) and the instantaneous channel-gain based selective combining scheme (i.e., when the receive antennas with larger norms than the others are selected) were considered, as well as the full selection scheme (i.e., when using all the receive antennas). Furthermore, $A=3$, i.e., when maximum two retransmissions for each packet. Unless specified otherwise, a low-density parity-check (LDPC) code of codeword length 576 and rate $5/6$ was considered as FEC [5], and the quadrature amplitude modulation (QAM) with $Q=64$ was considered for the modulation. Chase combining was considered as the HARQ retransmission strategy, i.e., the retransmitted signal for a packet was identical to the initially transmitted signal for the packet. The exponential correlation model with the assumption of uniform planar arrays (UPAs) was considered for the spatial correlation model [27,28], i.e., $\mathbf{R}={\mathbf{R}}_{\mathrm{h}}\otimes {\mathbf{R}}_{\mathrm{v}}$ with ${\left[{\mathbf{R}}_{\mathrm{h}}\right]}_{i,n}={\left[{\mathbf{R}}_{\mathrm{v}}\right]}_{i,n}={\rho }^{|i-n|}$ for the spatial correlation factor $\rho$, where the horizontal $\left({\mathbf{R}}_{\mathrm{h}}\right)$ and vertical (${\mathbf{R}}_{\mathrm{v}}$) correlation matrices were square and had the same size. In addition, no temporal correlation (i.e., when ${\mathbf{G}}_l$ and ${\mathbf{G}}_{l^{\prime }}$ are independent for different l and $l^{\prime }$) and quasi-static fading (i.e., when ${\mathbf{G}}_l={\mathbf{G}}_{l^{\prime }}$ regardless of l and $l^{\prime }$) were considered for the temporal fading model. Unless specified otherwise, both $\mathbf{R}$ and ${\mathbf{H}}_l$ were fully known at the receiver, i.e., there were no channel estimation errors. BLC and KC were considered as the HARQ combining scheme after the selection, where the LMMSE-based detection and LLR calculation were considered for BLC. Further, the min-sum algorithm was employed at the decoder, where the number of decoding iterations was set to 20 for each packet. After the decoding, the 32-bit cyclic redundancy check (CRC) code was used to check whether each decoded packet(s) contained errors or not, and ACK/NACK messages were sent according to the error detection results of CRC. Unless specified otherwise, the ACK/NACK messages, according to the error detection results, were sent through error-free channels.

Figure 4 and Figure 5 show the average PER results that were obtained under the MIMO Rayleigh fading channels of no temporal correlation for the cases of $P=1$ and $P=N$, respectively, where $N=24$, $M=36$, $S=24$, and the spatial correlation factor for the exponential correlation model, $\rho$, was 0.8, i.e., there were severe spatial correlations [18,28]. It is shown that the proposed scheme outperformed the instantaneous channel-gain based scheme and round-robin scheme when BLC was employed. Specifically, for BLC, the SNR gains of the proposed scheme with $K=1$ over the instantaneous channel-gain based selective combining scheme and round-robin scheme at the average PER of ${10}^{-2}$ were about 1.5 dB and 2.4 dB, respectively, regardless of P. Meanwhile, when KC was employed, the proposed scheme outperformed the round-robin scheme and achieved a slightly better average PER than the instantaneous channel-gain based scheme. Further, it is shown that KC with the selective combining scheme was able to outperform BLC with a full combining by a large SNR margin. Considering that KC and BLC require a similar level of computational complexity [13], the selective combining for MIMO systems can be considered an effective approach for MIMO systems with the receiver spatial correlation in terms of both error performance and computational complexity. Note that the cases of $K>1$, for the proposed scheme, were not considered in Figure 4 and Figure 5 because of no temporal correlation, as explained in Section 3.

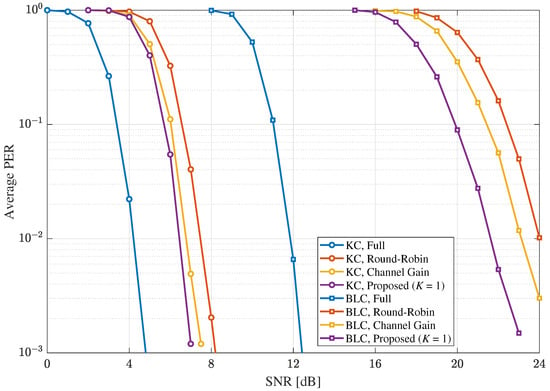
Figure 4. The average PERs under the MIMO Rayleigh fading channels of no temporal correlation with $\rho =0.8$ and $S=24$ in $24\times 36$ MIMO systems when $P=1$.

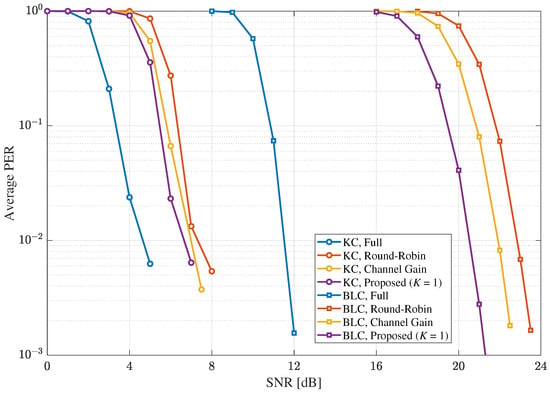
Figure 5. The average PERs under the MIMO Rayleigh fading channels of no temporal correlation with $\rho =0.8$ and $S=24$ in $24\times 36$ MIMO systems when $P=N$.

Next, Figure 6 and Figure 7 show the average PER results under the MIMO Rayleigh quasi-static channel for the cases of $P=1$ and $P=N$, respectively, where $N=24$, $M=36$, $S=24$, and $\rho =0.8$. Similar to the results for no temporal correlation in Figure 4 and Figure 5, the proposed scheme outperformed the other selective combining schemes for both BLC and KC. Specifically, for BLC, the SNR gains of the proposed scheme with $K=4$ over the instantaneous channel-gain based selective combining scheme and round-robin scheme at the average PER of ${10}^{-2}$ were about 1.9 dB and 2.9 dB for $P=1$, respectively, which were increased to about 2.9 dB and 3.8 dB for $P=N$. Meanwhile, the SNR gains of the proposed scheme with $K=1$ over the other selective combining schemes were similar to the cases of Figure 4 and Figure 5. Thus, the performance improvement by the proposed scheme was clearly observed for the multiple HARQ processes (e.g., uplink MIMO) under the quasi-static fading by increasing K for the diversity effect. Meanwhile, for KC, the SNR gain of the proposed scheme over the other selective combining schemes was decreased compared with the cases of BLC. Further, the SNR improvement by increasing K was also reduced due to the SLC nature of KC. Nonetheless, in cases of the proposed scheme and the instantaneous channel-gain based scheme, KC with the selective combining scheme outperformed BLC with a full combining for the cases of quasi-static fading, as well as for the cases of no temporal correlation.

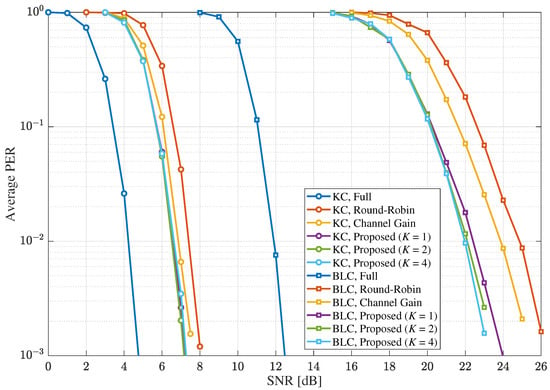
Figure 6. The average PERs under the MIMO Rayleigh quasi-static fading channel with $\rho =0.8$ and $S=24$ in $24\times 36$ MIMO systems when $P=1$.

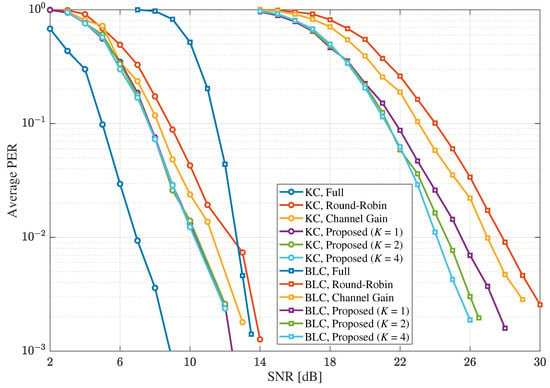
Figure 7. The average PERs under the MIMO Rayleigh quasi-static fading channel with $\rho =0.8$ and $S=24$ in $24\times 36$ MIMO systems when $P=N$.

Figure 8 and Figure 9 show the average PER results under the MIMO Rayleigh quasi-static channel for the cases of $P=1$ and $P=N$, respectively, where $N=48$, $M=64$, $S=48$, and $\rho =0.8$. Compared with the results in Figure 6 and Figure 7, the SNR gain of the proposed scheme over the other selective combining schemes were decreased. Specifically, for BLC, the SNR gains of the proposed scheme with $K=4$ over the instantaneous channel-gain based selective combining scheme and round-robin scheme at the average PER of ${10}^{-2}$ were about 0.5 dB and 1.0 dB for $P=1$, respectively, which were about 1.9 dB and 2.3 dB for $P=N$. However, the SNR gain of the KC with the selective combining scheme over the BLC with the full combining was significantly increased from the results in Figure 6 and Figure 7 for both $P=1$ and $P=N$. This happened because the gain of SLC, such as KC over BLC, increased with the size of MIMO systems, even if the load factor was fixed [9].

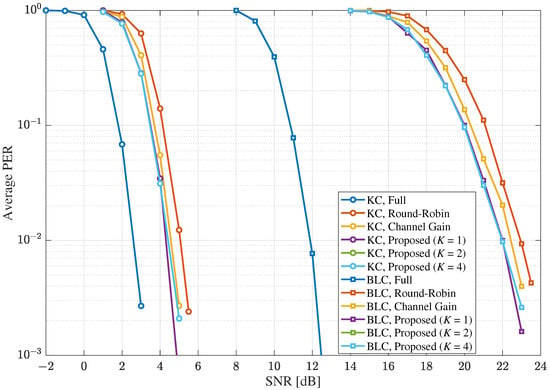
Figure 8. The average PERs under the MIMO Rayleigh quasi-static fading channel with $\rho =0.8$ and $S=48$ in $48\times 64$ MIMO systems when $P=1$.

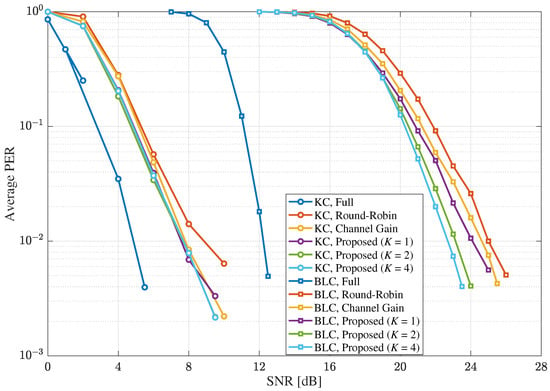
Figure 9. The average PERs under the MIMO Rayleigh quasi-static fading channel with $\rho =0.8$ and $S=48$ in $48\times 64$ MIMO systems when $P=N$.

In Figure 10, the average PER results under the MIMO Rayleigh quasi-static fading channel for the case of $P=N$, where $N=24$, $M=36$, $S=30$, and $\rho =0.8$, are shown. By increasing the number of the receive antennas used for the reception procedure, the error performance of each scheme was improved from the case shown in Figure 7 with $S=24$. In addition, the performance characteristics similar to the case of $S=24$ shown in Figure 7 were observed for the case of $S=30$ shown in Figure 10, and the proposed scheme outperformed the other selective combining schemes at a reduced SNR gain compared with the SNR gain when $S=24$. For BLC, the SNR gains of the proposed scheme over the instantaneous channel-gain based selective combining scheme and round-robin scheme at the average PER of ${10}^{-2}$ were about 0.8 dB and 1.1 dB, respectively. This happened because the difference between the selective combining schemes was reduced as S increased.

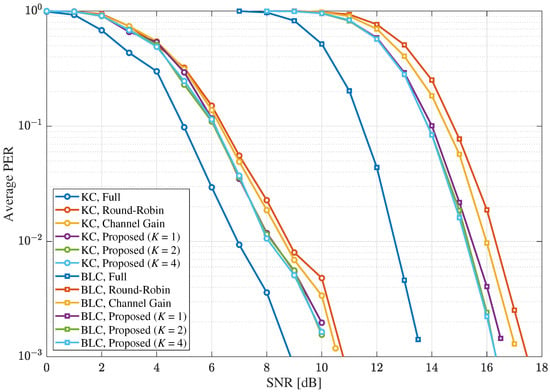
Figure 10. The average PERs under the MIMO Rayleigh quasi-static fading channel with $\rho =0.8$ and $S=30$ in $24\times 36$ MIMO systems when $P=N$.

Figure 11 shows the average PER results under the MIMO Rayleigh quasi-static fading channel when the rate 1/2 LDPC code and 4-QAM modulation were considered, where $N=24$, $M=36$, $S=24$, $P=N$, $\rho =0.8$. By considering a low modulation and coding scheme (MCS) level, the performance of each scheme significantly improved compared to the results in Figure 7. Therefore, the performance gain of the proposed scheme over the other selective combining schemes could be reduced. Specifically, the SNR gains of the proposed scheme with $K=4$ over the instantaneous channel-gain based selective combining scheme and round-robin scheme at the average PER of ${10}^{-2}$ were about 0.6 dB and 1.2 dB for BLC, respectively, which were about 0.4 dB and 1.0 dB for KC. In addition, unlike the other results, BLC with full combining achieved a better error performance than KC with the selective combining schemes. Therefore, it was observed that the selective combining scheme can be more effective with a higher MCS level.

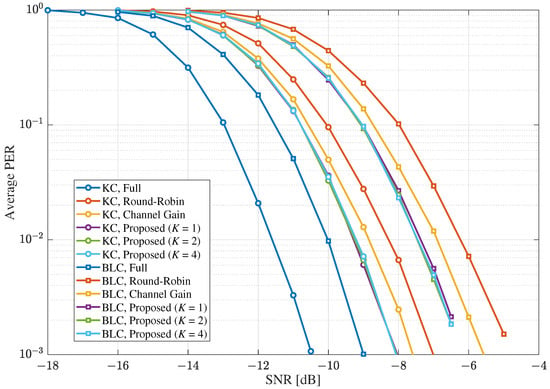
Figure 11. The average PERs under the MIMO Rayleigh quasi-static fading channel with $P=N$, $\rho =0.8$, and $S=24$ in $24\times 36$ MIMO systems when the rate 1/2 LDPC code and 4-QAM modulation are considered.

In Figure 12, the average PER results under the MIMO Rayleigh quasi-static fading channel when ACK/NACK messages are sent through non-error-free channels, where $N=24$, $M=36$, $S=24$, $P=N$, and $\rho =0.8$, are shown. The average ACK/NACK message error probability was set to 0.002, and it was assumed that the ACK(NACK) message sent from the receiver is converted to a NACK(ACK) message at the transmitter if the error occurs. Compared to the error-free cases shown in Figure 7, although the performance of each scheme was somewhat degraded by the ACK/NACK message errors, the difference in error performance between each scheme remained at a similar level. Specifically, for BLC, the SNR gains of the proposed scheme with $K=4$ over the instantaneous channel-gain based selective combining scheme and round-robin scheme at the average PER of ${10}^{-2}$ were about 2.8 dB and 3.9 dB, respectively, and the SNR gains shown in Figure 7 for BLC were 2.9 dB and 3.8 dB. Thus, it was shown that the proposed scheme is effective even when non-error-free channels are considered for ACK/NACK messages, as is the case in practical systems.

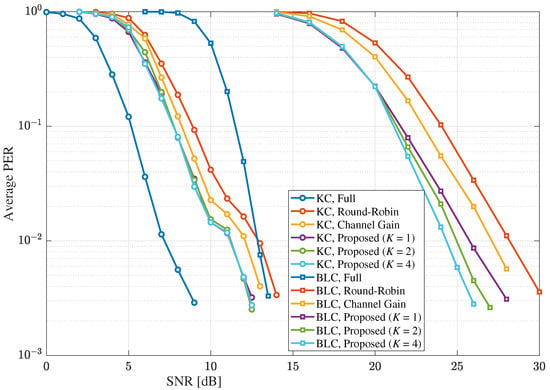
Figure 12. The average PERs under the MIMO Rayleigh quasi-static fading channel with $P=N$, $\rho =0.8$, and $S=24$ in $24\times 36$ MIMO systems when the average ACK/NACK message error probability is 0.002.

As shown in Figure 13 and Figure 14, the average PER results of the selective combining schemes, according to $\rho$ under the MIMO Rayleigh quasi-static fading channel, were compared for the cases of KC and BLC, respectively, where $N=24$, $M=36$, $S=24$, and $P=N$. It is also shown that the proposed scheme outperformed the other selective combining in cases of lower $\rho$, although the SNR gain could be decreased as $\rho$ is decreased. This is expected because the proposed scheme selects the receive antennas based on only the receiver spatial correlation. Further, it is shown that the performance improvement by the proposed scheme was larger for the cases of BLC than the cases of KC, as observed in the previous results.

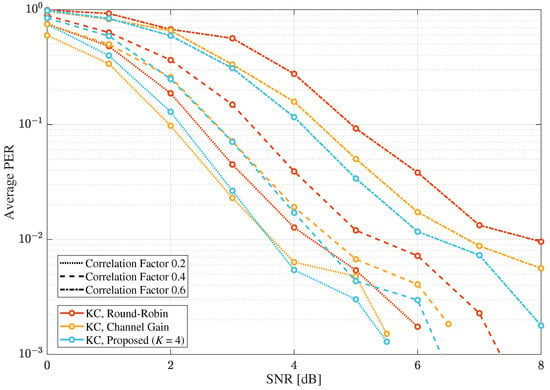
Figure 13. The average PERs of selective combining schemes with KC according to the spatial correlation factor $\rho$ under the MIMO Rayleigh quasi-static fading channel in $24\times 36$ MIMO systems, where $S=24$ and $P=N$.

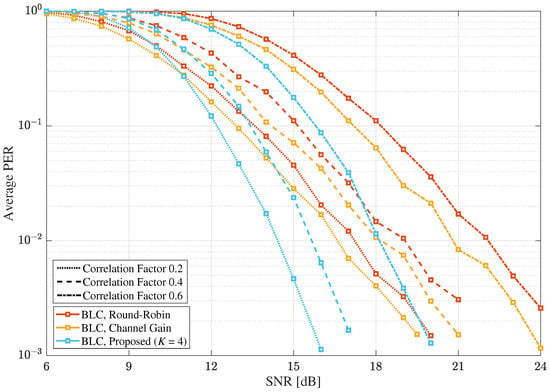
Figure 14. The average PERs of selective combining schemes with BLC according to the spatial correlation factor $\rho$ under the MIMO Rayleigh quasi-static fading channel in $24\times 36$ MIMO systems, where $S=24$, $P=N$, and $\rho =0.8$.

Figure 15 shows the average PER results of the proposed scheme under the MIMO Rayleigh quasi-static fading channel when the $\mathbf{R}$ estimated at the receiver contained errors, i.e., a non-perfect estimation, where $N=24$, $M=36$, $S=24$, $P=N$, and $\rho =0.8$. As shown in Figure 15, the SNR of the pilot signal was identical to the SNR of the data signal, and the orthogonal pilot transmission per transmit antenna was considered with least-square (LS) estimation. To see the effect by the errors in the estimated $\mathbf{R}$ to the proposed scheme only, it was assumed that the instantaneous CSI of the data channel, i.e., $\mathbf{H}$, was perfectly known at the receiver. The results in Figure 15 show that the estimation errors in $\mathbf{R}$ did not have a significant impact on the performance of the proposed scheme, e.g., the proposed scheme with one pilot symbol per transmit antenna showed a slightly degraded performance from the proposed scheme with the perfect $\mathbf{R}$. Thus, it was shown that the proposed scheme was robust against the estimation error in the receiver correlation matrix $\mathbf{R}$.

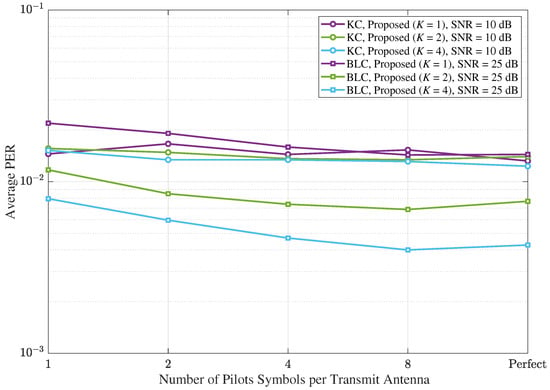
Figure 15. The average PERs of the proposed scheme according to the spatial correlation estimation interval under the MIMO Rayleigh quasi-static fading channel in $24\times 36$ MIMO systems, where $S=24$, $\rho =0.8$, and $P=N$.

Finally, as shown in Table 2, the numerical simulation results for the proposed scheme were summarized. As described in Table 2, it was verified that the proposed scheme is an effective approach in terms of error performance in various system environments.

Table 2. Summary of the numerical simulation results for the proposed scheme.

• Outperforming the instantaneous channel-gain based selective combining scheme and round-robin scheme regardless of the simulation environment (i.e., the number of selected antennas, numbers of transmit and receive antennas, number of HARQ processes, HARQ combining scheme, temporal correlation, spatial correlation, MCS level, and ACK/NACK message errors)

• Additional performance improvement by increasing K (i.e., the number of subsets of selected antennas used for selective combining in each TTI) under the quasi-static fading channels

• Robustness against the estimation errors in the receiver correlation matrix

5. Conclusions

This paper proposes the selective combining scheme for HARQ-employed MIMO systems. By the receiver correlation matrix-based selection without using instantaneous CSI, the proposed scheme outperformed the instantaneous channel-gain based selective combining scheme in various system environments. In addition, it was shown that switching the subset of the receiver antennas can further improve the error performance for the channels with high-temporal correlation. Furthermore, when the receiver spatial correlation is high, the KC scheme with the proposed scheme can outperform the full BLC scheme at a lower computational complexity. Although the proposed scheme does not need to be performed for every TTI, the computational complexity can be significantly large when the number of receive antennas is very large, i.e., in ultra-massive MIMO systems. For such cases, the modification of the algorithm for the complexity reduction could be studied in detail, e.g., the parallelization or stopping criterion, and this could be a future work.