Pairing-Free Certificate-Based Proxy Re-Encryption Plus Scheme for Secure Cloud Data Sharing

Abstract

The popularity of secure cloud data sharing is on the rise, but it also comes with significant concerns about privacy violations and data tampering. While existing Proxy Re-Encryption (PRE) schemes effectively protect data in the cloud, challenges persist with certificate administration and key escrow. Moreover, the increasing number of users and prevalence of lightweight devices demand functional and cost-effective solutions. To address these issues, this paper presents a novel Pairing-free Certificate-Based Proxy Re-Encryption Plus scheme that leverages elliptic curve groups for improved effectiveness and performance. This scheme successfully resolves challenges related to certificate management and key escrow in traditional PRE schemes, while also introducing non-transferable and message-level fine-grained control characteristics. These enhancements bolster data security during sharing and minimize the risk of malicious information leakage. Our proposed scheme’s correctness, security, and effectiveness are rigorously verified and analyzed. The results demonstrate that the scheme achieves the chosen ciphertext security in the random oracle model. Compared to current PRE schemes, our approach offers greater advantages, lower computational overhead, and enhanced suitability for practical cloud computing applications.

1. Introduction

1.1. Background

With the rapid advancement and convergence of cloud computing, big data, and related technologies, public cloud storage has become immensely popular. Users increasingly depend on cloud storage solutions for online data storage and sharing. However, this convenience comes with security concerns. When users store their data in the cloud, they lose direct control, leading to potential issues such as privacy breaches and compromised data confidentiality. The semi-trustworthy nature inherent in third-party cloud service providers poses a challenge for users in conferring absolute trust. Consequently, the predominant strategy for ensuring data protection rests on the shoulders of the cloud subscribers themselves, who rightfully own and safeguard their data.

Data confidentiality is typically guaranteed via the pre-upload encryption of data to the cloud. Nevertheless, challenges arise in scenarios where data sharing among diverse users is essential. In the context of sharing data between User A and User B, User A is required to download and decrypt the data before transmitting it to User B. Upon reception, User B must re-encrypt the data before uploading it to the cloud storage platform. This method exhibits inefficiency and introduces the potential for data leakage during transmission, thereby compromising the security and convenience that public cloud storage platforms aim to provide.

Blaze et al. [1] introduced the concept of Proxy Re-Encryption (PRE) at the 1998 Euromonitor conference to address these challenges. In the PRE system, users can convert ciphertext encrypted by an authorized party into ciphertext that can be decrypted by another authorized party with the assistance of a semi-trusted third party. This process ensures that the third party cannot access the plaintext information of the data, providing an efficient and secure solution for cloud data sharing.

Utilizing a Proxy Re-Encryption (PRE) scheme empowers data owners to delegate access to their stored data, enabling designated individuals to download and access the data directly from the cloud. Proxy re-encryption serves to diminish the direct interaction between the authorizer and the authorized party, consequently elevating data-sharing security and mitigating overhead for the cloud subscriber.

1.2. Our Contribution

This paper introduces a novel scheme called Pairing-Free Certificate-Based Proxy Re-Encryption Plus (PCBPRE⁺), which combines the features of Pairing-free Proxy Re-Encryption (PPRE) and Certificate-Based Proxy Re-Encryption Plus (CBPRE⁺). The main contributions of this scheme are outlined below:

• This paper introduces the PCBPRE⁺ scheme, which combines the properties of PPRE and CBPRE⁺ schemes. The proposed scheme improves computational efficiency by eliminating the reliance on bilinear pairs, effectively addressing the issue of high computation overhead present in existing schemes. As a result, the PCBPRE⁺ scheme is highly suitable for deployment on computationally or power-constrained devices.
• The scheme presented in this paper effectively addresses the challenges related to certificate management and key escrow in traditional CBPRE schemes. Additionally, it incorporates non-transferable and message-level fine-grained control features. Through fine-grained data control and permission management, the scheme ensures that only authorized users can access the data, thereby preventing unauthorized information leakage and tampering.
• This paper offers a formal conceptual description of the PCBPRE⁺ scheme, along with a defined security model. We designed a concrete PCBPRE⁺ scheme and rigorously verified and analyzed its correctness, security, and performance. Detailed empirical evidence and evaluation demonstrate the feasibility and practicality of the scheme.

1.3. Organization

This paper is structured as follows: Section 2 provides a review of the relevant literature for our strategy. In Section 3, background information is presented. The security model of the system is described in Section 4. Section 5 introduces the new PCBPRE⁺ scheme. Its accuracy and security are confirmed in Section 6, while Section 7 contains a study of its performance.

2. Related Work

Proxy Re-Encryption (PRE) has received increased academic attention recently, leading to the development of several well-known PRE schemes [2,3,4,5,6]. However, many of these schemes rely on traditional public-key cryptosystems (PKC) [7,8,9,10] or identity-based cryptosystems [11,12,13,14], which can introduce certain limitations and challenges.

Traditional proxy re-encryption schemes based on public-key cryptosystems face challenges in certificate management, while identity-based cryptosystems have inherent key escrow issues. To address these concerns, Sur introduced the concept of certificateless proxy re-encryption (CLPRE) within the framework of certificateless public-key cryptography (CLPKC) [15]. This approach allows users to overcome key escrow problems by combining a partially trusted key generation center (KGC) with a user-selected key value, generating an independent private key. This ensures that the KGC remains unaware of any user’s private key. However, the introduction of various CLPRE schemes [16,17] has revealed that the KGC still needs to securely transmit a portion of the private key to the user, leading to a new key distribution challenge. Consequently, CLPRE still has limitations in cloud storage applications.

Sur et al. proposed a scheme known as Certificate-Based Proxy Re-Encryption (CBPRE) that addresses the limitations and shortcomings of earlier proxy Re-Encryption (PRE) schemes [18]. CBPRE leverages the implicit certificate property of the Certificate-Based Encryption (CBE) paradigm, achieving a balance between identity-based encryption and conventional public-key encryption. This approach effectively tackles the challenge of certificate revocation in conventional public-key encryption and overcomes the issues of key escrow and distribution in identity-based encryption. As a result, CBPRE has emerged as an ideal solution for achieving secure and efficient cloud storage sharing [19,20].

Furthermore, Sur et al. established the first provably secure CBPRE scheme and provided a formal conception of CBPRE. Following this, Li et al. [21] proposed the Certificate-Based Conditional Proxy Re-Encryption (CB-CPRE) scheme and demonstrated its chosen ciphertext security in the random oracle model. The CB-CPRE scheme allows for conditional filtering of stored data; however, the authorized party can only obtain either all plaintexts or no plaintexts after decrypting the re-encrypted ciphertexts, thus lacking the ability to achieve fine-grained sharing at the message level.

Liu et al. [22] developed the CBPRE+ technique to address fine-grained sharing at the message level. This scheme combines the advantageous features of CBPRE and Proxy Re-Encryption Plus (PRE⁺) [23,24,25]. PRE⁺ was initially proposed by Wang et al., utilizing distinct ephemeral random values chosen by the authorizer to achieve fine-grained sharing and non-transferability features at the message level, which are highly desirable characteristics for cloud storage scenarios [26,27].

Currently, certificate-based proxy re-encryption schemes typically rely on computationally intensive bilinear pairings. However, with the continuous development of cloud computing technology and the widespread adoption of Internet of Things (IoT) applications in recent years, there is a geometric growth trend in both user numbers and data volume. This trend is particularly evident in various fields such as medical IoT and vehicular IoT, where the increase in data volume is accompanied by a more urgent demand for rapid data responsiveness. Consequently, the efficiency issues of cloud storage have drawn considerable attention, as the process of data sharing often consumes significant amounts of network and computational resources. Despite some progress in the implementation of bilinear pairings, they remain the most time-consuming and least efficient part of encryption operations. Therefore, proposing a more efficient data-sharing solution has become imperative.

To address this issue, Lu et al. introduced a certificate-based proxy re-encryption scheme in their paper [28], which eliminates the reliance on bilinear pairings and adopts a non-bilinear pairing approach. This method significantly improves computational efficiency and is better suited to the data development trends in modern society. However, achieving a balance between functionality and efficiency remains a challenge under the prerequisite of meeting both aspects.

3. Preliminary

3.1. Elliptic Curve Group and Computational Assumption

To begin, a brief summary of the elliptic curve group, which serves as the foundation for the scheme, is provided.

Let $F_p$ be a finite field with the following operations, and let p be a prime number:

• Addition: If $a,b\in F_p$, then $a+b=r$ mod p, where $0\le r\le p-1$.
• Multiplication: If $a,b\in F_p$, then $a·b=r$ mod p, where $0\le r\le p-1$.
• Inversion: If a is a non-zero element in $F_p$, then the inverse of a is the only element $c\in F_p$ that satisfies $a·c=r$ mod p.

Let $F_p$ be a p element finite field and a and b be two elements of $F_p$ satisfying the discriminant $△=4a^3+27b^2\ne 0$. The elliptic curve over the finite field $F_p$, denoted as $E\left(F_p\right)$, is formally defined as the set of all points $(x,y)$ on $F_p$ that satisfy the Weierstrass equation $y^2=x^3+ax+b$, along with the inclusion of point O at infinity. In other words, all the points on $E\left(F_p\right)$ collectively form an exchange group denoted as $G=\left\{(x,y)\mid x,y\in F_{p}and{y}^2=x^3+ax+b\right\}\cup \left\{O\right\}$.

The binary operation “+” on group G is formally defined as follows: Let $P,Q\in G$, L be the line through P and L (if $P=Q$, then L represents the tangent line to group G at point P ), L intersects G at a third point, denoted $R^{\prime }$, and reflecting $R^{\prime }$ on the x-axis gives a point R, defining $P+Q=R$. Quantitative multiplication in group G: $tP=P+P+\cdots +P$ (t times).

The security of this scheme relies on the underlying assumption of the Computational Diffie–Hellman (CDH) problem. This problem can be defined as follows:

Definition 1.

Let G be a large prime elliptic curve group of order q and P a generating element of group G. Then, the CDH problem on group G is as follows: Given $P,aP,bP\in G^3$, compute $abP=P\in G$ for any $a,b\in Z_q^{*}$. Let us assume the existence of a probabilistic polynomial-time (PPT) algorithm, denoted as $A_{CDH}$, that can effectively solve the Computational Diffie–Hellman (CDH) problem with a certain probability:

$$Adv\left(A_{CDH}\right)=Pr[A_{CDH}(G,q,P,aP,bP)=abP]$$

If the probability $Adv\left(A_{CDH}\right)$ of success for all PPT algorithms $A_{CDH}$ is negligible, then the CDH problem in group G is considered computationally hard to solve.

3.2. Program Definition

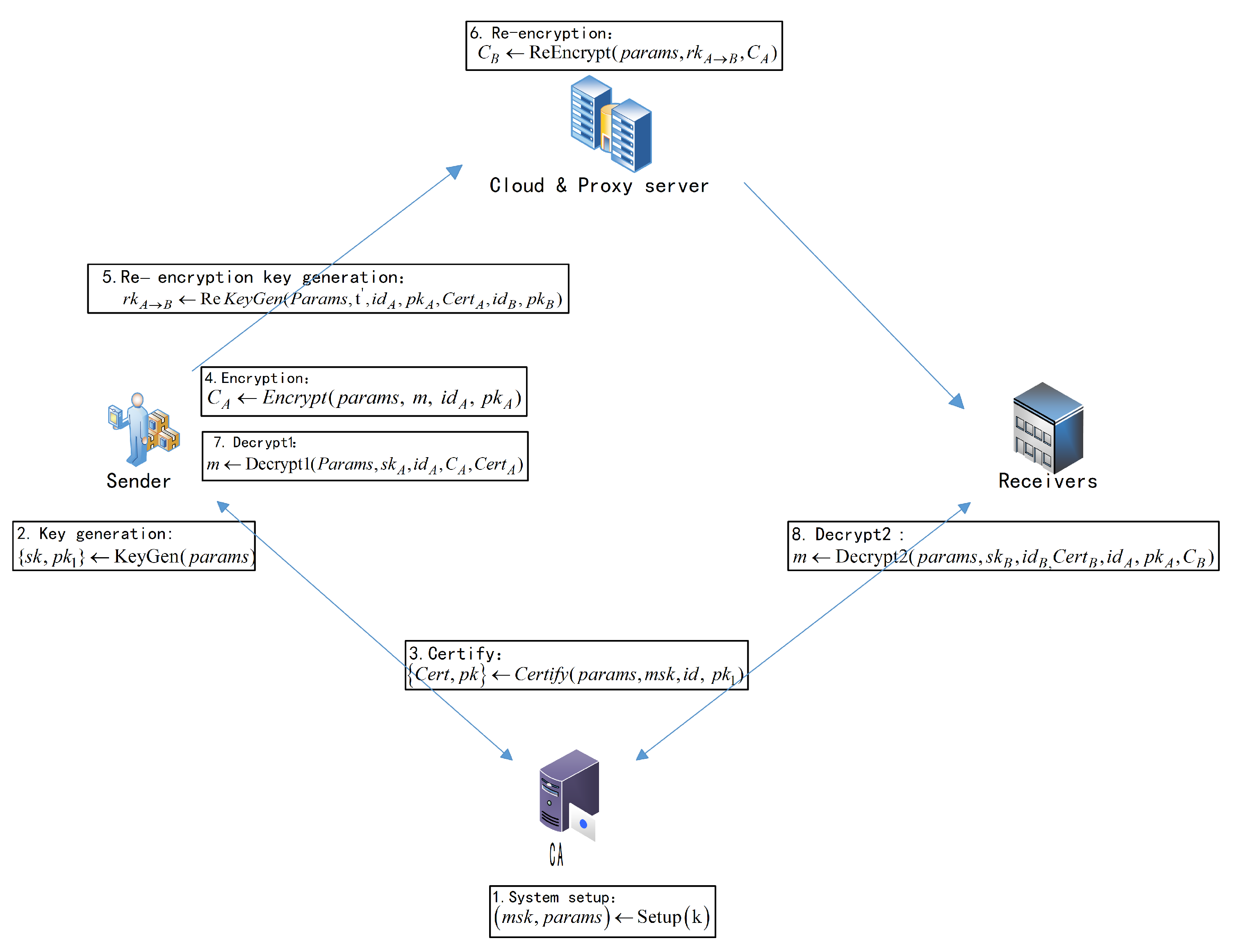
This scheme involves four key roles, including the sender, receiver, semi-trusted proxy, and Certificate Authority (CA). The CA is primarily responsible for authenticating the identities of the sender and receiver and issuing certificates. The sender is tasked with key generation, message encryption, and re-encryption key generation. The semi-trusted proxy is responsible for re-encrypting the ciphertext, and upon receiving the re-encrypted ciphertext, the receiver can decrypt it using their private key. Each role plays a unique and crucial part in the scheme, collectively constituting the complete operation of the proxy re-encryption scheme. In this collaborative system, each role contributes significantly to the overall functionality.

• Setup (k): Given the security parameter k as input, the algorithm outputs the system’s public parameter $params$ and the master key $msk$.
• KeyGen ($params$): Given the system’s public parameter $params$ as input, the algorithm generates and outputs the user’s private key $sk$ and partial public key $p{k}_1$.
• Certify ($params,msk,id,pk$): Given the system’s public parameter $params$, master key $msk$, user identity $id$, and partial public key $p{k}_1$ as input, the algorithm generates and outputs all public keys $pk=(p{k}_1,p{k}_2)$ and user certificate $Cert$.
• Encrypt ($params,m,i{d}_A,p{k}_A$): Given the ephemeral randomness $t^{\prime }$, message m, user identity $i{d}_A$, public key $p{k}_A$, and the system’s public parameter $params$ as input, the algorithm creates and outputs the message’s original ciphertext $C_A$.
• ReKeyGen ($params,t^{\prime },p{k}_A,Cer{t}_A,i{d}_B,p{k}_B$): Given the ephemeral randomness $t^{\prime }$, the private key $s{k}_A$ of user A, certificate $Cer{t}_A$, Identity $i{d}_B$ of authorized user B, public key $p{k}_B$, and the system’s public parameter $params$ as input, the encryption key $r{k}_{A\to B}$ is created and output by the algorithm.
• ReEncrypt ($params,C_A,r{k}_{A\to B}$): Given the original ciphertext $C_A$, the re-encryption key $r{k}_{A\to B}$, and the system’s public parameter $params$ as input, the algorithm outputs the re-encryption ciphertext $C_B$.
• Decrypt1 ($params,s{k}_A,Cer{t}_A,C_A$): Given the system’s public parameter $params$, the private key $s{k}_A$ of the authorizer, the certificate $Cer{t}_A$ and the original ciphertext $C_A$ as input, the algorithm outputs either the message m or the invalid symbol ⊥.
• Decrypt2 ($params,s{k}_B,Cer{t}_B,C_B$): Given the system’s public parameter $params$, the private key $s{k}_B$ of the authorized party, the certificate $Cer{t}_B$, and the original ciphertext $C_B$ as input, the algorithm outputs either the message m or the invalid symbol ⊥.

4. Security Model

In the PCBPRE+ scheme’s security model, the adversaries can be divided into two groups: $A_1$ and $A_2$. Adversary $A_1$ simulates an unauthenticated user who lacks access to the system’s master key. However, adversary $A_1$ has the ability to request the certificate of any user except for the target user. On the other hand, adversary $A_2$ acts as a malicious Certification Authority ($CA$) by simulating its behavior to gain access to the system’s master key. $A_2$ has the ability to request the private key of any user except for the private key of the target user.

The security of the scenario can be characterized by the interactive game $IND$-$CCA2$-$Game$, involving adversaries $A_1$ and $A_2$, as well as the challenger. A security model diagram is shown in Figure 1.

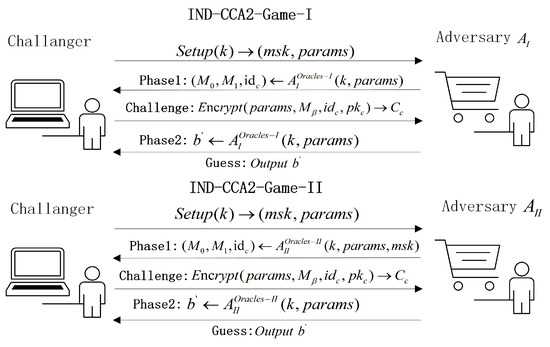
Figure 1. Security Architecture.

4.1. Game IND-CCA2-I

• System parameter setting: The challenger executes the algorithm $Setup\left(\lambda \right)$ to generate the system’s public parameter set $params$, with $CA$ corresponding to master key $msk$. The challenger outputs the master key $msk$ and outputs the system parameter set $params$ to adversary $A_1$.
• Phase 1: Adversary $A_1$ is able to make the following inquiries in an adaptive manner.
  • Users generation oracle: The challenger keeps track of the user’s private key, public key, and certificate in a table called $L_{user}$ that is initially empty. Adversary $A_1$ inputs the identity $i{d}_u$, and if there is already a record in table $L_{user}$, the challenger outputs the public key $i{d}_u$ to adversary $A_1$; otherwise, the challenger generates the public key $p{k}_u$, private key $s{k}_u$, and certificate $Cer{t}_u$ corresponding to the identity $i{d}_u$, records them in $L_{user}$, and outputs the public key $p{k}_u$ to $A_1$.
  • Private key generation oracle: Adversary $A_1$ enters the identity $i{d}_u$, and the challenger extracts the private key $s{k}_u$ from the $L_{user}$ table and outputs it to the $A_1$.
  • Certificate generation oracle: Certificate Inquiry: Adversary $A_1$ enters the identity $i{d}_u$, and the challenger obtains the certificate $Cer{t}_u$ from table $L_{user}$ and outputs it to $A_1$.
  • Re-encryption key generation oracle: Adversary $A_1$ inputs the identity $(i{d}_i,i{d}_j)$, randomly selects ephemeral randomness $t\in Z_q^{*}$, and the challenger generates a re-encryption key $r{k}_{i\to j}$, and outputs the re-encryption key $r{k}_{i\to j}$ to adversary $A_1$.
  • Re-encryption oracle: Adversary $A_1$ inputs an original ciphertext $C_i$ and the identity$(i{d}_i,i{d}_j)$, and the challenger generates a re-encrypted ciphertext $C_j$, and outputs the re-encrypted ciphertext $C_j$ to adversary $A_1$.
  • Decryption oracle: Adversary $A_1$ inputs identity $i{d}_i$ and a ciphertext $C_i$, and the challenger performs the decryption algorithm on $C_i$ and outputs the resulting value to $A_1$.
• Challenge stage: After the Stage 1 inquiries, adversary $A_1$ produces an identity $i{d}_c$ and two plaintexts of equal length, denoted as $m_0$, $m_1$. The restriction is that adversary $A_1$ has not made an inquiry about the certificate corresponding to the identity $i{d}_c$. The challenger randomly chooses $\beta \in \left\{0,1\right\}$, runs the algorithm $Encrypt$ to generate the original ciphertext $C_c$ of $m_{\beta }$, and outputs it as the challenge ciphertext to $A_1$, where $A_1$ does not interrogate the re-encryption key for $(i{d}_c,i{d}_i)$.
• Phase 2: The same as the phase 1 interrogation, with the following restrictions: adversary $A_1$ cannot interrogate the certificate of the challenging identity $i{d}_c$; for any $i{d}_i\ne i{d}_c$, adversary $A_1$ cannot make an inquiry about the $(i{d}_c,i{d}_i)$ with the re-encryption key; adversary $A_1$ cannot interrogate the $(i{d}_c,C_c)$ and the $(i{d}_d,C_d)$ with the decryption key, and in the process, $C_d$ interrogates the output of the $(i{d}_c,i{d}_d,C_c)$ for the re-encryption.
• Guess: Adversary $A_1$ outputs a guess ${\beta }^{\prime }$ for $\beta$. If ${\beta }^{\prime }=\beta$, then adversary $A_1$ wins the game. The advantage for adversary $A_1$ to win is $Adv\left(A_1\right)=\left|Pr\left[{\beta }^{\prime }=\beta \right]-1/2\right|$.

4.2. Game IND-CCA2-II

• System parameter setting: The challenger executes the algorithm $Setup\left(\lambda \right)$ to generate the system’s public parameter $params$, with $CA$ corresponding to the master key $msk$. The challenger outputs the master key $msk$ and outputs the system parameter set $params$ to adversary $A_2$.
• Phase 1: Adversary $A_2$ is able to make the following inquiries in an adaptive manner.

  1.

  Users generation oracle: The challenger keeps track of the user’s private key, public key, and certificate in a table called $L_{user}$ that is initially empty. Adversary $A_2$ inputs the identity $i{d}_u$, and if there is already a record in table $L_{user}$, the challenger outputs the public key $p{k}_u$ to adversary $A_2$; otherwise, the challenger generates the public key $p{k}_u$, private key $s{k}_u$, and certificate $Cer{t}_u$ corresponding to the identity $i{d}_u$, records them in $L_{user}$, and outputs the public key $p{k}_u$ to $A_2$.

  2.

  Private key generation oracle: Adversary $A_2$ enters the identity $i{d}_u$, and the challenger obtains the private key $s{k}_u$ from the table $L_{user}$ and outputs it to $A_2$.

  3.

  Re-encryption key generation oracle: Adversary $A_2$ inputs the identity $(i{d}_i,i{d}_j)$, randomly selects ephemeral randomness $t\in Z_q^{*}$, and the challenger generates a re-encryption key $r{k}_{i\to j}$, and outputs the re-encryption key $r{k}_{i\to j}$ to adversary $A_2$.

  4.

  Re-encryption oracle: Adversary $A_2$ inputs an original ciphertext $C_i$, and identity $(i{d}_i,i{d}_j)$, and the challenger generates a re-encrypted ciphertext $C_j$, and outputs the re-encrypted ciphertext $C_j$ to adversary $A_2$.

  5.

  Decryption oracle: Adversary $A_2$ inputs identity $i{d}_i$ and a ciphertext $C_i$, and the challenger performs the decryption algorithm on $C_i$ and outputs the resulting value to $A_2$.

• Challenge stage: Following the Stage 1 inquiries, adversary $A_2$ produces an identity $i{d}_c$ along with two plaintexts of equal length, denoted as $m_0$ and $m_1$. The restriction is that adversary $A_2$ has not asked for the private key corresponding to identity $i{d}_c$. The challenger randomly chooses $\beta \in \left\{0,1\right\}$, runs the algorithm $Encrypt$ to generate the original ciphertext $C_c$ of $m_{\beta }$, and outputs it as the challenge ciphertext to $A_2$, where $A_2$ does not interrogate the re-encryption key for $(i{d}_c,i{d}_i)$.
• Phase 2: The same as the phase 1 interrogation, with the following restrictions: Adversary $A_2$ cannot ask for the private key of the challenge identity $i{d}_c$; for any $i{d}_i\ne i{d}_c$, adversary $A_2$ cannot inquiry the $(i{d}_c,i{d}_i)$ with the re-encryption key; adversary $A_2$ cannot interrogate the $(i{d}_c,C_c)$ and the $(i{d}_d,C_d)$ with the decryption key, and in the process, the $C_d$ interrogates the output of the $(i{d}_c,i{d}_d,C_c)$ for the re-encryption.
• Guess: Adversary $A_2$ outputs a guess ${\beta }^{\prime }$ for $\beta$. If ${\beta }^{\prime }=\beta$, then adversary $A_2$ wins the game. The advantage for adversary $A_2$ to win is $Adv\left(A_2\right)=\left|Pr\left[{\beta }^{\prime }=\beta \right]-1/2\right|$.

Definition 2.

A certificate-based proxy re-encryption scheme is considered to satisfy indistinguishable security under adaptive chosen ciphertext attacks (IND-CCA2 security) if no PPT adversary can gain a significant advantage in winning the aforementioned game.

5. Pairing-Free Certificate-Based Proxy Re-Encryption Plus Scheme

The PCBPRE⁺ scheme consists of eight algorithms, and Figure 2 provides a concise depiction of the scheme.

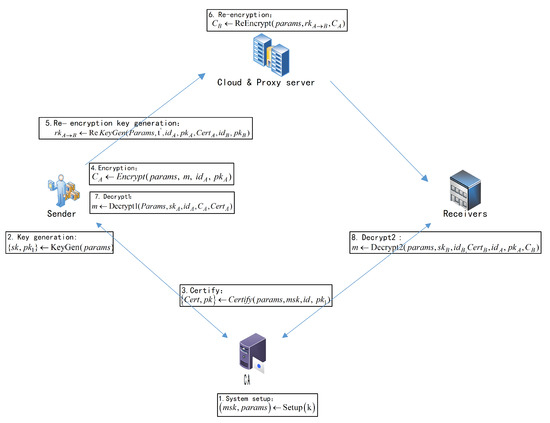
Figure 2. Flowchart of the CBPRE⁺.

• Setup: On inputting security parameters k, generate the master key $msk$ and the set of public parameters $params$ as follows:

  (a)

  The k-bit prime q is chosen to produce a cyclic additive group, where group G comprises elliptic curves whose order is the large prime q and P is the generating element of G.

  (b)

  Choose five hash functions, where n and l denote the length of the random bit string used by the plaintext and encryption algorithms, respectively:

  $$H_1:{\left\{0,1\right\}}^{*}\times G^2\to Z_q^{*}$$

  $$H_2:{\left\{0,1\right\}}^n\times {\left\{0,1\right\}}^l\times {\left\{0,1\right\}}^{*}\times G^2\to Z_q^{*}$$

  $$H_3:G\to {\left\{0,1\right\}}^{n+l}$$

  $$H_4:G\times Z_q^{*}\times G\times {\left\{0,1\right\}}^{n+l}\times G\to Z_q^{*}$$

  $$H_5:{\left\{0,1\right\}}^{*}\times {\left\{0,1\right\}}^{*}\times G\to Z_q^{*}$$

  (c)

  CA randomly selects $\alpha \in Z_q^{*}$, calculates $P_{pub}=\alpha P$, and outputs the master key $msk=\alpha$ and the set of public parameters:

  $params=\left\{G,q,P,P_{pub},n,l,H_1,H_2,H_3,H_4,H_5\right\}$.

• KeyGen: On inputting public parameters $params$, this algorithm randomly selects $s{k}_i=x_i\in Z_q^{*}$ as the user i private key and computes the partial public key $p{k}_{i1}=x_{i}P$. Output user i’s private keys $s{k}_i$ and partial public key $p{k}_{i1}$.
• Certify: On inputting public parameter $params$, master key $msk$, identity $i{d}_i$, and the partial public key $p{k}_{i1}$.

  (a)

  The algorithm randomly selects $y_i\in Z_q^{*}$, user i’s public key $p{k}_i=(p{k}_{i1},p{k}_{i2})=(x_{i}P,y_{i}P)$.

  (b)

  The algorithm calculates user i’s certificate $Cer{t}_i=y_i+\alpha H_1(i{d}_i,p{k}_i).$

• Encrypt: On inputting message $m\in {\left\{0,1\right\}}^n$, identity $i{d}_A$, the public key $p{k}_A=(p{k}_{A1},p{k}_{A2})$, and public parameter $params$, the user does the following:

  (a)

  Choose ephemeral randomness $c\in Z_q^{*}$ at random.

  (b)

  Randomly select a l-bit $\delta \in {\left\{0,1\right\}}^l$, and calculate $r=H_2(m,\delta ,i{d}_A,p{k}_A)$, $f=cr$.

  (c)

  Computer the ciphertext $C_1=rP$, $C_2=r$, $C_3=crP$, $C_4=(m\Vert \delta )\oplus H_3\left(f{Q}_A\right)$, where $Q_A=p{k}_{A1}+p{k}_{A2}+h_A{P}_{pub}$, $h_A=H_1(i{d}_A,p{k}_A)$.

  (d)

  Randomly select $t\in Z_q^{*}$, and compute the ciphertext $C_5=tP$, $C_6=t+cr{H}_4(C_1,C_2,C_3,C_4,C_5)$.

  (e)

  Output the original ciphertext $C=(C_1,C_2,C_3,C_4,C_5,C_6)$.

• ReKeyGen: On inputting ephemeral randomness c, public parameter $params$, identity $i{d}_A$, certificate $Cer{t}_A$, the public key $p{k}_A$ of sender A, and the identity $i{d}_B$ and public key $p{k}_B=(p{k}_{B1},p{k}_{B2})$ of receiver B, this algorithm performs as follows:

  (a)

  Calculate $s=H_5(i{d}_A,i{d}_B,p{k}_{B1}+p{k}_{B2}+h_B{P}_{pub})$, where $h_B=H_1(i{d}_B,P{K}_B)$.

  (b)

  Then, compute $r{k}_1=s^{-1}·c·Cer{t}_A$, $r{k}_2=s^{-1}·c·p{k}_{A1}$, $r{k}_3=s^{-1}·Cer{t}_A$.

  (c)

  Set the proxy re-encryption key $r{k}_{A\to B}=(r{k}_1,r{k}_2,r{k}_3)$.

• ReEncrypt: On inputting a re-encryption key $r{k}_{A\to B}$, ciphertext C, and public parameter $params$, the steps that the proxy takes are as follows:

  (a)

  If $C_{6}P=C_5+H_4(C_1,C_2,C_3,C_4,C_5)C_3$, then continue; otherwise, output ⊥.

  (b)

  Compute $C_1^{\prime }=r{k}_1·C_1$, $C_2^{\prime }=r{k}_2·C_2$, $C_3^{\prime }=C_4$, $C_4^{\prime }=r{k}_3·C_1$, and output a new ciphertext $C^{\prime }=(i{d}_A,C_1^{\prime },C_2^{\prime },C_3^{\prime },C_4^{\prime })$.

• Decrypt1: On inputting ciphertext C, identity $i{d}_A$, private keys $s{k}_A$, the certificate $Cer{t}_A$ of sender A, and public parameter $params$, the receiver A operates as follows:

  (a)

  If $C_{6}P=C_5+H_4(C_1,C_2,C_3,C_4,C_5)C_3$, then proceed; if not, output ⊥.

  (b)

  Compute $(m\Vert \delta )=C_4\oplus H_3(s{k}_A+Cer{t}_A)C_5$.

  (c)

  If $C_3=crP$, where $r=H_2(m,\delta ,i{d}_A,P{K}_A)$, the algorithm returns m as the message. Otherwise, it outputs ⊥, indicating a failure or invalid condition.

• Decrypt2: On inputting ciphertext $C^{\prime }$, identity $i{d}_A$, the public key $p{k}_A$ of sender A and identity $i{d}_B$, private keys $s{k}_B$, the certificate $Cer{t}_B$ of receiver B, and public parameter $params$, the receiver B operates as follows:

  (a)

  Compute $s^{\prime }=H_5(i{d}_A,i{d}_B,(s{k}_B+Cer{t}_B)P)$.

  (b)

  Compute $(m\Vert \delta )=C_3^{\prime }\oplus H_3\left(s^{\prime }(C_1^{\prime }+C_2^{\prime })\right)$.

  (c)

  If $C_4^{\prime }={\left(s^{\prime }\right)}^{-1}r(p{k}_{A2}+h_A{P}_{pub})$, where $h_A=H_1(i{d}_A,p{k}_A),r=H_2(m,\delta ,i{d}_A,p{k}_A)$, the algorithm returns m as the message. Otherwise, it outputs ⊥, indicating a failure or invalid condition.

6. Security Analysis

6.1. Correctness Analysis

Original ciphertext verification:

$$\begin{array}{cc}\hfill C_{6}P& =(t+cr{H}_4(C_1,C_2,C_3,C_4,C_5))P\hfill \\ \hfill & =C_5+H_4(C_1,C_2,C_3,C_4,C_5)C_3\hfill \end{array}$$

Original ciphertext decryption verification:

$$\begin{array}{cc}\hfill & C_4\oplus H_3\left((s{k}_A+Cer{t}_A)C_3\right)\hfill \\ \hfill & =C_4\oplus H_3\left((x_A+y_A+\alpha H_1(i{d}_A,p{k}_A))crP\right)\hfill \\ & =C_4\oplus H_3\left((p{k}_{A1}+p{k}_{A2}+H_1(i{d}_A,p{k}_A)P_{p}ub)cr\right)\hfill \\ & =C_4\oplus H_3\left(cr{Q}_A\right)\hfill \\ & =(m\Vert \delta )\oplus H_3\left(cr{Q}_A\right)\oplus H_3\left(cr{Q}_A\right)\hfill \\ & =(m\Vert \delta )\hfill \end{array}$$

Re-encryption ciphertext decryption verification:

$$\begin{array}{cc}\hfill s^{\prime }& =H_5(i{d}_A,i{d}_B,(s{k}_B+Cer{t}_B)P)\hfill \\ & =H_5(i{d}_A,i{d}_B,(p{k}_{B1}+p{k}_{B2}+h_B{P}_{pub}))\hfill \\ & =s\hfill \end{array}$$

$$\begin{array}{cc}\hfill & C_3^{\prime }\oplus H_3\left(s^{\prime }(C_1^{\prime }+C_2^{\prime })\right)\hfill \\ \hfill =& C_3^{\prime }\oplus H_3(s^{\prime }(r{k}_1·C_1+r{k}_2·C_2)\hfill \\ \hfill =& C_3^{\prime }\oplus H_3\left(s(s^{-1}·Cer{t}_A·c·rP+s^{-1}·p{k}_{A1}·cr)\right)\hfill \\ \hfill =& C_3^{\prime }\oplus H_3(Cer{t}_A·crP+p{k}_{A1}·cr)\hfill \\ \hfill =& (m\Vert \delta )\oplus H_3\left(cr{Q}_A\right)\oplus H_3\left(cr(Cer{t}_A·P+p{k}_{A1})\right)\hfill \\ \hfill =& (m\Vert \delta )\oplus H_3\left(cr{Q}_A\right)\oplus H_3\left(cr\right((y_A+\alpha H_1(i{d}_A,p{k}_A))P\hfill \\ & +p{k}_{A1}\left)\right)\hfill \\ \hfill =& (m\Vert \delta )\oplus H_3\left(cr{Q}_A\right)\oplus H_3\left(cr(p{k}_{A2}+h_A{P}_{hub}+p{k}_{A1})\right)\hfill \\ \hfill =& (m\Vert \delta )\oplus H_3\left(cr{Q}_A\right)\oplus H_3\left(cr{Q}_A\right)\hfill \\ \hfill =& (m\Vert \delta )\hfill \end{array}$$

6.2. Security Analysis

Theorem 1.

Assuming that $H_1-H_5$ are random prophecies, if there exists a first class adversary $A_1$ about the security of this scheme IND-CCA2 with advantage ε, asking at most $q_{cu}$ user-generated queries, $q_k$ private key queries, $q_{cer}$ certificate queries, $q_{rek}$ re-encryption key queries, $q_{ren}$ re-encryption queries, $q_{dec}$ decryption queries, and $q_i$ random prophecy $H_i$ queries $(1\le i\le 5)$, then the CDH problem on group G is solved by the $A_{CDH}$ algorithm with advantage ${\epsilon }^{\prime }\ge \frac{1}{q_3}\left(\frac{\epsilon }{q_{cu}}-\frac{q_{ren}+q_{dec}}{2^{\lambda }}-\frac{q_2}{2^{l+1}}\right)$.

Proof. 

In this paper, an algorithm $A_{CDH}$ is constructed to mimic the challenger of IND-CCA2, a CDH problem example is given as $(G,q,P,aP,bP)$, and the algorithm $A_{CDH}$ interacts with the first class adversary $A_1$ to solve the CDH problem:

• System parameter setting: The algorithm $A_{CDH}$ probabilistically selects an index value $\theta \in \left[1,q_{cu}\right],a\in Z_q^{*}$,$P_{pub}=aP$ and $A_{CDH}$ outputs $\{q,P,G,n,l,H_1,H_2,H_3,H_4,H_5,$$P_{pub}\}$ to adversary $A_1$ as an open parameter set $params$.
• Hash Oracle Queries: Adversary $A_1$ generates a random prophecy $H_1-H_5$ query, algorithm $A_{CDH}$ maintains table $L_{H_1}-L_{H_5}$, where $L_{H_1}-L_{H_5}$ is initially empty, and algorithm $A_{CDH}$ interacts with adversary $A_1$ as follows:

  –

  $H_1$ Queries: Adversary $A_1$ inputs $(i{d}_i,p{k}_i)$, if table $L_{H_1}$ already has records $(i{d}_i,p{k}_i,h_1)$, algorithm $A_{CDH}$ outputs $h_1$ to adversary $A_1$; otherwise, algorithm $A_{CDH}$ randomly selects $h_1\in Z_q^{*}$, records $(i{d}_i,p{k}_i,h_1)$ into $L_{H_1}$, and outputs $h_1$ to adversary $A_1$.

  –

  $H_2$ Queries: Adversary $A_1$ inputs $(m,\delta ,i{d}_i,p{k}_i)$, if table $L_{H_2}$ already has records $(m,\delta ,i{d}_i,p{k}_i,h_2,f)$, algorithm $A_{CDH}$ outputs $h_2$ to adversary $A_1$; otherwise, algorithm $A_{CDH}$ randomly selects $h_2\in Z_q^{*}$, records $(m,\delta ,i{d}_i,p{k}_i,h_2,f)$ into $L_{H_2}$, and outputs $h_2$ to adversary $A_1$.

  –

  $H_3$ Queries: Adversary $A_1$ inputs R, if table $L_{H_3}$ already has records $(R,h_3)$, algorithm $A_{CDH}$ outputs $h_3$ to adversary $A_1$; otherwise, algorithm $A_{CDH}$ randomly selects $h_3\in {\left\{0,1\right\}}^{n+l}$, records $(R,h_3)$ into $L_{H_3}$, and outputs $h_3$ to adversary $A_1$.

  –

  $H_4$ Queries: Adversary $A_1$ inputs $(C_1,C_2,C_3,C_4,C_5)$, if table $L_{H_4}$ already has records $(C_1,C_2,C_3,C_4,C_5,h_4)$, algorithm $A_{CDH}$ outputs $h_4$ to adversary $A_1$; otherwise, algorithm $A_{CDH}$ randomly selects $h_4\in Z_q^{*}$, records $C_1,C_2,C_3,C_4,C_5,h_4)$ into $L_{H_4}$, and outputs $h_4$ to adversary $A_1$.

  –

  $H_5$ Queries: Adversary $A_1$ inputs $(i{d}_i,i{d}_j,S)$, if table $L_{H_5}$ already has records $(i{d}_i,i{d}_j,S,h_5)$, algorithm $A_{CDH}$ outputs $h_5$ to adversary $A_1$; otherwise, algorithm $A_{CDH}$ randomly selects $h_5\in Z_q^{*}$, records $(i{d}_i,i{d}_j,S,h_5)$ into $L_{H_5}$, and outputs $h_5$ to adversary $A_1$.

• Phase 1: Adversary $A_1$ adaptively makes the following queries, and the algorithm $A_{CDH}$ maintains the table below as initially empty.
• User generation query: Adversary $A_1$ enters $i{d}_i$:

  (1)

  If there is already a record $(i{d}_i,p{k}_i,s{k}_i,y_i,Cer{t}_i)$ in table $L_{user}$, algorithm $A_{CDH}$ outputs $p{k}_i$ to adversary $A_1$.

  (2)

  If $i{d}_i$ is the user identity $i{d}_{\theta }(\theta \in \left[1,q_{cu}\right])$ asked by adversary $A_1$, that is, $i{d}_i=i{d}_{\theta }$, the algorithm $A_{CDH}$ randomly selects $x_{\theta },y_{\theta }\in Z_q^{*},p{k}_{\theta }=(x_{\theta }P,y_{\theta }P),s{k}_{\theta }=x_{\theta }$, records $(i{d}_{\theta },p{k}_{\theta },s{k}_{\theta },y_{\theta },\perp )$ into table $L_{user}$, and outputs $p{k}_{\theta }$ to adversary $A_1$.

  (3)

  If $i{d}_i\ne i{d}_{\theta }$, algorithm $A_{CDH}$ randomly select $x_i,s_i,t_i\in Z_q^{*}$, let $p{k}_i=(p{k}_{i1},$$p{k}_{i2})=(x_{i}P,t_{i}P-s_i{P}_{pub}),s{k}_i=x_i,Cer{t}_i=t_i$, add $(i{d}_i,p{k}_i,s_i)$ and $(i{d}_i,p{k}_i,s{k}_i,\perp ,$$Cer{t}_i)$ to table $L_{H_1}$ and table $L_{user}$, respectively, and output $p{k}_i$ to adversary $A_1$.

• Private key generation query: Adversary $A_1$ inputs $i{d}_i$, algorithm $A_{CDH}$ obtains the records $(i{d}_i,p{k}_i,s{k}_i,Cer{t}_i)$ from table $L_{user}$, and outputs $s{k}_i$ to adversary $A_1$.
• Certificate generation query: Adversary $A_1$ inputs $i{d}_i$, if $i{d}_i=i{d}_{\theta }$, Algorithm $A_{CDH}$ stops the game; otherwise, Algorithm $A_{CDH}$ obtains the records $(i{d}_i,p{k}_i,s{k}_i,Cer{t}_i)$ from Table $L_{user}$ and outputs $Cer{t}_i$ to Adversary $A_1$.
• Re-encryption key generation query: Adversary $A_1$ inputs $(i{d}_i,i{d}_j)$, if $i{d}_i=i{d}_{\theta }$, algorithm $A_{CDH}$ aborts the game; otherwise, algorithm $A_{CDH}$ obtains ephemeral randomness c, certificate $Cer{t}_i$, and public key $p{k}_j$, executes algorithm $ReKeyGen$ to produce a new re-encryption key $r{k}_{i\to j}=(r{k}_1,r{k}_2,r{k}_3)$, which is then output to adversary $A_1$.
• Re-encryption query: Adversary $A_1$ inputs $(i{d}_i,i{d}_j,C_i=(C_1,C_2,C_3,C_4,C_5,C_6))$, Algorithm $A_{CDH}$ first verifies the equation $C_{6}P=C_5+H_4(C_1,C_2,C_3,C_4,C_5)C_3$. If the equation does not hold, Algorithm $A_{CDH}$ rejects the query; if it does, Algorithm $A_{CDH}$ executes as follows:

  (1)

  If $i{d}_i=i{d}_{\theta }$, then algorithm $A_{CDH}$ searches the table $L_{H_2}$ for the record $(m,\delta ,i{d}_i,p{k}_i,$$h_2)$ satisfying $C_1=h_{2}P,C_2=h_2,C_3=h_{2}cP,C_4=(m\Vert \delta )\oplus H_3\left(f{Q}_i\right)$, where $Q_i=p{k}_{i1}+p{k}_{i2}+h_i{P}_{pub}$, $h_i=H_1(i{d}_i,p{k}_i)$. If there is no such record, the algorithm $A_{CDH}$ rejects the query; if it exists, then $C_1^{\prime }=s^{-1}·c·(p{k}_{i2}+H_1(i{d}_i,p{k}_i)P_{pub})·h_2$, $C_2^{\prime }=s^{-1}·p{k}_{i1}·h_{2}c$, $C_3^{\prime }=C_4$, $C_4^{\prime }=s^{-1}·(p{k}_{i2}+H_1(i{d}_i,p{k}_i)P_{pub})·h_2$. where $s=H_5(i{d}_i,i{d}_j,p{k}_{j1}+p{k}_{j2}+H_1(i{d}_j,p{k}_j)P_{pub})$. Algorithm $A_{CDH}$ outputs $C_j=(i{d}_i,C_1^{\prime },C_2^{\prime },C_3^{\prime },C_4^{\prime })$ to adversary $A_1$.

  (2)

  If $i{d}_i\ne i{d}_{\theta }$, algorithm $A_{CDH}$ undergoes a re-encryption key query on $(i{d}_i,i{d}_j)$ to obtain $r{k}_{i\to j}$, then outputs $C_j=ReEncrypt(params,r{k}_{i\to j},C_i)$ to adversary $A_1$.

• Decryption query: Adversary $A_1$ inputs $(i{d}_i,C_i)$, and the algorithm $A_{CDH}$ is executed as follows:

  (1)

  If $i{d}_i=i{d}_{\theta }$, $C_i=(C_1,C_2,C_3,C_4,C_5,C_6)$ is an original ciphertext, Algorithm $A_{CDH}$ checks $C_{6}P=C_5+H_4(C_1,C_2,C_3,C_4,C_5)C_3$, if the query is not valid, Algorithm $A_{CDH}$ rejects the query; otherwise, algorithm $A_{CDH}$ searches the table $L_{H_2}$ for records $(m,\delta ,i{d}_i,p{k}_i,h_2)$ that satisfy $C_1=h_{2}P, C_2=h_2, C_3=h_{2}cP,$ $C_4=(m\Vert \delta )\oplus H_3\left(f{Q}_i\right)$, where $Q_i=p{k}_{i1}+p{k}_{i2}+h_i{P}_{pub}$, $h_i=H_1(i{d}_i,p{k}_i)$. If there is no such record, Algorithm $A_{CDH}$ rejects the query; if it exists, it outputs m to adversary $A_1$ as the decryption of ciphertext $C_i$.

  (2)

  If $i{d}_i=i{d}_{\theta }$, $C_i=(i{d}_j,C_1^{\prime },C_2^{\prime },C_3^{\prime },C_4^{\prime })$ is a re-encrypted ciphertext, the algorithm $A_{CDH}$ performs the re-encryption key interrogation $(i{d}_i,i{d}_j)$ to obtain the re-encryption key $r{k}_{i\to j}=(r{k}_1,r{k}_2,r{k}_3)$, and computes $C_1={\left(r{k}_1\right)}^{-1}·C_1^{\prime },$ $C_2={\left(r{k}_2\right)}^{-1}·C_2^{\prime }, C_4={\left(r{k}_3\right)}^{-1}·C_1^{\prime }$. Algorithm $A_{CDH}$ searches the table $L_{H_2}$ for records $(m,\delta ,i{d}_j,p{k}_j,h_2)$ that satisfy $C_1=h_{2}P, C_2=h_2, C_3=h_{2}cP,$ $C_4=(m\Vert \delta )\oplus H_3\left(f{Q}_j\right)$, where $Q_j=p{k}_{j1}+p{k}_{j2}+h_j{P}_{pub}$, $h_j=H_1(i{d}_j,p{k}_j)$. If there is no such record, algorithm $A_{CDH}$ rejects the query; if it exists, it outputs m to adversary $A_1$ as the decryption of ciphertext $C_i$.

  (3)

  If $i{d}_i\ne i{d}_{\theta }$, the algorithm $A_{CDH}$ obtains $s{k}_i$ and $Cer{t}_i$, decrypts $C_i$ using the appropriate decryption algorithm, then outputs m to adversary $A_1$.

• Challenge: After phase 1 queries, adversary $A_1$ outputs identity $i{d}_c$ and two plaintexts of equal length $m_0,m_1$. Adversary $A_1$ does not make a re-encryption key query for $(i{d}_c,i{d}_i)$. If $i{d}_c\ne i{d}_{\theta }$, the algorithm $A_{CDH}$ terminates the game, resulting in a failed simulation; otherwise, the algorithm $A_{CDH}$ probabilistically selects a value $\beta \in \left\{0,1\right\}, e^{*}\in Z_q^{*}, {C_4}_c\in {\left\{0,1\right\}}^{n+l},{C_6}_c$, calculates ${C_1}_c=bP, {C_2}_c=b,$ ${C_3}_c=cbP,$ ${C_5}_c={C_6}_{c}P-e^{*}\left(cbP\right)$, records $({C_1}_c,{C_2}_c,{C_3}_c,{C_4}_c,{C_5}_c,e^{*})$ in table $L_{H_4}$, and gives $C_c=({C_1}_c,{C_2}_c,{C_3}_c,{C_4}_c,{C_5}_c,{C_6}_c)$ to $A_1$ as the challenge ciphertext. Obviously, ${C_6}_{c}P={C_5}_c+H_4({C_1}_c,{C_2}_c,{C_3}_c,{C_4}_c,{C_5}_c){C_3}_c$ holds.
  Decrypt $C_c$:

  $$\begin{array}{cc}& C_{4_c}\oplus H_3\left((s{k}_{\theta }+Cer{t}_{\theta })C_{3_c}\right)\hfill \\ \hfill & =C_{4_c}\oplus H_3\left((x_{\theta }+y_{\theta }+a{H}_1(i{d}_{\theta },p{k}_{\theta }))cbp\right)\hfill \end{array}$$

  where $H_2(m_{\beta },{\delta }^{*},i{d}_{\theta },p{k}_{\theta })=b,{\delta }^{*}\in {\left\{0,1\right\}}^l$.
• Phase 2: The algorithm $A_{CDH}$ answers the same as the phase 1 interrogation with the following constraints: adversary $A_1$ cannot interrogate the certificate of challenge identity $i{d}_c$; for any $i{d}_i\ne i{d}_c$, no re-encryption key interrogation can be performed on $(i{d}_c,i{d}_i)$; no decryption interrogation can be performed on $(i{d}_c,C_c)$ and $(i{d}_d,C_d)$. The result of the re-encryption query $(i{d}_c,i{d}_d,C_c)$ is $C_d$ during the procedure.
• Guess: Adversary $A_1$ outputs a guess ${\beta }^{\prime }$ for $\beta$. If ${\beta }^{\prime }=\beta$, then $A_1$ wins the game.
  During the challenge, if adversary $A_1$ chooses the identity $i{d}_{\theta }$ as the challenge identity, which is $i{d}_{\theta }=i{d}_c$, then Algorithm $A_{CDH}$ does not abort the game. Algorithm $A_{CDH}$ selects a random record $(R,h_3)$ in table $L_{H_3}$ and uses $T={\left(c{H}_1(i{d}_{\theta },p{k}_{\theta })\right)}^{-1}$$(R-x_{\theta }cbP-y_{\theta }cbP)$ as the solution to the given CDH problem.

□

Analysis: We define the following events in order to calculate the benefit of $A_{CDH}$ in solving the specified CDH problem:

(1)

$Ask{H}_2^{*}$: Adversary $A_1$ makes a random oracle $H_2$ query on $(m_{\theta },{\delta }^{*},i{d}_{\theta },p{k}_{\theta })$.

(2)

$Ask{H}_3^{*}$: Adversary $A_1$ makes a random oracle $H_3$ query on $(x_{\theta }+y_{\theta }+a{H}_1(i{d}_{\theta },p{k}_{\theta }))cbp$.

(3)

$Abort$: During the simulation, $A_{CDH}$ stops the game.

(4)

$ReEncErr$:$A_{CDH}$ rejects a legitimate re-encryption query.

(5)

$DecErr$:$A_{CDH}$ rejects a legitimate decryption query.

Let $E=(ReEncErr\vee DecErr\vee Ask{H}_2^{*}\vee Ask{H}_3^{*})\mid \neg Abort$, obviously, $Pr\left[{\beta }^{\prime }=\beta \mid \neg E\right]\le 1/2$, we have

$$\begin{array}{cc}& Pr\left[{\beta }^{\prime }=\beta \right]\hfill \\ & =Pr\left[{\beta }^{\prime }=\beta \mid \neg E\right]Pr\left[\neg E\right]+Pr\left[{\beta }^{\prime }=\beta \mid E\right]Pr\left[E\right]\hfill \\ & \le Pr\left[\neg E\right]/2+Pr\left[E\right]\hfill \\ & =1/2+Pr\left[E\right]/2\hfill \end{array}$$

The scheme of [28] in the literature specifically proves that since the advantage of adversary $A_1$ to win is $\epsilon$, there is.

$$\begin{array}{cc}\hfill \epsilon =& \le 2\left|Pr\left[{\beta }^{\prime }=\beta \right]-1/2\right|\hfill \\ \hfill \le & Pr\left[E\right]\hfill \\ \hfill \le & Pr\left[(ReEncErr\vee DecErr\vee Ask{H}_2^{*}\vee Ask{H}_3^{*})\mid \neg Abort\right]\hfill \\ \hfill \le & (Pr\left[ReEncErr\right]+Pr\left[DecErr\right]+Pr\left[Ask{H}_2^{*}\right]\hfill \\ & +Pr\left[Ask{H}_3^{*}\right])/Pr\left[\neg Abort\right]\hfill \end{array}$$

where $Pr\left[\neg Abort\right]=1/q_{cu}$, $Pr\left[ReEncErr\right]\le q_{ren}/2^{\lambda }$, $Pr\left[DecErr\right]\le q_{dec}/2^{\lambda }$, $Pr\left[Ask{H}_2^{*}\right]\le q_2/2^{l+1}$. Therefore

$$\begin{array}{cc}\hfill Pr\left[Ask{H}_3^{*}\right]\ge & Pr\left[\neg Abort\right]\epsilon -Pr\left[ReEncErr\right]\hfill \\ & -Pr\left[DecErr\right]-Pr\left[Ask{H}_2^{*}\right]\hfill \\ \hfill \ge & \epsilon /q_{cu}-q_{ren}/2^{\lambda }-q_{dec}/2^{\lambda }-q_2/2^{l+1}\hfill \end{array}$$

If the event $Ask{H}_3^{*}$ occurs, the algorithm $A_{CDH}$ obtains a correct record in $L_{H_3}$, then:

$$\begin{array}{cc}\hfill {\epsilon }^{\prime }& \ge Pr\left[Ask{H}_3^{*}\right]/q_3\ge \frac{1}{q_3}\left(\frac{\epsilon }{q_{cu}}-\frac{q_{ren}+q_{dec}}{2^{\lambda }}-\frac{q_2}{2^{l+1}}\right)\hfill \end{array}$$

Theorem 2.

Assuming that $H_1$–$H_5$ are random prophecies, if there exists a second class adversary $A_2$ about the security of this scheme IND-CCA2 with advantage ε, asking at most $q_{cu}$ user-generated queries, $q_k$ private key queries, $q_{rek}$ re-encryption key queries, $q_{ren}$ re-encryption queries, $q_{dec}$ decryption queries, and $q_i$ random prophecy $H_i$ queries $(1\le i\le 5)$, then the CDH problem on group G is solved by the $A_{CDH}$ algorithm with advantage ${\epsilon }^{\prime }\ge \frac{1}{q_3}\left(\frac{\epsilon }{q_{cu}}-\frac{q_{ren}+q_{dec}}{2^{\lambda }}-\frac{q_2}{2^{l+1}}\right)$.

Proof. 

In this paper, an algorithm $A_{CDH}$ is constructed to mimic the challenger of IND-CCA2, given a CDH problem example $(G,q,P,aP,bP)$, and the algorithm $A_{CDH}$ interacts with the first class adversary $A_2$ to solve the CDH problem:

• System parameter setting: The algorithm $A_{CDH}$ randomly selects an index value $\theta \in \left[1,q_{cu}\right],\alpha \in Z_q^{*}$,$P_{pub}=\alpha P$, master private key $msk=\alpha$, and $A_{CDH}$ outputs public parameters $params=\left\{q,P,G,n,l,H_1,H_2,H_3,H_4,H_5,P_{pub}\right\}$ and master private key $msk$ to adversary $A_2$.
• Phase 1: Adversary $A_2$ adaptively makes the following queries, and the algorithm $A_{CDH}$ maintains the table below as initially empty.
• User generation query: Adversary $A_2$ inputs $i{d}_i$:

  (1)

  If there is already a record $(i{d}_i,p{k}_i,s{k}_i,y_i,Cer{t}_i)$ in table $L_{user}$, algorithm $A_{CDH}$ outputs $p{k}_i$ to adversary $A_2$.

  (2)

  If $i{d}_i$ is the user identity $i{d}_{\theta }(\theta \in \left[1,q_{cu}\right])$ asked by adversary $A_2$, that is, $i{d}_i=i{d}_{\theta }$, the algorithm $A_{CDH}$ randomly selects $h_{\theta },y_{\theta }\in Z_q^{*},p{k}_{\theta }=(aP,y_{\theta }P),Cer{t}_{\theta }=y_{\theta }+\alpha h_{\theta }$, Record $(i{d}_{\theta },p{k}_{\theta },h_{\theta })$ and $(i{d}_{\theta },p{k}_{\theta },\perp ,y_{\theta },Cer{t}_{\theta })$ into table $L_{H_1}$ and table $L_{user}$, respectively, and output $p{k}_{\theta }$ to adversary $A_2$.

  (3)

  If $i{d}_i\ne i{d}_{\theta }$, algorithm $A_{CDH}$ randomly select $x_i,y_i,h_i\in Z_q^{*}$, let $p{k}_i=(p{k}_{i1},$$p{k}_{i2})=(x_{i}P,y_{i}P),s{k}_i=x_i,Cer{t}_i=y_i+\alpha h_i$, add $(i{d}_i,p{k}_i,h_i)$ and $(i{d}_i,p{k}_i,s{k}_i,y_i,$$Cer{t}_i)$ to table $L_{H_1}$ and table $L_{user}$, respectively, and output $p{k}_i$ to adversary $A_2$.

• Private key generation query: Adversary $A_2$ inputs $i{d}_i$, if $i{d}_i=i{d}_{\theta }$, algorithm $A_{CDH}$ aborts the game; otherwise, algorithm $A_{CDH}$ obtains the records $(i{d}_i,p{k}_i,s{k}_i,y_i,Cer{t}_i)$ from table $L_{user}$ and outputs $s{k}_i$ to adversary $A_2$.
• Certificate generation query: Adversary $A_1$ inputs $i{d}_i$, if $i{d}_i=i{d}_{\theta }$, Algorithm $A_{CDH}$ stops the game; otherwise, Algorithm $A_{CDH}$ obtains the records $(i{d}_i,p{k}_i,s{k}_i,Cer{t}_i)$ from Table $L_{user}$ and outputs $Cer{t}_i$ to Adversary $A_1$.
• Re-encryption key generation query: Adversary $A_1$ inputs $(i{d}_i,i{d}_j)$, if $i{d}_i=i{d}_{\theta }$, algorithm $A_{CDH}$ aborts the game; otherwise, algorithm $A_{CDH}$ obtains ephemeral randomness c, certificate $Cer{t}_i$ and public key $p{k}_j$, executes algorithm $ReKeyGen$ to produce a new re-encryption key $r{k}_{i\to j}=(r{k}_1,r{k}_2,r{k}_3)$, which is then output to adversary $A_1$.
• Re-encryption query: Adversary $A_1$ inputs $(i{d}_i,i{d}_j,C_i=(C_1,C_2,C_3,C_4,C_5,C_6))$, Algorithm $A_{CDH}$ first verifies the equation $C_{6}P=C_5+H_4(C_1,C_2,C_3,C_4,C_5)C_3$. If the equation does not hold, Algorithm $A_{CDH}$ rejects the query; if it does, Algorithm $A_{CDH}$ executes as follows:

  (1)

  If $i{d}_i=i{d}_{\theta }$, the algorithm $A_{CDH}$ searches the table $L_{H_2}$ for the record $(m,\delta ,i{d}_i,p{k}_i,$$h_2)$ satisfying $C_1=h_{2}P,C_2=h_2,C_3=h_{2}cP,C_4=(m\Vert \delta )\oplus H_3\left(f{Q}_i\right)$, where $Q_i=p{k}_{i1}+p{k}_{i2}+h_i{P}_{pub}$, $h_i=H_1(i{d}_i,p{k}_i)$. If there is no such record, the algorithm $A_{CDH}$ rejects the query; if it exists, then $C_1^{\prime }=s^{-1}·c·(p{k}_{i2}+H_1(i{d}_i,p{k}_i)$$P_{pub})·h_2$, $C_2^{\prime }=s^{-1}·p{k}_{i1}·h_{2}c$, $C_3^{\prime }=C_4$, $C_4^{\prime }=s^{-1}·(p{k}_{i2}+H_1(i{d}_i,p{k}_i)P_{pub})·h_2$. where $s=H_5(i{d}_i,i{d}_j,p{k}_{j1}+p{k}_{j2}+H_1(i{d}_j,p{k}_j)P_{pub})$. Algorithm $A_{CDH}$ output $C_j=(i{d}_i,C_1^{\prime },C_2^{\prime },C_3^{\prime },C_4^{\prime })$ to adversary $A_1$.

  (2)

  If $i{d}_i\ne i{d}_{\theta }$, algorithm $A_{CDH}$ does re-encryption key query on $(i{d}_i,i{d}_j)$ to obtain $r{k}_{i\to j}$, then output $C_j=ReEncrypt(params,r{k}_{i\to j},C_i)$ to adversary $A_1$.

• Decryption query: Adversary $A_1$ inputs $(i{d}_i,C_i)$, and the algorithm $A_{CDH}$ is executed as follows:

  (1)

  If $i{d}_i=i{d}_{\theta }$, $C_i=(C_1,C_2,C_3,C_4,C_5,C_6)$ is an original ciphertext, Algorithm $A_{CDH}$ checks $C_{6}P=C_5+H_4(C_1,C_2,C_3,C_4,C_5)C_3$, if the query is not valid, Algorithm $A_{CDH}$ rejects the query; otherwise, algorithm $A_{CDH}$ searches the table $L_{H_2}$ for records $(m,\delta ,i{d}_i,p{k}_i,h_2)$ that satisfy $C_1=h_{2}P,C_2=h_2,C_3=h_{2}cP,$$C_4=(m\Vert \delta )\oplus H_3\left(f{Q}_i\right)$, where $Q_i=p{k}_{i1}+p{k}_{i2}+h_i{P}_{pub}$, $h_i=H_1(i{d}_i,p{k}_i)$. If there is no such record, Algorithm $A_{CDH}$ rejects the query; if it exists, it outputs m to adversary $A_1$ as the decryption of ciphertext $C_i$.

  (2)

  If $i{d}_i=i{d}_{\theta }$, $C_i=(i{d}_j,C_1^{\prime },C_2^{\prime },C_3^{\prime },C_4^{\prime })$ is a re-encrypted ciphertext, the algorithm $A_{CDH}$ performs the re-encryption key interrogation $(i{d}_i,i{d}_j)$ to obtain the re-encryption key $r{k}_{i\to j}=(r{k}_1,r{k}_2,r{k}_3)$, and computes $C_1={\left(r{k}_1\right)}^{-1}·C_1^{\prime },$$C_2={\left(r{k}_2\right)}^{-1}·C_2^{\prime },C_4={\left(r{k}_3\right)}^{-1}·C_1^{\prime }$. Algorithm $A_{CDH}$ searches the table $L_{H_2}$ for records $(m,\delta ,i{d}_j,p{k}_j,h_2)$ that satisfy $C_1=h_{2}P,C_2=h_2,C_3=h_{2}cP,C_4=(m\Vert \delta )\oplus H_3\left(f{Q}_j\right)$, where $Q_j=p{k}_{j1}+p{k}_{j2}+h_j{P}_{pub}$, $h_j=H_1(i{d}_j,p{k}_j)$. If there is no such record, algorithm $A_{CDH}$ rejects the query; if it exists, it outputs m to adversary $A_1$ as the decryption of ciphertext $C_i$.

  (3)

  If $i{d}_i\ne i{d}_{\theta }$, the algorithm $A_{CDH}$ obtains $s{k}_i$ and $Cer{t}_i$, decrypts $C_i$ using the appropriate decryption algorithm, then outputs m to adversary $A_1$.

• Challenge: After phase 1 queries, adversary $A_2$ outputs identity $i{d}_c$ and two plaintexts of equal length $m_0,m_1$. Adversary $A_2$ does not make re-encryption key query for $(i{d}_c,i{d}_i)$. If $i{d}_c\ne i{d}_{\theta }$, the algorithm $A_{CDH}$ terminates the game, resulting in a failed simulation; otherwise, the algorithm $A_{CDH}$ probabilistically selects a value $\beta \in \left\{0,1\right\},e^{*}\in Z_q^{*},{C_4}_c\in {\left\{0,1\right\}}^{n+l},{C_6}_c$, calculates ${C_1}_c=bP,{C_2}_c=b,{C_3}_c=cbP,$${C_5}_c={C_6}_{c}P-e^{*}\left(cbP\right)$, records $({C_1}_c,{C_2}_c,{C_3}_c,{C_4}_c,{C_5}_c,e^{*})$ in table $L_{H_4}$, and gives $C_c=({C_1}_c,$${C_2}_c,{C_3}_c,{C_4}_c,{C_5}_c,{C_6}_c)$ to $A_1$ as the challenge ciphertext. Obviously, ${C_6}_{c}P={C_5}_c+H_4({C_1}_c,{C_2}_c,{C_3}_c,{C_4}_c,{C_5}_c){C_3}_c$ holds.
  Decrypt $C_c$:

  $$\begin{array}{cc}& C_{4_c}\oplus H_3\left((s{k}_{\theta }+Cer{t}_{\theta })C_{3_c}\right)\hfill \\ & =C_{4_c}\oplus H_3\left((a+y_{\theta }+\alpha H_1(i{d}_{\theta },p{k}_{\theta }))cbp\right)\hfill \end{array}$$

  where $H_2(m_{\beta },{\delta }^{*},i{d}_{\theta },p{k}_{\theta })=b,{\delta }^{*}\in {\left\{0,1\right\}}^l$.
• Phase 2: The algorithm $A_{CDH}$ answers the same as the phase 1 interrogation with the following constraints: adversary $A_2$ cannot interrogate the private key of challenge identity $i{d}_c$; for any $i{d}_i\ne i{d}_c$, no re-encryption key interrogation can be performed on $(i{d}_c,i{d}_i)$; no decryption interrogation can be performed on $(i{d}_c,C_c)$ and $(i{d}_d,C_d)$. The result of the re-encryption query $(i{d}_c,i{d}_d,C_c)$ is $C_d$ during the procedure.
• Guess: Adversary $A_2$ produces a guess ${\beta }^{\prime }$ for $\beta$. If ${\beta }^{\prime }=\beta$, then $A_2$ wins the game.
  During the challenge, if adversary $A_2$ chooses the identity $i{d}_{\theta }$ as the challenge identity, which is $i{d}_{\theta }=i{d}_c$, then Algorithm $A_{CDH}$ does not abort the game. Algorithm $A_{CDH}$ selects a random record $(R,h_3)$ in table $L_{H_3}$ and uses $T=c^{-1}(R-y_{\theta }cbP-\alpha H_1$$(i{d}_{\theta },p{k}_{\theta })cbp)$ as the solution to the given CDH problem.

As proved in Theorem 1, the advantage of the algorithm $A_{CDH}$ to solve the CDH problem is as follow:

$$\begin{array}{cc}\hfill {\epsilon }^{\prime }& \ge Pr\left[Ask{H}_3^{*}\right]/q_3\ge \frac{1}{q_3}\left(\frac{\epsilon }{q_{cu}}-\frac{q_{ren}+q_{dec}}{2^{\lambda }}-\frac{q_2}{2^{l+1}}\right)\hfill \end{array}$$

□

7. Performance Analysis

In this section, we conduct a comprehensive comparison between the PCBPRE⁺ scheme proposed in this paper and several existing PRE schemes, focusing on both functional and efficiency aspects.

For the functional analysis, we compare the properties of various existing PRE schemes used for data sharing. We consider aspects such as fine-grained sharing capabilities, non-transferability, and security, and compare them with other PRE schemes. This comparison highlights the advantages and features of the PCBPRE⁺ scheme in terms of functionality.

In the efficiency analysis, we perform both theoretical analysis and experimental simulations. The theoretical analysis evaluates the performance of each PRE scheme by analyzing its algorithmic complexity and computational overhead. The experimental simulation, on the other hand, assesses the performance of each scheme in a real scenario, constructing an actual test environment and data set. We thoroughly evaluate the efficiency of each PRE scheme, considering the findings from both the theoretical study and the experimental simulation.

7.1. Property Analysis

In this section, we provide a comparison between our scheme and existing PRE schemes from the literature [5,18,19,21,22], as shown in Table 1. Our scheme offers several advantages over other schemes, which are as follows:

Table 1. Properties analysis and comparison of the schemes.

Scheme	Sur [18]	Li [21]	Kan [5]	Liu [22]	Xu [19]	Ours
Pairing-free	No	No	No	No	Yes	Yes
Conditional	No	Yes	No	Yes	Yes	Yes
Complexity assumption	BDH	BDH	CDH	BDH	CDH	CDH
Non-transferable delegation	No	No	Yes	Yes	No	Yes
Solve the key distribution problem	Yes	Yes	No	Yes	Yes	Yes
Fine-grained delegation (message level)	No	No	No	Yes	No	Yes
Re-encryption authority of the encryptor	No	No	Yes	Yes	No	Yes

• Improved Efficiency: In contrast to the predominant proxy re-encryption schemes relying on bilinear pairings, our study introduces a bilinear pair-free approach employing elliptic curves for construction. This innovative methodology substantially diminishes the computational overhead, amplifies efficiency, and elevates the scalability of the scheme in comparison to prevailing methods. Noteworthy is the adaptability of our scheme, especially in scenarios involving power-constrained devices, rendering it highly applicable across diverse settings.
• Fine-Grained Message-Level Delegation: In our scheme, fine-grained control at the message level is attained via the utilization of ephemeral random values. This distinctive feature bestows upon the authorizer the ability to encrypt specific data intended for sharing, utilizing the same ephemeral random value, while employing distinct values for encrypting other messages. Through the strategic selection of diverse ephemeral random values, the authorizer acquires meticulous control over data access, facilitating the nuanced and selective sharing of information. This heightened level of flexibility and precision empowers users to authorize and share data with the utmost accuracy, finely tailored to their specific needs.
• Non-Transferability Guarantee: Our PCBPRE⁺ scheme integrates ephemeral randomness, the message, and the sender’s public key in the computation and generation of the re-encryption key. This approach guarantees complete independence among sender A, receiver B, and proxy P, preventing any collusion between P and B to deduce the ephemeral random value generated by A. Consequently, authorized users are unable to transfer their decryption privileges to others, ensuring data security and maintaining ownership control. This robust protection mechanism prevents authorized users from transferring their decryption rights to unauthorized parties, thus mitigating unauthorized data dissemination and misuse. By upholding the independence of decryption rights, our scheme enhances data protection and control, fostering secure and accountable data sharing.
• Enhanced Functionality: Our proxy re-encryption scheme, founded on certificate-based encryption (CBE), presents notable advancements compared to conventional public-key proxy re-encryption. By harnessing the advantageous properties inherent in CBE, we adeptly tackle the challenge associated with certificate revocation. Moreover, our scheme proficiently eradicates both the key escrow and distribution challenges inherent in identity-based proxy re-encryption, thereby augmenting its functionality and applicability.
• Re-encryption Control Capability: In our scheme, the cryptographer encrypts the original ciphertext by generating unique ephemeral random values for each message. This strategy guarantees the resilience of the original ciphertext decryption, even in scenarios where the encryption algorithm fails to produce a corresponding random number for the message. However, this also signifies that decrypting the re-encrypted ciphertext becomes impractical, granting the encryptor full control over the re-encryption process.

The PCBPRE⁺ scheme presented in this paper introduces an innovative and efficient solution for secure cloud storage sharing. It incorporates notable advantages such as fine-grained sharing, non-transferable characteristics, and computational efficiency. These advantages bear substantial implications for fostering secure cloud storage sharing and have the potential to contribute significantly to the advancement of this field.

7.2. Efficiency Analysis

The performance of the proposed scheme is assessed in the subsequent analysis. Table 2 presents a comparison of the attributes between our scheme and the scheme mentioned in the literature [18,19,21,22]. The comprehensive cost analysis of our scheme is presented in Table 3. In these tables, we use the notations P, E, M, and H to represent the bilinear pair operation, exponential operation in group $G_T$, multiplicative operation in group G, and the Hash operation, respectively, along with their respective coefficients indicating the number of operations performed.

Table 2. Efficiency analysis.

Scheme	Encrypt	ReKeyGen	ReEncrypt	Decrypt1	Decrypt2
Sur [18]	2P + 2E + 3M	2P + 2E + 3M	8P	2P + E + 2M	4P + E + M
Li [21]	3P + 2E + 3M	2P + E + 5M	5P	4P + 2E	4P + E + M
Liu [22]	3P + 2E + 4M	2P + 2E + 2M	6P	2P + E + M	4P + E + M
Xu [19]	5M	5M	3M	4M	5M
Ours	5M	2M	5M	4M	4M

Table 3. Computation cost in proposed scheme.

Process	Encrypt	ReKeyGen	ReEncrypt	Decrypt1	Decrypt2
Calculation volume	5M + 4H	2M + 2H	5M + H	4M + 3H	4M + 4H

To provide a comprehensive time complexity analysis of the comparison scheme, we refer to Boyen [29], who offers estimated relative times for individual asymmetric operations when instantiating group elements in super singular curves with 80 bits of security (SS/80) and MNT curves with 80 bits of security (MNT/80).

We denote the time complexities of pairing, exponential operations in group $G_T$, multiplication operations in group G, and hash operations as $T_p$, $T_e$, $T_m$, and $T_h$ respectively. The relevant information can be found in Table 4. Utilizing the data from Table 4, we computed the time complexities of the comparison schemes, presented in Table 5 and Table 6. The results demonstrate that our proposed strategy outperforms the previous pairing-based PRE scheme in terms of computational efficiency.

Table 4. Temporal overhead of cryptographic operations (Relative time: 1 unit = 1$T_m$).

Curves	${\mathit{T}}_{\mathit{p}}$	${\mathit{T}}_{\mathit{e}}$	${\mathit{T}}_{\mathit{m}}$	${\mathit{T}}_{\mathit{h}}$
MNT/80	150	36	1	1
SS/80	20	4	1	1

Table 5. Time complexities of MNT/80.

Scheme	Encrypt	ReKeyGen	ReEncrypt	Decrypt1	Decrypt2
Sur [18]	375 $T_m$	375 $T_m$	1200 $T_m$	338 $T_m$	637 $T_m$
Li [21]	525 $T_m$	341 $T_m$	750 $T_m$	602 $T_m$	637 $T_m$
Liu [22]	526 $T_m$	374 $T_m$	900 $T_m$	337 $T_m$	637$T_m$
Xu [19]	5 $T_m$	5 $T_m$	3 $T_m$	4 $T_m$	5 $T_m$
Ours	5 $T_m$	2 $T_m$	5 $T_m$	4 $T_m$	4 $T_m$

Table 6. Time complexities of SS/80.

Scheme	Encrypt	ReKeyGen	ReEncrypt	Decrypt1	Decrypt2
Sur [18]	51 $T_m$	51 $T_m$	160 $T_m$	46 $T_m$	85 $T_m$
Li [21]	71 $T_m$	49 $T_m$	100 $T_m$	82 $T_m$	85 $T_m$
Liu [22]	72 $T_m$	50 $T_m$	120 $T_m$	45 $T_m$	85 $T_m$
Xu [19]	5 $T_m$	5 $T_m$	3 $T_m$	4 $T_m$	5 $T_m$
Ours	5 $T_m$	2 $T_m$	5 $T_m$	4 $T_m$	4 $T_m$

Finally, we conducted simulations to implement the scheme using the MIRACL library (version 7.0.0) and the PBC library (version 0.5.14). The experiments took place on a personal computer with an AMD Ryzen 7 5800H CPU operating at a frequency of 3.20 GHz. The simulation platform ran on Windows 11.

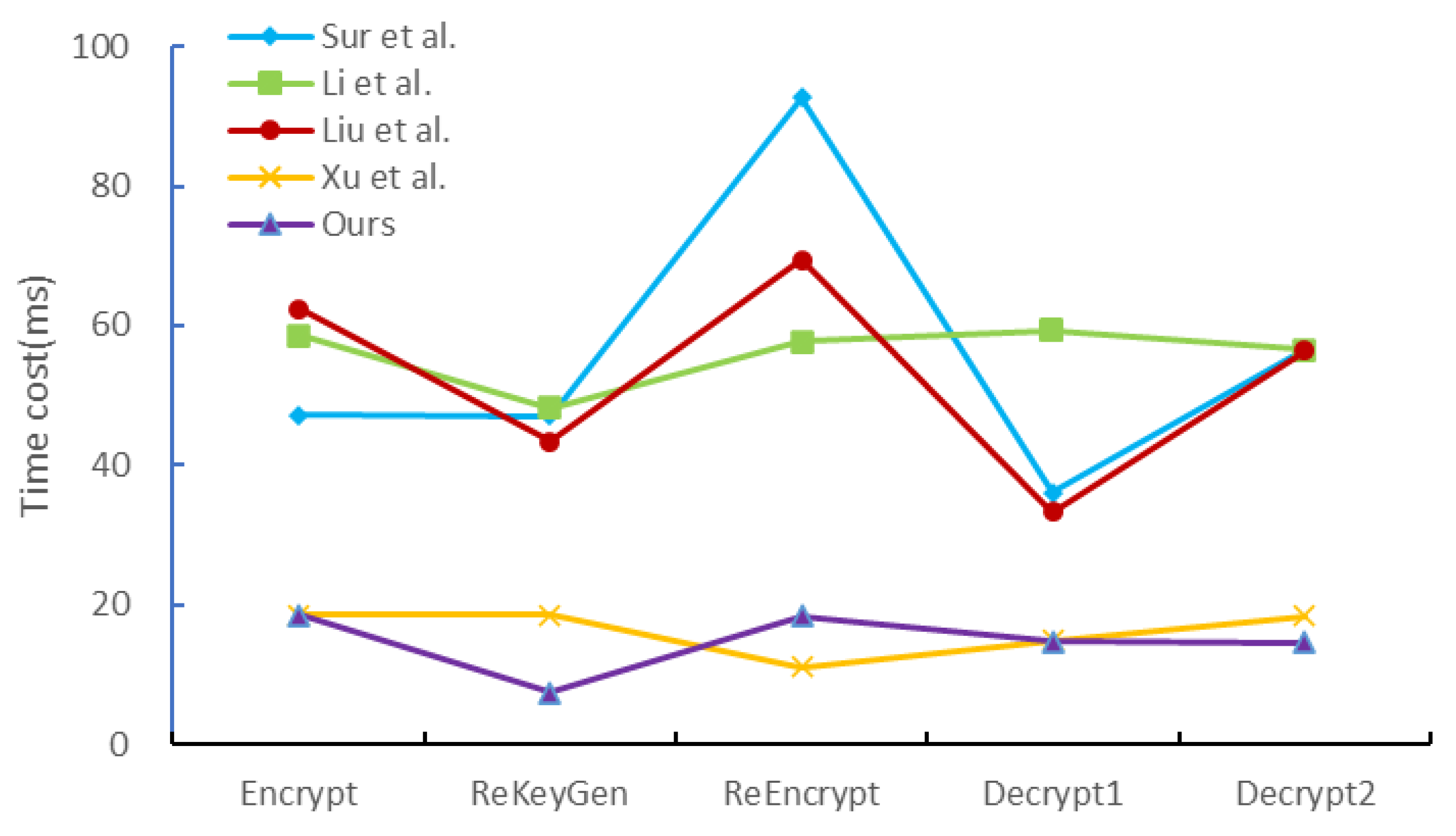
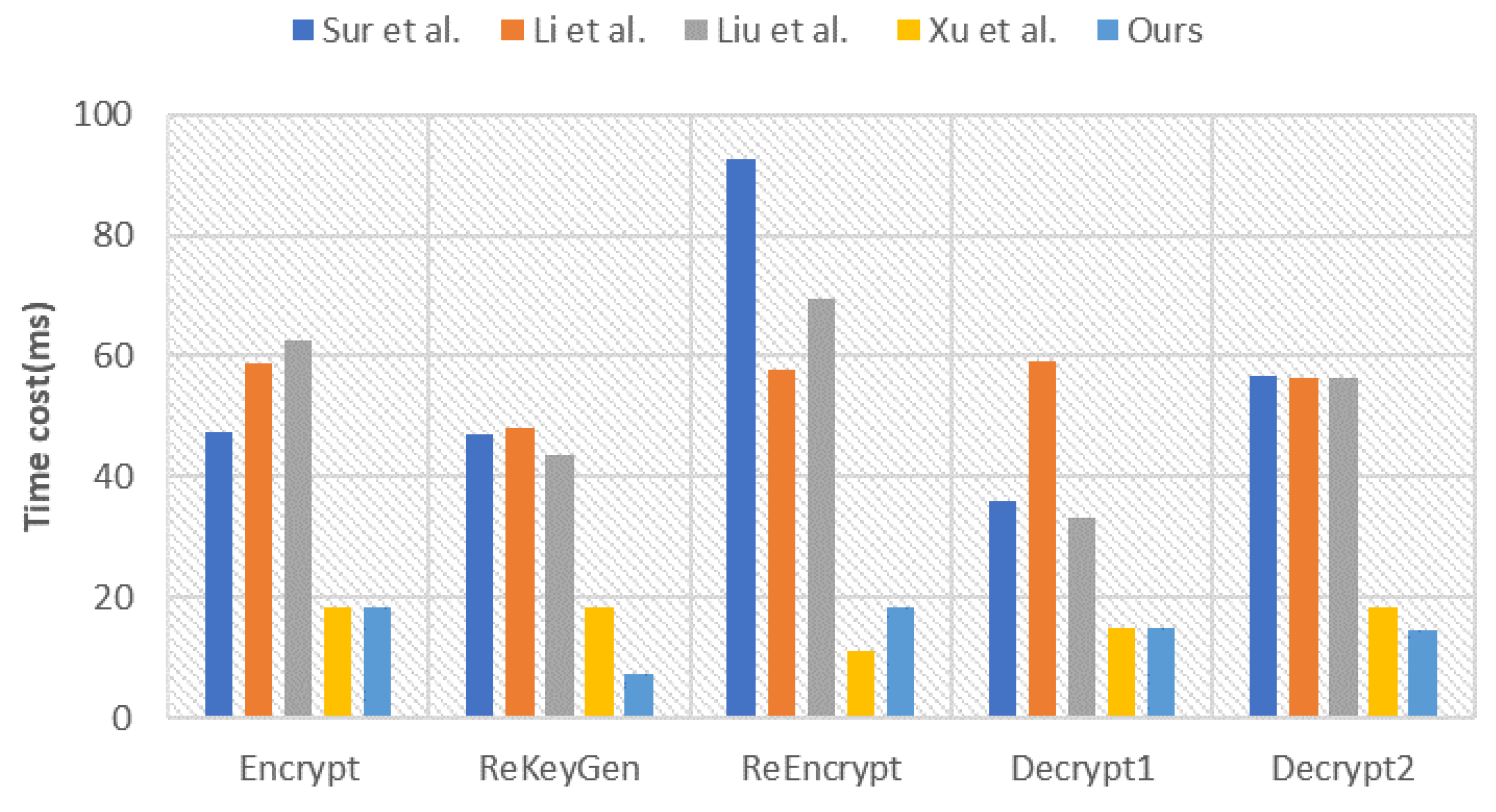
In this study, our main focus was on time-consuming operations, including exponential operations, scalar multiplication on elliptic curves, and bilinear pairing operations. We disregarded the computational costs associated with elliptic curve addition, modular multiplication, and regular hashing, as their impact was considered negligible. For detailed information about the symbols and execution times of these operations, please refer to Table 7. The comparison of computational costs between the scheme [18,19,21,22] and our proposed scheme is presented in Table 8, Figure 3 and Figure 4.

Table 7. Executing time.

Symbol	Operation	Time Cost (ms)
$T_p$	Bilinear pairing	11.571
$T_e$	Exponential operation in group $G_T$	6.469
$T_m$	Multiplicative operation in group G	3.690
$T_h$	Hash to points operation	4.017

Table 8. Efficiency comparison (ms).

Scheme	Encrypt	ReKeyGen	ReEncrypt	Decrypt1	Decrypt2
Sur [18]	47.241	47.069	92.650	36.080	56.534
Li [21]	58.632	48.152	57.746	59.131	56.476
Liu [22]	65.457	43.399	69.420	33.293	56.352
Xu [19]	18.501	18.458	11.091	14.795	18.431
Ours	18.490	7.405	18.417	14.769	14.542

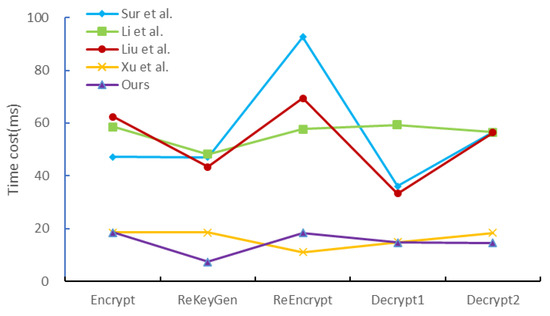
Figure 3. Efficiency Analysis Line Chart [18,19,21,22].

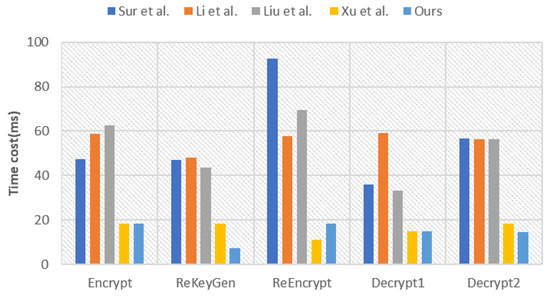
Figure 4. Average running time of each phase [18,19,21,22].

The PCBPRE⁺ scheme proposed in this paper not only overcomes the limitations of existing schemes but also offers significant advantages in terms of efficiency, security, and functionality. These advancements are crucial for ensuring secure and efficient sharing of cloud storage and providing a viable solution for applications on computationally or power-constrained devices.

7.3. Application Analysis

In specific scenarios, our solution demonstrates irreplaceable advantages, especially in data transmission within the context of the Medical Internet of Things (MIoT). The emergence of MIoT has facilitated the expansion and implementation of remote medical care, allowing patients to comfortably receive real-time medical services at home. MIoT technology leverages cloud storage, thereby increasing storage capacity and computing power, driving the development of the MIoT framework. Our proposed solution offers three key advantages in this domain.

Firstly, it achieves fine-grained access control, enabling seamless data sharing at the message level. In the extensive backdrop of medical data, where some may be confidential and sensitive, and others have limited value to healthcare practitioners, this capability becomes crucial. By implementing fine-grained access control, our solution effectively regulates the sharing of medical data. This empowers the sender to exercise significant control over the data-sharing process, including the content that is re-encrypted, ensuring that only important medical data is transmitted and preventing unnecessary leakage of personal and sensitive privacy data.

Secondly, our solution possesses the non-transferable characteristic. Given the sensitivity of medical data, it is imperative to ensure that only authorized healthcare institutions have access to individuals’ health information. The non-transferability of our solution effectively prevents malicious disclosure, as only authorized recipients are allowed to transmit data within the framework.

Thirdly, the efficient implementation of our solution enables effective data sharing even in scenarios of rapid data growth or when the computational power of healthcare institutions is moderate.

Certainly, we should also consider potential limitations or conditions under which the solution may not perform as expected, such as excessive data storage, insufficient device computational power, or issues with third-party server failures. Adequate contingency plans should be prepared for such situations.

8. Conclusions

In this paper, we present a novel scheme called Pairing-free Certificate-Based Proxy Re-Encryption Plus (PCBPRE⁺) that facilitates the secure delegation of decryption privileges from one user to another, enabling flexible sharing of encrypted data among cloud users. Our innovative approach allows users to efficiently and securely send their encrypted data to recipients using public cloud storage, without the need for bilinear pairs. This results in improved efficiency and enhanced suitability for practical application environments. Moreover, PCBPRE⁺ addresses the challenges of certificate management and key distribution encountered in traditional PRE schemes. A key advantage of our scheme is the incorporation of non-transferability and message-level fine-grained delegation mechanisms, ensuring exclusive sharing of user data with authorized individuals and preventing any malicious leaks. We rigorously verify and evaluate the correctness, security, and performance of the proposed approach, demonstrating its ability to satisfy the chosen ciphertext security in the random oracle model. Overall, the PCBPRE⁺ scheme offers several advantages and significant application potential compared to existing PRE schemes. It provides a secure and efficient solution for data sharing in cloud environments, making it well suited for various practical scenarios.