Observer-Based Fixed-Time Consensus Tracking for a Class of Nonlinear Multi-Agent Systems

Abstract

In this paper, the problem of fixed-time consensus tracking for a class of nonlinear multi-agent systems (MASs) with uncertainties and external disturbances is addressed. To solve this problem, a new fixed-time consensus tracking protocol with disturbance rejection abilities is proposed that consists of a fixed-time distributed observer (FTDO), a fixed-time disturbance observer (FDO), and a nonsmooth backstepping controller with lumped disturbance compensation (NBCDC). The fixed-time stabilities are analyzed correspondingly. Firstly, an FTDO is designed to estimate a leader’s output by using the topology of communication networks for each follower. Second, an FDO is developed to observe the lumped disturbances composed of model uncertainties and external disturbances. Finally, an NBCDC is proposed for improving the closed-loop performance. The simulation results show that the proposed method is effective.

1. Introduction

Motivated by increasing military and civilian demands, the cooperative control problems of MASs have attracted increasing attention in both the academic and industrial communities. The cooperative control technology of a multi-agent system has important application prospects in many fields, such as the formation control of robots, posture coordination and formation control of multiple aircraft [1,2,3], internet congestion control [4], and joint attacks of multiple missiles [5]. There are several topics involved in cooperative control technology, such as clustering, formation, and consensus. A fundamental and critical topic in terms of MASs is the leader–follower consensus problem. This problem involves the development of a distributed cooperative protocol that enables all followers to track the output of the leader. Although considerable research has been performed on this topic [6,7], it is challenging to design a protocol with fixed-time convergence and disturbance rejection abilities for nonlinear MASs. As a concentrated expression of traditional control performance specifications, the convergence rate for achieving consensus is critical in practical applications. The synchronization and coordination of UAVs for surveillance or search and rescue operations require efficient consensus tracking to ensure cohesive behavior. Rapid consensus tracking is essential for maintaining safe distances and coordinated movement among multiple vehicles in the context of connected and automated vehicles. In modern energy systems, multi-agent systems that manage energy consumption and distribution must rely on fast consensus tracking to optimize resource allocation and response to demand fluctuations. In the deployment of robotic teams to assist in search and rescue operations, effective consensus tracking enables seamless collaboration in dynamic and uncertain environments. In industrial environments, collaborative robotics working alongside human operators need prompt consensus tracking to ensure safety and efficiency during joint tasks. Therefore, an increasing number of researchers have focused on consensus protocols with specific convergence requirements.

In general, research on fast convergence is performed to enhance the performance and robustness of a system. Similar to the development of control theory, this research objective naturally leads to investigations on asymptotic consensus, finite-time consensus [8], and fixed-time consensus [9,10,11,12] for distributed cooperative control design. The conventional linear distributed protocols [13,14,15,16] only achieve asymptotic stability, implying that consensus is reached when time approaches infinity. A linear consensus protocol for MASs is researched in [17]. The results demonstrate a correlation between the convergence rate and the algebraic connectivity of an interaction graph. Inspired by [17], Kim [18] tried to find a proper interaction topology with a larger algebraic connectivity. The main limitation of asymptotic consensus is that consensus is reached only as time approaches infinity. Furthermore, stability analysis of the consensus protocol cannot be achieved via the “separation principle”.

Subsequently, various finite-time stabilizing control algorithms have been proposed using continuous state feedback and output feedback controllers. Recent advancements in finite-time stabilizing control algorithms highlight the benefits of nonsmooth finite-time controllers, particularly regarding tracking accuracy and disturbance rejection capabilities [19]. The adoption of finite-time consensus strategies in MASs has become increasingly prevalent to address various consensus challenges [20,21,22,23]. The literature has explored the finite-time consensus problem across different dynamics, including both first-order and second-order systems, as well as configurations with unidirectional and intermittent communication links [24,25]. Various approaches have been introduced, such as discontinuous finite-time protocols leveraging signum functions [26] and strategies for leader–follower interactions and switched topologies [27]. Additionally, distributed finite-time attitude containment control for multiple rigid bodies has been addressed [28].

However, the convergence time of finite-time consensus is contingent on the initial states of the agents. As the initial conditions deviate from equilibrium, the convergence time of the finite-time control design notably escalates. Therefore, as an improvement to finite-time consensus, fixed-time consensus was initially introduced and defined in [29,30]. The earliest exploration of fixed-time consensus for MASs can be found in [31], which proposed a nonlinear control protocol to ensure fixed-time convergence for MASs with simple integrator dynamics. Additionally, Zuo and Tie [32] presented a class of nonlinear consensus protocols for MASs, while Fu and Wang [33] enhanced the results in [32] by providing an upper bound estimate for the settling time of MASs with limited input uncertainties. Given the exceptional properties of fixed-time consensus, the primary focus of this paper is on the fixed-time consensus tracking problem for a specific class of nonlinear MASs.

Disturbances exist in a wide number of control systems, such as chemical process systems, mechanical control systems, drone swarms, traffic systems, smart grids, mobile manipulators, and aeroengines, and they negatively affect the performance of the control systems. Therefore, antidisturbance or disturbance rejection is a key topic in high-performance control design [19,34] and also presents a significant challenge in the field of consensus tracking control for MASs. Wang and He [35] presented a leader-following bipartite consensus approach for nonlinear MASs subject to disturbances, introducing new output feedback control protocols and a disturbance observer. In [36], the proposed control strategy ensures that all agents can track a predetermined trajectory within a fixed time, with both the consensus tracking error and disturbance estimation error converging to a small neighborhood around the origin while keeping all signals in the closed-loop system bounded. Yang and Wang [37] utilized neural networks to approximate the nonlinear functions present in MASs. An extended state observer was employed to estimate the unmeasured states and unknown disturbances. Xiong and Gu [38] explored the fixed-time consensus control problem for nonlinear second-order MASs that experience measurement noise. The paper uses the concept of lumped disturbances, which include unmodeled dynamics, parameter perturbations, external disturbances and nonlinear couplings. In traditional control methods, high gain is often used to suppress lumped disturbances, and its drawbacks are obvious. Therefore, we develop a fixed-time disturbance observation for feedforward compensation to improve the closed-loop performance of each follower.

In the references mentioned above [29,30,31,32,33,39] and in the recent work [40], the dynamics of agents in MASs are mostly simple integral series systems and their variants. For a class of nonlinear MASs with uncertainties and external disturbances, there are still some valuable issues to study for the leader–follower consensus problem. There are two main reasons for this situation. First, designing an FTDO for nonlinear MASs is challenging. Second, it is nontrivial to design a nonsmooth backstepping tracking controller with lumped disturbance compensation for each follower. Motivated by the need to solve the aforementioned problems, the main contributions of this paper are summarized as follows:

• For a class of nonlinear MASs with uncertainties and external disturbances, the output of the leader is not available to all followers. An FTDO is designed for each follower to estimate the leader’s output using the topology of communication networks. The fixed-time stability is uniquely analyzed by Lyapunov theory, graph theory, and the mean value theorem.
• As the lumped disturbances represent model uncertainties and external disturbances in each follower, we develop an FDO to rapidly estimate the lumped disturbances. A proof for the fixed-time stability of the FDO is also given based on Lyapunov theory.
• We propose an effective nonsmooth control scheme for command tracking in followers based on an FTDO and an FDO. Since they all converge at a fixed time, we can design them separately. With lumped disturbance feedforward compensation, this NBCDC greatly improves the closed-loop performance.

The subsequent sections of this paper are structured as follows: Section 2 provides essential assumptions and lemmas, followed by the formulation of the problem of fixed-time consensus tracking for a class of nonlinear MASs with uncertainties and external disturbances. In Section 3, the technical details and theoretical proof of the proposed fixed-time consensus tracking protocol are presented. To illustrate the effectiveness of the proposed method, simulations and analyses are conducted in Section 4. Finally, Section 5 concludes the paper.

2. Preliminaries and Problem Formulation

Notation: For any nonnegative real number $\alpha$, the function $x\mapsto {⌈x⌋}^{\alpha }$ is defined as ${⌈x⌋}^{\alpha }={\left|x\right|}^{\alpha }\mathrm{sign}\left(x\right)$ for any $x\in R$. We also define $\underline{n}=\{1,2,\dots ,n\}$ and $x{⌈x⌋}^{\alpha }={\left|x\right|}^{\alpha +1}$. For any $\mathit{x}={\left[x_1,x_2,\dots ,x_N\right]}^{\mathrm{T}}\in {\mathbb{R}}^N$, we define $\mathrm{abs}\left(\mathit{x}\right)={\left[\left|x_1\right|,\left|x_2\right|,\dots ,\left|x_N\right|\right]}^{\mathrm{T}}$, $\mathit{x}={\left[x_i\right]}_{N\times 1}$ and ${⌈\mathit{x}⌋}^{\alpha }={\left[\mathrm{sign}\left(x_1\right){\left|x_1\right|}^{\alpha },\mathrm{sign}\left(x_2\right){\left|x_2\right|}^{\alpha },\dots ,\mathrm{sign}\left(x_N\right){\left|x_N\right|}^{\alpha }\right]}^{\mathrm{T}}$. $∥\mathit{x}∥$ and ${∥\mathit{x}∥}_1$ denote the 2-norm and 1-norm of vector $\mathit{x}$, respectively. Throughout the paper, ⊗ denotes the Kronecker product and $\mathbf{1}$ denotes a vector with all elements equal to one.

2.1. Lemmas

Consider the system

$$\dot{\mathit{x}}\left(t\right)=f(t,\mathit{x}),\mathit{x}\left(0\right)={\mathit{x}}_{\mathbf{0}},$$

(1)

where $f:{\mathbb{R}}_{+}\times {\mathbb{R}}^n\to {\mathbb{R}}^n$ and $\mathit{x}\in {\mathbb{R}}^n$. Suppose the origin is an equilibrium point of (1).

Lemma 1.

According to [30,31], if there exists a continuous, radially unbounded, and positive definite function $V\left(x\right)$ such that

$$\begin{array}{c}\dot{V}\left(x\right)\le -\alpha V^q-\beta V^p,\hfill \end{array}$$

for some $\alpha ,\beta >0,q>1,0<p<1,$ then the origin of the system (1) is globally fixed-time stable. The settling time function T can be approximated by the inequality

$$\begin{array}{c}T\le T_{max}:={\displaystyle \frac{1}{\alpha (q-1)}}+{\displaystyle \frac{1}{\beta (1-p)}}.\hfill \end{array}$$

Moreover, if $q=1+{\displaystyle \frac{1}{\vartheta }}$ and $p=1-{\displaystyle \frac{1}{\vartheta }}$ with $\vartheta >1$ are chosen, the settling time function T can be estimated by a less conservative bound:

$$\begin{array}{c}{T}_{max}:={\displaystyle \frac{\pi \vartheta }{2\sqrt{\alpha \beta }}}.\hfill \end{array}$$

Lemma 2.

In accordance with [32], for ${\zeta }_1,{\zeta }_2,\dots ,{\zeta }_N\ge 0$ and $0<u<1,v>1$, the following inequalities hold:

$$\begin{array}{c}\sum _{i=1}^N{\zeta }_i^u\ge {\left(\sum _{i=1}^N{\zeta }_i\right)}^u,\sum _{i=1}^N{\zeta }_i^v\ge N^{1-v}{\left(\sum _{i=1}^N{\zeta }_i\right)}^v.\hfill \end{array}$$

2.2. Problem Formulation

Consider a multi-agent system composed of one leader and N followers, labeled as 0 and $i=1,2,\dots ,N$, respectively. The dynamics of the leader are described as follows:

$$\left\{\begin{array}{c}{\dot{x}}_{01}=f_{01}\left({\overline{\mathit{x}}}_{01}\right)+x_{02},\hfill \\ {\dot{x}}_{02}=f_{02}\left({\overline{\mathit{x}}}_{02}\right)+x_{03},\hfill \\ ⋮\hfill \\ {\dot{x}}_{0n}=f_{0n}\left({\overline{\mathit{x}}}_{0n}\right)+u_0,\hfill \\ y_0=x_{01},\hfill \end{array}\right.$$

(2)

where ${\mathit{x}}_{\mathbf{0}}={\left[x_{01},x_{02},\dots ,x_{0n}\right]}^{\mathrm{T}}\in {\mathbb{R}}^n$ represents the state vector, ${\overline{\mathit{x}}}_{\mathbf{0}\mathit{j}}={[x_{01},\dots x_{0j}]}^{\mathrm{T}}$, $u_0\in \mathbb{R}$ represents the control input, and $y_0$ represents the control output of the leader. In addition, $f_{0j}(·)$, $j=1,2,\dots ,n$ are assumed to be continuously differentiable with locally Lipchitz derivatives. The dynamics of the followers are delineated as

$$\left\{\begin{array}{c}{\dot{x}}_{i1}=f_{i1}\left({\overline{\mathit{x}}}_{i1}\right)+x_{i2}+d_{i1},\hfill \\ {\dot{x}}_{i2}=f_{i2}\left({\overline{\mathit{x}}}_{i2}\right)+x_{i3}+d_{i2},\hfill \\ ⋮\hfill \\ {\dot{x}}_{in}=f_{in}\left({\overline{\mathit{x}}}_{in}\right)+u_i+d_{in},\hfill \\ y_i=x_{i1},\hfill \end{array}\right.$$

(3)

where ${\mathit{x}}_{\mathit{i}}={\left[x_{i1},\dots x_{in}\right]}^{\mathrm{T}}\in {\mathbb{R}}^n$ is the state vector of the $i\mathrm{th}$ follower, $u_i\in \mathbb{R}$ is the control input of the $i\mathrm{th}$ follower, ${\overline{\mathit{x}}}_{\mathit{ij}}={[x_{i1},\dots x_{ij}]}^{\mathrm{T}}$, $d_{ij}\left(j=1,\dots n-1\right)$ denote the mismatching disturbances, $d_{in}$ represents the matching disturbance, $y_i$ is the output, and $f_{ij}\left(·\right)$ denotes the known system model terms. Notably, the disturbances $d_{ij}\left(j=1,\dots n\right)$ can be considered as unknown lumped disturbances composed of model uncertainties and external disturbances.

It is essential to point out that such strictly feedback nonlinear systems with disturbances can be found in many practical applications, including robot control, aerospace, autonomous vehicles, and unmanned boats. Conducting consensus research on these multi-agent system models would be very meaningful.

Similar to the approach in [41], the communication topology among the N followers can be represented by an edge set $\mathbb{E}\subseteq \mathbb{V}\times \mathbb{V}$ of a graph $\mathbb{G}=\left\{\mathbb{V},\mathbb{E}\right\}$, in which the N followers are depicted by a node set $\mathbb{V}=\left\{1,2,\dots ,N\right\}$. The adjacency matrix $\mathbb{A}=\left[a_{ij}\right]\in {\mathbb{R}}^{N\times N}$ is defined such that $a_{ij}>0$ if follower i can connect with follower j, and $a_{ij}=0$ otherwise. In this paper, we assume that $a_{ii}=0$ and that the topology is undirected. The degree diagonal matrix is denoted by $\mathbb{D}=\mathrm{diag}\{d_{1,}{d}_2,\dots ,d_N\}$, where $d_i={\sum }_{j=1}^N{a}_{ij}$ for $i\in \mathbb{V}$. The graph Laplacian matrix is denoted as $\mathbb{L}=\left[l_{ij}\right]=\mathbb{D}-\mathbb{A}$. We define the diagonal matrix $\mathbb{B}=\mathrm{diag}\{b_1,b_2,\dots ,b_N\}$ to represent the interconnection relationship between the leader and followers, where $b_i=1$ if the $i\mathrm{th}$ follower can obtain the information of the leader, and $b_i=0$ otherwise.

Assumption 1.

The generalized input $u_0$ of the leader is unknown to any followers, but its upper bound, denoted by $u^{max}$, is available to all followers.

Assumption 2.

The graph $\mathbb{G}$ is connected, and at least one follower in graph $\mathbb{G}$ is accessible to the states of the leader, denoted as $\mathbb{B}\ne 0$.

The control objective is to devise a fixed-time consensus tracking protocol $u_i$ solely using local information for each follower to achieve fixed-time consensus. In other words, for all initial states $y_i\left(0\right)$, $i\in \mathbb{V}$, there should exist a constant $T_{max}$ such that

$$\left\{\begin{array}{c}\underset{t\to T_{max}}{lim}∥y_i\left(t\right)-y_0\left(t\right)∥=0\hfill \\ y_i\left(t\right)=y_0\left(t\right),\forall t>T_{max}.\hfill \end{array}\right.$$

3. Fixed-Time Consensus Tracking Protocol

A novel fixed-time consensus tracking protocol with disturbance rejection abilities, which consists of an FTDO, an FDO, and an NBCDC, is detailed in this section.

3.1. Fixed-Time Distributed Observer

Since the leader’s state information is available only to some followers rather than all, we are inspired by [41] to design an observer for system (2). This allows each follower to observe the output of the leader within a fixed time. The estimate of the leader’s state $x_{0k}$ is denoted by ${\hat{x}}_{0k}^i$, where $k=1,2,\dots ,n$ for the $i\mathrm{th}$ follower, $i\in \mathbb{V}$. The FTDO is designed as follows:

$$\begin{array}{cc}\hfill {\dot{\hat{x}}}_{0k}^i=& {\alpha }_k{⌈\sum _{j=1}^N{a}_{ij}({\hat{x}}_{0k}^i-{\hat{x}}_{0k}^j)+b_i({\hat{x}}_{0k}^i-x_{0k})⌋}^{{\displaystyle \frac{1}{2}}}+{\beta }_k{⌈\sum _{j=1}^N{a}_{ij}({\hat{x}}_{0k}^i-{\hat{x}}_{0k}^j)+b_i({\hat{x}}_{0k}^i-x_{0k})⌋}^{{\displaystyle \frac{3}{2}}}\hfill \\ \hfill & +f_{0k}\left({\overline{\hat{\mathit{x}}}}_{\mathbf{0}\mathit{k}}^{\mathit{i}}\right)+{{\overline{\hat{x}}}^i}_{0k+1}+{\gamma }_k\mathrm{sign}\left[\sum _{j=1}^N{a}_{ij}({\hat{x}}_{0k}^i-{\hat{x}}_{0k}^j)+b_i({\hat{x}}_{0k}^i-x_{0k})\right]\hfill \\ \hfill & \times \sum _{m=1}^k\sum _{i=1}^N\left|\sum _{j=1}^N{a}_{ij}({\hat{x}}_{0m}^i-{\hat{x}}_{0m}^j)+b_i({\hat{x}}_{0m}^i-x_{0m})\right|,\hfill \\ \hfill k=1,& 2,\dots ,n-1,\hfill \\ \hfill & ⋮\hfill \\ \hfill {\dot{\hat{x}}}_{0n}^i=& {\alpha }_n{⌈\sum _{j=1}^N{a}_{ij}({\hat{x}}_{0n}^i-{\hat{x}}_{0n}^j)+b_i({\hat{x}}_{0n}^i-x_{0n})⌋}^{{\displaystyle \frac{1}{2}}}+{\beta }_n{⌈\sum _{j=1}^N{a}_{ij}({\hat{x}}_{0n}^i-{\hat{x}}_{0n}^j)+b_i({\hat{x}}_{0n}^i-x_{0n})⌋}^{{\displaystyle \frac{3}{2}}}\hfill \\ \hfill & +f_{0n}\left({\overline{\hat{\mathit{x}}}}_{\mathbf{0}\mathit{n}}^{\mathit{i}}\right)+c_n\mathrm{sign}\left[\sum _{j=1}^N{a}_{ij}({\hat{x}}_{0n}^i-{\hat{x}}_{0n}^j)+b_i({\hat{x}}_{0n}^i-x_{0n})\right]\hfill \\ \hfill & +{\gamma }_n\mathrm{sign}\left[\sum _{j=1}^N{a}_{ij}({\hat{x}}_{0k}^i-{\hat{x}}_{0k}^j)+b_i{\tilde{x}}_{0k}^i\right]·\sum _{m=1}^n\sum _{i=1}^N\left|\sum _{j=1}^N{a}_{ij}({\hat{x}}_{0m}^i-{\hat{x}}_{0m}^j)+b_i({\hat{x}}_{0m}^i-x_{0m})\right|.\hfill \end{array}$$

(4)

The observation errors are defined as follows:

$$\begin{array}{c}{\tilde{x}}_{0k}^i={\hat{x}}_{0k}^i-x_{0k}.\hfill \end{array}$$

(5)

Combining (2), (4), and (5) yields the dynamics of the observation error as

$$\begin{array}{cc}{\dot{\tilde{x}}}_{0k}^i=\hfill & {\alpha }_k{⌈\sum _{j=1}^N{a}_{ij}({\tilde{x}}_{0k}^i-{\tilde{x}}_{0k}^j)+b_i{\tilde{x}}_{0k}^i⌋}^{{\displaystyle \frac{1}{2}}}+{\beta }_k{⌈\sum _{j=1}^N{a}_{ij}({\tilde{x}}_{0k}^i-{\tilde{x}}_{0k}^j)+b_i{\tilde{x}}_{0k}^i⌋}^{{\displaystyle \frac{3}{2}}}\hfill \\ \hfill & +f_{0k}\left({\overline{\hat{\mathit{x}}}}_{\mathbf{0}\mathit{k}}^{\mathit{i}}\right)-f_{0k}\left({\overline{x}}_{0k}^i\right)\hfill \\ \hfill & +{\tilde{x}}_{0,k+1}^i+{\gamma }_k\mathrm{sign}\left[\sum _{j=1}^N{a}_{ij}({\tilde{x}}_{0k}^i-{\tilde{x}}_{0k}^j)+b_i{\tilde{x}}_{0k}^i\right]·\sum _{m=1}^k\sum _{i=1}^N\left|\sum _{j=1}^N{a}_{ij}({\tilde{x}}_{0m}^i-{\tilde{x}}_{0m}^j)+b_i{\tilde{x}}_{0m}^i\right|,\hfill \\ \hfill & k=1,2,\dots ,n-1,\hfill \\ {\dot{\tilde{x}}}_{0n}^i=\hfill & {\alpha }_n{⌈\sum _{j=1}^N{a}_{ij}({\tilde{x}}_{0n}^i-{\tilde{x}}_{0n}^j)+b_i{\tilde{x}}_{0n}^i⌋}^{{\displaystyle \frac{1}{2}}}+{\beta }_n{⌈\sum _{j=1}^N{a}_{ij}({\tilde{x}}_{0n}^i-{\tilde{x}}_{0n}^j)+b_i{\tilde{x}}_{0n}^i⌋}^{{\displaystyle \frac{3}{2}}}\hfill \\ \hfill & +f_{0n}\left({\overline{\hat{\mathit{x}}}}_{\mathbf{0}\mathit{n}}^{\mathit{i}}\right)-f_{0n}\left({\overline{x}}_{0n}^i\right)-u_0+c_n\mathrm{sign}\left[\sum _{j=1}^N{a}_{ij}({\tilde{x}}_{0n}^i-{\tilde{x}}_{0n}^j)+b_i{\tilde{x}}_{0n}^i\right]\hfill \\ \hfill & +{\gamma }_n\mathrm{sign}\left[\sum _{j=1}^N{a}_{ij}({\tilde{x}}_{0n}^i-{\tilde{x}}_{0n}^j)+b_i{\tilde{x}}_{0n}^i\right]·\sum _{m=1}^n\sum _{i=1}^N\left|\sum _{j=1}^N{a}_{ij}({\tilde{x}}_{0m}^i-{\tilde{x}}_{0m}^j)+b_i{\tilde{x}}_{0m}^i\right|.\hfill \end{array}$$

Let ${\mathit{z}}_{\mathit{i}}={\left[{\tilde{x}}_{0i}^1,{\tilde{x}}_{0i}^2,\cdots ,{\tilde{x}}_{0i}^N\right]}^{\mathrm{T}}$ for $i\in 1,2,\dots ,n$. We can express the above formula more concisely as

$$\begin{array}{cc}\hfill {\dot{\mathit{z}}}_{\mathit{k}}=& {\alpha }_k{⌈(\mathbb{L}+\mathbb{B}){\mathit{z}}_{\mathit{k}}⌋}^{{\displaystyle \frac{1}{2}}}+{\beta }_k{⌈(\mathbb{L}+\mathbb{B}){\mathit{z}}_{\mathit{k}}⌋}^{{\displaystyle \frac{3}{2}}}\hfill \\ \hfill & +{\gamma }_k·\mathrm{diag}\left\{\mathrm{sign}\left[(\mathbb{L}+\mathbb{B}){\mathit{z}}_{\mathit{k}}\right]\right\}·\sum _{m=1}^k\mathbf{1}\otimes {∥(\mathbb{L}+\mathbb{B}){\mathit{z}}_{\mathit{m}}∥}_1\hfill \\ \hfill & +{\left[\nabla f_{0k}^{\mathrm{T}}\left({\xi }_{\mathit{ik}}\right)·({\overline{\hat{\mathit{x}}}}_{\mathbf{0}\mathit{k}}^{\mathit{i}}-{\overline{\mathit{x}}}_{\mathbf{0}\mathit{k}})\right]}_{N\times 1}+{\mathit{z}}_{\mathit{k}+\mathbf{1}}\hfill \\ \hfill & k=1,2,\dots n-1,\hfill \\ \hfill {\dot{\mathit{z}}}_{\mathit{n}}=& {\alpha }_n{⌈(\mathbb{L}+\mathbb{B}){\mathit{z}}_{\mathit{n}}⌋}^{{\displaystyle \frac{1}{2}}}+{\beta }_n{⌈(\mathbb{L}+\mathbb{B}){\mathit{z}}_{\mathit{n}}⌋}^{{\displaystyle \frac{3}{2}}}\hfill \\ \hfill & +{\gamma }_n·\mathrm{diag}\left\{\mathrm{sign}\left[(\mathbb{L}+\mathbb{B}){\mathit{z}}_{\mathit{n}}\right]\right\}·\sum _{m=1}^n\mathbf{1}\otimes {∥(\mathbb{L}+\mathbb{B}){\mathit{z}}_{\mathit{m}}∥}_1\hfill \\ \hfill & +{\left[\nabla f_{0n}^{\mathrm{T}}\left({\xi }_{\mathit{in}}\right)·({\overline{\hat{x}}}_{0n}^i-{\overline{\mathit{x}}}_{\mathbf{0}\mathit{n}})\right]}_{N\times 1}-\mathbf{1}\otimes u_0+c_n·\mathrm{sign}\left[(\mathbb{L}+\mathbb{B}){\mathit{z}}_{\mathit{n}}\right].\hfill \end{array}$$

The mean value theorem of multivariable functions is employed here, where ${\xi }_{\mathit{ik}}$ and ${\eta }_{\mathit{ik}}$ are vectors between ${\overline{\hat{\mathit{x}}}}_{\mathbf{0}\mathit{k}}^{\mathit{i}}$ and ${\overline{\mathit{x}}}_{\mathbf{0}\mathit{k}}$ that satisfy the following conditions:

$$\begin{array}{cc}\hfill & {\overline{\hat{\mathit{x}}}}_{\mathbf{0}\mathit{k}}^{\mathit{i}}={\left[{\hat{x}}_{01}^i,{\hat{x}}_{02}^i,\cdots ,{\hat{x}}_{0k}^i\right]}^{\mathrm{T}},{\overline{\mathit{x}}}_{\mathbf{0}\mathit{k}}={\left[x_{01},x_{02},\cdots x_{0k}\right]}^{\mathrm{T}},\hfill \\ \hfill & \nabla f_{0k}\left({\xi }_{\mathit{ik}}\right)={{\left[{\displaystyle \frac{\partial f_{0k}}{\partial x_{01}}},{\displaystyle \frac{\partial f_{0k}}{\partial x_{02}}},\cdots ,{\displaystyle \frac{\partial f_{0k}}{\partial x_{0k}}}\right]}^{\mathrm{T}}}_{{\overline{\mathit{x}}}_{\mathbf{0}\mathit{k}}={\xi }_{\mathit{ik}}},\hfill \\ \hfill & k=1,2,\dots ,n.\hfill \end{array}$$

Theorem 1.

Assuming that Assumptions 1 and 2 hold, and the observer parameters are in compliance with the requirements

$$\left\{\begin{array}{c}{\alpha }_k={\displaystyle \frac{\epsilon }{{\left[2{\lambda }_{min}(\mathbb{L}+\mathbb{B})\right]}^{\frac{3}{4}}}},\hfill \\ {\beta }_k={\displaystyle \frac{\epsilon ·N^{\frac{1}{4}}}{{\left[2{\lambda }_{min}(\mathbb{L}+\mathbb{B})\right]}^{\frac{5}{4}}}},\hfill \\ c_n+\left|u_0^{max}\right|\le 0,\hfill \\ {\gamma }_k{\lambda }_{min}(\mathbb{L}+\mathbb{B})+\underset{i\in \mathbb{V}}{max}∥\nabla f_{0k}^{\mathrm{T}}\left({\xi }_{\mathit{ik}}\right)∥\le 0\hfill \\ \forall k=1,2,\dots ,n,\hfill \end{array}\right.$$

where $\epsilon <0$, then the observation errors of the distributed observer (4) converge to zero in a fixed time, which is bounded by

$$\begin{array}{c}{T}_o:={\displaystyle \frac{2n\pi }{\left|\epsilon \right|}}.\hfill \end{array}$$

Remark 1.

For the proof of stability, please refer to our published paper [42]. Unlike the distributed observers utilized in [41,43], which treat the nonlinear terms as bounded lumped disturbances and eliminate them using the sign function with a large gain, our approach fully utilizes the observed state information and the network topology structure to construct the adaptive gain “${\gamma }_k{\sum }_{m=1}^k{\sum }_{i=1}^N|{\sum }_{j=1}^N{a}_{ij}({\hat{x}}_{0m}^i-{\hat{x}}_{0m}^j)+b_i({\hat{x}}_{0m}^i-x_{0m})|$”. This adaptive gain decreases to zero when the observation errors converge to zero. Therefore, our proposed observer (4) removes the requirement for knowledge of the upper bound of the nonlinear terms and alleviates the inherent chattering issue of high-gain sliding mode control.

3.2. Fixed-Time Disturbance Observer

Inspired by [44,45], an FDO is introduced to estimate the lumped disturbance using the sliding mode technique. The FDO for estimating the lumped disturbances is expressed as

$$\left\{\begin{array}{cc}\hfill {\dot{z}}_{ij}^1=& z_{ij}^2-k_{ij}^1{⌈z_{ij}^1-x_{ij}⌋}^{{\rho }_1}-k_{ij}^2{⌈z_{ij}^1-x_{ij}⌋}^{{\varrho }_1}+f_{ij}\left({\overline{\mathit{x}}}_{\mathit{ij}}\right)+x_{i(j+1)}\hfill \\ \hfill {\dot{z}}_{ij}^2=& z_{ij}^3-k_{ij}^3{⌈z_{ij}^1-x_{ij}⌋}^{{\rho }_2}-k_{ij}^4{⌈z_{ij}^1-x_{ij]}⌋}^{{\varrho }_2}\hfill \\ \hfill ⋮\\ \hfill {\dot{z}}_{ij}^{l-1}=& z_{ij}^l-k_{ij}^{2l-3}{⌈z_{ij}^1-x_{ij}⌋}^{{\rho }_{l-1}}-k_{ij}^{2l-2}{⌈z_{ij}^1-x_{ij}⌋}^{{\varrho }_{l-1}}\hfill \\ \hfill {\dot{z}}_{ij}^l=& -k_{ij}^{2l-1}{⌈z_{ij}^1-x_{ij}⌋}^{{\rho }_{l-1}}-k_{ij}^{2l}{⌈z_{ij}^1-x_{ij}⌋}^{{\varrho }_l}\hfill \\ \hfill & j=1,\dots ,n-1,\hfill \end{array}\right.$$

(6)

$$\left\{\begin{array}{cc}\hfill {\dot{z}}_{in}^1=& z_{in}^2-k_{in}^1{⌈z_{in}^1-x_{in}⌋}^{{\rho }_1}-k_{in}^2{⌈z_{in}^1-x_{in}⌋}^{{\varrho }_1}+f_{in}\left({\overline{\mathit{x}}}_{\mathit{in}}\right)+u_i\hfill \\ \hfill {\dot{z}}_{in}^2=& z_{in}^3-k_{in}^3{⌈z_{in}^1-x_{in}⌋}^{{\rho }_2}-k_{in}^4{⌈z_{in}^1-x_{in]}⌋}^{{\varrho }_2}\hfill \\ \hfill ⋮\\ \hfill {\dot{z}}_{in}^{l-1}=& z_{in}^l-k_{in}^{2l-3}{⌈z_{in}^1-x_{in}⌋}^{{\rho }_{l-1}}-k_{in}^{2l-2}{⌈z_{in}^1-x_{in}⌋}^{{\varrho }_{l-1}}\hfill \\ \hfill {\dot{z}}_{in}^l=& -k_{in}^{2l-1}{⌈z_{in}^1-x_{in}⌋}^{{\rho }_{l-1}}-k_{in}^{2l}{⌈z_{in}^1-x_{in}⌋}^{{\varrho }_l}\hfill \end{array}\right.$$

(7)

where ${\rho }_m\in (0,1)$, ${\varrho }_m>1$, and $m=1,2,\dots ,l$, satisfy that ${\rho }_i=i\rho -(i-1)$, ${\varrho }_i=i\varrho -(i-1)$, and $\rho \in (1-{\iota }_1,1)$ and $\varrho \in (1,1+{\iota }_2)$ for sufficiently small ${\iota }_1>0$, ${\iota }_2>0$. The observer gains $k_{ij}^g,g=1,2,\dots ,2l$ are assigned such that the matrices $A_1$ and $A_2$ are Hurwitz:

$$\begin{array}{c}{A}_1=\left[\begin{array}{ccccc}-k_{ij}^1& 1& 0& \cdots & 0\\ -k_{ij}^3& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ -k_{ij}^{2l-3}& 0& 0& \cdots & 1\\ -k_{ij}^{2l-1}& 0& 0& 0& 0\end{array}\right],A_2=\left[\begin{array}{ccccc}-k_{ij}^2& 1& 0& \cdots & 0\\ -k_{ij}^4& 0& 1& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ -k_{ij}^{2l-2}& 0& 0& \cdots & 1\\ -k_{ij}^{2l}& 0& 0& 0& 0\end{array}\right],\hfill \end{array}$$

observer variables $z_{ij}^1,z_{ij}^2,\cdots ,z_{ij}^l$, ($j=1,2,\cdots ,n$) represent the observations of $x_{ij},d_{ij},\cdots ,d_{ij}^{(l-2)}$.

Theorem 2.

Given strict feedback affine nonlinear uncertain systems (3), the observation errors of the FDO (6) and (7) for lumped disturbances $d_{ij}(j=1,\dots ,n)$ and their derivatives ${\dot{d}}_{ij},\cdots ,d_{ij}^{(l-2)}$ converges to the neighborhood of the origin within a fixed time, and the convergence time is expressed as

$$\begin{array}{c}{T}_{ij\_\mathrm{ob}}\le {\displaystyle \frac{{\lambda }_{max}^r\left(P_1\right)}{r_{1}r}}+{\displaystyle \frac{1}{r_2\sigma {{\rm Y}}^{\sigma }}}\hfill \end{array}$$

where $r=1-\rho$, $\sigma =\varrho -1$, $r_1={\displaystyle \frac{{\lambda }_{min}\left(Q_1\right)}{{\lambda }_{max}\left(P_1\right)}}$, $r_2={\displaystyle \frac{{\lambda }_{min}\left(Q_2\right)}{{\lambda }_{max}\left(P_2\right)}}$, positive real number ${\rm Y}\le {\lambda }_{min}\left(P_2\right)$, positive definite matrix $Q_1,Q_2\in {\mathbb{R}}^{n\times n}$, and $P_1$, $P_2$ satisfy $P_1{A}_1+A_1^{\mathrm{T}}{P}_1=-Q_1$ and $P_2{A}_2+A_2^{\mathrm{T}}{P}_2=-Q_2$.

Proof. 

Defining ${\chi }_{ij}^1=x_{ij}-z_{ij}^1,{\chi }_{ij}^2=d_{ij}-z_{ij}^2,\dots ,{\chi }_{ij}^l=d_{ij}^{(l-2)}-z_{ij}^l$ and combining (6) and (7) with (3), we can derive the dynamical equation of the estimation errors as

$$\left\{\begin{array}{cc}\hfill {\dot{\chi }}_{ij}^1=& {\chi }_{ij}^2-k_{ij}^1{⌈{\chi }_{ij}^1⌋}^{{\rho }_1}-k_{ij}^2{⌈{\chi }_{ij}^1⌋}^{{\varrho }_1}\hfill \\ \hfill {\dot{\chi }}_{ij}^2=& {\chi }_{ij}^3-k_{ij}^3{⌈{\chi }_{ij}^1⌋}^{{\rho }_2}-k_{ij}^4{\left.⌈{\chi }_{ij}^1\right]}^{{\varrho }_2}\hfill \\ \hfill ⋮\\ \hfill {\dot{\chi }}_{ij}^{l-1}=& {\chi }_{ij}^l-k_{ij}^{2l-3}{⌈{\chi }_{ij}^1⌋}^{{\rho }_{ij}^{l-1}}-k_{ij}^{2l-2}{⌈{\chi }_{ij}^1⌋}^{{\varrho }_{l-1}}\hfill \\ \hfill {\dot{\chi }}_{ij}^l=& -k_{ij}^{2l-1}{⌈{\chi }_{ij}^1⌋}^{{\rho }_l}-k_{ij}^{2l}{⌈{\chi }_{ij}^1⌋}^{{\varrho }_l}+d^{(l-1)}\hfill \end{array}.\right.$$

(8)

The following proof process is consistent with Theorem 1 in [45], which is omitted here for brevity. According to [44,45], the observation errors in Equation (8) converge to a neighborhood of the origin within a fixed time. Furthermore, there exits a fixed time $T_{ij\_\mathrm{ob}}$, independent of the initial observation errors, such that when $t>T_{ij\_\mathrm{ob}}$, $z_{ij}^1,z_{ij}^2,\cdots ,z_{ij}^l$, ($j=1,2,\cdots ,n$) converges to a neighborhood of $x_{ij},d_{ij},\cdots ,d_{ij}^{(l-2)}$, i.e., ${\tilde{d}}_{ij}={\hat{d}}_{ij}-d_{ij}\le {\delta }_{ij}$. □

Remark 2.

The total upper bound convergence time $T_{i\_ob}$ for the ith follower, considering all lumped disturbances $d_{ij}(j=1,\dots ,n)$, can be calculated in two modes. In serial mode, $T_{i\_ob}$ is the sum of individual convergence times $T_{ij\_ob}$ for each disturbance. In parallel mode, $T_{i\_ob}$ is determined by the maximum value among all individual convergence times $T_{ij\_ob}$.

3.3. Nonsmooth Backstepping Controller with Lumped Disturbance Compensation

3.3.1. Nonsmooth Backstepping Controller Design

For the $i\mathrm{th}$ ($i=1,\dots ,N$) follower, we propose an effective control scheme for command tracking. In this NBCDC, the follower receives the tracking command from the leader through the FTDO and obtains estimates of the lumped disturbances through the FDO.

Define the state tracking error as $e_{ij}=x_{ij}-x_{ijc}$ and filtering error as ${\xi }_{ij}=x_{i(j+1)c}-x_{i(j+1)d}$, where i denotes the ith follower and j denotes the jth state variable. The process for designing the controller is as follows.

Step 1: In order to enable the state $x_{i1}$ to track $x_{i1\mathrm{c}}$, we consider $x_{i2}$ as an intermediate virtual control input. As a result, the dynamics of $e_{i1}$ can be expressed as

$$\begin{array}{c}{\dot{e}}_{i1}={\dot{x}}_{i1}-{\dot{x}}_{i1\mathrm{c}},\hfill \end{array}$$

(9)

where ${\dot{x}}_{i1\mathrm{c}}$ is the derivative of $x_{i1\mathrm{c}}$, which is observed by the FTDO.

Then, the stabilization function, which is denoted by the desired intermediate control input $x_{i2\mathrm{d}}$, can be formulated as

$$\begin{array}{cc}\hfill x_{i2\mathrm{d}}=& -f_{i1}\left({\overline{\mathit{x}}}_{\mathit{i}\mathbf{1}}\right)-K_{i1}^1{⌈e_{i1}⌋}^{{\mu }_1}-K_{i1}^2{e}_{i1}-K_{i1}^3{⌈e_{i1}⌋}^{{\mu }_2}+{\dot{x}}_{i1\mathrm{c}}-{\hat{d}}_{i1},\hfill \end{array}$$

(10)

where $K_{i1}^1$, $K_{i1}^2$, $K_{i1}^3$ are positive gains and $0<{\mu }_1<1,{\mu }_2>1$.

We design the first nonsmooth command filter as

$$\begin{array}{cc}\hfill {\tau }_{i1}·{\dot{x}}_{i2\mathrm{c}}=& -{\kappa }_{i1}^1{⌈x_{i2\mathrm{c}}-x_{i2\mathrm{d}}⌋}^{{\mu }_1}-{\kappa }_{i1}^2\left(x_{i2\mathrm{c}}-x_{i2\mathrm{d}}\right)-{\kappa }_{i1}^3{⌈x_{i2\mathrm{c}}-x_{i2\mathrm{d}}⌋}^{{\mu }_2}.\hfill \end{array}$$

Obviously, the dynamic of ${\xi }_{i1}$ is

$$\begin{array}{cc}\hfill {\tau }_{i1}{\dot{\xi }}_{i1}=& -{\kappa }_{i1}^1{⌈{\xi }_{i1}⌋}^{{\mu }_1}-{\kappa }_{i1}^2{\xi }_{i1}-{\kappa }_{i1}^3{⌈{\xi }_{i1}⌋}^{{\mu }_2}-{\tau }_{i1}{\dot{x}}_{i2\mathrm{d}},\hfill \end{array}$$

where the filter parameter ${\tau }_{i1}$ is a time constant, and ${\kappa }_{i1}^1$, ${\kappa }_{i1}^2$, and ${\kappa }_{i1}^3$ are appropriate positive gains. We suppose that ${\dot{x}}_{i2\mathrm{d}}$ is bounded and there exists a known positive constant $B_{i1}$ satisfying that $B_{i1}=\sup ∥{\dot{x}}_{i2\mathrm{d}}∥$.

Combining ${\xi }_{i1}=x_{i2\mathrm{c}}-x_{i2\mathrm{d}}$ with $e_{i2}=x_{i2}-x_{i2\mathrm{c}}$ yields

$$\begin{array}{c}{x}_{i2}=x_{i2\mathrm{d}}+e_{i2}+{\xi }_{i1}.\hfill \end{array}$$

(11)

Then, substituting (9), (10), and (11) into (3) yields

$$\begin{array}{cc}{\dot{e}}_{i1}=\hfill & -K_{i1}^1{⌈e_{i1}⌋}^{{\mu }_1}-K_{i1}^2{e}_{i1}-K_{i1}^3{⌈e_{i1}⌋}^{{\mu }_2}-{\hat{d}}_{i1}+d_{i1}+{\xi }_{i1}+e_{i2}.\hfill \end{array}$$

Step j: We treat $x_{i(j+1)},j=2,\cdots ,n-1$ as an intermediate virtual control input to make $x_{ij}$ track $x_{ij\mathrm{c}}$. The dynamics of $e_{ij}$ are expressed as

$$\begin{array}{c}{\dot{e}}_{ij}={\dot{x}}_{ij}-{\dot{x}}_{ij\mathrm{c}}.\hfill \end{array}$$

(12)

Subsequently, the desired intermediate control input $x_{i(j+1)\mathrm{d}}$ can be formulated as

$$\begin{array}{cc}{x}_{i(j+1)\mathrm{d}}=\hfill & -f_{ij}\left({\overline{\mathit{x}}}_{\mathit{ij}}\right)-K_{ij}^1{⌈e_{ij}⌋}^{{\mu }_1}-K_{ij}^2{e}_{ij}-K_{ij}^3{⌈e_{ij}⌋}^{{\mu }_2}+{\dot{x}}_{ij\mathrm{c}}-{\hat{d}}_{ij}-e_{i(j-1)},\hfill \end{array}$$

(13)

where $K_{ij}^1$, $K_{ij}^2$, and $K_{ij}^3$ are positive gains.

Subsequently, we design the nonsmooth command filter as

$$\begin{array}{cc}{\tau }_{ij}·{\dot{x}}_{i(j+1)\mathrm{c}}=\hfill & -{\kappa }_{ij}^1{⌈x_{i(j+1)\mathrm{c}}-x_{i(j+1)\mathrm{d}}⌋}^{{\mu }_1}-{\kappa }_{ij}^2\left(x_{i(j+1)\mathrm{c}}-x_{i(j+1)\mathrm{d}}\right)-{\kappa }_{ij}^3{⌈x_{i(j+1)\mathrm{c}}-x_{i(j+1)\mathrm{d}}⌋}^{{\mu }_2}\hfill \end{array}$$

the dynamics of ${\xi }_{ij}$ are

$$\begin{array}{cc}{\tau }_{ij}{\dot{\xi }}_{ij}=\hfill & -{\kappa }_{ij}^1{⌈{\xi }_{ij}⌋}^{{\mu }_1}-{\kappa }_{ij}^2{\xi }_{ij}-{\kappa }_{ij}^3{⌈{\xi }_{ij}⌋}^{{\mu }_2}-{\tau }_{ij}{\dot{x}}_{i(j+1)\mathrm{d}},\hfill \end{array}$$

where the filter parameter ${\tau }_{ij}$ is a time constant, and ${\kappa }_{ij}^1$, ${\kappa }_{ij}^2$, and ${\kappa }_{ij}^3$ are appropriate positive gains. We suppose that ${\dot{x}}_{i(j+1)\mathrm{d}}$ is bounded and there exists a known positive constant $B_{ij}$ satisfying that $B_{ij}=\sup ∥{\dot{x}}_{i(j+1)\mathrm{d}}∥$.

Combining ${\xi }_{ij}=x_{i(j+1)\mathrm{c}}-x_{i(j+1)\mathrm{d}}$ with $e_{i(j+1)}=x_{i(j+1)}-x_{i(j+1)\mathrm{c}}$ yields

$$\begin{array}{c}{x}_{i(j+1)}=x_{i(j+1)\mathrm{d}}+e_{i(j+1)}+{\xi }_{ij}.\hfill \end{array}$$

(14)

Then, combining (12), (13), and (14) with (3) yields

$$\begin{array}{cc}{\dot{e}}_{ij}=\hfill & -K_{ij}^1{⌈e_{ij}⌋}^{{\mu }_1}-K_{ij}^2{e}_{ij}-K_{ij}^3{⌈e_{ij}⌋}^{{\mu }_2}-{\hat{d}}_{ij}+d_{ij}+{\xi }_{ij}+e_{i(j+1)}-e_{i(j-1)}\hfill \end{array}$$

Step n: Differing from above, the dynamics of $e_{in}$ is

$$\begin{array}{c}{\dot{e}}_{in}={\dot{x}}_{in}-{\dot{x}}_{in\mathrm{c}}=f_{in}\left({\overline{\mathit{x}}}_{in}\right)+u_i+d_{in}-{\dot{x}}_{in\mathrm{c}}.\hfill \end{array}$$

(15)

To make state $x_{in}$ track $x_{in\mathrm{c}}$, we design the control law $u_i$ as follows:

$$\begin{array}{cc}{u}_i=\hfill & -f_{in}\left({\overline{\mathit{x}}}_{in}\right)-K_{in}^1{⌈e_{in}⌋}^{{\mu }_1}-K_{in}^2{e}_{in}-K_{in}^3{⌈e_{in}⌋}^{{\mu }_2}+{\dot{x}}_{in\mathrm{c}}-{\hat{d}}_{in}-e_{n-1},\hfill \end{array}$$

(16)

where $K_{in}^1,K_{in}^2,$ and $K_{in}^3>0$ are positive gains.

Substituting (15) and (16) into (3) yields

$$\begin{array}{cc}{\dot{e}}_{in}=\hfill & -K_{in}^1{⌈e_{in}⌋}^{{\mu }_1}-K_{in}^2{e}_{in}-K_{in}^3{⌈e_{in}⌋}^{{\mu }_2}-{\hat{d}}_{in}+d_{in}-e_{n-1}.\hfill \end{array}$$

3.3.2. Stability Analysis

Theorem 3.

For the strict feedback affine nonlinear system with disturbances described by Equation (3), we can obtain its closed loop form based on (10), (13), and (16) as follows:

$$\left\{\begin{array}{cc}\hfill {\dot{e}}_{i1}=& -K_{i1}^1{⌈e_{i1}⌋}^{{\mu }_1}-K_{i1}^2{e}_{i1}-K_{i1}^3{⌈e_{i1}⌋}^{{\mu }_2}-{\hat{d}}_{i1}+d_{i1}+{\xi }_{i1}+e_{i2}\hfill \\ \hfill {\dot{e}}_{ij}=& -K_{ij}^1{⌈e_{ij}⌋}^{{\mu }_1}-K_{ij}^2{e}_{ij}-K_{ij}^3{⌈e_{ij}⌋}^{{\mu }_2}-{\hat{d}}_{ij}+d_{ij}+{\xi }_{ij}+e_{i(j+1)}-e_{i(j-1)}\hfill \\ \hfill & (j=2,\cdots ,n-1)\hfill \\ \hfill {\dot{e}}_{in}=& -K_{in}^1{⌈e_{in}⌋}^{{\mu }_1}-K_{in}^2{e}_{in}-K_{in}^3{⌈e_{in}⌋}^{{\mu }_2}-{\hat{d}}_{in}+d_{in}-e_{n-1}\hfill \\ \hfill {\tau }_{ij}{\dot{\xi }}_{ij}& =-{\kappa }_{ij}^1{⌈{\xi }_{ij}⌋}^{{\mu }_1}-{\kappa }_{ij}^2{\xi }_{ij}-{\kappa }_{ij}^3{⌈{\xi }_{ij}⌋}^{{\mu }_2}-{\tau }_{ij}{\dot{x}}_{i(j+1)\mathrm{d}}\hfill \\ \hfill & (j=1,\cdots ,n-1).\hfill \end{array}\right.$$

If the control gains satisfy

$$\left\{\begin{array}{cc}{\eta }_i=\hfill & 2^{{\displaystyle \frac{1+{\mu }_1}{2}}}min\{\underset{j\in \underline{n-1}}{min}min\{{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}},K_{ij}^1\},K_{in}^1\}>0,\hfill \\ {\sigma }_i=\hfill & 2min\{\underset{j\in \underline{n-1}}{min}min\{{\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}-1,K_{ij}^2-1\},K_{in}^2-{\displaystyle \frac{1}{2}}\}=0\hfill \\ {\zeta }_i=\hfill & 2^{{\displaystyle \frac{1+{\mu }_2}{2}}}{(2n-1)}^{{\displaystyle \frac{1-{\mu }_2}{2}}}min\{\underset{j\in \underline{n-1}}{min}min\{{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}},K_{ij}^3\},K_{in}^3\}>0,\hfill \end{array}\right.$$

the tracking errors and filtering errors of the closed-loop system will all converge to a small neighborhood near the origin within a fixed time $T_{ic}$, independent of their initial errors.

$$\begin{array}{c}{T}_{ic}=T_{i\_ob}+{\displaystyle \frac{2}{{\zeta }_i({\mu }_2-1)}}+{\displaystyle \frac{1}{{\eta }_i(2^{\frac{1+{\mu }_1}{2}}-1)}}{\displaystyle \frac{2}{1-{\mu }_1}}.\hfill \end{array}$$

Proof. 

The following Lyapunov function $W_i$ is selected for stability analysis:

$$\begin{array}{c}{W}_i=\frac{1}{2}{\sum }_{k=1}^n{e}_{ik}^{\mathrm{T}}·e_{ik}+\frac{1}{2}{\sum }_{k=1}^{n-1}{\xi }_{ik}^{\mathrm{T}}·{\xi }_{ik}.\hfill \end{array}$$

(17)

Obviously, if $∥e_{ik}∥\ne 0$ and $∥{\xi }_{ik}∥\ne 0$ hold, $W_i>0$. The time derivative of (17) is

$$\begin{array}{cc}\hfill {\dot{W}}_i=& {\sum }_{j=1}^n{e}_{ij}·{\dot{e}}_{ij}+{\sum }_{j=1}^{n-1}{\xi }_{ij}·{\dot{\xi }}_{ij}\hfill \\ \hfill \le & {\sum }_{j=1}^n\left(-K_{ij}^1{\left|e_{ij}\right|}^{1+{\mu }_1}-K_{ij}^2{e}_{ij}^2-K_{ij}^3{\left|e_{ij}\right|}^{1+{\mu }_2}+\frac{1}{2}{e}_{ij}^2+\frac{1}{2}{\tilde{d}}_{ij}^2\right)\hfill \\ \hfill & +{\sum }_{j=1}^{n-1}\left(\frac{-{\kappa }_{ij}^1}{{\tau }_{ij}}{\left({\xi }_{ij}^2\right)}^{1+{\mu }_1}-\frac{{\kappa }_{ij}^2}{{\tau }_{ij}}{\xi }_{ij}^2-\frac{{\kappa }_{ij}^3}{{\tau }_{ij}}{\left({\xi }_{ij}^2\right)}^{1+{\mu }_2}+{\xi }_{ij}^2+\frac{1}{2}{\dot{x}}_{i(j+1)\mathrm{d}}^2+\frac{1}{2}{e}_{ij}^2\right)\hfill \\ \hfill \le & -min\{\underset{j\in \underline{n-1}}{min}min\{{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}},K_{ij}^1\},K_{in}^1\}·\left[{\sum }_{j=1}^n{\left(e_{ij}^2\right)}^{\frac{1+{\mu }_1}{2}}+{\sum }_{j=1}^{n-1}{\left({\xi }_{ij}^2\right)}^{\frac{1+{\mu }_1}{2}}\right]\hfill \\ \hfill & -min\{\underset{j\in \underline{n-1}}{min}min\{{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}},K_{ij}^3\},K_{in}^3\}·\left[{\sum }_{j=1}^n{\left(e_{ij}^2\right)}^{\frac{1+{\mu }_2}{2}}+{\sum }_{j=1}^{n-1}{\left({\xi }_{ij}^2\right)}^{\frac{1+{\mu }_2}{2}}\right]\hfill \\ \hfill & -min\{\underset{j\in \underline{n-1}}{min}min\{{\displaystyle \frac{{\kappa }_{ij}^2}{{\tau }_{ij}}}-1,K_{ij}^2-1\},K_{in}^2-{\displaystyle \frac{1}{2}}\}·\left[{\sum }_{j=1}^n{e}_{ij}^2+{\sum }_{j=1}^{n-1}{\xi }_{ij}^2\right]+{\mathsf{\Theta }}_i\hfill \end{array}$$

where ${\mathsf{\Theta }}_i=\frac{1}{2}{\sum }_{j=1}^n{\tilde{d}}_{ij}^2+{\sum }_{j=1}^{n-1}\frac{1}{2}{\dot{x}}_{i(j+1)\mathrm{d}}^2$ is positive and bounded and the Lemma A.2 appearing in [46] is used.

Based on Lemma 2, we can derive

$$\begin{array}{cc}\hfill \dot{W_i}\le & -2^{{\displaystyle \frac{1+{\mu }_1}{2}}}min\{\underset{j\in \underline{n-1}}{min}min\{{\displaystyle \frac{{\kappa }_{ij}^1}{{\tau }_{ij}}},K_{ij}^1\},K_{in}^1\}·{\left(\frac{1}{2}{\sum }_{j=1}^n{e}_{ij}^2+\frac{1}{2}{\sum }_{j=1}^{n-1}{\xi }_{ij}^2\right)}^{\frac{1+{\mu }_1}{2}}\hfill \\ \hfill & -2min\{\underset{j\in \underline{n-1}}{min}min\{\frac{{\kappa }_{ij}^2}{{\tau }_{ij}}-1,K_{ij}^2-1\},K_{in}^2-\frac{1}{2}\}·(\frac{1}{2}{\sum }_{j=1}^n{e}_{ij}^2+\frac{1}{2}{\sum }_{j=1}^{n-1}{\xi }_{ij}^2)\hfill \\ \hfill & -2^{{\displaystyle \frac{1+{\mu }_2}{2}}}{(2n-1)}^{{\displaystyle \frac{1-{\mu }_2}{2}}}min\{\underset{j\in \underline{n-1}}{min}min\{{\displaystyle \frac{{\kappa }_{ij}^3}{{\tau }_{ij}}},K_{ij}^3\},K_{in}^3\}·(\frac{1}{2}{\sum }_{j=1}^n{e}_{ij}^2+\frac{1}{2}{\sum }_{j=1}^{n-1}{{\xi }_{ij}^2)}^{\frac{1+{\mu }_2}{2}}+{\mathsf{\Theta }}_i\hfill \\ \hfill \le & -{\eta }_i{W}_i^{{\displaystyle \frac{1+{\mu }_1}{2}}}-{\zeta }_i{W}_i^{{\displaystyle \frac{1+{\mu }_2}{2}}}+{\mathsf{\Theta }}_i.\hfill \end{array}$$

(18)

According to (18), we can easily see that the Lyapunov function $W_i$ will not diverge to infinity within a finite time $\left[0,T_{i\_ob}\right]$. When $t>T_{i\_ob}$, ${\mathsf{\Theta }}_i\le \frac{1}{2}{\sum }_{j=1}^n{\delta }_{ij}^2+\frac{1}{2}{\sum }_{j=1}^{n-1}{B}_{ij}^2$ can be guaranteed by Theorem 2.

Define ${\mathsf{\Xi }}_i={[e_{i1},\dots ,e_{in},{\xi }_{i1},\dots ,{\xi }_{i(n-1)}]}^{\mathrm{T}}$ as the error vector of the closed-loop system. Theorem 2 in [45] and Lemma 1 thus guarantee that the error vector $\mathsf{\Xi }$ converges to an arbitrarily small neighborhood of the origin:

$$\begin{array}{c}\mathsf{\Omega }=\left\{{\mathsf{\Xi }}_i\mid W_i\le {\left[{\displaystyle \frac{{\mathsf{\Theta }}_i}{{\eta }_i\left(2-2^{\frac{1+{\mu }_1}{2}}\right)}}\right]}^{{\displaystyle \frac{2}{{\mu }_1+1}}}\right\}.\hfill \end{array}$$

When ${\mathsf{\Xi }}_i\in \overline{\mathsf{\Omega }}$, the inequality (18) becomes

$$\begin{array}{cc}\hfill {\dot{W}}_i\le & -{\eta }_i{W}_i^{{\displaystyle \frac{1+{\mu }_1}{2}}}-{\zeta }_i{W}_i^{{\displaystyle \frac{1+{\mu }_2}{2}}}+{\mathsf{\Theta }}_i\hfill \\ \hfill \le & -{\eta }_i(2^{{\displaystyle \frac{1+{\mu }_1}{2}}}-1)W_i^{{\displaystyle \frac{1+{\mu }_1}{2}}}-{\zeta }_i{W}_i^{{\displaystyle \frac{1+{\mu }_2}{2}}}.\hfill \end{array}$$

(19)

The convergence time is bounded by a constant, as given by Equation (20)

$$\begin{array}{c}{T}_{ic}=T_{i\_ob}+{\displaystyle \frac{2}{{\zeta }_i({\mu }_2-1)}}+{\displaystyle \frac{1}{{\eta }_i(2^{\frac{1+{\mu }_1}{2}}-1)}}{\displaystyle \frac{2}{1-{\mu }_1}}.\hfill \end{array}$$

(20)

It is evident from Equation (20) that the upper boundary of the convergence time is independent of the initial tracking and filtering errors. This concludes the proof. □

4. Simulation Results

In this section, we verify the effectiveness of the proposed fixed-time consensus tracking control protocol with disturbance rejection abilities.

The following second-order nonlinear systems [11] are used to demonstrate the effectiveness of the proposed fixed-time consensus tracking protocol. The MASs utilized in the simulation consist of one leader and five followers.

The leader’s model is

$$\begin{array}{cc}\hfill & {\dot{x}}_{01}\left(t\right)=0.1sin\left(x_{01}\left(t\right)\right)+x_{02}\left(t\right)\hfill \\ \hfill & {\dot{x}}_{02}\left(t\right)=0.1sin\left(x_{01}\left(t\right)\right)x_{02}\left(t\right)+u_0\left(t\right).\hfill \end{array}$$

The models of the five followers are

$$\begin{array}{c}{\dot{x}}_{i1}\left(t\right)=s_{i}sin\left(x_{i1}\left(t\right)\right)+x_{02}\left(t\right)+d_{i1}\hfill \\ {\dot{x}}_{i2}\left(t\right)=s_{i}sin\left(x_{i1}\left(t\right)\right)x_{i2}\left(t\right)+u_i\left(t\right)+d_{i2}.\hfill \end{array}$$

where $x_{01},x_{02}$, and $u_0$ represent the two states and control input of the leader, and $x_{i1},x_{i2}$, and $u_i$$(i=1,\dots ,5)$ represent the states and control inputs of the five followers, respectively. $d_{i1}$ represent mismatching disturbances, while $d_{i2}$$(i=1,2,\dots 5)$ represents matching disturbances in the five followers, in which the coefficient $s_i$ takes the values 0.1, 0.2, 0.3, 0.4, and 0.5, sequentially. During the simulation process, the backstepping method is used to enable the leader to output the expected sine and step trajectories for control.

For the MASs example, which consists of one leader and five followers, the communication topology between the leader and followers is shown in Figure 1. The Laplacian matrix corresponding to this network topology is

$$L=\left[\begin{array}{ccccc}2& -1& -1& 0& 0\\ -1& 2& 0& -1& 0\\ -1& 0& 2& -1& 0\\ 0& -1& -1& 3& -1\\ 0& 0& 0& -1& 1\end{array}\right],$$

the leader accessibility matrix is $B=\mathrm{diag}\{1,0,0,0,0\}$ and ${\lambda }_{min}(\mathbb{L}+\mathbb{B})$ can be calculated as 0.1338.

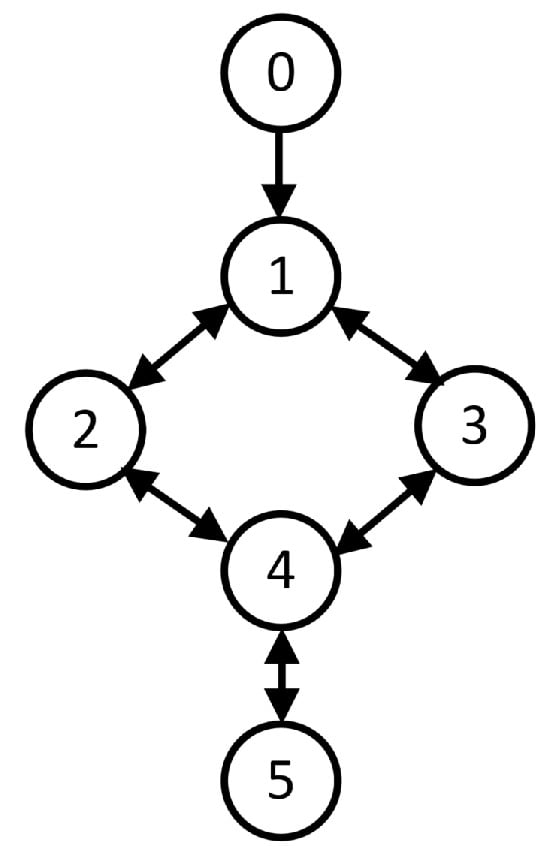
Figure 1. Information flow between the leader and followers in MASs.

To demonstrate the tracking performance of the proposed method, two types of tracking scenarios are provided. In scenario 1, the leader outputs a sinusoidal command, and in scenario 2, the leader outputs the step command. At the same time, two different initial states are set for each scenario:

$$\begin{array}{cc}\hfill & \left(\mathrm{i}\right)x_0={[0,0]}^{\mathrm{T}},x_1={[3,0]}^{\mathrm{T}},x_2={[2,0]}^{\mathrm{T}},\hfill \\ \hfill & x_3={[0,0]}^{\mathrm{T}},x_4={[-2,0]}^{\mathrm{T}},x_5={[-3,0]}^{\mathrm{T}},\hfill \\ \hfill & {\hat{x}}_0^1={[2,0]}^{\mathrm{T}},{\hat{x}}_0^2={[1,0]}^{\mathrm{T}},{\hat{x}}_0^3={[0,0]}^{\mathrm{T}},\hfill \\ \hfill & {\hat{x}}_0^4={[-1,0]}^{\mathrm{T}},{\hat{x}}_0^5={[-2,0]}^{\mathrm{T}},\hfill \\ \hfill & \left(\mathrm{ii}\right)x_0={[0,0]}^{\mathrm{T}},x_1={[30,0]}^{\mathrm{T}},x_2={[20,0]}^{\mathrm{T}},\hfill \\ \hfill & x_3={[0,0]}^{\mathrm{T}},x_4={[-20,0]}^{\mathrm{T}},x_5={[-30,0]}^{\mathrm{T}},\hfill \\ \hfill & {\hat{x}}_0^1={[20,0]}^{\mathrm{T}},{\hat{x}}_0^2={[10,0]}^{\mathrm{T}},{\hat{x}}_0^3={[0,0]}^{\mathrm{T}},\hfill \\ \hfill & {\hat{x}}_0^4={[-10,0]}^{\mathrm{T}},{\hat{x}}_0^5={[-20,0]}^{\mathrm{T}},\hfill \end{array}$$

where $x_i={[x_{i1},x_{i2}]}^{\mathrm{T}}$, $(k=0,\dots ,5)$ is the initial states of the agents and ${\hat{x}}_0^i={[x_{01}^i,x_{02}^i]}^{\mathrm{T}}$, $(i=1,\dots ,5)$ denotes the initial states of the FTDO.

In scenario 1, the sinusoidal command is

$$\begin{array}{c}{x}_{01\mathrm{d}}=sin\left(\pi t\right).\hfill \end{array}$$

The matching disturbance applied to all five followers is given by $d_{i2}=4.8+5sin\left(\pi t\right)$, while the mismatching disturbance is expressed as $d_{i1}=5.2+5sin\left(\pi t\right)+0.5sin\left({\displaystyle \frac{x_{i2}}{5}}\right)cos{x}_{i1}$. Here, $5.2+5sin\left(\pi t\right)$ represents the external disturbance and $0.5sin\left({\displaystyle \frac{x_{i2}}{5}}\right)cos{x}_{i1}$ accounts for the model uncertainty.

Remark 3.

The parameters of the FTDO in all five followers are selected as ${\alpha }_1={\alpha }_2=-2.7$, ${\beta }_1={\beta }_2=-7.8,$ ${\gamma }_1=-{\displaystyle \frac{0.1}{{\lambda }_{min}(\mathbb{L}+\mathbb{B})}},{\gamma }_2=-{\displaystyle \frac{0.4}{{\lambda }_{min}(\mathbb{L}+\mathbb{B})}}$, and ${\mathrm{c}}_2=-10$. The parameters of the FDO are $l=4$, $k_{ij}^1=24,k_{ij}^2=24,k_{ij}^3=216,k_{ij}^4=216,k_{ij}^5=864,k_{ij}^6=864,k_{ij}^7=1296,$ $k_{ij}^8=1296,\rho =0.8$, and $\varrho =1.2$. The parameters of the NBCDCs in all five followers are ${\mu }_1=0.5$, ${\mu }_2=1.1$, $K_{i1}^1=5,K_{i1}^2=1,K_{i1}^3=1$, $K_{i2}^1=5,K_{i2}^2=0.5,K_{i2}^3=1$, ${\kappa }_{i1}^1=5,{\kappa }_{i1}^2=0.1,{\kappa }_{i1}^3=0.1$, and ${\tau }_{i1}=0.1$. The simulation is conducted utilizing the Euler method with a fixed step of ${10}^{-4}$ s. The selection of the observer gain parameter for the FTDO is based on the equality and inequality constraints presented in Theorem 1. However, excessively high gains can cause oscillations in the observed values, reducing the accuracy of the distributed observer, which in turn may lead to discrepancies between the tracking commands of the followers and the actual trajectory of the leader. The observer parameters for the FDO must satisfy the Hurwitz conditions for matrices $A_1$ and $A_2$ in Theorem 2, while also considering the convergence time. For the NBCDC, the selection of the control gain must fulfill the equality and inequality constraints outlined in Theorem 3. Similarly, overly high gains can have detrimental effects on the closed-loop system, such as causing the control action to exceed the saturation limits of the actuators, thereby degrading control quality.

In scenario 2, the command is

$$x_{01\mathrm{d}}=\left\{\begin{array}{c}0,t\le 1,\hfill \\ 5,t>1.\hfill \end{array}\right.$$

The matching disturbances, mismatching disturbances, and the parameters of the FTDO, FDO, and NBCDC, except for ${\gamma }_1=-{\displaystyle \frac{20}{{\lambda }_{min}(\mathbb{L}+\mathbb{B})}},{\gamma }_2=-{\displaystyle \frac{20}{{\lambda }_{min}(\mathbb{L}+\mathbb{B})}}$, and $c_2=-50$, are all the same as those in scenario 1. Before the given command is passed to the leader, it goes through a low-pass filter with a transfer function of ${\displaystyle \frac{1}{0.1s+1}}$ to enable a smooth transition process.

In order to compare and analyze the performances of the aforementioned methods, the ITAE index is utilized as the control performance specification in this paper. The ITAE index is defined as $J_{\mathrm{ITAE}}={\int }_0^{T_f}t\left|e\left(t\right)\right|dt$, where $e\left(t\right)$ represents the tracking error and $T_f$ is the simulation time.

The performance of the proposed NBCDC and the comparative nonsmooth backstepping controller (NBC) without lumped disturbance compensation are presented in Table 1. The simulation results are depicted in Figure 2, Figure 3, Figure 4 and Figure 5.

Table 1. ITAE indexes in NBCDC and NBC.

Follower	Sine		Step
	NBCDC	NBC	NBCDC	NBC
Follower 1	0.2301	5.2869	0.33	4.4095
Follower 2	0.1096	4.9809	0.3109	4.3570
Follower 3	0.0772	4.6551	0.2753	4.2560
Follower 4	0.1466	4.5612	0.2855	4.2506
Follower 5	0.1978	4.5372	0.2989	4.2562

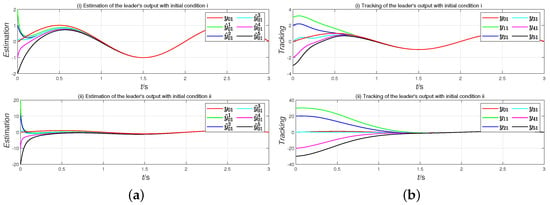
Figure 2. (a) Estimation of the leader’s output with different initial conditions (scenario 1); (b) tracking of the leader’s output with different initial conditions (scenario 1).

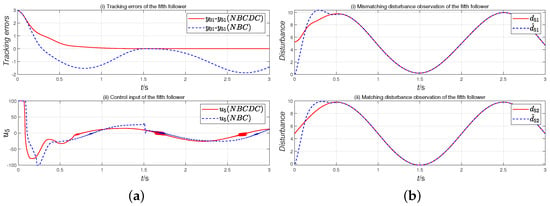
Figure 3. (a) Tracking errors (i) and control input (ii) of the fifth follower (scenario 1); (b) disturbance observation of the fifth follower (scenario 1).

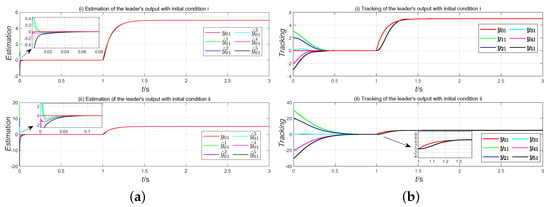
Figure 4. (a) Estimation of the leader’s output with different initial conditions (scenario 2); (b) tracking of the leader’s output with different initial conditions (scenario 2).

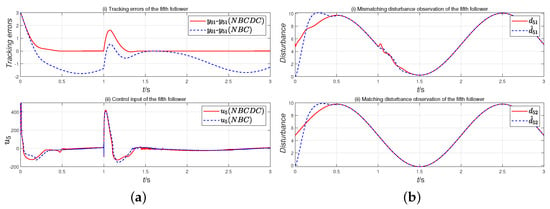
Figure 5. (a) Tracking errors (i) and control input (ii) of the fifth follower (scenario 2); (b) disturbance observation of the fifth follower (scenario 2).

Remark 4.

In scenario 1 and scenario 2, we choose follower 5 as a representative example. The remaining followers exhibit similar behavior to these given examples. Due to space constraints, we cannot provide further elaboration here. Figure 2a and Figure 4a demonstrate that the distributed state observer achieves fixed-time convergence within 1.5 s regardless of the initial conditions of the FTDO, thus confirming the validity of Theorem 1.

Remark 5.

Figure 2b and Figure 4b show that all the followers converge within 2 s under two different initial conditions, indicating that the proposed protocol achieves consensus tracking within a fixed time.

Remark 6.

Figure 3a and Figure 5a show that the proposed controller adeptly tracks the desired trajectory for the specified commands in the initial states (i) by utilizing the NBCDC. Furthermore, relative to the method lacking disturbance compensation (NBC), the proposed controller’s control performance is significantly enhanced with approximate control inputs. The performance specifications of all followers are detailed in Table 1, providing comprehensive evidence for the validity of Theorem 3.

Remark 7.

Figure 3b and Figure 5b show that the proposed FTDO demonstrates rapid estimation of matching and mismatching disturbances under different command signals within a fixed time. This validates the correctness of Theorem 2.

5. Conclusions

In this paper, we address the fixed-time consensus tracking problem for a class of MASs with dynamics in the form of strict feedback affine nonlinearities. A novel fixed-time consensus tracking protocol with disturbance rejection abilities is introduced. The protocol consists of an FTDO, an FDO, and an NBCDC. The novel FTDO converges rapidly within a fixed time to estimate the output from the leader. The FDO can quickly observe lumped disturbances. The designed nonsmooth backstepping controller with lumped disturbance compensation can also achieve fixed-time convergence. The fixed-time stability is conducted based on Lyapunov theory. The simulation results demonstrate that the proposed method is effective.