Joint Wideband Spectrum Sensing and Carrier Frequency Estimation in the Multi-Path Propagation Environment Based on Sub-Nyquist Sampling

Abstract

We consider the wideband spectrum sensing within a multi-path propagation environment, where a multi-antenna base station (BS) is tasked with identifying the frequency positions of multiple narrowband transmissions distributed across a broad range of frequencies. To tackle this, we propose a sub-Nyquist sampling structure that incorporates a phased array system. Specifically, each antenna is connected to two separate sampling channels, i.e., one for direct sampling and another for delayed sampling, with the latter incorporating a specified time delay factor. The cross-correlation matrices associated with the samples, which are characterized by different time lags, are calculated. These matrices are represented in tensor form, and the factor matrices are extracted through CANDECOMP/PARAFAC (CP) decomposition. By these factor matrices, the carrier frequencies and the power spectra of the far-field signals of interest are estimated. Numerical simulations are conducted to evaluate the performance of the proposed method, and the results reveal the feasibility and effectiveness of the approach, demonstrating its potential for accurate and efficient wideband spectrum sensing in complex multi-path propagation environments.

1. Introduction

Cognitive radio (CR) represents a promising approach to enhancing spectrum utilization and addressing the critical issue of spectrum resource depletion [1]. Its primary goal is to maximize the spectral efficiency by allowing secondary users to access the spectrum only when it is not being used by primary users. The “cognitive” features in a cognitive radio system include sensing ability, learning ability, adaptive ability, intelligent decision-making ability, etc. One of the fundamental requirements for an effective CR system, i.e., sensing ability, is the ability to accurately identify occupied spectrum bands and dynamically access unoccupied frequency resources. Based on the information gathered during spectrum sensing, cognitive systems formulate dynamic spectrum access strategies to enable the secondary users to access and utilize underutilized frequency bands without causing interference to primary users.

To achieve the goal of sensing the spectrum and providing the necessary information for a CR system to manage the dynamic spectrum access strategies, it is essential to continuously and periodically monitor spectrum usage to ensure efficient spectrum management and to respond to changing conditions [2,3,4]. However, directly performing Nyquist sampling across a wideband range—potentially extending up to several gigahertz (GHz)—can result in prohibitively high sampling rates. This not only leads to significant challenges in terms of managing and processing the vast number of data generated but also imposes substantial demands on data storage and computational resources [5]. As a result, the problem of wideband signal sampling becomes a critical issue that must be addressed to enable effective wideband spectrum sensing (WSS). Overcoming these challenges is crucial for developing systems that can efficiently handle large bandwidths and provide accurate spectrum analysis, thereby enhancing the overall performance and utility of CR networks.

To overcome the challenge of high sampling rates and realize the real-time WSS, several schemes based on sub-Nyquist sampling have been proposed, e.g., analog-to-information converter-based solutions [6,7,8], modulated wideband converter-based solutions [9,10,11], multi-coset sampling-based solutions [12,13,14], and direct-delay path sampling-based solutions [15,16,17]. These methods exploit the sparsity in the frequency domain and formulate the WSS problem as a compressive sensing problem, which can be efficiently solved by off-the-shelf algorithms, e.g., orthogonal matching pursuit and sparse Bayesian learning [18,19]. Recent works have proposed the compressive covariance sensing-based WSS technique [20,21,22], in which power spectra rather than original signals are reconstructed. Such a compressive covariance sensing-based approach makes it possible to reduce the number of samples to achieve the WSS. In addition, the sparse array, benefiting from its enhanced degrees of freedom, has also been employed to jointly estimate the directions of arrival (DOAs) and carrier frequencies of far-field sources [23,24,25].

The aforementioned studies assume that signals are received via the line-of-sight (LOS) path. However, the multi-path propagation environment is mostly involved in the practice, especially in dense urban areas, in which both the LOS and non-LOS (NLOS) paths are co-existent. Therefore, severe performance degradation is witnessed in these solutions that are based on the LOS assumption. To address the aforementioned challenges, early works [16,17] presented a new sub-Nyquist sampling framework based on a phased array, along with a WSS method via tensor representation and CP decomposition. Specifically, this sampling framework includes two sampling channels at each antenna: the direct sampling channel and the delayed sampling channel with a specified time delay. The collected data are utilized to compute a set of cross-correlation matrices characterized by the time lags, which are then represented by two tensors. The CP decomposition is performed on these two different tensors to obtain the associated factor matrices, which are subsequently used to estimate the carrier frequencies after eliminating scaling and permutation ambiguities. However, such an elimination procedure may fail in low signal-to-noise-ratio (SNR) scenarios, which in turn degrades the performance. To address the issue, we propose a novel signal processing scheme, in which only one CP decomposition is involved and the complicated scaling and permutation ambiguities elimination step is avoided. The superiority of the proposed method is revealed via simulation results.

This paper is organized as follows. Section 2 provides the signal model as well as the proposed sub-Nyquist sampling architecture. The proposed method is presented in Section 3, while the CRB analysis is shown in Section 4. Numerical simulation results are presented in Section 5, followed by the conclusions in Section 6.

Notation: in this paper, vectors are denoted by boldface lowercase letters and matrices by boldface uppercase letters. The conjugate transpose, transpose, and inverse of a matrix are denoted by ${(·)}^H$, ${(·)}^T$, and ${(·)}^{-1}$, respectively. Additionally, $Tr(·)$ and $diag(·)$ represent the trace of a matrix and the diagonal matrix, respectively. The ${\mathcal{l}}_2$-norm and Frobenius norm of a vector and matrix are denoted by ${\parallel ·\parallel }_2$ and ${\parallel ·\parallel }_F$, respectively.

2. Signal Model and Sub-Nyquist Sampling

2.1. Signal Model

Consider a scenario with the scattering-rich environment, as illustrated in Figure 1, where a receiver with M antennas is employed to deal with the WSS problem. There are K far-field narrowband signals spreading over a wide frequency band. In addition, these signals are assumed to be wide-sense stationary and uncorrelated. The involved multi-band signal is modeled by

$$\begin{array}{c}\hfill s\left(t\right)=\sum _{k=1}^K{s}_k\left(t\right)=\sum _{k=1}^K{s}_k^b\left(t\right)e^{j2\pi f_{k}t}\end{array}$$

(1)

where $s_k^b\left(t\right)$ is the baseband signal of the kth narrowband far-field signal, and $f_k$ denotes its carrier frequency.

Figure 1. The considered scenario.

Unlike most existing works in which far-field signals are received via an LOS path, we consider the multi-path propagation environment, which is more practical. To this end, we denote ${\mathit{h}}_k\in {\mathbb{C}}^M$ the channel between the kth source signal and the receiver, and hence the received signal at the receiver can thus be expressed as

$$\begin{array}{c}\hfill \mathit{x}\left(t\right)=\mathit{H}\mathit{s}\left(t\right)+\mathit{w}\left(t\right)\end{array}$$

(2)

where $\mathit{H}\triangleq [{\mathit{h}}_1\cdots {\mathit{h}}_K]\in {\mathbb{C}}^{M\times K}$, $\mathit{x}\left(t\right)\triangleq {[x_1\left(t\right)\phantom{0}\dots \phantom{0}{x}_M\left(t\right)]}^T\in {\mathbb{C}}^{M\times 1}$, with $x_m\left(t\right)$ being the received signal at the mth antenna, $\mathit{s}\left(t\right)\triangleq {[s_1\left(t\right)\phantom{0}\dots \phantom{0}{s}_K\left(t\right)]}^T\in {\mathbb{C}}^{K\times 1}$ is a collection of the K modulated signals, and $\mathit{w}\left(t\right)$ denotes the additive complex Gaussian noise with ${\sigma }^2\mathit{I}$ as its covariance matrix.

In this work, our assumptions regarding the far-field source signals are as follows:

• The number of antennas is no less than that of the far-field signals, i.e., $M\ge K$;
• The baseband signals $\left\{s_k^b\left(t\right)\right\}$ are mutually uncorrelated;
• The baseband signals associated with the far-field sources are all bandlimited;
• The far-field sources are narrowband signals and have distinct power spectra.

2.2. Sub-Nyquist Sampling Framework

To achieve the WSS, we in this work utilize a phased array-based sub-Nyquist sampling architecture, which is illustrated in Figure 2. Each antenna is connected to two channels, i.e., a direct channel and $\Delta$-delayed channel. The analog signals are sampled by a well-synchronized ADC at a sub-Nyquist sampling rate, i.e., $f_s=1/T_s\ll f_{nyq}$, where $f_{nyq}$ is the Nyquist sampling rate. In this sampling architecture, the time delay factor, $\Delta$, is chosen to satisfy $\Delta ·f_k<1,\forall k$ and $\Delta \ll 1/B$. In addition, the sampling rate is no less than the largest bandwidth among these sources, i.e., $f_s\ge B$.

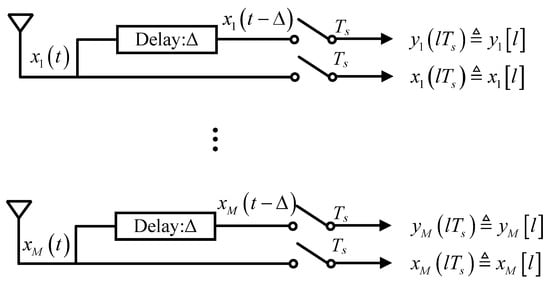
Figure 2. The sampling architecture for our proposed method.

This sub-Nyquist sampling architecture was originally proposed in [26], in which the DOAs and carrier frequencies of source signals were jointly estimated via an ESPRIT-based method. In this work, we present a novel signal processing approach that utilizes samples from this sampling architecture to sense the wideband spectrum in a multi-path propagation environment.

Define ${\mathit{s}}^b\left[l\right]\triangleq {[s_1^b\left(l{T}_s\right)\phantom{0}\dots \phantom{0}{s}_K^b\left(l{T}_s\right)]}^T$ and $\mathit{E}\left(t\right)\triangleq \mathrm{diag}(e^{j2\pi f_{1}t}\phantom{0}\dots \phantom{0}{e}^{j2\pi f_{K}t})$. Therefore, the sampled data at the $l{T}_s$th instant of the direct path are given by

$$\begin{array}{c}\hfill \mathit{x}\left[l\right]=\mathit{H}\mathit{E}\left(l{T}_s\right){\mathit{s}}^b\left[l\right]+\mathit{w}\left[l\right]\end{array}$$

(3)

where $\mathit{x}\left[l\right]\triangleq {[x_1\left(l{T}_s\right)\phantom{0}\dots \phantom{0}{x}_M\left(l{T}_s\right)]}^T$. Similarly, the sampled data of the delayed channels across all antennas can be expressed as

$$\begin{array}{cc}\hfill \mathit{y}\left[l\right]& =\mathit{H}\mathit{E}(l{T}_s-\Delta ){\mathit{s}}^b(l{T}_s-\Delta )+\mathit{w}(l{T}_s-\Delta )\hfill \\ \hfill & \stackrel{\left(a\right)}{\approx }\mathit{H}\mathit{E}(t-\Delta ){\mathit{s}}^b\left[l\right]+{\mathit{w}}^{\prime }\left[l\right]\hfill \end{array}$$

(4)

where in (a) we define ${\mathit{w}}^{\prime }\left[l\right]=\mathit{w}(l{T}_s-\Delta )$, $\mathit{y}\left[l\right]$ is similarly defined, and the approximation holds due to the fact that $\Delta \ll 1/B$. In the next section, we discuss how to estimate the key WSS parameters associated to the sources signals from these sampled data.

3. Proposed Method

Consider the direct sampling path. Given any two time instants, say, $l_1{T}_s$ and $l_2{T}_s$, the cross-correlation covariance of these two samples can be written as

$$\begin{array}{cc}\hfill {\mathit{R}}^x(l_1,l_2)& \triangleq E\left[\mathit{x}\left[l_1\right]{\mathit{x}}^H\left[l_2\right]\right]\hfill \\ \hfill & =\mathit{H}\mathit{E}\left(\tau \right){\mathit{R}}^b\left(\tau \right){\mathit{H}}^H+E\left[\mathit{w}\left[l_1\right]{\mathit{w}}^H\left[l_2\right]\right]\hfill \end{array}$$

(5)

where $\tau =l_1{T}_s-l_2{T}_s$, and ${\mathit{R}}^b\left(\tau \right)$ is a diagonal matrix given by

$$\begin{array}{c}\hfill {\mathit{R}}^b\left(\tau \right)=E\left[{\mathit{s}}^b\left[l_1\right]{\mathit{s}}^b\left[l_2\right]\right]=\mathrm{diag}\left\{r_k^b\left(\tau \right)\right\}\end{array}$$

(6)

with the kth diagonal entry $r_k^b\left(\tau \right)$ being defined by

$$\begin{array}{c}\hfill r_k^b\left(\tau \right)=E\left[s_k^b(t+\tau ){\left(s_k^b\left(t\right)\right)}^{*}\right]\end{array}$$

(7)

It is apparent that ${\mathit{R}}^x(l_1,l_2)$ depends only on the time difference, $\tau$, and hence we utilize ${\mathit{R}}^x\left(\tau \right)$ to represent ${\mathit{R}}^x(l_1,l_2)$ hereafter. Considering the fact that $\mathit{w}\left(t\right)$ is white Gaussian noise, we can simplify (5) as

$$\begin{array}{c}\hfill {\mathit{R}}^x\left(\tau \right)=\left\{\begin{array}{cc}\mathit{H}{\mathit{R}}^b\left(0\right){\mathit{H}}^H+{\sigma }^2\mathit{I},\hfill & \tau =0\hfill \\ \mathit{H}\mathit{E}\left(\tau \right){\mathit{R}}^b\left(\tau \right){\mathit{H}}^H,\hfill & \tau \ne 0\hfill \end{array}\right.\end{array}$$

(8)

where $\mathit{E}\left(0\right)$ is an identity matrix. Define ${\tilde{\mathit{R}}}^x\left(\tau \right)$ as

$$\begin{array}{c}\hfill {\tilde{\mathit{R}}}^x\left(\tau \right)=\left\{\begin{array}{cc}{\mathit{R}}^x\left(\tau \right)-{\sigma }^2\mathit{I},\hfill & \tau =0\hfill \\ {\mathit{R}}^x\left(\tau \right),\hfill & \tau \ne 0\hfill \end{array}\right.\end{array}$$

(9)

Then we can rephrase (8) as

$$\begin{array}{c}\hfill {\tilde{\mathit{R}}}^x\left(\tau \right)=\mathit{H}\mathit{E}\left(\tau \right){\mathit{R}}^b\left(\tau \right){\mathit{H}}^H\end{array}$$

(10)

Similarly, the cross-correlation between the sampled data from the direct path and the delayed path can be given by

$$\begin{array}{cc}\hfill {\tilde{\mathit{R}}}^y\left(\tau \right)& \triangleq E\left[\mathit{x}\left[l_1\right]{\mathit{y}}^H\left[l_2\right]\right]\hfill \\ \hfill & =\mathit{H}\mathit{E}(\tau +\Delta ){\mathit{R}}^b\left(\tau \right){\mathit{H}}^H\hfill \end{array}$$

(11)

With ${\left\{{\tilde{\mathit{R}}}^x\left(\tau \right)\right\}}_{\tau =-L{T}_s}^{L{T}_s}$ and ${\left\{{\tilde{\mathit{R}}}^y\left(\tau \right)\right\}}_{\tau =-L{T}_s}^{L{T}_S}$, we can naturally express them by a third-order tensor $\mathcal{R}\in M\times M\times 2(2L+1)$. Three modes of $\mathcal{R}$, respectively, stand for the antenna indices of the receiver and the time difference, as illustrated in Figure 3. We use $\kappa$ as an index to denote the time difference mode. It is clear that $\kappa \in S\triangleq \{\kappa \in \mathbb{Z},1\le \kappa \le 4L+2\}$. Define $S_1\triangleq \{\kappa \in \mathbb{Z},1\le \kappa \le 2L+1\}$ and $S_2\triangleq \{\kappa \in \mathbb{Z},2L+2\le \kappa \le 4L+2\}$.

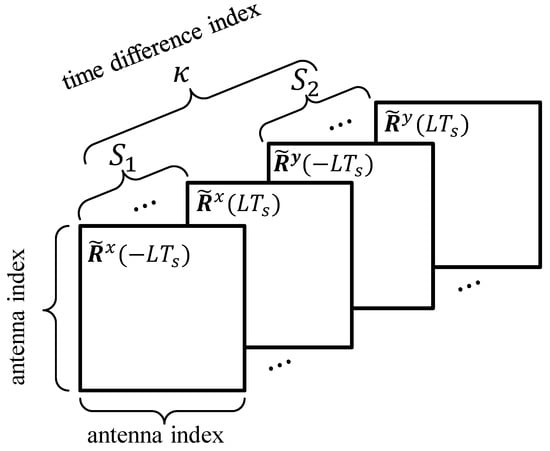
Figure 3. The illustration of our constructed tensor.

Notice that the $\kappa$th slice of the tensor $\mathcal{R}$ can be represented by

$$\begin{array}{c}\hfill \mathcal{R}(:,:,\kappa )=\sum _{k=1}^K{\lambda }_{\kappa ,k}\circ {\mathit{h}}_k\circ {\mathit{h}}_k^{*}\end{array}$$

(12)

where ${\lambda }_{\kappa ,k}$ is given by

$$\begin{array}{c}\hfill {\lambda }_{\kappa ,k}=\left\{\begin{array}{cc}{r}_k^b\left({\tau }_1\right)e^{j2\pi f_k{\tau }_1},\hfill & \kappa \in S_1\hfill \\ r_k^b\left({\tau }_2\right)e^{j2\pi f_k({\tau }_2+\Delta )},\hfill & \kappa \in S_2\hfill \end{array}\right.\end{array}$$

(13)

in which ${\tau }_1\triangleq (\kappa -L-1)T_s$ and ${\tau }_2\triangleq (\kappa -3L-2)T_s$. Therefore, the tensor $\mathcal{R}$ can be decomposed as follows via a CP decomposition:

$$\begin{array}{c}\hfill \mathcal{R}=\sum _{k=1}^K{\mathit{\lambda }}_k\circ {\mathit{h}}_k\circ {\mathit{h}}_k^{*}\end{array}$$

(14)

where ${\mathit{\lambda }}_k\triangleq {[{\lambda }_{1,k},\cdots ,{\lambda }_{4L+2,k}]}^T$.

Define $\mathbf{\Lambda }\triangleq [{\mathit{\lambda }}_1,\cdots ,{\mathit{\lambda }}_K]\in {\mathbb{C}}^{2(2L+1)\times K}$. The matrices $\{\mathit{H},{\mathit{H}}^{*},\mathbf{\Lambda }\}$ are the factor matrices of the tensor $\mathcal{R}$, which can be estimated via implementing the CP decomposition on $\mathcal{R}$. Note that $\mathbf{\Lambda }$ encompasses details pertaining to both the carrier frequencies and power spectra of these far-field signals. Therefore, we can estimate the carrier frequencies as well as the power spectra of these sources from the estimated value of $\mathbf{\Lambda }$.

3.1. CP Decomposition and Its Uniqueness

Let us first consider the scenario where K is known a priori. Under such a circumstance, the CP decomposition of $\mathcal{R}$ involves the following optimization problem:

$$\begin{array}{c}\hfill \{\widehat{\mathit{H}},{\widehat{\mathit{H}}}^{*},\widehat{\mathbf{\Lambda }}\}=arg\underset{\mathit{H},\mathbf{\Lambda }}{min}{∥\mathcal{R}-\sum _{k=1}^K{\mathit{h}}_k\circ {\mathit{h}}_k^{*}\circ {\mathit{\lambda }}_k∥}_F^2\end{array}$$

(15)

As we will discuss later, the CP decomposition of $\mathcal{R}$ is unique. We therefore replace ${\mathit{H}}^{*}$ by an auxiliary matrix, $\mathit{A}$. The optimization problem in (15) is then efficiently solved by the following iterative procedure:

$$\begin{array}{cc}\hfill {\widehat{\mathit{H}}}^{\left(i\right)}& =arg\underset{\mathit{H}}{min}{∥{\mathit{R}}_{\left(1\right)}^T-\left({\widehat{\mathbf{\Lambda }}}^{(i-1)}\odot {\widehat{\mathit{A}}}^{(i-1)}\right){\mathit{H}}^T∥}_F^2\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\widehat{\mathit{A}}}^{\left(i\right)}& =arg\underset{\mathit{A}}{min}{∥{\mathit{R}}_{\left(2\right)}^T-\left({\widehat{\mathbf{\Lambda }}}^{(i-1)}\odot {\widehat{\mathit{H}}}^{\left(i\right)}\right){\mathit{A}}^T∥}_F^2\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill {\widehat{\mathbf{\Lambda }}}^{\left(i\right)}& =arg\underset{\mathbf{\Lambda }}{min}{∥{\mathit{R}}_{\left(3\right)}^T-\left({\widehat{\mathit{A}}}^{\left(i\right)}\odot {\widehat{\mathit{H}}}^{\left(i\right)}\right){\mathbf{\Lambda }}^T∥}_F^2\hfill \end{array}$$

(18)

where i denotes the iteration index, and ${\mathit{R}}_{\left(x\right)}$ represents the mode-x unfolding of $\mathcal{R}$.

The above CP decomposition requires K as prior information. However, in real applications, K is generally unavailable due to the complex electromagnetic environment. To deal with this challenge, several solutions were developed to implement the CP decomposition for a tensor when its rank (i.e., K) is unknown. One commonly utilized approach is employing a model selection strategy. Specifically, the information criteria, like the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC), are adopted to select the best-fitting model with the optimal rank. Another approach involves formulating the CP decomposition as a Bayesian inference problem and imposing a sparsity-inducing prior to automatically determine the rank. While these solutions offer better performance, they are relatively complicated. To this end, we here introduce a simpler approach based on alternative least squares and an error-checking strategy to jointly estimate K and the factor matrices of the tensor. It should be noted that most existing solutions, as discussed above, can be readily employed to solve the problem when K is unknown.

Specifically, we have the following optimization problem:

$$\begin{array}{cc}\hfill \underset{\mathit{H},\mathit{A},\mathbf{\Lambda }}{min}& {\parallel \mathcal{R}-\mathcal{Y}\parallel }_F^2+\mu \left(\mathrm{tr}(\widehat{\mathit{H}}{\mathit{H}}^H+\mathit{A}{\mathit{A}}^H\mathbf{\Lambda }{\mathbf{\Lambda }}^H)\right)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \mathcal{Y}=\sum _{k=1}^{\overline{K}}{\mathit{h}}_k\circ {\mathit{a}}_k\circ {\mathit{\lambda }}_k\hfill \end{array}$$

(19)

where $\mu$ is a parameter to balance the fitting error and the low-rankness of the factor matrices, and $\overline{K}\gg K$ is the over-estimated tensor rank. The above optimization can also be solved via the alternative least square method. Specifically, we have the following update procedure:

$$\begin{array}{cc}\hfill {\widehat{\mathit{H}}}^{\left(i\right)}& =arg\underset{\mathit{H}}{min}{∥\left[\begin{array}{c}{\mathit{R}}_{\left(1\right)}^T\\ 0\end{array}\right]-\left[\begin{array}{c}\left({\widehat{\mathbf{\Lambda }}}^{(i-1)}\odot {\widehat{\mathit{A}}}^{(i-1)}\right)\\ \sqrt{\mu }\mathit{I}\end{array}\right]{\mathit{H}}^T∥}_F^2\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\widehat{\mathit{A}}}^{\left(i\right)}& =arg\underset{\mathit{A}}{min}{∥\left[\begin{array}{c}{\mathit{R}}_{\left(2\right)}^T\\ 0\end{array}\right]-\left[\begin{array}{c}\left({\widehat{\mathbf{\Lambda }}}^{(i-1)}\odot {\widehat{\mathit{H}}}^{\left(i\right)}\right)\\ \sqrt{\mu }\mathit{I}\end{array}\right]{\mathit{A}}^T∥}_F^2\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\widehat{\mathbf{\Lambda }}}^{\left(i\right)}& =arg\underset{\mathbf{\Lambda }}{min}{∥\left(\begin{array}{c}{\mathit{R}}_{\left(3\right)}^T\\ 0\end{array}\right)-\left(\begin{array}{c}\left({\widehat{\mathit{A}}}^{\left(i\right)}\odot {\widehat{\mathit{H}}}^{\left(i\right)}\right)\\ \sqrt{\mu }\mathit{I}\end{array}\right){\mathbf{\Lambda }}^T∥}_F^2\hfill \end{array}$$

(22)

Once $\{\widehat{\mathit{H}},\widehat{\mathit{A}},\widehat{\mathbf{\Lambda }}\}$ is obtained, the estimate of K (i.e., the rank of the constructed tensor $\mathcal{R}$), denoted by $\widehat{K}$, can be assigned by delating the negligible rank-one components.

3.2. Uniqueness of CP Decomposition

The uniqueness of the CP decomposition is the necessary condition for our method. Refs. [27,28] studied the condition for the uniqueness property of the CP decomposition, and, based on what we know, that if

$$\begin{array}{c}\hfill k_{\mathit{H}}+k_{{\mathit{H}}^{*}}+k_{\mathbf{\Lambda }}\ge 2K+2\end{array}$$

(23)

where $k_{\mathit{A}}$ represents the Kruskal-rank of a matrix $\mathit{A}$, then the CP decomposition of $\mathcal{R}$ is essentially unique up to scaling and permutation ambiguities. Since ${\mathit{H}}^{*}$ is the complex conjugate of $\mathit{H}$, we only need to check Kruskal’s rank of $\mathit{H}$ and $\mathbf{\Lambda }$. In multi-path propagation environments, $\mathit{H}$ can be modeled as a random matrix consisting of independent complex Gaussian entries. In this case, $\mathit{H}$ is with full column rank, and hence $k_{\mathit{H}}=K$ is almost true, i.e., $P(k_{\mathit{H}}=K)=1$. In addition, it is assumed that any two baseband signals are with distinct power spectra, meaning that any two columns of $\mathbf{\Lambda }$ are linearly independent and furthermore implying $k_{\mathbf{\Lambda }}\ge 2$. Via the above discussion, it can be concluded that the uniqueness condition of the CP decomposition can be satisfied. In the next section, we will develop a method to estimate the WSS parameters according to the estimation of these factor matrices.

3.3. Carrier Frequency and Power Spectrum Estimation

As discussed previously, the CP decomposition incurs both the scaling and permutation ambiguities. The permutation ambiguity can be neglected because we only rely on $\widehat{\mathbf{\Lambda }}$ to estimate $\left\{f_k\right\}$ and power spectra of source signals, and each column of $\widehat{\mathbf{\Lambda }}$ corresponds to a specific source signal.

Taking the scaling ambiguity into account, each element of the kth column of $\widehat{\mathbf{\Lambda }}$ is given by

$$\begin{array}{c}\hfill {\widehat{\lambda }}_{\kappa ,k}=\left\{\begin{array}{cc}{a}_k{r}_k^b\left({\tau }_1\right)e^{j(2\pi f_k{\tau }_1-{\varphi }_k)}\hfill & \kappa \in S_1\hfill \\ a_k{r}_k^b\left({\tau }_2\right)e^{j(2\pi f_k({\tau }_2+\Delta )-{\varphi }_k)}\hfill & \kappa \in S_2\hfill \end{array}\right.\end{array}$$

(24)

where ${\varphi }_k$ and $a_k$ are, respectively, the phase and amplitude ambiguities caused by the CP decomposition. Considering our assumption that $\Delta ·f_k<1$, the carrier frequency, $f_k$, can be estimated as

$$\begin{array}{c}\hfill {\widehat{f}}_k={\displaystyle \frac{1}{2L+1}}\sum _{p=1}^{2L+1}{\displaystyle \frac{\mathrm{mod}\left(\arg ({\widehat{\lambda }}_{p+2L+1,k}/{\widehat{\lambda }}_{p,k}),2\pi \right)}{2\pi \Delta }}\end{array}$$

(25)

in which $\mathrm{mod}(a,b)$ denotes the modulo operator and $arg\left(z\right)=\mathrm{mod}(\varphi ,2\pi )$, where $z=r{e}^{j\varphi }$.

Now we show how to estimate the power spectra of the involved source signals. Based on the relationship between the power spectrum and the DFT of the autocorrelation sequence, we have

$$\begin{array}{c}\hfill {\widehat{S}}_k\left(\omega \right)\approx \sum _{\tau =-L{T}_s}^{L{T}_s}{r}_k^b\left(\tau \right)e^{j2\pi f_k\tau }{e}^{-j\omega \tau }\end{array}$$

(26)

When L is sufficiently large, the approximation error in (26) is negligible. With the estimated carrier frequency, according to (24), $r_k^b\left({\tau }_1\right)e^{j2\pi f_k{\tau }_1}$ can be estimated by

$$\begin{array}{c}\hfill r_k^b\left({\tau }_1\right)e^{j2\pi f_k{\tau }_1}={\widehat{\lambda }}_{\kappa ,k}{a}_k^{-1}{e}^{j{\varphi }_k}\end{array}$$

(27)

Since $a_k$ and ${\varphi }_k$ are unknown due to the scaling ambiguity during the CP decomposition, we simply use ${\widehat{\lambda }}_{\kappa ,k}$ to replace $r_k^b\left({\tau }_1\right)e^{j2\pi f_k{\tau }_1}$ to estimate the power spectrum. Such a replacement, however, will result in a scaled power spectrum of the kth source signal. Despite the scaling ambiguity, the wide-spectrum sensing task can still be effectively accomplished. This is because, even though the exact scaling factor may be uncertain, we can accurately determine which frequency bands are unoccupied. Consequently, we can identify and allocate these available bands for use by secondary users, ensuring efficient spectrum utilization and avoiding interference with primary users.

Apparently, there are three main portions in the proposed WSS solution, i.e., obtaining the correlation matrices of samples from both the direct sampling branch and the delayed sampling branch, computing the factor matrices of the formulated tensor via the CP decomposition, and estimating the carrier frequencies and the autocorrelation sequence. There are a total of $4L+2$ correlation matrices involved in our method, and the computational complexity of forming one correlation matrix is $\mathcal{O}\left(2M^2{N}_s\right)$. Therefore, the computational complexity of the first part is $\mathcal{O}\left(2M^2{N}_s(4L+2)\right)$. We adopt the alternative least squares to achieve the CP decomposition of the involved tensor in an iterative manner. Assuming that there are J iteration loops involved, it can be determined that the complexity of the second part is $\mathcal{O}\left(J{M}^{2}K(4L+2)\right)$. The computational complexity of the third part is relatively small and can be neglected. Therefore, the overall complexity of the proposed method is $\mathcal{O}(2M^2{N}_s(4L+2)+J{M}^{2}K(4L+2))$. It should be noted that such a computational complexity is a slightly higher computational complexity compared with the matrix-based methods, and is similar to that of most of the existing tensor-based solutions, e.g., [13,17]. In addition, the proposed method can be efficiently implemented in real applications where the computational resources like the FPGA are employed.

4. CRB Analysis

The CRB provides a lower bound on the variance of unbiased estimators and can establish the best possible accuracy that can be achieved by any unbiased estimator for a given parameter, given the statistical model and the data available. Therefore, it is generally regarded as a benchmark for evaluating the performance of estimation algorithms. In this section, we provide the CRB analysis of the estimation problem under consideration, which will help evaluate the performance of the proposed wideband spectrum sensing solution.

According to (2), the sampled data in the direct sampling channel are given by

$$\begin{array}{c}\hfill \mathit{x}\left[l\right]=\mathit{H}\mathit{s}\left[l\right]+\mathit{w}\left[l\right]\end{array}$$

(28)

Define $\mathit{X}\triangleq [\mathit{x}\left[1\right],\cdots ,\mathit{x}\left[N_s\right]]$, $\mathit{S}\triangleq [\mathit{s}\left[1\right],\cdots ,\mathit{s}\left[N_s\right]]$, and $\mathit{W}\triangleq [\mathit{w}\left[1\right],\cdots ,\mathit{w}\left[N_s\right]]$. We can rewrite (28) as

$$\begin{array}{c}\hfill \mathit{X}=\mathit{H}\mathit{S}+\mathit{W}\end{array}$$

(29)

In addition, the vectorization format of the above equation can be expressed with the aid of the Kronecker product as

$$\begin{array}{c}\hfill \overline{\mathit{x}}=\overline{\mathit{H}}\overline{\mathit{s}}+\overline{\mathit{w}}\end{array}$$

(30)

where $\overline{\mathit{x}}\triangleq \mathrm{vec}\left(\mathit{X}\right)$, $\overline{\mathit{s}}\triangleq \mathrm{vec}\left(\mathit{S}\right)$, $\overline{\mathit{w}}\triangleq \mathrm{vec}\left(\mathit{W}\right)$, and $\overline{\mathit{H}}=\mathit{H}\otimes \mathit{I}$.

The entire collected in the delayed sampling channel can be similarly represented as

$$\begin{array}{c}\hfill \overline{\mathit{y}}=\overline{\mathit{G}}\overline{\mathit{s}}+{\overline{\mathit{w}}}^{\prime }\end{array}$$

(31)

where the definitions of $\{\overline{\mathit{y}},\overline{\mathit{s}},{\overline{\mathit{w}}}^{\prime }\}$ are omitted due to the similarity, and $\overline{\mathit{G}}$ is defined as $\overline{\mathit{G}}=\mathit{G}\otimes \mathit{I}$, where $\mathit{G}$ is computed as

$$\begin{array}{c}\hfill \mathit{G}=\mathit{H}\mathit{E}(\Delta )\end{array}$$

(32)

Combining (30) and (31) results in the following unified signal model

$$\begin{array}{c}\hfill \mathit{z}=\mathit{F}\overline{\mathit{s}}+\mathit{v}\end{array}$$

(33)

where $\mathit{z}\triangleq {[{\overline{\mathit{x}}}^T,{\overline{\mathit{y}}}^T]}^T$, $\mathit{F}\triangleq [\mathit{H};\mathit{G}]$, and $\mathit{v}\triangleq {[{\mathit{w}}^T,{\left({\mathit{w}}^{\prime }\right)}^T]}^T$. Since each element in $\mathit{v}$ is a circularly symmetric complex Gaussian distribution (i.e., $\mathbb{CN}(0,{\sigma }^2)$) and mutually independent, we know that the covariance of $\mathit{z}$ is given by

$$\begin{array}{c}\hfill {\mathit{R}}_z=\mathit{F}{\mathit{R}}_s{\mathit{F}}^H+{\sigma }^2{\mathit{I}}_{2N{N}_s}\end{array}$$

(34)

where ${\mathit{R}}_s\triangleq \mathbb{E}\left(\overline{\mathit{s}}{\overline{\mathit{s}}}^H\right)$ is the source covariance to be estimated along with other parameters such as the carrier frequencies and the components in the channel matrix. Denote the parameter to be estimated by $\mathit{\beta }$. The log-likelihood function with respect to the unknown parameter $\mathit{\beta }$ can be expressed as

$$\begin{array}{c}\hfill \mathcal{L}\left(\mathit{\beta }\right)=-ln|{\mathit{R}}_z|-{\mathit{z}}^H{\mathit{R}}_z^{-1}\mathit{z}\end{array}$$

(35)

It is evident that $\mathit{z}$ is a circularly symmetric Gaussian random variable, and hence the Fisher information matrix (FIM) can be obtained via the Slepian–Bangs formula. Denote the FIM matrix as $\mathbf{\Theta }$, and the $(i,j)$th element of $\mathbf{\Theta }$ is given by

$$\begin{array}{c}\hfill \mathbf{\Theta }(i,j)=\mathrm{Tr}\left({\mathit{R}}_z^{-1}{\displaystyle \frac{\partial {\mathit{R}}_z}{\partial {\beta }_i}}{\mathit{R}}_z^{-1}{\displaystyle \frac{\partial {\mathit{R}}_z}{\partial {\beta }_j}}\right)\end{array}$$

(36)

where ${\beta }_i$ and ${\beta }_j$ are the ith and jth components of $\mathit{\beta }$, respectively. Once the FIM matrix is obtained, the CRB can be calculated by taking the inverse of the FIM matrix, i.e.,

$$\begin{array}{c}\hfill \mathrm{CRB}\left(\mathit{\beta }\right)={\mathbf{\Theta }}^{-1}\end{array}$$

(37)

In the following, we focus on determining the components in $\mathit{\beta }$ as well as the partial derivative involved in (36).

We first consider ${\mathit{R}}_s$. Due to the fact that the far-field sources are mutually independent, ${\mathit{R}}_s$ is essentially a block-diagonal matrix, i.e.,

$$\begin{array}{c}\hfill {\mathit{R}}_s=\mathrm{blkdiag}({\mathit{P}}_1,\cdots ,{\mathit{P}}_K)\end{array}$$

(38)

where ${\mathit{P}}_k(1\le k\le K)$ is the autocorrelation matrix of the kth far-field source signal. In addition, the considered far-field source is wide-sense stationary, and ${\mathit{P}}_k$ is a Hermitian Toeplitz matrix, which can be parameterized by the entries on the first row. For convenience, we denote the first row of ${\mathit{P}}_k$ as ${\mathit{p}}_k$, and hence ${\mathit{P}}_k$ can be presented as ${\mathit{P}}_k=\mathit{a}\left({\mathit{p}}_k\right)$. In addition, according to the definition of $\mathit{F}$, its kth column is

$$\begin{array}{c}\hfill {\mathit{f}}_k={[h_{1k},\cdots ,h_{Nk},h_{1k}{e}^{-j2\pi f_k{\Delta }_1},\cdots ,h_{Nk}{e}^{-j2\pi f_k{\Delta }_N}]}^T\end{array}$$

(39)

Utilizing $\mathit{F}(:,k)$ and the block-diagonal property of ${\mathit{R}}_s$, we can rewrite (34) as

$$\begin{array}{c}\hfill {\mathit{R}}_z=\sum _{k=1}^K\left({\mathit{f}}_k{\mathit{f}}_k^H\right)\otimes P_k+{\sigma }^2{\mathit{I}}_{2N{N}_s}\end{array}$$

(40)

Based on the above discussions, we can now define the parameters to be estimated as

$$\begin{array}{c}\hfill \mathit{\beta }\triangleq \{\left\{h_{nk}\right\},\left\{f_k\right\},{\sigma }^2,\{\Re \left({\mathit{p}}_k\right),\Im \left({\mathit{p}}_k\right)\}\}\end{array}$$

According to the definition of ${\mathit{f}}_k$, we have the following relationships:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\mathit{f}}_k}{\partial h_{nk}}}& =[0,\cdots ,1,\cdots ,0,\cdots ,e^{-j{\omega }_k{\Delta }_n},\cdots ,0]\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\mathit{f}}_k^H}{\partial h_{nk}}}& =[0,\cdots ,1,\cdots ,0,\cdots ,e^{j{\omega }_k{\Delta }_n},\cdots ,0]\hfill \end{array}$$

(42)

In addition, we redefine the parameter ${\varphi }_k\triangleq 2\pi f_k/c$ to ensure ${\varphi }_k$ and $h_{nk}$ are on the same order to avoid the numerical issue. It is readily verified that

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\mathit{f}}_k}{\partial {\varphi }_k}}& =-jc\mathrm{diag}[0,\cdots ,0,{\Delta }_1,\cdots ,{\Delta }_N]{\mathit{f}}_k\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\mathit{f}}_k^H}{\partial {\varphi }_k}}& =jc{\mathit{f}}_k^H\mathrm{diag}[0,\cdots ,0,{\Delta }_1,\cdots ,{\Delta }_N]\hfill \end{array}$$

(44)

With the relationships in (41)–(44), we can further derive that

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\mathit{R}}_z}{\partial h_{nk}}}& =\left({\displaystyle \frac{\partial {\mathit{f}}_k}{\partial h_{nk}}}{\mathit{f}}_k^H+{\mathit{f}}_k{\displaystyle \frac{\partial {\mathit{f}}_k^H}{\partial h_{nk}}}\right)\otimes {\mathit{P}}_k\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\mathit{R}}_z}{\partial {\varphi }_k}}& =\left({\displaystyle \frac{\partial {\mathit{f}}_k}{\partial {\varphi }_k}}{\mathit{f}}_k^H+{\mathit{f}}_k{\displaystyle \frac{\partial {\mathit{f}}_k^H}{\partial {\varphi }_k}}\right)\otimes {\mathit{P}}_k\hfill \end{array}$$

(46)

Other involved partial derivatives can be obtained by

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\mathit{R}}_z}{\partial {\sigma }^2}}& ={\mathit{I}}_{2N{N}_s}\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\mathit{R}}_z}{\partial \Re \left({\mathit{p}}_k\right)}}& =\left({\mathit{f}}_k{\mathit{f}}_k^H\right)\otimes \left({\mathbf{\Pi }}_l+{\mathbf{\Pi }}_l^T\right)\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\mathit{R}}_z}{\partial \Im \left({\mathit{p}}_k\right)}}& =\left({\mathit{f}}_k{\mathit{f}}_k^H\right)\otimes \left(-j{\mathbf{\Pi }}_l+j{\mathbf{\Pi }}_l^T\right)\hfill \end{array}$$

(49)

where ${\mathbf{\Pi }}_l$ is the $(l-1)$th super diagonal identity matrix. Substituting the above partial derivatives into (36) and then applying the inverse operation on the FIM matrix will yield the required CRB.

5. Numerical Simulation

In this section, we demonstrate the performance of the proposed WSS scheme by comparing it with the method proposed in [17], which is labeled as the dual CPD method. In our simulation, the receiver equips $M=8$ antennas, and $\Delta T$ of the different antennas are identically set to ${10}^{-9}$. Denote $\mathcal{U}(a,b)$ as the uniform distribution, with a and b being the control parameters. We consider $K=3$ far-field sources, and their carrier frequencies and the corresponding bandwidths are set to $f_1=\mathcal{U}(50,150)$ MHz, $f_2=\mathcal{U}(200,300)$ MHz, $f_3=\mathcal{U}(350,450)$ MHz, $B_1=10$ MHz, $B_2=15$ MHz, and $B_3=20$ MHz. We consider the channel matrix $\mathit{H}\triangleq [{\mathit{h}}_1,{\mathit{h}}_2,{\mathit{h}}_3]$, where each component is generated via

$$\begin{array}{c}\hfill {\mathit{h}}_k=\sum _{i=1}^L{\alpha }_i\mathit{a}\left({\theta }_i\right),k=1,2,3\end{array}$$

(50)

where i is the index of the propagation path, ${\alpha }_i\sim \mathbb{CN}(0,1)$ is the complex channel gain of the ith signal path, ${\theta }_i$ the angle of arrival associated with the ith path, and $\mathit{a}(·)$ is the steering vector of the ULA. The complex baseband signals are generated by bandlimited Gaussian noises, which are obtained by low-pass filters with different cutoff frequencies. $f_s$ is set to 28 MHz, which is slightly higher than 20 MHz. L is set to 95, which is sufficient large to calculate the power spectral. The signal-to-noise ratio is defined as SNR = ${\mathbb{E}\left(\right|s\left(t\right)|}^2)/{\sigma }^2$. For clarity, the simulation parameters are summarized in Table 1.

Table 1. The simulation parameters.

Simulation Parameter	Value	Simulation Parameter	Value
M	8	$\Delta T$	${10}^{-9}$
K	3	L	95
$f_s$	28 MHz	${\alpha }_i$	$\mathbb{CN}(0,1)$
$f_1$	$\mathcal{U}(50,150)$ MHz	$B_1$	10 MHz
$f_2$	$\mathcal{U}(200,300)$ MHz	$B_2$	15 MHz
$f_3$	$\mathcal{U}(350,450)$ MHz	$B_3$	20 MHz

We employ the normalized mean absolute error (NMAE) to qualify the estimation accuracy of the carrier frequencies. The NMAE is defined as

$$\begin{array}{c}\hfill \mathrm{NMAE}=E\left\{\right|f_k-{\widehat{f}}_k|/f_{\mathrm{nyq}}\}\end{array}$$

(51)

where $f_k$ and ${\widehat{f}}_k$ denote the kth true frequency and estimated frequency of users, and $f_{\mathrm{nyq}}=1$ GHz.

The NMAE along with the SNR is plotted in Figure 4 when $N_s$ is set to ${10}^4$, while the NMAE’s relationship with the number of samples is illustrated in Figure 5. Apparently, the proposed method outperforms the dual CPD method. This improvement is likely due to the simpler signal processing procedure in our method, as compared with the dual CPD method, which involves a matching procedure to align the information from the same far-field source signal with the factor matrices from two tensors.

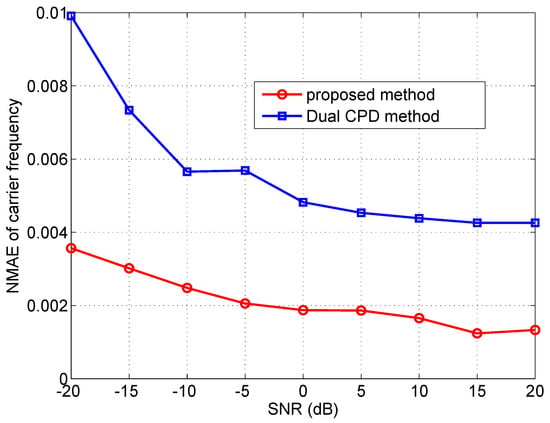
Figure 4. The NMAE of carrier frequency versus SNR when $N_s={10}^4$.

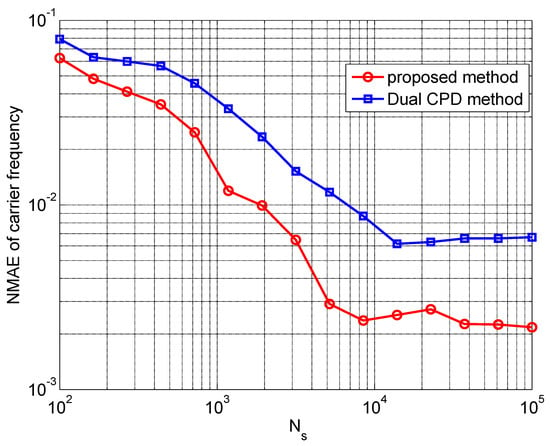
Figure 5. The NMAE of carrier frequency versus the number of samples when $\mathrm{SNR}=-15$ dB.

In addition, we show the original and reconstructed power spectra of one implementation when the SNR is 10dB and $N_s={10}^5$ in Figure 6. It can be observed that the proposed method can accurately recover the power spectra of the considered wideband (despite there existing the scaling ambiguity) with a sampling rate significantly lower than $f_{\mathrm{nyq}}$. Although the CP decomposition and the unknown channel introduce amplitude deviation in the estimated power spectrum, the proposed method can still provide information about a vacant spectrum for secondary access.

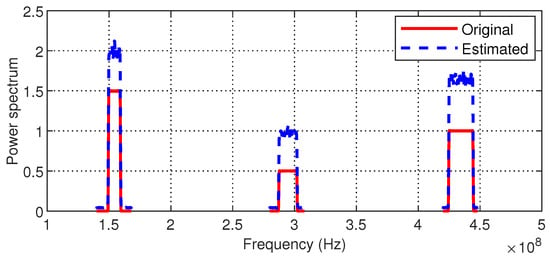
Figure 6. The original and estimated power spectrum when $\mathrm{SNR}=10$ dB.

Figure 7 shows the MSE and CRB as a function of the number of the samples (i.e., $N_s$) when the SNRs are set to 5 dB and 15 dB. It can be observed that both the MSE and the CRB exhibit a similar decreasing trend, indicating that increasing the number of the samples benefits the estimation of the carrier frequency. However, it should be noted that the gap between the CRB and the MSE for the same $N_s$ is similar for the case both with $\mathrm{SNR}=5$ dB and with $\mathrm{SNR}=15$ dB. This result is consistent with the findings in Figure 4, suggesting that our method is not highly sensitive to SNRs within regions with a relatively large value (generally above 0 dB).

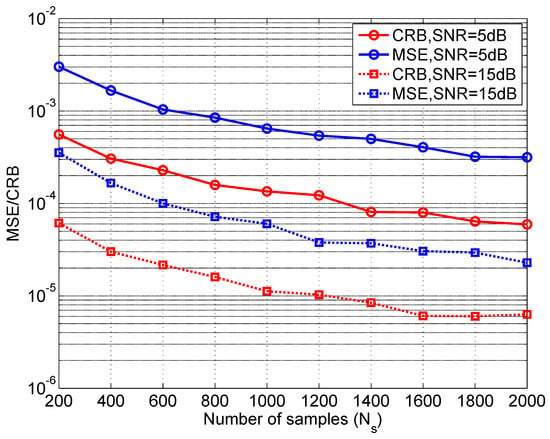
Figure 7. MSE and CRB of the scaled carrier frequencies versus $N_s$.

6. Conclusions

In this paper, we have considered the WSS problem in the multi-antenna-based receiver in the multi-path propagation environment. We have proposed a novel method to reconstruct the WSS parameters of the far-field sources. Numerical simulations have revealed that our proposed method outperforms the existing solutions.