Optimized Decode-and-Forward Multirelay Selection and Power Allocation in Cooperative Wireless Networks

Abstract

To combat the high outage probability, high complexity calculation, and low resource utilization rate of collaborative communications, an optimal decode-and-forward (DF) multirelay selection and power allocation is proposed in cooperative wireless sensor networks. It is suitable for cooperative communications equipped with a large number of relay nodes. It uses the Lagrange multiplier method to perform the power pre-distribution of the source nodes and all relay nodes before the relay selection. In addition, it also optimally exploits the power of the distributed source and relay nodes according to statistics channel status information (CSI). By optimizing the selection of the multirelay nodes and the allocation of the power with the water-filling algorithm, the proposed scheme totally exploits the whole power to greatly reduce the resource waste. Especially, it chooses an optimal relay node in cooperative communications without a large number of instantaneous channel information, and it only need to arrange the relay nodes according to the increase in the equivalent channel gain order for the optimal relay node collection at the proper signal-to-noise ratios (SNRs). Simulation results show that the outage probability of the scheme outperforms those of the existing single selective decode-and-forward (SDF) counterparts by about 2.1 dB at an outage probability of ${10}^{-2}$.

1. Introduction

Cooperative communication introduced a new spatial degree due to the existence of relay nodes [1]. It effectively reduced the information loss in transmission and also improved the reliability of wireless communication links [2]. Thus, it became one of the research hot spots in wireless communications [3]. Traditionally, cooperative wireless sensor networks were generally composed of a source node, a destination node, and several relay nodes. Signals sent by the source node were affected by multipath and Rayleigh fading in transmissions [4]. Most cooperative communications methods had been focused on the amplify-and-forward (AF) [5] and decode-and-forward (DF) approaches [6]. For the former, AF, the relay amplified both the signals and noises simultaneously; thus, it failed to improve the signal-to-noise ratio (SNR) of received signals. For the latter, DF, at low SNRs, it caused the error propagation of messages [7,8]. To overcome the deficiencies brought by both AF and DF, selective DF (SDF) was then proposed to address the noise amplification of the AF and error propagation of the DF to greatly improve the reliability [9].

For the above three forwarding methods, the cooperation of relay nodes and power allocation was needed to enhance the overall performance. Therefore, the selection and power allocation of relay nodes were the research hot spots on cooperative communications. To efficiently select relay nodes, there was a two-hop multirelay network mode. The all-relay cooperation scheme required all relay nodes to forward the received messages from the source node. So, it brought about much redundancy, which degraded the bandwidth utilization. To address this deficiency, an opportunistic cooperative relay scheme was proposed to select relay nodes according to the instantaneous channel state information (CSI) [10]. This scheme forwarded the received signals from the source node by selecting only one single relay. Compared with the all-relay cooperation, the single relay scheme had much higher spectrum utilization [11]. For the power allocation of single-relay selection, a power allocation scheme, to minimize the systematic outage probability, was proposed to improve the performance [12]. However, it cannot accomplish adaptive transmission in time-varying wireless fading channels. It needed to constantly select the optimal relay node in the dynamically variant channels with large transmission overhead. Hence, multiple relays were selected for cooperation with the wireless transmission channel quality among the relay and source nodes [13]. To select multiple relay nodes in the DF cooperation, the optimal relay nodes are selected from all the relay nodes for better cooperation to minimize the outage probability [14]. However, most of these schemes relied on the equal power allocation of the source and relay nodes. Simultaneously, after the optimal relay selection, the lack of power redistribution of the optimal relay node still caused power wastage. In addition, a simultaneous wireless information and power transfer (SWIPT)-enabled cooperative cognitive network was proposed to address energy scarcity and spectral scarcity in recent 5G wireless communications [15]. Then, a self-sustainable, SWIPT-enabled relay was used to assist in the primary user’s transmission, and the SWIPT relay employed the proposed energy-assisted decode-and-forward (EDF) protocol to enhance the conventional decode-and-forward (DF) protocol with energy dimension-augmented information decoding. Furthermore, to overcome wasted resources through single DF or amplify-and-forward (AF) collaboration in traditional collaborative communication, a non-orthogonal multiple access (NOMA) and orthogonal multiple access (OMA) hybrid access method was proposed for narrowband Internet of Things (NB-IoT) [16]. The whole transmission process has been classified into five states after deriving the outage probability of each link. The system had been discussed as a discrete-time Markov model, where the closed expressions of the system outage probability and throughput were derived by using the steady-state probability. With the rapid growing demand for latency-critical and computation-intensive Internet of Things (IoT) services, an IoT-oriented network architecture, as well as mobile edge computing (MEC), was proposed to increase the computation capability of the resource-constrained IoT system. In a multiuser cache-assisted MEC, the preferences for different types of services played an important role in the joint design of communication, computation, and service caching. A deep learning (DL)-based offline cache placement scheme was adopted by using a novel stochastic quantization-based discrete-action generation method [17]. The proposed hybrid learning framework leveraged both benefits from the model-free DL approach and the model-based optimization. In addition, to meet the demand for large-scale device access in narrowband Internet of Things, a non-orthogonal multiple access and orthogonal multiple access hybrid access method in NB-IoT was proposed for a new hybrid transmission protocol with adapatively selectable relay collaboration [18]. Then, the throughput performance of a full-duplex two-way energy harvesting (EH)-capable relay system was investigated, and a practical EH strategy, or time switching-based relaying, was adopted for the EH and the decode-and-forward for efficient information transmission [19]. In addition, to ensure reliable, secure, and low-latency communication in IoT applications, rateless codes (RCs) were employed for forward error correction (FEC) at the physical layer (PHY) in a cooperative delay-constrained environment [20]. The probability of violation was used as a performance metric, and the RCs can adjust the rate on the fly, when the receiver either accumulated energy or mutual information (MI) from the received signals. Therefore, cooperative communications have numerous applications, and the high outage probability and low power efficiency should be improved for better transmission performance.

To combat high outage probability and low power efficiency of existing cooperative schemes, this paper mainly proposes a multirelay selection scheme by using the channel state information (CSI) and reallocating the power of the optimal relay. The proposed scheme first pre-allocates the power of the source node and all relay nodes by using the Lagrange multiplier method before relay selection. It counts the power allocation factors of the source node and all relay nodes. Subsequently, it utilizes the allocated source node power and also the relay node power to select the optimal multirelay node according to the statistical CSI. Subsequently, the well-known water-filling algorithm [21] in the classic information theory is used to re-allocate the power of the selected optimal relay nodes. Hence, the proposed scheme makes full use of the total power of the entire system and it greatly reduces the waste of transmission resources. In summary, this paper mainly proposes a multirelay selection and power allocation scheme by the outage performance to solve high outage probability and system power waste. Given the fixed total power, the power expression is solved by using the Lagrange multiplier method with the objective of minimizing the systematic outage probability. In addition, the systematic capacity of different relay numbers is accumulated and the relay set of the largest value is chosen as the optimal relays for message forwarding. Finally, the contributions of the proposed scheme are detailed as follows:

• Joint cooperative model construction by the optimal DF multirelay selection and power allocation to overcome the high outage probability, high complexity calculation, and low resource utilization.
  A joint cooperative model of the DF multirelay selection and power allocation is constructed and analyzed in cooperative wireless sensor networks. Based on the outage probability performance, it incorporates both the optimal multirelay selection for efficient transmission and the distributed power allocation for better power utilization. Thus, the multirelay selection and the distributed power allocation are combined closely to jointly improve the integrated transmission performance.
• Optimal power pre-distribution of the source and relay nodes by the Lagrange multiplier method and the statistics CSI to enhance relay selection performance.
  To optimize the relay selection, the Lagrange multiplier method is mainly used to perform the power pre-distribution of the source nodes and all relay nodes. In addition, it also optimally utilizes the power property of the distributed source and relay nodes by exploiting the statistics of the channel status information (CSI). Therefore, the relay selection is performed optimally with both transmission and power for efficient resource utilization.
• Joint power allocation by the water-filling algorithm with the relay nodes of the increase order of the equivalent channel gain for globally optimal power efficiency.
  Through the optimized selection of the multirelay nodes and allocation of the power with the water-filling algorithm, the proposed scheme totally exploits the whole power to significantly reduce the resource waste. Primarily, it chooses an optimal relay node in cooperative communications without a large number of instantaneous channel information. It only needs to arrange the relay nodes by the increase order of the equivalent channel gain for the optimal relay node collection at the given SNRs.

The rest of the paper is organized as follows: Section 2 introduces the cooperative network model of multirelay SDF and power allocation. Section 3 discusses the optimal multirelay selection scheme with the outage probability minimization by the statistical CSI. Additionally, the optimal power allocation is also proposed with the water-filling algorithm. Section 4 simply compares and analyzes the computational complexity. Subsequently, Section 5 provides numerical simulations and result analyses to validate the good performance of the proposed scheme. Finally, Section 6 concludes the paper.

2. Cooperative Network Model for Multirelay Selection and Power Allocation

A typical cooperative network model for multirelay selection and power allocation is shown in Figure 1. It consists of a source node S, a destination node D and N relay nodes $R_i(i=1,2,\cdots ,N)$. It is assumed that M relay nodes are pre-selected from n relay nodes to participate in the cooperation and they receive the messages from the source node. In this system, m relay nodes can correctly decode the received messages from the source node, and they form a set $B_M$. Then, K relay nodes are found from these m relay nodes to forward the received messages from the source node to the destination node. These K relay nodes are the optimal relay nodes and they form a set $B_{opt}$. Each node adopts half duplex mode in transmissions, and each transmission requires to consume a fixed time slot. Simultaneously, suppose that each channel link is determined on the scenarios of the Rayleigh fading, the unchanged channel gain in a transmission process, and each channel link independent of each other. In addition, the signals are further affected by the additive Gaussian white noise (AWGN) in transmissions.

Figure 1. Cooperative network model for multirelay selection and power allocation.

The entire cooperation is divided into two stages. In the first stage, the source node S transmits the signals $X_S$ to the destination node D and all relay nodes $R_i\left(i\in B_M\right)$ can correctly decode the source signals. Then, they are received by the relay and destination nodes. Finally, they are expressed as

$$y_{sd}=\sqrt{P_S}{h}_{sd}{x}_S+w_{sd},$$

(1)

$$y_{s{r}_i}=\sqrt{P_S}{h}_{s{r}_i}{x}_S+w_{s{r}_i},i\in B_M,$$

(2)

where $y_{sd}$ and $y_{s{r}_i}$ represent the signals received by the destination node D and the relay node $R_i\left(i\in B_M\right)$ in the first stage, respectively. They represent the transmission power of the source S. $X_S$ represents the transmitted signals by the source node S. $h_{sd}$ and $h_{s{r}_i}$ represent the channel coefficients from the source node S to the destination node D, from source node S to the i-th relay node $R_i\left(i\in B_M\right)$, respectively. They all obey the complex Gaussian distribution with zero mean and circular symmetry, and the variance is ${\eta }_{sd}^2$ and ${\eta }_{s{r}_i}^2$, respectively. $w_{sd}$ and $w_{s{r}_i}$ are the additive white Gaussian noises (AWGNs) of the related channels, respectively. They both obey the complex Gaussian distribution with zero mean, circular symmetry and variance $N_0$.

In the second stage, the optimal relay is selected from the candidate relay set $B_M$ to form the set $B_{opt}$. All relay nodes in $B_{opt}$ decode and re-encode the received signals before sending them to the destination D. Then, the signals received at the destination D are expressed as

$$y_{r_{i}d}=\sqrt{{\mathrm{P}}_{r_i}}{h}_{r_{i}d}{x}_{r_i}+w_{r_{i}d},$$

(3)

where $y_{r_{i}d}$ represents the signals received by the destination D, and ${\mathrm{P}}_{r_i}\left(i=1,2,3,\cdots ,N\right)$ represents the transmission power of the relay node. $h_{r_{i}d}$ represents the channel coefficient between relay node $R_i\left(i\in B_{opt}\right)$ and destination node D. It follows the complex Gaussian distribution with zero mean and circular symmetry, and the variance is ${\eta }_{r_{i}d}^2$. $w_{r_{i}d}$ represents the AWGN on this channel, and it follows the complex Gaussian distribution with zero mean, circular symmetry and variance $N_0$.

In the DF cooperative network, for n relay nodes, a complete transmission requires $n+1$ time slots, and the channel capacity is expressed as follows.

$$I_N={\displaystyle \frac{1}{N+1}}{log}_2\left(1+P_S{\left|h_{sd}\right|}^2\gamma +{{\displaystyle \sum _{i\in B_M}}{\mathrm{P}}_{r_i}\left|h_{r_{i}d}\right|}^2\gamma \right),$$

(4)

where there is $\gamma =1/N_0$. The reason for the multiplication by $1/(N+1)$ is that the whole cooperation procedure requires $N+1$ time slots to form the $N+1$ mutually orthogonal channels.

When the channel capacity is less than the transmission rate r of the system, the transmission is interrupted. The outage probability is used to represent $P_{out,DF}\left(N\right)$ to express the frequency of interruption events in cooperative wireless sensor networks. It is an index to measure the reliability of the system. On the condition of high signal-to-noise ratios, the expression of the systematic outage probability is expressed as follows:

$$\begin{array}{c}{P}_{out,DF}\left(N\right)=Pr\left(I_N<R\right)\hfill \\ =Pr\left({\displaystyle \frac{1}{N+1}}{log}_2\left(1+P_S{\left|h_{sd}\right|}^2\gamma +{\displaystyle \sum _{i=1}^N}{\mathrm{P}}_{r_i}{\left|h_{r_{i}d}\right|}^2\gamma \right)<R\right)\hfill \\ =Pr\left(P_S{\left|h_{sd}\right|}^2\gamma +{\displaystyle \sum _{i=1}^N}{\mathrm{P}}_{r_i}{\left|h_{r_{i}d}\right|}^2\gamma <2^{\left(N+1\right)R}-1\right)\hfill \\ =C\left(N\right){\displaystyle \frac{1}{P_S{\left|h_{sd}\right|}^2\gamma }}{\displaystyle \prod _{i=1}^N}{\displaystyle \frac{1}{{\mathrm{P}}_{r_i}{\left|h_{r_{i}d}\right|}^2\gamma }}\hfill \end{array},$$

(5)

where there is

$$C\left(N\right)={\displaystyle \frac{{\left[2^{\left(N+1\right)R}-1\right]}^{N+1}}{\left(N+1\right)!}}.$$

(6)

3. Proposed DF Multirelay Selection and Power Allocation Scheme

This part mainly describes the pre-allocated power to the source node S and all relay nodes, and then it finds the relay node set $B_M$ that can correctly decode the source node messages from all relay nodes. After that, the optimal relay node set $B_{opt}$ is obtained from the relay node set $B_M$ to correctly decode the source node messages according to the CSI. Finally, the power of all relay nodes in the optimal relay node set $B_{opt}$ is redistributed for better power utilization.

A.

Power pre-distribution

To search a relay node to correctly decode the source node messages, it is necessary to know the channel state information of each channel and the power of the source node S and all relay nodes. So, it is necessary to pre-allocate the power of the source nodes and all relay nodes.

The purpose of power pre-allocation is just to make full use of the total power on the constraint of a certain total power of the entire system. It can be addressed by the minimization of the systematical outage probability expressed in (5).

Suppose that the total power of the system is $P_{total}$, which is a constant. If the power allocation factor of the source node is ${\delta }_0$ and the power allocation factor of the relay node is ${\delta }_i\left(i=1,2,\cdots ,N\right)$, there are

$$P_S={\delta }_0{P}_{total},$$

(7)

$${\mathrm{P}}_{r_i}={\delta }_i{P}_{total}.$$

(8)

Simultaneously, the constraints are required to be met as

$$\sum _{i=0}^N{\delta }_i=1.$$

(9)

Subsequently, the expression of outage probability in (5) turns into

$$\begin{array}{c}{P}_{out,DF}\left(N\right)=Pr\left(I_N<R\right)\hfill \\ =C\left(N\right){\displaystyle \frac{1}{P_S{\left|h_{sd}\right|}^2\gamma }}{\displaystyle \prod _{i=1}^N}{\displaystyle \frac{1}{{\mathrm{P}}_{r_i}{\left|h_{r_{i}d}\right|}^2\gamma }}\hfill \\ =C\left(N\right){\displaystyle \frac{1}{{\delta }_0{P}_{total}{\left|h_{sd}\right|}^2\gamma }}{\displaystyle \prod _{i=1}^N}{\displaystyle \frac{1}{{\delta }_i{P}_{total}{\left|h_{r_{i}d}\right|}^2\gamma }}\hfill \\ =C\left(N\right){\displaystyle \frac{1}{{\delta }_0{\left|h_{sd}\right|}^2{\left(P_{total}\gamma \right)}^{N+1}}}{\displaystyle \prod _{i=1}^N}{\displaystyle \frac{1}{{\delta }_i{\left|h_{r_{i}d}\right|}^2}}\hfill \end{array}.$$

(10)

Obviously, $P_{out,DF}\left(N\right)$ in the above Equation (10) is greater than zero. To facilitate the following calculation, the logarithms are performed on both sides of the above equations, and there are

$$\begin{array}{c}ln\left[P_{out,DF}\left(N\right)\right]=ln\left[C\left(N\right){\displaystyle \frac{1}{{\left|h_{sd}\right|}^2{\left(P_{total}\gamma \right)}^{N+1}}}\right]-ln\left({\delta }_0\right)\begin{array}{cc}& -{\displaystyle \sum _{i=1}^N}ln\left({\delta }_i{\left|h_{r_{i}d}\right|}^2\right)\end{array}\hfill \end{array}.$$

(11)

Given the determined communication system, the first term in the above Equation (11) is a constant and it has no influence on the final result. Therefore, it is directly ignored for the sake of conciseness in the calculation of the power allocation factors for the source and all relay nodes. Subsequently, it is only necessary to calculate the minimum value of the two latter terms to satisfy the limiting conditions of Equation (9). Finally, the problem is turned into the following mathematical model as

$$\begin{array}{cc}min& -ln\left({\delta }_0\right)-{\displaystyle \sum _{i=1}^N}ln\left({\delta }_i{\left|h_{r_{i}d}\right|}^2\right)\\ s.t.& {\displaystyle \sum _{i=0}^N}{\delta }_i=1\end{array}.$$

(12)

The above Equation (12) can be regarded as the objective of searching the extreme value with limited conditions. Subsequently, for this purpose, the Lagrange multiplier method is adopted to address the above problem efficiently. If $\lambda$ is the Lagrange constant, the Lagrange function is constructed for the above model as follows:

$$\begin{array}{c}L\left(\begin{array}{cc}{P}_{out,DF}& \lambda \end{array}\right)=-ln\left({\delta }_0\right)-{\displaystyle \sum _{i=1}^N}ln\left({\delta }_i{\left|h_{r_{i}d}\right|}^2\right)+\lambda \left({\displaystyle \sum _{i=0}^N}{\delta }_i-1\right)\hfill \end{array}.$$

(13)

Let the above Equation (13) to be calculated with the partial derivatives of ${\delta }_i$$\left(i=0,1,2,3,\cdots ,N\right)$ and $\lambda$, respectively, and then make them equal to zero, there are

$$\left\{\begin{array}{c}-{\displaystyle \frac{1}{{\delta }_0}}+\lambda =0\hfill \\ \begin{array}{cc}-{\displaystyle \frac{1}{{\delta }_i}}+\lambda =0,& i=1,\cdots ,N\end{array}\hfill \\ {\displaystyle \sum _{i=0}^N}{\delta }_i-1=0\hfill \end{array}\right..$$

(14)

To solve the Lagrange multiplier method, the constant for the channel coefficients between relay nodes and the destination node must be assumed to be kept as fixed instantaneously. Otherwise, the method fails due to the change in the constant coefficient condition necessary for the method to be correctly solved. By solving the above equations, the following conclusion is obtained:

$${\delta }_0={\delta }_i\left(i=1,\cdots ,N\right)={\displaystyle \frac{1}{N+1}}.$$

(15)

Therefore, it is solved just by the optimized function with Lagrange multiplier method. It is actually calculated by the Equations (13) and (14) with the Lagrange multiplier method, and they are calculated as the equal value to obtain the minimized objective for the initial optimization function, i.e., Equation (13). Therefore, under the pre-allocating power of the source and all relay nodes, the average power allocation is exactly the optimal power allocation.

B.

Optimal relay node selection

Previously, the power of the source node S and all relay nodes $R_i\left(i=1,2,3,\cdots ,N\right)$ have been pre-allocated, and the power allocation factors of source node S and relay nodes have been obtained. Therefore, before selecting the optimal relay node, it is necessary to find the relay node set $B_M$ to correctly decode the source node message from all relay nodes. In summary, the selection is represented as follows:

To enable the relay node to correctly decode the source node messages, it is necessary to satisfy the fact that the channel capacity of any channel generated between the relay and the source nodes is greater than the transmission rate r of the given system. The channel capacity between the source and relay nodes is expressed as follows:

$$I_{s{r}_i}\left(N\right)={\displaystyle \frac{1}{N+1}}{log}_2\left(1+P_S{\left|h_{s{r}_i}\right|}^2\gamma \right).$$

(16)

Suppose that the relay node can correctly decode the message of the source node; it is necessary to ensure that the channel capacity between the source and relay nodes is larger than or equal to the system transmission rate r, and it is expressed as

$${\displaystyle \frac{1}{N+1}}{log}_2\left(1+P_S{\left|h_{s{r}_i}\right|}^2\gamma \right)\ge R.$$

(17)

To ensure that the relay node can decode the source node message correctly, the transmission power $P_S$ of the original transmission node also needs to satisfy the following requirements.

$$P_S\ge {\displaystyle \frac{2^{\left(N+1\right)R}-1}{{\left|h_{s{r}_i}\right|}^2\gamma }}.$$

(18)

Since the transmission power $P_S$ of the source node has been determined after the power is pre-allocated, according to the CSI between the source node and any single relay node, the relay node that satisfies the requirement of Equations (17) and (18) is just the relay node that correctly decodes the correct information from the source node. Then, it is put into the set $B_M$. Channel coefficients are estimated by current channel estimation algorithms and the result is used to decide whether it is efficient for transmission. Then, they are selected to obtain these M relay nodes in the set $B_M$ via the channel quality from the received signals.

If there is no relay node in the system to correctly decode the source node information, the set $B_M$ is empty. Then, the direct transmission is adopted in the second stage. Otherwise, if there are relay nodes in the system to correctly decode the source node messages, the set $B_M$ is not empty, and the optimal relay node is directly chosen.

Next, the case about the non-empty set $B_M$ is studied. After searching the relay nodes to correctly decode the source node messages, the optimal relay node is analyzed from these relay nodes to forward the received source node messages. Suppose that there are M relay nodes in the set $B_M$. For M relay nodes, the channel capacity is expressed as

$$\begin{array}{cc}\hfill I_M& ={\displaystyle \frac{1}{M+1}}{log}_2\left(1+P_S{\left|h_{sd}\right|}^2\gamma +{\displaystyle \sum _{i\in B_M}}{\mathrm{P}}_{r_i}{\left|h_{s{r}_i}\right|}^2\gamma \right)\hfill \\ & ={\displaystyle \frac{1}{M+1}}{log}_2\left(1+{\delta }_0{P}_{total}{\left|h_{sd}\right|}^2\gamma +{\displaystyle \sum _{i\in B_M}}{\delta }_i{P}_{total}{\left|h_{s{r}_i}\right|}^2\gamma \right)\hfill \end{array}.$$

(19)

In the case of M relay nodes, given the channel capacity is less than the transmission rate r of the system, the outage occurs. The channel capacity decides the total capacity of the multiple user channel and the practical transmission rate is used, to be compared with the above channel capacity for the theoretical computation of the outage probability. Simultaneously, the systematic outage probability is expressed as $P_{out,DF}\left(M\right)$, and it is presented as

$$\begin{array}{c}{P}_{out,DF}\left(M\right)=Pr\left(I_M<R\right)\hfill \\ =Pr\left({\displaystyle \frac{1}{M+1}}{log}_2\left(1+{\delta }_0{P}_{total}{\left|h_{sd}\right|}^2\gamma +{\displaystyle \sum _{I\in B_M}}{\delta }_i{P}_{total}{\left|h_{r_{i}d}\right|}^2\gamma \right)<R\right)\hfill \\ =Pr\left({\delta }_0{P}_{total}{\left|h_{sd}\right|}^2\gamma +{\displaystyle \sum _{I\in B_M}}{\delta }_i{P}_{total}{\left|h_{r_{i}d}\right|}^2\gamma <2^{\left(M+1\right)R}-1\right)\hfill \\ =C\left(M\right){\displaystyle \frac{1}{{\delta }_0{P}_{total}{\left|h_{sd}\right|}^2\gamma }}{\displaystyle \prod _{i\in B_M}}{\displaystyle \frac{1}{{\delta }_i{P}_{total}{\left|h_{r_{i}d}\right|}^2\gamma }}\hfill \\ =C\left(M\right){\displaystyle \frac{1}{{\delta }_0{\left|h_{sd}\right|}^2{\left(P_{total}\gamma \right)}^{M+1}}}{\displaystyle \prod _{i\in B_M}}{\displaystyle \frac{1}{{\delta }_i{\left|h_{r_{i}d}\right|}^2}}\hfill \end{array},$$

(20)

where there is

$$C\left(M\right)={\displaystyle \frac{{\left[2^{\left(M+1\right)R}-1\right]}^{M+1}}{\left(M+1\right)!}}.$$

(21)

In Equation (20), only $1/{\delta }_i{\eta }_{s{r}_i}^2$ in the system outage probability is related to the relay channel itself. To facilitate the subsequent calculation, first define the equivalent channel gain $w_i\left(i\in B_M\right)$ with the expression of the relay node $R_i\left(i\in B_M\right)$ as

$$w_i={\displaystyle \frac{1}{1/{\delta }_i{\eta }_{s{r}_i}^2}}={\delta }_i{\eta }_{s{r}_i}^2,i=1\sim M.$$

(22)

After calculating the equivalent channel gain $w_i$ of each relay node in the set $B_M$, it is arranged in descending order. In (20), the outage probability is inversely proportional to the equivalent channel gain $w_i$ of the relay node. Therefore, after $w_i$ is arranged in descending order, the outage probability of the related relay node is arranged in ascending order. To find the optimal relay node set $B_{opt}$ from the set $B_M$, it is assumed that there are K relay nodes in $B_{opt}$. Then, K relay nodes are selected from N relay nodes, and the outage probability is denoted as

$$P_{out,DF}\left(K\right)=C\left(K\right){\displaystyle \frac{1}{{\delta }_0{\eta }_{sd}^2}}{\displaystyle \frac{1}{{\left(P_{total}\gamma \right)}^{K+1}}}{\displaystyle \prod _{i\in B_{opt}}}{\displaystyle \frac{1}{{\delta }_i{\eta }_{s{r}_i}^2}},$$

(23)

where there is

$$C\left(K\right)={\displaystyle \frac{{\left[2^{\left(K+1\right)R}-1\right]}^{K+1}}{\left(K+1\right)!}}.$$

(24)

If the systematic signal-to-noise ratio is represented by ${\gamma }_{th}$, then there is

$${\gamma }_{th}=P_{total}\gamma ={\displaystyle \frac{P_{total}}{N_0}}.$$

(25)

Subsequently, the optimal value of the set of K relay nodes in $B_M$ is represented as

$$R_{opt}=\left\{\begin{array}{c}\begin{array}{ccc}0,& & {\gamma }_{eq,1}\ge {\gamma }_{th}\end{array}\hfill \\ arg\underset{K}{max}\left\{{\gamma }_{eq,K}<{\gamma }_{th}\right\},{\gamma }_{eq,1}<{\gamma }_{th}\hfill \end{array}\right.,$$

(26)

where there is

$${\gamma }_{eq,K}={\displaystyle \frac{f\left(K\right)p\left(K\right){\delta }_{0,K-1}}{{\delta }_{0,K}}},$$

(27)

$$f\left(K\right)={\displaystyle \frac{{\left[2^{\left(K+1\right)R}-1\right]}^{K+1}}{{\left(2^{KR}-1\right)}^K\left(K+1\right)}},$$

(28)

$$p\left(K\right)={\displaystyle \frac{{\displaystyle \prod _{i\in B_{opt}}}\frac{1}{{\delta }_i{\eta }_{s{r}_i}^2}}{{\displaystyle \prod _{i\in B_{opt-1}}}\frac{1}{{\delta }_i{\eta }_{s{r}_i}^2}}},$$

(29)

where ${\delta }_{0,K-1}$ and ${\delta }_{0,K}$ represent the power allocation factors obtained by the source node in the procedure of the power pre-allocation under the number of relay nodes of $K-1$ and K, respectively. Therefore, the optimal relay node set, i.e., $B_{opt}$, are expressed as

$$B_{opt}=\left\{R_1,R_2,R_3,\cdots ,R_{\mathrm{opt}}\right\}.$$

(30)

Proof. 

When the equivalent channel gain $w_i$ of the relay nodes in $B_M$ is arranged in descending order, the outage probability of the related relay nodes is then arranged in ascending order too. After finding the optimal relay set and $B_{opt}$, the systematic outage probability is minimized. Therefore, the following inequality is obtained as

$$P_{out,DF}\left(K\right)<P_{out,DF}\left(K-1\right)<\cdots <P_{out,DF}\left(1\right),$$

(31)

$$P_{out,DF}\left(K\right)>P_{out,DF}\left(K+1\right)>\cdots >P_{out,DF}\left(M\right).$$

(32)

By combining Equations (31), (32) and (23) together, we obtain

$$w_j>{\displaystyle \frac{f\left(j\right)}{{\gamma }_{th}}},j=1,2,\cdots ,K,$$

(33)

$$w_j<{\displaystyle \frac{f\left(j\right)}{{\gamma }_{th}}},j=K+1,\cdots ,M.$$

(34)

Because $f\left(K\right)$ and $p\left(K\right)$ increase monotonically along with the increase in K, and $w_K$ decreases monotonically along with the increase in K as well, the following results are obtained according to Equations (33) and (34) as

$$w_K>{\displaystyle \frac{f\left(K\right)}{{\gamma }_{th}}},$$

(35)

$$w_K<{\displaystyle \frac{f\left(K+1\right)}{{\gamma }_{th}}}.$$

(36)

By further simplifying the above two equations, there is

$${\gamma }_{eq,K}={\displaystyle \frac{f\left(K\right)}{w_K}}<{\gamma }_{th}<{\displaystyle \frac{f\left(K+1\right)}{w_{K+1}}}={\gamma }_{eq,K+1}.$$

(37)

Since Equations (28) and (29) are monotonically increasing with K, Equation (27) can be further written in the form of Equation (26). In addition, given the smaller signal-to-noise ratio, there is ${\gamma }_{th}<{\gamma }_{eq,1}$. Then, none of $B_M$, or the relay nodes, can meet the requirement of minimizing the outage probability. Subsequently, the relay node is not used to participate in the cooperation, and both the source and destination nodes are directly utilized for transmissions. Otherwise, given the much larger signal-to-noise ratio, there is ${\gamma }_{th}>{\gamma }_{eq,M}$. Only all relay nodes in the $B_M$ that participated in cooperation can be adopted to minimize the systematic outage probability. In addition, there is another special case, ${\gamma }_{th}={\gamma }_{eq,1}$. It shows that the outage probability is related to select a relay node from the $B_M$ to participate in cooperation. To save resources, in this case, the direct transmission is utilized to accomplish the transmissions. This phenomenon is consistent with the results derived from Equation (26). □

Analyses of the Proposed Multirelay Selection and Power Allocation

According to the above derivations of the proposed scheme, the optimal relay node set $B_{opt}$ under power pre-allocation can be selected according to a simple inequality. First, the equivalent channel gains of all relay nodes in $B_M$ after power pre-allocation is required to be calculated according to Equation (22) and it is arranged in descending order. Second, ${\gamma }_{eq,K}$, related to each relay node, is calculated by the Equation (27). It is compared with the current system signal-to-noise ratio ${\gamma }_{th}$ to search the value of $R_{opt}$ to satisfy the requirements. Simultaneously, the optimal relay node set is $B_{opt}=\left\{R_1,R_2,R_3,\cdots ,R_{\mathrm{opt}}\right\}$. At different signal-to-noise ratio ${\gamma }_{th}$, the calculated optimal relay value of $R_{opt}$ is also different, and monotonically decreases.

To compare the performance, two other relay selection algorithms are given here, namely the single-relay SDF (short for SDF) scheme and all-relay SDF (short for ADF) schemes. The SDF scheme refers to finding the set of relay nodes to correctly decode the messages of the source node, and then it searches the relay node with the lowest systematic outage probability to participate in the cooperation, i.e., $K=1$. The ADF scheme searches the set of relay nodes to correctly decode the source node messages, and it does not select the optimal relay. All-relay selection cooperation means that they can correctly decode the source node messages that participated in the cooperation, i.e., $K=M$.

In the SDF scheme, with the selected optimal relay node K, the outage probability is expressed by being transformed from Equation (23) to

$$P_{out,SDF}\left(K\right)={\displaystyle \frac{{\left(2^{2R}-1\right)}^2}{2{\left(P_{total}\gamma \right)}^2{\delta }_0{\eta }_{sd}^2{w}_K}}.$$

(38)

By selecting a relay with a minimal outage probability of the entire system, the selected relay is expressed as

$$R_{opt,SDF}=arg\underset{K}{min}\left(P_{out,SDF}\left(K\right)\right)=arg\underset{K}{max}\left(w_K\right).$$

(39)

Finally, the case of the empty set $B_M$ is investigated. Since there is no suitable relay node to participate in the cooperation, direct transmission is adopted for communications in the second stage. Simultaneously, to avoid the waste of system resources, all the power of the system needs to be allocated to the source node, i.e., $P_S=P_{total}$. Therefore, the channel capacity of the system is expressed as

$$I={log}_2\left(1+P_{total}{\left|h_{sd}\right|}^2\gamma \right).$$

(40)

Because there is only one channel link in the cooperation system that is instantaneous, the coefficient of the channel capacity is set as 1. When the channel capacity of this link is less than the system transmission rate R, the transmission is terminated.

C.

Power redistribution

After finding the optimal relay node set $B_{opt}$, to ensure the transmission reliability, it is necessary to redistribute the power of the relay nodes in $B_{opt}$, and the power allocation is still carried out under the total power $P_{total}$ in the transmission system.

The algorithm for the power redistribution is the well-known water-filling algorithm in the traditional information theory [21]. Its fundamental conception is to maximize the total channel capacity of the transmission system under the total systematic power $P_{total}$. Different from the previous power pre-allocation, the purpose of the proposed scheme is to minimize the outage probability of the entire system. For the power redistribution in this scheme, more power should be allocated to the link with a high signal-to-noise ratio.

There are two cases for the optimal relay node set $B_{opt}$. In the first case, the set $B_{opt}$ is not empty. The second case can be expressed in Equation (26).

Suppose that there are K relay nodes in the relay set $B_{opt}$, and the source node does not participate in the information transmission in the second stage. A complete transmission requires K time slots. Simultaneously, for the i-th relay, $R_i,i\in B_{opt}$, the channel capacity of the link composed of the i-th relay and the destination node D is presented as

$$I_{r_{i}d}={\displaystyle \frac{1}{K}}{log}_2\left(1+{\mathrm{P}}_{r_i}{\left|h_{r_{i}d}\right|}^2\gamma \right).$$

(41)

At this moment, the systematic outage probability is expressed as

$$\begin{array}{c}{P}_{out,DF}=Pr\left(I_K={\displaystyle \sum _{i\in B_{opt}}}{I}_{r_{i}d}<R\right)\hfill \\ \begin{array}{cc}& =C\left(K-1\right){\displaystyle \frac{1}{{\left(P_{total}\gamma \right)}^K}}{\displaystyle \prod _{i\in B_{opt}}}{\displaystyle \frac{1}{{\delta }_i{\eta }_{s{r}_i}^2}}\end{array}\hfill \end{array}.$$

(42)

To maximize the channel capacity of the whole system under a certain total power $P_{total}$ of the system, it is expressed by the following model as

$$\begin{array}{cc}max& I_K={\displaystyle \sum _{i\in B_{opt}}}{\displaystyle \frac{1}{K}}{log}_2\left(1+{\mathrm{P}}_{r_i}{\left|h_{r_{i}d}\right|}^2\gamma \right)\\ s.t.& {\displaystyle \sum _{i\in B_M}}{\mathrm{P}}_{r_i}=P_{total}\end{array}.$$

(43)

Furthermore, the above model is still equivalent to the problem of finding extreme value with limited conditions. It can be solved by the well-known Lagrange multiplier method. Therefore, the Lagrange formula is constructed as

$$\begin{array}{c}L\left(\begin{array}{cc}{I}_K& \lambda \end{array}\right)={\displaystyle \sum _{i\in B_{opt}}}{\displaystyle \frac{1}{K}}{log}_2\left(1+{\mathrm{P}}_{r_i}{\left|h_{r_{i}d}\right|}^2\gamma \right)\hfill \\ \begin{array}{ccc}\begin{array}{cc}& \end{array}& & +\lambda \left({\displaystyle \sum _{i\in B_{opt}}}{\mathrm{P}}_{r_i}-P_{total}\right)\end{array}\hfill \end{array}.$$

(44)

Let the above Lagrange Formula (44) calculate the partial derivative of ${\mathrm{P}}_{r_i}$$(i=1,2,3,\cdots ,$$K\left)\right)$ and $\lambda$, respectively, and then make them equal to zero; subsequently, there are

$$\left\{\begin{array}{c}{\displaystyle \sum _{i\in B_{opt}}}{\displaystyle \frac{{\left|h_{r_{i}d}\right|}^2\gamma }{Kln2\left(1+{\mathrm{P}}_{r_i}{\left|h_{r_{i}d}\right|}^2\gamma \right)}}+\lambda =0\hfill \\ {\displaystyle \sum _{i\in B_{opt}}}{\mathrm{P}}_{r_i}-P_{total}=0\hfill \end{array}\right..$$

(45)

For the Equation (45), there is

$${\mathrm{P}}_{r_i}={\displaystyle \frac{P_{total}+\frac{1}{\gamma }{\displaystyle \sum _{i\in B_{opt}}}\frac{1}{{\left|h_{r_{i}d}\right|}^2}}{K}}-{\displaystyle \frac{1}{\gamma {\left|h_{r_{i}d}\right|}^2}}.$$

(46)

According to the above equation that the power allocated to each relay node in the relay set $B_{opt}$ is only related to the channel coefficient $h_{r_{i}d}$ of the channel formed between each relay and destination node D in the $B_{opt}$. Therefore, by counting the channel coefficient $h_{r_{i}d}$ of the channel formed between each relay node and destination node D in the set $B_{opt}$. The power allocated to the relay node $R_i\left(i\in B_{opt}\right)$ is also calculated according to the above equation.

Finally, the second case is analyzed as follows: The set is empty, and it is just presented as the first case in Equation (26). Because there is no optimal relay node set, direct transmission is adopted for the cooperative communication in the second stage. To avoid the resource waste, total power of the system is still allocated to the source node, i.e., $P_S=P_{total}$. Thus, it is the same as that of the previous empty set $B_M$.

In summary, the specific steps of the proposed scheme are detailed as follows:

(a)

The Lagrange multiplier method is used to allocate the total power to the source and all relay nodes $R_i\left(i=1,2,\cdots ,N\right)$ in the system on the condition of minimizing the system outage probability and making full use of the total system power;

(b)

According to the allocated source node power and relay node power ${\mathrm{P}}_{r_i}$$\left(i=1,2,3,\cdots ,N\right)$, use Equations (16), (17) and (18) to find the relay node set $B_M$ that can correctly decode the source node information. Then, use Equation (22) to calculate and count the equivalent channel gain $w_i$ of all relay nodes in the relay node set $B_M$ and arrange it in a descending order. Then, calculate the ${\gamma }_{eq,K}$ of each relay node in the $B_M$ according to Equation (27) and compare it with the signal-to-noise ratio ${\gamma }_{th}$. Finally, the optimal relay node set $B_{opt}=\left\{R_1,R_2,R_3,\cdots ,R_{opt}\right\}$ is obtained by Equation (26);

(c)

Redistribute power to all relay nodes in the optimal relay node set $B_{opt}$ according to Equation (46), and notify all relay nodes in $B_{opt}$ of the allocation result.

4. Complexity Analysis

The proposed scheme only needs to allocate power twice under the selection of the optimal relay node set $B_{opt}$. Suppose that the algorithm complexity of power allocation is t, the operation complexity of the proposed algorithm is about $2T$. The enumeration method needs to allocate ${\sum }_{L=0}^N{C}_N^L=2^N$ secondary power. The total computational complexity of the enumeration method is about $2^{N}T$. Therefore, the proposed scheme greatly reduces the computational complexity.

5. Simulation Results and Analysis

The simulation parameters are set as follows. Each channel is set as an independent Rayleigh fading channel. The modulation is the binary phase shift keying (BPSK). The total number N of relays is set to 5. Since the SNR involved in the simulation is the systematic SNR, there is $SNR=10{log}_{10}\left({\gamma }_{th}\right)$. In the experimental, we mainly choose the simulation parameters in Table 1 via the actual experiment parameters, which are measured from the true experimental measurement. The channel coefficients are obtained by the average amplitude measurement with a sequence of fixed “1’’ bit sequence transmission and the amplitude of it is normalized as 1 in the experiment, because the average calculation is actually the expectation in statistics and the zero mean property of the additive Gaussian white noises help to eliminate the influence of it. So, the channel coefficients can be easily measured and calculated as the square of the average amplitude of the received signals. The experimental parameters in Table 1 are determined and selected, particularly they are adopted for the simulations and related analyses in the context of all the following presented figures. Therefore, they are rational experiment parameters to be used in simulations.

Table 1. Simulation parameter values under different channel conditions.

Parameter	Value
${\eta }_{sr1}^2$	1.7
${\eta }_{sr2}^2$	1.06
${\eta }_{sr3}^2$	0.7
${\eta }_{sr4}^2$	1.25
${\eta }_{sr5}^2$	0.3
${\eta }_{r1d}^2$	1.7
${\eta }_{r2d}^2$	1.06
${\eta }_{r3d}^2$	0.7
${\eta }_{r4d}^2$	1.25
${\eta }_{r5d}^2$	0.3
${\eta }_{sd}^2$	1
R	1 bit/s
$P_{total}$	10 W

In Figure 2, the Monte Carlo experimental and theoretical values of different relay set points are simulated and compared. By (5) and (6), much larger N leads to the smaller $C\left(N\right)$, and thus there is the smaller $P_{out,DF}\left(N\right)$, i.e., the outage probability. In this figure, under the condition of large signal-to-noise ratio (SNR > 22 dB), the curve of experimental and theoretical values basically coincides with the expected result of Equation (5), which verifies that the outage probability expression obtained by the proposed method is quite correct.

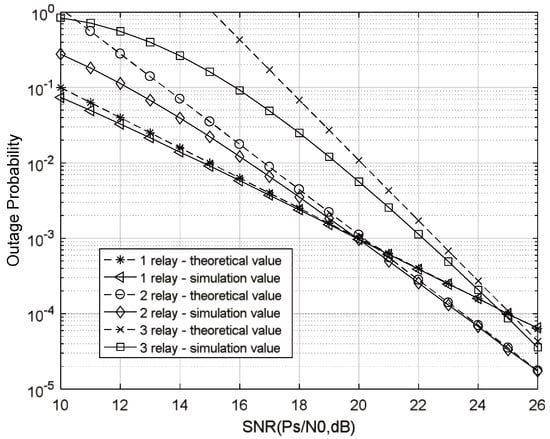
Figure 2. Theoretical and simulation values of outage probability for different number of relay nodes.

In Figure 3, the outage probability of the proposed relay selection scheme is simulated and compared with different relay cooperation under the proposed power pre-allocation. The outage probability of the proposed scheme is always the lowest under any signal-to-noise ratio, indicating that the proposed scheme can always select the optimal relay for cooperation. Meanwhile, according to Equation (27), ${\gamma }_{eq,1}=10.25$ dB, ${\gamma }_{eq,2}=19.08$ dB and ${\gamma }_{eq,3}=26.99$ dB can be calculated. In addition, according to Equations (26) and (30), when ${\gamma }_{th}<{\gamma }_{eq,1}$, no relay participates in cooperation, when ${\gamma }_{eq,1}<{\gamma }_{th}<{\gamma }_{eq,2}$, select one relay to participate in cooperation, when ${\gamma }_{eq,2}<{\gamma }_{th}<{\gamma }_{eq,3}$, select two relays to participate in cooperation, and when ${\gamma }_{th}>{\gamma }_{eq,3}$, all relays participate in cooperation. The simulation results in the figure are basically consistent with the theoretical results, which verifies the reliability of the proposed scheme.

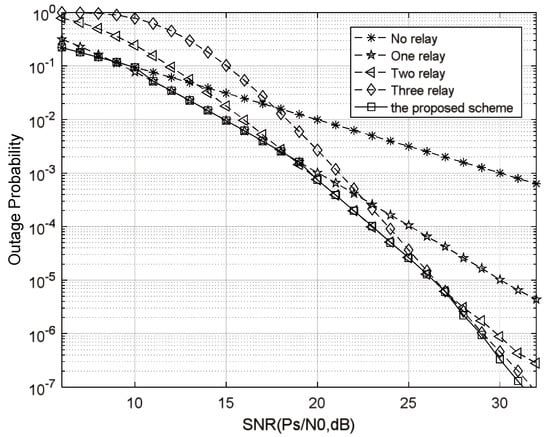
Figure 3. Outage probability curves of the proposed relay selection scheme and different relay numbers under the proposed power pre-allocation scheme.

In Figure 4, the outage probabilities of different relay selection schemes are simulated and compared under the proposed power allocation scheme. The SDF scheme is adopted to select the best relay node among all relay nodes to correctly decode the source node messages to participate in the cooperation. The ADF refers to all relay nodes that correctly decode the messages from the source node to participate in the cooperation. An exhaustive method is used to select the best relay set among all possible relay sets for cooperation. Under the same signal-to-noise ratio, the performance of the proposed scheme is better than those of the SDF and the ADF, respectively. At the systematic outage probability of ${10}^{-4}$, the signal-to-noise ratio required by the proposed relay selection is 2.1 dB lower than that of the SDF scheme, and 0.9 dB lower than that of the ADF scheme. In addition, the outage probability curve of the proposed scheme almost coincides with that of the exhaustive method. Therefore, the proposed scheme can not only reduce the complexity of the exhaustive method, but also has the same outage probability performance as the exhaustive method, which is globally optimal.

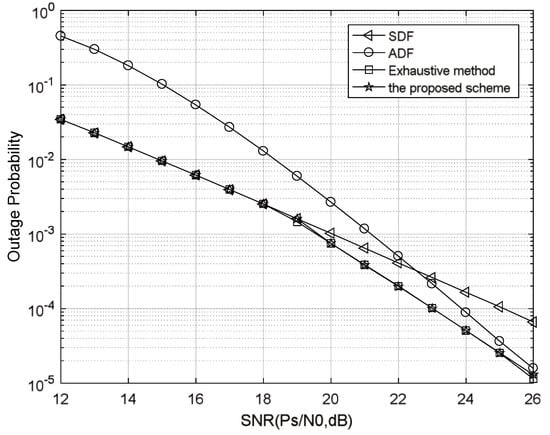
Figure 4. Outage probability curves of different options under the proposed power allocation scheme.

In Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, the simulation and comparison of the terminal probability curves of different power allocation schemes under different numbers of relay nodes is depicted. The equal power allocation (EPA) scheme refers to the equal power allocation between the any relay node and source node. The proposed scheme uses Equation (46) to allocate power to the relay node. In these figures, when the number of relay nodes is one and two, the outage probability of the proposed power allocation scheme is greater than that of the EPA scheme. With the increase in the number of relay nodes, the curve of the proposed power allocation gradually approaches the curve related to the EPA scheme. When the number of relay nodes is three, the two curves almost overlap. Given the relay number of four and five, the systematic outage probability of the proposed power allocation is less than that of the EPA scheme. With a relay number of five, the performance gain is about 1.5 dB between the proposed scheme and the counterpart EPA scheme at the outage probability of ${10}^{-4}$. It is explained as follows: With the alteration of the optimal relay number, the power allocation of Equation (12) also changes accordingly. Combined with the objective equation and constraints of Equation (12), the proposed power allocation scheme always makes full use of system resources and minimizes the outage probability. Therefore, with the further increase in the relay number, the curve of the proposed power allocation gradually moves away from that of the EPA scheme with much more performance gains. Thus, it is verified that the proposed power allocation has better performance, when the number of relay nodes is large. More relay nodes leads to the lower outage probability of the proposed power allocation, and thus it obtains better transmission performance. Therefore, the proposed power allocation outperforms the EPA.

Figure 5. Outage probability curves of different power allocation schemes under one relay node.

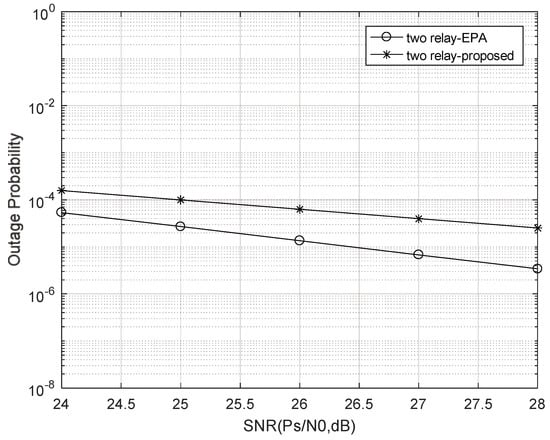
Figure 6. Outage probability curves of different power allocation schemes under two relay nodes.

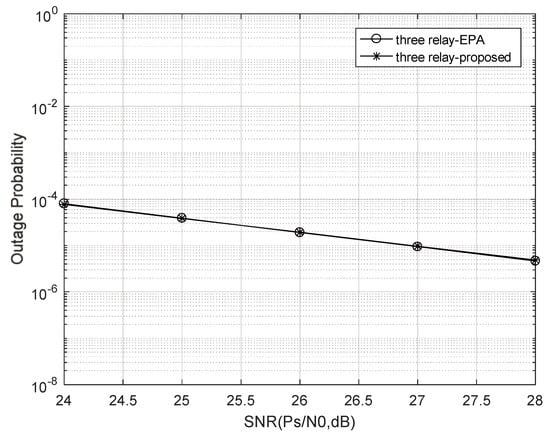
Figure 7. Outage probability curves of different power allocation schemes under three relay nodes.

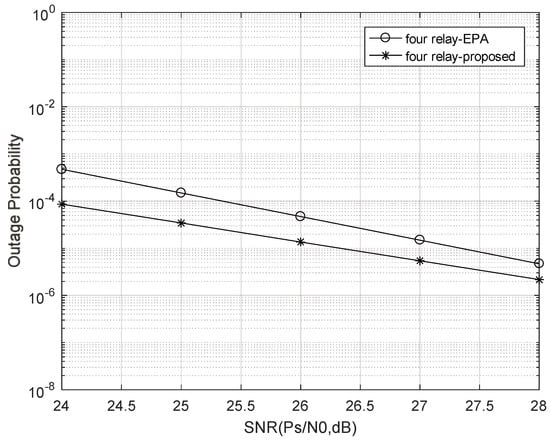
Figure 8. Outage probability curves of different power allocation schemes under four relay nodes.

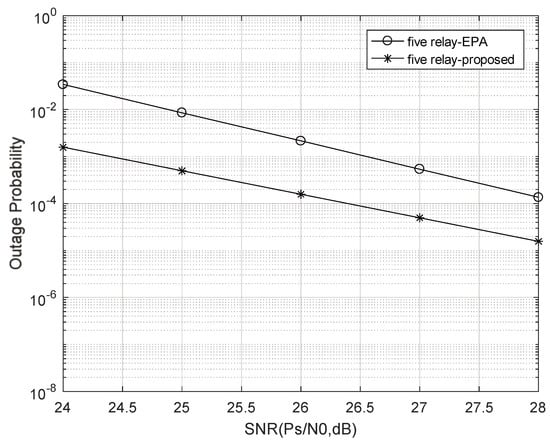
Figure 9. Outage probability curves of different power allocation schemes under five relay nodes.

6. Conclusions

This paper mainly studies the optimal relay selection and power allocation in the multirelay SDF cooperation by statistical channel characteristics. It pre-allocates power to all relay and source nodes before selecting relay nodes, and it redistributes power to the best relay nodes after optimal relay selection. Moreover, the outage probability performance of the proposed scheme is compared with those of the single-relay SDF, all-relay ADF and exhaustive method through numerical simulations. The outage probability performance of the proposed scheme is significantly improved and almost approaches that of the exhaustive scheme, when compared with those of the SDF, ADF and exhaustive scheme. With a lower number of relay nodes, the terminal performance of the proposed scheme is just slightly inferior to those of the existing equal power allocation scheme. However, under a large number of relay nodes, it significantly outperforms the counterparts, especially with the increase in the number of relay nodes. Therefore, the proposed scheme is more suitable for ultra dense networks (UDNs) of the next-generation mobile communication systems, with high complexity and a large number of relay nodes.

In a future work, the proposed scheme is planned to be adjusted to work at low SNRs via the modern channel codes, especially the low-density parity-check (LDPC) codes, the polar codes, and so on. Also, the proposed scheme can be combined with the secure cooperative relaying (SCR) protocol, the hybrid non-orthgonal multiple access (NOMA) protocol, a relay adaptive amplify-and-forward/decode-and-forward (AF/DF) collaboration, energy harvesting, and so on, to achieve ever-better comprehensive performance.