The ZVS Class E/F3 Inverter Using Piezoelectric Transformers for Energy Extraction

Abstract

Enhanced class E inverters (EF_n or E/F_n) reduce the high peak switch voltage that is prevalent in class E inverters. Additionally, their stability and load regulation capabilities are improved as compared to class E inverters. This paper proposes an enhanced class E inverter (E/F₃) with a piezoelectric transformer (PT) replacing the auxiliary resonant networks. This class E/F₃ inverter is designed by adding a tuned auxiliary LC network at the third harmonic of the switching frequency to the class E inverter. Both the primary and auxiliary resonant networks are realized using a piezoelectric transformer (PT). The converter is simulated in LTspice and an experimental prototype is built and tested. It is found that the experimental results concur with the simulation results, with a measured efficiency of 90%. Thus, the theoretical design is verified and the concept of energy extraction is achieved.

1. Introduction

The compact architecture of class E inverters, which has a low component count and a simultaneous high power transmission capability, is largely responsible for their popularity. Additionally, if combined with zero voltage switching (ZVS) or zero derivative voltage switching (ZVDS) approaches, they can function at very high switching frequencies with excellent efficiency. The ZVS/ZVDS class E inverters’ analyses and modeling have been thoroughly documented in the literature [1,2,3]. This architecture does have one significant drawback, though. This is seriously concerning, because the peak switch voltage is so large (3.5 to 5 times, depending on the duty ratio) [4,5,6,7,8]. The upgraded class E configurations are suggested, among other things, to address this problem, and the LC networks are tuned at the nth harmonic of the switching frequency [9,10,11,12,13,14,15,16,17,18]. In this paper, a class E/F₃ inverter is designed. The inverter’s topology is shown in Figure 1a. A piezoelectric transformer (PT-T1PP0361) is used for energy extraction in the primary and auxiliary resonant networks. This PT is shown in Figure 1b, along with its mason equivalent circuit being demonstrated in Figure 1c. In Figure 1a, the inverter has primary and secondary resonant networks tuned at different resonant frequencies. In this design, either the primary or secondary resonant network is replaced by the PT, or the PT is used to realize the other network using conventional magnetic components. The experimental prototype is constructed and put through testing, while the inverter is simulated in LTSPICE utilizing a PT emulation circuit. The following sections provide details on the testing’s design and outcomes. In Section 2, the circuit configuration and modes of operation are described. In Section 3, the circuit design is explained. In Section 4, the simulation and experimental verification process is described. Section 5 concludes the paper.

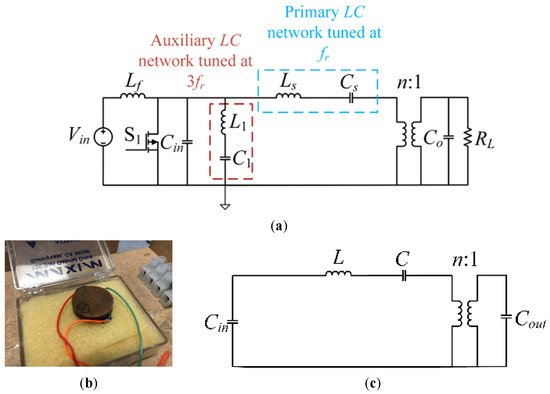
Figure 1. (a) The class E/F3 topology with primary and auxiliary resonant networks tuned at f_r and 3f_r, respectively. (b) The radial mode PT (T1PP0361). (c) The PT mason equivalent circuit.

2. The Circuit Configuration and Modes of Operation

In Figure 1a, the inductance L_s and capacitance C_s make up the primary resonant tank of the class E/F₃ inverter, which resonates at a resonant frequency (f_r) in accordance with a quality factor (Q). The input inductance (L_f) is designed to deliver an extremely low ripple current while maintaining a steady DC current. The input capacitance C_in absorbs the drain-to-source (non-linear) capacitance (C_ds) of the switch. The auxiliary resonant branch consists of the auxiliary resonant inductance (L₁) and capacitance (C₁). The primary resonant frequency is f_r, and the auxiliary resonant frequency is 3f_r. The primary resonant frequency f_r and the switching frequency f_s are both chosen to be equal, or the f_s is slightly higher than the f_r. To accomplish the ZVS operation, the switch S₁ is run at its optimal duty ratio D_opt. The switching pattern is depicted as follows.

$$\mathrm{Switch}=\{\begin{array}{l}\mathrm{Turned} \mathrm{ON}, 0\le \theta <2\pi D\\ \mathrm{Turned} \mathrm{OFF}, 2\pi D\le \theta <2\pi \end{array}$$

(1)

When the switch S₁ is ON in mode 1, the voltage across the capacitor C_in is forced to zero. The L_f is charged as the input current (I_in) passes through S₁. The resonant current flows through the switch in the resonant tank, transferring the stored energy from the C_s to the L_s and completing one half of the resonant cycle. At the conclusion of this cycle, the energy transfer is completed and the current starts to decline. When S₁ opens at θ = 2πD in mode 2, the I_in charges the input capacitor C_in, which eventually achieves the peak switch voltage (V_S1,peak), before being discharged through the primary resonant tank. Due to the inductive nature of the load network in mode 2, the output current (I_out) lags the input voltage to the resonant tank (V_S1) in mode 2. This ensures that the ZVS is operating for the designed inverter. On that note, the following conditions must be met to achieve ZVS or ZVDS,

$$V_{S1}(2\pi )=0 \mathrm{and} \frac{d}{d\theta }{V}_{S1}(2\pi )=0$$

(2)

In Figure 1b, the PT mason equivalent circuit replaces the primary or the secondary resonant tank in the class E/F₃ resonant inverter.

3. Circuit Design

In this section, the circuit components are designed [7,8] according to the specifications that are stated in Table 1. As mentioned earlier, the primary and auxiliary resonant tank is replaced by the PT. The PT characteristic component values are measured using a Bode 100 Network Analyzer. The measured parameters are stated in Table 2.

Table 1. Design specifications.

Parameters	Symbols	Values
Input voltage	Vin	10 V
Primary resonant frequency	fr	26.67 kHz
Auxiliary resonant frequency	3fr	80 kHz
Capacitance ratio	k (C1/Cin)	10
Quality factor of the conventional resonant tank	Qaux	0.707

Table 2. Characteristic component values of PT.

Parameter	Symbol	Value
Series resistance	RPT	8.69 Ω
Resonant inductor	LS	4.86 mH
Resonant capacitor	CS	0.814 nF
Input capacitor	Cin	2.53 nF
Output capacitor	Co	4.58 nF
Turns ratio	n:1	1:0.45
Quality factor of the PT	QPT	281.30

As can be calculated from Table 2, the PT resonant frequency (f_r−PT) is

$$f_{r-PT}=\frac{1}{2\pi \sqrt{LC}}=\frac{1}{2\pi \sqrt{4.86\times {10}^{-3}\times 0.814\times {10}^{-9}}}\approx 80 \mathrm{kHz}$$

(3)

An input inductor L_f = 100 µH is selected for both designs involving the PT, as the primary or auxiliary resonant network.

A.

The PT as Primary Resonant Tank

In this subsection, the inverter is designed while the primary resonant tank is replaced by a PT. In Figure 2, the circuit diagram with the PT mason equivalent circuit is shown. In this case, as can be derived from Table 2, L_s = L_PT = 4.86 mH, C_s = C_PT = 0.814 nF, n ≈ 2.22, C_in = C_in−PT = 2.53 nF, and C_o = C_out−PT = 4.58 nF. The L_ofC_of filter is designed with a cutoff frequency of f_c = 120 kHz. Alternatively, without the L_ofC_of filter, a large output capacitor, C_of = 330 µH, can be used to reduce the high frequency harmonics, as shown in Figure 2b. As the PT replaces the primary resonant tank, the primary resonant frequency f_r is 80 kHz. The auxiliary circuit has to resonate at f_raux = 3f_r. The components L₁ and C₁ are selected for Q = 0.707 from Table 1 and for R_L = 100 Ω.

$$L_1=\frac{Q\times R_L}{\omega }=\frac{0.707\times 100}{2\pi \times 240\times {10}^3}\approx 46.90 \mathsf{\mu }\mathrm{H}$$

(4)

$$C_1=\frac{1}{4{\pi }^2{L}_1{f}^2{}_{raux}}=\frac{1}{4{\pi }^2\times 46.90\times {10}^{-6}\times {(3\times 80\times {10}^3)}^2}\approx 9.38 \mathrm{nF}$$

(5)

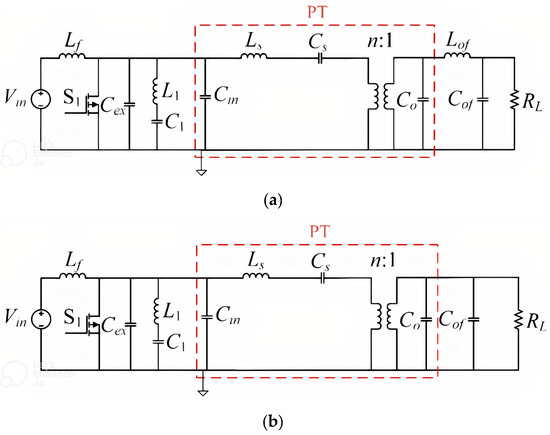
Figure 2. PT as primary resonant tank, (a) with an output LC filter, and (b) with output filter capacitor (C_of).

The input capacitance can be calculated from [12] by using the k from Table 1.

$$\begin{array}{l}\omega R_{L,opt}{C}_{in}=\frac{0.6428k+0.3598}{k+0.0875}\\ \Rightarrow C_{in}=\frac{0.6428\times 10+0.3598}{2\pi \times 26670\times 100\times (10+0.0875)}=40.15 \mathrm{nF}\end{array}$$

(6)

As C_in−PT = 2.53 nF, an external input capacitance C_ex = C_in − C_in−PT = (40.15 − 2.53)nF = 37.62 nF has to be added. Practically, C_ex ≈ 47 nF is selected with consideration to its availability. The circuit parameters are stated in Table 3.

Table 3. The circuit parameters with PT as primary resonant tank.

Parameter		Values
PT input capacitance	Cin	2.53 nF
External input capacitance	Cex	47 nF
PT output capacitance	Co	4.70 nF
PT transformer ratio	n	≈2.22
Load resistance	RL	100 Ω
Primary resonant inductance	Ls	4.77 mH
Primary resonant capacitance	Cs	814 pF
Auxiliary resonant inductance	L1	46.90 µH
Auxiliary resonant capacitance	C1	9.10 nF
Output filter inductor	Lof	200 µH
Output filter capacitance	Cof	100 nF

B.

The PT as Auxiliary Resonant Tank

In Figure 3, the circuit diagram, with the PT replacing the auxiliary resonant network, is shown. In this case, as can be derived from Table 2, L₁ = L_PT = 4.86 mH, C₁ = C_PT = 0.814 nF, n ≈ 2.22, and C_in = C_in−PT = 2.53 nF. For the structure of the PT, the C_out−pri comes in parallel to the C₁. This is due to the PT output capacitance (C_out−PT) being reflected to the primary side and can be computed as:

$$C_{out-pri}=C_{out-PT}\times n^2=4.58\times {(2.22)}^2 \mathrm{nF}=22.57 \mathrm{nF}$$

(7)

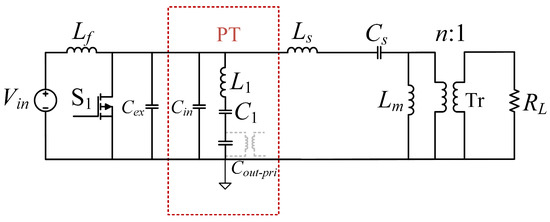
Figure 3. The class E/F₃ topology with PT as auxiliary resonant tank and magnetic transformer.

In (6), the required C_in is calculated. Hence, an external input capacitance, C_ex ≈ 47 nF, is added to the required design. The magnetic transformer (Tr) has a magnetic inductance of L_m = 18 µH. The circuit parameters are stated in Table 4.

Table 4. The circuit parameters with PT as auxiliary resonant tank.

Parameter		Values
PT input capacitance	Cin−PT	2.53 nF
External input capacitance	Cex	47 nF
PT output capacitance	Cout−PT	4.57 nF
Transformer ratio	n:1	2:1
Load resistance	RL	100 Ω
PT auxiliary resonant inductance	L1	4.86 mH
PT auxiliary resonant capacitance	C1	814 pF
PT output capacitance	Cout−pri (n2 ∗ Cout−PT)	18.28 nF
Equivalent capacitance in the auxiliary branch	Ceq = C1||Cout−pri	778 pF
Primary resonant inductance	Ls	300 µH
Primary resonant capacitance	Cs	124 nF

4. Simulation and Experimental Verification

The class E/F₃ inverter with the integrated PT is simulated in an LTSPICE simulation platform and prototypes are built. In Figure 4, the LTSPICE simulation circuit is shown. In this configuration, the PT emulator (i.e., the mason equivalent) replaces the primary resonant tank. The component design is presented in the previous section and utilizes a PT as the primary or auxiliary resonant network. In the rest of this section, the results for the simulation and experimentation of the designed inverter are presented and described. The experimental setup is shown in Figure 5.

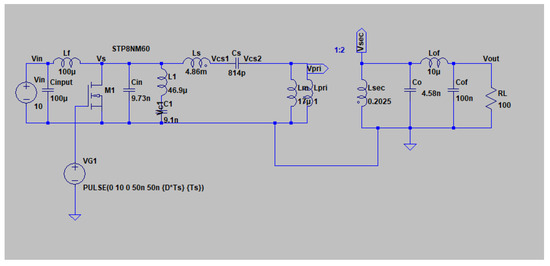
Figure 4. Simulation circuit: the class E/F₃ topology with PT as primary resonant tank.

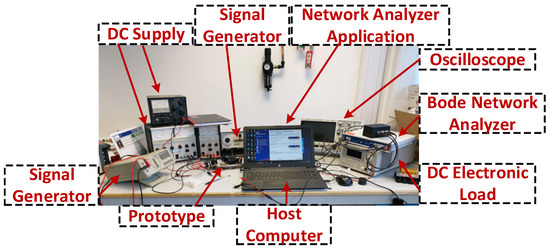
Figure 5. Experimental setup.

A.

The PT as Primary Resonant Tank

In Figure 5, the LTSPICE simulation circuit is shown. In this configuration, the PT emulator (i.e., the mason equivalent) replaces the primary resonant tank.

In Figure 6a, the switch voltage from the LTSPICE simulation is demonstrated. As can be seen, the peak switch voltage is 34 V. From Figure 6b, it is obvious that the output voltage (V_out) is smooth and contains less harmonics. However, the reverse diode’s conduction shows that the inverter is not performing at its best. The inverter’s output power is determined as follows:

$$P_{out,sim}=\frac{V_{rms}{}^2}{R_L}\approx \frac{{\left(18\times 0.707\right)}^2}{100}=1.62 \mathrm{W}$$

(8)

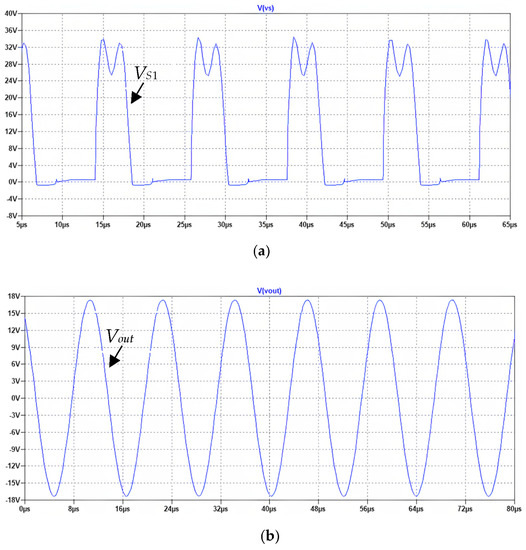
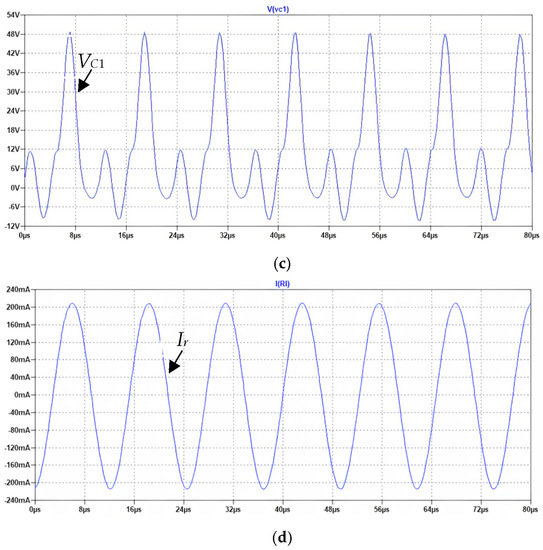
Figure 6. Simulation results: the class E/F3 topology with PT as auxiliary resonant tank. (a) The switch voltage, (b) the output voltage, V_out (c) the auxiliary resonant capacitor voltage, V_C1, and (d) the primary resonant current, I_r.

The experimental findings are shown in Figure 7. As can be seen, the switch’s reverse diode (S₁) conducts for a brief length of time, achieving the ZVS/ZDS in the sub-optimal zone. This output power is determined as follows:

$$P_{out,\exp }=\frac{V_{rms}{}^2}{R_L}\approx \frac{{\left(20\times 0.707\right)}^2}{100}=1.99 \mathrm{W}$$

(9)

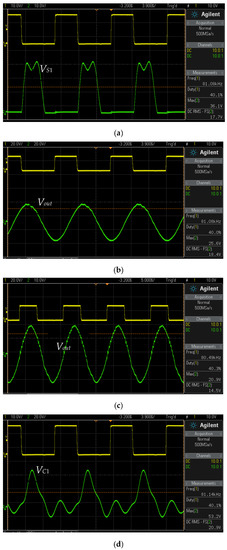
Figure 7. Experimental results for class E/F₃ topology with piezoelectric transformer as primary resonant tank. (a) The switch voltage, V_S1, (b) the output voltage with LC output filter, V_out, (c) the output voltage with output filter capacitance, V_out, and (d) the auxiliary resonant capacitor voltage, V_C1.

The high frequency harmonics in the V_out can be decreased using an LC low pass filter or an output capacitor, as shown in Figure 7b,c. Additionally, it is clear that the simulation and experimental results closely support the theoretical design. Table 5 compiles the findings to show how comparable they are.

Table 5. The simulation and experimental prototype results.

Parameter	Simulation	Experimental
PT as primary resonant tank
Vout	18 V	20.9 V
VS1,peak	34 V	36.1 V
VC1,peak	48 V	53.2 V
PT as auxiliary resonant tank
Vout	2.6 V	3.2 V
VS1,peak	70 V	45.9 V

B.

The PT as Auxiliary Resonant Tank

In Figure 8, the LTSPICE simulation circuit is shown for the PT that replaces the conventional auxiliary resonant network. In this configuration, the PT emulator (i.e., the mason equivalent) is used for simulation purposes.

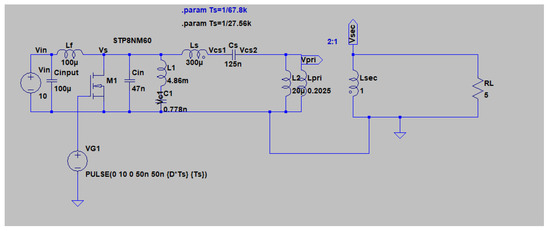
Figure 8. Simulation circuit: the class E/F3 topology with PT as auxiliary resonant tank.

The simulation results are shown in Figure 9. The ZVS is attained, as seen by the switch voltage waveform in Figure 9b. However, the reverse diode’s conduction also suggests that the converter is not performing at its best.

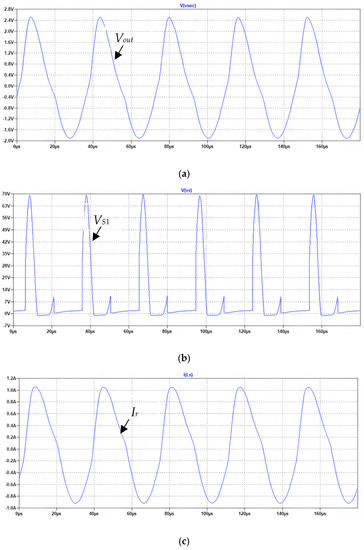
Figure 9. Simulation results for class E/F₃ topology with PT as auxiliary resonant tank. (a) The output voltage, V_out, (b) the switch voltage, V_S1, and (c) The primary resonant current, I_r.

The experimental findings for the PT working as an auxiliary resonant tank are shown in Figure 10. It is clear from Figure 10a that a higher harmonic content dominates the output voltage (V_out). To get rid of the higher frequency harmonics, a 100 kHz output low pass filter can be used. Additionally, the ZVS is attained in the sub-optimal region, as seen in Figure 9b and Figure 10b. It should be noticed that the peak switch voltage (V_S1,peak) is still high, despite employing the auxiliary network (i.e., the PT). By increasing the capacitance ratio k, this high switch peak voltage can be reduced. However, the latter necessitates the use of a different PT, which is not executed in this work because of the non-availability of the required PT. Nevertheless, the idea of utilizing a PT for the energy extraction in a class E/F3 inverter is confirmed. In Figure 11, the power versus the efficiency (η) curve is shown. The efficiency is measured under the specified conditions, as described in Table 1. As observed, the converter operates at approximately 90%, while the output power (P_out) is 5 W or lower. Overall, the simulation and experimental results are shown in Table 5. It can be observed that the results are quite consistent with one another and conform to the theoretical design. The slight differences in the results are due to the deviations of the parametric values of the PT equivalent circuit at a high frequency.

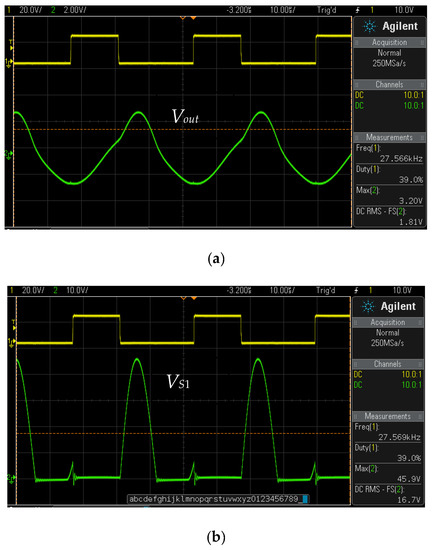
Figure 10. Experimental results for class E/F₃ topology with PT as primary resonant tank. (a) The output voltage, V_out, and (b) the switch voltage, V_S1.

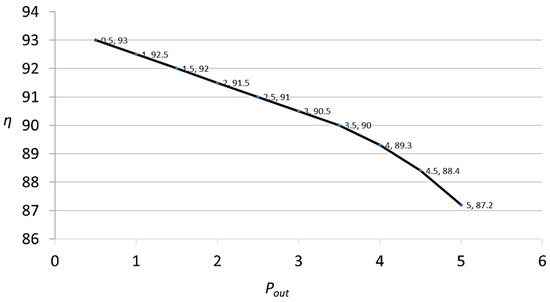
Figure 11. The output power (P_out) versus measured efficiency (η).

5. Conclusions

In this paper, the primary or auxiliary resonant tank is replaced with a PT in a class E/F₃ inverter. According to the circuit analysis, this inverter can be used in ZVS mode while the PT replaces the traditional resonant tanks. The inverter is simulated in LTspice and an experimental prototype of the inverter is tested. The simulation and experimental results are consistent with one another, indicating the validity of the theoretical design. Additionally, by raising the value of k, the inverter’s peak switch voltage in the class E/F₃ can be further reduced, which remains a future scope for this work. A compact and low-power inverter can be realized by replacing its traditional magnetic components with a PT. This concept is also applicable for other enhanced class E inverters. However, there are opportunities for further investigation into this topic.