Parameter Extraction of Solar Module Using the Sooty Tern Optimization Algorithm

Abstract

Photovoltaic module parameter estimation is a critical step in observing, analyzing, and optimizing the efficiency of solar power systems. To find the best value for unknown parameters, an efficient optimization strategy is required. This paper presents the implementation of the sooty tern optimization (STO) algorithm for parameter assessment of a solar cell/module. The simulation findings were compared to four pre-existing optimization algorithms: sine cosine (SCA) algorithm, gravitational search algorithm (GSA), hybrid particle swarm optimization and gravitational search algorithm (PSOGSA), and whale optimization (WOA). The convergence rate and root mean square error evaluations show that the STO method surpasses the other studied optimization techniques. Additionally, the statistical results show that the STO method is superior in average resilience and accuracy. The superior performance and reliability of the STO method are further validated by the Friedman ranking test.

1. Introduction

Recently, clean energy usage has increased significantly as demand for all other fuels declined because of environmental concerns. As a result,, the scientific community made substantial efforts to harvest energy from different ambient sources [1,2,3,4,5]. Solar energy harvesting has become the most ideal option since it surpasses all traditional nonrenewable and renewable resources [6]. As a result, the worldwide solar electricity sector is expanding significantly, with a current value of more than $10 billion each year [6,7,8].

Solar energy is converted into electrical energy by employing photovoltaic (PV) panels [9]. Numerous PV panels are linked together in serial and/or parallel arrangements to create bulky solar energy plants equipped with maximum power point tracking (MPPT) systems to increase power generation. The primary goal of MPPT systems is to regulate the parameters of the PV system to generate optimum power [9]. The rapid deviation of electrical energy production is a well-known property of solar plants [9]. Many solar facilities are linked to local grids, and their operation at the same time as the grids causes voltage instability in distribution lines [10]. Hence, stable and maximized power generation from solar plants is an essential requirement of the green energy movement. To obtain maximum power density, both theoretical and experimental studies were performed to optimize the parameters of PV panels [4,11,12,13]. Single, double, and triple diode models of PV cells are widely employed to identify the current-voltage parameters [14,15,16]. These parameters are helpful for determining the accuracy and steadiness of the models. However, parameter assessment is not an easy task because of unbalanced operational cases such as faults and ageing. In most cases, the single diode model is employed because of ease and acceptance. On the other hand, the double diode model is anticipated to be more than the three-diode model accurate in case of lower solar irradiance.

Different types of algorithms were proposed and studied to get more accurate and precise parameters from nonlinear implicit equations with high accuracy [17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33]. The merits and demerits of these algorithms are categorized because of the trade-off between exploration and exploitation capabilities [17]. Some became caught in local optima solutions because of a lack of exploration capabilities for finding an optimal solution in the search space. Heuristic and deterministic are the two main groups of algorithms. Heuristic algorithms contain particle swarm optimization (PSO) [18], cuckoo search algorithm [19], harmony search [20], cat swarm optimization (CSO) [21], differential evolution (DE) [22], artificial bee colony [23], chaos CPSO [24], simulated annealing [25], biogeography-based optimization algorithm with mutation strategies [26], genetic algorithms [27], improved adaptive differential evolution [28], pattern search [29], generalized opposition-based teaching-learning-based optimization [30], and Nelder–Mead modified PSO [31]. The Lambert W-functions [32], least squares [33], iterative curve-fitting methods [34], conductivity method [35], Levenberg–Marquardt algorithm [36], Newton–Raphson, and nonlinear least square are categorized as deterministic algorithms. The applicability of deterministic algorithms is restricted because of continuity, differentiability, and convexity related to objective functions. These algorithms are likewise sensitive to the starting solution and settle at local optima in most cases. Because they do not include difficult mathematics, biorelated algorithms are more realistic and robust optimization methods for simplifying complex transcendental equations.

The sooty tern optimization (STO) algorithm mimics the attack and migration behavior of sooty terns (birds of tropical oceans). This algorithm provides a good balance between exploration and exploitation strategy and thus reaches optimal solution without getting trapped in a local solution. These benefits allow researchers to apply the STO for parameter extraction of a solar module. The key purposes of this research investigation are as follows:

• To first present the experimental results that verify the performance of the STO in handling the parameter extraction problem of the solar module.
• To use two test cases—R.T.C France solar cell and SS2018P polycrystalline PV module—to evaluate the effectiveness of the STO and compare it with other metaheuristic algorithms.
• To use the experimental results to comprehensively confirm that STO is competitive compared to other existing methods in literature.

This study utilizes the STO algorithm for the parameter assessment of PV cells/modules. Initially, the mathematical model for PV cell/module and problem formulation is discussed. At the second stage, the STO algorithm is briefly introduced and used to assess the optimal magnitude of undetermined parameters. Next, the output results are examined with a measured dataset, and the algorithm is compared to pre-existing metaheuristic algorithms. Section 5 contains the discussion and conclusion of manuscript.

2. Problem Formulation and Methodology

2.1. Mathematical Modeling of Solar Panels

Figure 1 depicts the PV panel’s comparable circuit model. At the output terminal, the correlation between voltage ($V_l$) and current ($I_l$) is expressed as:

$$I_l=I_p-I_{sd}\left[exp\left(\frac{q\left(V_l/N_s+R_s{I}_l/N_p\right)}{a_{ }{k}_{B}T}\right)-1\right]-\frac{V_l/N_s+R_s{I}_l/N_p}{R_{sh}}$$

(1)

where $N_p$ and $N_s$ denote the count of solar cells interconnected in parallel and series combinations. The $k_B$ is the Boltzmann constant (1.3806 × 10⁻²³ m²kgK⁻¹s⁻²), $T$ is the cell/module temperature, $q$ is elementary charge, $I_p$ is photovoltaic current, $I_{sd}$ is diode saturation current, $R_s$ series resistance, $R_{sh}$ shunt resistance, and $a$ is the module quality factor. Only five parameters ($I_p$, $I_{sd}$, $a$, $R_s$, $R_{sh}$) are required to calculate the minimum value of root mean square error (RMSE).

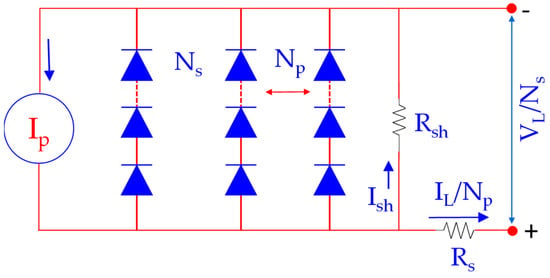
Figure 1. PV panel module equivalent circuit.

2.2. Objective Function

The main objective of the presented study is to lessen the variance among experimental and estimated data by optimizing unknown parameters for the single-diode model. Unknown parameters ($I_p$, $I_{sd}$, $a$, $R_s$, $R_{sh}$) are employed as decision variables during the optimization process. The accumulative squared variation between calculated and observed data is applied as an objective function. The error objective function is denoted as follows [37,38]:

$$\mathrm{RMSE}=\sqrt{\frac{1}{k}{\displaystyle \sum }_{N=1}^{k}f{\left(V_l,I_l,X\right)}^2}$$

(2)

where $V_l$ and $I_l$ denote the observed value of voltage and current of the PV module. The range of experimental datasets is specified by the parameter ‘$k$’ and the algorithm’s best answer is indicated by a vector $X$. In the case of the PV panel module:

$$\left(\begin{array}{c}{f}_{single}\left(V_l, I_l, X\right)=I_p-I_{sd}\left[exp\left(\frac{q\left(\frac{V_l}{N_s}+\frac{R_s{I}_l}{N_p}\right)}{a_1{k}_{B}T}\right)-1\right]-\frac{\frac{V_l}{N_s}+\frac{R_s{I}_l}{N_p}}{R_{sh}}-\frac{I_l}{N_p} \\ \left(X=I_p, I_{sd}, a, R_s, R_{sh} \right) \end{array}\right)$$

(3)

3. Sooty Tern Optimization

The sooty tern optimization (STO) algorithm was proposed in 2019 [39,40]. The algorithm is inspired by the attacking behavior of sooty tern birds. Generally, sooty terns live in groups. They employ their intelligence to locate and attack a target. The most notable characteristics of sooty terns are their migrating and assaulting behaviors. The following provide insights into sooty tern birds:

• Sooty terns travel in groups during migration. To avoid collisions, the initial positions of sooty terns are different.
• In a group, sooty terns with low fitness levels can nevertheless travel the same distance that the fittest among them can.
• Sooty terns with low fitness can upgrade their preliminary locations on the basis of the fittest sooty tern.

3.1. Migration Behavior

A sooty tern must meet three requirements during a migration:

Collision avoidance: SA is used to compute a new search agent location to avoid collisions with its neighborhood search agents (i.e., sooty terns).

$${\overrightarrow{C}}_{st}=s_A·{\overrightarrow{P}}_{st}\left(z\right)$$

(4)

where ${\overrightarrow{C}}_{st}$ denotes the position of a sooty tern that does not collide with other terns. ${\overrightarrow{P}}_{st}$ represents the current location of the sooty tern. $z$ signifies the current iteration, and $s_A$ denotes the migration of a sooty tern in the solution space.

Converge in the direction of best neighbor: Following collision evasion, the search agents converge in the path of the finest neighbor.

$${\overrightarrow{M}}_{st}=C_B·{\overrightarrow{P}}_{st}\left(z\right)\left({\overrightarrow{P}}_{bst}\left(z\right)-{\overrightarrow{P}}_{st}\left(z\right)\right)$$

(5)

where ${\overrightarrow{M}}_{st}$ denotes a different position of a search agent (i.e., sooty tern). ${\overrightarrow{P}}_{bst}\left(z\right)$ shows the best location of a search agent, and $C_B$ signifies the random variable and can be computed as follows:

$$C_B=0.5 R_{and}$$

(6)

where $R_{and}$ represents any arbitrary number in the range of 0 and 1.

Updating corresponding to best search agent: Finally, the sooty tern can revise its location in relation to the best search agent.

$${\overrightarrow{D}}_{st}={\overrightarrow{C}}_{st}+{\overrightarrow{M}}_{st}$$

(7)

where ${\overrightarrow{D}}_{st}$ signifies the difference between the search agent and the best fittest search agent.

3.2. Attacking Behavior

Sooty terns can modify their speed and attack angle during migration. They gain altitude by flapping their wings. They produce spherical behavior in the air while attacking prey, which is explained below.

$$x\prime = R_{adius}\sin \left(i\right)$$

(8)

$$y\prime = R_{adius}\cos \left(i\right)$$

(9)

$$z\prime = R_{adius}i$$

(10)

$$r=u{e}^{kv}$$

(11)

where, $R_{adius}$ denotes the radius of each spiral turn, $i$ signifies the value in the range of [0 ≤ $k$ ≤ 2π], and the $u$ and $v$ are the constant values.

3.3. Execution Steps of STO for Parameter Estimation

Figure 2 illustrates the flowchart of the STO algorithm for optimized parameter estimation of a solar cell/module. The algorithm works as follows:

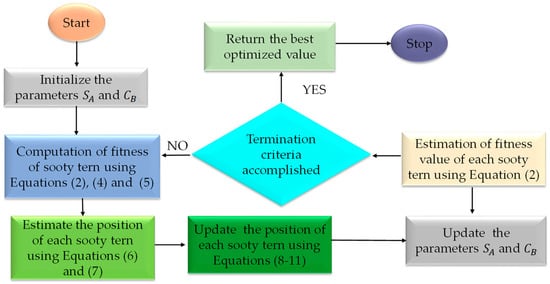
Figure 2. Process flowchart of STO algorithm for parameter estimation of PV cell/module.

• Step 1. In the search space, begin the population of search agents of the fifth order dimension. The photovoltaic current ($I_p$), diode saturation current ($I_{sd}$), series resistance ($R_s$), shunt resistance ($R_{sh}$), and diode ideality factor are all represented by the fifth order dimension ($a$).
• Step 2. In the search space, control the fitness of all agents using Equation (2).
• Step 3. At each iteration, the STO is employed to adjust the position of the agents. Because the algorithm is intended to function in the minimization mode, the location of the particles with the least cost suggests the best SDM parameters with the minimum RMSE.

4. Results and Discussion

In this section, we examine the validity of the STO algorithm and describe how we tested it under standard temperature conditions (1000 W/m² at 25 °C) utilizing primarily one R.T.C France solar cell and polycrystalline PV module (SS2018P). The extracted PV module characteristics were tracked and employed to generate simulated I-V and P-V data sets. The dependability of the STO algorithm was examined and compared to four metaheuristic algorithms: GSA [41], SCA [42], GWO [43], and WOA [44]. The size of the sample and the objective function evaluations for the experiment were fixed to 30 and 50,000, respectively. In addition, at least 30 independent runs were performed to avoid duplication.

The effectiveness of the proposed method was evaluated using several empirical constraints, e.g., internal absolute error (IAE), correctness of the curve-fitting, and global minimum convergence rates. The current and voltage data for the R.T.C France solar cell [45] and the SS2018P polycrystalline PV module [38] were collected experimentally. In the SS2018P PV module, 36 polycrystalline cells were connected serially [38]. Table 1 tabulates the exploration ranges for every parameter (i.e., upper and lower bounds). These ranges were utilized by investigators in this study. The STO algorithm [46] was simulated on a MATLAB 2018a (MathWorks, Mexico, DF, Mexico) platform with an Intel ^® core TM i5-HQ CPU running at turbo frequency of 4.8 GHz and 8 GB of RAM.

Table 1. The parameter range for SDM of a solar cell and a PV module.

Parameters	R.T.C France Solar Cell		SS2018P PV Module
	Lower Bound	Upper Bound	Lower Bound	Upper Bound
$I_p$(A)	0	1	0	10
$R_s$(Ω)	0.01	0.5	0.01	2
$R_{sh}$(Ω)	0.001	100	0.001	2000
$I_{sd}$(µA)	0	0.5	0	50
$a$	1	2	1	100

4.1. Parameter Extraction of the R.T.C France Solar Cell

For a single-diode model, five parameters ($I_p$, $I_{sd}$, $a$, $R_s$, $R_{sh}$) must be estimated. The values of simulated current and power with their IAE are charted in Table 2. Table 3 shows the values of the STO-optimized parameters and RMSE for comparison. The STO algorithm has the lowest RMSE of 8.6106 × 10⁻⁴ when compared to other algorithms. In this case, RMSE values are obtained as an index for evaluating results with previously constructed techniques by the researchers. Figure 3 depicts a redrawn current-voltage (I-V) and power-voltage (P-V) characteristics curve for a single-diode model based on the optimum optimized parameters achieved by executing the STO method. The computed data generated by the STO was found to be very close to the experimental data set across the whole voltage range.

Table 2. The calculated current and absolute error results of the STO for SDM of the R.T.C France solar cell.

Observations	${\mathit{V}}_{\mathit{l}}\left(\mathbf{V}\right)$	Il (A)	Isimulated (A)	IAE (A)	Pmeasured (W)	Psimulated (W)	IAE (W)
1	0.0057	0.7605	0.7817	0.0212	0.0043	0.0044	0.0001
2	0.0646	0.7600	0.7764	0.0164	0.0490	0.0501	0.0010
3	0.1185	0.7590	0.7714	0.0124	0.0899	0.0914	0.0014
4	0.1678	0.7570	0.7669	0.0099	0.1270	0.1287	0.0016
5	0.2132	0.7570	0.7627	0.0057	0.1613	0.1626	0.0012
6	0.2545	0.7555	0.7588	0.0033	0.1922	0.1931	0.0008
7	0.2924	0.7540	0.754	0.0007	0.2204	0.2206	0.0002
8	0.3269	0.7505	0.7501	0.0003	0.2453	0.245	0.0001
9	0.3585	0.7465	0.7441	0.0023	0.2676	0.2667	0.0008
10	0.3873	0.7385	0.7351	0.0033	0.2860	0.2847	0.0012
11	0.4137	0.7280	0.7208	0.0071	0.3011	0.2982	0.0029
12	0.4373	0.7065	0.6987	0.0077	0.3089	0.3055	0.0034
13	0.459	0.6755	0.6648	0.0106	0.3100	0.3051	0.0049
14	0.4784	0.6320	0.6173	0.0146	0.3023	0.2953	0.0070
15	0.496	0.5730	0.5544	0.0185	0.2842	0.2750	0.0091
16	0.5119	0.4990	0.4772	0.0217	0.2554	0.2443	0.0111
17	0.5265	0.4130	0.3857	0.0272	0.2174	0.2030	0.0143
18	0.5398	0.3165	0.2945	0.0219	0.1708	0.1590	0.0118
19	0.5521	0.2120	0.1728	0.0391	0.1170	0.0954	0.0215
20	0.5633	0.1035	0.0582	0.0452	0.0583	0.0328	0.0254
Sum of IAE				0.2891

Table 3. Comparison between the STO and other algorithms for parameter estimation techniques for R.T.C France solar cell.

Algorithms	${\mathit{I}}_{\mathit{p}}\left(\mathbf{A}\right)$	${\mathit{R}}_{\mathit{s}}\left(\mathsf{\Omega }\right)$	${\mathit{R}}_{\mathit{s}\mathit{h}}\left(\mathsf{\Omega }\right)$	${\mathit{I}}_{\mathit{s}\mathit{d}}\left(\mathsf{\mu }\mathbf{A}\right)$	$\mathit{a}$	RMSE
STO	0.7850	0.0394	10.9985	0.1770	1.4474	8.6106 × 10−4
GSA [41]	0.7607	0.0339	63.7784	0.0500	1.5486	1.2012 × 10−3
SCA [42]	0.7595	0.0519	90.0685	0.002	1.2641	1.9123 × 10−3
GWO [43]	0.7695	0.0269	47.9136	1	1.6232	9.4095 × 10−4
WOA [44]	0.7573	0.053	58.5839	0.016	1.2476	9.9529 × 10−4

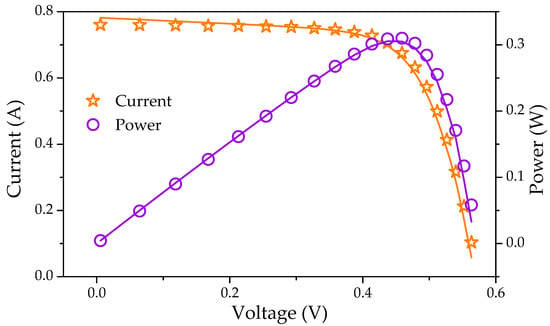
Figure 3. The simulated and experimental I-V and P-V characteristics curves for the single-diode model of the R.T.C France solar cell. Symbols indicate measured data, while solid lines indicate optimized data.

4.2. Parameter Extraction of the SS2018P PV Module

To properly assess the efficacy of the STO algorithm, parameters for the SS2018P PV module were computed at 1000 W/m² and 25 ℃, using the SDM model. The values of simulated current and power with their IAE are tabulated in Table 4. Table 5 shows the optimized value of all five parameters ($I_p$, $I_{sd}$, $a$, $R_s$, $R_{sh}$) for SDM of the PV module at standard temperature condition. Figure 4 depicts a redrawn I-V and P-V characteristics curve for a single-diode model based on the optimum optimized parameters achieved by executing the STO method. It was observed that the simulated data provided by the STO was extremely closely related to the experimental data set.

Table 4. The simulated current and absolute error results of the STO for SDM of the SS2018 PV module.

Observations	${\mathit{V}}_{\mathit{l}}\left(\mathbf{V}\right)$	${\mathit{I}}_{\mathit{l}}\left(\mathbf{A}\right)$	Isimulated (A)	IAE (A)	Pmeasured (W)	Psimulated (W)	IAE (W)
1	0.0844	1.1698	1.2096	0.0397	0.0988	0.1021	0.00336
2	0.2558	1.1697	1.2088	0.0390	0.2993	0.3093	0.0100
3	0.5550	1.1697	1.2075	0.0377	0.6492	0.6702	0.0210
4	1.0896	1.1697	1.2051	0.0353	1.2745	1.3131	0.0386
5	2.1529	1.1697	1.2003	0.0306	2.5183	2.5843	0.0659
6	2.8780	1.1697	1.1971	0.0273	3.3666	3.4454	0.0788
7	3.8696	1.1697	1.1926	0.0229	4.5265	4.6153	0.0888
8	4.5833	1.1697	1.1895	0.0197	5.3613	5.4518	0.0906
9	5.5482	1.1697	1.1851	0.0154	6.4901	6.5757	0.0856
10	6.2780	1.1697	1.1819	0.0121	7.3436	7.4201	0.0765
11	7.2243	1.1697	1.1776	0.0079	8.4505	8.5079	0.0574
12	8.0501	1.1697	1.1739	0.0042	9.4164	9.4506	0.0342
13	8.7878	1.1696	1.1706	0.0009	10.2789	10.2874	0.00852
14	9.7689	1.1696	1.1662	0.0034	11.4259	11.3926	0.0333
15	10.5181	1.1695	1.1627	0.0067	12.3009	12.2302	0.0707
16	11.3167	1.1692	1.1590	0.0102	13.2324	13.1166	0.11160
17	12.1901	1.1688	1.1548	0.0140	14.2485	14.0774	0.1710
18	12.9947	1.1680	1.1506	0.0174	15.1790	14.9522	0.227
19	13.9457	1.1663	1.1449	0.0213	16.2656	15.9678	0.2980
20	14.6556	1.1638	1.1398	0.0240	17.0574	16.7051	0.3520
21	15.5347	1.1583	1.1312	0.0270	17.9941	17.5742	0.4200
22	16.4330	1.1471	1.1177	0.0294	18.8509	18.3673	0.4840
23	17.1324	1.1312	1.1007	0.0305	19.3812	18.8578	0.5230
24	18.0801	1.0907	1.0600	0.0306	19.7206	19.1662	0.5540
25	18.8065	1.0325	1.0033	0.0291	19.4190	18.8700	0.5490
26	19.7423	0.8906	0.8658	0.0248	17.5832	17.0933	0.4900
27	20.5628	0.6493	0.6315	0.0178	13.3533	12.9868	0.3660
28	21.3013	0.2582	0.2516	0.0065	5.5007	5.3614	0.1390
Sum of IAE				0.5840

Table 5. Comparison of the STO with other parameter estimation methods for the SS2018 PV module.

Algorithms	${\mathit{I}}_{\mathit{p}}\left(\mathbf{A}\right)$	${\mathit{R}}_{\mathit{s}}\left(\mathsf{\Omega }\right)$	${\mathit{R}}_{\mathit{s}\mathit{h}}\left(\mathsf{\Omega }\right)$	${\mathit{I}}_{\mathit{s}\mathit{d}}\left(\mathsf{\mu }\mathbf{A}\right)$	$\mathit{a}$	RMSE
STO	1.1276	2	2000	0.5000	89.85	6.19 × 10−5
GSA [41]	1.0959	0.001	455.528	0.0010	53.59	1.68 × 10−1
SCA [42]	1.1742	0.0011	139.676	0.0092	1.415	1.51 × 10−3
GWO [43]	1	0.001	100	0.0010	1.263	1.59 × 10−1
WOA [44]	1.1810	0.0024	18.166	0.0190	1.289	7.82 × 10−4

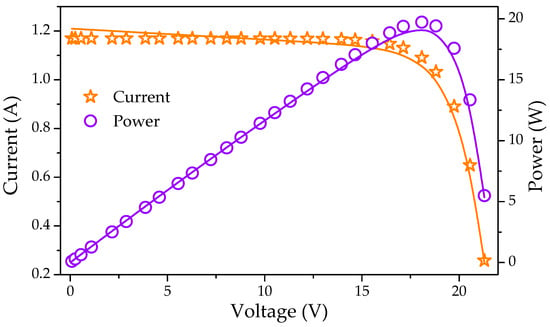
Figure 4. I-V and P-V characteristics curves for anticipated and experimental values for the SS2018 PV module. Symbols indicate measured data, while solid lines indicate optimized data.

4.3. Convergence Analysis

Figure 5 and Figure 6 depict the convergence curves of the R.T.C France solar cell and the SSS2018 polycrystalline PV cell for examining the computational competency of the STO. The convergence rate analysis shows that the STO algorithm is more accurate than the GSA, SCA, GWO, and WOA algorithms. Thus, the STO algorithm produces a realistic answer for the same amount of evaluation functions (i.e., 50,000).

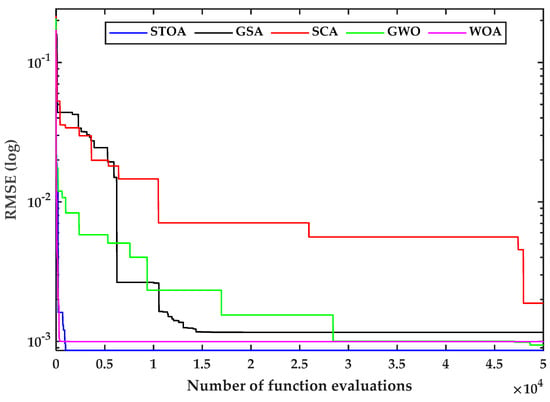
Figure 5. Convergence plot for the RTC France solar cell.

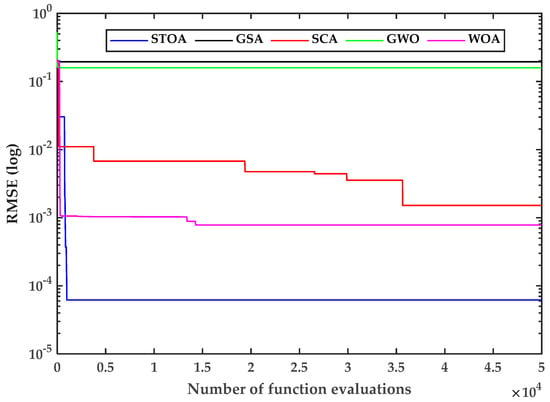
Figure 6. Convergence plot for the SS2018 PV module.

4.4. Statistical and Robustness Analysis

This subsection offers statistical assessments of the mean, minimum, maximum, and standard deviation (SD) of RMSE for all recently created strategies. The accuracy and reliability comparison of the various algorithms in 30 runs is summarized in Table 6. The RMSE mean and standard deviation were calculated to investigate the durability of the parameter estimation algorithms. According to the statistical data presented in Table 6, the STO is found to be the most precise and trustworthy parameter optimization technique.

Table 6. Statistical RMSE results for various techniques for the R.T.C France solar cell and the SS2018 PV module.

	Algorithm	RMSE
		Minimum	Mean	Maximum	SD
R.T.C France Solar Cell	STO	8.6106 × 10−4	9.4761 × 10−4	2.6964 × 10−2	1.0836 × 10−5
	GSA [41]	1.2012 × 10−3	5.4701 × 10−3	2.4211 × 10−1	1.3129 × 10−3
	SCA [42]	1.9123 × 10−3	9.6515 × 10−3	2.1642 × 10−1	9.4066 × 10−3
	GWO [43]	9.4095 × 10−4	1.0441 × 10−3	1.3506 × 10−3	1.4050 × 10−5
	WOA [44]	9.9529 × 10−4	9.2032 × 10−4	7.1240 × 10−3	9.0250 × 10−3
SS2018 PV Module	STO	6.1900 × 10−5	5.2500 × 10−4	3.0407 × 10−2	2.3643 × 10−5
	GSA [41]	1.6800 × 10−1	1.9462 × 10−1	2.0011 × 10−1	4.4500 × 10−3
	SCA [42]	1.5100 × 10−3	5.2657 × 10−3	2.0345 × 10−1	1.0058 × 10−2
	GWO [43]	1.5900 × 10−1	1.5940 × 10−1	5.2494 × 10−1	1.6793 × 10−2
	WOA [44]	7.8200 × 10−4	1.8268 × 10−3	2.1078 × 10−2	1.3639 × 10−3

In addition to the conventional statistical analysis, we also applied the Friedman rank test [47] to determine the relevance of the presented study. It is a nonparametric test which is employed to decide the rank of algorithms for the analysis of PV modules; lower the rank, better the algorithm. Table 7 illustrates the Friedman ranking test results of different algorithms. The Friedman ranking test results show that the STO has the highest ranking compared to WOA, SCA, GWO and GSA. In the Friedman test, the null hypothesis $H_0$ (p-value > 5%) suggests that there are no noteworthy alterations among the compared algorithms. For all 30 runs, the contrary hypothesis $H_1$ indicates a significant difference between the compared methods. Each algorithm is ranked in this test depending on its efficiency.

Table 7. Friedman ranking of different algorithms for all modules.

Algorithm	Friedman Ranking	Final Ranking
STO	1	1
GSA [41]	5.12	5
SCA [42]	3.01	3
GWO [43]	4.29	4
WOA [44]	2.03	2

5. Conclusions

In this study, the STO algorithm was employed to assess the parameters of the R.T.C France solar panel and the SS2018 polycrystalline PV module at typical temperature conditions. The single-diode model theory was considered for parameter estimation. We also want to point out that the STO method was being used for the parameter estimation of PV models for the first time. The main observations of this study are as follows:

• The RMSE values confirm that the STO is generally more accurate and trustworthy to generate the best optimized parameters than GSA, SCA, GWO, and WOA.
• The IV and PV characteristic curves as well as IAE results show that the STO can successfully optimize the parameters for different types of PV cells.
• The statistical study illustrates the robustness of the implemented STO technique on the parameter estimation problem in standard operational conditions.
• The convergence curve confirms that the STO obtains the best values of estimated parameters in terms of RMSE of 8.6106 × 10⁻⁴ and 6.19 × 10⁻⁵ for solar cells and PV modules respectively.

According to the preceding discussion, the STO is an efficient and reliable technique for estimating the unknown optimum parameters of a solar PV module model under typical operating conditions.