An Investigation into the Comprehensive Impact of Self-Heating and Hot Carrier Injection

Abstract

As the device feature size shrinks, the dissipation of power increases and further raises the carrier and lattice temperature, which finally affects device performance. In this paper, we analyze the comprehensive influence of the self-heating effect and hot carrier injection (HCI) using TCAD simulations. Based on the hydrodynamic and thermodynamic models, it is demonstrated that the thermal surface resistance had a positive impact on the carrier and lattice temperature and that the drain saturation current is reduced dramatically due to the self-heating effect. Moreover, the impact of HCI on device performance is discussed. Finally, it is concluded that the self-heating effect exacerbates the influence of HCI on device characteristics.

1. Introduction

With the continuous shrinking of the device feature size, the self-heating effect becomes more important [1]. The self-heating effect is mainly due to the fact that the carriers are accelerated to obtain higher energy under a high electric field at the drain region, and part of the energy of the carriers is transferred to the lattice by phonon scattering, which finally results in a local lattice temperature higher than the ambient temperature [2]. Because of the scattering, the carrier mobility decreases, and thus the saturation current reduces [3], which affects the performance and reliability of the device [4]. Therefore, a recent popular issue is the investigation of the influence of the self-heating effect on device performance using different device structures and new materials [5,6,7,8,9,10,11,12,13,14,15].

The energy gained by the carriers exceeds the energy delivered to the lattice, which causes the carriers to become hot carriers and the channel region to become filled with hot carriers [12]. The hot carriers with energy higher than the barrier of the Si/SiO₂ interface are injected into the gate oxide, and thereby trapped charges are generated. Furthermore, the increasing lattice temperature raises the probability of energy bond breakage at the Si/SiO₂ interface and further increases the number of trapped charges. Through the analysis of trapped charges [16,17,18,19,20,21,22], the impact of hot carrier injection (HCI) on device performance is typically discussed. However, the self-heating effect is not considered in these studies.

In this paper, the impact of the self-heating effect for different devices are analyzed. Simultaneously, we also investigate the comprehensive influence of the self-heating effect and HCI on the performance of a 22 nm n-channel bulk FinFET (NFinFET). The self-heating characteristics, including carrier mobility, lattice temperature, heat generation and thermal surface resistance (SR), are discussed. Moreover, the characteristic variations under HCI are revealed. Based on the above analysis, we disclose the impact of the self-heating effect and HCI on the device output characteristics.

The remainder of our work is organized as follows. Section 2 introduces the device parameters and the simulation setup. Section 3 reports the simulation results and discussion, and Section 4 provides a conclusion.

2. Experimental Setup

Since the self-heating effect has become increasingly important in small-scale devices, in our experiment, the 65 nm planar NMOS was used as a reference device to investigate the impact of self-heating on device performance by 2D electrothermal simulation. In order to better illustrate the self-heating effect, we compared the performance of 65 nm with 22 nm planar NMOS and 22 nm three-dimensional NFinFET under self-heating. These devices are available in the Sentaurus TCAD application library [23]. Compared with the structures of the other two planar NMOSs, the channel region of the NFinFET is a fin-shaped semiconductor surrounded by a gate, which increases the control area of the gate to the channel and greatly enhances the gate control capability, thereby effectively suppressing the short-channel effect and reducing the subthreshold leakage current. The physical parameters of the NMOS and the NFinFET are listed in Table 1 and Table 2, respectively. To simulate the characteristics of the devices, we adopted the Lombardi piezoresistance and high-field saturation models to simulate carrier mobility. The hydrodynamic and thermodynamic transport models were also coupled with the carrier transport model. Specially, the hydrodynamic model estimated the carrier temperature, and the lattice temperature was calculated by the thermodynamic model. To solve the lattice temperature, the ambient temperature was set to 300 K for the thermal boundary condition, and the thermal conductivity parameters used for the thermodynamic simulation are listed in Table 3. In addition, in order to simulate the self-heating effect, the temperature model was also coupled to the solver. With respect to HCI, the trap degradation model and lucky electron injection model were adopted to calculate the performance when the initial trapped charge concentration in the Si/SiO₂ interface was assumed to be 1 × 10⁸ cm⁻³. The trap degradation model describes the process of depassivation of the dangling silicon bonds at the Si-SiO₂ interface based on the reaction–diffusion with hydrogen atom transport in the gate oxide [23]. The lucky electron injection model was used to calculate the lucky electron current from an interface to a gate contact [23] (Figure 1).

Table 1. The physical parameters of NMOS used for TCAD simulations.

Parameter	Symbol	Value
Channel length (nm)	L	65, 22
Gate oxide thickness (nm)	Tox	0.6
High-k oxide thickness (nm)	THf	20
Souce/Drain junction depth (nm)	Xj	40
Souce/Drain extension junction depth (nm)	Xjs	8
Halo pocket depth (nm)	XjHalo	50
Halo pocket concentration (cm−3)	NHalo	4 × 1018
Souce/Drain concentration (cm−3)	NS/D	1.5 × 1020
Souce/Drain extension concentration (cm−3)	NExtension	1 × 1019
Substrate concentration (cm−3)	Nsub	5 × 1015
Surface Resistance (cm2 KW−1)	SR	1 × 10−5–1 × 10−4
Drain to source voltage (V)	Vds	0–1
Gate to source voltage (V)	Vgs	0–1

Table 2. The physical parameters of NFinFET used for TCAD simulations.

Parameter	Symbol	Value
Channel length (nm)	L	22
Gate oxide thickness (nm)	Tox	1
High-k oxide thickness (nm)	THf	2
Fin Height (nm)	HFin	40
Fin Width (nm)	WFin	17
Souce/Drain concentration (cm−3)	NS/D	5 × 1015
Substrate concentration (cm−3)	Nsub	1 × 1015
Surface Resistance (cm2 KW−1)	SR	1 × 10−5–1 × 10−4
Drain to source voltage (V)	Vds	0–1
Gate to source voltage (V)	Vgs	0–1

Table 3. The thermal parameters used for self-heating simulations.

Material	Thermal Conductivity (WK−1 cm−1)
SiO2	0.014
Si (bulk)	1.48
Si (Fin)	0.13
Poly Si	1.5
HfO2	0.023
Si3N4	0.185
TiN	0.192

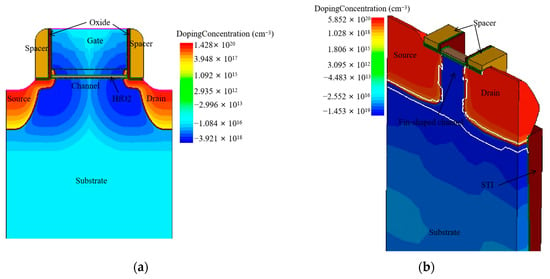
Figure 1. The device structures. (a) The structure of planar NMOS; (b) the cross-section view of NFinFET.

3. Simulation Results and Discussion

To investigate the impact of self-heating, the thermal performances of different devices were compared. We took the lattice temperature and heat profiles under SR = 5 × 10⁻⁵ cm² KW⁻¹ as an example to illustrate that self-heating becomes increasingly serious in small-scale devices, as shown in Figure 2. This is because the shrinking of voltage is not proportional to the device size [24], leading to an enhancement of the electric field in the channel, which further results in an increase in the thermal energy, as shown in Figure 3. In particular, the heat generation of the NFinFET was higher than the 65 nm and 22 nm NMOS. This is because the narrow fin-shaped channel region results in enhanced phonon-boundary scattering, which significantly affects thermal conductivity and increases thermal resistance. In addition, since the thermal conductivities of SiO₂ and HfO₂ surrounding the channel in the FinFET are 0.014 WK⁻¹ cm⁻¹ and 0.023 WK⁻¹ cm⁻¹, respectively, which is less than the thermal conductivity of the silicon substrate in the NMOSs, the heat accumulates. Therefore, we adopted the NFinFET for further investigation of the impact of the self-heating effect and HCI.

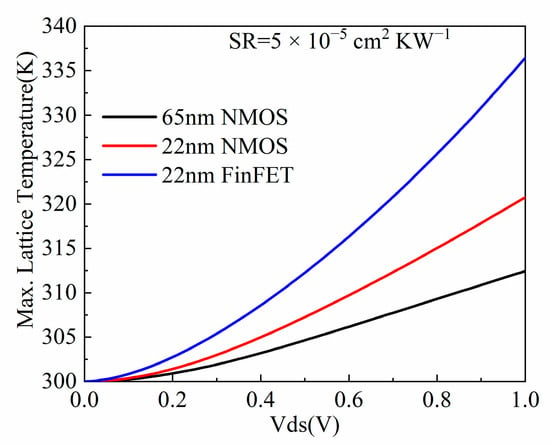
Figure 2. The lattice temperature profiles for different devices.

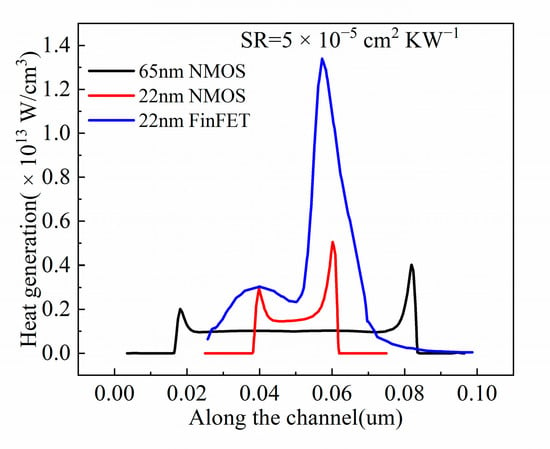
Figure 3. The heat profiles for different devices along the channel.

3.1. Performance Characteristics under the Self-Heating Effect

Figure 4 lists the variations of the maximum electron temperature and electron mobility against the drain voltage when SR = 5 × 10⁻⁵ cm² KW⁻¹. It can be inferred from Figure 4 that the electron temperature increases slowly when V_ds is less than 0.1 V. Conversely, it increases dramatically when V_ds is greater than 0.1 V.

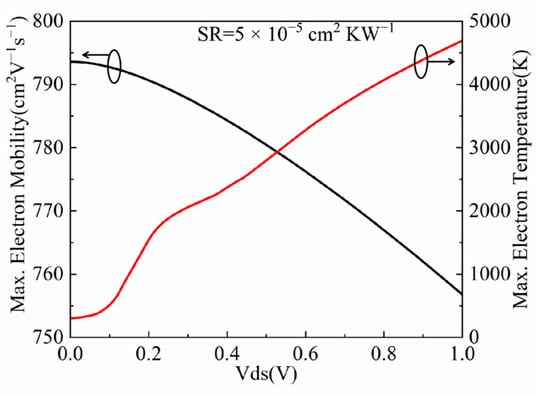
Figure 4. The maximum electron temperature and electron mobility of NFinFET against the drain voltage.

This happens because the electrons are in low field transport in the linear region where the kinetic energy is lower, which leads to a lower electron temperature. On the contrary, in the saturation region, the electrons are in high field transport and absorb higher kinetic energy, which leads to an increase in the electron temperature. In this case, there are collisions between electrons and phonons. Because of the short relaxation of the electron and phonon scattering, the phonons accumulate, resulting in the enhancement of scattering, which further leads to a decrease in electron mobility. Through the collisions, the electron energy is delivered to the lattice, leading to an increase in the lattice temperature, as shown in Figure 5. It should be noticed that the maximum lattice temperature is near the drain region. This is because electrons are scattered with a large number of phonons near the drain, thereby transferring the electron energy to the lattice. Thus, the heat generation near the drain is much larger than that in the channel and source, which indicates that the heat distribution is non-uniform.

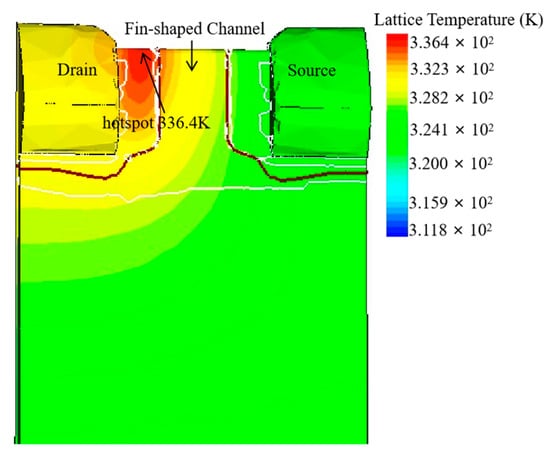
Figure 5. The temperature distribution of NFinFET with SR = 5 × 10⁻⁵ cm² KW⁻¹.

Figure 6 illustrates the effect of self-heating on the device output characteristics. Compared with the drain current of an NFinFET without the self-heating effect and that of an NFinFET under the self-heating effect, the drain current in the linear region is almost unchanged, while the drain saturation current is reduced under the self-heating effect. The essential reason is that the carrier mobility decreases due to phonons scattering.

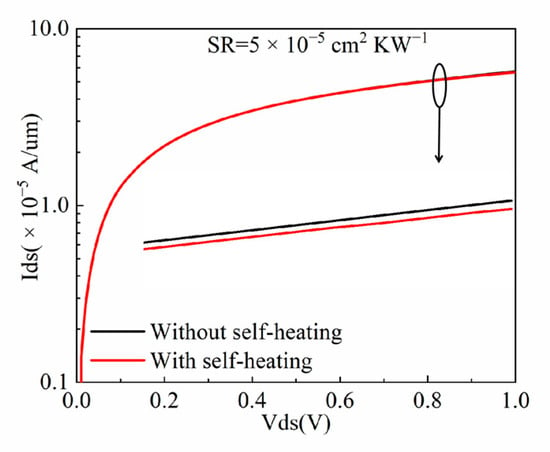
Figure 6. Comparison of the drain current for an NFinFET without the self-heating effect and an NFinFET under the self-heating effect.

In addition, SR plays an important role in thermal characteristics. It can be inferred from Figure 7 that under the same operating voltage, as SR increases from 1 × 10⁻⁵ cm² KW⁻¹ to 1 × 10⁻⁴ cm² KW⁻¹, the drain saturation current decreases. This is because the increasing SR leads to a reduction in electron mobility from 790.254 cm² V⁻¹s⁻¹ to 705.194 cm² V⁻¹s⁻¹. Moreover, the increasing SR raises the maximum lattice temperature from 314.37 K to 360.76 K, as illustrated in Figure 8. This is because the increasing SR offers a low-speed thermal conduction path for heat flow from the source and drain contacts [3]. The higher lattice temperature further increases the probability of the phonons scattering and decreases the carrier mobility, which finally reduces the saturation current.

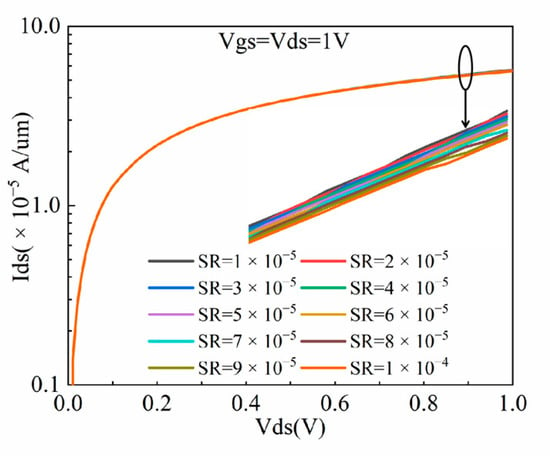
Figure 7. The saturation current variation of NFinFET under different surface resistances.

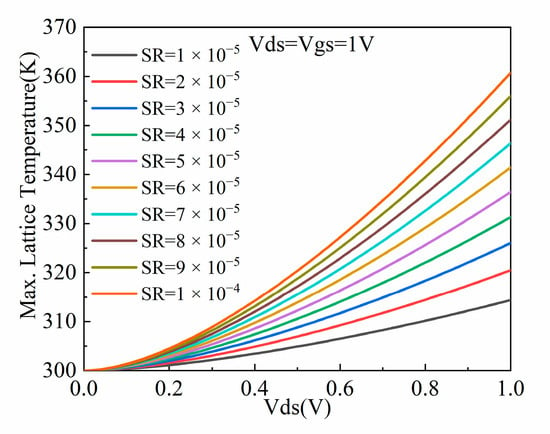
Figure 8. The maximum lattice temperature variation of NFinFET under different surface resistances.

3.2. Performance Characteristics under HCI

Figure 9 shows the variation of the threshold voltage against time under HCI. It can be concluded from Figure 9 that with an increase in operating time, the threshold voltage increases, which is consistent with the threshold voltage variation trend shown in [25]. This is because the carriers in the channel are continuously accelerated under the high electric field at the drain, the carriers acquire higher kinetic energy and thus become hot carriers. The hot carriers with high enough energy can cross the barrier of the Si/SiO₂ interface and be injected into the gate oxide layer, then break the covalent bond, which finally generates the trapped charges. Due to the fact that the trapped charges cancel out part of the gate voltage, the threshold voltage increases.

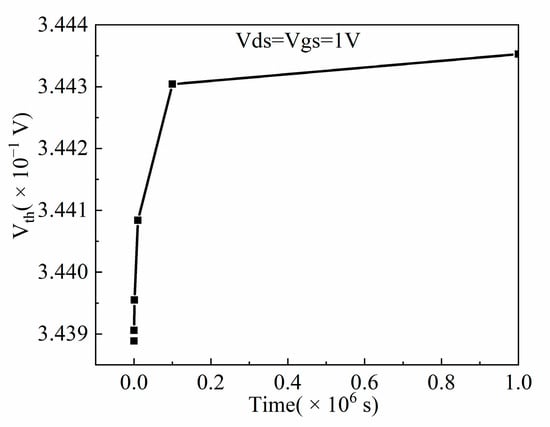
Figure 9. The threshold voltage variation of NFinFET under HCI for different times.

According to the drain saturation current formula [26]:

$$I_{dsat}=\frac{W{\mu }_n{C}_{ox}}{L}\left(V_{gs}-V_{th}\right){\nu }_{sat},$$

(1)

the saturation current and threshold voltage are negatively related. Therefore, with the increase in operating time, the saturation current gradually decreases, as illustrated in Figure 10.

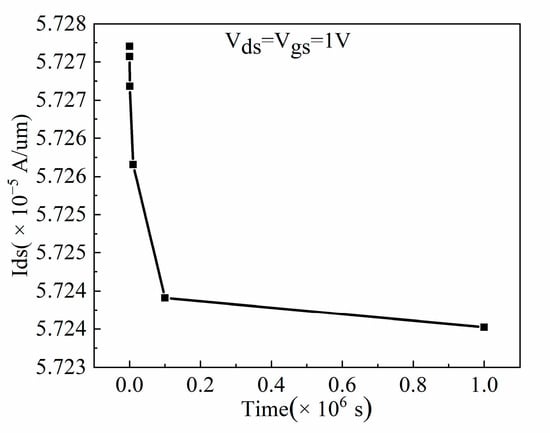
Figure 10. The saturation current variation of NFinFET under HCI for different times.

3.3. Performance Characteristics under the Self-Heating Effect and HCI

Figure 11 illustrates the saturation current variation under HCI and HCI with the self-heating effect when SR is 5 × 10⁻⁵ cm² KW⁻¹. The red curve denotes the variation of the saturation current under HCI against time, and the black curve represents the output characteristic variation under HCI with the self-heating effect. It can be seen from Figure 11 that the saturation current variation under HCI with the self-heating effect is greater than that under HCI as the operating time increases.

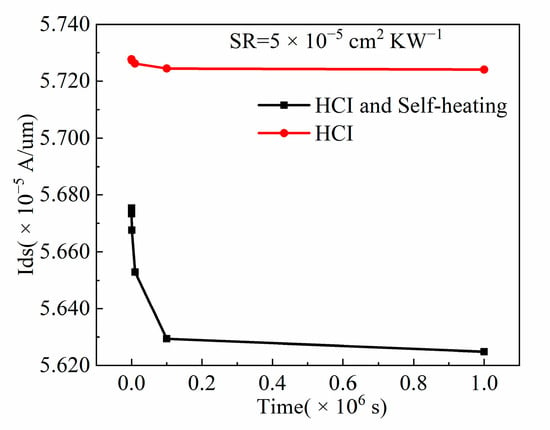
Figure 11. Comparison of results of the saturation current of NFinFET between HCI and HCI with self-heating effect at different time.

This is because as the operating time increases, the dissipation power increases, and so does the carrier temperature. Consequently, the carrier temperature exceeds the lattice temperature. Moreover, the hot carriers transfer energy to the lattice by phonon emission, which increases the lattice temperature. An increase in the lattice temperature promotes the probability of energy bond breakage at the Si/SiO₂ interface and the probability of trapped charges in the oxide layer. Because the trapped charges cancel out part of the gate voltage, the saturation current at the drain decreases. From the above analysis, we can conclude that the self-heating effect exacerbates the influence of HCI on the device saturation current.

Moreover, we also investigate the impact of HCI with the self-heating effect on the saturation current of the NFinFET under different SRs at different times. It should be noted that the saturation current decreases gradually with an increase in SR, as shown in Figure 12. We took electric field and electron mobility under different SRs at a time of 1000 s as an example to illustrate the reason for the decreasing saturation current. As SR increases, the effective electric field decreases from 1.01 × 10⁹ Vcm⁻¹ to 7.30869 × 10⁸ Vcm⁻¹, which results in a reduction in electron mobility from 790.254 cm² V⁻¹s⁻¹ to 705.826 cm² V⁻¹s⁻¹ [27]. Moreover, the increasing SR hinders the thermal conduction speed from the source to the drain contacts [3], and the thermal conductivity of SiO₂ and HfO₂ is relatively low, which makes the heat dissipation slow, resulting in an increase in the maximum lattice temperature from 314.367 K to 360.3 K. The high lattice temperature enhances the phonon scattering and increases the probability of the Si-H bond breakage in the gate oxide, resulting in an increase in interface trapped charges, as shown in Figure 13, which finally leads to a reduction in the saturation current. In addition, the dissipated heat of NFinFET is less than the electrical power, as shown in Table 4. The reason for this phenomenon is that the SR provides resistance to the heat generation of the NFinFET, and the heat of the NFinFET is generated by electrons colliding with phonons in the drain, ignoring the heat caused by the collision of the electrons and phonons in other regions, which is consistent with [28].

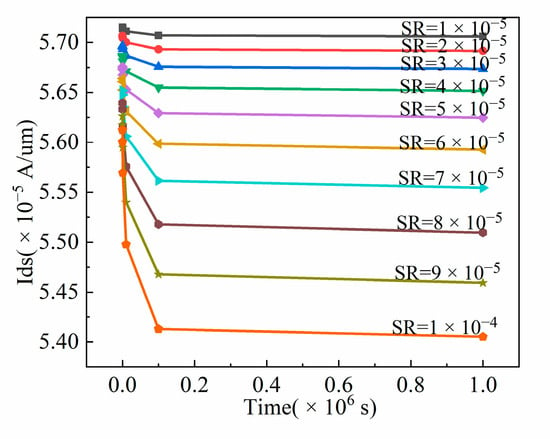
Figure 12. The saturation current variations of NFinFET against time at different SRs.

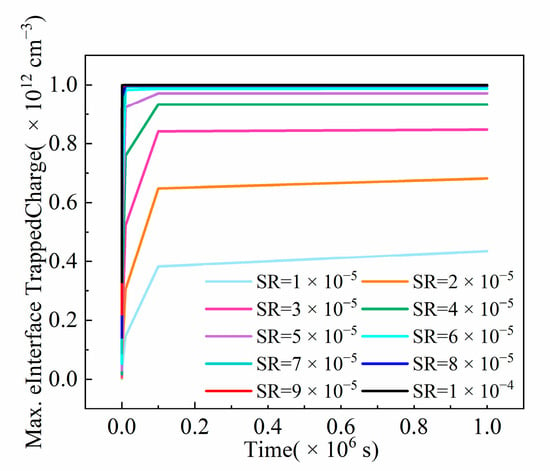
Figure 13. The maximum interface trapped charge variation of NFinFET against time at different SRs.

Table 4. Comparison of results between heat and electric power under different SRs at different times.

SR (cm2 KW−1)	Time (s)	Total Heat (W)	Electric Power (W)
1 × 10−5	10	5.46388 × 10−5	5.71516813464 × 10−5
	100	5.463616 × 10−5	5.71481694648 × 10−5
	1000	5.463014 × 10−5	5.71384276547 × 10−5
	10,000	5.46018 × 10−5	5.71127985774 × 10−5
	100,000	5.455764 × 10−5	5.70695061607 × 10−5
	1,000,000	5.454896 × 10−5	5.70600452826 × 10−5
2 × 10−5	10	5.466508 × 10−5	5.70651366756 × 10−5
	100	5.466068 × 10−5	5.70593219536 × 10−5
	1000	5.464068 × 10−5	5.70432883455 × 10−5
	10,000	5.461038 × 10−5	5.70012833352 × 10−5
	100,000	5.453421 × 10−5	5.69307354766 × 10−5
	1,000,000	5.452013 × 10−5	5.69155432188 × 10−5
3 × 10−5	10	5.466111 × 10−5	5.69675211279 × 10−5
	100	5.465413 × 10−5	5.6958350135 × 10−5
	1000	5.46283 × 10−5	5.69331548613 × 10−5
	10,000	5.45705 × 10−5	5.68673603157 × 10−5
	100,000	5.446274 × 10−5	5.67580419574 × 10−5
	1,000,000	5.443128 × 10−5	5.67351230947 × 10−5
4 × 10−5	10	5.463975 × 10−5	5.68634327628 × 10−5
	100	5.461902 × 10−5	5.6849418515 × 10−5
	1000	5.459479 × 10−5	5.68110640842 × 10−5
	10,000	5.450186 × 10−5	5.67114134919 × 10−5
	100,000	5.432998 × 10−5	5.6548435426 × 10−5
	1,000,000	5.429868 × 10−5	5.65152385571 × 10−5
5 × 10−5	10	5.459634 × 10−5	5.6753961365 × 10−5
	100	5.460443 × 10−5	5.67330566528 × 10−5
	1000	5.453399 × 10−5	5.6676030086 × 10−5
	10,000	5.439573 × 10−5	5.65291425804 × 10−5
	100,000	5.415387 × 10−5	5.62936626834 × 10−5
	1,000,000	5.410054 × 10−5	5.62481972882 × 10−5
6 × 10−5	10	5.455347 × 10−5	5.66394452119 × 10−5
	100	5.451982 × 10−5	5.66088826268 × 10−5
	1000	5.444668 × 10−5	5.65258175509 × 10−5
	10,000	5.424986 × 10−5	5.63144653359 × 10−5
	100,000	5.391934 × 10−5	5.59850969861 × 10−5
	1,000,000	5.385224 × 10−5	5.59258497826 × 10−5
7 × 10−5	10	5.449223 × 10−5	5.65197687632 × 10−5
	100	5.444807 × 10−5	5.64758360032 × 10−5
	1000	5.435171 × 10−5	5.63571430317 × 10−5
	10,000	5.40695 × 10−5	5.6059792514 × 10−5
	100,000	5.362063 × 10−5	5.56146013132 × 10−5
	1,000,000	5.353012 × 10−5	5.55423612409 × 10−5
8 × 10−5	10	5.4423 × 10−5	5.63945236534 × 10−5
	100	5.436438 × 10−5	5.63323025709 × 10−5
	1000	5.422656 × 10−5	5.61657278472 × 10−5
	10,000	5.383865 × 10−5	5.57567909814 × 10−5
	100,000	5.324494 × 10−5	5.51782929022 × 10−5
	1,000,000	5.315336 × 10−5	5.509621932 × 10−5
9 × 10−5	10	5.434621 × 10−5	5.62629974705 × 10−5
	100	5.425804 × 10−5	5.61761841972 × 10−5
	1000	5.406845 × 10−5	5.59465483844 × 10−5
	10,000	5.355166 × 10−5	5.53977980035 × 10−5
	100,000	5.281394 × 10−5	5.46793156284 × 10−5
	1,000,000	5.270793 × 10−5	5.45942119901 × 10−5
1 × 10−4	10	5.426152 × 10−5	5.61241803495 × 10−5
	100	5.414727 × 10−5	5.60047540938 × 10−5
	1000	5.388327 × 10−5	5.56935774279 × 10−5
	10,000	5.320421 × 10−5	5.49777477636 × 10−5
	100,000	5.231724 × 10−5	5.412926789 × 10−5
	1,000,000	5.222591 × 10−5	5.40506290857 × 10−5

4. Conclusions

Based on TCAD simulation results, we revealed that the self-heating effect is more pronounced in NFinFET by comparing the thermal characteristics of different devices. According to the thermal simulation of NFinFET, we demonstrated that the self-heating effect increases the local lattice temperature and decreases the carrier mobility, which led to a reduction in the saturation current. Finally, we revealed that the self-heating effect exacerbates the impact of HCI on the drain saturation current.