Abstract
Convolutional neural networks (CNNs) have demonstrated promising results in various applications such as computer vision, speech recognition, and natural language processing. One of the key computations in many CNN applications is matrix multiplication, which accounts for a significant portion of computation. Therefore, hardware accelerators to effectively speed up the computation of matrix multiplication have been proposed, and several studies have attempted to design hardware accelerators to perform better matrix multiplications in terms of both speed and power consumption. Typically, accelerators with either a two-dimensional (2D) systolic array structure or a single instruction multiple data (SIMD) architecture are effective only when the input matrix has shapes that are close to or similar to a square. However, several CNN applications require multiplications of non-squared matrices with various shapes and dimensions, and such irregular shapes lead to poor utilization efficiency of the processing elements (PEs). This study proposes a configurable engine for neural network acceleration, called CONNA, whose computation engine can conduct matrix multiplications with highly utilized computing units, regardless of the access patterns, shapes, and dimensions of the input matrices by changing the shape of matrix multiplication conducted in the physical array. To verify the functionality of the CONNA accelerator, we implemented CONNA as an SoC platform that integrates a RISC-V MCU with CONNA on Xilinx VC707 FPGA. SqueezeNet on CONNA achieved an inference performance of 100 frames per second (FPS) with 2.36 mm2 and 83.55 mW in a 65 nm process, improving efficiency by up to 34.1 times better than existing accelerators in terms of FPS, silicon area, and power consumption.
1. Introduction
Convolutional neural networks (CNNs) have emerged as a key technology in several applications, such as object detection [1,2,3], image/video classification [4,5,6,7], and translation [8,9], and they generally achieve superior accuracy when compared to humans. CNN typically consists of computationally intensive convolution layers, which impose challenges in achieving high-performance and real-time processing [10,11,12]. In particular, inference latency is critical when a CNN is employed in safety-critical applications, such as autonomous driving [13]. In general, graphic processing units (GPUs) are advantageous for accelerating large amounts of computation through parallel processing [14,15]. However, they are not capable of achieving low latency [16]. Further, the energy efficiency of GPUs is poor. Therefore, numerous studies have attempted to design CNN hardware accelerators with improved low latency and energy efficiency [16,17,18,19,20,21,22,23,24,25,26].
Many of these studies target matrix multiplication to accelerate convolution layers [17,18,19,20,21,22,23,24,25,26]. Convolution layers perform element-wise multiplication and additions between input feature maps and convolution kernels to generate output feature maps. Convolution layers are generally implemented by lowering three-dimensional tensors to matrix multiplication, which accounts for more than 70% of the total operations in many CNN applications [11]. Therefore, efficient handling of matrix multiplication is crucial for accelerating CNN.
Recently, state-of-the-art hardware accelerators have employed systolic array structure or SIMD architecture as the main computing fabric for accelerating matrix multiplication [17,18,19,20,21,22,24,25,26]. In general, systolic array architecture and SIMD structure are implemented by interconnecting computing units to form a two-dimensional (2D) array. Many CNN accelerators employ a systolic array architecture and SIMD structure in which multiply-accumulate (MAC) operators form a 2D array [17,18,25]. Because the 2D array commonly has a size of 2N × 2N, the utilization efficiency of the computing units is maximized when the input is a square matrix [23]. However, computing efficiency degrades considerably when the shapes of the input matrices are tall or fat [17,18,19,21,22,23,25,26]. It should be noted that many matrices in CNN applications have tall (or fat) shapes for various reasons, such as the type of convolution layers (e.g., group, depth-wise, and normal), type of layers, and weight factorization [23,27,28]. Therefore, it is important to design an accelerator that can efficiently perform matrix multiplications of various shapes.
In this study, we propose a configurable matrix multiplication engine and a neural network acceleration method using this engine. We name the proposed hardware accelerator CONNA, which stands for configuring the shape of matrix multiplication conducted in the physical array following the shape and dimension of the matrix, which is used in convolution layers in neural networks. In addition, we have introduced a set of application programming interfaces (APIs) for the proposed accelerator, allowing the accelerator to be controlled by a processor. We verified that it is possible to effectively accelerate matrix multiplication of tall (or fat) shape matrices in the system on a chip (SoC) platform in which the proposed accelerator and RISC-V processor are integrated.
The remainder of this paper is organized as follows: Section 2 explains CNNs and matrix multiplication in general. In addition, we have discussed some challenges in implementing CNN accelerators. Section 3 describes the proposed matrix multiplication engine and the CONNA architecture. Section 4 describes the experimental environment and results. The CONNA was compared with existing neural accelerators and general-purpose processors in terms of performance, silicon area, power consumption, and computational efficiency, and the details are provided in Section 5 and Section 6.
Finally, Section 7 concludes the paper.
2. Background and Related Works
In this section, CNNs and matrix multiplications are discussed briefly. We have also detailed two mainstream neural processing unit (NPU) architectures: single instruction multiple data (SIMD) and systolic array (SA). Issues in conducting various shapes and dimensions of matrix multiplication in CNN accelerators are discussed in subsequent sections.
2.1. Convolutional Neural Network
CNN has been adopted to solve many difficult problems, which include computer vision and natural language processing [1,2,3,4,5,6]. Most CNNs consist of three different types of processing layers: convolution layer, pooling layer, and fully connected layer. These layers are arranged in a feed-forward structure [11]. CNN recognizes an object by feature extraction and classification. The main function of the convolution and pooling layers is feature extraction, and that of the fully connected layer is classification.
In the convolution layer, element-wise multiplications are performed between an input feature map and a convolution kernel. Figure 1 depicts an example of computation in a convolution layer. First, the input feature map is convolved with a convolution kernel. In the convolution layer, Cin-channels of Hin × Win input feature map are convolved with Ck × Ck × Cin kernels by shifting the kernel window to generate one pixel in the Hout × Wout output feature map. Cout denotes the number of channels in the output feature map. Second, the sum of weighted results from the first stage and bias is calculated. Finally, the sum is filtered using an activation function, such as sigmoid, tanh, and ReLU.
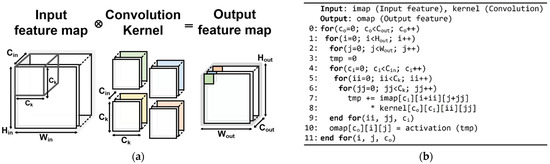
Figure 1.
Example computation in a convolution layer: (a) Illustration of a convolution operation between an input feature map and convolution kernel; (b) Pseudocode for a typical computation in a convolution layer.
Following the execution of the convolution layer, the pooling layer reduces the size of feature maps. A fully connected layer follows feature extraction using multiple convolutions and pooling layers. The output feature map from the multiple convolutions and pooling layers represents the high-level features of the input image, and the output of the fully connected layer is the classification result.
2.2. Matrix Multiplication
Matrix multiplication is a key operation in accelerating CNN applications [12,27,28,29]. In a CNN, the convolution and fully connected layers area are often implemented with matrix multiplication. In widely used deep learning frameworks, such as PyTorch and TensorFlow, the convolution kernel and input feature map are transformed into matrices, and this transformation process is called packing [27,28,29,30,31]. After the packing is completed, the output feature map is generated by multiplying the transformed matrices.
For example, image-to-image (im2col) is generally used in the convolution and fully connected layers [27,28], as shown in Figure 2. The im2col method makes a feature map into patches of Ck × Ck × Cin, where Ck, and Cin indicate the size and channel of the convolution filter, respectively. The n feature map patches are reshaped into a (Ck × Ck × Cin) × n matrix before being multiplied by a Cout × (Ck × Ck × Cin) filter matrix to generate a Cout × (Hout × Wout) output feature map, where Cout, Hout, Wout, n represent the number of filter type, the height, width of the output feature map, and the number of feature map patches correspond to the size of the output feature map, respectively.
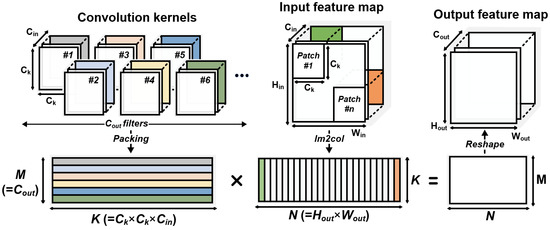
Figure 2.
Matrix to matrix multiplication of matrices A (M × K) and B (K × N).
2.3. Accelerating CNN on Neural Processing Unit
The acceleration of CNN becomes pivotal as the computational complexity of CNN grows rapidly [11,12,14]. Several NPUs have been designed to enhance the computing performance and energy efficiency of CNNs [17,18,19,20,21,22,23,24,25,26]. In such NPUs, when two matrices, A and B, are multiplied, the first matrix A and the second matrix B are partitioned into tiles with shapes that fit the hardware accelerator structure, as depicted in Figure 3a. The tiled matrices of matrix A and matrix B are loaded into buffers (activation/weight buffers in Figure 3b,c), and multiplication is performed by an array of processing elements (PEs).
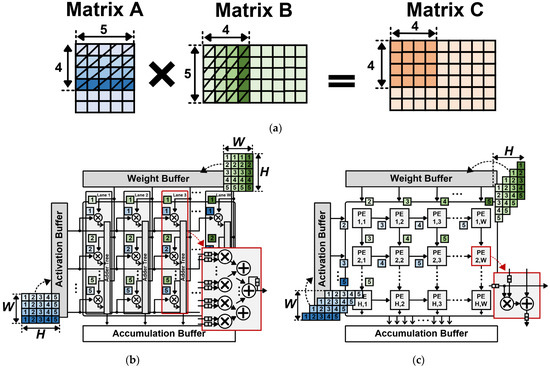
Figure 3.
Matrix multiplication dimension, tiling, and mapping of two types of accelerators: (a) Tiled matrix on CNN matrix multiplication; (b) Matrix multiplication on SIMD; and (c) Systolic array.
The SIMD architecture is a hardware unit in which multiple computing units perform a single operation on different sets of data concurrently [32]. They are widely used in various commercial processors [33,34]. Several state-of-the-art NPUs employ the SIMD architecture as their main computation unit [16,19,21,22,24]. In a SIMD-based implementation, each lane typically performs a dot-product operation [24]. A typical SIMD architecture computes W dot-product operations in parallel, as illustrated in Figure 3b. To perform W dot-product operations in parallel, the SIMD requires a dedicated data distribution fabric (i.e., bus, tree, or mesh) for high-bandwidth data exchange to keep W lanes busy.
The SA architecture is a class of NPU that exploits computational parallelism by utilizing an array of PEs [17,18,20,25,26]. In SA-based accelerators, there are two conventional dataflows: weight stationary (WS) and output stationary (OS). In the SA architecture, each PE typically conducts a MAC operation. In general, matrix multiplication in the SA architecture is carried out as follows: (1) Data are received from neighboring PEs, as depicted in Figure 3c. (2) W × H MAC operations are performed simultaneously. (3) The results are stored in each PE and remain stationary until the final results are computed. This dataflow is called the OS because the outputs are stored in each PE to minimize the movement cost of the partial sums. On the other hand, when the weights are pre-loaded into the MAC array and the activations are marched in from the activation storage buffer, the dataflow is called WS. In both cases, one element of the output feature map is computed for every clock cycle for each read input element.
2.4. Handling Various Shapes and Dimensions of Matrix Multiplication in NPU
As mentioned earlier, the transformed feature maps and kernels are computed in the form of matrix multiplication and various types of matrix multiplications in terms of shapes and dimensions are carried out in a CNN [23,31]. As listed in Table 1, in the conv1 layer of SqueezeNet v1.1 [4], the shape of the input feature map is fat-short (N >> K). However, in fire5/expand 1 × 1 and conv10 layer, the shape of the kernel matrix is tall-skinny (M >> K). In addition, the input feature maps of conv1 and fire2/squeeze1 × 1 are fat-short, but the dimensions of conv 1 are significantly larger than those of fire2/squeeze1 × 1.

Table 1.
Matrix multiplication parameter in SqueezeNet v1.1 with im2col [4,28].
These various shapes and dimensions may decrease the efficiency of matrix multiplication on both systolic array structure and SIMD architecture [17,18,19,21,22,23,25,26]. Most NPU architectures have an inflexible structure where they are effective only for square matrix multiplications [16,17,18,19,20,21]. Therefore, the acceleration performance of a CNN accelerator may not be consistently good. In this section, the key issues in implementing a CNN accelerator are discussed from three perspectives: computing unit utilization, latency, and throughput.
2.4.1. Computing Unit Utilization
Table 2 lists the MAC utilization rates and computing performance achieved when accelerating SqueezeNet on various NPUs [17,18,19,20,21]. In the case of 3 × 3 convolution layers (conv1, fire2/expand3 × 3), most NPUs have high MAC utilization on average. However, in the case of 1 × 1 convolution layers (fire2/squeeze1 × 1 and expand1 × 1), the utilization rates are considerably lower. In particular, the utilization rates of KOP3, Angle-Eye, and TPU are less than 10%. Figure 4 depicts the matrix multiplication of convolution layers on a 32 × 32 PE array in Gemmini. For the 3 × 3 convolution layer, approximately 85% (=27 × 32/(32 × 32)) of the PEs in Gemmini were utilized. However, for 1 × 1 convolution layers, only 50% (=32 × 16/(32 × 32)) of the PEs were utilized. The main reasons for the low utilization are that the dimensions of the transformed tensors are considerably smaller than those of the PE array on the NPU, and the shape of the transformed tensors and that of the PE array on the NPU are not identical [17,21,23,24].

Table 2.
Acceleration utilization of SqueezeNet v1.1 on NPUs.
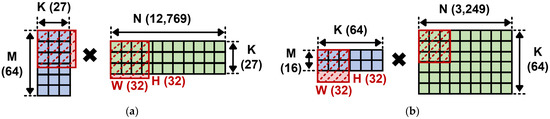
Figure 4.
Matrix multiplication with 32 × 32 PE array Gemmini: (a) Case of 3 × 3, and (b) 1 × 1 convolution layers in SqueezeNet.
In previous studies, the following three methods were mainly used to compute the various shapes and dimensions of matrices in a CNN: zero padding, gating technique, and reconfigurable hardware [17,18,19,20,21,23,24]. Zero padding is a method that transforms non-square matrices into square-shaped ones using zero values [35]. Zero padding has been employed in Angle-Eye, TPU, and Gemmini [17,18,19]. Although zero padding makes a squares matrix, certain unnecessary computations are performed; thus, quite a few meaningless operations such as multiplication by zero will be carried out. Therefore, it can reduce the utilization of MAC utilization. Gating technique and reconfigurable hardware are methods to increase MAC utilization. Eyeriss and KOP3 employ a clock gating logic that controls new input loading and avoids unnecessary computation [20,21]. Unlike zero padding, unnecessary operations are avoided using this gating logic, but overhead for the control hardware is costly. In reconfigurable hardware, MAC engines with reconfigurable interconnections allow for the effective computation of matrix multiplication of various shapes and dimensions [23,24]. It employs switchable adder and multiplier logic and forwards the data to the selected interconnections according to the shape and dimension of matrices. However, it requires a large amount of power consumption. More than 50% of power is dissipated in switchable logics. In addition, these logics take more than a quarter of the total silicon area [24].
2.4.2. Latency and Throughput
Figure 5 depicts an example of the computation of a non-square-shaped matrix multiplication in an SA-based architecture. Before propagating data into a systolic array, the matrices must be zero-padded so that their dimensions become multiples of the size of the systolic array [17,18,23]. It requires clock cycles to pad zeros in the input matrix to propagate from the buffer to each PE. Also, the PEs do not perform meaningful MAC computations on zero-padded parts, resulting in unnecessary latencies and low throughput [18,23].
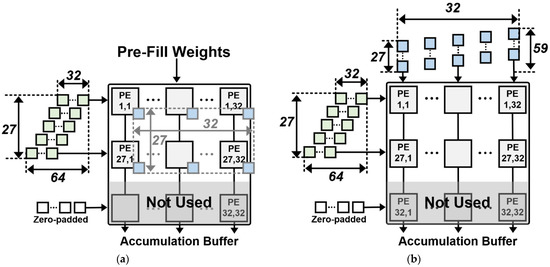
Figure 5.
Matrix multiplication of conv1 layer in 32 × 32 systolic array: (a) Weight Stationary (WS) and (b) Output Stationary (OS).
Table 3 lists the number of clock cycles, latency, and throughput of processing a zero-padded SqueezeNet v1.1 running on Gemmini [18]. First, fire2/squeeze1 × 1 and fire5/expand1 × 1 underwent the same number of MAC operations. However, the latency of fire2/squeeze1 × 1 was approximately twice as long as that of fire5/expand1 × 1. In addition, the throughput was approximately half. Second, while fire5/squeeze1 × 1 required fewer MAC operations than fire2/expand1 × 1, the latency and throughput were similar. These large differences in computing performance were also observed in the SIMD-based accelerators [18,20]. As shown in Table 4, KOP3 exhibited considerable differences in latency and throughput among other convolution layers [21]. In KOP3, the fire2/expand3 × 3 layer requires more computation than that of fire2/expand1 × 1, but the latency and throughput are similar. These results imply that NPU architectures cannot consistently perform matrix multiplication for various shapes and dimensions.

Table 3.
Latency and throughput of 32 × 32 Gemmini (1024 GOPS) running at 500 MHz [18].

Table 4.
Latency and throughput of KOP3 [21].
The main reason for the longer latency and lower throughput is that the zero value is forwarded and calculated through the connection between connected operators for data reuse within the accelerator [17,18,21]. Several existing accelerators have attempted to resolve this issue by connecting adjacent computing units only in a horizontal or vertical direction, called 1D systolic array [25,26]. The independent 1D systolic array of the accelerator can be mapped into individual rows or columns of a 2D systolic array. This method improves the latency by reducing unnecessary data forwarding, but the data reusability is reduced compared to typical SA and requires additional memory and hardware logic to increase data reuse.
3. CONNA Architecture
This section describes the architecture of CONNA and the computation of a convolution layer on CONNA. CONNA includes special hard circuits for the multiplication of tall-or-fat matrices by dynamically reconfiguring the matrix form. We have discussed the advantages of this configurable matrix multiplication engine in terms of MAC utilization, latency, and throughput. We have explained the computation of various matrix multiplications in a CNN by using this hardware engine.
3.1. Architecture Overview
Figure 6 depicts the hardware structure of the CONNA. It consists of a system bus interface and a computation engine to multiply tall-or-fat matrices. Through the system bus, data and control signals are delivered to CONNA, and the result of convolution operations is stored in external memory. This matrix multiplication engine consists of several components for control and memory (I/O control, weight buffer, feature buffer, and accumulation buffer) and computation (vector lane, vector lane scheduler, activation unit).
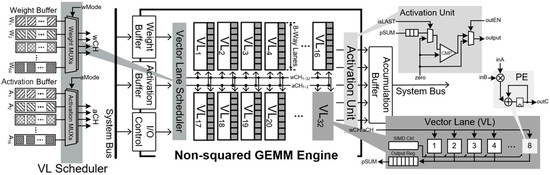
Figure 6.
Hardware block diagram of CONNA architecture.
I/O control is a hardware interface for controlling the CONNA. CONNA starts its operation by receiving commands from the host processor. These commands include data movement operations (e.g., copying data from the external memory to a buffer inside CONNA) and multiplication operations (e.g., 32 × 8 matrix multiplication). The activation buffer and weight buffer store a portion of the input feature map and weight of the convolution kernel, respectively.
The data for a convolution layer is passed to the component for computation through a special hardware module that configures the data path to the computational logic depending on the dimension and shape of the input matrices. This special hardware is called a vector lane scheduler (VL scheduler). This has been detailed in Section 3.2. Vector lanes (VLs) conduct MAC operations in parallel. Each VL consists of processing elements (PEs) that multiply the input feature map and weight of the convolution layer and accumulate the result of multiplication to obtain a partial sum and a register to hold the partial sum. An activation unit performs activation functions, such as a series of rectifier linear units (e.g., ReLU and ReLU6). When the output feature map is completed, the result is forwarded to the accumulation buffer, and the result is eventually stored in the external memory.
3.2. Proposed Configurable Matrix Engine
As mentioned in Section 2.4, the acceleration of multiplications of tall-and-fat matrices on CNN accelerators is inefficient in most of the existing PE arrays [17,18,19,21,22,23,25,26]. Therefore, it is important to find a way to accelerate matrix multiplication regardless of the shapes and dimensions of the matrices.
The CONNA includes a special hardware module that realizes the configuration of the data path between the buffer and computation unit using multiplexers (MUXs). Figure 7 depicts the architecture of the VL scheduler and interconnections between the VL scheduler and VLs for multiplications of 8 activations and 32 weights. It consists of a register called mode control, a module called activation scheduler (actSH), and four modules called weight schedulers (wSH1~4). Mode control generates the selection signals (aMode, wMode) of multiplexers in actSH and wSH1~4 to select the shape and dimension of matrix multiplication that can be computed in the CONNA.
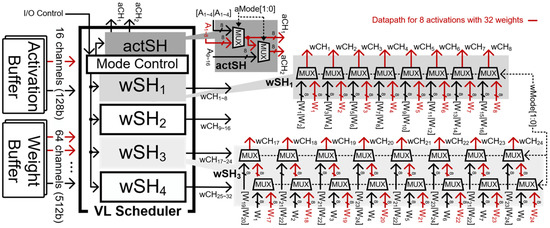
Figure 7.
Architecture of the VL scheduler for multiplications of 8 activations and 32 weights.
The data path is divided into two parts: the path from the activation and weight buffers to the VL scheduler (A1~16 and W1~64) and thereafter to VLs (aCH1~2 and wCH1~32). The activation values and weights to be used for multiplication were selectively delivered to the VL scheduler through actSH and wSH1~4, respectively. This selection logic circuit realizes matrix multiplications of various shapes and dimensions efficiently in the CONNA architecture. The VL scheduler, which consists of 32 weight channels (wCH1~32) and 2 activation channels (aCH1~2), was connected to 32 VLs. The activation values were distributed into 2 channels (aCH1~2), which means that 16 VLs share the same activation value, and the weight values were passed to the VLs through 32 channels (wCH1~32), which means that each VL has its own weight. VLs performed the matrix multiplication of activation values and weights in parallel.
Figure 8 depicts an 8 × 32 matrix multiplication of 8 × N activations and N × 32 weights in CONNA, where N represents the number of columns in the activation matrix and the number of rows in the weight matrix. Matrix multiplication is conducted as the sum of the outer products of the columns of activations and rows of weights, as depicted in Figure 8a. An 8 × 32 matrix multiplication was performed in the CONNA architecture as follows: The activation scheduler (actSH) selected A1~8 and the weight schedulers (wCH1~4) selected W1~32, and the selected values were delivered to 32 VLs. The activation channel aCH1 delivered 8 activations (A1~8) to 16 VLs, and the other activation channel aCH2 carried A1~8 to the other 16 VLs. Then, 32 weights (W1~32) were propagated to 32 VLs, which means that each VL had its own weight (e.g., VL1 to W1). As depicted in Figure 8b, each VL multiplied A1~8 by the assigned weight to generate values in the corresponding column of the output matrix. The results were stored in a register in the VL. After completing the multiplication of A1~8 and W1~32, the multiplication of the next pair of the column of activations (A9~16) and row of weights (W33~64) proceeded, and the results were accumulated in a register in each VL. These computations were repeated until the operations of all pairs of columns of activations and rows of weights were completed. The accumulated result was stored in an accumulation buffer through the activation unit, as depicted in Figure 6.
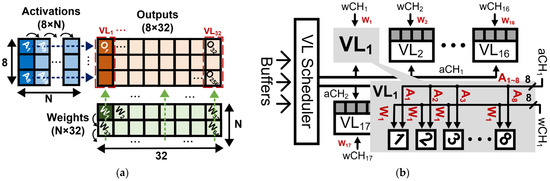
Figure 8.
Example of matrix multiplication between 8 × N activations and N × 32 weights inside CONNA: (a) 8 × 32 matrix multiplication and (b) matrix multiplication conducted in CONNA.
The CONNA conducted matrix multiplication of various shapes and dimensions, as well as 8 × 32 matrix multiplication. This architecture sets the shape and dimension of matrix multiplication by configuring the data path. Table 5 lists the forms of matrix multiplications that can be performed using the CONNA. This setting is called operation mode. In each operation mode, the CONNA multiplied tm × N activations by N × tn weights and generated a tm × tn matrix, where tm and tn indicate the size of a row in the activation matrix and that of a column in the weight matrix, respectively. For instance, in operation mode 1, it conducts a matrix multiplication of 16 × N activations and N × 16 weights, and a 16 × 16 result matrix will be generated.

Table 5.
Operation modes of CONNA.
3.3. Convolution Operation inside CONNA
This section details the convolution operation mentioned in Section 3.2. The main goal of the CONNA is to maximize the utilization of computational units to improve latency and throughput. The efficiency of a neural network accelerator decreases significantly when the structure of the PE array does not match the shape and dimension of the required matrix multiplication. That is, the efficiency depends on the shape of the tensor. The CONNA employed a configurable computational engine to address this problem.
Figure 9 depicts the pseudocodes of the convolution operation conducted in the CONNA. The tensor of a CNN was transformed into a matrix so that it could be computed via matrix multiplication, which is conducted with tiling in the CONNA. Once a feature map of dimension (M × K) and a weight matrix of the convolution kernel of dimension (K × N) are loaded into the buffers, these matrices are tiled into the shape of tm × K and K × tn matrices, respectively, as depicted in Figure 10a, where tm refers to the number of convolution windows (e.g., A1 and A2) in a feature map and tn indicates the number of types of convolution kernels used for the convolution operation. The convolution operation with tm activations and tn convolution kernels is depicted in Figure 10b.

Figure 9.
Pseudocodes of convolution operations in a convolution layer.
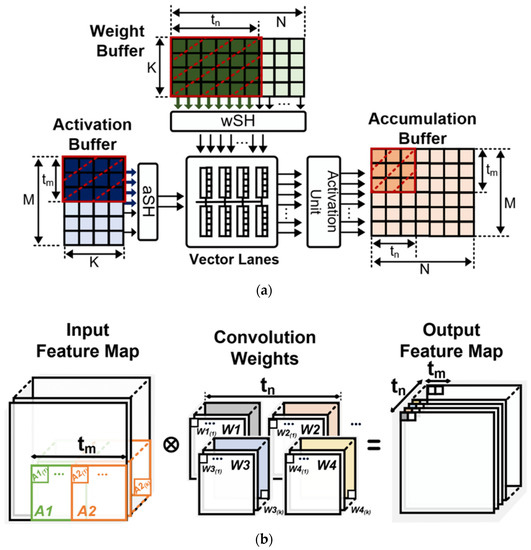
Figure 10.
Convolution operation inside CONNA architecture: (a) Illustration of a convolution operation using matrix multiplication; (b) Convolution operation with tm activations and tn convolution kernels.
Figure 11 depicts the execution flow of the CONNA. The execution flow is pipelined into the following five stages: (1) Loading activations/weights from a buffer to VL; (2–3) Performing multiplication and addition (MUL and ADD) in VL; (4) Activation to generate an output feature map; and (5) Storing the result in the accumulation buffer. During the loading stage, the activations and weights stored in the buffer are transferred to each VL with the data path set according to the operation mode. In this step, a set of data is continuously fetched and transferred to VLs in every cycle. For example, the first tm activations (A1(1)~Atm(1)) and tn weights (W1(1)~Wtn(1)) are fetched and transferred to VLs at clock cycle t1. The second set of values, A1(2)~Atm(2) and W1(2)~Wtn(2), are fetched at t2, as depicted in Figure 11. In the computation stage, matrix multiplication is performed, and partial sums are generated by accumulating the values. Eventually, after obtaining the output feature map through the activation operation (Activation), the result is stored in the accumulation buffer (Store).
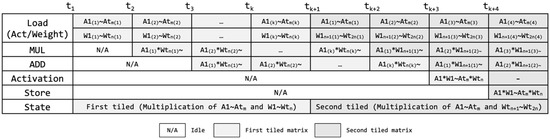
Figure 11.
Illustration of the five-stage pipelined execution in CONNA: Load, two stages for computation, activation, and store.
4. Hardware Implementation
4.1. CONNA Implmentation
The hardware design of CONNA was implemented using the Chisel language [36]. A chisel is a hardware description language that directly generates synthesizable RTL Verilog HDL codes. The CONNA hardware implementation was verified using a Xilinx FPGA VC707. We integrated the CONNA with a RISC-V microcontroller unit (MCU) [37]. The details of the hardware configuration and SoC platform are discussed in Section 4.2. After the functionality was verified, the hardware design was synthesized using Synopsys Design Compiler Ultra with Samsung 65 nm LP libraries under the worst-case operating conditions (1.08 V, 125 °C). The energy dissipation of CONNA was estimated using the Synopsys Power Compiler. In addition, CACTI v7.0 was used to estimate the amount of SRAM power consumption and area using the Samsung 65 nm technology [38]. Each SRAM was organized into 4 banks with a 128-bit data width. The area and power consumption of a 172 KB SRAM were 1.92 mm2 and 75.256 mW, respectively.
For comparison, we implemented the RTL designs of OS and WS SAs and SIMDs (16 × 16, 32 × 8/8 × 32, 64 × 4/4 × 64), including 8-bit multipliers and 32-bit adders. We set the operating frequency at 200 MHz to satisfy the timing constraints. The results are summarized in Table 6. Figure 12 depicts the hardware cost for each accelerator. The circuit area and power consumption of the multipliers were compared to each other. However, the costs of other parts were different from one another.

Table 6.
Summary of implementation evaluation on three types of neural network accelerators.
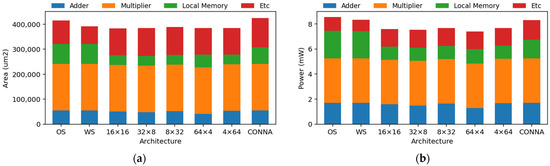
Figure 12.
Detailed hardware implementation cost of each accelerator excluding the SRAM: (a) silicon area (μm2); (b) power consumption (mW).
The hardware costs were analyzed in more detail. First, except for SIMDs, the adders for other accelerators had comparable areas and power consumption. In SIMD-based accelerators, the number of lanes and elements combined in each lane affected the area and power consumption of the adders. It is also one of the factors that determine the required memory size in SIMD-based accelerators. For memory, SA accelerators require a large memory size when compared to SIMDs and CONNA accelerators. Because each PE in SA should hold activations, weights, and partial sums, it requires a large memory size. The hardware cost to implement auxiliary blocks for SIMDs (e.g., broadcasting hardware from local memory to PEs) depended on the type of SIMD. The CONNA utilized a slightly larger silicon area than the other compared designs. The larger silicon area was due to the circuit size of the VL Scheduler. To achieve high utilization of computation units, the VL Scheduler configures the data path between the SRAM and VLs. However, the area and power overhead were negligible (0.4% and 0.23% of the total silicon area and power consumption, respectively). The achieved computing performance of the CONNA was up to 1.68 times faster than that of other accelerators by raising the utilization rate. In addition, the efficiency is 1.66 times more effective than that of other accelerators. The details of the hardware performance are discussed in Section 5.
4.2. Integration of CONNA and RISC-V MCU
To configure the operation of the CONNA to deal with various shapes and dimensions of matrix multiplication, the proposed CONNA accelerator was integrated with a RISC-V-based Rocket SoC [37]. In the Rocket SoC, a RISC-V core called Rocket adopts the RV64G RISC-V instruction set architecture (ISA) with a single-issue five-stage pipeline. The Rocket SoC included hardware components such as a processor core, an L2 cache, an external interface (TileLink), and a co-processor called the Rocket custom co-processor (RoCC) [39]. Because the CONNA was implemented as a RoCC, the RISC-V core and CONNA communicated with each other through the TileLink interface, which enabled the host core to send a stream of instructions and data to the CONNA, as depicted in Figure 13. The RoCC interface also enabled the accelerator to be integrated into a cache coherent TileLink memory system. The core of the CONNA SoC was the same as the SiFive U54 standard core, which had a 128 KB L2 cache, a 16 KiB 4-way set-associative instruction L1 cache, and a data L1 cache of the same structure. [40].
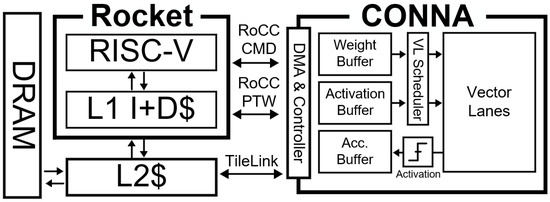
Figure 13.
Block diagram of CONNA SoC.
The CONNA was controlled using the RISC-V core. The operation mode of the CONNA was configured via a stream of custom RISC-V instructions from the host core to the CONNA accelerator. It was controlled by a mixture of the extended RISC-V and RoCC instruction sets. The instructions designed for the CONNA are listed in Table 7. There are seven instructions of three different types: data movement, computation, and configuration.

Table 7.
Extended instructions for CONNA.
Two instructions, VLOAD and VSTORE, were added for the data movement. These instructions use the direct memory access (DMA) hardware unit of the CONNA to copy the feature map and convolution weight from the main memory to the CONNA’s local memory space, such as the weight buffer, activation buffer, and accumulation buffer. Once matrices have been brought in from the main memory, the CONNA executes the computation instructions that can be configured according to the operation mode. The COMPUTE_MAT instruction conducts the matrix multiplication of activations and weights and generates an output matrix that stores the result in the accumulation buffer. After the matrix multiplication, the COMPUTE_ACT instruction performs an activation function. SET_MAT is an instruction to set the matrix parameter, and SET_TMAT is an instruction to set the parameters for the matrix tiling. The SET_ACT instruction is an instruction to configure the type of the activation function. To make the CONNA accelerator user-friendly, these instructions were wrapped in a C language in-line assembly.
Figure 14 lists the examples of pseudocodes of the matrix multiplication in the CONNA. First, the matrix and the tiled matrix parameters are configured (SET_MAT/SET_TMAT). This allows the PE array to be configured to fit the matrix multiplication of tm × tn. Also, the SET_ACT instruction sets the type of the activation function. After completing the configuration, the data is copied from DRAM to the buffer inside the CONNA, and matrix multiplication is performed using the VLOAD and COMPUTE_MAT, respectively. Finally, the data stored in the accumulation buffer is copied to the DRAM through the activation function (COMPUTE_ACT and VSTORE).

Figure 14.
Pseudocode of the convolution layer with CONNA instructions.
5. Evaluation
Because the neural network accelerators are significantly different from one another, it is difficult to compare the performance of the CONNA with that of the other accelerators. Also, neural networks are characterized by various features, such as architecture style, amount of computation, and arithmetic precision. In CONNA, a small CNN model, SqueezeNet v1.1 [4], with various shapes and dimensions of matrices, was used as a benchmark. Table 8 lists the structural information, such as tensors and matrix shapes. To evaluate the performance of CONNA, we compare CNN accelerators by considering two cases: the number of PE is fixed and the state-of-the-art accelerators. For a fair comparison of performance, the number of PEs in all accelerators was fixed at 256. CNN accelerators, namely SIMD and SA, were implemented and compared, representing the state-of-the-art accelerators [17,18,21]. Also, we discuss the CONNA accelerator in comparison to the SIMD/SA-based accelerator with different numbers and shapes of PE arrays.

Table 8.
Computation of SqueezeNet v1.1 [4] by matrix multiplication.
In this section, computing performance is discussed in terms of computing unit utilization, latency, and throughput. Next, we compare CONNA with state-of-the-art accelerators in terms of performance, throughput, and efficiency.
5.1. Computing Unit Utilization of CONNA
Figure 15 depicts the per-layer PE utilization of SqueezeNet v1.1 on all the accelerator architectures that were compared (SIMD, OS/WS SA, and CONNA). First, the utilization rate of the CONNA was up to four times higher than that of SIMD.
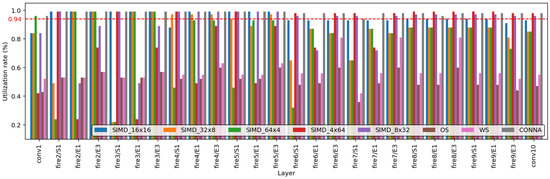
Figure 15.
PE utilization rates of SIMD, OS-SA, WS-SA and CONNA for SqueezeNet v1.1.
SIMD-based accelerators (16 × 16, 64 × 4, 32 × 8, 4 × 64, 8 × 32) were classified according to the shape of the PE array. In general, for a SIMD accelerator with an X × Y PE array, the matrix parameter K should be a multiple of Y to be fully utilized. SIMD_16 × 16 employed a dataflow structure that computed 2D 16 × 16 pixels of an image in parallel [41]. Although SIMD accelerators demonstrated reasonably decent utilization rates, the conv1 layer, where the kernel matrix was tall-and-skinny, attained a relatively low utilization rate. This was because the matrix parameter K was not close to the multiple of Y. For instance, to compute the matrix multiplications when K is equal to 27 on SIMD_16 × 16, only 84% (=27/32) of the PEs were utilized. In SIMD_64 × 4, 96% (27/28) of the PEs were utilized to conduct this matrix multiplication. In contrast, for some layers (e.g., fire3/s1), the utilization rate of SIMD_64 × 4 was significantly low owing to the size mismatch. A similar result was achieved for SIMD_32 × 8. In short, SIMD_32 × 8 and SIMD_64 × 4 were effective when the kernel matrix was tall-and-skinny, whereas SIMD_4 × 64 and SIMD_8 × 32 were effective when the kernel matrix was short-and-fat. In the case of SIMD 4 × 64, as it approached the last layer of the neural network, the utilization rate increased. However, for the first layer, the utilization rate was significantly lower (42%), owing to the size mismatch.
Overall, the CONNA achieved a higher utilization rate than SIMDs because it was capable of configuring the PE array to adjust the shape of the computation. In the conv1 layer, operation mode 3 was activated by multiplying 4 × N activations by N × 64 weights. In this case, the size of the computation was a multiple of 4 (12,772), and 99.97% (=12,769/12,772) of the PEs were meaningfully utilized. In the fire7/S1 layer, the utilization rate of CONNA was 96.98% (=225/232) by multiplying 8 × N activations by N × 32 weights, operation mode 5. The lowest utilization rate of the CONNA was 93.75% (=225/240) for fire7/S1, running operation mode 1. SIMDs achieved a low utilization rate because the size of matrices is small, and the matrix parameter K (384) does not fit well in the multiple of Y in this layer. In this layer, compared to SIMD-based accelerators, the CONNA outperforms them by up to 1.56 times.
In general, SA-based accelerators take longer to load data and collect the final output than SIMDs do [42]. This is mainly due to the increased idle time of the PEs. Generally, the OS SA propagates weights more often than the WS SA, and the utilization of the OS SA is lower than that of the WS SA. In addition, in both OS SA and WS SA, relatively low utilization of PEs is achieved [18]. In fire7/s1, the utilization rate of both OS and WS SA is lower than that of other layers. This is because it takes more time than the computation to forward data to PE, resulting in longer idle time. Overall, the CONNA achieves a utilization rate up to 3.13 times higher utilization rate compared to SA-based accelerators.
5.2. Latency and Throughput of CONNA
To calculate the latency and throughput of the accelerators, the number of clock cycles required to compute each layer was measured. Figure 16 depicts the number of computation cycles per layer for SqueezeNet v1.1. The computational cycle was closely related to the amount of computation required to process each layer. Each layer requires a large amount of computation. For instance, the fire2/E1 (expand_1 × 1) and fire2/E3 (expand_3 × 3) layers have approximately 6 M and 60 M operations, respectively.
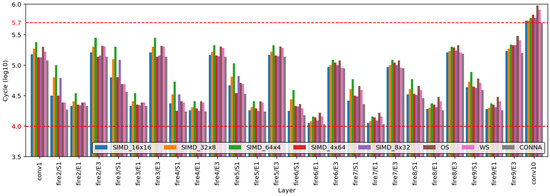
Figure 16.
Computation cycles of SIMD, OS SA, WS SA, and CONNA on SqueezeNet v1.1.
Although fire2/S1 and fire2/E1 had approximately the same amount of computation, there was a large gap in the number of computation cycles required to process each layer. There were some cases where more computation cycles were required, although the amount of computation was smaller. Although fire2/S1 required 3% less computation than fire4/E1, it took 1.74 times more clock cycles in SIMD_16 × 16.
As mentioned earlier, to effectively conduct multiplications in SIMD_16 × 16, the dimension of matrix multiplication is a multiple of the size of the PE array. However, the size of the matrix parameter N was 3249, and it was computed as 3264 to fit a multiple of 16. Therefore, additional computations were required for the remaining 15 elements (=3264–3249) in fire2/S1. In addition, in the case of fire4/E1, the size of the matrix parameter N was 841, and the computed size of N was 848 to fit a multiple of 16. Therefore, additional computations were required for the remaining 7 elements (=848–841). In the SIMD architecture, the effectiveness of performing matrix multiplications in a CNN depends on whether the dimensions of the matrices match the structure of the processing hardware.
On SqueezeNet v1.1, the CONNA required a smaller number of computation cycles when compared to the SIMD-based accelerators. This is related to computing unit utilization. SIMDs perform unnecessary computations to fit the shape of the PE array, which corresponds to zero padding [35]. Zero padding makes the matrix multiplication shape the PE array but reduces the computing unit utilization so that it takes more latencies. However, CONNA can configure the PE array to adjust the matrix shape and can achieve reduced unnecessary computations. In the conv10 layer, CONNA takes about 501.200 clock cycles, which is the longest time. Compared to SIMD-based accelerators, it takes up to 1.3 times fewer computation clock cycles.
SA is advantageous from the perspective of data reuse. It loads data once and reuses it through communication between PEs [17,18]. However, if the shape of the matrix is not a square shape, the input of SA contains zero values to match the shape of the PE array. In terms of the number of computation cycles, it often required more clock cycles to pass the information on feature maps, weights, and partial sums to several PEs. In the conv10 layer, SA required more cycles than all the other accelerators, especially when the matrix computations in those layers involved matrices with various shapes and dimensions.
The throughput of the accelerator was measured by the number of frames processed per second (FPS) when the inference was conducted on SqueezeNet v1.1. Table 9 presents the comparison results in terms of throughput and efficiency. Efficiency was measured in frames per watt. In the CONNA, the total number of computation cycles was 2,002,956, and the corresponding throughput was 100, which is up to 1.68 times better than that of the other accelerators compared. Furthermore, CONNA demonstrated up to 1.67 times better efficiency than the other SIMDs and SAs.

Table 9.
Utilization, cycle, and throughput comparison with SIMD and OS/WS-based accelerators.
5.3. Comparision with the State-of-the-Art Accelerators
The proposed accelerator, CONNA, was compared with the state-of-the-art accelerators in terms of various design metrics. Because the hardware structures and dataflows of each accelerator were diverse, it was difficult to compare the performance of the CONNA with those of the other accelerators. Therefore, we performed the comparisons in terms of several metrics: achieved computing performance, throughput, implementation cost, power consumption, silicon area, and multiple efficiencies. The performance efficiency metric was computed by dividing the throughput metric by the implementation cost. The power efficiency metric was computed by dividing the throughput by the power consumption (FPS/W), and the area efficiency metric was computed by dividing the throughput by the silicon area (FPS/mm2). The overall efficiency was estimated by dividing the throughput by the product of the power consumption and silicon area (FPS/(W*mm2)).
Several platforms were compared: CPU (i3-6100U), GPU (Tesla T4), and well-known accelerators such as SIMD and SA-based implementation [21,22,34,43]. The results are summarized in Table 10 and Table 11. Both CPU and GPU platforms suffered from low power efficiency as well as low area efficiency. However, SIMD and SA-based accelerators are relatively more efficient than processors [20,21]. In this section, we compare the performance of CONNA with SIMD-based accelerators and SA-based accelerators.

Table 10.
Efficiency comparison with processors and the SIMD-based accelerators [21,22,24,43].

Table 11.
Efficiency comparison with the state-of-the-art accelerators [17,18,20,25].
5.3.1. SIMD-Based Accelerators
The SIMD-based accelerator is classified by the number of hardware that performs a dot-product operation. KOP3 was a SIMD-type accelerator with an optimized hardware structure for the computation of a 3 × 3 convolution kernel [21]. It possessed 26 dot-product computation units, each of which performs 9 multiplications in parallel and combines them. It uses clock gating and enables unnecessary computations and power consumption. It consumed lower power when compared to the CONNA. However, it exhibited lower power efficiency and area efficiency than the CONNA. This is because the hardware was designed to achieve the best performance for 3 × 3 convolution operations, further resulting in performance degradation when performing 1 × 1 convolution operations. CONV is an optimized acceleration architecture when the kernel matrix is high [22]. It consists of a multiplier array and adder trees that combine the multiplication results for each row. This architecture is similar to that of the SIMD_32 × 32. In the inference process of SqueezeNet v1.1, the computing performance achieved by CONV was 51.07 GOPS, which is only 33% of the peak computing performance. Only a fraction of the peak computing performance was achieved because the acceleration performance decreased when the kernel matrices were not tall. Compared to the CONNA, it required a lower silicon area and lower power consumption. However, the CONNA exhibited a higher power and area efficiency. MAERI has a special MAC engine that allows data to be forwarded to the selected interconnections [24]. It has switchable logic and employs a method increasing the efficiency by forwarding the data to all multipliers and adders according to the shape and dimension of matrix multiplication. This architecture is similar to that of the SIMD_1 × 374, which is optimized for combining 374 multiplication results into 1. The achieved computing performance and throughput are 1.52 and 1.51 times better than that of the CONNA, respectively. However, it requires a large amount of power consumption from switchable logic. It also requires more area, and all efficiencies are much lower than that of the CONNA.
5.3.2. SA-Based Accelerators
The SA-based accelerator performs high computational parallelism by communication between a large number of PE arrays [17,18,20,25]. It is classified by dataflow: Weight Stationary (WS), Output Stationary (WS), and Row Stationary (RS). TPU is a WS base SA accelerator that stores weight in the register at PE and remains stationary to minimize the movement of the weights [17]. Because TPU is designed for high-performance inference on cloud platforms, it includes large PE arrays and memory. As shown in Table 10, TPU has a significantly higher achieved computing performance throughput than that of other accelerators. However, only 15% of the peak performance is achieved. As mentioned earlier, the effectiveness of performing matrix multiplications depends on whether the dimensions of the matrices match the structure of the processing hardware. This implies that a large PE array can increase the inference performance, but it reduces the efficiency of the computation. Compared to the CONNA, it requires more silicon-area and power consumption, which are related to lower efficiencies. Eyeriss is an SA-type accelerator that employs an efficient dataflow model called Row Stationary (RS) [20]. The RS is a dataflow model that increases the reusability of feature maps and weights. It is designed to maximize data reusability by assigning the processing of a 1-D row convolution to each PE. However, it consumed 3.33 times more power and required up to 5.19 times larger silicon area than that of the CONNA. A large amount of power was dissipated, and a large silicon area was consumed by the PE network block, including the clock network and PE controller hardware logic for gating. In terms of power and area efficiencies, the CONNA outperformed Eyeriss. Gemmini is a flexible acceleration architecture that adjusts dataflows depending on the CNN structure [18]. Inside Gemmini, each PE performs a MAC operation in one cycle using either the WS or OS dataflow. Before feeding data into the PE array, zero-padding operations must be performed to guarantee that the dimension of the matrix multiplication is a multiple of the size of the PE array. This operation incurs significant overhead, leading to an increased number of computation cycles and a decreased utilization rate of the computing units. It achieved 1.56 times lower throughput and required 3.74 times more power than the CONNA. In addition, it demonstrated a 5.84 times lower power efficiency. Chain-NN is an implementation that reduces the forwarding of zero values between PE arrays using a 1D systolic array [25]. In typical communication structures in the OS and WS dataflow, one PE is connected to multiple PEs to maximize data reuses and MAC utilization. In contrast, in 1D chain architecture, only one adjacent PE is connected like a chain structure. Chain-NN targets to maximize the computing performance; it requires more SRAM and logics than other accelerators. However, in terms of power and area efficiencies, Chain-NN is much better than that of the CONNA. When compared based on the 65 nm technology, Chain-NN requires 10.52 and 15.77 times more silicon area and power consumption than CONNA, respectively.
In the overall efficiency that considers all throughput, power consumption, and silicon area, the CONNA is up to 34.1 times better than the dedicated accelerators that were compared. In conclusion, the CONNA excels in performing diverse matrix multiplications compared to other dedicated accelerators and can achieve a high utilization rate of the computing units, further leading to low computation latencies.
6. Discussion
The CONNA focuses on hardware design to effectively perform various shapes and dimensions of matrix multiplication, which takes a large portion of CNN applications. With a negligible amount of hardware cost, the computing performance of the CONNA is consistently higher regardless of various matrix multiplications. Furthermore, the CONNA shows a significant power, area, and overall efficiency on SqueezeNet v1.1 against the existing CNN accelerators, as shown in Section 5.3
Accelerating various matrix multiplication effectively is a challenging task from a hardware architecture design point of view. The accelerator design complexity and hardware implementation cost become much higher due to additional control logic and memory. This has resulted in Table 10 and Table 11. In addition, it makes an additional latency, which is related to a reduced throughput. However, CONNA demonstrates a hardware design that can accelerate various matrix multiplications with high MAC utilization, throughput, and efficiencies compared to existing accelerators.
It is worth noting that high efficiencies provide by configuring the shape of MAC units to adjust the shape of the computation. Currently, CONNA does not consider consisting of a large number of PE arrays, but this can be implemented with an accelerating larger CNN model. This would enable our design approach to accelerate various matrix multiplication faster.
7. Conclusions
In this study, we presented a neural network accelerator called CONNA with a configurable engine to efficiently perform matrix multiplications with various shapes and dimensions. Existing studies have employed a computing engine optimized for matrices of either square or particular shapes and dimensions. Such architectures suffer from inefficiency when matrices in the CNN layers have various shapes and dimensions. The CONNA can maximize the utilization rate of computing units using a novel configurable engine. Using the proposed configurable computing engine, the shape and dimension of the matrix multiplication conducted inside the accelerator were configured such that the utilization rate of the computing units could be maximized. Compared to conventional accelerators, the CONNA achieved a high utilization rate, further leading to excellent computing performance. Furthermore, in terms of the overall efficiency considering throughput, power consumption, and silicon area, the CONNA was up to 34.1 times better than the state-of-the-art accelerators and processors.
Author Contributions
S.-S.P. was responsible for initial conceptualization and writing the draft manuscript. S.-S.P. and K.-S.C. declared that they have participated in the research and editing of the manuscript. K.-S.C. read and approved the final manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Institute of Information and Communications Technology Planning and Evaluation (IITP) grant funded by the Korean government (MSIT) (No. 2022-0-01304, Development of Self-learnable Mobile Recursive Neural Network Processor Technology).
Acknowledgments
The EDA tool was supported by the IC Design Education Center (IDEC), Korea.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (ECCV), Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Farhadi, A.; Redmon, J. Yolov3: An incremental improvement. In Proceedings of the Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Zhao, Q.; Sheng, T.; Wang, Y.; Tang, Z.; Chen, Y.; Cai, L.; Ling, H. M2det: A single-shot object detector based on multi-level feature pyramid network. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Iandola, F.N.; Han, S.; Moskewicz, M.W.; Ashraf, K.; Dally, W.J.; Keutzer, K. SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5 MB model size. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Tan, M.; Le, Q. Efficientnet: Rethinking model scaling for convolutional neural networks. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 9–15 June 2019. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Karpathy, A.; Toderici, G.; Shetty, S.; Leung, T.; Sukthankar, R.; Fei-Fei, L. Large-scale video classification with convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Stockholm, Sweden, 24–28 August 2014. [Google Scholar]
- Guo, D.; Zhou, W.; Li, H.; Wang, M. Hierarchical LSTM for sign language translation. In Proceedings of the AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Devlin, J.; Chang, M.W.; Lee, K.; Toutanova, K. Bert: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies (NAACL-HLT), Minneapolis, MN, USA, 2–7 June 2019. [Google Scholar]
- Ogden, S.S.; Guo, T. Characterizing the deep neural networks inference performance of mobile applications. arXiv 2019, arXiv:1909.04783. [Google Scholar]
- Cong, J.; Xiao, B. Minimizing computation in convolutional neural networks. In Proceedings of the International Conference on Artificial Neural Networks (ICANN), Hamburg, Germany, 15–19 September 2014. [Google Scholar]
- Lavin, A.; Gray, S. Fast algorithms for convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Strobel, K.; Zhu, S.; Chang, R.; Koppula, S. Accurate, low-latency visual perception for autonomous racing: Challenges, mechanisms, and practical solutions. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020. [Google Scholar]
- Kim, Y.D.; Park, E.; Yoo, S.; Choi, T.; Yang, L.; Shin, D. Compression of deep convolutional neural networks for fast and low power mobile applications. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, PR, USA, 2–4 May 2016. [Google Scholar]
- Aguilera, C.A.; Aguilera, C.; Navarro, C.A.; Sappa, A.D. Fast CNN Stereo Depth Estimation through Embedded GPU Devices. Sensors 2020, 20, 3249. [Google Scholar] [CrossRef] [PubMed]
- NVDIA Deep Learning Accelerator. 2021. Available online: https://nvldla.org (accessed on 28 June 2022).
- Jouppi, N.P.; Young, C.; Patil, N.; Patterson, D.; Agrawal, G.; Bajwa, R.; Yoon, D.H. In-datacenter performance analysis of a tensor processing unit. In Proceedings of the International Symposium on Computer Architecture (ISCA), Toronto, ON, Canada, 24–28 June 2017. [Google Scholar]
- Genc, H.; Kim, S.; Amid, A.; Haj-Ali, A.; Iyer, V.; Prakash, P.; Zhao, J.; Grubb, D.; Liew, H.; Mao, H.; et al. Gemmini: Enabling systematic deep-learning architecture evaluation via full-stack integration. In Proceedings of the Design Automation Conference (DAC), San Francisco, CA, USA, 7–10 December 2021. [Google Scholar]
- Guo, K.; Sui, L.; Qiu, J.; Yu, J.; Wang, J.; Yao, S.; Yang, H. Angel-eye: A complete design flow for mapping CNN onto embedded FPGA. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2017, 37, 35–47. [Google Scholar] [CrossRef]
- Chen, Y.-H.; Emer, J.; Sze, V. Eyeriss: A spatial architecture for energy-efficient dataflow for convolutional neural networks. In Proceedings of the International Symposium on Computer Architecture (ISCA), Seoul, Korea, 18–22 June 2016. [Google Scholar]
- Yue, J.; Liu, Y.; Yuan, Z.; Wang, Z.; Guo, Q.; Li, J.; Yang, H. A 3.77 TOPS/W convolutional neural network processor with priority-driven kernel optimization. IEEE Trans. Circuits Syst. 2018, 66, 277–281. [Google Scholar]
- Chong, Y.S.; Goh, W.L.; Ong, Y.S.; Nambiar, V.P.; Do, A.T. An Energy-efficient Convolution Unit for Depthwise Separable Convolutional Neural Networks. In Proceedings of the International Symposium on Circuits and Systems (ISCAS), Virtual, 23–26 May 2021. [Google Scholar]
- Qin, E.; Samajdar, A.; Kwon, H.; Nadella, V.; Srinivasan, S.; Das, D.; Krishna, T. Sigma: A sparse and irregular gemm accelerator with flexible interconnects for DNN training. In Proceedings of the IEEE International Symposium on High Performance Computer Architecture (HPCA), San Diego, CA, USA, 22–26 February 2020. [Google Scholar]
- Kwon, H.; Samajdar, A.; Krishna, T. Maeri: Enabling flexible dataflow mapping over dnn accelerators via reconfigurable interconnects. In ACM SIGPLAN Notices; Association for Computing Machinery: New York, NY, USA, 2018; pp. 461–475. [Google Scholar]
- Wang, S.; Zhou, D.; Han, X.; Yoshimura, T. Chain-NN: An energy-efficient 1D chain architecture for accelerating deep convolutional neural networks. arXiv 2017, arXiv:1703.01457. [Google Scholar]
- Selvam, S.; Ganesan, V.; Kumar, P. Fuseconv: Fully separable convolutions for fast inference on systolic arrays. In Proceedings of the Design, Automation & Test in Europe Conference & Exhibition (DATE), Virtual, 14–23 March 2022. [Google Scholar]
- Anderson, A.; Gregg, D. Optimal DNN primitive selection with partitioned boolean quadratic programming. In Proceedings of the 2018 International Symposium on Code Generation and Optimization (CGO), New York, NY, USA, 24–28 February 2018. [Google Scholar]
- Anderson, A.; Vasudevan, A.; Keane, C.; Gregg, D. Low-memory gemm-based convolution algorithms for deep neural networks. arXiv 2017, arXiv:1709.03395. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. Tensorflow: A system for large-scale machine learning. In Proceedings of the USENIX Symposium on Operating Systems Design and Implementation (OSDI), Savannah, GA, USA, 2–4 November 2016. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Chintala, S. Pytorch: An imperative style, high-performance deep learning library. arXiv 2019, arXiv:1912.01703. [Google Scholar]
- Chen, J.; Xiong, N.; Liang, X.; Tao, D.; Li, S.; Ouyang, K.; Chen, Z. TSM2: Optimizing tall-and-skinny matrix-matrix multiplication on GPUs. In Proceedings of the ACM International Conference on Supercomputing (ICS), Phoenix, AZ, USA, 26–28 June 2019. [Google Scholar]
- Mitra, G.; Johnston, B.; Rendell, A.P.; McCreath, E.; Zhou, J. Use of SIMD vector operations to accelerate application code performance on low-powered ARM and Intel platforms. In Proceedings of the International Symposium on Parallel & Distributed Processing (IPDPS), Chicago, IL, USA, 23–27 May 2016. [Google Scholar]
- Stephens, N.; Biles, S.; Boettcher, M.; Eapen, J.; Eyole, M.; Gabrielli, G.; Walker, P. The ARM scalable vector extension. IEEE Micro 2018, 37, 26–39. [Google Scholar] [CrossRef] [Green Version]
- Lee, W.J.; Shin, Y.; Lee, J.; Kim, J.W.; Nah, J.H.; Jung, S.; Lee, S.; Park, H.S.; Han, T.D. SGRT: A mobile GPU architecture for real-time ray tracing. In Proceedings of the High-Performance Graphics Conference (HPG), Anaheim, CA, USA, 19–21 July 2013. [Google Scholar]
- Kang, H.J. Accelerator-aware pruning for convolutional neural networks. IEEE Trans. Circuits Syst. Video Technol. 2019, 30, 2093–2103. [Google Scholar] [CrossRef] [Green Version]
- Bachrach, J.; Vo, H.; Richards, B.; Lee, Y.; Waterman, A.; Avižienis, R.; Asanović, K. Chisel: Constructing hardware in a scala embedded language. In Proceedings of the Design Automation Conference (DAC), San Francisco, CA, USA, 3–7 June 2012. [Google Scholar]
- Asanovic, K.; Avizienis, R.; Bachrach, J.; Beamer, S.; Biancolin, D.; Celio, C.; Waterman, A. The Rocket Chip Generator; Tech. Rep. UCB/EECS-2016-17; EECS Department, University of California: Berkeley, CA, USA, 2016. [Google Scholar]
- Balasubramonian, R.; Kahng, A.B.; Muralimanohar, N.; Shafiee, A.; Srinivas, V. CACTI 7: New tools for interconnect exploration in innovative off-chip memories. ACM Trans. Archit. Code Optim. (TACO) 2017, 14, 1–25. [Google Scholar] [CrossRef]
- Cook, H.; Terpstra, W.; Lee, Y. Diplomatic design patterns: A TileLink case study. In Proceedings of the Workshop on Computer Architecture Research with RISC-V (CARRV), Boston, MA, USA, 14 October 2017. [Google Scholar]
- SiFive U54. Available online: https://www.sifive.com/cores/u54 (accessed on 25 April 2022).
- Moons, B.; Verhelst, M. An energy-efficient precision-scalable ConvNet processor in 40-nm CMOS. IEEE J. Solid State Circuits 2016, 52, 903–914. [Google Scholar] [CrossRef]
- Gonzalezm, A.; Hong, A. A Chipyard Comparison of NVDLA and Gemmini. Berkely, CA, USA, Tech. Rep. EE, 2020, 290-2. Available online: https://charleshong3.github.io/projects/nvdla_v_gemmini.pdf (accessed on 28 June 2022).
- Nebullvm. Available online: https://github.com/nebuly-ai/nebullvm (accessed on 25 April 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).