Asymmetric Bipartite Consensus of Multi-Agent Systems under Periodic Detection Event-Triggered Mechanism

Abstract

This paper investigates the periodic event-triggered asymmetric bipartite consensus problem of multi-agent systems (MASs) under structurally balanced undirected signed graphs. In order to reduce the consumption of communication resources and continuous detection in the control process of MASs, a novel periodic detection event-triggered asymmetric bipartite consensus control protocol is proposed. In particular, each agent samples only in a fixed period. For each agent, two event conditions are given, and only when state error satisfies this event condition can the event be triggered. A new type of Laplacian matrix is constructed to achieve asymmetric bipartite consensus. The control method can guarantee the performance of MASs and have less communication resources. Based on the Lyapunov stability theorem and algebraic graph theory, the proposed periodic event-triggered control strategy is able to implement the asymmetric bipartite consensus when the topology is structurally balanced undirected signed graphs. The proposed method in this paper can reduce the restriction on the sampling period and automatically exclude Zeno behavior. Finally, the validity of the conclusion is verified by numerical simulation.

1. Introduction

MASs have been widely considered by scholars in the field of control and have been widely used in aircraft formations, sensor networks, multi-manipulator collaborative devices and other fields [1,2,3,4,5,6]. The consensus problem has become the research hotspot. Much research is concentrated on the cooperative network. In 2013, Altafini [7] proposed the concept of competitive relationship, which expressed the weight of edges as negative numbers. Most of the achievements related to cooperative and competitive networks are the bipartite consensus, which achieve a consensus with the same modulus but opposite sign [8,9,10,11]. However, the degree of trust/distrust and like/dislike between people is not the same in real life. Therefore, asymmetric bipartite consensus has a more general and practical significance. Bipartite consensus can be regarded as a special case of asymmetric bipartite consensus. Guo et al. [12,13,14] extended the bipartite consensus problem of MASs to asymmetric bipartite consensus. In Ref [15], the authors studied the finite-time asymmetric bipartite consensus problem based on iterative learning control.

With the development of control science, communication engineering and other disciplines, the battery capacity of an agent is limited in practical applications. At the same time, the loss caused by the mutual communication between agents is also very huge. To solve the above problems, many researchers have conducted much work. In the traditional control method, each individual must sample the information of its neighbor agent periodically. In terms of system design and analysis, this method is easy to analyze and implement in theory. However, after the system runs stably, timing sampling will lead to a series of unnecessary communication and control tasks, resulting in a certain waste of resources. Therefore, the communication and control mode of this mechanism is conservative [16,17]. Unlike time sampling, event-triggered control is triggered on “demand” to save communication resources. The advantages of event-triggered control focus on ensuring system performance, saving network and computing resources. In 2009, Dimarogonas et al. [18] applied the event-triggered mechanism to MASs for the first time. They designed centralized and distributed event-triggered control algorithms, respectively. When the error is greater than the set threshold, the event will be triggered. Otherwise, the event will not be triggered. Fan et al. [19] proposed a combined measurement method for event design and developed a basic event-triggered control algorithm. Seyboth et al. [20] expressed the triggering condition as a time function with exponential decline to ensure that the agent states asymptotic convergence to average consensus. Wei et al. [21] considered the consensus problem of event-based general linear MASs. Nowzari and Cortes [22] designed a new distributed event-triggered control protocol to realize the average consensus of MASs and also proved that Zeno behavior can be avoided. Zeno behavior refers to the behavior of triggers infinitely triggered within a limited time, and this behavior does not conform to the physical characteristics of communication between individuals in the actual system. Therefore, the most important problem is how to avoid Zeno behavior. In Ref [23], the average consensus problem is studied for MASs with distributed event-triggered communication and control strategy. In Refs [24,25], a new analysis method was proposed, and it was concluded that there is no Zeno behavior.

Generally, event-triggered control uses the hardware device to continuously test the controlled object to judge the triggering condition, which determines the triggering moment of the control task. In order to avoid continuous event detection caused by Zeno behavior, the event-triggered control method derives periodic event-triggered control. In other words, a fixed period is given, and the control task is executed when the triggering condition meets the periodic sampling time, which completely avoids continuous communication from the design of the triggering condition. Meng et al. [26] considered the combination of period detection and control protocol to solve the problem of continuous judgment by the event detector. In the literature [27,28], in order to reduce the number of events, a new event-triggered consensus algorithm based on periodic sampling was proposed. In Ref [29], a periodic event-triggered controller was designed. In addition, Dong et al. [30] discussed the design of event-triggered controllers in networked control systems.

However, the current research on event-triggered control mainly focuses on bipartite consensus in MASs. There are relatively few studies on the asymmetric bipartite consensus of MASs triggered by periodic detection events. This article adopts the periodic detection event-triggered control method in the MASs. The main innovation of this paper is the design of two different triggering conditions. They can directly avoid Zeno behavior and implement asymmetric bipartite consensus in MASs. The advantage of the first triggering condition is that there is no need to know the state information of the agent and its neighbors during detection. It converges quickly. The second triggering condition makes the sampling period not limited to the limit of topology and widens the range of the sampling period. Therefore, the second triggering condition further reduces the number of communications between agents.

This paper is arranged as follows. We introduce the preliminaries and problem formulation in Section 2. According to the Lyapunov stability theory, two kinds of triggering conditions are constructed, and the sufficient conditions for the system state to achieve asymmetric bipartite consensus are obtained. Examples are shown in Section 4. Finally, Section 5 concludes this paper.

2. Preliminaries and Problem Formulation

2.1. Preliminaries

Consider a MAS with $n$ agents, simplify each agent to a point, and simplify the communication between agents to an edge. $G=(V,E,A)$ represents the communication topology diagram with $n$ nodes. $V=(v_1,v_2,\dots ,v_n)$ represents the set of points, and $E\subseteq (V\times V)$ represents the set of edges. $(v_i,v_j)\in E$ represents the two nodes of an edge. Nodes $v_i$ and $v_j$ can communicate with each other. In this case, node $v_j$ is said to be the neighbor of node $v_i$. $A={[a_{ij}]}_{n\times n}$ is the adjacency matrix of the undirected graph, and $a_{ij}$ represents the weight of the edge $(v_j,v_i)$. If $(v_i,v_j)\in E$, then $a_{ij}\ne 0$, otherwise $a_{ij}=0$. $D=diag\left\{d_1,d_2,\dots ,d_n,\right\}$ represents the degree matrix of the graph, where $d_i={\displaystyle \sum _{j=1,i\ne j}^n{a}_{ij}}$.

Definition 1.

A gauge transformation is a change of orthant order in$R^n$performed by a matrix$H=diag(h)$. Denote$H=diag(h)$,$h={[h_1,\dots ,h_n]}^T$,$h_i\in \{\pm 1\}$the set of all gauge transformations in$R^n$[7].

Definition 2.

A signed graph$G(A)$is said to be structurally balanced if it admits a bipartition of the nodes$V_1,V_2$,$V_1\cup V_2=V,V_1\cap V_2=\varnothing$, such that$a_{ij}\ge 0$,$\forall v_i,v_j\in V_q$,$\left(q\in \left\{1,2\right\}\right)$,$a_{ij}\le 0$,$\forall v_i\in V_q$,$v_j\in V_r$,$q\ne r$$\left(q,r\in \left\{1,2\right\}\right)$[7].

Lemma 1.

For a Laplacian matrix$L$, it has one zero eigenvalue, and all non-zero eigenvalues are in the right half plane. There is also a left eigenvector$\overrightarrow{\xi }={({\xi }_1,{\xi }_2,\dots ,{\xi }_n)}^T$corresponding to the zero eigenvalue of the Laplacian matrix, and satisfying${\xi }_i>0$for$i\in V_1$and${\xi }_i<0$for$i\in V_2$[12].

Lemma 2.

Assuming that the sign graph$G(A)$is structurally balanced, there are the following conclusions [7]:

(1) 

There exists a diagonal matrix$H=diag\{h_1,h_2,\dots \dots ,h_n\}$, so that entries of$HAH$are all nonnegative, where$h_i\in \{1,-1\}$for$i\in V$;

(2) 

Laplacian matrix$\tilde{L}=HLH$is positive semi-definite;

(3) 

For a vector$x$that satisfies$1^{T}x=0$, the following formula holds

(4) 

$\underset{x\ne 0}{\min }\frac{x^T\tilde{L}x}{x^{T}x}={\lambda }_2(\tilde{L}),$

where${\lambda }_2(\tilde{L})$is the smallest positive eigenvalue of$\tilde{L}$.

2.2. Problem Formulation

Assuming the MAS is composed of n agents, the dynamic behavior of the i-th agent is as follows

$${\dot{x}}_i(t)=u_i(t)\begin{array}{c},\end{array}i\in N$$

(1)

where $N\in \{1,\dots ,n\}$, $x_i(t)$ is the state of the agent, and $u_i(t)$ is the control input.

The goal of this paper is to propose an event-triggered control based on periodic detection to ensure that the minimum trigger interval is the sampling period. At the same time, based on the existing literature, we can further reduce the communication times and achieve asymmetric bipartite consensus. The measurement error is

$$e_i(t_k^i+lh)=x_i(t_k^i)-x_i(t_k^i+lh),l=1,2,\dots$$

(2)

where $h$ is the defined detection period, $t_k^i$ is the kth trigger moment for the agent, and $t_k^i$ is an integer multiple of $h$, and $e_i(t_k^i+lh)$ is the difference between the state at the time of the last event-triggered and the current sampled state. All trigger moment states $x_i(t_k^i)$ are a subset of the sampled state $x_i(kh)$. That is to say, the event-triggered moment is $\{t_0^i,t_1^i,\dots \}\subseteq \{0,h,2h,\dots \}$. This means that the least low bound of the event-triggered interval $\{t_{k+1}^i-t_k^i,k=0,1,\dots \}$ of all agents is greater than or equal to $h$. Furthermore, the occurrence of Zeno behavior is avoided from the design of triggering conditions.

At each detection moment, each agent transmits its own state information to its neighbors and receives the status information of the neighbors for event detection. If the event-triggered condition is met, agent $i$ does not need to take the next step; otherwise, agent $i$ will update its state and transmit the current state information to its neighbors, resetting the measurement error $e_i(t_k^i+lh)$ to zero.

To reduce confusion in the notation, we define

$${\widehat{x}}_i(t)\stackrel{\Delta }{=}{x}_i(t_k^i),t_k^i\le t<t_{k+1}^i$$

which convert discrete time signal $x_i(t_k^i)$ into continuous time signal ${\widehat{x}}_i(t)$.

For a given undirected signed graph, $G(A)$ is a structurally balanced strongly connected graph. Without loss of generality, we suppose $n$ agents can be divided into two groups $V_1,V_2$, $V_1\in \{v_1,v_2,\dots ,v_m\}$ and $V_2\in \{v_{m+1},v_{m+2},\dots ,v_n\}$. For the convenience of expression, we denote $V_1\in \{1,\dots ,m\}$ and $V_2\in \{m+1,\dots ,n\}$. The control protocol $u_i(t)$ is designed as follows

$$u_i(t)=\{\begin{array}{l}-{\displaystyle \sum _{j=1}^m{a}_{ij}(sign(a_{ij}){\widehat{x}}_i(t)-{\widehat{x}}_j(t))}\\ -{\displaystyle \sum _{j=m+1}^n{a}_{ij}(qsign(a_{ij}){\widehat{x}}_i(t)-{\widehat{x}}_j(t)),\begin{array}{cc}& i\in V_1\end{array}}\\ -{\displaystyle \sum _{j=1}^m{a}_{ij}(\frac{1}{q}sign(a_{ij}){\widehat{x}}_i(t)-{\widehat{x}}_j(t))}\\ -{\displaystyle \sum _{j=m+1}^n{a}_{ij}(sign(a_{ij}){\widehat{x}}_i(t)-{\widehat{x}}_j(t)),\begin{array}{cc}& i\in V_2\end{array}}\end{array}$$

(3)

where $q>0$ is the given influence coefficient, $\widehat{x}(t)={[{\widehat{x}}_1(t),{\widehat{x}}_2(t),\dots ,{\widehat{x}}_n(t)]}^T$ is the latest propagation state of the agent, and $sign(\cdot )$ is the sign function, $t\in [t_k^i,t_{k+1}^i)$. The control protocol is not a segmentation constant between event times $\{t_0^i,t_1^i,\dots \}$ but a segmentation constant between sampling moments $\{0,h,2h,\dots \}$. Because the control protocol will be updated at its own event time $\{t_0^i,t_1^i,\dots \}$ and its neighbor’s event time ${\cup }_{j\in N_i}\{t_0^i,t_1^i,\dots \}$.

Define the general Laplacian matrix $L=C-A$, where $C={[c_{i,j}]}_{n\times n}=diag\begin{array}{c}\end{array}[c_{11},c_{22},\dots \dots ,c_{nn}]$ is a diagonal matrix with diagonal elements

$$c_{ii}=\{\begin{array}{c}{\displaystyle \sum _{j=1}^m\left|a_{ij}\right|+{\displaystyle \sum _{j=m+1}^{n}q\left|a_{ij}\right|,\begin{array}{cc}& i\in V_1\end{array}}}\\ {\displaystyle \sum _{j=1}^m\frac{1}{q}\left|a_{ij}\right|+{\displaystyle \sum _{j=m+1}^n\left|a_{ij}\right|,\begin{array}{cc}& i\in V_2\end{array}}}\end{array}$$

From the measurement error of the agent (2), it can be obtained

$$x_i(t_k^i)=x_i(t_k^i+lh)+e_i(t_k^i+lh)$$

(4)

$$x_j(t_{k^{\prime }}^j)=x_j(t_k^i+lh)+e_j(t_k^i+lh)$$

(5)

The dynamic equation of agent $i$ can be expressed as

$${\dot{x}}_{\mathrm{i}}(t)=\{\begin{array}{c}\begin{array}{l}-{\displaystyle \sum _{j=1}^m{a}_{ij}(sign(a_{ij}){\widehat{x}}_i(t)-{\widehat{x}}_j(t))}\\ -{\displaystyle \sum _{j=m+1}^n{a}_{ij}(qsign(a_{ij}){\widehat{x}}_i(t)-{\widehat{x}}_j(t)),\begin{array}{cc}& i\in V_1\end{array}}\end{array}\\ \begin{array}{l}-{\displaystyle \sum _{j=1}^m{a}_{ij}(\frac{1}{q}sign(a_{ij}){\widehat{x}}_i(t)-{\widehat{x}}_j(t))}\\ -{\displaystyle \sum _{j=m+1}^n{a}_{ij}(sign(a_{ij}){\widehat{x}}_i(t)-{\widehat{x}}_j(t)),\begin{array}{cc}& i\in V_2\end{array}}\end{array}\end{array}$$

(6)

Definition 3.

In the MAS (1), if there exists a constant$\alpha$, such that$\underset{t\to \infty }{\lim }{x}_i(t)=\alpha$for$i\in V_1$and$\underset{t\to \infty }{\lim }{x}_i(t)=-q\alpha$for$i\in V_2$, then the MAS (1) can achieve asymmetric bipartite consensus, where$\overrightarrow{\alpha }={({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n)}^T$,${\alpha }_1={\alpha }_2=\dots ={\alpha }_m=1$,${\alpha }_{m+1}={\alpha }_{m+2}=\dots ={\alpha }_n=-q$[7].

Lemma 3.

Under the control protocol (3), the MAS (1) can achieve asymmetric bipartite consensus, and the final convergence state is$\underset{t\to \infty }{\lim }x(t)=\frac{{(\overrightarrow{\xi })}^{T}x(0)}{{(\overrightarrow{\xi })}^T\overrightarrow{\alpha }}\overrightarrow{\alpha }$[12].

Substituting Equations (4) and (5) into Equation (6), when $i\in V_1$, we obtain

$$\begin{array}{lll}{\dot{\mathit{x}}}_i(t)& =& -{\displaystyle \sum _{j=1}^m{a}_{ij}(sign(a_{ij}){\mathit{x}}_i(t_k^i)-{\mathit{x}}_j(t_{k^{\prime }}^j))}-{\displaystyle \sum _{j=m+1}^n{a}_{ij}(qsign(a_{ij}){\mathit{x}}_i(t_k^i)-{\mathit{x}}_j(t_{k^{\prime }}^j))}\\ & =& -{\displaystyle \sum _{j=1}^m{a}_{ij}sign(a_{ij})\left({\mathit{x}}_i(t_k^i+lh)+{\mathit{e}}_i(t_k^i+lh)\right)}+{\displaystyle \sum _{j=1}^m{a}_{ij}\left({\mathit{x}}_j(t_k^i+lh)+{\mathit{e}}_j(t_k^i+lh)\right)}\\ & & -{\displaystyle \sum _{j=m+1}^n{a}_{ij}qsign(a_{ij})\left({\mathit{x}}_i(t_k^i+lh)+{\mathit{e}}_i(t_k^i+lh)\right)}+{\displaystyle \sum _{j=m+1}^n{a}_{ij}\left({\mathit{x}}_j(t_k^i+lh)+{\mathit{e}}_j(t_k^i+lh)\right)}\\ & =& -{\displaystyle \sum _{j=1}^m{a}_{ij}\left(sign(a_{ij}){\mathit{x}}_i(t_k^i+lh)-{\mathit{x}}_j(t_k^i+lh)\right)}\\ & & -{\displaystyle \sum _{j=m+1}^n{a}_{ij}\left(qsign(a_{ij}){\mathit{x}}_i(t_k^i+lh)-{\mathit{x}}_j(t_k^i+lh)\right)}\\ & & -{\displaystyle \sum _{j=1}^m{a}_{ij}\left(sign(a_{ij}){\mathit{e}}_i(t_k^i+lh)-{\mathit{e}}_j(t_k^i+lh)\right)}\\ & & -{\displaystyle \sum _{j=m+1}^n{a}_{ij}\left(qsign(a_{ij}){\mathit{e}}_i(t_k^i+lh)-{\mathit{e}}_j(t_k^i+lh)\right)}\end{array}$$

Substituting Equations (4) and (5) into Equation (6), when $i\in V_2$, we obtain

$$\begin{array}{lll}{\dot{\mathit{x}}}_i(t)& =& -{\displaystyle \sum _{j=1}^m{a}_{ij}\left(\frac{1}{q}sign(a_{ij}){\mathit{x}}_i(t_k^i)-{\mathit{x}}_j(t_{k^{\prime }}^j)\right)}-{\displaystyle \sum _{j=m+1}^n{a}_{ij}\left(sign(a_{ij}){\mathit{x}}_i(t_k^i)-{\mathit{x}}_j(t_{k^{\prime }}^j)\right)}\\ & =& -{\displaystyle \sum _{j=1}^m{a}_{ij}\frac{1}{q}sign(a_{ij})\left({\mathit{x}}_i(t_k^i+lh)+{\mathit{e}}_i(t_k^i+lh)\right)}\\ & & -{\displaystyle \sum _{j=1}^m{a}_{ij}\left({\mathit{x}}_j(t_k^i+lh)+{\mathit{e}}_j(t_k^i+lh)\right)}\\ & & -{\displaystyle \sum _{j=m+1}^n{a}_{ij}sign(a_{ij})\left({\mathit{x}}_i(t_k^i+lh)+{\mathit{e}}_i(t_k^i+lh)\right)}\\ & & +{\displaystyle \sum _{j=m+1}^n{a}_{ij}\left({\mathit{x}}_j(t_k^i+lh)+{\mathit{e}}_j(t_k^i+lh)\right)}\\ & =& -{\displaystyle \sum _{j=1}^m{a}_{ij}\left(\frac{1}{q}sign(a_{ij}){\mathit{x}}_i(t_k^i+lh)-{\mathit{x}}_j(t_k^i+lh)\right)}\\ & & -{\displaystyle \sum _{j=m+1}^n{a}_{ij}\left(sign(a_{ij}){\mathit{x}}_i(t_k^i+lh)-{\mathit{x}}_j(t_k^i+lh)\right)}\\ & & -{\displaystyle \sum _{j=1}^m{a}_{ij}\left(\frac{1}{q}sign(a_{ij}){\mathit{e}}_i(t_k^i+lh)-{\mathit{e}}_j(t_k^i+lh)\right)}\\ & & -{\displaystyle \sum _{j=m+1}^n{a}_{ij}\left(sign(a_{ij}){\mathit{e}}_i(t_k^i+lh)-{\mathit{e}}_j(t_k^i+lh)\right)}\end{array}$$

where $t_{k^{\prime }}^i=\max \left\{t\right|t\in \{t_k^j,k=0,1,\dots \},t\le t_k^i+lh\}$.

From the Laplacian matrix defined above, in the $t\in [kh,(k+1)h)$ interval, the compact form of the dynamic Equation (6) can be expressed as

$${\dot{x}}_i(t)=-L(x_i(kh)+e_i(kh))$$

(7)

Since the symbol graph adjacency matrix has positive and negative elements, it is not easy to follow up theoretical analysis. We use gauge transformation to change the adjacency matrix to non-negative.

By Definition 1, take the transformation matrix $H=diag(h),h=[h_1,h_2,\dots \dots ,h_n]$, where $h_i=1$ if $i\in V_1$ and $h_i=-1$ if $i\in V_2$. The Laplacian matrix after the gauge transformation is $\tilde{L},\tilde{L}=HLH$, $\tilde{x}(t)=Hx(t),\tilde{e}(t)=He(t),$ then, after the gauge transformation, the compact form of the dynamic equation can be rewritten as follows

$$\dot{\tilde{x}}(t)=-\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh))$$

(8)

3. The Analysis of Asymmetric Bipartite Consensus

In this section, we construct two Lyapunov functions and obtain two sets of sufficient conditions, respectively. It proves that the triggering condition can reduce system resources under the premise of satisfying system performance.

Theorem 1.

Consider the MAS (1), the communication topology is an undirected signed graph with a balanced structure, and the distributed event-triggered protocol (3) is adopted. If the triggering condition meets

$${\Vert {\tilde{e}}_i(t_k^i+lh)\Vert }_2^2\le {\delta }_i{\Vert z_i(t_k^i)\Vert }_2^2,l=1,2,\dots$$

(9)

and satisfies $0<h\le \frac{1}{2{\lambda }_n}$, $0<{\delta }_i\le \frac{1}{{\lambda }_n^2}$, ${\lambda }_n$ refers to the largest eigenvalue of the Laplacian matrix. All agents can converge to asymmetric bipartite consensus, and the final convergence state is $\underset{t\to \infty }{\lim }x(t)=\frac{{(\overrightarrow{\xi })}^{T}x(0)}{{(\overrightarrow{\xi })}^T\overrightarrow{\alpha }}\overrightarrow{\alpha }$. Where $x(0)$ is the initial state of the system, and $z_i(t_k^i+lh)={\displaystyle \sum _{j\in N_i}(x_i(t_k^i+lh)-x_j(t_k^j+lh))}$, $\overrightarrow{\xi }$ is the left eigenvector of $L$ in Definition 3, $\overrightarrow{\alpha }={({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n)}^T$, ${\alpha }_1={\alpha }_2=\dots ={\alpha }_m=1$, ${\alpha }_{m+1}={\alpha }_{m+2}=\dots ={\alpha }_n=-q$.

Proof. 

Introduce the Lyapunov function as follows

$$V(t)=\frac{1}{2}{\tilde{x}}^T(t)\tilde{x}(t),t\in [kh,(k+1)h)$$

(10)

Taking the time derivative of $V(t)$ yields

$$\begin{array}{ll}\dot{V}(t)& ={\tilde{x}}^T(t)\dot{\tilde{x}}(t)\\ & =-{\tilde{x}}^T(t)\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh))\\ & =-{(\tilde{x}(kh)+\dot{\tilde{x}}(t)(t-kh))}^T\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh))\\ & =(t-kh){(\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh)))}^T\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh))-{\tilde{x}}^T(kh)(\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh)))\end{array}$$

(11)

Because of $t\in [kh,(k+1)h)$, the maximum value of $(t-kh)$ is $h$, then

$$\dot{V}(t)\le h{(\tilde{x}(kh)+\tilde{e}(kh))}^T{\tilde{L}}^T\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh))-{\tilde{x}}^T(kh)\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh))$$

(12)

Additionally, because ${\lambda }_2(\tilde{L}){\tilde{x}}^T\tilde{L}\tilde{x}\le {\tilde{x}}^T{\tilde{L}}^2\tilde{x}\le {\lambda }_n(\tilde{L}){\tilde{x}}^T\tilde{L}\tilde{x}$

$$\begin{array}{lll}\dot{V}(t)& \le & h{\lambda }_n{(\tilde{x}(kh)+\tilde{e}(kh))}^T\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh))-{\tilde{x}}^T(kh)\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh))\\ & =& -(1-h{\lambda }_n){\tilde{x}}^T(kh)\tilde{L}\tilde{x}(kh)-{\tilde{x}}^T(kh)\tilde{L}\tilde{e}(kh)\\ & & +h{\lambda }_n{\tilde{e}}^T(kh)\tilde{L}\tilde{e}(kh)+2h{\lambda }_n{\tilde{x}}^T(kh)\tilde{L}\tilde{e}(kh)\end{array}$$

(13)

Due to inequality

$${\tilde{e}}^T(kh)\tilde{L}z(kh)\le \frac{1}{2}{\tilde{e}}^T(kh)\tilde{L}\tilde{e}(kh)+\frac{1}{2}{z}^T(kh)\tilde{L}z(kh)$$

(14)

Then

$$\dot{V}(t)\le (2h{\lambda }_n-\frac{3}{2}){\tilde{x}}^T(kh)\tilde{L}\tilde{x}(kh)+(2h{\lambda }_n-\frac{1}{2}){\tilde{e}}^T(kh)\tilde{L}\tilde{e}(kh)$$

(15)

Let $2h{\lambda }_n\le 1$, it can be derived that

$$\begin{array}{ll}\dot{V}(t)& \le -\frac{1}{2}{\tilde{x}}^T(kh)\tilde{L}\tilde{x}(kh)+\frac{1}{2}{\tilde{e}}^T(kh)\tilde{L}\tilde{e}(kh)\\ & \le -\frac{1}{2{\lambda }_n}{\tilde{x}}^T(kh){\tilde{L}}^2\tilde{x}(kh)+\frac{1}{2}{\lambda }_n{\tilde{e}}^T(kh)\tilde{e}(kh)\end{array}$$

(16)

Let $z(kh)=\tilde{L}\tilde{x}(kh)$, then we have

$$\dot{V}(t)\le -\frac{1}{2{\lambda }_n}{z}^T(kh)z(kh)+\frac{1}{2}{\lambda }_n{\tilde{e}}^T(kh)\tilde{e}(kh)$$

(17)

Substituting the triggering condition (9) into the above formula, we obtain

$$\begin{array}{ll}\dot{V}(t)& \le -\frac{1}{2{\lambda }_n}{z}^T(kh)z(kh)+\frac{1}{2}{\delta }_i{\lambda }_n{z}^T(kh)z(kh)\\ & \le (\frac{1}{2}{\delta }_i{\lambda }_n-\frac{1}{2{\lambda }_n})z^T(kh)z(kh).\end{array}$$

(18)

To guarantee stability, a sufficient condition is $\frac{1}{2}{\delta }_i{\lambda }_n-\frac{1}{2{\lambda }_n}\le 0$. Since $0<h\le \frac{1}{2{\lambda }_n},$ a sufficient condition to ensure $\dot{V}(t)\le 0$ is $0<{\delta }_i\le \frac{1}{{\lambda }_n^2}.$ Combined with Lemma 3, the MAS (1) can achieve asymmetric bipartite consensus, and the final convergence state is $\underset{t\to \infty }{\lim }x(t)=\frac{{(\overrightarrow{\xi })}^{T}x(0)}{{(\overrightarrow{\xi })}^T\overrightarrow{\alpha }}\overrightarrow{\alpha }$. □

Remark 1.

The advantages of triggering condition (9) are shown in the following three aspects. First of all, the triggering conditions in Equation (9) are different from centralized event detectors. The event detectors in Equation (9) are distributed, which means that each agent only needs information from its neighbors to determine the update time. Secondly, different from continuous event detectors, this triggering condition neither requires continuous local event detection nor continuous communication with neighboring agents. Finally, the result of the existing distributed mechanism can only guarantee the nonexistence of aggregation point, but there is no complete theoretical framework to provide the minimum event-triggered interval. The event detector in Equation (9) essentially recognizes a minimum event interval is h, so Zeno behavior will not occur.

Theorem 2.

Consider the MAS (1), the communication topology is an undirected signed graph with a balanced structure, and the distributed event-triggered protocol (3) is adopted. If the triggering conditions are met

$${\Vert {\tilde{e}}_i(t_k^i+lh)\Vert }_2^2\le \frac{{\sigma }_i}{a}\left(\frac{2}{{\lambda }_n}-\frac{1}{a}-2h\right){\Vert z_i(t_k^i)\Vert }_2^2,\begin{array}{c}\end{array}l=1,2,\dots$$

(19)

and satisfy $0<h\le \frac{1}{{\lambda }_n}-\frac{1}{2a}$, $0<{\sigma }_i<1$, ${\lambda }_n$ refers to the largest eigenvalue of the Laplacian matrix $\tilde{L}$. All agents can converge to asymmetric bipartite consensus, and the final convergence state is $\underset{t\to \infty }{\lim }x(t)=\frac{{(\overrightarrow{\xi })}^{T}x(0)}{{(\overrightarrow{\xi })}^T\overrightarrow{\alpha }}\overrightarrow{\alpha }$. Where $z_i(t_k^i)={\displaystyle \sum _{j\in N_i}\left(x_i(t_k^i)-x_j(t_k^j)\right)}$.

Proof. 

Introduce the Lyapunov function as follows

$$V(t)=\frac{1}{2}{\tilde{x}}^T(t)\tilde{L}\tilde{x}(t),t\in [kh,(k+1)h)$$

(20)

Taking the time derivative of $V(t)$ yields

$$\begin{array}{ll}\dot{V}(t)& ={\tilde{x}}^T(t)\tilde{L}\dot{\tilde{x}}(t)\\ & =-{\tilde{x}}^T(t)\tilde{L}(\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh)))\\ & =-{(\tilde{x}(kh)+\dot{\tilde{x}}(t)(t-kh))}^T\tilde{L}(\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh)))\\ & =(t-kh){(\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh)))}^T\tilde{L}(\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh)))-{\tilde{x}}^T(kh)(\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh)))\end{array}$$

(21)

Substitute $z(kh)=\tilde{L}(\tilde{x}(kh)+\tilde{e}(kh))$ into the above formula to obtain

$$\dot{V}(t)=(t-kh)z^T(kh)\tilde{L}z(kh)-{\tilde{x}}^T(kh)z(kh)$$

(22)

Because of $t\in [kh,(k+1)h)$, the maximum value of $(t-kh)$ is $h$, then

$$\begin{array}{ll}\dot{V}(t)& \le h{z}^T(kh)\tilde{L}z(kh)+{(\tilde{L}\tilde{e}(kh)-z(kh))}^{T}z(kh)\\ & \le h{z}^{{\rm T}}(kh)\tilde{L}z(kh)+{\tilde{e}}^{{\rm T}}(kh)\tilde{L}z(kh)-z^{{\rm T}}(kh)z(kh)\end{array}$$

(23)

Then, we use the primary inequality

$${\tilde{e}}^T(kh)\tilde{L}z(kh)\le \frac{a}{2}{\tilde{e}}^T(kh)\tilde{L}\tilde{e}(kh)+\frac{1}{2a}{z}^T(kh)\tilde{L}z(kh)$$

(24)

where $a>0$, thus we obtain $\dot{V}(t)$ as

$$\dot{V}(t)\le h{z}^T(kh)\tilde{L}z(kh)+\frac{a}{2}{\tilde{e}}^T(kh)\tilde{L}\tilde{e}(kh)+\frac{1}{2a}{z}^T(kh)\tilde{L}z(kh)-z^T(kh)z(kh)$$

(25)

Due to ${\lambda }_2(\tilde{L}){\tilde{x}}^T\tilde{L}\tilde{x}\le {\tilde{x}}^T{\tilde{L}}^2\tilde{x}\le {\lambda }_n(\tilde{L}){\tilde{x}}^T\tilde{L}\tilde{x}$, then one has

$${\lambda }_n\ge \frac{{\tilde{x}}^T\tilde{L}\tilde{x}}{{\tilde{x}}^T\tilde{x}}$$

(26)

Therefore, we obtain

$$\begin{array}{ll}\dot{V}(t)& \le h{\lambda }_n{z}^T(kh)z(kh)+\frac{a}{2}{\lambda }_n{\tilde{e}}^T(kh)\tilde{e}(kh)+\frac{1}{2a}{\lambda }_n{z}^T(kh)z(kh)-z^T(kh)z(kh)\\ & \le \left({\lambda }_n(h+\frac{1}{2a})-1\right)z^T(kh)z(kh)+\frac{a}{2}{\lambda }_n{\tilde{e}}^T(kh)\tilde{e}(kh)\end{array}$$

(27)

Substituting the triggering condition (19) into the above formula, we obtain

$$\dot{V}(t)\le \left({\lambda }_n(h+\frac{1}{2a})-1+\frac{a{\lambda }_n}{2}\frac{{\sigma }_i}{a}(\frac{2}{{\lambda }_n}-\frac{1}{a}-2h)\right){\Vert z_i(kh)\Vert }_2^2$$

(28)

where $a>0$. To guarantee stability, a sufficient condition is ${\lambda }_n(h+\frac{1}{2a})-1+\frac{a{\lambda }_n}{2}\frac{{\sigma }_i}{a}(\frac{2}{{\lambda }_n}-\frac{1}{a}-2h)\le 0$. Since $0<{\sigma }_i<1$, a sufficient condition to ensure $\dot{V}(t)\le 0$ is $0<h\le \frac{1}{{\lambda }_n}-\frac{1}{2a}.$ Combined with Lemma 3, the MAS (1) can achieve asymmetric bipartite consensus, and the final convergence state is $\underset{t\to \infty }{\lim }x(t)=\frac{{(\overrightarrow{\xi })}^{T}x(0)}{{(\overrightarrow{\xi })}^T\overrightarrow{\alpha }}\overrightarrow{\alpha }$. □

Remark 2.

In the existing literature, the sampling period is mostly limited by the topology of the system itself. That is, the topology determines the range of the sampling period. In this paper, triggering condition (19) can reduce the influence of system topology on the sampling period. In addition, triggering condition (19) changes with the changes of system parameters. Therefore, we can set an appropriate sampling period to adjust the number of events. In addition, compared with the continuous event-triggered communication strategy, for agent i in triggering condition (19), only the neighbor sampling information $x_i(t_k^i)$is needed instead of continuous state$x_i(t)$. The triggering condition only needs to be checked and calculated at each sampling instant, which means that no additional hardware devices are required for continuous measurement and calculation.

Remark 3.

The triggering conditions (9) and (19) only need to be periodically measured and calculated at a constant sampling time. Compared with the continuous event-triggered strategy, the lower bound of the event-triggered interval of this discrete event-triggered strategy is the sampling period. This means that Zeno behavior is absolutely excluded.$z_i(t_k^i+lh)$, $z_i(t_k^i+lh)={\displaystyle \sum _{j\in N_i}\left(x_i(t_k^i+lh)-x_j(t_k^j+lh)\right)}$in the triggering condition (9) indicates that the triggering condition needs to update $z_i(t_k^i+lh)$at all detection times. In this process, the agent needs to exchange the state information with its neighbors. This will cause a lot of communication loss and consume system resources. $z_i(t_k^i)={\displaystyle \sum _{j\in N_i}(x_i(t_k^i)-x_j(t_k^j))}$in triggering condition (19) retains the advantages of triggering condition (9). At the same time, it is not necessary to know the state information of the agent and its neighbor agent at the current time at the detection time, which significantly reduces the update times of the variable. Each agent only needs to obtain the status information of its neighbor at the corresponding event trigger time and then perform control input update. Compared with triggering condition (9), the sampling period of triggering condition (19) is not only affected by the topology but can also change with the change of parameter a, so that the range of sampling period h is twice that of triggering condition (9).

4. Simulation Results

In this section, we consider a MAS in Equation (1) which consists of six agents. The communication topology is shown in Figure 1, where $V_1=\{v_1,v_2\}$, $V_2=\{v_3,v_4,v_5,v_6\}$ satisfied the structural balance. Let $q=0.5$. The Laplacian matrix $L$ can be obtained as follows

$$L=\left[\begin{array}{cccccc}1.5& -1& 0& 0& 0& 1\\ -1& 1.5& 1& 0& 0& 0\\ 0& 1& 4& -1& -1& 0\\ 0& 0& -1& 2& -1& 0\\ 0& 0& -1& -1& 3& -1\\ 1& 0& 0& 0& -1& 3\end{array}\right]$$

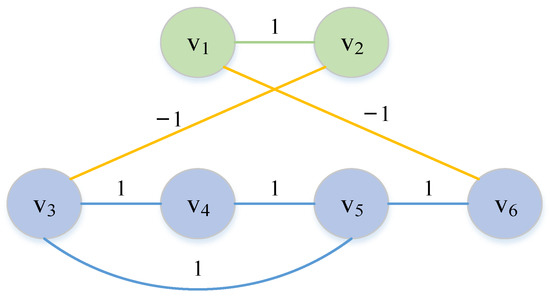
Figure 1. Communication topology.

The eigenvalue of $L$ is ${\lambda }_1=0$, ${\lambda }_2=0.91$, ${\lambda }_3=1.8$, ${\lambda }_4=3$, ${\lambda }_5=4.29$, ${\lambda }_6=5$. The left eigenvector is $\overrightarrow{\xi }={[\begin{array}{cccccc}0.58& 0.58& -0.29& -0.29& -0.29& -0.29\end{array}]}^T$ corresponding to zero eigenvalue, and the initial state is $x(0)={[\begin{array}{cccccc}1& 2& 3& 5& 6& 7\end{array}]}^T$, $\overrightarrow{\alpha }={[\begin{array}{cccccc}1& 1& -0.5& -0.5& -0.5& -0.5\end{array}]}^T$, $x(\infty )={[\begin{array}{cccccc}-2.5& -2.5& 1.25& 1.25& 1.25& 1.25\end{array}]}^T$ can be obtained from Theorem 1. We conduct simulation experiments to verify the triggering conditions (9) and (19), respectively.

Example 1.

By Theorem 1, system (1) driven by the triggering condition (9) can achieve asymmetric bipartite consensus. We choose the parameters${\delta }_1=0.01,{\delta }_2=0.03,{\delta }_3=0.02,{\delta }_4=0.01,{\delta }_5=0.03,{\delta }_6=0.02$, the sampling period$h=0.05$. The above parameters satisfy$0<h\le \frac{1}{2{\lambda }_n}$and$0<{\delta }_i\le \frac{1}{{\lambda }_n^2}$.

Example 2.

By Theorem 2, system (1) driven by the event-triggered condition (19) can achieve asymmetric bipartite consensus. We choose the parameters${\sigma }_1=0.09,{\sigma }_2=0.08,{\sigma }_3=0.04,{\sigma }_4=0.05,{\sigma }_5=0.08,{\sigma }_6=0.02$,$a=16$, the sampling period$h=0.15$. The above parameters satisfy$0<h\le \frac{1}{{\lambda }_n}-\frac{1}{2a}$and$0<{\sigma }_i<1$.

The following Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 shows the simulation results of Example 1 and Example 2. From the simulation results shown in Figure 2 and Figure 6, it can be seen that when the triggering conditions (9) and (19) are met, the system state can achieve asymmetric bipartite consensus. The state of the agents $v_1,v_2$ converges to −2.5, $v_3,v_4,v_5,v_6$ converges to 1.25 when $t\to \infty$. Figure 3 and Figure 7 show the curve of the control input corresponding to each agent over time. Since the control input remains unchanged at the time of an event being triggered, there will be a short-term level change. Figure 4 and Figure 8 show the evolution of errors. In these figures, an event is generated when the measurement error exceeds the set threshold, and therefore, the event is triggered. Figure 5 and Figure 9 show the trigger interval of the proposed triggering conditions (9) and (19), respectively. The data in Table 1 can be obtained from Figure 5 and Figure 9.

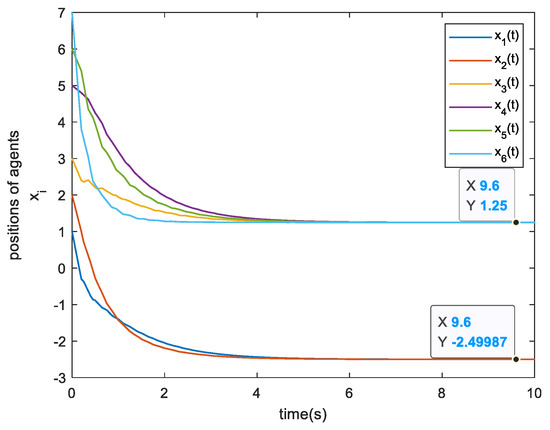
Figure 2. The states of agents.

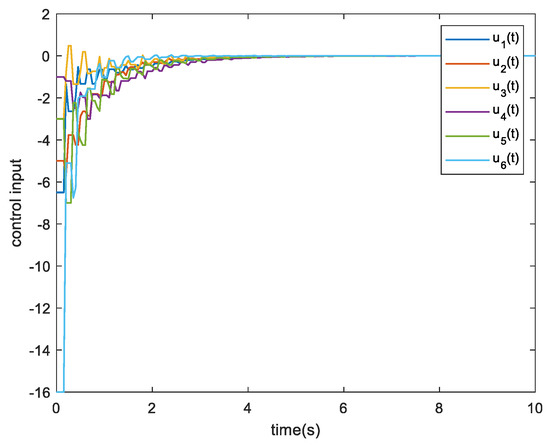
Figure 3. Control inputs for the agents.

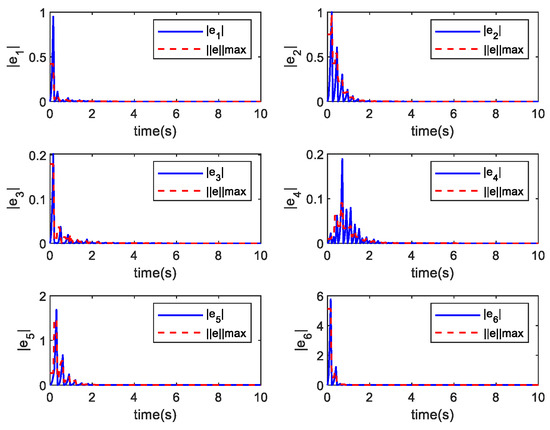
Figure 4. Evolution of error signals for each agent.

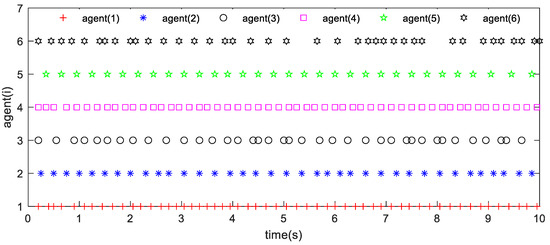
Figure 5. Event times for each agent.

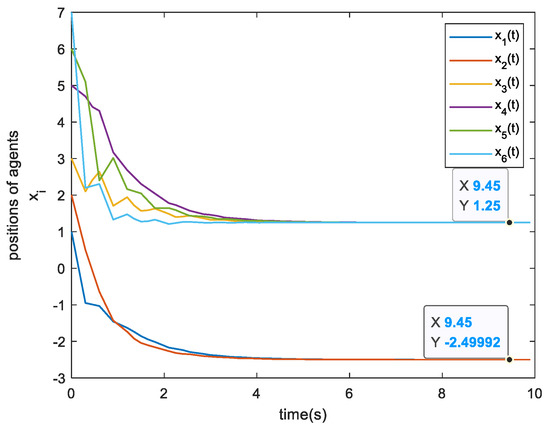
Figure 6. The states of agents.

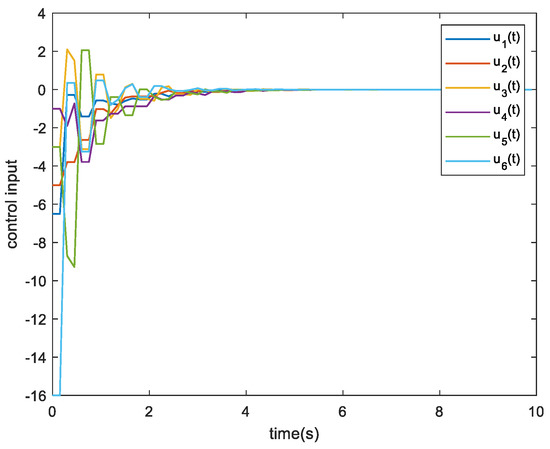
Figure 7. Control inputs for the agents.

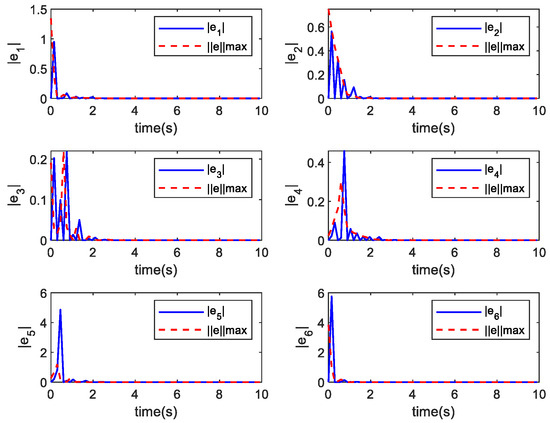
Figure 8. Evolution of error signals for each agent.

Figure 9. Event times for each agent.

Table 1. The number of events per agent.

agent	agent 1	agent 2	agent 3	agent 4	agent 5	agent 6
No. Event of (9)	56	37	38	53	32	39
No. Event of (19)	24	24	24	30	23	30

It can be seen from Table 1. that the trigger times of triggering condition (19) are reduced by 56%, 35%, 36%, 43%, 28% and 23%, respectively, compared with those of triggering condition (9). Therefore, triggering condition (19) has more advantages in reducing resource consumption. Compared with the event-triggered control adopted in reference [31], the periodic detection event-triggered control proposed in this paper effectively reduces the energy consumption in the system control and avoids Zeno behavior.

5. Conclusions

In this paper, asymmetric bipartite consensus is implemented in MASs by considering the periodic event-triggered control method. For undirected sign graphs, a new type of Laplacian matrices is constructed. A distributed control protocol based on periodic detection event triggering is designed. At the same time, two kinds of triggering conditions are derived, which enables the sampling period to not be limited to the topological structure. This enables dynamic adjustment of the sampling period to further reduce system resources. By using classical control theory and mathematical knowledge, the sufficient conditions for the system to achieve asymmetric bipartite consensus and the final convergence value are derived. In addition, this control strategy essentially avoids Zeno behavior. Although the event-triggered condition proposed in this paper can dynamically adjust the sampling period, the future work is to study the asymmetric bipartite consensus problem of MASs with fuzzy rough digraph topology.