Abstract
A memristor is a vital circuit element that can mimic biological synapses. This paper proposes the memristive version of a recently proposed map neuron model based on the phase space. The dynamic of the memristive map model is investigated by using bifurcation and Lyapunov exponents’ diagrams. The results prove that the memristive map can present different behaviors such as spiking, periodic bursting, and chaotic bursting. Then, a ring network is constructed by hybrid electrical and chemical synapses, and the memristive neuron models are used to describe the nodes. The collective behavior of the network is studied. It is observed that chemical coupling plays a crucial role in synchronization. Different kinds of synchronization, such as imperfect synchronization, complete synchronization, solitary state, two-cluster synchronization, chimera, and nonstationary chimera, are identified by varying the coupling strengths.
1. Introduction
The memristor is the fourth fundamental circuit element besides the three primary circuit elements, namely resistor, inductor, and capacitor, presented by Chua in 1971 [1]. A memristor, a memory resistor, has become well known since the investigation of Strukov et al. in 2008 [2] on memristor properties. Different applications such as self-programming logic circuits [3], digital memory [4], signal and image processing [5], cellular neural networks [6], etc., have been introduced for memristors. Moreover, memristors can intrinsically provide high nonlinearity to the system [7]. This feature has led many studies to focus on proposing or improving memristor models to bring higher nonlinearities [8,9,10]. Besides, memristors are one of the best candidates to model electromagnetic induction in biological systems and neuronal models, and circuits [11,12]. For this reason, some researchers have proposed memristive neuronal models by adding the magnetic flux to the membrane potential of a neuron model. The memristive Hindmarsh–Rose neuronal model [13,14,15], memristive Hodgkin–Huxley model [16], and memristive Morris–Lecar neuronal model [17] are some examples.
In addition to the flow-based neuronal models, the map-based neuronal models have also been investigated as they are computationally efficient, fast, flexible, and simple to implement [18]. Some map-based neuronal models can be found in [19,20,21,22]. In order to propose or implement the memristive maps, some discrete memristors have been introduced [23,24,25]. Employing the discrete memristors, the memristive version of the Rulkov map was proposed in [26]. Apart from investigating the neuron models, the memristors are able to mimic the biological synapses [7]. Synapses are the main parts of neuronal systems as they enable neurons to connect with other neurons for information transferring [27]. As mentioned in [27], chemical and electrical synapses are two well-known types of defined synapses for neurons. However, some researchers have used memristors as synaptic couplings between neurons [28,29]. Xu et al. [28] investigated the behavior of neurons coupled by memristor and found that memristive coupling can lead to enhanced synchronization.
By considering the synapses in neuronal models, neuronal networks can be constructed to discover the neurons’ collective behaviors [30]. Synchronization is one of the essential collective behaviors of neuronal networks. This behavior refers to the states in which all neurons, or generally all oscillators, are simultaneously in the same dynamics [31,32]. Complete synchronization [33], imperfect synchronization [34], phase synchronization [35], lag synchronization [36], cluster synchronization [37], and partial synchronization [38] are some well-known synchronization types. Two specific types of partial synchronization are chimeras [39] and solitary states [40]. In a solitary state, almost all oscillators are synchronized except a few ones, which are randomly positioned in the network. However, the chimera refers to the state in which oscillators split into coherent and incoherent groups [41]. These neuronal collective behaviors have been studied in numerous flow-based [42,43,44], and also map-based, neuronal models [45,46,47].
In this paper, firstly, the memristive version of a recently proposed neuronal map is introduced. The dynamics of the memristive model are investigated by varying parameters, and the bifurcation and Lyapunov exponents’ diagrams are presented. Secondly, the collective behavior of the network of memristive maps is investigated wherein the neurons are coupled via both electrical and chemical synapses. The synchronization error of the network is computed for different synaptic couplings. It is observed that the chemical synapses play a more critical role in synchronization. The behavior of the network before complete synchronization is also investigated, and several partial synchronization patterns are found. Therefore, the description and investigation of the memristive neuron map model are presented in Section 2. The collective behavior of the network of the proposed map is detailed in Section 3. Finally, Section 4 concludes the most important results.
2. Memristive Neuron Map Model
In 2020, Zandi et al. [21] introduced a one-dimensional neuronal map based on the phase space analysis that can exhibit different neuronal behaviors such as action potential, spiking, bursting, chaotic bursting, and myocardial action potential. In this paper, we modify this model with the aim of considering the electromagnetic effects. Consequently, a discrete memristor defined by Li et al. in 2021 [26] is added to the model, which is defined as follows:
Here, , , and are memristor’s voltage, memristor’s current, and the flux variable, respectively, is the control variable, and is an integer simulation step. Thus, , where is the total number of samples. Using the presented discrete memristors, the neuron map model can be described as follows:
where and are the control parameters, and . Moreover, is described as mentioned below [21]:
The parameters are set at , , , , , , , , , , , , and . Considering and , Figure 1 shows the phase diagrams and time series of the memristive model in plane for different values of . The initial conditions are . Figure 1a,b show the spiking behavior of the model in . Similarly, Figure 1c,d present periodic bursting in , and Figure 1e,f demonstrate chaotic bursting in .
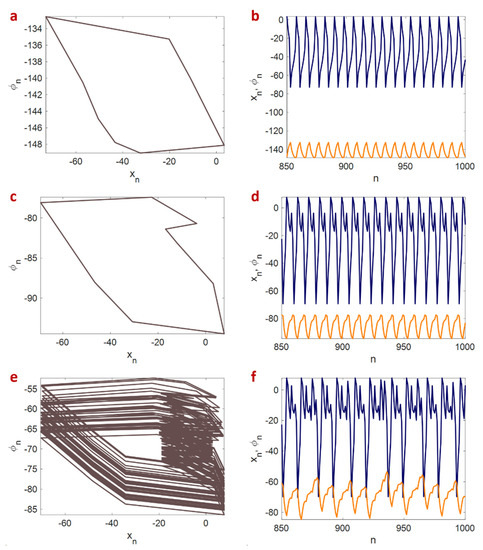
Figure 1.
The phase diagram in the x- plane (left panel) and the time series of (navy blue) and (orange) variables of the memristive map model (right panel) for different values. (a,b) Spiking behavior for . (c,d) Periodic bursting for . (e,f) Chaotic bursting for . Other parameters are , , , , , , , , , , , , , and . The used initial condition is .
To study the different dynamics of the memristive neuron map, the bifurcation diagram and the Lyapunov exponents are obtained and investigated. Figure 2 shows the bifurcation diagram and the corresponding Lyapunov exponents according to the variation of parameter considering the initial condition of and , , , , , , , , , , , , , , and . It is attained that the neuron’s behavior is mostly periodic by varying ; however, the period and amplitude of the oscillations change. In the special ranges of , such as , , , , and , the chaotic bursting can be observed. It should be noted that many periodic windows can be observed. For example, , , , and are four significantly observed periodic windows among which is the biggest one. Moreover, boundary crises, period-doubling, and period-halving bifurcation can be observed in these periodic windows. Furthermore, period-doubling bifurcations can be observed for . Therefore, it can be concluded that the neuron can exhibit period bursting of period n in this range of parameter.
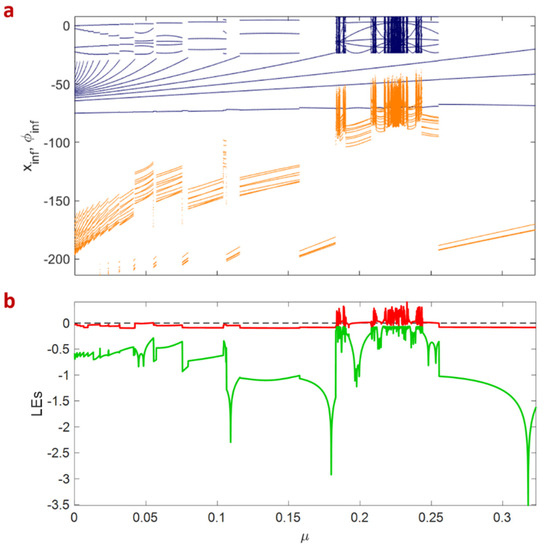
Figure 2.
(a) The bifurcation diagram (navy blue and orange colors refer to the and variables) and (b) the Lyapunov exponents’ diagram of the memristive map model by the variation of with considering , , , , , , , , , , , , , , and . The initial condition is . Periodic behavior is the most noticeable behavior of the neuron; however, for , the periodic bursting can also be observed.
Figure 3 presents the bifurcation diagram and the corresponding Lyapunov exponents by varying the parameter. The assumed initial condition is and the other parameters are , , , , , , , , , , , , , , and . It can be observed that for , the neuron has periodic behavior, and chaotic bursting emerges for . In addition, many periodic windows can be noticed in ; however, , , and are the three most prominent ones. The most significant detected behaviors in these periodic windows are period-halving and period-doubling bifurcations.
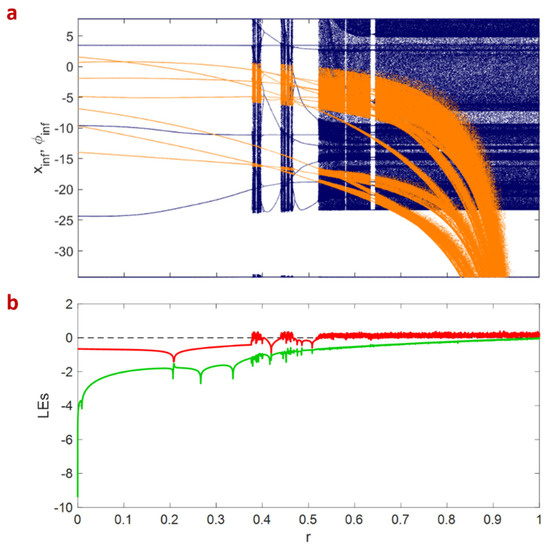
Figure 3.
(a) The bifurcation diagram (navy blue and orange colors refer to the and variables) and (b) the Lyapunov exponents’ diagram of the memristive map model by the variation of with considering , , , , , , , , , , , , , , and . The initial condition is . The neuron has periodic behavior for ; however, by increasing the parameter, the most significant behavior of the neuron is chaotic bursting.
3. Network’s Dynamics
The collective behavior of the coupled proposed memristive map is also investigated. The neurons are assumed to be coupled via simultaneous electrical and chemical synapses in a bidirectional ring topology. Thus, the implemented network can be formulated as follows:
where and are, respectively, the electrical and chemical synaptic strengths, and , , and are the control parameters. Here, these parameters are set at , , and . Moreover, is the square matrix that determines the bidirectional ring topology. The parameters of the model are set at , , , , , , , , , , , , , , and , where the neuron exhibits chaotic bursting.
Considering a ring network of 100 memristive neuron maps, the synchronization error is calculated as a criterion for evaluating the synchronization of the neurons. This criterion is defined as follows:
Here, and are, respectively, the network size and the run time (number of samples) of the map. Considering the mentioned parameters, the synchronization error is obtained under three conditions. In the first condition, is set to zero, which means the neurons are coupled only through chemical synapses, and the synchronization error is obtained for 100 chemically coupled neurons. Similarly, in the second condition, is set to zero, and the synchronization error is calculated for the ring network of electrically coupled neurons. Figure 4a represents the synchronization error of the chemically coupled neurons for different chemical synaptic strengths. The network reaches complete synchronization only for a small range of chemical coupling strengths (). For , the neurons become unstable. Figure 4b shows the synchronization error of the neurons coupled through electrical synapses. It is observed that the synchronization error is high for any electrical coupling strength. Therefore, the electrically coupled neurons cannot become synchronized.
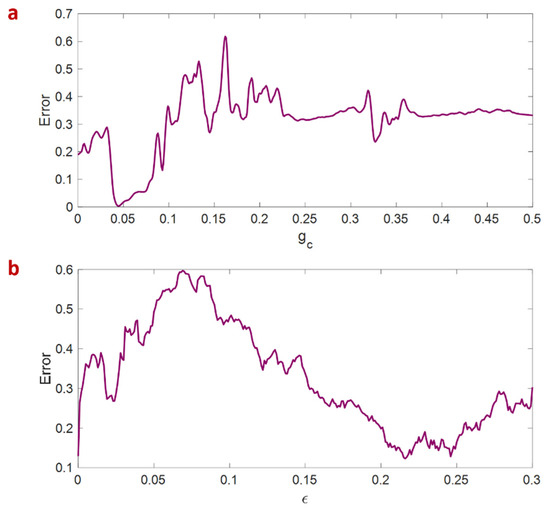
Figure 4.
Synchronization error of the network of 100 memristive neuron maps connected through (a) chemical and (b) electrical synapses by the variation of coupling strengths. The network parameters are , , and . Complete synchronization can be observed in chemically coupled neurons for .
In the third condition, the effects of the simultaneous alteration of both chemical and electrical coupling strengths are investigated on the synchronization state. Figure 5 represents the synchronization error by the variation of chemical and electrical synaptic strengths. As shown in Figure 5, the complete synchronization can only be obtained in small ranges of chemical coupling strengths for any electrical coupling strength. However, by increasing the electrical coupling strength, the synchronous region firstly shrinks until and then enlarges again. Dark magenta in this figure represents the region of complete synchronization state. Consequently, it seems that in this case, chemical synaptic coupling plays an essential role in reaching complete synchronization.
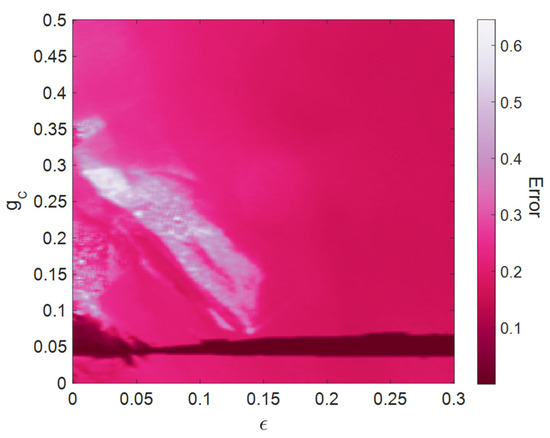
Figure 5.
Synchronization error of the ring network of 100 memristive maps connected through both chemical and electrical synaptic couplings by the variation of coupling strengths. The network parameters are , , and . Complete synchronization can be observed for a small range of chemical coupling strength.
By looking more closely at the network dynamics, other collective behaviors can be observed among the neurons connected through chemical couplings. Figure 6 illustrates three different behaviors of the network named imperfect synchronization, complete synchronization, and solitary state for different values. The spatiotemporal patterns along with the snapshots and the time series of neurons are shown for each state. Figure 6a,b show an imperfect synchronization for . In this case, although the majority of the neurons are synchronous, a few of them have escaped from synchronization. The behavior of the escaped neurons is the same as those synchronized. Therefore, the pattern can be called imperfect synchronization. Figure 6c,d represent the complete synchronization for . For a stronger chemical coupling strength, the solitary state can be observed. Figure 6e,f illustrate the solitary state for ; in this case, the escaped neurons oscillate with a different firing pattern from the synchronized ones.
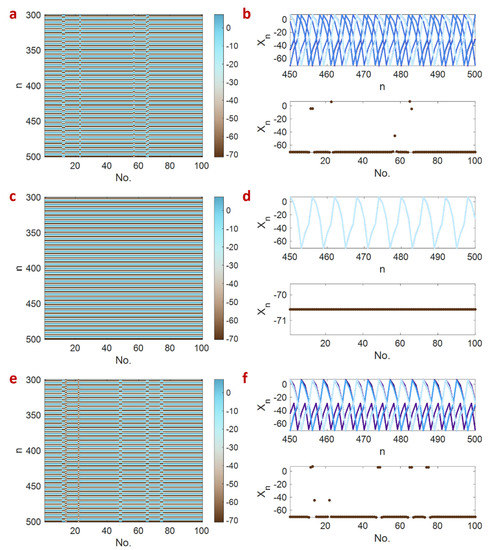
Figure 6.
The spatiotemporal patterns (left panel) and the time series and snapshots (right panel) of the network of 100 memristive neuron maps coupled via chemical synapses. (a,b) For , imperfect synchronization is observed. (c,d) For , complete synchronization is achieved. (e,f) For , the solitary state appears.
By increasing the electrical synaptic strengths, more types of collective behaviors can be observed. Figure 7 demonstrates the network’s spatiotemporal patterns along with its time series and snapshots in three states, namely, two-cluster synchronization, chimera, and nonstationary chimera. In Figure 7a,b, which are plotted for and , it can be observed that the neurons are synchronized in two groups; thus, the pattern is called two-cluster synchronization. Figure 7c,d present the chimera state for and . As two groups of coherent and incoherent neurons are formed, the pattern is the chimera state. Another type of chimera with moving incoherent clusters, i.e., the nonstationary chimera, can be seen in Figure 7e,f for and . In this case, the positions of incoherent neurons vary in time.
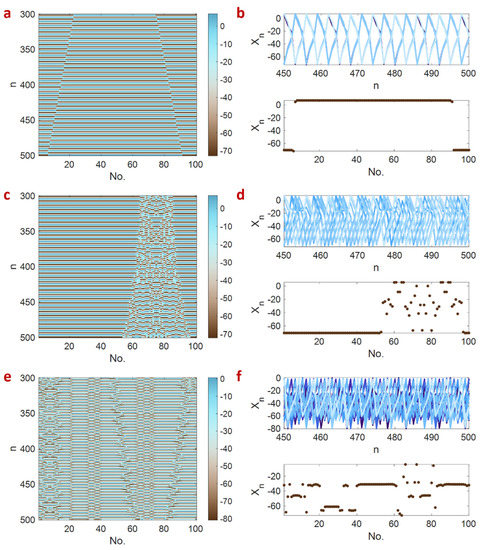
Figure 7.
The spatiotemporal patterns (left panel) and the time series and snapshots (right panel) of the network of 100 memristive neuron maps coupled via electrochemical synapses. (a,b) For and , imperfect synchronization is formed. (c,d) For and , the chimera state is observed. (e,f) For and , the nonstationary chimera appears.
4. Conclusions
The presented paper was mainly divided into two parts. Firstly, the memristive version of a newly proposed neuron map model was introduced. A one-dimensional map-based neuronal model was defined based on the phase space by Zandi et al. in 2020 [21]. Here, we modified this map by adding a discrete memristor, as in [26], to consider the electromagnetic effects. The bifurcation diagrams and the Lyapunov exponents were obtained to study the dynamics of the proposed memristive model. These diagrams showed that the memristive map could exhibit different neuronal behaviors, such as spiking, periodic bursting, and chaotic bursting.
Secondly, the collective behavior of the proposed memristive map was investigated by locating 100 neurons in a bidirectional ring network with both electrical and chemical synaptic couplings. The synchronization error was computed to find whether the network could become completely synchronized. This criterion was calculated under three conditions considering only electrical synapses, only chemical synapses, and both electrical and chemical synapses. The results showed that the ring network of chemically coupled maps could be completely synchronized, while the network could not become synchronized through electrical synaptic couplings. Besides, when coupled through both electrical and chemical synapses, the complete synchronization state could be observed in a small range of chemical coupling strength. This range can become wider by the increase of electrical coupling strength. In addition to the complete synchronization, imperfect synchronization, solitary states, two-cluster synchronization, chimera, and nonstationary chimera were detected in different electrical and chemical coupling strengths.
Author Contributions
Conceptualization, K.R. and S.J.; methodology, F.P.; software, B.R. and M.M.; validation, F.P. and K.R.; investigation, B.R. and M.M.; writing—original draft preparation, M.M. and B.R.; writing—review and editing, F.P. and S.J.; visualization, K.R.; supervision, S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work is partially funded by Centre for Nonlinear Systems, Chennai Institute of Technology, India vide funding number CIT/CNS/2021/RD/064.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
References
- Chua, L. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef]
- Borghetti, J.; Li, Z.; Straznicky, J.; Li, X.; Ohlberg, D.A.; Wu, W.; Stewart, D.R.; Williams, R.S. A hybrid nanomemristor/transistor logic circuit capable of self-programming. Proc. Natl. Acad. Sci. USA 2009, 106, 1699–1703. [Google Scholar] [CrossRef] [Green Version]
- Strukov, D.B.; Williams, R.S. Four-dimensional address topology for circuits with stacked multilayer crossbar arrays. Proc. Natl. Acad. Sci. USA 2009, 106, 20155–20158. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Hu, M.; Li, Y.; Jiang, H.; Ge, N.; Montgomery, E.; Zhang, J.; Song, W.; Dávila, N.; Graves, C.E. Analogue signal and image processing with large memristor crossbars. Nat. Electron. 2018, 1, 52–59. [Google Scholar] [CrossRef]
- Duan, S.; Hu, X.; Dong, Z.; Wang, L.; Mazumder, P. Memristor-based cellular nonlinear/neural network: Design, analysis, and applications. IEEE Trans. Neural Netw. Learn. Syst. 2014, 26, 1202–1213. [Google Scholar] [CrossRef]
- Tan, Y.; Wang, C. A simple locally active memristor and its application in HR neurons. Chaos 2020, 30, 053118. [Google Scholar] [CrossRef]
- Mladenov, V.; Kirilov, S. A nonlinear drift memristor model with a modified biolek window function and activation threshold. Electronics 2017, 6, 77. [Google Scholar] [CrossRef] [Green Version]
- Mladenov, V.; Kirilov, S. A Memristor Model with a Modified Window Function and Activation Thresholds. In Proceedings of the 2018 IEEE International Symposium on Circuits and Systems (ISCAS), Florence, Italy, 27–30 May 2018; pp. 1–5. [Google Scholar]
- Mladenov, V.; Kirilov, S. Learning of an Artificial Neuron with Resistor-Memristor Synapses. In Proceedings of the ANNA ‘18; Advances in Neural Networks and Applications 2018, St. Konstantin and Elena Resort, Bulgaria, 15–17 September 2018; pp. 1–5. [Google Scholar]
- Thomas, A. Memristor-based neural networks. J. Phys. D 2013, 46, 093001. [Google Scholar] [CrossRef] [Green Version]
- Hua, M.; Wu, H.; Xu, Q.; Chen, M.; Bao, B. Asymmetric memristive Chua’s chaotic circuits. Int. J. Electron. 2020, 108, 1106–1123. [Google Scholar] [CrossRef]
- Usha, K.; Subha, P. Hindmarsh-Rose neuron model with memristors. Biosystems 2019, 178, 1–9. [Google Scholar]
- Bao, H.; Hu, A.; Liu, W.; Bao, B. Hidden bursting firings and bifurcation mechanisms in memristive neuron model with threshold electromagnetic induction. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 502–511. [Google Scholar] [CrossRef]
- Lin, H.; Wang, C.; Sun, Y.; Yao, W. Firing multistability in a locally active memristive neuron model. Nonlinear Dyn. 2020, 100, 3667–3683. [Google Scholar] [CrossRef]
- Hu, X.; Liu, C. Dynamic property analysis and circuit implementation of simplified memristive Hodgkin–Huxley neuron model. Nonlinear Dyn. 2019, 97, 1721–1733. [Google Scholar] [CrossRef]
- Morris, C.; Lecar, H. Voltage oscillations in the barnacle giant muscle fiber. Biophys. J. 1981, 35, 193–213. [Google Scholar] [CrossRef] [Green Version]
- Ibarz, B.; Casado, J.M.; Sanjuán, M.A. Map-based models in neuronal dynamics. Phys. Rep. 2011, 501, 1–74. [Google Scholar] [CrossRef]
- Rulkov, N.F. Modeling of spiking-bursting neural behavior using two-dimensional map. Phys. Rev. E 2002, 65, 041922. [Google Scholar] [CrossRef] [Green Version]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef] [Green Version]
- Zandi-Mehran, N.; Panahi, S.; Hosseini, Z.; Golpayegani, S.M.R.H.; Jafari, S. One dimensional map-based neuron model: A phase space interpretation. Chaos Soliton. Fractal. 2020, 132, 109558. [Google Scholar] [CrossRef]
- Mesbah, S.; Moghtadaei, M.; Golpayegani, M.R.H.; Towhidkhah, F. One-dimensional map-based neuron model: A logistic modification. Chaos Soliton. Fractal. 2014, 65, 20–29. [Google Scholar] [CrossRef]
- Bao, B.-C.; Li, H.; Wu, H.; Zhang, X.; Chen, M. Hyperchaos in a second-order discrete memristor-based map model. Electron. Lett. 2020, 56, 769–770. [Google Scholar] [CrossRef]
- Bao, H.; Hua, Z.; Li, H.; Chen, M.; Bao, B. Discrete Memristor Hyperchaotic Maps. IEEE Trans. Circuits Syst. I 2021, 68, 4534–4544. [Google Scholar] [CrossRef]
- Li, H.; Hua, Z.; Bao, H.; Zhu, L.; Chen, M.; Bao, B. Two-dimensional memristive hyperchaotic maps and application in secure communication. IEEE Trans. Ind. Electron. 2021, 68, 9931–9940. [Google Scholar] [CrossRef]
- Li, K.; Bao, H.; Li, H.; Ma, J.; Hua, Z.; Bao, B.-C. Memristive Rulkov Neuron Model with Magnetic Induction Effects. IEEE Trans. Ind. Inf. 2021, 18, 1726–1736. [Google Scholar] [CrossRef]
- Volos, C.K.; Kyprianidis, I.; Stouboulos, I.; Tlelo-Cuautle, E.; Vaidyanathan, S. Memristor: A New Concept in Synchronization of Coupled Neuromorphic Circuits. J. Eng. Sci. Technol. 2015, 8, 157–173. [Google Scholar]
- Xu, Y.; Jia, Y.; Ma, J.; Alsaedi, A.; Ahmad, B. Synchronization between neurons coupled by memristor. Chaos Soliton. Fractal. 2017, 104, 435–442. [Google Scholar] [CrossRef]
- Bao, H.; Zhang, Y.; Liu, W.; Bao, B. Memristor synapse-coupled memristive neuron network: Synchronization transition and occurrence of chimera. Nonlinear Dyn. 2020, 100, 937–950. [Google Scholar] [CrossRef]
- Chavez, M.; Hwang, D.-U.; Boccaletti, S. Synchronization processes in complex networks. Eur. Phys. J. Spec. Top. 2007, 146, 129–144. [Google Scholar] [CrossRef]
- Chowdhury, S.N.; Majhi, S.; Ozer, M.; Ghosh, D.; Perc, M. Synchronization to extreme events in moving agents. New J. Phys. 2019, 21, 073048. [Google Scholar] [CrossRef]
- Rajagopal, K.; Jafari, S.; Karthikeyan, A.; Srinivasan, A. Effect of magnetic induction on the synchronizability of coupled neuron network. Chaos 2021, 31, 083115. [Google Scholar] [CrossRef]
- Rybalova, E.; Strelkova, G.; Schöll, E.; Anishchenko, V. Relay and complete synchronization in heterogeneous multiplex networks of chaotic maps. Chaos 2020, 30, 061104. [Google Scholar] [CrossRef]
- Bukh, A.V.; Schöll, E.; Anishchenko, V. Synchronization of spiral wave patterns in two-layer 2D lattices of nonlocally coupled discrete oscillators. Chaos 2019, 29, 053105. [Google Scholar] [CrossRef] [PubMed]
- Andrzejak, R.G.; Ruzzene, G.; Malvestio, I.; Schindler, K.; Schöll, E.; Zakharova, A. Mean field phase synchronization between chimera states. Chaos 2018, 28, 091101. [Google Scholar] [CrossRef] [PubMed]
- Ibrahim, M.M.; Kamran, M.A.; Mannan, M.M.N.; Jung, I.H.; Kim, S. Lag synchronization of coupled time-delayed FitzHugh–Nagumo neural networks via feedback control. Sci. Rep. 2021, 11, 3884. [Google Scholar] [CrossRef] [PubMed]
- Della Rossa, F.; Pecora, L.; Blaha, K.; Shirin, A.; Klickstein, I.; Sorrentino, F. Symmetries and cluster synchronization in multilayer networks. Nat. Commun. 2020, 11, 3179. [Google Scholar] [CrossRef]
- Rybalova, E.; Vadivasova, T.; Strelkova, G.; Anishchenko, V.S.; Zakharova, A. Forced synchronization of a multilayer heterogeneous network of chaotic maps in the chimera state mode. Chaos 2019, 29, 033134. [Google Scholar] [CrossRef] [PubMed]
- zur Bonsen, A.; Omelchenko, I.; Zakharova, A.; Schöll, E. Chimera states in networks of logistic maps with hierarchical connectivities. Eur. Phys. J. B 2018, 91, 65. [Google Scholar] [CrossRef] [Green Version]
- Rybalova, E.; Anishchenko, V.; Strelkova, G.; Zakharova, A. Solitary states and solitary state chimera in neural networks. Chaos 2019, 29, 071106. [Google Scholar] [CrossRef] [PubMed]
- Parastesh, F.; Jafari, S.; Azarnoush, H.; Shahriari, Z.; Wang, Z.; Boccaletti, S.; Perc, M. Chimeras. Phys. Rep. 2021, 898, 1–114. [Google Scholar] [CrossRef]
- Hussain, I.; Jafari, S.; Ghosh, D.; Perc, M. Synchronization and chimeras in a network of photosensitive FitzHugh–Nagumo neurons. Nonlinear Dyn. 2021, 104, 2711–2721. [Google Scholar] [CrossRef]
- Majhi, S.; Perc, M.; Ghosh, D. Chimera states in a multilayer network of coupled and uncoupled neurons. Chaos 2017, 27, 073109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shafiei, M.; Jafari, S.; Parastesh, F.; Ozer, M.; Kapitaniak, T.; Perc, M. Time delayed chemical synapses and synchronization in multilayer neuronal networks with ephaptic inter-layer coupling. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105175. [Google Scholar] [CrossRef]
- Sun, X.; Perc, M.; Lu, Q.; Kurths, J. Effects of correlated Gaussian noise on the mean firing rate and correlations of an electrically coupled neuronal network. Chaos 2010, 20, 033116. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, Q.; Perc, M.; Duan, Z.; Chen, G. Synchronization transitions on scale-free neuronal networks due to finite information transmission delays. Phys. Rev. E 2009, 80, 026206. [Google Scholar] [CrossRef] [Green Version]
- Rakshit, S.; Ray, A.; Bera, B.K.; Ghosh, D. Synchronization and firing patterns of coupled Rulkov neuronal map. Nonlinear Dyn. 2018, 94, 785–805. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).