Abstract
This paper presents inductance simulators using the voltage differencing differential input buffered amplifier (VD-DIBA) as an active building block. Three types of inductance simulators, including floating lossless inductance, series inductance-resistance, and parallel inductance-resistance simulators, are proposed, in addition to their application to the 4th order elliptic lowpass ladder filter. The simple design procedures of these inductance simulators using a circuit block diagram are also given. The proposed inductance simulators employ two VD-DIBAs and two passive elements. The complementary metal oxide semiconductor (CMOS) VD-DIBA used in this design utilizes the multiple-input metal oxide semiconductor (MOS) transistor technique in order to achieve a compact and simple structure with a minimum count of transistors. Thanks to this technique, the VD-DIBA offers high performances compared to the other CMOS structures presented in the literature. The CMOS VD-DIBAs and their applications are designed and simulated in the Cadence environment using a 0.18 µm CMOS process from Taiwan semiconductor manufacturing company (TSMC). Using a supply voltage of ±0.9 V, the linear operation of VD-DIBA is obtained over a differential input range of −0.5 V to 0.5 V. The lowpass (LP) ladder filter realized with the proposed inductance simulators shows a dynamic range (DR) of 80 dB for a total harmonic distortion (THD) of 2% at 1 kHz and a 1.8 V peak-to-peak output. In addition, the experimental results of the floating inductance simulators and their applications are obtained by using VD-DIBA constructed from the available commercial components LM13700 and AD830. The simulation results are in agreement with the experimental ones, confirming the advantages of the inductance simulators and their application.
1. Introduction
The realization of inductance simulators to be used instead of the passive inductor in the analog signal processing system is an interesting research topic which has been constantly gaining attention. The use of inductance simulators in circuit design also presents several advantages compared to the passive inductor, such as inductance controllability, a small chip area, a high quality factor, low noise, and low power consumption [1]. Moreover, the procedure employed to synthesize the analog circuits by replacing the passive inductors with inductance simulators is easy to understand and implement without using advanced or complicated mathematics [2,3,4]. For example, the design of the 4th ladder bandpass filter consisting of the passive inductors L1 and L2, passive resistors R1 and R2, and passive capacitors C1 and C2 in Figure 1 is easily achieved by replacing the grounded inductance simulator and the floating inductance simulator instead of these passive inductors [2].
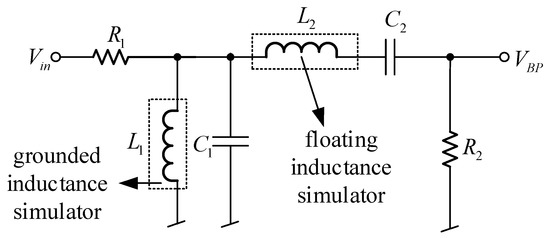
Figure 1.
Design of the 4th ladder bandpass filter by replacing the inductance simulators instead of passive inductors [2].
In analog circuit synthesis and design, active building blocks (ABBs) are very useful devices [5]. They provide flexibility and convenience when synthesizing high performance circuits connecting a small number of passive elements, such as resistors or capacitors (the use of passive inductors is not popular for circuit design). Most typical designs rely on the connection of sub-circuits, so voltage-mode ABBs with a high input impedance and low output impedance or current-mode ABBs with a low input impedance and high output impedance can provide a cascading ability, without the use of buffer devices at input and output stages. Additionally, ascertaining the circuit properties from ABB-based circuit analysis is easier than ascertaining those of transistor-based circuits. Moreover, some electronically controllable ABBs, which are required for modern circuits, are easily and automatically controlled by a microprocessor or microcomputer [5].
Many examples of different active building blocks have been proposed in [5], where the operational transconductance amplifier (OTA) is combined with other active sub-blocks, such as a current follower (CF), a current differencing unit (CDU), a voltage buffer (BF), or a voltage differencing unit (VDU). One of the ABBs which can be developed using the above-mentioned sub-blocks is the voltage differencing buffered amplifier (VDBA). This active device is composed of OTA at the input stage, and a voltage buffer at the output. With this structure, the VDBA has a low output impedance and high input impedance, which is useful in circuit design, since active blocks can be cascaded in voltage-mode circuits, without the requirement of additional voltage buffers [5,6]. VDBA-based circuits can be found in the open literature [7,8,9,10,11,12,13,14,15,16,17]. However, in some applications, the unity gain voltage differencing circuit is required, which cannot be directly realized with VDBAs. Therefore, the voltage differencing differential input buffered amplifier (VD-DIBA) was proposed to extend the universality of the VDBA, by combining OTA and a voltage differencing unit with a low output impedance. There are many applications of VD-DIBA presented in the literature, such as filters [18,19,20,21,22,23,24], sinusoidal oscillators [25,26,27,28,29,30], and inductance simulators [31,32,33].
Although the VD-DIBA is an interesting active block, its CMOS structures presented in the literature thus far are rather complex and show many limitations. Usually, the transconductance stage of the VD-DIBA is realized as a simple differential amplifier, which limits its linearity. The voltage differencing stage is realized with two differential pairs that increase the number of MOS transistors and current branches, and consequently, the current consumption of the circuits [23,29,30]. In order to avoid the above limitations, a new CMOS structure of VD-DIBA is presented in this paper. The multiple-input gate-driven technique (MI-GD) is employed to reduce the number of differential pairs required to build this active block. The transconductance stage is realized by an MI-GD two-stage OTA with unity gain feedback. Thanks to the MI-GD technique and the unity gain feedback, the linearity of the transconductor is significantly improved. The voltage differencing stage is realized with only one MI-GD differential pair, which decreases the total power dissipation of the circuit.
Recently, Khateb et al. presented the principle and experimental results of the multiple-input MOS transistor technique [34,35,36]. The multiple-input MOS transistor is obtained with a simple analog summing circuit composed of parallel connections of capacitors and large resistances, connecting each input of this composite device with the input terminal of the MOS transistor. The input terminal can be the bulk [34,37], the bulk along with the quasi-floating-gate [35], the bulk along with the gate (DTMOS) [38], or the gate [39,40]. The main advantages of this technique are the simplification of the CMOS structure of some active blocks, reduction of the current consumption, and increase of the dynamic range of the circuit due to the input capacitive divider [34,35,36]. This technique can also simplify the realization of some applications, which results in lower power dissipation and a reduced silicon area.
This paper presents the realization of inductance simulators using VD-DIBA based on the multiple-input technique and shows their application in the 4th order elliptic lowpass ladder filter. The paper is organized as follows: Section 2 and Section 3 present the CMOS structure of the VD-DIBA and its simulated performances; the floating inductance simulators and filter application are presented in Section 4; Section 5 and Section 6 present the simulation and experimental results of floating inductance simulators and an exemplary filter; Section 7 presents a comparison of the proposed inductance simulators with previous works; and finally, Section 8 concludes the paper.
2. The Compact CMOS Structure of the VD-DIBA
2.1. Basic Concept of VD-DIBA
The VD-DIBA is a connection of OTA and a voltage differencing unit. The circuit symbol is shown in Figure 2a. The high-impedance input voltage terminals are v+, v−, z, and v. The low-impedance output voltage terminal is w. Note that the z terminal is also the output current terminal. Figure 2b shows the equivalent schematic of VD-DIBA in an ideal case. The circuit performance is described by the matrix Equation (1) [18].
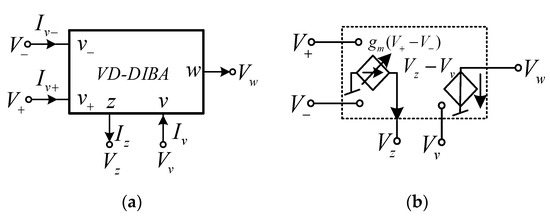
Figure 2.
(a) The symbolic representation of the voltage differencing differential input buffered amplifier (VD-DIBA) and (b) VD-DIBA equivalent circuit [18].
2.2. Internal Construction of Compact CMOS VD-DIBA
Figure 3 shows the realization of VD-DIBA with two multiple-input OTAs. The OTA1 with a negative feedback connection and the resistor Rset create a transconductance stage (gm). The transconductance is adjustable with Rset and its value is approximately given by gm≈1/Rset [41]. If the transconductance value needs to be electronically controlled, then Rset can be replaced, for instance, by a voltage-controlled resistance based on a simple CMOS circuitry. It is worth noting that the negative feedback connection of OTA1 significantly enhances the linearity of the transconductor compared with conventional OTA, which uses the bias current to set its transconductance value [41]. The second multiple-input OTA2 with unity gain feedback is used to transfer the voltage difference between z and v terminals to the output terminal w.
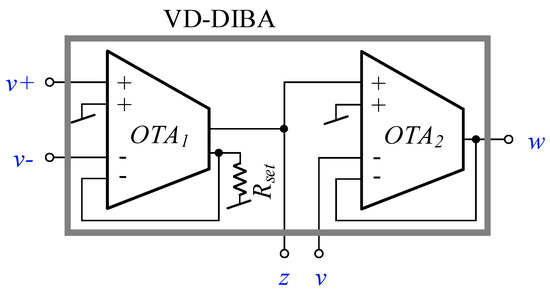
Figure 3.
The VD-DIBA based on a multiple-input operational transconductance amplifier (OTA).
The CMOS structure of the proposed VD-DIBA is shown in Figure 4. The OTA1 consists of a differential stage (M1, M2, M5, M10, and M11), followed by two class AB output stages (M6 and M12 and M7 and M13). The Cc1 is the frequency compensation capacitor that ensures the stability of the OTA. The large resistance RMOS1 is used to set the DC bias voltage Vb at the gates of M12 and M13, whereas the capacitor C1 creates an AC signal path, so class AB output stages are obtained. The differential pair (M1 and M2) is based on multiple-input transistors, realized by an MOS transistor with its gate connected to a parallel connection of a couple of large value resistances RMOSi along with capacitor CGi (i = 1, 2, …, n), where n is the number of required inputs, as depicted in Figure 5. The resistor RMOS is realized by two MOS transistors operating in a cut-off region, so the chip area occupied by this resistor is minimal. Note that unlike the conventional multiple-input OTA that requires multiple differential pairs, which increase the circuit complexity and power consumption, the proposed only OTA requires one differential pair. Consequently, the CMOS circuitries that use the multiple-input MOS transistors are compact, with a reduced power consumption [34,35,36,37,40,42,43]. The bias current Ib and the transistor M17 set the bias currents and voltages for the OTA. The OTA2 is a copy of OTA1 with one output stage that serves as a voltage differencing unit. It is worth mentioning that the principle of the multiple-input MOS transistor was first presented and experimentally verified in [34,35,36].
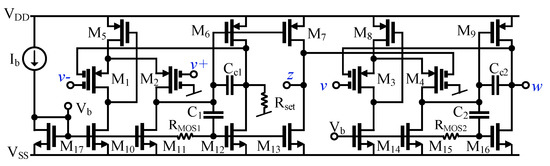
Figure 4.
The CMOS structure of the VD-DIBA.
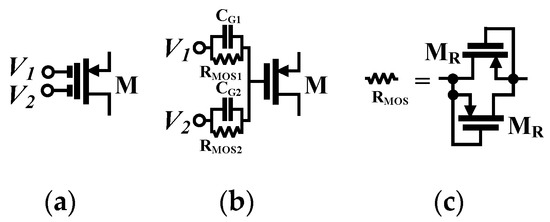
Figure 5.
The multiple-input MOS transistor: (a) Symbol; (b) realization; and (c) realization of RMOS [34].
3. Simulation Result of VD-DIBA’s Performances
To validate the performances of the voltage differencing differential input buffered amplifier (VD-DIBA) in Figure 4, extensive simulations in the Cadence/Spectre environment were performed, assuming the 0.18 μm TSMC CMOS technology. The transistor aspect ratios, capacitors, voltage supply, and bias current values are included in Table 1. The total power consumption was 0.99 mW. Figure 6 shows the DC transfer characteristic of the transconductance stage for different resistances Rset = 15, 20, 25, and 30 kΩ. It is worth noting the tunability and the good linearity obtained over a differential input range of −0.5 to 0.5 V. Figure 7 shows the output voltage Vw against the input voltage Vv for different values of Vz. The correct operation of the voltage differential unit is clearly visible. The frequency responses of Vw/Vv and Vw/Vz are shown in Figure 8. The histogram of the low frequency gain at 1 kHz and the −3 dB bandwidth of these responses with Monte Carlo (MC) analysis are shown in Figure 9, Figure 10, Figure 11 and Figure 12. For Figure 9 and Figure 10, the mean value of the gain is −7.07 and 5.79 mdB, while the standard deviation is 0.19 and 0.39 mdB for the Vw/Vv and Vw/Vz gain, respectively. For Figure 11 and Figure 12, the mean value of the −3 dB bandwidth is 6.37 and 6.11 MHz, while the standard deviation is 121.5 and 89 kHz for the Vw/Vv and Vw/Vz gain, respectively. The MC analysis confirms the low sensitivity of the VD-DIBA to transistor mismatch.

Table 1.
Transistor aspect ratios and component values.
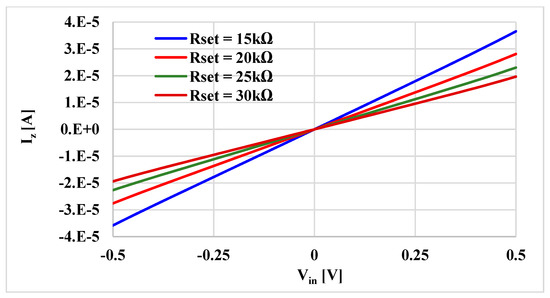
Figure 6.
The DC transfer characteristic of the transconductor for different Rset.
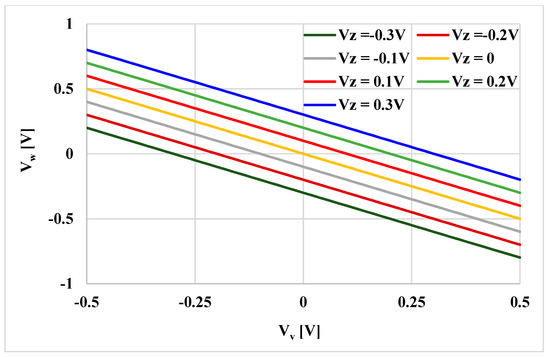
Figure 7.
The output voltage VW versus the input voltage Vv for different Vz.
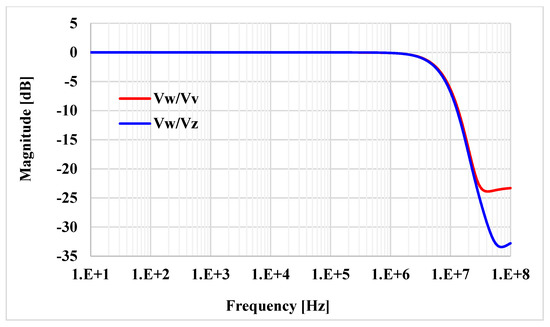
Figure 8.
The frequency responses of Vw/Vv and Vw/Vz.
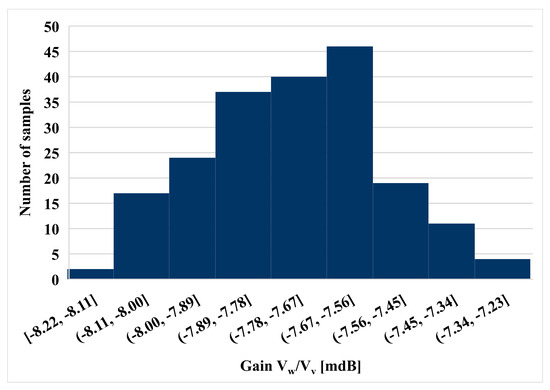
Figure 9.
A histogram of the voltage gain Vw/Vv with 200 runs Monte Carlo (MC) analysis.
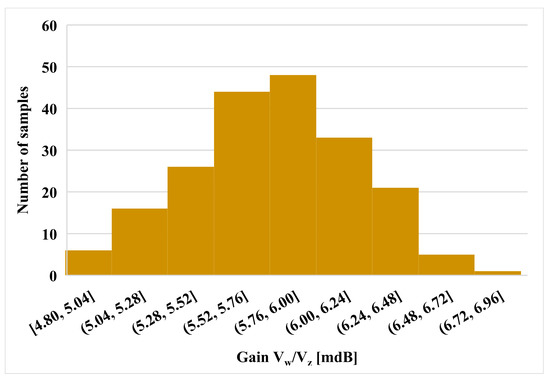
Figure 10.
A histogram of the voltage gain Vw/Vz with 200 runs MC analysis.
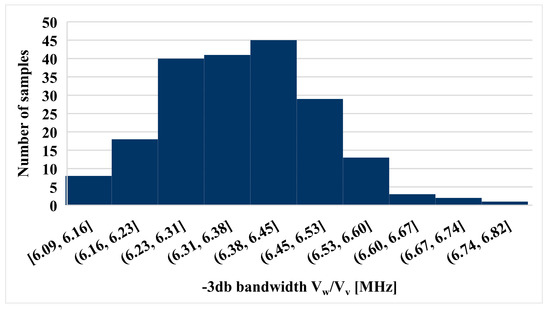
Figure 11.
A histogram of the −3 dB bandwidth Vw/Vv with 200 runs MC analysis.
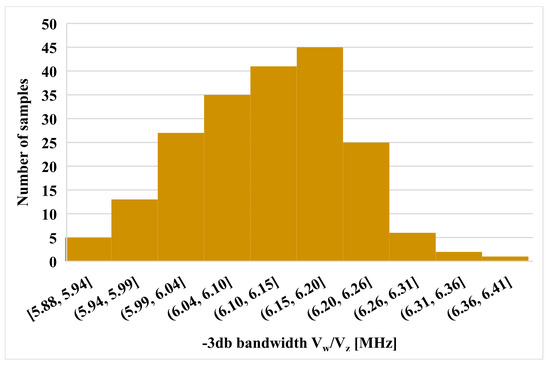
Figure 12.
A histogram of the −3 dB bandwidth Vw/Vz with 200 runs MC analysis.
The process, voltage, temperature (PVT) corner analysis was also performed for the proposed VD-DIBA. The MOS transistor corners were [ss, sf, fs, ff], the capacitor corners were [slow, fast], the temperature corners were [−10 °C, 80 °C], and the voltage supply corners +VDD = −VSS were [895 mV, 905 mV]. The results of this analysis, including the minimum, typical, and maximum values, are summarized in Table 2 and confirm the acceptable performance of the circuit under PVT variations.

Table 2.
Process, voltage, temperature (PVT) corner analysis.
4. The Proposed Floating Inductance Simulators Using VD-DIBAs
4.1. The Proposed Floating Lossless Inductance Simulator
There are many methods for synthesizing analog circuits in a signal processing system. Synthesizing based on a circuit block diagram attracts the most attention. This method is easy to understand and implement without using advanced or complicated mathematics. Therefore, the procedure for synthesizing the floating lossless inductance simulator in this paper is based on the block diagram in Figure 13. The circuit uses three kinds of sub-circuits, namely, two voltage to current converters (V to I converters), a voltage-mode lossy integrator, and two voltage differencing circuits. This block diagram can be considered a modified version of the one in [44], where the active building block has three input voltage terminals, which are not available for VD-DIBA. The time constant of the integrator is denoted as τ, while the transconductance gain of the V to I converter is denoted as k. The voltages at the first and second ports are denoted as v1 and v2, respectively. Moreover, the currents at the first and second port are denoted as i1 and i2, respectively. The magnitudes of currents i1 and i2 are the output current of the first and second voltage to current converters, respectively. Ideally, the currents i1 and i2 must be equal. Therefore, the transconductance gains of both voltage to current converters are set to be equal to each other (k1 = k2 = k). The input impedance between the first and second ports in Figure 13 is given by
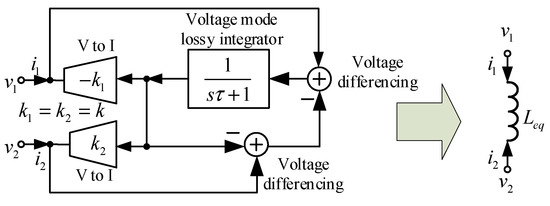
Figure 13.
Block diagram presenting the synthesis of the floating lossless inductance simulator.
Note that the voltage differencing unit at the output stage of VD-DIBA is very useful for realizing the voltage difference v1 − v2. Equation (2) obviously shows that the input impedance of the block diagram presented in Figure 13 can be considered the impedance of a floating lossless inductance simulator, where its equivalent inductance is given by
Equation (3) shows that the inductance value can be tuned with the time constant of an integrator and the transconductance gain of a V to I converter.
The VD-DIBA will be used as an active element to synthesize the floating lossless inductance simulator. Referring to the block diagram in Figure 13, the first V to I converter and voltage differencing part are realized with VD-DIBA1, while the second V to I converter and voltage differencing part are implemented by the VD-DIBA2. The voltage mode lossy integrator is realized from a simple RC voltage divider circuit, where the capacitor is connected to the ground. By connecting sub-circuits based on the block diagram presented in Figure 13, the proposed floating lossless inductance simulator is achieved as shown in Figure 14. For gm1 = gm2 = gm, the input impedance between the first and second ports of Figure 14 is given by
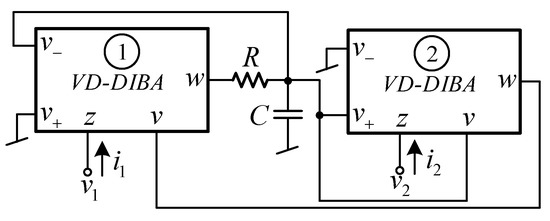
Figure 14.
The floating lossless inductance simulator based on VD-DIBAs.
Equation (4) shows that the circuit exhibited in Figure 14 simulates the impedance of the floating lossless inductance simulator, where its equivalent inductance value is given by
Note that the inductance value can be tuned by R, C, and gm.
Comparing the proposed structure in Figure 14 with the floating lossless inductance simulator using VD-DIBA as an active element in [32] and [33], it is found that the active inductor in [32] requires a matching condition of the passive resistor and transconductance of VD-DIBA, while the floating inductance simulator proposed in [33] employs three VD-DIBAs. In addition, these inductance simulators are based on a lossless integrator.
4.2. The Proposed Floating Series Inductance-Resistance Simulator
For the proposed floating series inductance-resistance (L-R) simulator, the synthesis procedure is based on the block diagram presented in Figure 15. Like the proposed lossless inductance simulator, there are three sub-circuits for synthesizing the series inductance resistance simulator. However, it requires only one voltage differencing circuit. For gm1 = gm2 = gm, the input impedance between the first and second port of Figure 15 is given by
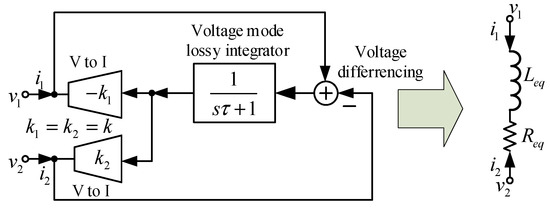
Figure 15.
Block diagram showing the synthesis of the floating series inductance-resistance simulator.
As can be concluded from (6), the input impedance of the block diagram in Figure 15 can be considered the impedance of the floating series connection of an inductor and a resistor, where its equivalent inductance value is the same as that given by (2) and the equivalent resistance value is given by
Equation (7) shows that the equivalent resistance can be controlled by the transconductance gain of a V to I converter.
Referring to Figure 15, the first V to I converter and the voltage differencing part are realized with VD-DIBA1, while the second V to I converter is implemented by VD-DIBA2. The voltage mode lossy integrator is realized with a simple RC voltage divider circuit, where the capacitor is connected to the ground. By connecting sub-circuits based on the block diagram in Figure 15, the proposed floating series inductance-resistance simulator is achieved, as shown in Figure 16. For gm1 = gm2 = gm, the input impedance between the first and second port of Figure 16 is given by
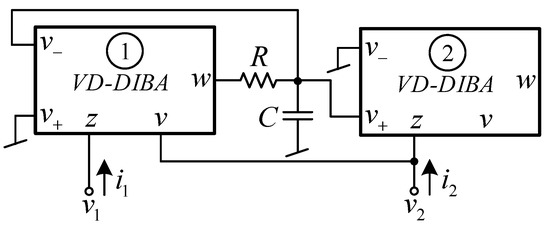
Figure 16.
The floating series inductance-resistance simulator based on VD-DIBAs.
Equation (8) shows that the circuit presented in Figure 16 simulates the impedance of the floating series connection inductor-resistor, where its equivalent inductance value is the same as that given by (4) and the series resistance is given by
Equation (9) shows that the resistance value can be controlled by gm.
Note that the proposed floating series L-R simulator in Figure 16 is synthesized from the same lossy integrator as proposed in [31]. However, the series L-R simulator in [31] only gives the grounded impedance. Additionally, the w terminal is connected to the v terminal to achieve two types of inductance value. With this connection, it is difficult to be modified as a floating type. Another advantage of the proposed floating series L-R simulator in Figure 16 is that, if the second port (v2) is assigned as an output voltage node, then a low output impedance is achieved.
4.3. The Proposed Floating Parallel Inductance-Resistance Simulator
A block diagram presenting the synthesis of the floating parallel inductance-resistance simulator is shown in Figure 17. It consists of two voltage to current converters (V to I), a voltage mode lossy integrator, and two voltage differencing circuits. For k1 = k2 = k, the input impedance between the first and second port in Figure 17 is given by
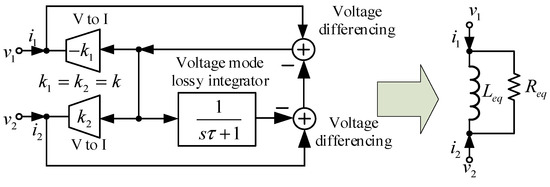
Figure 17.
Block diagram demonstrating the synthesis of the floating parallel inductance-resistance simulator.
Equation (10) shows that the input impedance of the block diagram presented in Figure 17 can be considered the impedance of the floating parallel inductor-resistor, where its equivalent inductance and resistance values are given by (3) and (7), respectively.
Based on the block diagram in Figure 17, the first V to I converter and the voltage differencing part are realized with VD-DIBA1, while the second V to I converter and the voltage differencing part are implemented by VD-DIBA2. The voltage mode lossy integrator is realized with a simple RC voltage divider circuit, where the capacitor is connected to the ground. By connecting sub-circuits based on the block diagram in Figure 17, the proposed floating parallel inductance-resistance simulator is achieved as shown in Figure 18. For gm1 = gm2 = gm, the input impedance between the first and second port of Figure 18 is given by
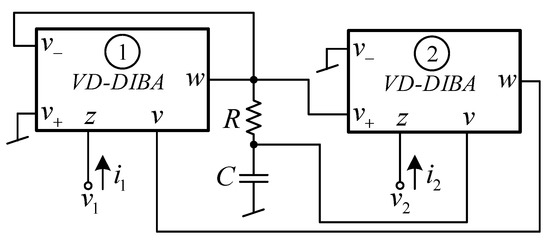
Figure 18.
The floating parallel inductance-resistance simulator based on VD-DIBAs.
Equation (11) obviously demonstrates that the circuit shown in Figure 18 simulates the impedance of the floating parallel inductor-resistor, where its equivalent inductance and resistance values are the same as those in (5) and (9), respectively.
5. Simulation Results of Inductance Simulators
The proposed floating inductance simulators using VD-DIBAs were designed and simulated in the Cadence environment using a 0.18 µm CMOS process from TSMC. The voltage supply was +VDD = −VSS = 0.9 V, and the bias current was Ib = 50 µA. The transistor aspect ratios of the VD-DIBA shown in Figure 4 are listed in Table 1. For the inductance simulators, the values of the passive components were selected as C = 1 nF and R = 10 kΩ, and the value of the resistor of the transconductors was Rset1 = Rset2 = 10 kΩ. Figure 19 shows the simulated impedance (both the magnitude and phase) of the floating lossless inductance simulator at the first port (v1) and second port (v2). The simulated inductance value was about 11.30 mH. The useful frequency range was around 3 decades. It was found that the parasitic resistances in VD-DIBA affect the workability of the active inductor and the performance of the proposed inductance simulator at a high frequency is affected by the parasitic capacitances. As described in (5), the inductance value of the lossless active inductor is adjusted by gm. This theoretical expectation was confirmed by the simulation result in Figure 20, where there are four values of Rset (10, 20, 30, and 40 kΩ). The inductance values simulated from these Rset values were 11.30, 21.51, 30.87, and 39.47 mH, respectively. As shown in the result, the inductance is proportional to the Rset value. The simulated results in Figure 20 are consistent with the expectation in (5).
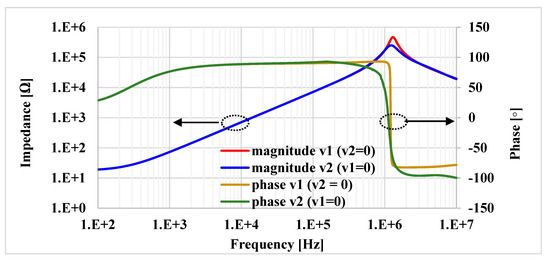
Figure 19.
The frequency and phase responses of the lossless L connection with Rset = 10 kΩ.
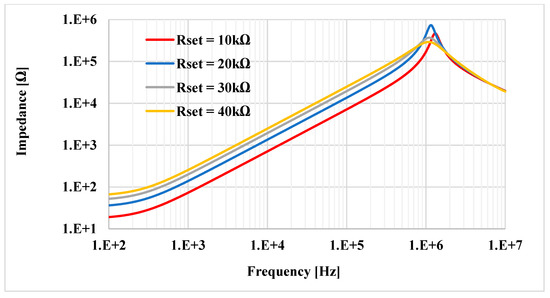
Figure 20.
The frequency responses of the lossless L connection with different Rset.
The simulated impedance (both the magnitude and phase) of the floating inductance-resistance simulator with Rset = 10 kΩ is shown in Figure 21. The simulated inductance and resistance values are about 12.39 mH and 9.22 kΩ, respectively. The impedance of the floating series L-R for different values of Rset is shown in Figure 22, where Rset had four values (10, 20, 30, and 40 kΩ). The inductance values simulated from these Rset values were 12.39, 23.38, 30.92 and 35.29 mH, respectively. Additionally, the resistance values simulated from these Rset values were 9.22, 16.88, 23.41, and 29.04 kΩ, respectively. The simulation performed on the floating parallel inductance-resistance simulator is shown in Figure 23. The simulated inductance and resistance values were about 11.28 mH and 9.43 kΩ, respectively. The impedance of the floating parallel L-R for different values of Rset is shown in Figure 24, where Rset was changed to four values (10, 20, 30, and 40 kΩ). The inductance values simulated from these Rset values were 11.28, 21.48, 30.81, and 39.41 mH, respectively. Furthermore, the resistance values simulated from these Rset values were 9.22, 17.36, 24.08, and 29.79 kΩ, respectively.
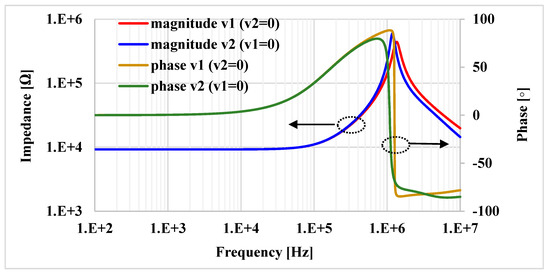
Figure 21.
The frequency and phase responses of the series L-R connection with Rset = 10 kΩ.
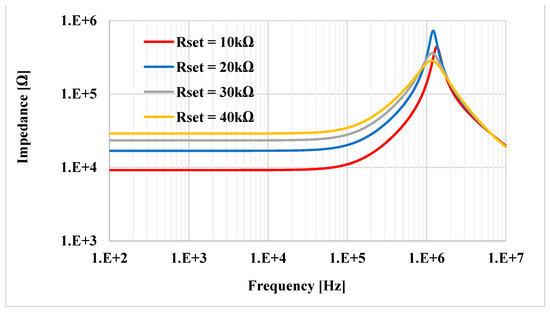
Figure 22.
The frequency responses of the series L-R connection with different Rset.
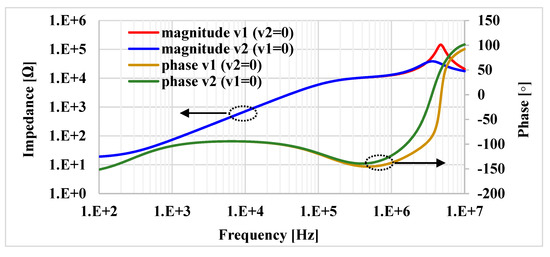
Figure 23.
The frequency and phase responses of the parallel L-R connection with Rset = 10 kΩ.
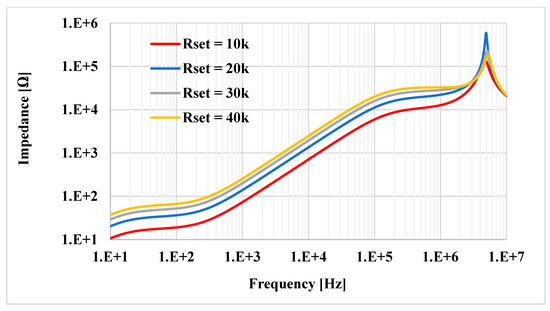
Figure 24.
The frequency responses of the parallel L-R connection with different Rset.
To show the usefulness of the floating inductance simulators, they were applied in the implementation of the 4th order elliptic lowpass ladder filter presented in Figure 25 [45]. The floating lossless inductance simulator in Figure 14 is used as Leq2, while the series Req1 and Leq1 circuit is implemented by the series inductance-resistance simulator shown in Figure 15. It should be noted that in the case of the input voltage signal applied at the first port (v1), only one VD-DIBA is required for the realization of the series L-R simulator. As mentioned in the Introduction section, the procedure used to synthesize the high order ladder filter is easy to understand and implement without using advanced or complicated mathematics by replacing the passive inductors with the proposed inductance simulators. The completed 4th order elliptic LP ladder filter using VD-DIBAs-based inductance simulators is shown in Figure 26. It can be seen that the input voltage node is a high impedance one.
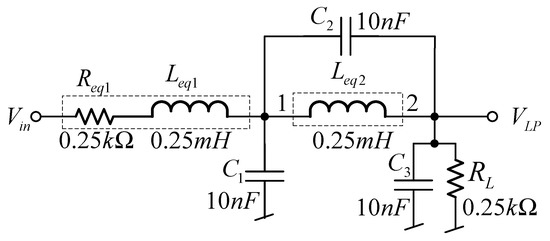
Figure 25.
The 4th elliptic LP ladder filter.
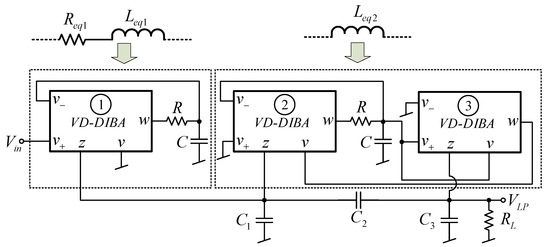
Figure 26.
The completed 4th order elliptic LP ladder filter based on VD-DIBAs.
The 4th order elliptic LP ladder filter was simulated by selecting C1 = C2 = C3 = 1.04 nF and RL = 10 kΩ. The resistors and capacitors in the inductance simulators were C = 1.04 pF and R = 10 kΩ, respectively, while the value of Rset was R1set = R2set = R3set = 9.07 kΩ. Figure 27 shows the frequency and responses of the 4th order elliptic LP ladder filter based on VD-DIBA and resistor-inductor-capacitor (RLC) circuit. The gain is −6.027 dB and the bandwidth (BW) is 13.31 kHz, while for the RLC, the gain is −6.02 dB and BW is 13.33 kHz. It is evident that the values are close to each other. Figure 28 shows the frequency responses of the LP ladder filter with different Rset1 and R = Rset1 = R2set = R3set = 7.07, 9.07, and 11.07 kΩ. The BW was 15.39, 13.31, and 11.8 kHz, respectively. The transient response of the 4th order LP ladder filter realized from the proposed inductance simulators is shown in Figure 29, where a sine wave signal with a peak-to-peak of 1 V at 1 kHz was applied to the input of the filter. The output signal has a total harmonic distortion (THD) of 1%. The THD versus the peak-to-peak value of the input signal is shown in Figure 30. The root mean square (RMS) value of the output noise of the filter is 60 µV, so the dynamic range is 80 dB for 2% THD.
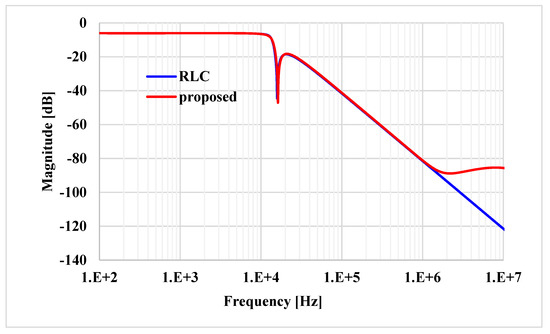
Figure 27.
The frequency responses of the LP ladder filter based on VD-DIBA and RLC.
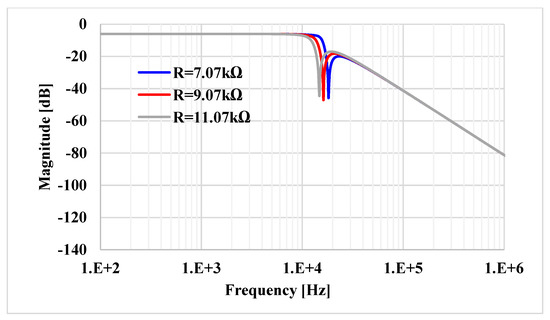
Figure 28.
The frequency responses of the LP ladder filter with different Rset.
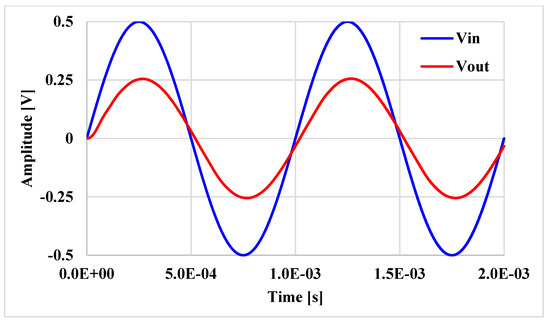
Figure 29.
The transient responses of the LP ladder filter.
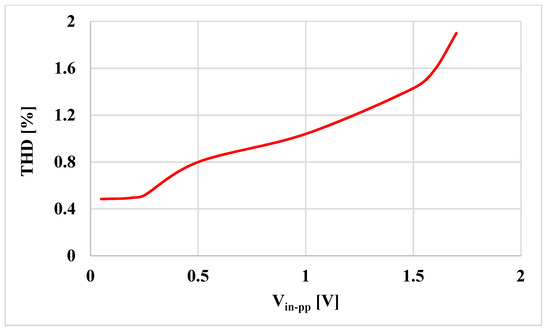
Figure 30.
The total harmonic distortion (THD) of the filter versus the Vin-pp.
6. Experimental Results of Inductance Simulators
The experiment was also conducted to verify the performances of the floating inductance simulators and the 4th order elliptic LP filter by implementing VD-DIBA from LM13700 and AD830 commercially available integrated circuits (IC), as shown in Figure 31. The transconductance of LM13700 is electronically controlled by gm = IB/2 VT, where the IB is the bias current and VT is the thermal voltage. To evaluate the impedance of the floating inductance simulators, the input current signal applied at the first (v1) and second (v2) ports was implemented by the voltage to current converter using AD844 and Rx, as shown in Figure 32 (the small value resistor, Rs, was connected to avoid oscillation in the tested circuits). The power supply voltage used was ±5 V, which was implemented by employing a GW Instek GPS-3303 power supply. C = 1 nF, R= 1 kΩ, and IB1 = IB2 = 180 μA, as measured by the Fluke 289 digital multimeter. From (5), the calculated inductance was 0.289 mH. The sinusoidal input signal and the measured output waveforms were registered with the Keysight DSOX1102G oscilloscope. Figure 33 shows the experimental impedance (both the magnitude and phase) of the floating lossless inductance simulator at the first port (v1) and second port (v2). The experimental inductance value was about 0.271 mH. The useful frequency range was more than two decades. It was found that the parasitic resistances in VD-DIBA affect the workability of the active inductor, as well as the performance of the proposed inductance simulator at a high frequency, which is affected by the parasitic capacitances. The transient responses of the input current (i1) and voltage v1 are shown in Figure 34, where a sine wave signal with a peak-to-peak of 20 mVpp at 200 kHz was applied to the input (vs) of the V to I converter in Figure 32. This yielded the input current i1 of 20 µApp. The theoretical voltage drop at port v1 should be 6.81 mVpp (v1 = i1 * 2πfLeq, where f = 200 kHz and Leq = 0.271 mH). The measured voltage drop at port v1 was 7.11 mVpp. It can be seen in Figure 34 that the phase of current was delayed compared to the phase of voltage by around 90 degrees, which proves that the proposed circuit works well as a passive inductor. The impedance at port v1 of the inductance simulator for different values of IB is shown in Figure 35, where the values of IB were set at 78, 180, and 358 µA. The experimental inductance values obtained from these IB values were 0.644, 0.271, and 0.138 mH, respectively. As shown in the result, the inductance is electronically controlled by IB.
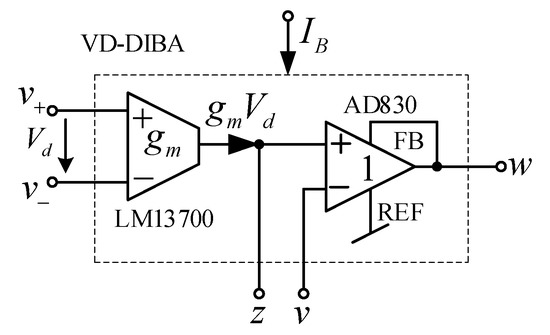
Figure 31.
VD-DIBA based on commercial components.
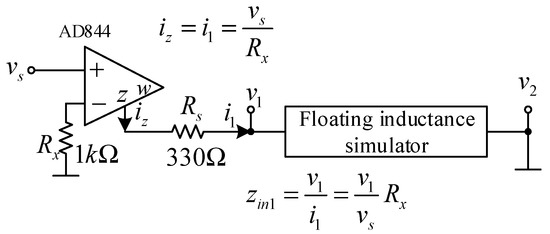
Figure 32.
Experimental setup used to measure the input impedance at the first port (v1).
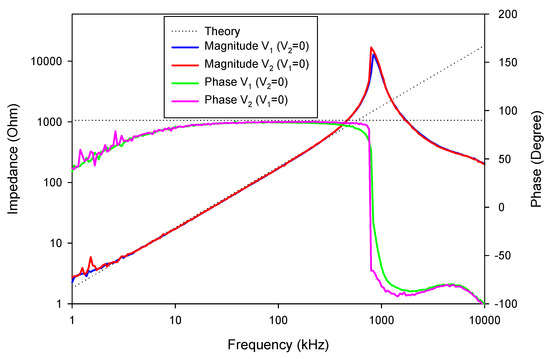
Figure 33.
Experimental setup used to measure the input impedance at the first port (v1).
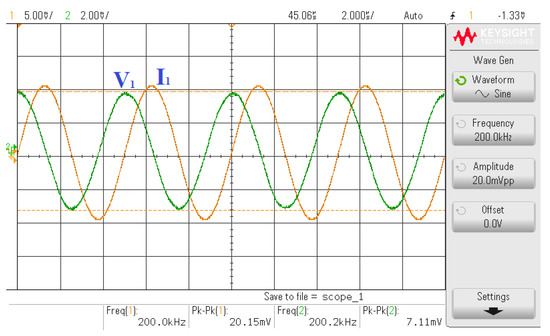
Figure 34.
The current and voltage measured at port v1 of the floating lossless inductance simulator.
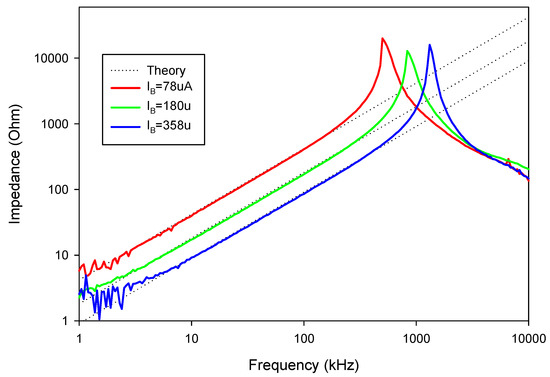
Figure 35.
The experimental frequency responses of lossless L with different IB.
The experimental impedance of the floating series inductance-resistance simulator is shown in Figure 36, where the inductance and resistance values are about 0.346 mH and 0.264 kΩ, respectively. The impedance of the floating series L-R connection for different values of IB is shown in Figure 37, where IB values were changed to obtain the three values of 78, 180, and 358 µA. The experimental inductance values obtained from these IB values were 1.38, 0.346, and 0.15 mH, respectively, while the experimental resistance values obtained from these IB values were 0.623, 0.264, and 0.135 kΩ, respectively. The experimental result for the floating parallel inductance-resistance simulator connection is shown in Figure 38, where the inductance and resistance values were about 0.269 mH and 0.25 kΩ, respectively. The impedance of the floating parallel inductance-resistance connection for different values of IB values is shown in Figure 39, where IB values were set as 78, 180, and 358 µA. The corresponding inductance values were 0.639, 0.269, and 0.132 mH, respectively, while the resistance values were 0.603, 0.25, and 0.121 kΩ, respectively.
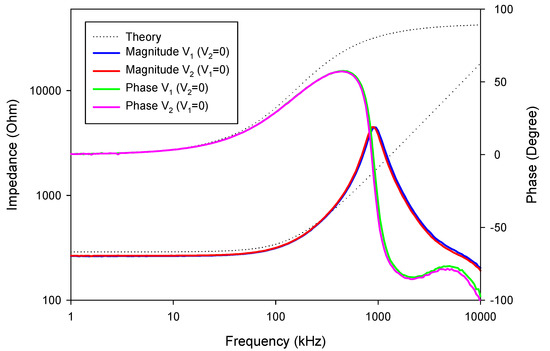
Figure 36.
The experimental frequency responses of lossless L with different IB.
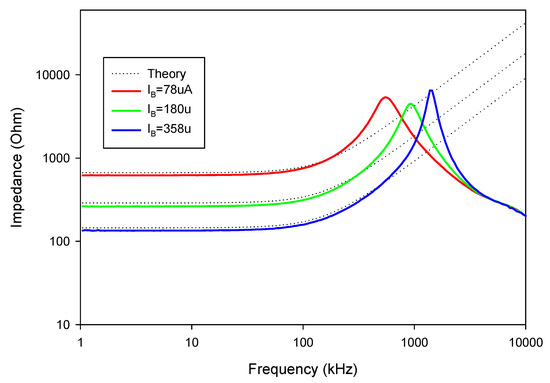
Figure 37.
The experimental frequency responses of the series L-R connection with different IB.
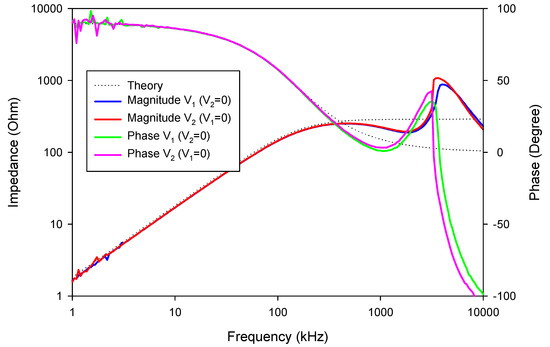
Figure 38.
The experimental frequency and phase responses of the parallel L-R connection.
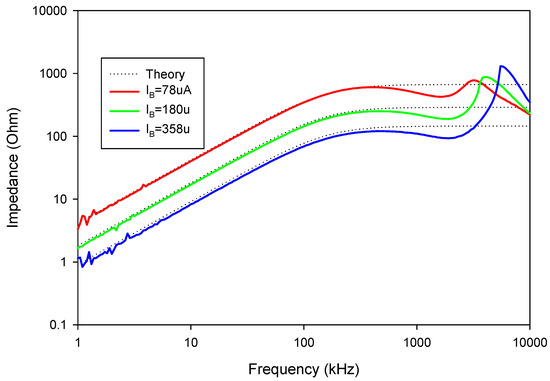
Figure 39.
The experimental frequency and phase responses of the parallel L-R connection.
The 4th order elliptic LP ladder filter realized from the proposed inductance simulators in Figure 26 was experimentally tested by selecting C1 = C2 = C3 = 10 nF and RL = 0.25 kΩ. The resistors and capacitors in the inductance simulators were C = 1 nF and R = 1 kΩ, respectively, while the value of the bias current was IB1 = IB2 = IB3 = 208 µA. This yielded Leq1 = Leq2 = 0.25 mH and Req1 = 0.25 kΩ. Figure 40 shows the experimental frequency responses of the 4th order elliptic LP ladder filter based on VD-DIBA compared with the theoretical response of the RLC prototype filter. The gain is −5.9 dB and bandwidth (BW) is 83.17 kHz, while for the RLC prototype, the gain is −6.02 dB and BW is 85.41 kHz. The transient responses of the LP ladder filter are shown in Figure 41, where sine wave signals with peak-to-peak of 20 mVpp at 10, 70, and 100 kHz were applied to the input of the filter. Figure 42 shows the experimental frequency and responses of the LP ladder filter with a different bias current and IB1 = IB2 = IB3 = 52, 104, and 208 µA, respectively. The BW was 19.95, 57.54, and 83.17 kHz, respectively. It was found that the BW or the cut-off frequency is electronically controlled by the bias currents.
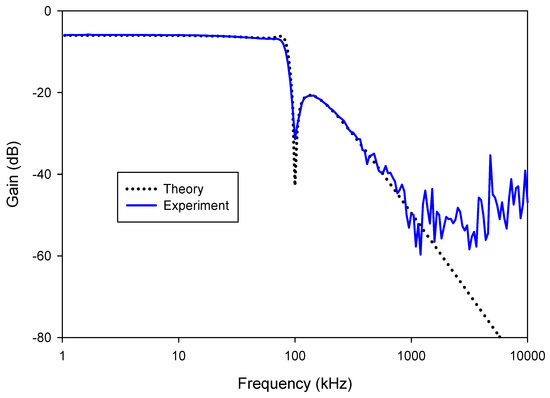
Figure 40.
The experimental frequency responses of the LP ladder filter based on VD-DIBA compared with the theoretical response of the RLC prototype filter.
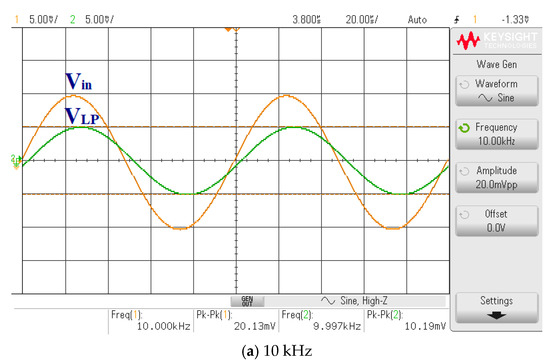
Figure 41.
The experimental transient responses of the LP ladder filter.
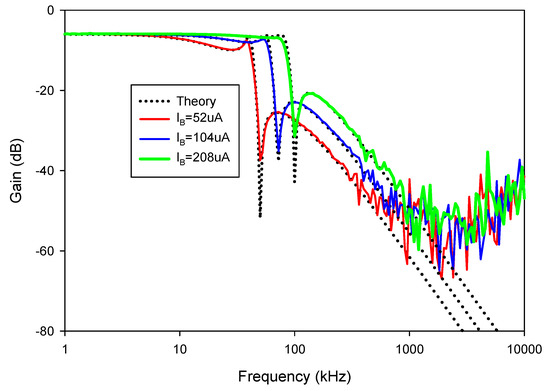
Figure 42.
The experimental frequency responses of the LP ladder filter with different IB.
7. Comparison
A comparison of the proposed inductance simulators with other inductance simulators [31,32,33,44,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60], is shown in Table 3. It can be seen that most of the simple inductance simulators using one active building block only perform grounded-type simulations [31,48,57,58,59,60]. The grounded inductance simulators in [33,52,53,56] use more than one active building block. The floating inductance simulators in [33,51,56] require three active elements. The prosed inductance simulators in [49,52,54,58] use a floating capacitor, but the proposed inductance simulators consist of a grounded capacitor, which is a benefit from an integration point of view. With two active and passive elements, the proposed floating inductance simulators can perform three functions, as a lossless inductor, series inductor-resistor, and parallel inductor-resistor. However, the inductance simulators realized in [31,32,33,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60] cannot perform three functions with the same number of active and passive elements. The inductance simulators in [50,55] were realized from the active building block with a multiple output terminal. The inductance simulators in [46,53,57,59] require a strict matching condition of the passive element. Most of the published papers [31,32,33,44,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60] on inductance simulator design do not show the procedure employed to design the topology. Therefore, new researchers or designers will not understand how to obtain the completed circuits. Therefore, the simple design procedures of the proposed inductance simulators using a circuit block diagram are also given in this work. Moreover, the performances of inductance simulators proposed in [31,32,33,48,50,52,55,56,60] were only verified through simulation, but the proposed inductance simulators were simulated in the Cadence environment using a 0.18 µm CMOS process from TSMC and experimentally tested by using VD-DIBA implemented by the available commercial IC. Additionally, thanks to the multiple-input MOS transistor technique, the CMOS structure of the VD-DIBA is compact and offers a high dynamic range.

Table 3.
Comparison of the proposed inductance simulators and other inductance simulators using an active building block.
8. Conclusions
The realization of floating inductance simulators (lossless inductor, series inductor-resistor connection, and parallel inductor-resistor connection) using compact CMOS VD-DIBA is proposed in this paper. In addition, these active inductors are applied to realize a 4th order elliptic LP ladder filter. All proposed inductance simulators use the same number of elements (two VD-DIBAs, one resistor, and grounded capacitor). A compact CMOS VD-DIBA based on the multiple-input MOS transistor technique is proposed in this paper. The compact CMOS VD-DIBA was supplied with ±0.9 V. The linear operation was obtained over a differential input range of −0.5 to 0.5 V. The total power consumption was 0.99 mW. The proposed floating inductance simulators and their filter application were designed using a 0.18 μm TSMC technology and commercially available ICs. Both simulation and experimental results are included in this paper to confirm the performance of the proposed circuits. The simulation result obtained from the 4th order elliptic LP ladder filter realized by the proposed inductance simulators shows a dynamic range (DR) of 80 dB for a total harmonic distortion (THD) of 2% at 1 kHz and a 1.8 V peak-to-peak output.
Author Contributions
Conceptualization, W.J. and F.K.; Methodology, W.J., S.B., F.K.; and T.K.; Validation, W.J., S.B., F.K. and T.K.; Formal Analysis, W.J., S.B., F.K. and P.S. (Piya Supavarasuwat); Investigation, W.J., S.B., F.K. and P.S. (Peerawut Suwanjan); Writing—Original Draft Preparation, W.J., S.B. and F.K.; Writing—Review and Editing, W.J., S.B., F.K.; T.K., P.S. (Peerawut Suwanjan), and P.S. (Piya Supavarasuwat). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Faculty of Industrial Education and Technology, King Mongkut’s Institute of Technology Ladkrabang (KMITL), under grant 2564-02-03-004.
Acknowledgments
The authors would like to thank the anonymous re-viewers for providing valuable comments which helped substantially improve the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yuan, E. CMOS Active Inductors and Transformers: Principle, Implementation, and Applications; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Sagbas, M.; Ayten, U.E.; Sedef, H.; Koksal, M. Electronically tunable floating inductance simulator. AEU Int. J. Electron. Commun. 2009, 63, 423–427. [Google Scholar] [CrossRef]
- Psychalinos, C.; Spanidou, A. Current amplifier based grounded and floating inductance simulators. AEU Int. J. Electron. Commun. 2006, 60, 68–171. [Google Scholar] [CrossRef]
- Metin, B.; Cicekoglu, O. A novel floating lossy inductance realization topology with NICs using current conveyors. IEEE Trans. Circuits Syst. II Express Briefs 2006, 53, 483–486. [Google Scholar] [CrossRef]
- Biolek, D.; Senani, R.; Biolkova, V.; Kolka, Z. Active elements for analog signal processing: Classification, review, and new proposals. Radioengineering 2008, 17, 15–32. [Google Scholar]
- Gupta, P.; Pandey, R. A low-power voltage differencing buffered amplifier. Int. J. Circ. Theor. Appl. 2019, 47, 1402–1416. [Google Scholar] [CrossRef]
- Mamatov, I.; Özçelep, Y.; Kaçar, F. Voltage differencing buffered amplifier based low power, high frequency and universal filters using 32 nm CNTFET technology. Microelectron. J. 2021, 107, 104948. [Google Scholar] [CrossRef]
- Yadav, N.; Rai, S.K.; Pandey, R. Novel Memristor Emulators using Fully Balanced VDBA and Grounded Capacitor. Iran. J. Sci. Technol. Trans. Elec Eng. 2021, 45, 229–245. [Google Scholar] [CrossRef]
- Tangsrirat, W.; Channumsin, O. Tunable Floating Capacitance Multiplier Using Single Fully Balanced Voltage Differencing Buffered Amplifier. J. Commun. Technol. Electron. 2019, 64, 797–803. [Google Scholar] [CrossRef]
- Tangsrirat, W. Linearly tunable voltage differencing buffered amplifier. Rev. Roum. Sci. Tech.-El. 2019, 64, 247–253. [Google Scholar]
- Gupta, P.; Pandey, R. Voltage differencing buffered amplifier based voltage mode four quadrant analog multiplier and its applications. Int. J. Eng. Trans. A Basics 2019, 32, 528–535. [Google Scholar]
- Gupta, P.; Pandey, N.; Pandey, R. High CMRR wide bandwidth instrumentation amplifier based on VDBA. Recent Adv. Electr. Electron. Eng. 2018, 11, 239–247. [Google Scholar] [CrossRef]
- Yeşil, A.; Kaçar, F. Current and voltage mode quadrature oscillator based on voltage differencing buffered amplifier. Istamb. Univ. J. Electr Electron. Eng. 2018, 18, 6–12. [Google Scholar]
- Yesil, A.; Kacar, F.; Gurkan, K. Design and Experimental Evaluation of Quadrature Oscillator Employing Single Fb-Vdba. J. Electr. Eng.-Slovak. 2016, 67, 137–142. [Google Scholar] [CrossRef]
- Tangsrirat, W. Simple Bicmos Realization of Full Balanced Voltage Differencing Buffered Amplifier. Rev. Roum. Sci. Tech.-El. 2015, 60, 409–415. [Google Scholar]
- Sotner, R.; Jerabek, J.; Herencsar, N. Voltage Differencing Buffered/Inverted Amplifiers and Their Applications for Signal Generation. Radioengineering 2013, 22, 490–504. [Google Scholar]
- Kacar, F.; Yesil, A.; Noori, A. New CMOS Realization of Voltage Differencing Buffered Amplifier and Its Biquad Filter Applications. Radioengineering 2012, 21, 333–339. [Google Scholar]
- Biolek, D.; Biolkova, V. First-order voltage-mode all-pass filter employing one active element and one grounded capacitor. Analog Integr. Circuits Signal. Process. 2010, 65, 123–129. [Google Scholar] [CrossRef]
- Pushkar, K.L.; Bhaskar, D.R.; Prasad, D. Voltage-Mode Universal Biquad Filter Employing Single Voltage Differencing Differential Input Buffered Amplifier. Circ. Syst. 2013, 4, 44–48. [Google Scholar] [CrossRef]
- Pushkar, K.L.; Bhaskar, D.R.; Prasad, D. A New MISO-Type Voltage-Mode Universal Biquad Using Single VD-DIBA. ISRN Electron. 2013, 2013, 1–5. [Google Scholar] [CrossRef]
- Ninsraku, W.; Biolek, D.; Jaikla, W.; Siripongdee, S.; Suwanjan, P. Electronically controlled high input and low output impedance voltage mode multifunction filter with grounded capacitors. AEU Int. J. Electron. Commun. 2014, 68, 1239–1246. [Google Scholar] [CrossRef]
- Jaikla, W.; Biolek, D.; Siripongdee, S.; Bajer, J. High input impedance voltage-mode biquad filter using VD-DIBAs. Radioengineering 2014, 23, 914–921. [Google Scholar]
- Jaikla, W.; Siripongdee, S.; Khateb, F.; Sotner, R.; Silapan, P.; Suwanjan, P.; Chaichana, A. Synthesis of Biquad filter using two VD-DIBAs with independent control of Quality factor and natural frequency. AEU Int. J. Electron. Commun. 2021, 132, 153601. [Google Scholar] [CrossRef]
- Jardrit, P.; Jaikla, W.; Siripogdee, S.; Chaichana, A.; Sotner, R.; Khateb, F. Design of High Input Impedance Voltage-mode Multifunction Biquad Filter with Independent Control of Natural Frequency and Quality Factor. In Proceedings of the International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phuket, Thailand, 24–27 June 2020; pp. 234–237. [Google Scholar]
- Pushkar, K.L.; Goel, R.K.; Gupta, K.; Vivek, P.; Ashraf, J. New VD-DIBA-Based Single-Resistance-Controlled Sinusoidal Oscillator. Circ. Syst. 2016, 7, 4145–4153. [Google Scholar] [CrossRef]
- Bajer, J.; Vavra, J.; Biolek, D. Voltage-mode quadrature oscillator using VD-DIBA active elements. In Proceedings of the IEEE Asia Pacific Conference on Circuits and Systems (APCCAS 2014), Ishigaki, Japan, 17–20 November 2014; pp. 197–200. [Google Scholar]
- Pushkar, K.L.; Bhaskar, D.R.; Prasad, D. Single-Resistance-Controlled Sinusoidal Oscillator Using Single VD-DIBA. Act. Passiv. Electron. Compon. 2013, 2013, 1–5. [Google Scholar] [CrossRef]
- Bhaskar, D.R.; Prasad, D.; Pushkar, K.L. Fully Uncoupled Electronically Controllable Sinusoidal Oscillator Employing VD-DIBAs. Circ. Syst. 2013, 4, 264–268. [Google Scholar] [CrossRef][Green Version]
- Prasad, D.; Bhaskar, D.R.; Pushkar, K.L. Electronically Controllable Sinusoidal Oscillator Employing CMOS VD-DIBAs. ISRN Electron. 2013, 2013, 1–6. [Google Scholar] [CrossRef]
- Pushkar, K.L. Electronically Controllable Quadrature Sinusoidal Oscillator Using VD-DIBAs. Circ. Syst. 2018, 9, 41–48. [Google Scholar] [CrossRef][Green Version]
- Srivastava, M.; Bhardwaj, K. Compact Lossy Inductance Simulators with Electronic Control. Iran. J. Electr. Electron. Eng. 2019, 15, 343–351. [Google Scholar]
- Bhaskar, D.R.; Prasad, D.; Pushkar, K.L. Electronically-Controllable Grounded-Capacitor-Based Grounded and Floating Inductance Simulated Circuits Using VD-DIBAs. Circ. Syst. 2013, 4, 422–430. [Google Scholar] [CrossRef]
- Prasad, D.; Bhaskar, D.R.; Pushkar, K.L. Realization of new electronically controllable grounded and floating simulated inductance circuits using Voltage Differencing Differential Input Buffered Amplifiers. Act. Passiv. Electron. Compon. 2011, 2011, 1–8. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Kumngern, M.; Psychalinos, C. Multiple-input bulk-driven MOS transistor for low-voltage low-frequency applications. Circuits Syst. Signal Process. 2019, 38, 2829–2845. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Veldandi, H.; Jaikla, W. Multiple-input bulk-driven quasi-floating-gate MOS transistor for low-voltage low-power integrated circuits. AEU Int. J. Electron. Commun. 2019, 100, 32–38. [Google Scholar] [CrossRef]
- Khateb, F.; Kulej, T.; Kumngern, M.; Jaikla, W.; Ranjan, R.K. Comparative performance study of multiple-input Bulk-driven and multiple-input Bulk-driven Quasi-floating-gate DDCCs. AEU Int. J. Electron. Commun. 2019, 108, 19–28. [Google Scholar] [CrossRef]
- Kumngern, M.; Kulej, T.; Stopjakova, V.; Khateb, F. 0.5 V Sixth-order Chebyshev band-pass filter based on multiple-input bulk-driven OTA. AEU Int. J. Electron. Commun. 2019, 111, 152930. [Google Scholar] [CrossRef]
- Kumngern, M.; Kulej, T.; Khateb, F.; Stopjakova, V.; Ranjan, R.K. Nanopower multiple-input DTMOS OTA and its applications to high-order filters for biomedical systems. AEU Int. J. Electron. Commun. 2021, 130, 153576. [Google Scholar] [CrossRef]
- Kumngern, M.; Aupithak, N.; Khateb, F.; Kulej, T. 0.5 V Fifth-Order Butterworth Low-Pass Filter Using Multiple-Input OTA for ECG Applications. Sensors 2020, 20, 7343. [Google Scholar] [CrossRef]
- Jaikla, W.; Khateb, F.; Kumngern, M.; Kulej, T.; Ranjan, R.K.; Suwanjan, P. 0.5 V Fully Differential Universal Filter Based on Multiple Input OTAs. IEEE Access. 2020, 8, 187832–187839. [Google Scholar] [CrossRef]
- Khateb, F.; Biolek, D. Bulk-Driven Current Differencing Transconductance Amplifier. Circuits Syst. Signal Process. 2011, 30, 1071–1089. [Google Scholar] [CrossRef]
- Kumngern, M.; Khateb, F.; Kulej, T. 0.3 V Differential Difference Current Conveyor Using Multiple-Input Bulk-Driven Technique. Circuits Syst. Signal Process. 2020, 39, 3189–3205. [Google Scholar] [CrossRef]
- Khateb, F.; Kumngern, M.; Kulej, T.; Psychalinos, C. 0.5 V Universal Filter Based on Multiple-Input FDDAs. Circuits Syst. Signal Process. 2019, 38, 5896–5907. [Google Scholar] [CrossRef]
- Jaikla, W.; Sotner, R.; Khateb, F. Design and analysis of floating inductance simulators using VDDDAs and their applications. AEU Int. J. Electron. Commun. 2019, 112, 152937. [Google Scholar] [CrossRef]
- Minaei, S.; Cicekoglu, O.; Kuntman, H.; Turkoz, S. Electronically tunable, active only floating inductance simulation. Int. J. Electron. 2002, 89, 905–912. [Google Scholar] [CrossRef]
- Singh, R.; Prasad, D. Comment- An Active Inductor Employing a New FTFNTA. Int. J. Electron. 2020, 107, 1406–1413. [Google Scholar] [CrossRef]
- Tarunkumar, H.; Shantikumar Singh, Y.; Ranjan, A. An active inductor employing a new four terminal floating nullor transconductance amplifier (FTFNTA). Int. J. Electron. 2020, 107, 683–702. [Google Scholar] [CrossRef]
- Safari, L.; Yuce, E.; Minaei, S.; Ferri, G.; Stornelli, V. A second-generation voltage conveyor (VCII)–based simulated grounded inductor. Int. J. Circ. Theor. Appl. 2020, 48, 1180–1193. [Google Scholar] [CrossRef]
- Abaci, A.; Yuce, E. Single DDCC−Based simulated floating inductors and their applications. IET Circuits Devices Syst. 2020, 14, 796–804. [Google Scholar] [CrossRef]
- Prasad, D.; Haseeb, Z.; Mainuddin; Akram, M. Realization of resistorless floating inductor using modified CDTA. Indian J. Pure Appl. Phys. 2019, 57, 29–32. [Google Scholar]
- Moonmuang, P.; Pukkalanun, T.; Unhavanich, S.; Tangsrirat, W. Actively simulated floating lossless inductor for short range wireless communication. J. Mob. Multimed. 2019, 15, 321–338. [Google Scholar]
- Yesil, A.; Yuce, E.; Minaei, S. Inverting voltage buffer based lossless grounded inductor simulators. AEU Int. J. Electron. Commun. 2018, 83, 131–137. [Google Scholar] [CrossRef]
- Dogan, M.; Yuce, E. CFOA based a new grounded inductor simulator and its applications. Microelectron. J. 2019, 90, 297–305. [Google Scholar] [CrossRef]
- Tangsrirat, W. Actively Floating Lossy Inductance Simulators Using Voltage Differencing Buffered Amplifiers. IETE J. Res. 2018, 65, 446–459. [Google Scholar] [CrossRef]
- Singh, A.K.; Kumar, P.; Senani, R. Electronically tunable grounded/floating inductance simulators using Z-copy CFCCC. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 1041–1055. [Google Scholar] [CrossRef]
- Singh, A.; Jain, M.K.; Wairya, S. Novel Lossless Grounded and Floating Inductance Simulators Employing a Grounded Capacitor Based on CC-CFA. J. Circuit Syst. Comput. 2019, 28. [Google Scholar] [CrossRef]
- Yuce, E.; Minaei, S. Commercially Available Active Device Based Grounded Inductor Simulator and Universal Filter with Improved Low Frequency Performances. J. Circuit Syst. Comput. 2017, 26, 4. [Google Scholar] [CrossRef]
- Siripongdee, S.; Jaikla, W. Electronically controllable grounded inductance simulators using single commercially available IC: LT1228. AEU Int. J. Electron. Commun. 2017, 76, 1–10. [Google Scholar] [CrossRef]
- Abaci, A.; Yuce, E. Modified DVCC based quadrature oscillator and lossless grounded inductor simulator using grounded capacitor(s). AEU Int. J. Electron. Commun. 2017, 76, 86–96. [Google Scholar] [CrossRef]
- Pathak, J.K.; Singh, A.K.; Senani, R. New canonic lossy inductor using a single CDBA and its application. Int. J. Electron. 2016, 103, 1–13. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).