Decoding Algorithms and HW Strategies to Mitigate Uncertainties in a PCM-Based Analog Encoder for Compressed Sensing
Abstract
1. Introduction
2. AIMC Testchip and Conductance Models
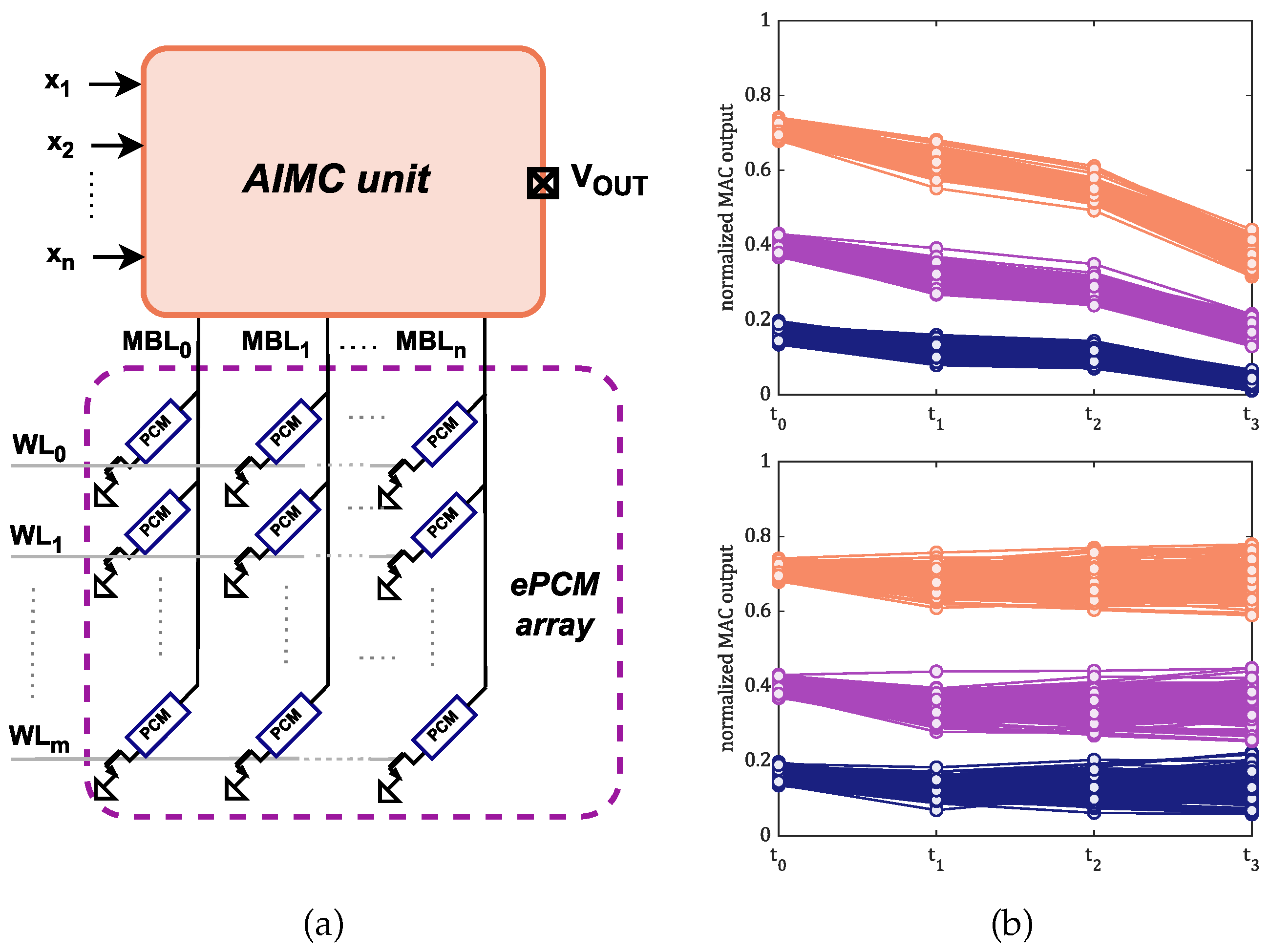
2.1. AIMC Testchip Structure
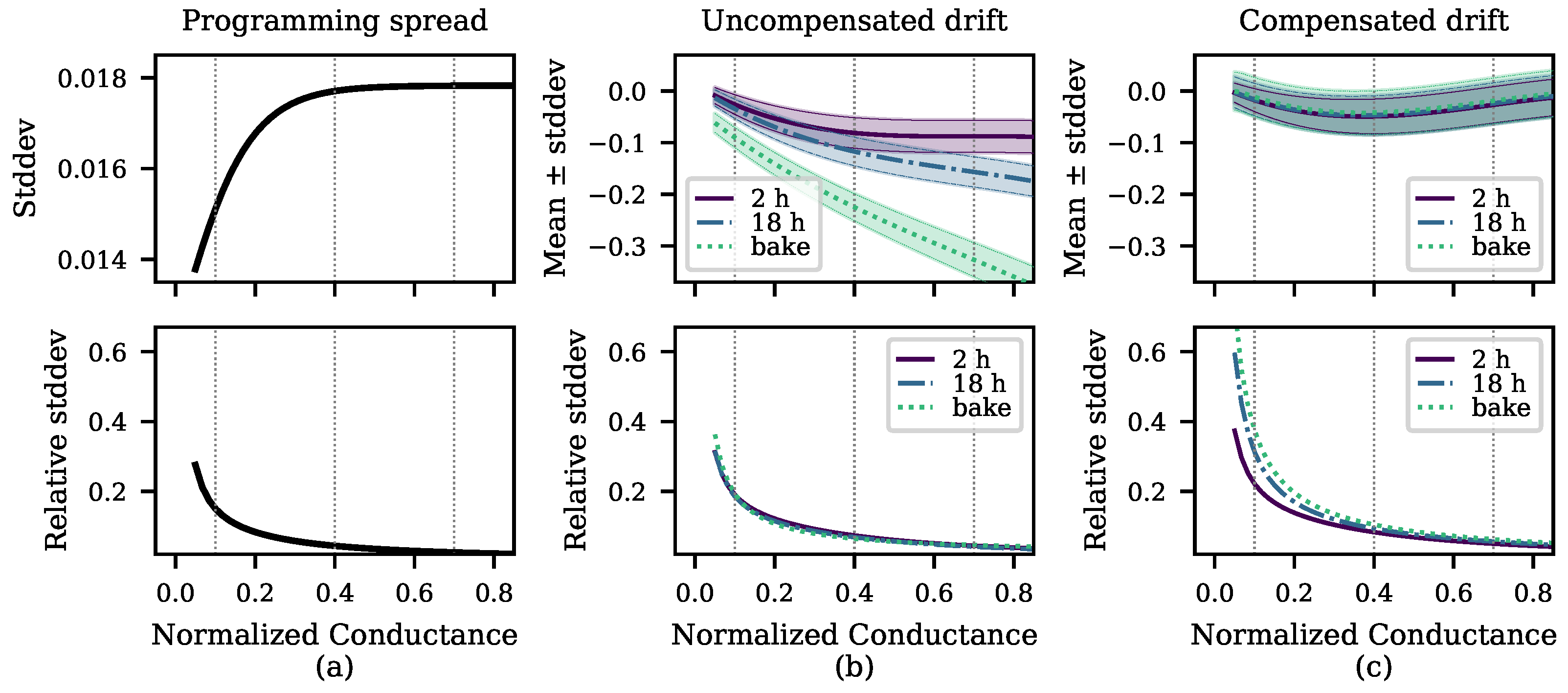
2.2. Modeling the Conductance Variability
3. Compressed Sensing Reconstruction
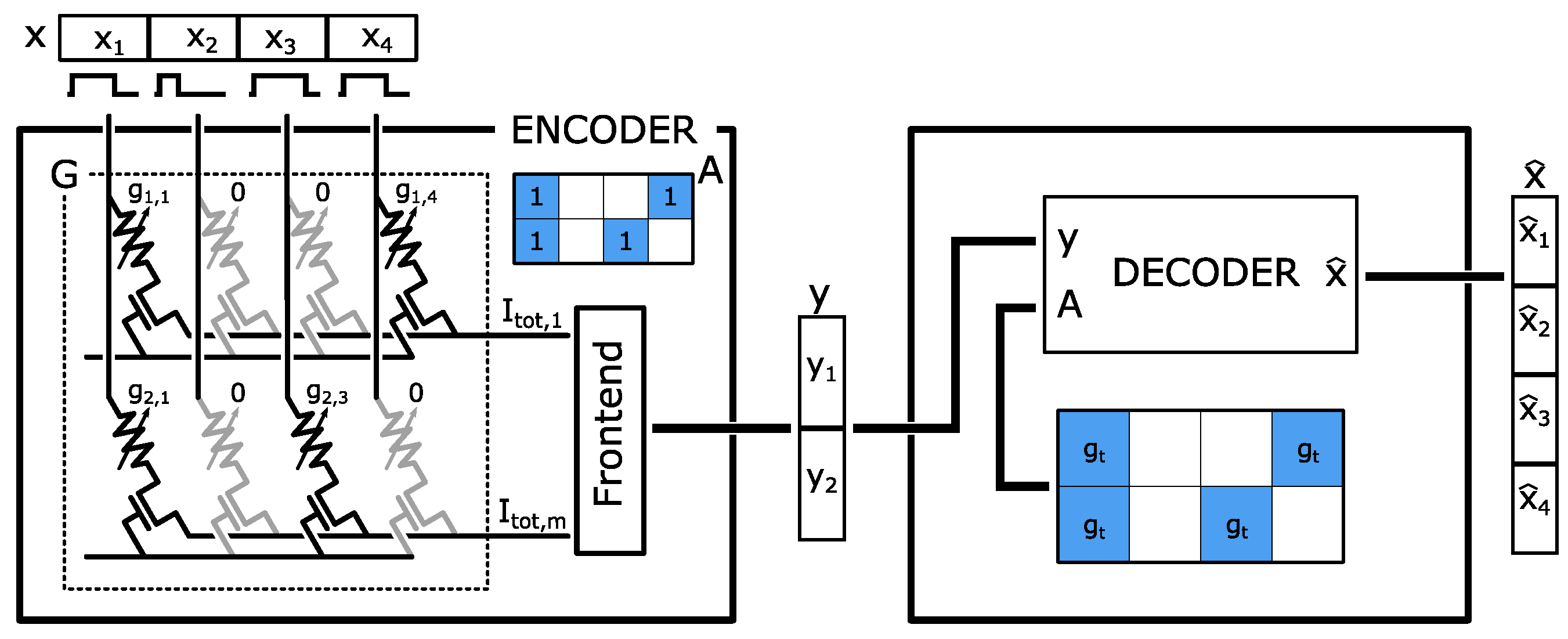
3.1. Acquisition Matrix Implementation
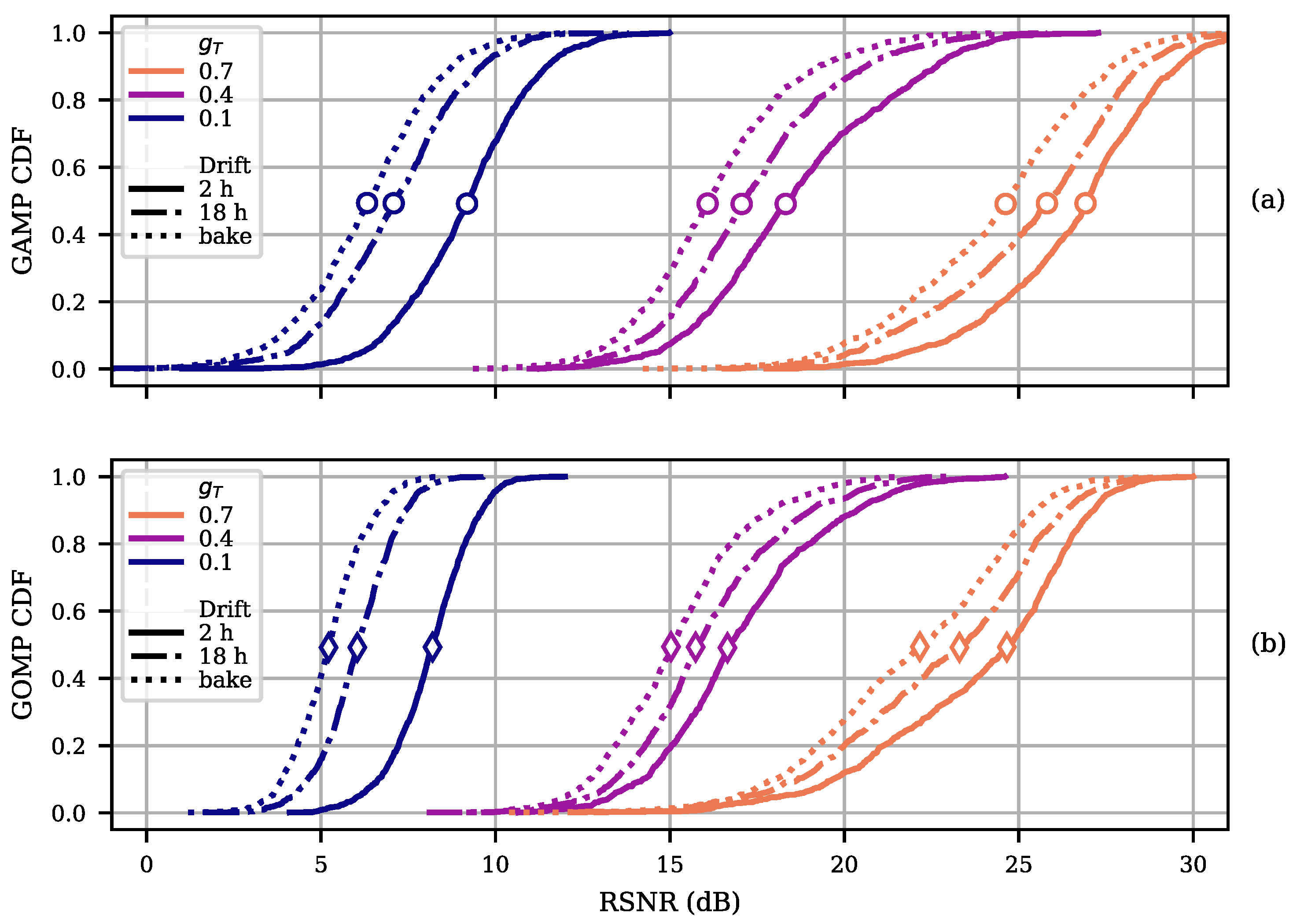
3.2. Reconstruction Algorithms
4. Experimental Validation
4.1. Effects of the Programming Variability
4.2. Effects of Drift
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Verma, N.; Jia, H.; Valavi, H.; Tang, Y.; Ozatay, M.; Chen, L.Y.; Zhang, B.; Deaville, P. In-Memory Computing: Advances and Prospects. IEEE Solid-State Circuits Mag. 2019, 11, 43–55. [Google Scholar] [CrossRef]
- Gao, S.; Yang, F.; Zhao, L.; Zhao, Y. Current Research Status and Future Prospect of the In-Memory Computing. In Proceedings of the 2021 IEEE 14th International Conference on ASIC (ASICON), Kunming, China, 26–29 October 2021; pp. 1–4. [Google Scholar] [CrossRef]
- Haensch, W.; Gokmen, T.; Puri, R. The Next Generation of Deep Learning Hardware: Analog Computing. Proc. IEEE 2019, 107, 108–122. [Google Scholar] [CrossRef]
- Sun, X.; Khwa, W.S.; Chen, Y.S.; Lee, C.H.; Lee, H.Y.; Yu, S.M.; Naous, R.; Wu, J.Y.; Chen, T.C.; Bao, X.; et al. PCM-Based Analog Compute-In-Memory: Impact of Device Non-Idealities on Inference Accuracy. IEEE Trans. Electron Devices 2021, 68, 5585–5591. [Google Scholar] [CrossRef]
- Mackin, C.; Rasch, M.; Chen, A. Optimised weight programming for analogue memory-based deep neural networks. Nat. Commun. 2022, 13, 3765. [Google Scholar] [CrossRef] [PubMed]
- Paolino, C.; Antolini, A.; Pareschi, F.; Mangia, M.; Rovatti, R.; Scarselli, E.F.; Gnudi, A.; Setti, G.; Canegallo, R.; Carissimi, M.; et al. Compressed Sensing by Phase Change Memories: Coping with Encoder non-Linearities. In Proceedings of the 2021 IEEE International Symposium on Circuits and Systems (ISCAS), Daegu, Republic of Korea, 23–26 May 2021; pp. 1–5. [Google Scholar] [CrossRef]
- Le Gallo, M.; Sebastian, A.; Cherubini, G.; Giefers, H.; Eleftheriou, E. Compressed Sensing With Approximate Message Passing Using In-Memory Computing. IEEE Trans. Electron Devices 2018, 65, 4304–4312. [Google Scholar] [CrossRef]
- Sun, Z.; Pedretti, G.; Ambrosi, E.; Bricalli, A.; Wang, W.; Ielmini, D. Solving matrix equations in one step with cross-point resistive arrays. Proc. Natl. Acad. Sci. USA 2019, 116, 4123–4128. [Google Scholar] [CrossRef]
- Chen, X.; Song, T.; Han, Y. RRAM-based Analog In-Memory Computing: Invited Paper. In Proceedings of the 2021 IEEE/ACM International Symposium on Nanoscale Architectures (NANOARCH), Virtual, 8–10 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Sebastian, A.; Le Gallo, M.; Khaddam-Aljameh, R.; Eleftheriou, E. Memory devices and applications for in-memory computing. Nat. Nanotechnol. 2020, 15, 529–544. [Google Scholar] [CrossRef]
- Kneip, A.; Bol, D. Impact of Analog Non-Idealities on the Design Space of 6T-SRAM Current-Domain Dot-Product Operators for In-Memory Computing. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 1931–1944. [Google Scholar] [CrossRef]
- Burr, G.W.; Brightsky, M.J.; Sebastian, A.; Cheng, H.Y.; Wu, J.Y.; Kim, S.; Sosa, N.E.; Papandreou, N.; Lung, H.L.; Pozidis, H.; et al. Recent Progress in Phase-Change Memory Technology. IEEE J. Emerg. Sel. Top. Circuits Syst. 2016, 6, 146–162. [Google Scholar] [CrossRef]
- Hartmann, J.; Cappelletti, P.; Chawla, N.; Arnaud, F.; Cathelin, A. Artificial Intelligence: Why moving it to the Edge? In Proceedings of the ESSCIRC 2021—IEEE 47th European Solid State Circuits Conference (ESSCIRC), Virtual, 13–22 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Carlos, E.; Branquinho, R.; Martins, R.; Kiazadeh, A.; Fortunato, E. Recent Progress in Solution-Based Metal Oxide Resistive Switching Devices. Adv. Mater. 2021, 33, 2004328. [Google Scholar] [CrossRef]
- Lin, H.; Wu, Z.; Liu, L.; Wang, D.; Zhao, X.; Cheng, L.; Lin, Y.; Wang, Z.; Xu, X.; Xu, H.; et al. Implementation of Highly Reliable and Energy Efficient in-Memory Hamming Distance Computations in 1 Kb 1-Transistor-1-Memristor Arrays. Adv. Mater. Technol. 2021, 6, 2100745. [Google Scholar] [CrossRef]
- Lin, H.; Xu, N.; Wang, D.; Liu, L.; Zhao, X.; Zhou, Y.; Luo, X.; Song, C.; Yu, G.; Xing, G. Implementation of Highly Reliable and Energy-Efficient Nonvolatile In-Memory Computing using Multistate Domain Wall Spin–Orbit Torque Device. Adv. Intell. Syst. 2022, 4, 2200028. [Google Scholar] [CrossRef]
- Wang, Y.; Tang, H.; Xie, Y.; Chen, X.; Ma, S.; Sun, Z.; Sun, Q.; Chen, L.; Zhu, H.; Wan, J.; et al. An in-memory computing architecture based on two-dimensional semiconductors for multiply-accumulate operations. Nat. Commun. 2021, 12. [Google Scholar] [CrossRef] [PubMed]
- Athmanathan, A.; Stanisavljevic, M.; Papandreou, N.; Pozidis, H.; Eleftheriou, E. Multilevel-Cell Phase-Change Memory: A Viable Technology. IEEE J. Emerg. Sel. Top. Circuits Syst. 2016, 6, 87–100. [Google Scholar] [CrossRef]
- Ielmini, D.; Pedretti, G. Device and Circuit Architectures for In-Memory Computing. Adv. Intell. Syst. 2020, 2, 2000040. [Google Scholar] [CrossRef]
- Khaddam-Aljameh, R.; Stanisavljevic, M.; Mas, J.F.; Karunaratne, G.; Braendli, M.; Liu, F.; Singh, A.; Müller, S.M.; Egger, U.; Petropoulos, A.; et al. HERMES Core—A 14nm CMOS and PCM-based In-Memory Compute Core using an array of 300ps/LSB Linearized CCO-based ADCs and local digital processing. In Proceedings of the 2021 Symposium on VLSI Technology, Kioto, Japan, 13–19 June 2021; pp. 1–2. [Google Scholar] [CrossRef]
- Antolini, A.; Lico, A.; Franchi Scarselli, E.; Gnudi, A.; Perilli, L.; Torres, M.L.; Carissimi, M.; Pasotti, M.; Canegallo, R.A. An embedded PCM Peripheral Unit adding Analog MAC In Memory Computing Feature addressing Non linearity and Time Drift Compensation. In Proceedings of the 2022 IEEE 48th European Solid State Circuit Research (ESSCIRC), Milan, Italy, 19–22 September 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Joshi, V.; Le Gallo, M.; Haefeli, S. Accurate deep neural network inference using computational phase-change memory. Nat. Commun. 2020, 11, 2473. [Google Scholar] [CrossRef]
- Antolini, A.; Franchi Scarselli, E.; Gnudi, A.; Romele, P.; Carissimi, M.; Pasotti, M.; Canegallo, R.A. Characterization and Programming Algorithm of Phase Change Memory Cells for Analog In-Memory Computing. Materials 2021, 14, 1624. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharjee, A.; Bhatnagar, L.; Panda, P. Examining and Mitigating the Impact of Crossbar Non-idealities for Accurate Implementation of Sparse Deep Neural Networks. In Proceedings of the 2022 Design, Automation & Test in Europe Conference & Exhibition (DATE), Online, 14–23 March 2022; pp. 1119–1122, ISSN 1558–1101. [Google Scholar] [CrossRef]
- He, Z.; Lin, J.; Ewetz, R.; Yuan, J.S.; Fan, D. Noise Injection Adaption: End-to-End ReRAM Crossbar Non-ideal Effect Adaption for Neural Network Mapping. In Proceedings of the 56th Annual Design Automation Conference, Las Vegas, NV, USA, 2–6 June 2019; Association for Computing Machinery: New York, NY, USA, 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Ding, F.; Peng, B.; Li, X.; Zhang, L.; Wang, R.; Song, Z.; Huang, R. A review of compact modeling for phase change memory. J. Semicond. 2022, 43, 023101. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed Sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candes, E.J.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theory 2005, 51, 4203–4215. [Google Scholar] [CrossRef]
- van den Berg, E.; Friedlander, M.P. Probing the pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. 2009, 31, 890–912. [Google Scholar] [CrossRef]
- Tropp, J.A.; Gilbert, A.C. Signal recovery from random measurements via orthogonal matching pursuit. Inf. Theory IEEE Trans. 2007, 53, 4655–4666. [Google Scholar] [CrossRef]
- Wang, J.; Kwon, S.; Li, P.; Shim, B. Recovery of Sparse Signals via Generalized Orthogonal Matching Pursuit: A New Analysis. IEEE Trans. Signal Process. 2016, 64, 1076–1089. [Google Scholar] [CrossRef]
- Rangan, S. Generalized approximate message passing for estimation with random linear mixing. In Proceedings of the 2011 IEEE International Symposium on Information Theory Proceedings, St. Petersburg, Russia, 31 July–5 August 2011; pp. 2168–2172. [Google Scholar] [CrossRef]
- Parker, J.T.; Cevher, V.; Schniter, P. Compressive sensing under matrix uncertainties: An Approximate Message Passing approach. In Proceedings of the 2011 Conference Record of the Forty Fifth Asilomar Conference on Signals, Systems and Computers (ASILOMAR), Pacific Grove, CA, USA, 6–9 November 2011; pp. 804–808. [Google Scholar] [CrossRef]
- Bortolotti, D.; Mangia, M.; Bartolini, A.; Rovatti, R.; Setti, G.; Benini, L. An ultra-low power dual-mode ECG monitor for healthcare and wellness. In Proceedings of the 2015 Design, Automation Test in Europe cOnference Exhibition (DATE), Grenoble, France, 9–13 March 2015; pp. 1611–1616. [Google Scholar] [CrossRef]
- Zigei, Y.; Cohen, A.; Katz, A. The weighted diagnostic distortion (WDD) measure for ECG signal compression. IEEE Trans. Biom. Eng. 2000, 47, 1422–1430. [Google Scholar] [CrossRef]
- Pasotti, M.; Zurla, R.; Carissimi, M.; Auricchio, C.; Brambilla, D.; Calvetti, E.; Capecchi, L.; Croce, L.; Gallinari, D.; Mazzaglia, C.; et al. A 32-KB ePCM for Real-Time Data Processing in Automotive and Smart Power Applications. IEEE J.-Solid-State Circuits 2018, 53, 2114–2125. [Google Scholar] [CrossRef]
- Ielmini, D.; Lacaita, A.L.; Mantegazza, D. Recovery and Drift Dynamics of Resistance and Threshold Voltages in Phase-Change Memories. IEEE Trans. Electron Devices 2007, 54, 308–315. [Google Scholar] [CrossRef]
- Volpe, F.G.; Cabrini, A.; Pasotti, M.; Torelli, G. Drift induced rigid current shift in Ge-Rich GST Phase Change Memories in Low Resistance State. In Proceedings of the 2019 26th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Genoa, Italy, 27–29 November 2019; pp. 418–421. [Google Scholar] [CrossRef]
- Antolini, A.; Paolino, C.; Zavalloni, F.; Lico, A.; Franchi Scarselli, E.; Mangia, M.; Pareschi, F.; Setti, G.; Rovatti, R.; Torres, M.; et al. Combined HW/SW Drift and Variability Mitigation for PCM-based Analog In-memory Computing for Neural Network Applications. J. Emerg. Sel. Top. Circuits Syst. 2023. early access. [Google Scholar] [CrossRef]
- Candes, E.J.; Romberg, J.; Tao, T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information. IEEE Trans. Inf. Theory 2006, 52, 489–509. [Google Scholar] [CrossRef]
- Lustig, M.; Donoho, D.L.; Santos, J.M.; Pauly, J.M. Compressed sensing MRI. IEEE Signal Process. Mag. 2008, 25, 72–82. [Google Scholar] [CrossRef]
- Mangia, M.; Pareschi, F.; Cambareri, V.; Rovatti, R.; Setti, G. Adapted Compressed Sensing for Effective Hardware Implementations: A Design Flow for Signal-Level Optimization of Compressed Sensing Stages; Springer International Publishing: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Oxvig, C.S.; Pedersen, P.S.; Arildsen, T.; Østergaard, J.; Larsen, T. Magni: A Python Package for Compressive Sampling and Reconstruction of Atomic Force Microscopy Images. J. Open Res. Softw. 2014, 2, e29. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paolino, C.; Antolini, A.; Zavalloni, F.; Lico, A.; Franchi Scarselli, E.; Mangia, M.; Marchioni, A.; Pareschi, F.; Setti, G.; Rovatti, R.; et al. Decoding Algorithms and HW Strategies to Mitigate Uncertainties in a PCM-Based Analog Encoder for Compressed Sensing. J. Low Power Electron. Appl. 2023, 13, 17. https://doi.org/10.3390/jlpea13010017
Paolino C, Antolini A, Zavalloni F, Lico A, Franchi Scarselli E, Mangia M, Marchioni A, Pareschi F, Setti G, Rovatti R, et al. Decoding Algorithms and HW Strategies to Mitigate Uncertainties in a PCM-Based Analog Encoder for Compressed Sensing. Journal of Low Power Electronics and Applications. 2023; 13(1):17. https://doi.org/10.3390/jlpea13010017
Chicago/Turabian StylePaolino, Carmine, Alessio Antolini, Francesco Zavalloni, Andrea Lico, Eleonora Franchi Scarselli, Mauro Mangia, Alex Marchioni, Fabio Pareschi, Gianluca Setti, Riccardo Rovatti, and et al. 2023. "Decoding Algorithms and HW Strategies to Mitigate Uncertainties in a PCM-Based Analog Encoder for Compressed Sensing" Journal of Low Power Electronics and Applications 13, no. 1: 17. https://doi.org/10.3390/jlpea13010017
APA StylePaolino, C., Antolini, A., Zavalloni, F., Lico, A., Franchi Scarselli, E., Mangia, M., Marchioni, A., Pareschi, F., Setti, G., Rovatti, R., Luigi Torres, M., Carissimi, M., & Pasotti, M. (2023). Decoding Algorithms and HW Strategies to Mitigate Uncertainties in a PCM-Based Analog Encoder for Compressed Sensing. Journal of Low Power Electronics and Applications, 13(1), 17. https://doi.org/10.3390/jlpea13010017







