Decision Algorithm of Teaching Quality Evaluation for Higher Education System Based on Intuitionistic Fuzzy Geometric Yager Heronian Mean Operators

Abstract

A reliable and data-based teaching quality evaluation is essential for the continuous improvement of higher-education systems. However, the inherent ambiguity of assessment indicators and the subjectivity of evaluators render traditional, crisp-value models insufficient. To address this challenge, we develop a novel intuitionistic fuzzy multi-attribute decision-making framework that integrates Yager triangular norms (t-norms) with the geometric Heronian mean. Specifically, we first introduce intuitionistic fuzzy operations based on Yager t-norms and Yager t-conorms and subsequently construct two aggregation operators: the intuitionistic fuzzy geometric Heronian mean operators and the intuitionistic fuzzy weighted geometric Heronian mean operators. The idempotency, monotonicity, and boundedness properties of these operators are formally proven. Next, the intuitionistic fuzzy weighted geometric Heronian mean operators are employed to develop an approach for multi-attribute decision-making in classroom teaching quality evaluation under intuitionistic fuzzy information. Moreover, an application case study of teaching quality evaluation in an intuitionistic fuzzy environment is presented to demonstrate the practicality and effectiveness of the proposed approach. Additionally, sensitivity and comparative analyses with other techniques are carried out to further confirm the coherence and superiority of the recommended approach. The research results clearly show that our proposed method is highly effective in accurately evaluating teaching quality and can serve as a valuable tool for educational institutions in enhancing their teaching quality management.

1. Introduction

In the era of data-driven education, traditional qualitative evaluations of teaching quality often lack objectivity and repeatability. Mathematical methods, including statistical analysis [1,2,3], fuzzy logic [4,5,6,7], and multi-criteria decision-making [8], provide systematic frameworks to quantify instructional effectiveness across multiple dimensions, such as student performance, engagement, and pedagogical strategies. These methods not only improve the accuracy and transparency of the evaluation, but also support comparative research, evidence-based teaching improvements and institutional decision-making. Therefore, the study of mathematics-driven teaching quality evaluation has solved the growing demand for strict, extensible and operable educational evaluation tools in modern academic environment.

In recent years, mathematical methods have achieved significant breakthroughs in the field of teaching quality evaluation. Yang [9] proposed a fuzzy comprehensive evaluation system that integrates AHP and FCES methods, effectively addressing uncertainty in online education assessment and providing a quantitative tool for quality assurance in distance learning. Bekesiene et al. [10] employed a fuzzy AHP-TOPSIS approach to evaluate remote learning modules, achieving objective assessments through a multi-attribute decision-making framework and significantly improving evaluation accuracy. Machine learning methods have shown strong potential in teaching evaluation. Sekeroglu et al. [11] utilized five machine learning algorithms for the prediction and classification of student performance, effectively predicting student outcomes. Ersozlu et al. [12] conducted a comprehensive analysis of machine learning in educational data mining, offering scientific guidance for algorithm selection. Multi-attribute decision-making methods are widely applied. Chen et al. [13] developed a teacher performance evaluation system based on fuzzy AHP, overcoming the limitations of traditional subjective assessments. Dou et al. [14] applied fuzzy TOPSIS to higher education evaluation in Vietnam, demonstrating the cross-cultural adaptability of mathematical methods. Bittencourt et al. [15] developed a deep neural network evaluation system that achieved high-precision student assessment in e-learning environments. These studies indicate that mathematical methods in teaching quality evaluation are increasingly integrated and diversified, providing scientific quantitative tools and decision-making support for educational quality improvement.

Intuitionistic fuzzy aggregation operators as complex mathematical tools, which can improve the flexibility and accuracy of multi-attribute decision-making, information fusion and uncertain information processing. They have found wide applications in areas such as economic forecasting [16,17], risk assessment [18,19,20], medical diagnosis [21,22,23], and supply chain management [24,25], achieving significant advances both theoretically and practically. In the study of intuitionistic fuzzy aggregation operators, their integration with Yager t-norms and the Heronian mean operator enables the simultaneous characterization of “fuzziness” (degree of membership), “hesitancy” (degree of non-membership and hesitation margin), and “interactivity” (nonlinear dependencies among attributes) in evaluation information. The Yager t-norm family provides tunable flexible logical operations, alleviating the sensitivity of traditional operators to extreme values. Meanwhile, the Heronian mean captures potential interrelationships among attributes through pairwise interaction terms, thereby avoiding the information loss caused by independence assumptions. The teaching quality evaluation is a typical higher-order fuzzy problem: evaluators often find it difficult to express “satisfaction” with precise numerical values, and the perspectives of peers, students, and supervisors inherently involve interactive conflicts. Ali et al. [26] indicated that neglecting weights and interactions under an interval-valued hesitant fuzzy environment can lead to distorted rankings. Chen et al. [27] further demonstrated that introducing a picture fuzzy framework with quadruple membership degrees can substantially reduce the loss of neutral and rejection information. Consequently, adopting an intuitionistic fuzzy aggregation operator that integrates Yager t-norms with the Heronian mean not only preserves the integrity of evaluation information but also effectively captures nonlinear dependencies among key indicators, such as “teacher-student interaction” and “course design”, thereby yielding more robust and interpretable quality ranking outcomes.

Teaching quality evaluation in higher education is essential for educational governance, but traditional models, particularly crisp-value models, often fail to adequately address the fuzziness and subjectivity inherent in evaluation data. This limitation underscores the need for more sophisticated methodologies that can capture the complexities of teaching assessments. While existing intuitionistic fuzzy aggregation operators, such as the intuitionistic fuzzy Aczel-Alsina weighted geometric (IFAAWG) operator [28], the intuitionistic fuzzy hybrid weighted arithmetic and geometric aggregation (IFHWAGA) operator [29], and the Einstein intuitionistic fuzzy weighted geometric (EIFWG) operator [30], have proven useful in multi-criteria decision-making, they are limited by fixed parameters and simplistic aggregation structures, which fail to account for the nuanced nature of teaching quality evaluation. The gap left by these models is particularly evident in two key areas: the lack of flexibility in handling dynamic evaluation criteria and the failure to capture the interdependencies between them. Furthermore, existing methods generally ignore evaluators’ varying risk preferences, a crucial factor in educational contexts.

To address the challenge of the inadequacy of traditional models, inspired by the classical works of [31,32], we propose the intuitionistic Fuzzy Yager geometric Heronian Mean (IFYWGHM) and its weighted version (IFYWGHM) operators by incorporating Yager t-norms and t-conorms into the Heronian mean structure. These operators contain three adjustable parameters. They allow decision makers to customize the aggregation process, which can make the aggregation behavior more flexible and detailed so that the evaluation framework can adapt to the subjectivity and situational sensitivity of education quality evaluation. To ensure theoretical reliability and that the aggregation method provides stable and reasonable results in complex decision-making processes, we have proven the idempotency, monotonicity, and boundedness of these aggregation operators. Then we develop a novel intuitionistic fuzzy multi-attribute decision-making framework based on the FYWGHM operator, which provides a comprehensive framework that takes into account multidimensional feedback from students, peers, and supervisors, while also incorporating evaluators’ preferences and addressing the nonlinear relationships between evaluation criteria, such as the interaction between “teacher-student interaction” and “course design”. Through an application case study in classroom teaching quality evaluation under intuitionistic fuzzy conditions, we demonstrate that the proposed IFYWGHM framework provides a more robust and reliable evaluation tool. Sensitivity analyses and comparative evaluations with existing techniques further confirm its coherence and superiority. This framework represents a significant advancement over existing fuzzy aggregation techniques, enhancing the scientific rigor and interpretability of teaching evaluations and providing educational institutions with a more effective tool for diagnosing instructional challenges and optimizing faculty development strategies.

2. Preliminaries

This section reviews the essential concepts underlying the proposed framework, which is built upon intuitionistic fuzzy sets, Yager t-norms, and aggregation operators that account for inter-attribute dependency.

A fuzzy set, first introduced by Zadeh, addresses uncertainty through the principle of gradualness.

Definition 1

([33]). Let X denote a universe of discourse. A fuzzy set A on X can be formally represented as

$$A=\{<x,{\mu }_A\left(x\right)>|x\in X\},$$

where the mapping ${\mu }_A:X\to [0,1]$ is referred to as the membership function of A. For each element $x\in X$, the value ${\mu }_A\left(x\right)$ quantifies the extent to which x belongs to the set A.

In the classical sense, a fuzzy set A over a universe X is characterized by its membership function ${\mu }_A\left(x\right)$, while the complementary value $1-{\mu }_A\left(x\right)$ is often interpreted as the degree of non-membership. However, in real applications, people often find it difficult to express the degree of hesitation or uncertainty they feel toward certain phenomena. To address this limitation, Atanassov extended the classical fuzzy set by incorporating an additional degree of uncertainty, thereby formulating the intuitionistic fuzzy set, formally defined as follows.

Definition 2

([34]). Let X denote a universe of discourse. An intuitionistic fuzzy set A over X is formally specified by two functions: a membership function ${\mu }_A:X\to [0,1]$ and a non-membership function ${\nu }_A:X\to [0,1]$. The set can thus be expressed as

$$A=\{⟨x,{\mu }_A\left(x\right),{\nu }_A\left(x\right)⟩\mid x\in X\}.$$

These functions are constrained for every $x\in X$ such that

$$0\le {\mu }_A\left(x\right)+{\nu }_A\left(x\right)\le 1.$$

The residual quantity

$${\pi }_A\left(x\right)=1-{\mu }_A\left(x\right)-{\nu }_A\left(x\right)$$

is interpreted as the degree of indeterminacy associated with element x in A. When ${\pi }_A\left(x\right)=0$ for all $x\in X$, the intuitionistic fuzzy set reduces to a classical fuzzy set.

For notational convenience, the ordered pair $\alpha =({\mu }_{\alpha },{\nu }_{\alpha })$ is referred to as an intuitionistic fuzzy number, subject to the restrictions ${\mu }_{\alpha },{\nu }_{\alpha }\in [0,1]$ and ${\mu }_{\alpha }+{\nu }_{\alpha }\le 1$. The collection of all intuitionistic fuzzy numbers is denoted by

$$\Theta =\{({\mu }_{\alpha },{\nu }_{\alpha })\mid {\mu }_{\alpha },{\nu }_{\alpha }\in [0,1],{\mu }_{\alpha }+{\nu }_{\alpha }\le 1\}.$$

To enable a more intuitive assessment of intuitionistic fuzzy numbers and to facilitate the analysis of their inherent properties, the concepts of the score function and the accuracy (or precision) function are introduced.

Definition 3

([35,36]). Let $\alpha =({\mu }_{\alpha },{\nu }_{\alpha })$ denote an intuitionistic fuzzy number. Then:

(1) 

The score function S of α is defined as

$$S\left(\alpha \right)={\mu }_{\alpha }-{\nu }_{\alpha },$$

which quantifies the net tendency of membership relative to non-membership.

(2) 

The accuracy function H of α is given by

$$H\left(\alpha \right)={\mu }_{\alpha }+{\nu }_{\alpha },$$

representing the overall determinacy associated with α.

Utilizing these functions, Xu and Yager [31] formulated a systematic approach for the comparison and ranking method of intuitionistic fuzzy numbers.

Definition 4

([31]). Consider two intuitionistic fuzzy numbers ${\alpha }_1$ and ${\alpha }_2$. Their comparison is governed by the following criteria:

(1) 

If $S\left({\alpha }_1\right)<S\left({\alpha }_2\right)$, then ${\alpha }_2$ is considered superior to ${\alpha }_1$, denoted as ${\alpha }_2>{\alpha }_1$.

(2) 

If $S\left({\alpha }_1\right)>S\left({\alpha }_2\right)$, then ${\alpha }_1$ is superior to ${\alpha }_2$, denoted as ${\alpha }_1>{\alpha }_2$.

(3) 

If $S\left({\alpha }_1\right)=S\left({\alpha }_2\right)$, the ranking is further determined by the accuracy function H:

(a) 

When $H\left({\alpha }_1\right)=H\left({\alpha }_2\right)$, the two numbers are deemed equal, denoted by ${\alpha }_1={\alpha }_2$.

(b) 

When $H\left({\alpha }_1\right)<H\left({\alpha }_2\right)$, it follows that ${\alpha }_2>{\alpha }_1$.

(c) 

When $H\left({\alpha }_1\right)>H\left({\alpha }_2\right)$, it follows that ${\alpha }_1>{\alpha }_2$.

Triangle norms (t-norms), initially conceptualized by Menger [37], emerged as a foundational component within the analytical framework he employed to investigate Banach spaces endowed with probabilistic structures. According to this research, t-norms and their corresponding t-conorms are fundamental operations in fuzzy set theory and its extensions, such as Hamacher t-norms and t-conorms [38], Frank t-norms and conorms [39], Einstein t-norms and t-conorms [30], Dombi t-norms and t-conorms [40], and so on.

Definition 5

([41]). A t-norm $T:{[0,1]}^2\to [0,1]$ is defined as a binary operation that is associative and commutative, admits $e=1$ as its neutral element, and exhibits monotonicity in each argument. Similarly, a t-conorm $S:{[0,1]}^2\to [0,1]$ is a binary operation that is both associative and commutative, possesses $e=0$ as its neutral element, and is non-decreasing with respect to each of its arguments.

From an axiomatic perspective, t-norms and t-conorms are distinguished primarily by their respective boundary conditions. Conceptually, these two structures exhibit a form of duality: for any binary t-norm T, the corresponding dual t-conorm S can be expressed as

$$S(x,y)=1-T(1-x,1-y),$$

whereas for any binary t-conorm S, its dual t-norm T is defined by

$$T(x,y)=1-S(1-x,1-y).$$

Among the class of t-norms, three particular instances are of notable interest due to their fundamental properties:

(1)

The minimum t-norm, $T_M(x,y)=min\{x,y\}$,

(2)

The product t-norm, $T_P(x,y)=x·y$,

(3)

The drastic product t-norm, defined as

$$\begin{array}{cc}\hfill T_D(x,y)& =\left\{\begin{array}{cc}0,\hfill & (x,y)\in {[0,1]}^2,\hfill \\ min\{x,y\},\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

Correspondingly, the dual t-conorms associated with $S_M$, $S_P$, and $S_D$ are given by:

(1)

The maximum t-conorm, $S_M(x,y)=max\{x,y\}$,

(2)

The probabilistic sum t-conorm, $S_P(x,y)=x+y-x·y$,

(3)

The drastic sum t-conorm, defined as

$$\begin{array}{cc}\hfill S_D(x,y)& =\left\{\begin{array}{cc}1,\hfill & (x,y)\in {[0,1]}^2,\hfill \\ max\{x,y\},\hfill & otherwise.\hfill \end{array}\right.\hfill \end{array}$$

Within the spectrum of families used to represent intersections of fuzzy sets, a particularly prominent class comprises certain t-norms and their corresponding t-conorms, a formulation originally introduced by Yager [42].

Definition 6

([42]). The family ${\left(T_Y^r\right)}_{r\in [0,\infty )}$ of Yager t-norms is given by

$$\begin{array}{cc}\hfill & T_Y^r(x,y)\hfill \\ \hfill & =\left\{\begin{array}{cc}{T}_D(x,y),\hfill & r=0,\hfill \\ T_M(x,y),\hfill & r=\infty ,\hfill \\ max\left\{1-{\left({(1-x)}^r+{(1-y)}^r\right)}^{{\displaystyle \frac{1}{r}}},0\right\},\hfill & r\in (0,\infty ).\hfill \end{array}\right.\hfill \end{array}$$

And the dual family ${\left(S_Y^r\right)}_{r\in [0,\infty )}$ of Yager t-conorms is present as

$$\begin{array}{cc}\hfill S_Y^r(x,y)& =1-T_Y^r(1-x,1-y)\hfill \\ \hfill & =\left\{\begin{array}{cc}{S}_D(x,y),\hfill & r=0,\hfill \\ S_M(x,y),\hfill & r=\infty ,\hfill \\ min\left\{{(x^r+y^r)}^{{\displaystyle \frac{1}{r}}},1\right\},\hfill & r\in (0,\infty ).\hfill \end{array}\right.\hfill \end{array}$$

Yager t-norms and t-conorms are two basic operations in fuzzy logic, which correspond to logical “AND” and logical “OR” respectively. When the Yager t-conorm $T_Y^r$ and the Yager t-conorm $S_Y^r$ are given, the Yager algorithm on intuitionistic fuzzy numbers is defined as follows.

Definition 7.

Let $\alpha =({\mu }_{\alpha },{\nu }_{\alpha })$, ${\alpha }_1=({\mu }_{{\alpha }_1},{\nu }_{{\alpha }_1})$ and ${\alpha }_2=({\mu }_{{\alpha }_2},{\nu }_{{\alpha }_2})$ be three intuitionistic fuzzy numbers, with $\lambda >0$ and $r\in (0,\infty )$. The following operations are considered:

(1) 

The complement ${\alpha }^c$ of α is defined as:

$${\alpha }^c=({\nu }_{\alpha },{\mu }_{\alpha }).$$

(2) 

The addition of ${\alpha }_1$ and ${\alpha }_2$ is given by

$$\begin{array}{cc}\hfill {\alpha }_1\oplus {\alpha }_2& =\left(S_Y^r({\mu }_{{\alpha }_1},{\mu }_{{\alpha }_2}),T_Y^r({\nu }_{{\alpha }_1},{\nu }_{{\alpha }_2})\right)\hfill \\ & =({({\mu }_{{\alpha }_1}^r+{\mu }_{{\alpha }_2}^r)}^{{\displaystyle \frac{1}{r}}},1-{\left({(1-{\nu }_{{\alpha }_1})}^r+{(1-{\nu }_{{\alpha }_2})}^r\right)}^{{\displaystyle \frac{1}{r}}});\hfill \end{array}$$

(3) 

The multiplication of ${\alpha }_1$ and ${\alpha }_2$ is defined as

$$\begin{array}{cc}\hfill {\alpha }_1\otimes {\alpha }_2& =\left(T_Y^r({\mu }_{{\alpha }_1},{\mu }_{{\alpha }_2}),S_Y^r({\nu }_{{\alpha }_1},{\nu }_{{\alpha }_2})\right)\hfill \\ & =\left((1-{\left({(1-{\mu }_{{\alpha }_1})}^r+{(1-{\mu }_{{\alpha }_2})}^r\right)}^{{\displaystyle \frac{1}{r}}},{({\nu }_{{\alpha }_1}^r+{\nu }_{{\alpha }_2}^r)}^{{\displaystyle \frac{1}{r}}}\right);\hfill \end{array}$$

(4) 

The scalar multiplication is given by

$$\lambda \alpha =\left({\left(\lambda {\mu }_{\alpha }^r\right)}^{1/r},1-{\left(\lambda {(1-{\nu }_{\alpha })}^r\right)}^{1/r}\right).$$

(5) 

The power operation is expressed as

$${\alpha }^{\lambda }=\left(1-{\left(\lambda {(1-{\mu }_{\alpha })}^r\right)}^{1/r},{\left(\lambda {\nu }_{\alpha }^r\right)}^{1/r}\right).$$

In intuitionistic fuzzy sets, the Yager t-norm is typically used in intuitionistic fuzzy sets to combine membership ($\mu$) and non-membership ($\nu$) values in a way that reflects the underlying uncertainty in the data. It ensures that the combination of memberships is logically consistent and that the aggregation respects the fuzzy nature of the data.

The the Bonferroni mean [43] and Heronian mean [44], which consider interrelationships of aggregated arguments. Yu et al. [32] explained the advantages of the Heronian mean over the Bonferroni mean in details, where they pointed out that the Heronian mean considers the correlation between an attribute and itself and can avoid the calculation redundancy. The Heronian mean allows for a more flexible aggregation of the membership and non-membership values. Unlike traditional geometric or arithmetic means, which focus purely on arithmetic operations, the Heronian mean introduces a more nuanced interaction between attribute pairs through a non-linear weighting mechanism.

Definition 8

([45]). The basic Heronian mean operator $BHM:{[0,1]}^n\to [0,1]$ for aggregating the non-negative numbers $x_1,x_2,\dots ,x_n$ is formulated as:

$$BHM(x_1,x_2,\dots ,x_n)={\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n\sqrt{x_i{x}_j}.$$

The basic Heronian mean, in its simplest manifestation, was originally conceived and applied within the realm of inequality theory and methodology. Subsequently, its efficacy in the realm of decision-making began to be recognized over time.

Based on the concept of the basic Heronian mean, Yu [32] introduced two non-negative parameters p and q to generalize the operator, thereby formulating a more flexible version of the Heronian mean.

Definition 9

([32]). Let $p,q\ge 0$ and $x_i$ ($i=1,2,\dots ,n$) denote a collection of non-negative real numbers. The Heronian mean $HM:{[0,1]}^n\to [0,1]$ between $x_i$ is presented in the following formula:

$$HM(x_1,x_2,\dots ,x_n)={\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{x}_i^p{x}_j^q\right)}^{{\displaystyle \frac{1}{p+q}}}.$$

It is noteworthy that the generalized Heronian mean reduces to the basic Heronian mean when $p=q={\displaystyle \frac{1}{2}}$.

Extending this framework, Yu [46] proposed the geometric Heronian mean (GHM) by leveraging the concept of the geometric Bonferroni mean [47].

Definition 10

([46]). For a set of non-negative real numbers $x_i$ ($i=1,2,\dots ,n$) and parameters $p,q\ge 0$, the geometric Heronian mean is expressed as

$$GHM(x_1,x_2,\dots ,x_n)={\displaystyle \frac{1}{p+q}}\left(\prod _{i=1,j=i}^n{(p{x}_i+q{x}_j)}^{{\displaystyle \frac{2}{n(n+1)}}}\right).$$

3. Intuitionistic Fuzzy Geometric Heronian Mean Operators Based on Yager t-Norms

In this section, we introduce the intuitionistic fuzzy geometric Heronian mean operators and the intuitionistic fuzzy weighted geometric Heronian mean operators, both formulated on the basis of the Yager t-norm. We also examine several fundamental properties of these operators.

Definition 11.

Let ${\alpha }_i$ ($i=1,2,\dots ,n$) denote a collection of intuitionistic fuzzy numbers, with parameters $p,q\ge 0$ such that p and q are not simultaneously zero, and $r>0$. Consider a mapping

$${YGHM}^{(p,q,r)}:{\Theta }^n\to \Theta$$

defined by

$${YGHM}^{(p,q,r)}({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n)={\displaystyle \frac{1}{p+q}}\underset{i=1,j=i}{\overset{n}{⨂}}{\left(p{\alpha }_i\oplus q{\alpha }_j\right)}^{{\displaystyle \frac{2}{n(n+1)}}}.$$

This mapping is referred to as an intuitionistic fuzzy geometric Heronian mean operator based on the Yager t-norm, or, for brevity, the intuitionistic fuzzy Yager geometric Heronian mean (IFYGHM) operator.

The Yager t-norm provides the mathematical foundation for combining positive membership information in a logically consistent way, ensuring that aggregation respects the properties of fuzzy sets. The Heronian mean builds on this foundation by adding a layer of flexibility through its non-linear structure. This allows it to model more complex relationships between membership and non-membership, and to handle situations where different attributes interact in non-trivial ways. In the IFYGHM operator, the Heronian mean is combined with the Yager t-norm to form a flexible and non-linear aggregation process. It offer a powerful mechanism for aggregating intuitionistic fuzzy numbers that accounts for both the uncertainty in the membership values and the compensatory effects between the various criteria.

For any pair of intuitionistic fuzzy numbers ${\alpha }_i=({\mu }_{{\alpha }_i},{\nu }_{{\alpha }_i})$ and ${\alpha }_j=({\mu }_{{\alpha }_i},{\nu }_{{\alpha }_j})$, according to the Yager algorithm (Definition 7) we have

$$\begin{array}{cc}\hfill p{\alpha }_i\oplus q{\alpha }_j& =\left({(p{\mu }_{{\alpha }_i}^r+q{\mu }_{{\alpha }_j}^r)}^{{\displaystyle \frac{1}{r}}},1-{\left(p{(1-{\nu }_{{\alpha }_i})}^r+q{(1-{\nu }_{{\alpha }_j})}^r\right)}^{{\displaystyle \frac{1}{r}}}\right).\hfill \end{array}$$

To streamline the subsequent discussions and avoid redundant explanations, we introduce the following notation:

${\hslash }_{{\alpha }_{ij}}={(p{\mu }_{{\alpha }_i}^r+q{\mu }_{{\alpha }_j}^r)}^{{\displaystyle \frac{1}{r}}}$, ${\ell }_{{\alpha }_{ij}}=1-{\left(p{(1-{\nu }_{{\alpha }_i})}^r+q{(1-{\nu }_{{\alpha }_j})}^r\right)}^{{\displaystyle \frac{1}{r}}}$.

Theorem 1.

Let ${\alpha }_i(i=1,2,\dots ,n)$ be a collection of intuitionistic fuzzy numbers. Then, the aggregation via the IFYGHM operator yields an intuitionistic fuzzy number, which can be explicitly expressed as

$${YGHM}^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=\left(\begin{array}{cc}\hfill & {\left[{\displaystyle \frac{1}{p+q}}{\left(1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{(1-{\hslash }_{{\alpha }_{ij}})}^r\right)}^{{\displaystyle \frac{1}{r}}}\right)}^r\right]}^{{\displaystyle \frac{1}{r}}},\hfill \\ \hfill & 1-{\left[{\displaystyle \frac{1}{p+q}}{\left(1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{\ell }_{{\alpha }_{ij}}^r\right)}^{{\displaystyle \frac{1}{r}}}\right)}^r\right]}^{{\displaystyle \frac{1}{r}}}\hfill \end{array}\right).$$

Proof. 

Given that the IFYWGHM operator is based on a Heronian mean structure, the proof relies on showing that the aggregation process defined by the IFYWGHM operator satisfies the required properties under the conditions of intuitionistic fuzzy sets. Specifically, we need to demonstrate that the operator properly handles the aggregation of intuitionistic fuzzy numbers while respecting the underlying t-norm structure and the interaction of positive, negative, and hesitant information.

For any pair of intuitionistic fuzzy numbers ${\alpha }_i$ and ${\alpha }_j$, we build a new intuitionistic fuzzy number

$$\begin{array}{c}\hfill p{\alpha }_i\oplus q{\alpha }_j=\left({\hslash }_{{\alpha }_{ij}},{\ell }_{{\alpha }_{ij}}\right).\end{array}$$

Applying the Yager geometric aggregation exponent ${\displaystyle \frac{2}{n(n+1)}}$ and the Yager t-norm composition, it follows that

${(p{\alpha }_i\oplus q{\alpha }_j)}^{{\displaystyle \frac{2}{n(n+1)}}}=\left(1-{\left({\displaystyle \frac{2}{n(n+1)}}{(1-{\hslash }_{{\alpha }_{ij}})}^r\right)}^{{\displaystyle \frac{1}{r}}},{\left({\displaystyle \frac{2}{n(n+1)}}{\ell }_{{\alpha }_{ij}}^r\right)}^{{\displaystyle \frac{1}{r}}}\right)$ and consequently,

$$\begin{array}{c}\hfill \underset{i=1,j=i}{\overset{n}{⨂}}{(p{\alpha }_i\oplus q{\alpha }_j)}^{{\displaystyle \frac{2}{n(n+1)}}}=\left(1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{(1-{\hslash }_{{\alpha }_{ij}})}^r\right)}^{{\displaystyle \frac{1}{r}}},{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{\ell }_{{\alpha }_{ij}}^r\right)}^{{\displaystyle \frac{1}{r}}}\right).\end{array}$$

Therefore, we have

$$\begin{array}{cc}\hfill {YGHM}^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)& ={\displaystyle \frac{1}{p+q}}\underset{i=1,j=i}{\overset{n}{⨂}}{\left(p{\alpha }_i\oplus q{\alpha }_j\right)}^{{\displaystyle \frac{2}{n(n+1)}}}\hfill \\ \hfill & =\left(\begin{array}{cc}\hfill & {\left[{\displaystyle \frac{1}{p+q}}{\left(1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{(1-{\hslash }_{{\alpha }_{ij}})}^r\right)}^{{\displaystyle \frac{1}{r}}}\right)}^r\right]}^{{\displaystyle \frac{1}{r}}},\hfill \\ \hfill & 1-{\left[{\displaystyle \frac{1}{p+q}}{\left(1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{\ell }_{{\alpha }_{ij}}^r\right)}^{{\displaystyle \frac{1}{r}}}\right)}^r\right]}^{{\displaystyle \frac{1}{r}}}\hfill \end{array}\right).\hfill \end{array}$$

Denote $(\mu ,\nu )={YGHM}^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)$, we now verify $(\mu ,\nu )$ is an intuitionistic fuzzy number. Since $0\le {\mu }_{{\alpha }_i}\le 1$, $0\le {\mu }_{{\alpha }_j}\le 1$, $p\ge 0$, $q\ge 0$ and $r>0$, we have $0\le {(p{\mu }_{{\alpha }_i}^r+q{\mu }_{{\alpha }_j}^r)}^{{\displaystyle \frac{1}{r}}}\le {(p+q)}^{{\displaystyle \frac{1}{r}}}$, which implies $0\le {\hslash }_{{\alpha }_{ij}}\le {(p+q)}^{{\displaystyle \frac{1}{r}}}$. Further, we can derive

$$0\le {\left[{\displaystyle \frac{1}{p+q}}{\left(1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{(1-{\hslash }_{{\alpha }_{ij}})}^r\right)}^{{\displaystyle \frac{1}{r}}}\right)}^r\right]}^{{\displaystyle \frac{1}{r}}}\le 1.$$

Hence $0\le \mu \le 1$. Similarly, the same argument applies to $\nu$, yielding $0\le \nu \le 1$.

According to the concept of intuitionistic fuzzy numbers, we get that ${\mu }_{{\alpha }_i}\le (1-{\nu }_{{\alpha }_i})$ and ${\mu }_{{\alpha }_j}\le (1-{\nu }_{{\alpha }_j})$. It follows that

$${(p{\mu }_{{\alpha }_i}^r+q{\mu }_{{\alpha }_j}^r)}^{{\displaystyle \frac{1}{r}}}\le {\left(p{(1-{\nu }_{{\alpha }_i})}^r+q{(1-{\nu }_{{\alpha }_j})}^r\right)}^{{\displaystyle \frac{1}{r}}},$$

that is, ${\hslash }_{{\alpha }_{ij}}\le 1-{\ell }_{{\alpha }_{ij}}$. And thus

$$\begin{array}{cc}\hfill \mu & ={\left[{\displaystyle \frac{1}{p+q}}{\left(1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{(1-{\hslash }_{{\alpha }_{ij}})}^r\right)}^{{\displaystyle \frac{1}{r}}}\right)}^r\right]}^{{\displaystyle \frac{1}{r}}}\hfill \\ \hfill & \le {\left[{\displaystyle \frac{1}{p+q}}{\left(1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{\ell }_{{\alpha }_{ij}}^r\right)}^{{\displaystyle \frac{1}{r}}}\right)}^r\right]}^{{\displaystyle \frac{1}{r}}}\hfill \\ \hfill & =1-\nu .\hfill \end{array}$$

Therefore, $\mu +\nu \le (1-\nu )+\nu =1$. Thus, the proof is completed.    □

In numerous fields such as multi-attribute decision analysis, fuzzy set theory, and information fusion, aggregation operators serve as core tools, undertaking the crucial task of integrating multiple attribute values or information sources into a single comprehensive result. In-depth research into the characteristics of aggregation operators, especially their monotonicity, boundedness, and idempotency, is of paramount importance for constructing a robust theoretical framework, meeting practical application needs, facilitating operator comparison and selection, optimizing algorithm design, and enhancing decision reliability.

In what follows, we systematically investigate several fundamental properties of the IFYGHM operator, including idempotency, monotonicity, and boundedness. These properties not only ensure consistent and interpretable aggregation of intuitionistic fuzzy information, but also provide critical insights into its applicability for aggregating intuitionistic fuzzy information under Yager t-norm-based geometric aggregation frameworks.

Idempotency means that when all input values are equal, the output value of the aggregation operator is the same as the input value. This property plays an important role in the computation process, as it can avoid redundant calculations and reduce the time complexity of the algorithm.

Theorem 2

(Idempotency). Let ${\alpha }_i=({\mu }_{{\alpha }_i},{\nu }_{{\alpha }_i})$ for $i=1,2,\dots ,n$ be a set of intuitionistic fuzzy numbers. If ${\alpha }_1={\alpha }_2=\dots ={\alpha }_n=\alpha =({\mu }_{\alpha },{\nu }_{\alpha })$, then

$${YGHM}^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=\alpha .$$

Proof. 

Under the assumption ${\alpha }_1={\alpha }_2=\dots ={\alpha }_n=\alpha =({\mu }_{\alpha },{\nu }_{\alpha })$, it follows directly that

$$\begin{array}{c}\hfill {\hslash }_{{\alpha }_{ij}}={(p+q)}^{{\displaystyle \frac{1}{r}}}{\mu }_{\alpha },{\ell }_{{\alpha }_{ij}}=1-{(p+q)}^{{\displaystyle \frac{1}{r}}}(1-{\nu }_{\alpha }).\end{array}$$

For notational simplicity, let $\hslash ={\hslash }_{{\alpha }_{ij}}$ and $\ell ={\ell }_{{\alpha }_{ij}}$. Substituting these into the IFYGHM formula yields

$$\begin{array}{cc}\hfill & {YGHM}^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)\hfill \\ \hfill & =\left({\left[{\displaystyle \frac{1}{p+q}}{\left(1-{\left({(1-\hslash )}^r\right)}^{{\displaystyle \frac{1}{r}}}\right)}^r\right]}^{{\displaystyle \frac{1}{r}}},1-{\left[{\displaystyle \frac{1}{p+q}}{\left(1-{\left({\ell }^r\right)}^{{\displaystyle \frac{1}{r}}}\right)}^r\right]}^{{\displaystyle \frac{1}{r}}}\right)\hfill \\ \hfill & =\left({\displaystyle \frac{1}{{(p+q)}^{\frac{1}{r}}}}\hslash ,1-{\displaystyle \frac{1}{{(p+q)}^{\frac{1}{r}}}}(1-\ell )\right)\hfill \\ \hfill & =({\mu }_{\alpha },{\nu }_{\alpha })\hfill \\ \hfill & =\alpha .\hfill \end{array}$$

This confirms that the IFYGHM operator preserves idempotency when all input intuitionistic fuzzy numbers are identical.    □

In multi-attribute decision problems, monotonicity is a crucial property of aggregation operators. It ensures that when the value of a certain attribute increases (or decreases), the overall evaluation result will not exhibit an unreasonable reverse change.

Theorem 3 (Monotonicity).

Let ${\alpha }_i=({\mu }_{{\alpha }_i},{\nu }_{{\alpha }_i})$ and ${\beta }_i=({\mu }_{{\beta }_i},{\nu }_{{\beta }_i})(i=1,2,\dots ,n)$ be two collections of intuitionistic fuzzy numbers. If ${\alpha }_i⪯{\beta }_i$ for all i, meaning ${\mu }_{{\alpha }_i}\le {\mu }_{{\beta }_i}$, ${\nu }_{{\alpha }_i}\ge {\nu }_{{\beta }_i}$, then

$${YGHM}^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)\le {YGHM}^{(p,q,r)}\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right).$$

Proof. 

To facilitate the description, we denote

$$\alpha =({\mu }_{\alpha },{\nu }_{\alpha })={\mathrm{YGHM}}^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)$$

and

$$\beta =({\mu }_{\beta },{\nu }_{\beta })={\mathrm{YGHM}}^{(p,q,r)}\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right).$$

Given ${\mu }_{{\alpha }_i}\le {\mu }_{{\beta }_i}$, ${\nu }_{{\alpha }_i}\ge {\nu }_{{\beta }_i}$ for every i, the Yager operations preserve order:

$${(p{\mu }_{{\alpha }_i}^r+q{\mu }_{{\alpha }_j}^r)}^{{\displaystyle \frac{1}{r}}}\le {(p{\mu }_{{\beta }_i}^r+q{\mu }_{{\beta }_j}^r)}^{{\displaystyle \frac{1}{r}}},$$

$$1-{\left(p{(1-{\nu }_{{\alpha }_i})}^r+q{(1-{\nu }_{{\alpha }_j})}^r\right)}^{{\displaystyle \frac{1}{r}}}\ge 1-{\left(p{(1-{\nu }_{{\beta }_i})}^r+q{(1-{\nu }_{{\beta }_j})}^r\right)}^{{\displaystyle \frac{1}{r}}},$$

that is, ${\hslash }_{{\alpha }_{ij}}\le {\hslash }_{{\beta }_{ij}}$ and ${\ell }_{{\alpha }_{ij}}\ge {\ell }_{{\beta }_{ij}}$.

These inequalities propagate through the identical convex–geometric aggregation (Theorem 1), yielding

$${\mu }_{\alpha }\le {\mu }_{\beta },{\nu }_{\alpha }\ge {\nu }_{\beta }.$$

By Definitions 3 and 4, we have

$$S\left(\alpha \right)\le S\left(\beta \right),$$

and so $\alpha \le \beta$. This means that

$${\mathrm{YGHM}}^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)\le {\mathrm{YGHM}}^{(p,q,r)}\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right).$$

Therefore, the proof of Theorem 3 is completed.    □

Boundedness is another important characteristic of aggregation operators. It restricts the range of values for the aggregation result, causing it to fluctuate within a reasonable interval. When dealing with uncertain and fuzzy data, bounded aggregation operators can ensure that the aggregation result will not fluctuate excessively due to small changes in the data, thereby guaranteeing the stability and reliability of the algorithm.

Theorem 4 (Boundedness).

Let ${\alpha }_i(i=1,2,\dots ,n)$ be a collection of intuitionistic fuzzy numbers. Define

$${\alpha }^{+}=\left(\underset{i}{max}\left\{{\mu }_{{\alpha }_i}\right\},\underset{i}{min}\left\{{\nu }_{{\alpha }_i}\right\}\right),{\alpha }^{-}=\left(\underset{i}{min}\left\{{\mu }_{{\alpha }_i}\right\},\underset{i}{max}\left\{{\nu }_{{\alpha }_i}\right\}\right).$$

Then, the aggregation via the IFYGHM operator satisfies

$${\alpha }^{-}\le {YGHM}^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)\le {\alpha }^{+}.$$

Proof. 

From Definition 5, we observe ${\alpha }^{-}⪯{\alpha }_i⪯{\alpha }^{+}$ for all i. Applying Theorems 2 and 3 yields

$$\begin{array}{cc}\hfill {\alpha }^{-}& ={\mathrm{YGHM}}^{(p,q,r)}\left({\alpha }^{-},{\alpha }^{-},\dots ,{\alpha }^{-}\right)\hfill \\ \hfill & \le {\mathrm{YGHM}}^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)\hfill \\ \hfill & \le {\mathrm{YGHM}}^{(p,q,r)}\left({\alpha }^{+},{\alpha }^{+},\dots ,{\alpha }^{+}\right)\hfill \\ \hfill & ={\alpha }^{+}.\hfill \end{array}$$

Hence, the proof is completed.    □

By assigning different values to the parameters p, q, and r, some special cases of the IFYGHM operator can be obtained as follows:

(1)

When $q\to 0$, the IFYGHM operator ${YGHM}^{(p,q,r)}$ reduces into the form of

$\begin{array}{c}{YGHM}^{(p,0,r)}({\alpha }_1,\dots ,{\alpha }_n)=\\ \left(\begin{array}{cc}& {\displaystyle \frac{1}{p^{1/r}}}\left[1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1}^n{\left(1-p^{1/r}{\mu }_{{\alpha }_i}\right)}^r\right)}^{1/r}\right],\hfill \\ & 1-{\displaystyle \frac{1}{p^{1/r}}}\left[1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1}^n{\left(1-p^{1/r}(1-{\nu }_{{\alpha }_i})\right)}^r\right)}^{1/r}\right]\hfill \end{array}\right).\end{array}$

It can be called as a generalized intuitionistic fuzzy geometric heavy Yager Heronian mean operator.

(2)

When $p=1,q\to 0$, the IFYGHM operator ${YGHM}^{(p,q,r)}$ reduces into the form of

$${\mathrm{YGHM}}^{(1,0,r)}({\alpha }_1,\dots ,{\alpha }_n)=\left(1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1}^n{(1-{\mu }_{{\alpha }_i})}^r\right)}^{1/r},{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1}^n{\nu }_{{\alpha }_i}^r\right)}^{1/r}\right)$$

which can be called as an intuitionistic fuzzy geometric heavy Yager Heronian mean operator.

(3)

When $p=1,q=1$, the IFYGHM operator ${\mathrm{YGHM}}^{(p,q,r)}$ reduces into the form of

$$\begin{array}{cc}\hfill & {\mathrm{YGHM}}^{(1,1,r)}({\alpha }_1,\dots ,{\alpha }_n)\hfill \\ \hfill & =\left(\begin{array}{cc}\hfill & {\left[{\displaystyle \frac{1}{2}}{\left(1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{\left(1-{({\mu }_{{\alpha }_i}^r+{\mu }_{{\alpha }_j}^r)}^{1/r}\right)}^r\right)}^{1/r}\right)}^r\right]}^{1/r},\hfill \\ \hfill & 1-{\left[{\displaystyle \frac{1}{2}}{\left(1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{\left(1-{\left[{(1-{\nu }_{{\alpha }_i})}^r+{(1-{\nu }_{{\alpha }_j})}^r\right]}^{1/r}\right)}^r\right)}^{1/r}\right)}^r\right]}^{1/r}\hfill \end{array}\right)\hfill \end{array}$$

which can be called as an intuitionistic fuzzy geometric linear Yager Heronian mean operator.

(4)

When $p={\displaystyle \frac{1}{2}},q={\displaystyle \frac{1}{2}}$, the IFYGHM operator ${\mathrm{YGHM}}^{(p,q,r)}$ reduces into the form of

$$\begin{array}{cc}\hfill & {\mathrm{YGHM}}^{\left({\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}},r\right)}({\alpha }_1,\dots ,{\alpha }_n)\hfill \\ \hfill & =\left(\begin{array}{cc}\hfill & {\left[1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{\left(1-{\left({\displaystyle \frac{{\mu }_{{\alpha }_i}^r+{\mu }_{{\alpha }_j}^r}{2}}\right)}^{1/r}\right)}^r\right)}^{1/r}\right]}^{1/r},\hfill \\ \hfill & 1-{\left[1-{\left({\displaystyle \frac{2}{n(n+1)}}\sum _{i=1,j=i}^n{\left(1-{\left({\displaystyle \frac{{(1-{\nu }_{{\alpha }_i})}^r+{(1-{\nu }_{{\alpha }_j})}^r}{2}}\right)}^{1/r}\right)}^r\right)}^{1/r}\right]}^{1/r}\hfill \end{array}\right)\hfill \end{array}$$

which can be called as an intuitionistic fuzzy geometric Yager Heronian mean operator.

Attribute weights play an essential role while aggregating different attributes during multiple attribute decision making (MADM) processes. In order to consider the importance of aggregated arguments, we define an intuitionistic fuzzy Yager weighted geometric Heronian mean (IFYWGHM) operator as follows.

Definition 12.

Let ${\alpha }_i=({\mu }_{{\alpha }_i},{\nu }_{{\alpha }_i})$ for $i=1,2,\dots ,n$ be intuitionistic fuzzy numbers with corresponding weights $w_i\in [0,1]$ such that ${\displaystyle \sum _{i=1}^n}{w}_i=1$. The intuitionistic fuzzy Yager weighted geometric Heronian mean operator is defined as a mapping ${YGHM}_w^{(p,q,r)}:{\Theta }^n\to \Theta$ by

$$\begin{array}{c}\hfill {YGHM}_w^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)={\displaystyle \frac{1}{p+q}}\left(\underset{i=1,j=i}{\overset{n}{⨂}}{\left(p{\alpha }_i\oplus q{\alpha }_j\right)}^{{\displaystyle \frac{w_i{w}_j}{\varpi }}}\right),\end{array}$$

where $\varpi =\sum _{i=1,j=i}^n\left(w_i{w}_j\right)$ is a normalization factor ensuring the pairwise weights sum to 1.

In particular, if  $w_1=w_2=\dots =w_n={\displaystyle \frac{1}{n}}$, then the IFYWGHM operator reduces to the IFYWHM operator.

Theorem 5.

Let ${\alpha }_i=({\mu }_{{\alpha }_i},{\nu }_{{\alpha }_i})(i=1,2,\dots ,n)$ be a collection of intuitionistic fuzzy numbers, and let the weights $w_i\in [0,1]$ satisfy ${\displaystyle \sum _{i=1}^n}{w}_i=1$. Then the value aggregated by the IFYWGHM operator is also an intuitionistic fuzzy number, given by

$$\begin{array}{c}\hfill {YGHM}_w^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=\left(\begin{array}{cc}\hfill & {\left[{\displaystyle \frac{1}{p+q}}{\left(1-{\left(\sum _{i=1,j=i}^n{\displaystyle \frac{w_i{w}_j}{\varpi }}{(1-{\hslash }_{{\alpha }_{ij}})}^r\right)}^{{\displaystyle \frac{1}{r}}}\right)}^r\right]}^{{\displaystyle \frac{1}{r}}},\hfill \\ \hfill & 1-{\left[{\displaystyle \frac{1}{p+q}}{\left(1-{\left(\sum _{i=1,j=i}^n{\displaystyle \frac{w_i{w}_j}{\varpi }}{\ell }_{{\alpha }_{ij}}^r\right)}^{{\displaystyle \frac{1}{r}}}\right)}^r\right]}^{{\displaystyle \frac{1}{r}}}\hfill \end{array}\right).\end{array}$$

Proof. 

The proof of Theorem 5 proceeds analogously to that of Theorem 1, and is therefore omitted.    □

Next, we present several properties associated with the intuitionistic fuzzy Yager weighted geometric Heronian mean aggregation operator. The proofs for these properties follow a similar approach to those utilized for the intuitionistic fuzzy Yager geometric Heronian mean operator.

Theorem 6.

Consider a collection of intuitionistic fuzzy numbers ${\alpha }_i(i=1,2,\dots ,n)$ with the weight vector $w=(w_1,w_2,\dots ,w_n)$ satisfying $w_i\in [0,1]$ and ${\displaystyle \sum _{i=1}^n}{w}_i=1$, we have:

(1) 

(Idempotency) If all intuitionistic fuzzy numbers ${\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n$ are identical and equal to the intuitionistic fuzzy number $\alpha =({\mu }_{\alpha },{\nu }_{\alpha })$, then

$${YGHM}_w^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)=\alpha .$$

(2) 

(Monotonicity) Suppose ${\beta }_i(i=1,2,\dots ,n)$ is another collection of intuitionistic fuzzy numbers, if ${\alpha }_i⪯{\beta }_i$ for all i, then

$$\begin{array}{c}\hfill {YGHM}_w^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)\le {YGHM}_w^{(p,q,r)}\left({\beta }_1,{\beta }_2,\dots ,{\beta }_n\right).\end{array}$$

(3) 

(Boundedness) Define two extreme intuitionistic fuzzy numbers ${\alpha }^{+}$ and ${\alpha }^{-}$ as

$$\begin{array}{c}\hfill {\alpha }^{+}=\left(\underset{i}{max}\left\{{\mu }_{{\alpha }_i}\right\},\underset{i}{min}\left\{{\nu }_{{\alpha }_i}\right\}\right),{\alpha }^{-}=\left(\underset{i}{min}\left\{{\mu }_{{\alpha }_i}\right\},\underset{i}{max}\left\{{\nu }_{{\alpha }_i}\right\}\right).\end{array}$$

Then we have

$${\alpha }^{-}\le {YGHM}_w^{(p,q,r)}\left({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_n\right)\le {\alpha }^{+}.$$

4. A MADM Framework for Classroom Teaching Quality Evaluation Based on the IFYWGHM Operator

Beyond the computational and decision-making perspectives, recent research has emphasized that effective teaching evaluation must address issues of measurement validity, bias, and reliability. For instance, Constantinou and Wijnen-Meijer demonstrated that teacher self-efficacy and instructional practices are key predictors of student outcomes, underscoring the need for multidimensional assessment frameworks [48]. Similarly, Li et al. critically reviewed the biases inherent in student evaluations of teaching, including gender and course-level effects, which threaten validity and fairness [49]. Bower et al. further suggested that integrating artificial intelligence and peer-assessment frameworks can improve reliability in educational evaluation [50]. In this context, the proposed intuitionistic fuzzy evaluation model complements modern frameworks by providing a structured mechanism to integrate subjective expert opinions and quantitative indicators under uncertainty, thereby enhancing both the fairness and interpretability of teaching-quality assessment.

In the following, we utilize the proposed intuitionistic fuzzy Yager weighted geometric Heronian mean operator to build an approach to multiple attribute decision-making of classroom teaching quality evaluation under intuitionistic fuzzy information.

As the core component of the teaching quality assurance system of undergraduate education, classroom teaching quality evaluation is a key measure to ensure the quality of personnel training. After fully grasping the presentation information of classroom teaching quality evaluation results, the school continued to promote teaching reform and connotation construction, strengthen the management of teaching process, and make accurate diagnosis, effective communication and targeted guidance on teachers’ teaching situation, thus improving teachers’ teaching level and classroom teaching quality, improving students’ learning experience and learning effectiveness, and helping the school to better achieve the goal of talent training.

4.1. Representation of Evaluation Information

Now consider a collection of m alternatives denoted as $\{T_1,T_2,\dots ,T_m\}$. In order to fully practice the concept of multi-subject participation and multi-dimensional perspective evaluation, the teaching quality evaluation mechanism covers three core plates: student evaluation, peer evaluation and teaching supervision evaluation. Giving each evaluation subject corresponding weight vectors $\{w_1,w_2,w_3\}$ can make the advantages of each evaluation subject complement each other, avoid the limitations of a single evaluation subject, and ensure the comprehensiveness and objectivity of the evaluation results.

The attribute set $C^{\left(1\right)}=\{C_1^{\left(1\right)},C_2^{\left(1\right)},\dots ,C_{n_1}^{\left(1\right)}\}$ of student evaluation focuses on students’ self-reflection and evaluation. According to the course syllabus, students review their learning attitude, learning methods, investment, and gains in knowledge, ability and value, and make self-evaluation on the achievement of course objectives. This link is organized by the school in terms of online evaluation, and the evaluation results are automatically counted by the system, which not only facilitates students’ participation, but also improves the evaluation efficiency. The weights assigned to the attribute set $C^{\left(1\right)}$ form a vector $\{w_1^{\left(1\right)},w_2^{\left(1\right)},\dots ,w_{n_1}^{\left(1\right)}\}$, where $w_j^{\left(1\right)}\in [0,1]$ and ${\displaystyle \sum _{j=1}^{n_1}}{w}_j^{\left(1\right)}=1$. When evaluating alternatives, decision makers are required to utilize an intuitionistic fuzzy number, denoted as ${\tilde{r}}_{ij}^{\left(1\right)}=({\tilde{\mu }}_{ij}^{\left(1\right)},{\tilde{\nu }}_{ij}^{\left(1\right)})$, to represent their preferences concerning the criteria $G_j^{\left(1\right)}$ of the alternative $T_i$. As a result, an intuitionistic fuzzy student evaluation decision matrix ${\tilde{R}}^{\left(1\right)}={\left({\tilde{r}}_{ij}^{\left(1\right)}\right)}_{m\times n_1}$ is constructed.

The attribute set $C^{\left(2\right)}=\{C_1^{\left(2\right)},C_2^{\left(2\right)},\dots ,C_{n_2}^{\left(2\right)}\}$ of teaching peer evaluation pays attention to the accuracy, scientificity, cutting-edge, development and inspiration of course content, the scientificity and rationality of teaching methods and assessment methods, and the implementation of the “student-centered” concept and the realization of course objectives. This link is evaluated by teachers of the same course, major, classmate or field to ensure the objectivity and professionalism of the evaluation. $\{w_1^{\left(2\right)},w_2^{\left(2\right)},\dots ,w_{n_2}^{\left(2\right)}\}$ is the assigned weight vector, where $w_j^{\left(2\right)}\in [0,1]$ and ${\displaystyle \sum _{j=1}^{n_2}}{w}_j^{\left(2\right)}=1$. An intuitionistic fuzzy peer teacher evaluation decision matrix ${\tilde{R}}^{\left(2\right)}={\left({\tilde{r}}_{ij}^{\left(2\right)}\right)}_{m\times n_2}$ is constructed by decision maker.

The attribute set $C^{\left(3\right)}=\{C_1^{\left(3\right)},C_2^{\left(3\right)},\dots ,C_{n_3}^{\left(3\right)}\}$ of teaching supervisors evaluation is mainly carried out from three dimensions: teaching attitude, standardization of teaching documents and teaching effect. Through classroom observation, consulting teaching files such as course syllabus, teaching plan, teaching calendar and course assessment, as well as individual interviews and exchanges with students and teachers, the teaching supervisor evaluates the teaching quality of the assessed object after comprehensively and deeply understanding its teaching situation. $\{w_1^{\left(3\right)},w_2^{\left(3\right)},\dots ,w_{n_3}^{\left(3\right)}\}$ is the assigned weight vector, where $w_j^{\left(3\right)}\in [0,1]$ and ${\displaystyle \sum _{j=1}^{n_3}}{w}_j^{\left(3\right)}=1$. An intuitionistic fuzzy teaching supervisors evaluation decision matrix ${\tilde{R}}^{\left(3\right)}={\left({\tilde{r}}_{ij}^{\left(3\right)}\right)}_{m\times n_3}$ is constructed by decision maker.

4.2. Calculate the Overall Weight of the Evaluation Criteria

At this stage, our integrated technology adopts an expert scoring method as the subject layer weight, and uses an objective weight calculated based on the grey relational analysis (GRA) method as the attribute weight under the subject, thereby ensuring a balanced and comprehensive evaluation.

Notations:

• $\omega =({\omega }_1,{\omega }_2,{\omega }_3)$: subject-level weights (given by experts).
• $w^{\left(k\right)}=\left(w_1^{\left(k\right)},\dots ,w_{n_k}^{\left(k\right)}\right)$: attribute weights under subject k (derived by GRA).

The grey relational analysis (GRA) method for determining weights in intuitionistic fuzzy sets is a decision-making technique used to handle uncertain and imprecise data. In the context of intuitionistic fuzzy sets, each element has both a membership degree and a non-membership degree, and the GRA method takes both of these into account when calculating the weights. Steps for weight calculation using the grey relational analysis method in intuitionistic fuzzy sets are as follows [51]:

Step 1. Construct the intuitionistic fuzzy decision matrix.

For each evaluation subject $k\in \{1,2,3\}$ construct

$${\tilde{R}}^{\left(k\right)}={\left({\tilde{r}}_{ij}^{\left(k\right)}\right)}_{m\times n_k}=\left({\mu }_{ij}^{\left(k\right)},{\nu }_{ij}^{\left(k\right)}\right),0\le {\mu }_{ij}^{\left(k\right)}+{\nu }_{ij}^{\left(k\right)}\le 1.$$

Step 2. Calculate the intuitionistic fuzzy positive ideal solution

$${\tilde{r}}_j^{\left(k\right)+}=\left({\mu }_j^{\left(k\right)+},{\nu }_j^{\left(k\right)+}\right)=\left(\underset{i}{max}{\mu }_{ij}^{\left(k\right)},\underset{i}{min}{\nu }_{ij}^{\left(k\right)}\right),j=1,\dots ,n_k.$$

Step 3. Calculate the grey relational coefficients.

Define the intuitionistic fuzzy Hamming distance

$${\Delta }_{ij}^{\left(k\right)}={\displaystyle \frac{1}{2}}\left[\left|{\mu }_{ij}^{\left(k\right)}-{\mu }_j^{\left(k\right)+}\right|+\left|{\nu }_{ij}^{\left(k\right)}-{\nu }_j^{\left(k\right)+}\right|+\left|{\pi }_{ij}^{\left(k\right)}-{\pi }_j^{\left(k\right)+}\right|\right],$$

where $\pi =1-\mu -\nu$. Choose $\rho \in [0,1]$ (usually $\rho =0.5$); then

$${\gamma }_{ij}^{\left(k\right)}={\displaystyle \frac{\underset{i}{min}{\Delta }_{ij}^{\left(k\right)}+\rho \underset{i}{max}{\Delta }_{ij}^{\left(k\right)}}{{\Delta }_{ij}^{\left(k\right)}+\rho \underset{i}{max}{\Delta }_{ij}^{\left(k\right)}}}.$$

Step 4. Calculate objective attribute weights.

Normalize the total grey relational degree per attribute:

$$w_j^{\left(k\right)}={\displaystyle \frac{{\sum }_{i=1}^m{\gamma }_{ij}^{\left(k\right)}}{{\sum }_{j=1}^{n_k}{\sum }_{i=1}^m{\gamma }_{ij}^{\left(k\right)}}},j=1,\dots ,n_k.$$

4.3. Obtain Alternative Ranks with the IFYWGHM Operator

To obtain the ranking of the alternatives in the MADM problem, the phases of the MADM algorithm based on the IFYWGHM operator are presented below. Additionally, a flowchart is shown in the Graphic Abstract (refer to Figure 1).

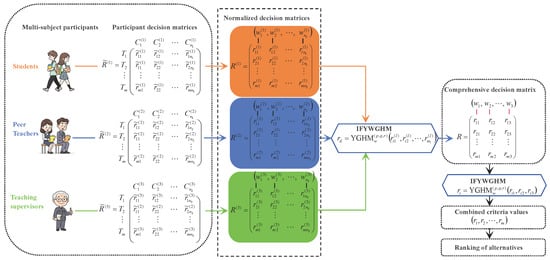
Figure 1. Flowchart of the MADM algorithm based on the GIFYWH operator.

The following steps outline the solution to an intuitionistic fuzzy multi-attribute decision-making problem using an IFYWGHM operator. The alternatives are then ranked in descending order, and the optimal choice is determined.

Step 1. Normalizing the participant decision matrices

$${\tilde{R}}^{\left(l\right)}={\left({\tilde{r}}_{ij}^{\left(l\right)}\right)}_{m\times n_l}=\begin{array}{cc}& \begin{array}{cccc}\hfill C_1^{\left(1\right)}\hfill & \hfill C_2^{\left(1\right)}& \dots \hfill & \hfill C_{n_l}^{\left(l\right)}\end{array}\\ \hfill \begin{array}{c}\hfill T_1\\ \hfill T_2\\ \hfill \dots \\ \hfill T_m\end{array}& \left(\begin{array}{cccc}{\tilde{r}}_{11}\hfill & \hfill {\tilde{r}}_{12}& \dots \hfill & \hfill {\tilde{r}}_{1n_l}\\ {\tilde{r}}_{21}\hfill & \hfill {\tilde{r}}_{22}& \dots \hfill & \hfill {\tilde{r}}_{2n_l}\\ \dots \hfill & \hfill \dots & \dots \hfill & \hfill \dots \\ {\tilde{r}}_{m1}\hfill & \hfill {\tilde{r}}_{m2}& \dots \hfill & \hfill {\tilde{r}}_{m{n}_l}\end{array}\right)\end{array}$$

into $R^{\left(l\right)}={\left(r_{ij}^{\left(l\right)}\right)}_{m\times n_l}$, where $l=1,2,3$.

In the context of a multi attribute decision making problem, there are generally two types of attributes: benefit type attributes and the cost type attributes. To ensure uniformity across all criteria, the following equation is employed to transform cost type attributes to benefit type attributes:

$$r_{ij}^{\left(l\right)}=({\mu }_{ij}^{\left(l\right)},{\nu }_{ij}^{\left(l\right)})=\left\{\begin{array}{cc}{\tilde{r}}_{ij}^{\left(l\right)},\hfill & C_j^{\left(l\right)}\in I_1,\hfill \\ {\tilde{r}}_{ij}^{\left(l\right)c},\hfill & C_j^{\left(l\right)}\in I_2,\hfill \end{array}\right.$$

(1)

where $I_1$ and $I_2$ represent the benefit type attributes and the cost type attributes, respectively.

Step 2. Aggregate the intuitionistic fuzzy numbers $r_{i1}^{\left(l\right)},r_{i2}^{\left(l\right)},\dots ,r_{i{n}_l}^{\left(l\right)}$ appeared in the decision matrices ${\tilde{R}}^{\left(1\right)}={\left(r_{ij}^{\left(1\right)}\right)}_{m\times n_1},{\tilde{R}}^{\left(2\right)}={\left(r_{ij}^{\left(2\right)}\right)}_{m\times n_2}$ and ${\tilde{R}}^{\left(3\right)}={\left(r_{ij}^{\left(3\right)}\right)}_{m\times n_3}$, respectively, to get the accumulated intuitionistic fuzzy number $r_{il}$ for constructing the collective decision matrix

$$\begin{array}{c}\hfill R={\left(r_{il}\right)}_{m\times 3}=\left(\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ ⋮& ⋮& ⋮\\ r_{m1}& r_{m2}& r_{m3}\end{array}\right)\end{array}$$

by using the IFYWGHM operator

$$\begin{array}{c}\hfill r_{il}={\mathrm{YGHM}}_w^{(p,q,r)}\left(r_{i1}^{\left(l\right)},r_{i2}^{\left(l\right)},\dots ,r_{i{n}_l}^{\left(l\right)}\right)={\displaystyle \frac{1}{p+q}}\left(\underset{j=1,k=j}{\overset{n_l}{⨂}}{(p{r}_{ij}^{\left(l\right)}\oplus q{r}_{ik}^{\left(l\right)})}^{{\displaystyle \frac{w_i^{\left(l\right)}{w}_j^{\left(l\right)}}{{\Lambda }^{\left(l\right)}}}}\right),\end{array}$$

(2)

where $i=1,2,\dots ,m$, $l=1,2,3$.

Step 3. Aggregate the intuitionistic fuzzy numbers $r_{i1},r_{i2},r_{i3}$ appeared in i-th row of the collective decision matrix $R={\left(r_{il}\right)}_{m\times 3}$ to obtain the overall aggregated intuitionistic fuzzy number $r_i$ of alternative $T_i$ by using the IFYWGHM operator

$$r_i={\mathrm{YGHM}}_w^{(p,q,r)}\left(r_{i1},r_{i2},r_{i3}\right),$$

(3)

where $i=1,2,\dots ,m$.

Step 4. Calculate the score value $S\left(r_i\right)$ of the overall aggregated intuitionistic fuzzy number $r_i=({\mu }_{r_i},{\nu }_{r_i})$, where

$$S\left(r_i\right)={\mu }_{r_i}-{\nu }_{r_i},$$

(4)

and calculate the accuracy value $H\left(r_i\right)$ of the overall aggregated intuitionistic fuzzy number $r_i=({\mu }_{r_i},{\nu }_{r_i})$, where

$$H\left(r_i\right)={\mu }_{r_i}+{\nu }_{r_i},$$

(5)

and $i=1,2,\dots ,m$.

Step 5. Rank all the alternatives $T_i(i=1,2,\dots ,m)$ in a decreasing order according to Definition 4, and choose the best alternative.

5. The Application of IFYWGHM Operators

To verify the viability and applicability of the proposed decision-making framework, this section applies the newly introduced method based on IFYWGHM operators to the evaluation of teaching quality in higher education institutions with sustainable and high-quality development goals. To further demonstrate the reliability and superiority of the method, sensitivity analysis and comparative studies are also conducted.

5.1. Illustrative Example

In this section, we present a numerical example to demonstrate the flexibility and effectiveness of the proposed IFYWGHM operators for the comprehensive evaluation of teachers’ teaching quality. Such evaluation plays an important role in promoting teachers’ professional development, improving teaching quality, and ensuring students’ learning rights and outcomes.

Here, the teaching quality of six teachers (denoted as $\{T_1,T_2,T_3,T_4,T_5,T_6\}$) at a public university in China is assessed. The evaluation system adopts a multi-dimensional and multi-subject model, consisting of student evaluations, peer teacher evaluations, and teaching supervisor evaluations. The process and results of a structured expert evaluation aimed at determining the relative importance of three key components in teaching evaluation: student evaluation, peer evaluation, and supervisory evaluation are as follows.

A panel of ten academic experts: 3 teaching administrators (E1, E2, E3), 2 distinguished scholars (E4, E5), 2 provincial-level outstanding teachers (E6, E7), and 3 senior professors (E8, E9, E10), used a 5-point Likert scale (1 = Very Unimportant, 2 = Unimportant, 3 = Neutral, 4 = Important, and 5 = Very Important) to assign importance scores to each component. Table 1 presents the individual ratings assigned by each expert.

Table 1. Expert ratings for teaching evaluation components.

Expert ID	Student Evaluation	Peer Evaluation	Supervisory Evaluation
E1	5	4	4
E2	5	3	3
E3	4	2	4
E4	4	4	3
E5	4	3	3
E6	3	4	3
E7	3	3	2
E8	4	2	3
E9	5	3	2
E10	3	2	3

The mean scores for each component were calculated as follows:

$$\begin{array}{cc}\hfill \mathrm{Student}\mathrm{Evaluation}& ={\displaystyle \frac{5+5+4+4+4+3+3+4+5+3}{10}}=4,\hfill \\ \hfill \mathrm{Peer}\mathrm{Evaluation}& ={\displaystyle \frac{4+3+2+4+3+4+3+2+3+2}{10}}=3,\hfill \\ \hfill \mathrm{Supervisory}\mathrm{Evaluation}& ={\displaystyle \frac{4+3+4+3+3+3+2+3+2+3}{10}}=3.\hfill \end{array}$$

The mean scores were normalized to obtain the final weights:

$$\begin{array}{cc}\hfill \mathrm{Total}& =4+3+3=10,\hfill \\ \hfill \mathrm{Student}\mathrm{Evaluation}\mathrm{Weight}& ={\displaystyle \frac{4}{10}}=0.40.\hfill \\ \hfill \mathrm{Peer}\mathrm{Evaluation}\mathrm{Weight}& ={\displaystyle \frac{3}{10}}=0.30.\hfill \\ \hfill \mathrm{Supervisory}\mathrm{Evaluation}\mathrm{Weight}& ={\displaystyle \frac{3}{10}}=0.30,\hfill \end{array}$$

hence the weight vector assigned to these three components is $w=\{0.4,0.3,0.3\}$. Student evaluations, as the direct beneficiaries of teaching, receive the highest weight ($w_1=0.4$), reflecting the ultimate goal of teaching-meeting students’ learning needs. Peer teacher evaluations are weighted at $w_2=0.3$ to ensure professional insight while mitigating subjectivity. Teaching supervision evaluation is weighted at $w_3=0.3$, strengthening institutional safeguards and process management. Together, these three components form a complementary mechanism that balances students’ experiences, professional standards, and institutional norms. The final comprehensive score is obtained through weighted aggregation, providing a scientific basis for both teacher improvement and school management.

To ensure the accuracy and fairness of teaching quality evaluation results, the evaluation criteria need to comprehensively incorporate diverse opinions from all stakeholders across the entire teaching chain, including student feedback as the main learner, professional judgment from peer teachers, effectiveness assessments from teaching management departments, and teachers’ own reflective growth needs. Based on this, this study systematically reviews the common characteristics and differentiated practices of the current evaluation methods of five universities—Yanshan University, Nanjing Forestry University, Anyang Normal University, Zhejiang Normal University, and Taiyuan University of Science and Technology—and, combined with cutting-edge research findings on “formative assessment” and “OBE education philosophy” in references [26,27,52], constructs a comprehensive evaluation framework (Table 2) encompassing dimensions such as teaching attitude, content design, methodological innovation, and outcome achievement.

Table 2. Evaluated indicators-adopted.

Evaluation Subjects	Evaluation Attributes and Symbols	Points of Evaluation Observation
Students	$C_1^{\left(1\right)}$: teaching attitude	Teachers are well prepared, careful in teaching, punctual in class and strict with students.
	$C_2^{\left(1\right)}$: teaching content	The teaching content is rich, the key points are prominent, the difficult points are clearly explained, and it is closely linked with practice.
	$C_3^{\left(1\right)}$: teaching method	The methods are flexible, good at inspiring students’ thinking and paying attention to cultivating students’ ability.
	$C_4^{\left(1\right)}$: teaching effectiveness	The students’ understanding and mastery of knowledge, the improvement of learning interest and enthusiasm, etc.
	$C_5^{\left(1\right)}$: teacher-student relationship	Teachers can give timely feedback on homework and tests, and communicate well with students.
Peer teachers	$C_1^{\left(2\right)}$: professional competence	Teachers have broad vision and solid professional knowledge, and can integrate the latest scientific research achievements into the teaching content.
	$C_2^{\left(2\right)}$: instructional design	Teachers can design teaching syllabus around training objectives and graduation requirements, with clear teaching objectives, reasonable teaching plan and appropriate teaching links.
	$C_3^{\left(2\right)}$: teaching implementation	Teachers have proper teaching methods, orderly teaching organization and strong classroom control ability.
	$C_4^{\left(2\right)}$: educational innovation	Teachers are brave enough to try new teaching methods and means and actively carry out teaching reform.
	$C_5^{\left(2\right)}$: construction of teaching team	Teachers actively participate in teaching team activities and teaching competitions, guide students’ competitions and guide the growth of young teachers.
Teaching supervisors	$C_1^{\left(3\right)}$: teaching norm	Teachers abide by teaching rules and regulations, and the teaching documents are complete and standardized.
	$C_2^{\left(3\right)}$: teaching management	Teachers obey teaching arrangements and cooperate with teaching management.
	$C_3^{\left(3\right)}$: teaching and research	Teacher actively participates in various teaching activities and teaching research and reform.
	$C_4^{\left(3\right)}$: teaching contribution	Teachers make contributions in discipline construction, specialty construction and curriculum construction.

Following expert review, the finalized questionnaire is presented in Table A1 of Appendix A, comprises 14 core items addressing teaching quality evaluation, supplemented by four general questions about the basic information of interviewees. Each core item collapses the five-point Likert scale into three interpretable zones—“strongly agree/agree”, “neutral”, and “strongly disagree/disagree”, which can be directly mapped to intuitive fuzzy numbers—the ratio of “strongly agree + agree” is recorded as the membership degree, the ratio of “neutral” is recorded as the degree of indeterminacy, and the ratio of “disagree + strongly disagree” is recorded as the non-membership degree. In this way, the subjective feelings of the five-point scale are completely encapsulated into $(\mu ,\pi ,\nu )$ triples, preserving all intuitionistic fuzzy information for subsequent aggregation, comparison, and diagnosis.

The six alternatives, namely $T_1,T_2,T_3,T_4,T_5$, and $T_6$, undergo assessment by three distinct groups: students, peer teachers, and teaching supervisors. Each group employs its specific set of evaluation criteria, based on the outcomes of data preparation and preprocessing, we can get the estimate of $T_i$ under criterion $C_j^{\left(l\right)}$ can be expressed with intuitionistic fuzzy numbers ${\tilde{r}}_{ij}^{\left(l\right)}$ (where $l=1,2,3$). Consequently, three decision matrices have been constructed: ${\tilde{R}}^{\left(1\right)}={\left(r_{ij}^{\left(1\right)}\right)}_{6\times 5}$, representing the student evaluations across five criteria for the six alternatives; ${\tilde{R}}^{\left(2\right)}={\left(r_{ij}^{\left(2\right)}\right)}_{6\times 5}$, capturing the peer teacher evaluations under the same five criteria; and ${\tilde{R}}^{\left(3\right)}={\left(r_{ij}^{\left(3\right)}\right)}_{6\times 4}$, reflecting the teaching supervisors’ assessments based on four criteria. These matrices are detailed in Table 3, Table 4 and Table 5.

Table 3. Intuitionistic fuzzy student evaluation decision matrix ${\tilde{R}}^{\left(1\right)}$.

	${\mathit{C}}_1^{\left(1\right)}$	${\mathit{C}}_2^{\left(1\right)}$	${\mathit{C}}_3^{\left(1\right)}$	${\mathit{C}}_4^{\left(1\right)}$	${\mathit{C}}_5^{\left(1\right)}$
$T_1$	$(0.85,0.12)$	$(0.82,0.15)$	$(0.82,0.13)$	$(0.86,0.13)$	$(0.88,0.08)$
$T_2$	$(0.75,0.18)$	$(0.91,0.08)$	$(0.84,0.15)$	$(0.76,0.21)$	$(0.73,0.25)$
$T_3$	$(0.81,0.17)$	$(0.88,0.07)$	$(0.83,0.14)$	$(0.85,0.14)$	$(0.89,0.08)$
$T_4$	$(0.78,0.19)$	$(0.85,0.13)$	$(0.75,0.18)$	$(0.82,0.15)$	$(0.86,0.11)$
$T_5$	$(0.84,0.15)$	$(0.89,0.10)$	$(0.85,0.12)$	$(0.85,0.12)$	$(0.91,0.06)$
$T_6$	$(0.78,0.22)$	$(0.87,0.09)$	$(0.78,0.15)$	$(0.87,0.11)$	$(0.72,0.26)$

Table 4. Intuitionistic fuzzy peer teacher evaluation decision matrix ${\tilde{R}}^{\left(2\right)}$.

	${\mathit{C}}_1^{\left(2\right)}$	${\mathit{C}}_2^{\left(2\right)}$	${\mathit{C}}_3^{\left(2\right)}$	${\mathit{C}}_4^{\left(2\right)}$	${\mathit{C}}_5^{\left(2\right)}$
$T_1$	$(0.91,0.05)$	$(0.88,0.08)$	$(0.85,0.13)$	$(0.75,0.15)$	$(0.83,0.15)$
$T_2$	$(0.92,0.06)$	$(0.84,0.15)$	$(0.78,0.17)$	$(0.81,0.18)$	$(0.72,0.25)$
$T_3$	$(0.86,0.13)$	$(0.92,0.06)$	$(0.92,0.05)$	$(0.85,0.12)$	$(0.88,0.08)$
$T_4$	$(0.89,0.09)$	$(0.85,0.13)$	$(0.83,0.16)$	$(0.89,0.11)$	$(0.65,0.28)$
$T_5$	$(0.87,0.12)$	$(0.91,0.09)$	$(0.88,0.10)$	$(0.84,0.15)$	$(0.82,0.13)$
$T_6$	$(0.85,0.14)$	$(0.92,0.07)$	$(0.78,0.21)$	$(0.55,0.38)$	$(0.84,0.14)$

Table 5. Intuitionistic fuzzy teaching supervisors evaluation decision matrix ${\tilde{R}}^{\left(3\right)}$.

	${\mathit{C}}_1^{\left(3\right)}$	${\mathit{C}}_2^{\left(3\right)}$	${\mathit{C}}_3^{\left(3\right)}$	${\mathit{C}}_4^{\left(3\right)}$
$T_1$	$(0.94,0.05)$	$(0.92,0.07)$	$(0.89,0.08)$	$(0.79,0.17)$
$T_2$	$(0.82,0.15)$	$(0.88,0.06)$	$(0.86,0.12)$	$(0.95,0.02)$
$T_3$	$(0.95,0.04)$	$(0.91,0.05)$	$(0.88,0.07)$	$(0.85,0.14)$
$T_4$	$(0.85,0.08)$	$(0.82,0.16)$	$(0.95,0.04)$	$(0.86,0.12)$
$T_5$	$(0.92,0.07)$	$(0.85,0.12)$	$(0.86,0.11)$	$(0.93,0.06)$
$T_6$	$(0.88,0.12)$	$(0.91,0.08)$	$(0.82,0.13)$	$(0.87,0.13)$

By applying the grey relational analysis method from Section 4.2 to process the evaluation data in Table 3, Table 4 and Table 5 respectively, the corresponding attribute weight vectors for student evaluation, peer teacher evaluation, and teaching supervisor evaluation can be obtained:

• Student evaluation:

  $$w^{\left(1\right)}=\{0.1699,0.2142,0.1967,0.2103,0.2089\};$$
• Peer teacher evaluation:

  $$w^{\left(2\right)}=\{0.2125,0.1964,0.1730,0.2217,0.1965\};$$
• Teaching supervisor evaluation:

  $$w^{\left(3\right)}=\{0.2589,0.2938,0.2205,0.2268\}.$$

Having obtained the three intuitionistic fuzzy decision matrices, we now apply the IFYWGHM-based procedure to derive the overall ranking. Our proposed methodology is applied to the given decision matrices by the decision-maker to determine the best alternative. The following steps are performed:

Step 1. Normalized the participants’ decision matrices. Since all attributes are of benefit type, we have $R^{\left(l\right)}={\tilde{R}}^{\left(l\right)}$ ($l=1,2,3$).

Step 2. Set parameters $p=1$, $q=1$, and $r=1$. The aggregated intuitionistic fuzzy numbers $r_{il}$ are computed to build the collective decision matrix $R={\left(r_{il}\right)}_{6\times 3}$ by aggregating the intuitionistic fuzzy numbers $r_{i1}^{\left(l\right)},r_{i2}^{\left(l\right)},\dots ,r_{i{n}_l}^{\left(l\right)}$, where $i=1,2,\dots ,6$, $l=1,2,3$, and $n_1=5,n_2=5,n_3=4$. The resulting collective decision matrix is:

$$\begin{array}{cc}\hfill R& ={\left(r_{il}\right)}_{6\times 3}\hfill \\ \hfill & =\left(\begin{array}{ccc}(0.8461,0.1222)& (0.8423,0.1115)& (0.8899,0.0891)\\ (0.8002,0.1735)& (0.8168,0.1604)& (0.8756,0.0874)\\ (0.8544,0.1172)& (0.8835,0.0908)& (0.9006,0.0717)\\ (0.8146,0.1498)& (0.8251,0.1513)& (0.8646,0.1046)\\ (0.8696,0.1080)& (0.8630,0.1195)& (0.8881,0.0915)\\ (0.8059,0.1632)& (0.7823,0.1922)& (0.8740,0.1122)\end{array}\right)\hfill \end{array}$$

Step 3. Calculate the comprehensive intuitionistic fuzzy number $r_i$ for each alternative $T_i$ by aggregating the intuitionistic fuzzy numbers $r_{i1},r_{i2},r_{i3}$ in the collective decision matrix $R={\left(r_{il}\right)}_{6\times 3}$, we have

$$\begin{array}{cc}{r}_1=(0.8577,0.1094),\hfill & r_2=(0.8270,0.1447),\hfill \\ r_3=(0.8763,0.0963),\hfill & r_4=(0.8322,0.1371),\hfill \\ r_5=(0.8731,0.1066),\hfill & r_6=(0.8189,0.1568).\hfill \end{array}$$

Step 4. The score values $S\left(r_i\right)$ of the overall aggregated intuitionistic fuzzy numbers $r_i=({\mu }_{r_i},{\nu }_{r_i})$$(i=1,2,\dots ,6)$ can be computed, the results are shown as follows: as:

$$\begin{array}{ccc}S\left(r_1\right)=0.7483,\hfill & S\left(r_2\right)=0.6823,\hfill & S\left(r_3\right)=0.7801,\hfill \\ S\left(r_4\right)=0.6951,\hfill & S\left(r_5\right)=0.7665,\hfill & S\left(r_6\right)=0.6620.\hfill \end{array}$$

Step 5. Rank all the six alternatives $T_i(i=1,2,\dots ,6)$ based on the score values $S\left(r_i\right)(i=1,2,\dots ,6)$ of the overall aggregated intuitionistic fuzzy numbers $r_i(i=1,2,\dots ,6)$. The ranking order of the alternatives $\{T_1,T_2,T_3,T_4,T_5,T_6\}$ is:

$$T_3\succ T_5\succ T_1\succ T_4\succ T_2\succ T_6,$$

where ≻ means superior. Therefore, $T_3$ is identified as the best alternative, and the corresponding teacher should be recommended for the outstanding teaching award.

The aggregated results provide valuable insights into the strengths and weaknesses of individual teaching evaluations across multiple stakeholders (students, peers, and supervisors). By using our proposed operators (IFYWGHM), institutions can gain a clearer, more balanced view of the teaching quality, which helps in making more informed decisions about course development, faculty performance reviews, and resource allocation. By incorporating multiple evaluators with different perspectives, the proposed framework fosters a more holistic and balanced approach to assessment. This is particularly important in educational settings where evaluation bias can sometimes occur, and a multi-perspective aggregation can mitigate the impact of individual biases. For educational policy-makers, the framework helps in making data-driven decisions about teaching quality. The results from our aggregation method can provide robust feedback for both individual instructors and overall academic strategies, such as teaching methodologies, course content, and evaluation approaches.

5.2. Consistency Analysis

By replacing the IFYWGHM operator in the above examples with IFAAWG [28], IFHWAGA [29], and EIFWG [30], the results presented in Table 6 can be achieved. Each of these operators represents a distinct methodology for aggregating intuitionistic fuzzy data, and the outcomes in Table 6 enable a comparative analysis of their effectiveness and suitability within the specific evaluation framework.

Table 6. Comparative analysis of different techniques and their ranking results.

Aggregation Operators	Score Values						Preference Order
	${\mathbf{T}}_{\mathbf{1}}$	${\mathbf{T}}_{\mathbf{2}}$	${\mathbf{T}}_{\mathbf{3}}$	${\mathbf{T}}_{\mathbf{4}}$	${\mathbf{T}}_{\mathbf{5}}$	${\mathbf{T}}_{\mathbf{6}}$
IFYWGHM ($p=1,q=1,r=1$)	0.7483	0.6823	0.7801	0.6951	0.7665	0.6620	$T_3\succ T_5\succ T_1\succ T_4\succ T_2\succ T_6$
IFAAWG ($\Im =1$, Senapati et al. [28])	0.7463	0.6781	0.7793	0.6917	0.7657	0.6524	$T_3\succ T_5\succ T_1\succ T_4\succ T_2\succ T_6$
IFHWAGA ($\lambda =0.5$, Ye [29])	0.7557	0.7001	0.7877	0.7052	0.7706	0.6754	$T_3\succ T_5\succ T_1\succ T_4\succ T_2\succ T_6$
EIFWG (Wang and Liu [30])	0.7481	0.6822	0.7807	0.6948	0.7666	0.6590	$T_3\succ T_5\succ T_1\succ T_4\succ T_2\succ T_6$

From the comparison presented in Table 6, we observe the following key points regarding the performance of the IFYWGHM operator in relation to other aggregation methods:

(1)

The results show that the IFYWGHM operator(with parameters $p=1$, $q=1$, $r=1$) performs quite similarly to the other operators, namely the IFAAWG, IFHWAGA, and EIFWG operators. All of these operators yield very similar ranking outcomes for the alternatives $T_1$ to $T_6$, with $T_3$ consistently ranked the highest and $T_6$ ranked the lowest across all methods.

(2)

The preference order across all methods—$T_3\succ T_5\succ T_1\succ T_4\succ T_2\succ T_6$—is identical for all operators. This indicates that, in terms of the final decision ranking, all aggregation methods agree on the relative importance of the alternatives, despite differences in their internal structures and parameterizations.

(3)

Given the similar performance of the IFYWGHM operator compared to other established methods, it suggests that the operator is flexible and effective in capturing a wide range of aggregation behaviors. This positions the IFYWGHM operator as a promising candidate for educational quality evaluations, where the data can be inherently uncertain and ambiguous.

In conclusion, the IFYWGHM operator provides a reliable, stable, and consistent aggregation approach that is comparable to well-established methods in the literature, while offering the flexibility of adjustable parameters to suit different decision-making needs. The similarity in ranking orders suggests that this operator can be confidently used in practice without significant loss of performance relative to alternative approaches.

5.3. Sensitivity Analysis of the Parameters p, q, and r

This section investigates how different values of the parameters p, q, and r influence the performance of the IFYWGHM operators. Specifically, we adjust p, q, and r in Step 2 and evaluate their effect on the resulting scores.

Firstly, we consider the case where the parameters p and q are fixed at $p=0.3$ and $q=0.4$, respectively. By varying the parameter r, different scores and corresponding rankings of the alternatives are obtained, as illustrated in Figure 2.

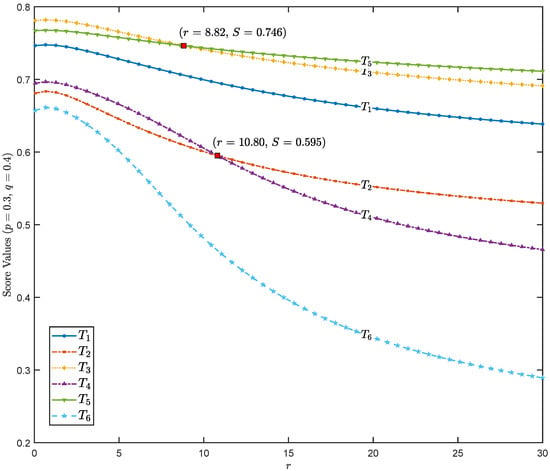
Figure 2. Scores of alternatives under fixed parameters $p=0.3$, $q=0.4$, and varying $r\in (0,30]$.

From Figure 2, the following observations can be made regarding the variation of scores with respect to r:

• At $r=8.82$, alternatives $T_3$ and $T_5$ both achieve a score of $0.746$, resulting in a tie.
• At $r=10.80$, alternatives $T_2$ and $T_4$ share the same score of $0.595$, providing another instance of tied outcomes.

Based on these observations, the rankings of the alternatives for different intervals of r can be summarized as follows:

• For $0<r<8.82$, the ranking is

  $$T_3\succ T_5\succ T_1\succ T_4\succ T_2\succ T_6.$$
  In this range, $T_3$ consistently occupies the top position, highlighting its relative strength.
• For $8.82<r<10.80$, the ranking changes to

  $$T_5\succ T_3\succ T_1\succ T_4\succ T_2\succ T_6.$$
  Here, $T_5$ surpasses $T_3$, which previously held the leading position.
• For $10.80<r\le 30$, the ranking becomes

  $$T_5\succ T_3\succ T_1\succ T_2\succ T_4\succ T_6.$$
  Although $T_5$ and $T_3$ remain the two leading alternatives, the order of $T_2$ and $T_4$ is reversed compared with the previous interval.

These results demonstrate that the ranking of alternatives is sensitive to variations in r, particularly near the points where score ties occur. Hence, decision-making procedures relying on such rankings should carefully account for this parameter-dependent instability.

Furthermore, as shown in Figure 3, when $q=0.5$ and $r=1$, varying the parameter p over the interval $(0,10]$ also alters the ranking of the alternatives. A critical threshold is observed at $p=5.11$, where alternatives $T_2$ and $T_4$ both attain a score of $0.685$, resulting in a tie.

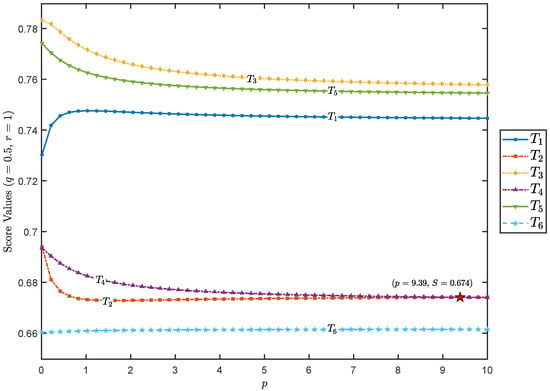
Figure 3. Scores of alternatives under varying p values ($p\in (0,10]$, $q=0.5$, and $r=1$).

• For $0<p<5.11$, the ranking is

  $$T_3\succ T_5\succ T_1\succ T_4\succ T_2\succ T_6.$$
• For $5.11<p\le 10$, the ranking changes to

  $$T_3\succ T_5\succ T_1\succ T_2\succ T_4\succ T_6.$$

These results indicate that small perturbations of p around the critical point $p=5.11$ may invert the relative order of $T_2$ and $T_4$, while the rankings of the top three alternatives ($T_3$, $T_5$, $T_1$) and the lowest-ranked alternative ($T_6$) remain invariant across the entire admissible range of p. This underscores the sensitivity of the IFYWGHM operator to parameter p, highlighting its pivotal role in fuzzy decision-making. Consequently, decision-makers should exercise careful judgment when specifying p, taking into account both the characteristics of the decision problem and the desired decision outcomes. Moreover, in cases where ties occur-such as the equality of $T_2$ and $T_4$ at $p=5.11$, it becomes necessary to employ auxiliary decision-making techniques or incorporate additional criteria to resolve the ambiguity and ensure robust conclusions.

From Figure 4, we observe the score values obtained under the parameter setting $p=0.5$, $q\in (0,10]$, and $r=1$. After analyzing both the score values and their corresponding rankings, we find that the ordering of alternatives is

$$T_3\succ T_5\succ T_1\succ T_2\succ T_4\succ T_6.$$

This indicates that, under these specific parameter settings, the ranking remains relatively stable compared with cases where p or r are varied. The observed stability suggests that certain parameter combinations may yield more consistent decision-making outcomes. Hence, decision-makers might prefer such settings when stability is prioritized. Nevertheless, it remains essential to perform a comprehensive analysis across all parameter configurations to ensure that the final decision is both well-informed and robust.

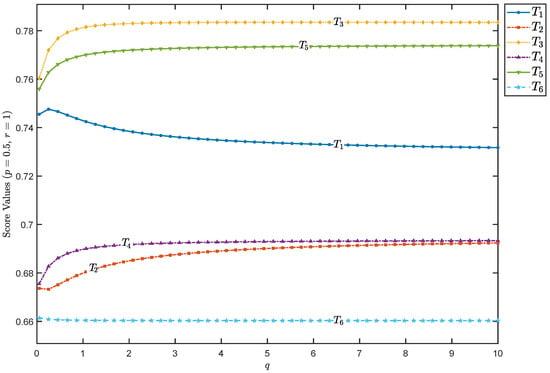
Figure 4. Scores of alternatives under varying q values ($p=0.5$, $q\in (0,10]$, and $r=1$).

By fixing the parameter at $r=1$, we can further investigate how simultaneous variations in the parameters p and q influence the ranking outcomes. As p and q vary, different score values are obtained for the six alternatives. Figure 5 illustrates the corresponding scores of the six alternatives, aggregated using the GIFYWHA operator.

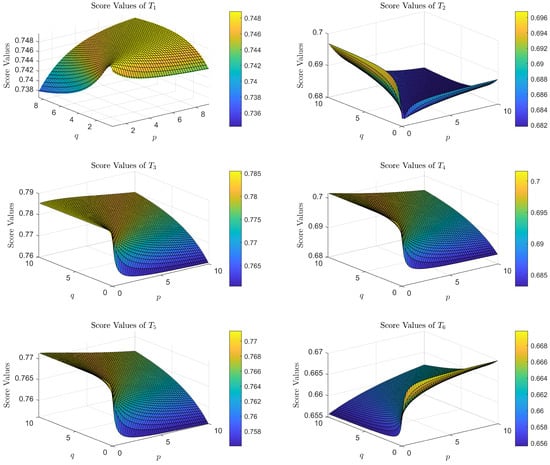
Figure 5. Scores of alternatives ($p,q\in (0,10]$, and $r=1$).

The 3D surface plots generated for the six alternatives ($T_1$ to $T_6$) demonstrate the sensitivity of the aggregated scores to variations in p and q within the range $(0,10]$, while r is fixed at 1. These plots provide deeper insights into the behavior of the Heronian mean aggregation under different parameter combinations. Based on the observed trends, the following key findings can be summarized:

• The aggregated scores of all six alternatives exhibit non-linear responses to changes in p and q. No consistent monotonic pattern emerges, as the score may increase with p for some values of q, yet decrease for others. This non-monotonicity highlights that the Heronian mean aggregation is strongly interactive: the influence of p and q is not additive but contingent on their joint configuration.
• For most alternatives, higher scores are concentrated in specific regions of the $(p,q)$ space (e.g., $p\approx 1-3$, $q\approx 1-3$). This suggests that intermediate parameter values generally yield more favorable evaluations, as they balance the weighting effects in the aggregation. By contrast, extreme values at the boundaries of $(0,10]$ may distort the balance, overemphasizing or underemphasizing certain attributes.
• Very small (<0.5) or very large (>5) values of p or q often result in unstable or skewed scores. Excessive emphasis on either parameter may disproportionately weight specific components of the aggregation, thereby destabilizing the overall evaluation.

Overall, the 3D plots confirm that the IFYWGHM operator is highly sensitive to p and q, with optimal performance typically concentrated in intermediate ranges. While some alternatives (e.g., $T_3$) remain relatively robust to parameter changes, others (e.g., $T_4$) require careful tuning to avoid instability. Decision-makers should therefore calibrate $(p,q)$ by balancing stability against peak performance, depending on the sensitivity profile of the alternatives under consideration.

In summary, the parameters p, q, and r in the IFYWGHM operator significantly enhance the flexibility of the proposed MCGDM framework, as they simultaneously capture interaction effects among criteria and accommodate heterogeneous risk preferences of decision-makers.

5.4. Comparative Analysis

To further show the advantages of the proposed IFYWGHM operator and the MADM algorithm based on it (described in Algorithm 1), we compare them with some existing method based on some operators, including IFAAWG [28], IFHWAGA [29], and EIFWG [30]. Considering that some of these aggregation operators, we compare their utility by the following cases (adopted from Ye [53]).

The implementation procedures of proposed approach for selecting the most efficient global supplier are as given below:

Algorithm 1 MADM algorithm based on IFYWGH operator

Require: alternatives $A=\{A_1,A_2,\dots ,A_m\}$, attributes $C=\{C_1,C_2,\dots ,C_n\}$, weight       vectors $W=\{w_1,w_2,\dots ,w_n\}$;   Input:$\tilde{R}={\left({\tilde{r}}_{ij}\right)}_{m\times n}$;   Output: The best alternative;   1. Normalized the intuitionistic fuzzy decision matrix $\tilde{R}={\left({\tilde{r}}_{ij}\right)}_{m\times n}$ into   $R={\left(r_{ij}\right)}_{m\times n}$ by the following equation: $$r_{ij}=\left\{\begin{array}{ccc}{\tilde{r}}_{ij},\hfill & C_j\in I_1,{\tilde{r}}_{ij}^c,\hfill & C_j\in I_2,\end{array}\right.$$ where $I_1$ and $I_2$ represent the benefit type attributes and the cost type attributes, respectively. 2. Aggregate the intuitionistic fuzzy numbers $r_{ij}(j=1,2,\dots ,n)$ for each alternatives $A_i(i=1,2,\dots ,m)$ into an overall intuitionistic fuzzy number $r_i$ by the proposed IFYWGH operator at fixed values of $p=1$, $q=1$, and $r=1$: $$r_i=YGH{M}_w^{(1,1,1)}\left(r_{i1},r_{i2},\dots ,r_{im}\right).$$ 3. Calculate the score values of comprehensive evaluation values $S\left(r_i\right)$ by the score function. If any two comprehensive evaluation value have the same score value, it requires to further calculate their accuracy values $H\left(r_i\right)$. 4. Rank all the alternatives $A_i(i=1,2,\dots ,m)$ and select the best one(s). 5. End

A mechanical designer typically focuses on the development of motion-related schemes for a press machine, such as the reduction and working mechanisms. Based on the functional requirements of the press machine, five preliminary design alternatives $A=A_1,A_2,A_3,A_4,A_5$ are proposed, drawing on expert analysis and the designer’s practical experience. To assess these alternatives, three evaluation attributes are specified: (1) $C_1$—manufacturing cost, (2) $C_2$—mechanical structure, and (3) $C_3$—transmission effectiveness. Each alternative $A_i(i=1,2,3,4,5)$ is evaluated by the chief designer (decision maker) with respect to these attributes using a suitability (fit) assessment. The corresponding evaluation values are expressed in terms of intuitionistic fuzzy numbers ${\tilde{r}}_{ij}=({\tilde{\mu }}_{ij},{\tilde{\nu }}_{ij})$, which can be constructed as the following intuitionistic fuzzy decision matrix:

$$\begin{array}{c}\hfill \tilde{R}={\left({\tilde{r}}_{ij}\right)}_{5\times 3}=\left(\begin{array}{ccc}(0.90,0.10)& (0.92,0.05)& (0.55,0.43)\\ (0.97,0.02)& (1.00,0.00)& (0.47,0.48)\\ (0.82,0.14)& (0.61,0.37)& (0.00,1.00)\\ (0.85,0.11)& (0.75,0.24)& (0.52,0.36)\\ (0.93,0.07)& (0.85,0.11)& (0.42,0.57)\end{array}\right)\end{array}$$

When the weight vector of the three attributes is considered as $w=(0.4,0.25,0.35)$ in the decision-making problem, We apply the proposed MADM algorithm to evaluate the given information of the five suppliers by the decision-maker, and record the changes in the decision results after replacing the IFYWGHM operator with the IFYWGA operator, the IFAAWG operator, the IFHWG operator, the IFHWAGA operator, and the EIFWG operator sequentially. A comparison of this article with the previous paper and the consequences of all discussed aggregation operators are summarized in Table 7 and are graphically illustrated in Figure 6.

Table 7. Comparative analysis of different techniques with Algorithm 1, and their ranking results.

Aggregation Operators	Score Values					Preference Order
	${\mathbf{A}}_{\mathbf{1}}$	${\mathbf{A}}_{\mathbf{2}}$	${\mathbf{A}}_{\mathbf{3}}$	${\mathbf{A}}_{\mathbf{4}}$	${\mathbf{A}}_{\mathbf{5}}$
IFYWGHM ($p=1,q=1,r=1$)	0.5774	0.6244	−0.0832	0.4828	0.2171	$A_2\succ A_1\succ A_4\succ A_5\succ A_3$
IFAAWG ($\Im =1$, Senapati et al. [28])	0.5391	0.5475	−0.9995	0.4559	−0.9994	$A_2\succ A_1\succ A_4\succ A_5\succ A_3$
IFHWAGA ($\lambda =0.5$, Ye [29])	0.6175	0.7592	−1.0000	0.4981	−1.0000	$A_2\succ A_1\succ A_4\succ A_5\approx A_3$
EIFWG (Wang and Liu [30])	0.5637	0.5961	−1.0000	0.4690	−1.0000	$A_2\succ A_1\succ A_4\succ A_5\approx A_3$

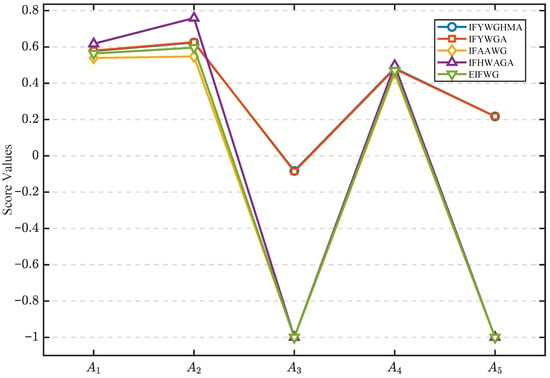
Figure 6. Comparison of the existing methods with Algorithm 1.

To highlight the advantages of the proposed IFYWGHM operator, we compare its performance with several existing aggregation operators. Observing the results of the comparison, the following are a few substantial benefits of the suggested technique:

(1)

Compared with the IFAAWG operator, IFHWAGA operator, and EIFWG operator, we find that the developed IFYWGHM operator offers stronger capability. One of its key advantages lies in the incorporation of three adjustable parameters $(p,q,r)$ within its Heronian mean structure. The three parameters $(p,q,r)$ serve distinct yet complementary roles: p and q regulate the relative contribution of positive and negative information, while r adjusts the sensitivity of the aggregation to pairwise attribute differences. This parametric structure provides decision-makers with an explicit interpretive control over how conservatively or optimistically the aggregation behaves. For example, higher values of r yield a smoother aggregation surface, reducing the influence of attribute disparity; smaller r values enhance sensitivity to local variations. Earlier operators, which rely on fixed or implicit parameterizations, are notably devoid of such fine-grained tunability. In contrast, the IFYWGHM operator, with its three adjustable parameters $(p,q,r)$ in the Heronian mean structure, empowers decision-makers to customize the aggregation process precisely in line with their specific preferences. On the other hand, methods like the IFYWGA operator (with a fixed $p=1$) and the IFAAWG operator (with a fixed $\Im =1$) simply do not possess this kind of adaptability.

(2)

Compared with the IFHWAGA operator, the IFYWGHM operator is better suited for cases where the attributes exhibit nonlinear dependence. The Heronian mean framework in IFYWGHM allows nonlinear weighting of attribute pairs with the term ${(1-{(p{\mu }_k^r+q{\mu }_l^r)}^{1/r})}^r$, enabling it to handle scenarios where the impact of one attribute depends on another. This is absent in simpler methods like IFHWAGA, which assume attribute independence. In contrast, EIFWG uses linear weighting, which fails to capture such complexities.

(3)

When comparing our proposed approach with the IFAAWG operator, IFHWAGA operator, and EIFWG operator, several distinct advantages of the IFYWGHM operator become evident. Firstly, in terms of numerical stability, the structure of the IFYWGHM operator sets it apart. Unlike the IFAAWG and EIFWG operators, which incorporate logarithmic and exponential transformations respectively, the Heronian mean employed in the IFYWGHM operator reduces the impact of extreme values through pairwise weight interactions, where $\varpi ={\displaystyle \sum _{i=1,j=i}^n}\left(w_i{w}_j\right)$. This avoidance is crucial as it prevents numerical instability when handling near-zero or near-one membership values. As a result, the IFYWGHM operator is particularly well-suited for high-dimensional, data-intensive applications. For instance, in large-scale educational assessments where a vast amount of student performance data needs to be processed, or in multi-criteria decision systems involving numerous experts providing their evaluations, the IFYWGHM operator can maintain stable performance. Secondly, our technique demonstrates greater robustness in dealing with outliers. The IFYWGHM operator is grounded in Yager t-norms and Heronian mean theory, providing a solid mathematical framework for aggregating intuitionistic fuzzy numbers. In contrast, the IFAAWG operator relies on logarithmic transformations, while the IFHWAGA and EIFWG operators utilize multiplicative products. These alternative approaches have a drawback in that they may over-penalize low $\mu /\nu$ values.

(4)

Furthermore, the IFYWGHM operator exhibits a higher degree of information preservation compared to other aggregation mechanisms. Traditional operators such as IFHWAGA and EIFWG typically emphasize either the membership or non-membership component, leading to potential loss of decision information when the hesitation degree is large. In contrast, the IFYWGHM operator integrates the Yager t-norm structure with the Heronian mean formulation, which simultaneously considers both the direct influence (through $\mu$) and the compensatory influence (through $\nu$). This dual-layered mechanism ensures that uncertainty and hesitation information are effectively captured during aggregation, resulting in a more comprehensive representation of intuitionistic fuzzy environments. Such balanced treatment is especially relevant in complex decision scenarios—such as teaching quality evaluation—where subjective judgments inherently contain hesitancy and partial reliability.

Therefore, the proposed IFYWGHM operator is recommended as an effective tool for intuitionistic fuzzy decision-making, particularly in scenarios requiring both robustness against outliers and flexibility in parameter adjustment.

6. Conclusions

This study develops an intuitionistic fuzzy geometric Heronian aggregation operator based on Yager t-norms and proposes the IFYWGHM multi-attribute decision-making model, which is further applied to the evaluation of teaching quality in higher education. Theoretical analysis and case study results demonstrate that the proposed operator possesses desirable properties such as idempotency, monotonicity, and boundedness, and can effectively capture nonlinear correlations among evaluation criteria. It achieves robust integration of heterogeneous information from students, peers, and supervisors while maintaining resistance to outliers. The flexible adjustment of parameters $p,q,r$ enables adaptation to different decision-makers’ risk preferences, thereby enhancing the discriminative power and reliability of the evaluation. Comparative experiments show that the proposed method outperforms existing operators such as IFYWGA and IFAAWG in terms of ranking stability and score rationality. This research provides educational authorities with a scientific, objective, and scalable tool for teaching diagnosis, offering practical implications for faculty development and the construction of quality assurance systems in higher education. Future work will extend the operator to multi-period dynamic evaluation and large-scale online learning scenarios, and a supporting software platform will be developed to further improve its practical applicability.

While this study demonstrates the effectiveness of the proposed intuitionistic fuzzy set-based model within the educational context, it is important to note that the model’s utility extends beyond this domain. Intuitionistic fuzzy sets are particularly useful for addressing complex, multi-criteria decision-making problems in environments characterized by uncertainty and imprecision. For instance, in healthcare, this model can aid in medical diagnosis by evaluating multiple, uncertain criteria such as symptoms, test results, and patient history. Moreover, the model can be applied to environmental risk assessments, where it can help evaluate the environmental impact of projects by considering a wide range of uncertain and qualitative factors. Future work will explore the application of this model to these and other domains to better understand its versatility and potential for practical use.