Strategic Decision-Making for Carbon Capture, Utilization, and Storage in Coal-Fired Power Plants: The Roles of Pollution Right Trading and Environmental Benefits
Abstract
1. Introduction
2. Literature Review
2.1. Real Options in the Power Industry
2.2. Development of the CCUS
3. Model Establishment
3.1. Problem Description and Assumptions
3.2. Investment Modeling of CCUS
3.3. Calculation
4. Discussion
4.1. Parameterization
4.2. Results and Analysis
4.2.1. Optimal Investment Results
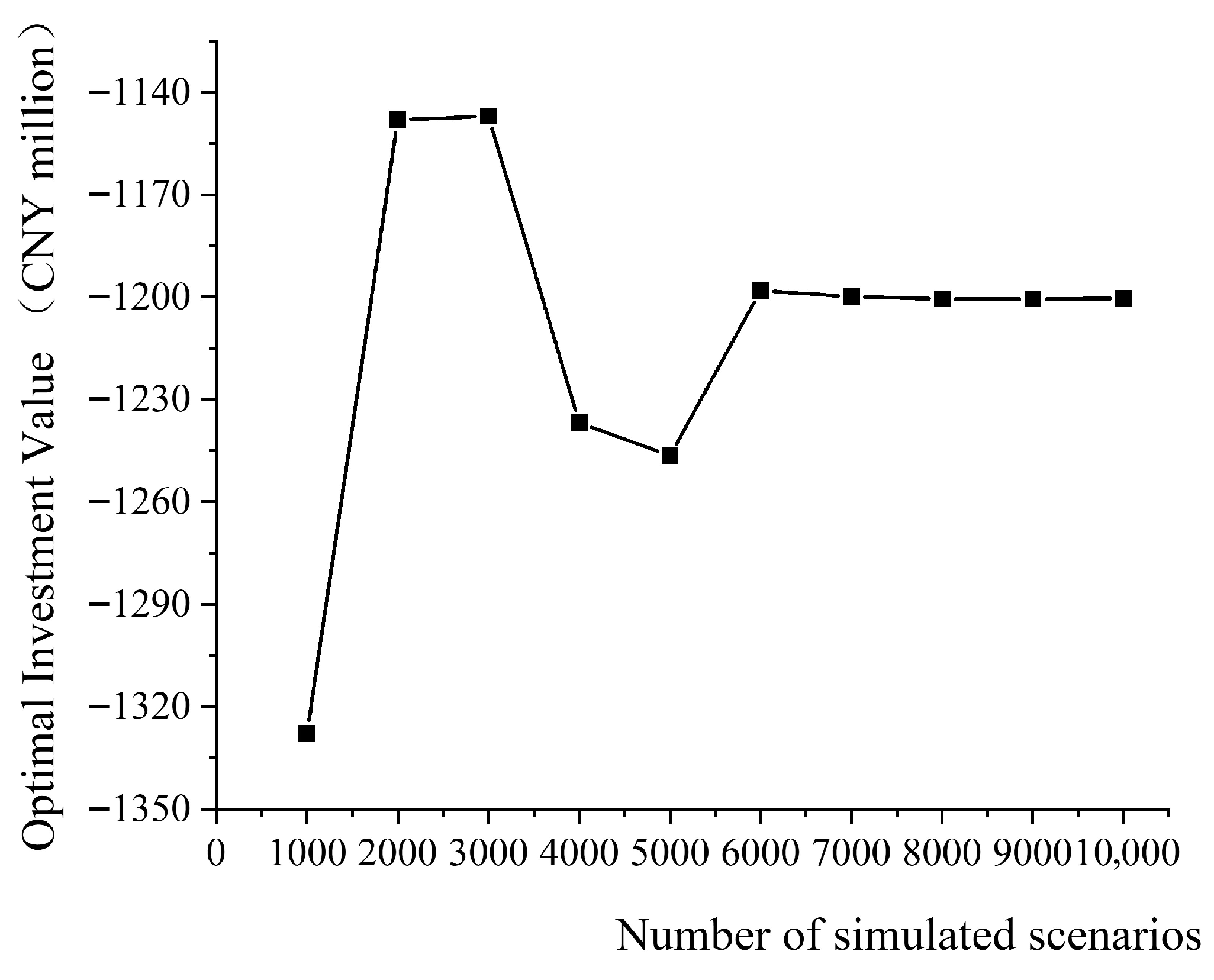
4.2.2. Monte Carlo Simulation Results
4.3. Comparative Analysis of Investment Decisions
4.4. Sensitivity Analysis
4.4.1. Impact of Carbon Trading Prices on Decision-Making
4.4.2. Impact of Government Subsidy Policy on Decision-Making
4.4.3. Carbon Capture and Utilization Ratio Impacts on Decision-Making
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nie, Y.; Zhang, G.; Duan, H.; Su, B.; Feng, Y.; Zhang, K.; Gao, X. Trends in energy policy coordination research on supporting low-carbon energy development. Environ. Impact Assess. Rev. 2022, 97, 106903. [Google Scholar] [CrossRef]
- Huang, L.; Zou, Y. How to promote energy transition in China: From the perspectives of interregional relocation and environmental regulation. Energy Econ. 2020, 92, 104996. [Google Scholar] [CrossRef]
- Cao, M.; Zhang, F.; Li, J. Trick or treat? Quasi-experimental evidence from electricity spot market policy in China. J. Environ. Plan. Manag. 2024, 68, 2957–2981. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, W. Abating carbon emissions at negative costs: Optimal energy reallocation in China’s industry. Environ. Impact Assess. Rev. 2024, 105, 107388. [Google Scholar] [CrossRef]
- Zhang, Z.; Yi, P.; Hu, S.; Jin, Y. Achieving artificial carbon cycle via integrated system of high-emitting industries and CCU technology: Case of China. J. Environ. Manag. 2023, 340, 118010. [Google Scholar] [CrossRef]
- Breukers, S.; Upham, P. Organisational aspects of public engagement in European energy infrastructure planning: The case of early-stage CCS projects. J. Environ. Plan. Manag. 2015, 58, 252–269. [Google Scholar] [CrossRef]
- Wang, Q.; Zhan, J.; Zhang, H.; Cao, Y.; Yang, Z.; Wu, Q.; Otho, A.R. China’s Carbon Emissions Trading Market: Current Situation, Impact Assessment, Challenges, and Suggestions. Land 2025, 14, 1582. [Google Scholar] [CrossRef]
- Tang, H.-L.; Liu, J.-M.; Mao, J.; Wu, J.-G. The effects of emission trading system on corporate innovation and productivity-empirical evidence from China’s SO2 emission trading system. Environ. Sci. Pollut. Res. 2020, 27, 21604–21620. [Google Scholar] [CrossRef] [PubMed]
- Du, Z.; Xu, C.; Lin, B. Does the Emission Trading Scheme achieve the dual dividend of reducing pollution and improving energy efficiency? Micro evidence from China. J. Environ. Manag. 2022, 323, 116202. [Google Scholar] [CrossRef]
- Liu, J.-Y.; Woodward, R.T.; Zhang, Y.-J. Has Carbon Emissions Trading Reduced PM2.5 in China? Environ. Sci. Technol. 2021, 55, 6631–6643. [Google Scholar] [CrossRef]
- Jiang, K.; Ashworth, P.; Zhang, S.; Liang, X.; Sun, Y.; Angus, D. China’s carbon capture, utilization and storage (CCUS) policy: A critical review. Renew. Sustain. Energy Rev. 2020, 119, 109601. [Google Scholar] [CrossRef]
- Wang, X.; Du, L. Study on carbon capture and storage (CCS) investment decision-making based on real options for China’s coal-fired power plants. J. Clean. Prod. 2016, 112, 4123–4131. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.; Wang, X.-P. Research on the Diffusion of Green Energy Technological Innovation from the Perspective of International Cooperation. Energies 2025, 18, 2816. [Google Scholar] [CrossRef]
- Kim, K.; Park, H.; Kim, H. Real options analysis for renewable energy investment decisions in developing countries. Renew. Sustain. Energy Rev. 2016, 75918–75926. [Google Scholar] [CrossRef]
- Agaton, C.B.; Guno, C.S.; Villanueva, R.O. Economic analysis of waste-to-energy investment in the Philippines: A real options approach. Appl. Energy 2020, 275, 115265. [Google Scholar] [CrossRef]
- Deeney, P.; Cummins, M.; Heintz, K.; Pryce, M.T. A real options based decision support tool for R&D investment: Application to CO2 recycling technology. Eur. J. Oper. Res. 2021, 289, 696–711. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, L.; Wang, Q.; Zhou, D. Valuing investment decisions of renewable energy projects considering changing volatility. Energy Econ. 2020, 92, 104954. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The Pricing of Options and Corporate Liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Cox, J.C.; Ross, S.A.; Rubinstein, M. Option Pricing: A Simplified Approach. J. Financ. Econ. 1979, 7, 229–263. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef]
- Barone-Adesi, G.; Whaley, R.E. Efficient Analytic Approximation of American Option Values. J. Financ. 2012, 42, 301–320. [Google Scholar] [CrossRef]
- Abadie, L.M.; Chamorro, J.M. European CO2 prices and carbon capture investments. Energy Econ. 2008, 30, 2992–3015. [Google Scholar] [CrossRef]
- Zhang, W.; Dai, C.; Luo, X.; Ou, X. Policy incentives in carbon capture utilization and storage (CCUS) investment based on real options analysis. Clean Technol. Environ. Policy 2021, 23, 1311–1326. [Google Scholar] [CrossRef]
- Fan, J.-L.; Xu, M.; Yang, L.; Zhang, X. Benefit evaluation of investment in CCS retrofitting of coal-fired power plants and PV power plants in China based on real options. Renew. Sustain. Energy Rev. 2019, 115, 109350. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Chen, J.; Xie, X.; Wang, K.; Wei, Y. A novel modeling based real option approach for CCS investment evaluation under multiple uncertainties. Appl. Energy 2014, 113, 1059–1067. [Google Scholar] [CrossRef]
- Koornneef, J.; Faaij, A.; Turkenburg, W. The screening and scoping of environmental impact assessment and strategic environmental assessment of carbon capture and storage in the Netherlands. Environ. Impact Assess. Rev. 2008, 28, 392–414. [Google Scholar] [CrossRef]
- Kemna, A.; Vorst, A. A pricing method for options based on average asset values. J. Bank. Financ. 1990, 14, 113–129. [Google Scholar] [CrossRef]
- Lin, B.; Tan, Z. How much impact will low oil price and carbon trading mechanism have on the value of carbon capture utilization and storage (CCUS) project? Analysis based on real option method. J. Clean. Prod. 2021, 298, 126768. [Google Scholar] [CrossRef]
- Boyle, P.; Broadie, M.; Glasserman, P. Monte Carlo methods for security pricing. J. Econ. Dyn. Control. 1997, 21, 1267–1321. [Google Scholar] [CrossRef]
- Longstaff, F.A.; Schwartz, E.S. Valuing american options by simulation: A simple least squares approach. Rev. Financ. Stud. 2001, 14, 113–147. [Google Scholar] [CrossRef]
- Zhu, L.; Fan, Y. Modelling the investment in carbon capture retrofits of pulverized coal-fired plants. Energy 2013, 57, 66–75. [Google Scholar] [CrossRef]
- Boomsma, T.K.; Meade, N.; Fleten, S.-E. Renewable energy investments under different support schemes: A real options approach. Eur. J. Oper. Res. 2012, 220, 225–237. [Google Scholar] [CrossRef]
- Hu, J.; Chen, H.; Zhou, P.; Guo, P. Optimal subsidy level for waste-to-energy investment considering flexibility and uncertainty. Energy Econ. 2022, 108, 105894. [Google Scholar] [CrossRef]
- Tsitsiklis, J.; Van Roy, B. Regression Methods for Pricing Complex American Style Options. IEEE Trans. Neural Netw. 2001, 12, 694–703. [Google Scholar] [CrossRef]
- Dusonchet, L.; Telaretti, E. Comparative economic analysis of support policies for solar PV in the most representative EU countries. Energy Rev. 2015, 42, 986–998. [Google Scholar] [CrossRef]
- Wang, X.; Tang, R.; Meng, M.; Su, T. Research on CCUS business model and policy incentives for coal-fired power plants in China. Int. J. Greenh. Gas Control 2023, 125, 103871. [Google Scholar] [CrossRef]
- Cheng, B.; Dai, H.; Wang, P.; Zhao, D.; Masui, T. Impacts of carbon trading scheme on air pollutant emissions in Guangdong Province of China. Energy Sustain. Dev. 2015, 27, 174–185. [Google Scholar] [CrossRef]
- Han, J.; Li, J.; Tang, X.; Wang, L.; Yang, X.; Ge, Z.; Yuan, F. Coal-fired power plant CCUS project comprehensive benefit evaluation and forecasting model study. J. Clean. Prod. 2023, 385, 135657. [Google Scholar] [CrossRef]
- Zhang, M.M.; Zhou, P.; Zhou, D.Q. A real options model for renewable energy investment with application to solar photovoltaic power generation in China. Energy Econ. 2016, 59, 213–226. [Google Scholar] [CrossRef]
- Yang, M.; Blyth, W.; Bradley, R.; Bunn, D.; Clarke, C.; Wilson, T. Evaluating the Power Investment Options with Uncertainty in Climate Policy. Energy Econ. 2008, 30, 1933–1950. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, L. Investment Decisions of Fired Power Plants on Carbon Utilization under the Imperfect Carbon Emission Trading Schemes in China. Processes 2019, 7, 828. [Google Scholar] [CrossRef]
- Jiang, K.; Ashworth, P. The development of Carbon Capture Utilization and Storage (CCUS) research in China: A bibliometric perspective. Renew. Sustain. Energy Rev. 2021, 138, 110521. [Google Scholar] [CrossRef]
- Guo, C.; Ma, W.; Yang, C.; Yang, R. Enterprise characteristics and incentive effect of environmental regulation. Int. Rev. Financ. 2025, 25, e70032. [Google Scholar] [CrossRef]
- Su, C.; Zha, X.; Ma, J.; Li, B.; Wang, X. Dynamic Optimal Control Strategy of CCUS Technology Innovation in Coal Power Stations Under Environmental Protection Tax. Systems 2025, 13, 193. [Google Scholar] [CrossRef]
- Su, C.; Xu, Z.; Wang, X.; Li, B. Research on the Co-Evolution Mechanism of Electricity Market Entities Enabled by Shared Energy Storage: A Tripartite Game Perspective Incorporating Dynamic Incentives/Penalties and Stochastic Disturbances. Systems 2025, 13, 817. [Google Scholar] [CrossRef]
- Sun, L.; Chen, W. Impact of carbon tax on CCUS source-sink matching: Finding from the improved ChinaCCS DSS. J. Clean. Prod. 2022, 333, 130027. [Google Scholar] [CrossRef]
- Cao, L.; Tang, Y.; Cai, B.; Wu, P.; Zhang, Y.; Zhang, F.; Xin, B.; Lv, C.; Chen, K.; Fang, K. Was it better or worse? Simulating the environmental and health impacts of emissions trading scheme in Hubei province, China. Energy 2021, 217, 119427. [Google Scholar] [CrossRef]
- Lindner, S.; Peterson, S.; Windhorst, W. An economic and environmental assessment of carbon capture and storage (CCS) power plants: A case study for the City of Kiel. J. Environ. Plan. Manag. 2010, 53, 1069–1088. [Google Scholar] [CrossRef]
- Zhang, X.; Gan, D.; Wang, Y.; Liu, Y.; Ge, J.; Xie, R. The impact of price and revenue floors on carbon emission reduction investment by coal-fired power plants. Technol. Forecast. Soc. Change 2020, 154, 119961. [Google Scholar] [CrossRef]
- Bruhn, T.; Naims, H.; Olfe-Kräutlein, B. Separating the debate on CO2 utilisation from carbon capture and storage. Environ. Sci. Policy 2016, 60, 38–43. [Google Scholar] [CrossRef]
- Laurikka, H.; Koljonen, T. Emissions trading and investment decisions in the power sector—A case study in Finland. Energy Policy 2004, 34, 1063–1074. [Google Scholar] [CrossRef]
- Wu, N.; Parsons, J.E.; Polenske, K.R. The impact of future carbon prices on CCS investment for power generation in China. Energy Policy 2013, 54, 160–172. [Google Scholar] [CrossRef]
- Shukla, R.; Ranjith, P.; Haque, A.; Choi, X. A review of studies on CO2 sequestration and caprock integrity. Fuel 2010, 89, 2651–2664. [Google Scholar] [CrossRef]
- CBEEX. 2023. Available online: https://www.cbeex.com.cn/ (accessed on 24 December 2023).
- Liu, J.; Zhang, Q.; Li, H.; Chen, S.; Teng, F. Investment decision on carbon capture and utilization (CCU) technologies—A real option model based on technology learning effect. Appl. Energy 2022, 322, 119514. [Google Scholar] [CrossRef]
- SEREX. 2023. Available online: http://www.sxerex.com/ (accessed on 24 December 2023).
- Tan, Z.; Zeng, X.; Lin, B. How do multiple policy incentives influence investors’ decisions on biomass co-firing combined with carbon capture and storage retrofit projects for coal-fired power plants? Energy 2023, 278, 127822. [Google Scholar] [CrossRef]
- Welkenhuysen, K.; Rupert, J.; Compernolle, T.; Ramirez, A.; Swennen, R.; Piessens, K. Considering economic and geological uncertainty in the simulation of realistic investment decisions for CO2-EOR projects in the North Sea. Appl. Energy 2017, 185, 745–761. [Google Scholar] [CrossRef]





| Related Articles | CCUS | Carbon Trading | Pollution Right Trading | Environmental Benefits | Methods |
|---|---|---|---|---|---|
| Dusonchet et al. [35] | √ | NPV | |||
| Wang et al. [36] | √ | √ | system dynamics method | ||
| Masui et al. [37] | √ | √ | Computable General Equilibrium | ||
| Han et al. [38] | √ | √ | Comprehensive Evaluation | ||
| Fan et al. [24] | √ | Real option (Tree model) | |||
| M.M. et al. [39] | √ | Real option (LSMC) | |||
| Hu, Huanyue, Peng, Peng [33] | √ | Real option (LSMC) | |||
| This paper | √ | √ | √ | √ | Real option (LSMC) |
| Description | Symbol | Values | Parameter Estimation Process |
|---|---|---|---|
| Operating life of CCUS | L | 30 | [46] |
| Investment period | T | 10 | Authors’ setting |
| Annual energy output | kWh | [41] | |
| Investment cost | 520 million CNY | Based on NZEC FEED, and authors made some adjustment | |
| Price of electricity | 0.35 CNY | [36] | |
| Coal price | 995 CNY/t | In late January 2024, the price of anthracite coal was 995 CNY/ton. | |
| Carbon trading price | 65 CNY/t | In January 2024, the average national carbon trading price was 65 CNY/ton | |
| Drift rate of carbon trading price | 0.03 | Calculated by the authors based on historical data from 2015–2024, with reference to [54] | |
| Drift rate of unit investment cost | −0.03 | Calculated by the authors based on historical data from 2015–2024, with reference to [36] | |
| Drift rate of electricity price | 0.04 | Calculated by the authors based on historical data from 2015–2024, with reference to [33] | |
| Drift rate of coal price | 0.04 | Calculated by the authors based on historical data from 2015–2024, with reference to [12] | |
| Volatility of carbon trading prices | 0.04 | Same as above, with reference to [54] | |
| Volatility of unit investment cost | 0.08 | Same as above, with reference to [36] | |
| Volatility of electricity price | 0.01 | Same as above, with reference to [33] | |
| Volatility of coal price | 0.04 | Same as above, with reference to [12] | |
| utilization | β | 20% | According to the current CCUS level, set by this article |
| prices for industry | 250 CNY | [41] | |
| price of food | 525 CNY | [41] | |
| Benefits of the EOR | 564.5 CNY | [55] | |
| Sulfur dioxide purification | 5414 t | [38] | |
| Nitrogen compound purification | 2639 t | [38] | |
| Amount of dust purification | 7031.8 t | [38] | |
| Purification value of sulfur dioxide | 450 CNY/t | Ecosystem assessment Guidelines for gross ecosystem product accounting | |
| Purification value of Nitrogen compounds | 540 CNY/t | Ecosystem assessment Guidelines for gross ecosystem product accounting | |
| Purification value of dust | 600 CNY/t | Ecosystem assessment Guidelines for gross ecosystem product accounting | |
| Trading price of sulfur dioxide | 6000 CNY/t | [56] | |
| Trading price of nitrogen compounds | 6000 CNY/t | [56] | |
| O&M costs | Ma | CNY | Based on NZEC FEED, and authors made some adjustment |
| Discount rate | 0.08 | A general discount rate | |
| capture cost | 400 CNY/t | [57] |
| Strategy Type | Optimal Investment Time (yr) | Best Investment Value (CNY Million) | |
|---|---|---|---|
| No carbon and emissions trading | Invest immediately | Not recommended for investment | −1545 |
| Deferred Options | Not recommended for investment | −1200.4 | |
| Carbon trading exists | Invest immediately | Not recommended for investment | −199 |
| Deferred Options | 10th year | 64.8 | |
| Pollution right trading exists | Invest immediately | Not recommended for investment | −878 |
| Deferred Options | Not recommended for investment | −695 | |
| With carbon and emissions trading | Invest immediately | Invest immediately | 321 |
| Deferred Options | 10th year | 462 |
| With/Without Carbon Trading | Optimal Investment Time (yr) | Best Investment Value (CNY Million) | |
|---|---|---|---|
| Disregard for environmental benefits | With carbon trading | Not recommended for investment | −63 |
| Without carbon trading | Not recommended for investment | −1283.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Xiao, X.; Su, C.; Li, B. Strategic Decision-Making for Carbon Capture, Utilization, and Storage in Coal-Fired Power Plants: The Roles of Pollution Right Trading and Environmental Benefits. Systems 2025, 13, 919. https://doi.org/10.3390/systems13100919
Wang X, Xiao X, Su C, Li B. Strategic Decision-Making for Carbon Capture, Utilization, and Storage in Coal-Fired Power Plants: The Roles of Pollution Right Trading and Environmental Benefits. Systems. 2025; 13(10):919. https://doi.org/10.3390/systems13100919
Chicago/Turabian StyleWang, Xinping, Xue Xiao, Chang Su, and Boying Li. 2025. "Strategic Decision-Making for Carbon Capture, Utilization, and Storage in Coal-Fired Power Plants: The Roles of Pollution Right Trading and Environmental Benefits" Systems 13, no. 10: 919. https://doi.org/10.3390/systems13100919
APA StyleWang, X., Xiao, X., Su, C., & Li, B. (2025). Strategic Decision-Making for Carbon Capture, Utilization, and Storage in Coal-Fired Power Plants: The Roles of Pollution Right Trading and Environmental Benefits. Systems, 13(10), 919. https://doi.org/10.3390/systems13100919






