Effect of the Variable Viscosity on the Peristaltic Flow of Newtonian Fluid Coated with Magnetic Field: Application of Adomian Decomposition Method for Endoscope

Abstract

In the present analysis, peristaltic flow was discussed for MHD Newtonian fluid through the gap between two coaxial tubes, where the viscosity of the fluid is treated as variable. In addition, the inner tube was considered to be at rest, while the outer tube had the sinusoidal wave traveling down its motion. Further, the assumptions of long wave length and low Reynolds number were taken into account for the formulation of the problem. A closed form solution is presented for general viscosity using the Adomian decomposition method. Numerical illustrations that show the physical effects and pertinent features were investigated for different physical included phenomenon. It was found that the pressure rise increases with an increase in Hartmann number, and frictional forces for the outer and inner tube decrease with an increase in Hartmann number when the viscosity is constant. It was also observed that the size of the trapping bolus decreases with an increase in Hartmann number, and increases with an increase in amplitude ratio when the viscosity is parameter.

1. Introduction

The study of peristaltic mechanism has gained considerable attention during the past few decades [1,2,3,4,5,6,7,8,9,10]. Peristaltic mechanism involves certain physiological phenomena, like swallowing food through the esophagus, vasomotion of small blood vessels, transport of urine from kidney to bladder, chyme motion in the gastrointestinal tract, and movement of spermatozoa in human reproductive tract.

Peristaltic pumping is a form of liquid transport that occurs when a progressive wave of area contraction or expansion propagates along the length of distensible duct. There are many engineering processes in which peristaltic pumps are used to handle a wider range of fluids, particularly in the chemical and pharmaceutical industries. This mechanism is also used in the transport of slurries, sanitary fluids, and noxious fluids in the nuclear industry [11,12,13]. Extensive analytical, numerical, and experimental studies have been undertaken involving such flows. Important studies to the present topic include the works done by [14,15,16,17,18,19]. In all previous studies, fluid viscosity is assumed to be constant. There are few attempts in which the variable viscosity in peristaltic phenomena has been used. Mention may be made of the works by [20,21,22].

There are various analytical techniques to solve the differential equations arising in physics and engineering. Thus, various perturbation and non perturbation techniques are in use. Recently, Adomian decomposition has acquired great credence in tackling the linear and non-linear problems, and sometimes gives the closed form solution in the form of general functions like trigonometric functions, Bessel functions, and so on. The impressive bibliography of the work done by the Adomian decomposition method has been presented in papers by [23,24,25,26,27,28,29,30].

The intent of the paper is to present an integrated solution for different facets of the problem. These include application of endoscopy in a viscous fluid with the variable viscosity and closed form Adomian solutions, which are presented for unknown (general $\mathsf{\mu }\left(r\right)$) variable viscosity. In Section 2, mathematical formulation of the present problem is described. Section 3 deals with the solution of the problem using the Adomian decomposition method. Three typical examples were chosen and their closed form solutions were presented, and comparison is given with the existing literature. In Section 4, graphical results are presented to gauge the effects of certain physical parameters. Finally, streamlines for the flow problems are also drawn.

2. Mathematical Formulation

Consider the magnetohydrodynamic flow of an electrically conducting viscous fluid through the gap between two coaxial tubes. It is assumed that a uniform magnetic field $B_0$ is applied transversely to the flow. Further, considering that the magnetic Reynolds number is small, the induced magnetic field is negligible. A schematic diagram of the geometry of the problem under consideration is shown in Figure 1.

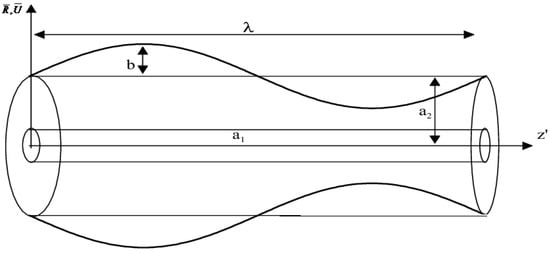
Figure 1. Effects of an endoscope on peristaltic motion.

The geometry of the wall surface is described as

$${\overline{R}}_1=a_1$$

(1)

$${\overline{R}}_2=a_2+b\cos \frac{2\mathsf{\pi }}{\mathsf{\lambda }}(\overline{Z}-c\overline{t})$$

(2)

where $a_1,$ and $a_2$ are the radii of the inner and the outer tubes, respectively; $b$ is the amplitude of the wave; $\mathsf{\lambda }$ is the wavelength; $c$ is the propagation velocity; and $\overline{t}$ is the time.

In the laboratory frame ($\overline{R}, \overline{Z}$), the flow is unsteady, but, by introducing a wave frame ($\overline{r} , \overline{z}$) moving with velocity $c$ away from the fixed frame, the flow can be treated as steady [10]. The coordinate frames are related by the transformations.

$$\overline{z}=\overline{Z}-c\overline{t}, \overline{r}=\overline{R}, \overline{w}=\overline{W}-c, \overline{u}=\overline{U}$$

(3)

where $\left(\overline{u}, \overline{w}\right)$ and $\left(\overline{U}, \overline{W}\right)$ are the velocity components in radial and axial directions in moving and fixed coordinates, respectively. Using the transformations (3), the equations that govern the flow are

$$\frac{\partial \overline{u}}{\partial \overline{r}}+\frac{\partial \overline{w}}{\partial \overline{z}}+\frac{\overline{u}}{\overline{r}}=0$$

(4)

$$\begin{array}{ll}\mathsf{\rho }\left[\overline{u}\frac{\partial \overline{u}}{\partial \overline{r}}+\overline{w}\frac{\partial \overline{u}}{\partial \overline{z}}\right]=& -\frac{\partial \overline{p}}{\partial \overline{r}}+\frac{\partial }{\partial \overline{r}}\left(2\mathsf{\mu }\left(\overline{r}\right) \frac{\partial \overline{u}}{\partial \overline{r}}\right) \\ & +\frac{2\mathsf{\mu }\left(\overline{r}\right)}{\overline{r}}\left[\frac{\partial \overline{u}}{\partial \overline{r}}-\frac{\overline{u}}{\overline{r}}\right] \\ & +\frac{\partial }{\partial \overline{z}}\left(\mathsf{\mu }\left(\overline{r}\right) \left(\frac{\partial \overline{u}}{\partial \overline{z}}+\frac{\partial \overline{w}}{\partial \overline{r}}\right)\right) \end{array}$$

(5)

$$\begin{array}{ll}\mathsf{\rho }\left[\overline{\mathrm{u}}\frac{\partial \overline{w}}{\partial \overline{r}}+\overline{w}\frac{\partial \overline{w}}{\partial \overline{z}}\right]=& -\frac{\partial \overline{p}}{\partial \overline{z}}+\frac{\partial }{\partial \overline{z}}\left(2\mathsf{\mu }\left(\overline{r}\right) \frac{\partial \overline{w}}{\partial \overline{z}}\right) \\ & +\frac{1}{\overline{r}}\frac{\partial }{\partial \overline{r}}\left(\overline{r}\mathsf{\mu }\left(\overline{r}\right) \left(\frac{\partial \overline{u}}{\partial \overline{z}}+\frac{\partial \overline{w}}{\partial \overline{r}}\right)\right) \\ & -\mathsf{\sigma }{B}_0^2\left(\overline{w}+c\right)\end{array}$$

(6)

where $\overline{u}$ and $\overline{w}$ are the velocity components in the $\overline{r}$ and $\overline{z}$ directions, respectively; $\mathsf{\rho }$ is the density; $\mathsf{\sigma }$ is the electrically conductivity of the fluid; and $\mathsf{\mu }$ is the variable viscosity. The governing equations can be dimensionalized by the following non-dimensional parameters.

$$\begin{array}{l}r=\frac{\overline{r}}{a_2},z=\frac{\overline{z}}{\mathsf{\lambda }},w=\frac{\overline{w}}{c},u=\frac{\lambda \overline{u}}{a_{2}c},p=\frac{a_2^2\overline{p}}{\mathsf{\lambda }c\mathsf{\mu }},r_1=\frac{{\overline{r}}_1}{a_2}, \mathsf{\delta }=\frac{a_2}{\mathsf{\lambda }}\\ r_2=\frac{{\overline{r}}_2}{a_2}=1+\mathsf{\phi }\cos \left(2\mathsf{\pi }z\right),\mathrm{Re}=\frac{\mathsf{\rho }c{a}_2}{\mathsf{\mu }},M=\sqrt{\frac{\mathsf{\sigma }}{\mathsf{\mu }}}{B}_0{a}_2\end{array}$$

(7)

where $\varphi$ is the amplitude ratio, $\mathrm{Re}$ is the Reynolds number, $\delta$ is the dimensionless wave number, and $M$ is the magnetic parameter.

Using the above non-dimensional parameters in Equations (4)–(6), the following system of equations is obtained.

$$\frac{1}{r}\frac{\partial \left(ru\right)}{\partial r}+\frac{\partial w}{\partial z}=0$$

(8)

$$\begin{array}{ll}\mathrm{Re}{\mathsf{\delta }}^3\left[u\frac{\partial u}{\partial r}+w\frac{\partial u}{\partial z}\right]=& -\frac{\partial p}{\partial r}+{\mathsf{\delta }}^2\frac{\partial }{\partial r}\left(2\mathsf{\mu }\left(r\right) \frac{\partial u}{\partial r}\right) +{\mathsf{\delta }}^2\left(\frac{2\mathsf{\mu }\left(r\right)}{r}\left(\frac{\partial u}{\partial r}-\frac{u}{r}\right)\right) \\ & +{\mathsf{\delta }}^2\left(\frac{\partial }{\partial z}\left(\mathsf{\mu }\left(r\right) \left(\frac{\partial u}{\partial z}{\mathsf{\delta }}^2+\frac{\partial w}{\partial r}\right)\right)\right)\end{array}$$

(9)

$$\begin{array}{ll}\mathsf{\delta }\mathrm{Re}\left[u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\right]=& -\frac{\partial p}{\partial z}+{\mathsf{\delta }}^2\frac{\partial }{\partial z}\left(2\mathsf{\mu }\left(r\right) \frac{\partial w}{\partial z}\right) \\ & +\frac{1}{r}\frac{\partial }{\partial r}\left(r\mathsf{\mu }\left(r\right) \left(\frac{\partial u}{\partial z}{\mathsf{\delta }}^2+\frac{\partial w}{\partial r}\right)\right)-M^{2}w\end{array}$$

(10)

Using the long wavelength approximation and dropping terms of order $\mathsf{\delta }$ and higher, the above equations reduce to

$$\frac{\partial p}{\partial r}=0$$

(11)

$$\frac{1}{r}\frac{\partial }{\partial r}\left(r\mathsf{\mu }\left(r\right) \frac{\partial w}{\partial r}\right)=\frac{\partial p}{\partial z}+M^{2}w$$

(12)

The relevant boundary conditions in new parameters are

$$\begin{array}{c}w=-1atr=r_1\\ w=-1atr=r_2\end{array}$$

(13)

3. Solution by Adomian Decomposition Method

In this section, the Adomian solution is determined for the velocity field. According to the Adomian decomposition method, Equation (12) can be written in the operator form as

$$L_{r}w=\frac{\mathrm{d}p}{\mathrm{d}z}+M^{2}w$$

(14)

where the differential operator $L_r$ is defined in the form

$$L_r=\frac{1}{r}\frac{\partial }{\partial r}\left(r\mathsf{\mu }\left(r\right) \frac{\partial }{\partial r}\right)$$

(15)

and the inverse operator $L_r^{-1}$ is defined by

$$L_r^{-1}(.)=\int \left[\frac{1}{r\mathsf{\mu }\left(r\right)}\int r(.) \mathrm{d}r\right] \mathrm{d}r$$

(16)

Applying the inverse operator, Equation (12) takes the form

$$\begin{array}{l}w\left(r, z\right)=L_r^{-1}\left[\frac{\mathrm{d}p}{\mathrm{d}z}+M^{2}w\right]+c_{1}r+c_2\\ w\left(r, z\right)=\frac{\mathrm{d}p}{\mathrm{d}z}I\left(r\right)+L_r^{-1}\left(M^{2}w\right)+c_{1}r+c_2\end{array}$$

(17)

in which

$$L_r^{-1}\left(\frac{\mathrm{d}p}{\mathrm{d}z}\right)=\int \left[\frac{1}{r\mathsf{\mu }\left(r\right)}\int r\left(\frac{\mathrm{d}p}{\mathrm{d}z}\right) \mathrm{d}r\right] \mathrm{d}r=\frac{\mathrm{d}p}{\mathrm{d}z}I\left(r\right)$$

(17a)

and $I\left(r\right)$ is given by

$$I\left(r\right)=\int \frac{r}{2\mathsf{\mu }\left(r\right)}\mathrm{d}r$$

(18)

According to Adomian decomposition, it can be written as

$$w={\displaystyle \sum }_{n=0}^{\infty }{w}_n$$

(19)

Using the Adomian decomposition method, the solution $w(r, z)$ can be elegantly computed by the recurrence relation

$$\begin{array}{ccc}\hfill w_0& =& c_{1}r+c_2\hfill \\ \hfill w_1& =& \frac{\mathrm{d}p}{\mathrm{d}z}I\left(r\right)+M^2{L}_r^{-1}\left(w_0\right)\hfill \\ \hfill w_{n+2}& =& M^2{L}_r^{-1}\left(w_{n+1}\right), n\ge 0\hfill \end{array}$$

(20)

The above equations give

$$w_n=M^{2n-2}\left(\frac{\mathrm{d}p}{\mathrm{d}z}+M^2{c}_2\right) {\left(L_r^{-1}\right)}^{n-1}I\left(r\right)+M^{2n}{c}_1{\left(L_r^{-1}\right)}^{n-1}{I}_1\left(r\right),n\ge 1$$

(21)

in which

$$I_1\left(r\right)=\int \frac{r^2}{3\mathsf{\mu }\left(r\right)}\mathrm{d}r$$

(22)

With the help of Equations (20) and (21), the closed form of $w$ can be written as

$$\begin{array}{l}w\left(r, z\right)=w_0+{\displaystyle \sum _{n=1}^{\infty }}{w}_n\\ w\left(r, z\right)=c_1\mathsf{\chi }\left(r\right)+c_2{\mathsf{\chi }}_1\left(r\right)+\frac{\mathrm{d}p}{\mathrm{d}z}{\mathsf{\chi }}_2\left(r\right)\end{array}$$

(23)

Using the boundary conditions (13), the values of constants $c_1$ and $c_2$ can be written as

$$\begin{array}{l}{c}_1=\frac{{\mathsf{\chi }}_{{}_1}\left(r_1\right)-{\mathsf{\chi }}_{{}_1}\left(r_2\right)}{\mathsf{\chi }\left(r_1\right) {\mathsf{\chi }}_{{}_1}\left(r_2\right)-\mathsf{\chi }\left(r_2\right) {\mathsf{\chi }}_{{}_1}\left(r_1\right)}-\frac{\mathrm{d}p}{\mathrm{d}z}\left[\frac{{\mathsf{\chi }}_{{}_2}\left(r_1\right) {\mathsf{\chi }}_{{}_1}\left(r_2\right)-{\mathsf{\chi }}_{{}_2}\left(r_2\right) {\mathsf{\chi }}_{{}_1}\left(r_1\right)}{\mathsf{\chi }\left(r_1\right) {\mathsf{\chi }}_{{}_1}\left(r_2\right)-\mathsf{\chi }\left(r_2\right) {\mathsf{\chi }}_{{}_1}\left(r_1\right)}\right]\\ c_2=-\frac{1}{{\mathsf{\chi }}_{{}_1}\left(r_2\right)}-\frac{\mathrm{d}p}{\mathrm{d}z}\frac{{\mathsf{\chi }}_{{}_2}\left(r_2\right)}{{\mathsf{\chi }}_{{}_1}\left(r_2\right)}-c_1\frac{\mathsf{\chi }\left(r_2\right)}{{\mathsf{\chi }}_{{}_1}\left(r_2\right)}\end{array}$$

(24)

where these ${\mathsf{\chi }}_s^{\prime }$ are defined in Appendix A.

The closed form solution (13) is represented in terms of integrals for any kind of general variable viscosity. These integrals can be computed for particular values of variable viscosity $\mathsf{\mu }$. Here, three cases of variable viscosity are taken into account, $\mathsf{\mu }(r)=1,$ $r,$ and $\frac{1}{r}.$

3.1. Case 1 (When μ = 1)

With the help of Equations (16), (18) and (22), the following are obtained:

$$I\left(r\right)=\frac{r}{2}\mathrm{d}r=\frac{r^2}{4}$$

(25)

$${\left(L_r^{-1}\right)}^{n}I\left(r\right)=\frac{{\left(\frac{r}{2}\right)}^{2n+2}}{{\left[\left(n+1\right)!\right]}^2}, n\ge 1, 2, 3,\dots$$

(26)

$${\left(L_r^{-1}\right)}^{n}I\left(r\right)=\frac{{\left(\frac{r}{2}\right)}^{2n+2}}{{\left[\left(n+1\right)!\right]}^2}, n\ge 1, 2, 3,\dots$$

(27)

$$I_1\left(r\right)=\int \frac{r^2}{3}\mathrm{d}r=\frac{r^3}{3^2},$$

$${\left(L_r^{-1}\right)}^n{I}_1\left(r\right)={\displaystyle \sum }_{n=0}^{\infty }\frac{r^{2n+3}}{3^2{.5}^2{.7}^2\dots .{\left(2n+3\right)}^2}$$

(28)

The closed form of $w\left(r, z\right)$ can be written as

$$w\left(r, z\right)=c_1{\mathsf{\chi }}_{{}_3}\left(r\right)+c_2{I}_0\left(Mr\right)+\frac{1}{M^2}\frac{\mathrm{d}p}{\mathrm{d}z}\left(-1+I_0\left(Mr\right)\right)$$

(29)

Using boundary conditions (13), the solution of (29) can be written as

$$w\left(r, z\right)=a_{14}{\mathsf{\chi }}_{{}_3}\left(r\right)+a_{15}{I}_0\left(Mr\right)+\frac{1}{M^2}\frac{\mathrm{d}p}{\mathrm{d}z}\left(-1-a_{15}{I}_0\left(Mr\right)-a_{14}{\mathsf{\chi }}_{{}_3}\left(r\right)\right)$$

(30)

The constants appearing in the above equations are defined in the equations and $I_0$ are the modified Bessel functions, with the first kind of order $0.$

3.1.1. Volume Flow Rate and Pressure Rise

The instantaneous volume flow rate $\overline{Q}\left(z\right)$ is given by

$$\overline{Q}\left(z\right)={\int }_{r_1}^{r_2}rw\left(r, z\right) \mathrm{d}r=\frac{\mathrm{d}p}{\mathrm{d}z}{a}_{22}+a_{20}+a_{21}$$

(31)

From Equation (31), the following is obtained:

$$\frac{\mathrm{d}p}{\mathrm{d}z}=\frac{1}{a_{22}}\left(\overline{Q}\left(z\right)-a_{20}-a_{21}\right)$$

(32)

The volume flow $Q$ over a period is obtained as

$$Q=\overline{Q}\left(z\right)+\left(1+\frac{{\mathsf{\phi }}^2}{2}\right)-r_1^2$$

(33)

and

$$\frac{\mathrm{d}p}{\mathrm{d}z}=\frac{1}{a_{22}}\left(Q-\left(1+\frac{{\mathsf{\phi }}^2}{2}\right)+r_1^2-a_{20}-a_{21}\right)$$

(34)

The pressure rise $\Delta p$ and the friction force (at the wall) on the outer and inner tubes are $F^{\left(0\right)}$ and $F^{\left(1\right)}$, respectively, are

$$\Delta p={\int }_0^1\frac{\mathrm{d}p}{\mathrm{d}z}\mathrm{d}z$$

(35)

$$\begin{array}{c}{F}^{\left(0\right)}={\int }_0^1{r}_2^2\left(-\frac{\mathrm{d}p}{\mathrm{d}z}\right) \mathrm{d}z\\ F^{\left(1\right)}={\int }_0^1{r}_1^2\left(-\frac{\mathrm{d}p}{\mathrm{d}z}\right) \mathrm{d}z\end{array}$$

(36)

3.1.2. Stream Function

The corresponding stream function $\left(u=-\frac{1}{r}\frac{\partial \mathsf{\Psi }}{\partial z}\mathrm{and}w=\frac{1}{r}\frac{\partial \mathsf{\Psi }}{\partial r}\right)$ can be written as

$$\mathsf{\Psi }=a_{14}g\left(r\right)-\frac{1}{M^2}\frac{\mathrm{d}p}{\mathrm{d}z}\left(a_{14}g\left(r\right)+\frac{r^2}{2}+a_{15}\frac{r}{M}{I}_1\left(Mr\right)\right)+a_{15}\frac{r}{M}{I}_1\left(Mr\right)$$

(37)

where the constants appears in the above equations are defined in Appendix A; $I_1$ is a modified Bessel functions of the first order; and $a_{14}$, $a_{15}$ are defined in Appendix A.

3.2. Case 2 (When μ = r)

Using Equations (16), (18), and (22), the following is implied for $\mathsf{\mu }=r$:

$$I\left(r\right)=\int \frac{r}{2.r}\mathrm{d}r=\frac{r}{2!}$$

(38)

$${\left(L_r^{-1}\right)}^{n}I\left(r\right)={\displaystyle \sum }_{n=0}^{\infty }\frac{r^{n+1}}{\left(n+2\right)!\left(1.2.3.4\dots .\left(n+1\right)\right)}$$

(39)

$$I_1\left(r\right)=\int \frac{r^2}{3.r}\mathrm{d}r=\frac{r^2}{3!}$$

(40)

$${\left(L_r^{-1}\right)}^n{I}_1\left(r\right)=\frac{r^2}{3!}+{\displaystyle \sum }_{n=1}^{\infty }\frac{r^{n+2}}{\left(n+3\right)!\left(3.4.5\dots .\left(n+2\right)\right)}$$

(41)

With the help of these values, and using boundary conditions, the closed form of $w\left(r, z\right)$ can be written as

$$w\left(r, z\right)=b_{14}{\mathsf{\chi }}_{{}_4}\left(r\right)+b_{18}{\mathsf{\chi }}_{{}_5}\left(r\right)+\frac{\mathrm{d}p}{\mathrm{d}z}\left({\mathsf{\chi }}_{{}_6}\left(r\right)+b_{19}{\mathsf{\chi }}_{{}_5}\left(r\right)-b_{15}{\mathsf{\chi }}_{{}_4}\left(r\right)\right)$$

(42)

The constants appearing in the above equations are defined in Appendix A.

3.2.1. Volume Flow Rate and Pressure Rise

The instantaneous volume flow rate $\overline{Q}\left(z\right)$ is given by

$$\overline{Q}\left(z\right)=\frac{\mathrm{d}p}{\mathrm{d}z}{b}_{29}+b_{27}+b_{25}$$

(43)

The volume flow rate and the pressure gradient can be calculated as

$$Q=\overline{Q}\left(z\right)+\left(1+\frac{{\mathsf{\phi }}^2}{2}\right)-r_1^2$$

(44)

The pressure rise $\Delta p$ and the friction force (at the wall) on the outer and inner tubes $F^{\left(0\right)}$ and $F^{\left(1\right)}$ can be computed using (35) and (36).

$$\frac{\mathrm{d}p}{\mathrm{d}z}=\frac{1}{b_{29}}\left(Q-\left(1+\frac{{\mathsf{\phi }}^2}{2}\right)+r_1^2-b_{25}-b_{27}\right)$$

(45)

The constants appearing in the above equations are defined in Appendix A

3.2.2. Stream Function

Stream function, in this case, is defined as

$$\mathsf{\Psi }=b_{14}{g}_{{}_0}\left(r\right)+b_{18}{g}_{{}_1}\left(r\right)+\frac{\mathrm{d}p}{\mathrm{d}z}\left(g_{{}_2}\left(r\right)+b_{19}{g}_{{}_1}\left(r\right)-b_{15}{g}_{{}_0}\left(r\right)\right)$$

(46)

3.3. Case 3 (When μ = $\frac{1}{r}$)

Using the similar procedure as discussed in previous sections, it can be written as

$$w\left(r, z\right)=d_{16}{\mathsf{\chi }}_{{}_7}\left(r\right)+d_{18}{\mathsf{\chi }}_{{}_8}\left(r\right)+\frac{\mathrm{d}p}{\mathrm{d}z}\left({\mathsf{\chi }}_{{}_9}\left(r\right)+d_{19}{\mathsf{\chi }}_{{}_8}\left(r\right)-d_{17}{\mathsf{\chi }}_{{}_7}\left(r\right)\right)$$

(47)

The constants appearing in the above equations are defined in Appendix A.

3.3.1. Volume Flow Rate and Pressure Rise

The instantaneous volume flow rate $\overline{Q}\left(z\right)$ is given by

$$\overline{Q}\left(z\right)=\frac{\mathrm{d}p}{\mathrm{d}z}{d}_{27}+d_{26}+d_{25}$$

(48)

The volume flow $Q$ over a period is obtained as

$$Q=\overline{Q}\left(z\right)+\left(1+\frac{{\mathsf{\phi }}^2}{2}\right)-r_1^2$$

(49)

The pressure rise $\Delta p$ and the friction force $F^{\left(0\right)}$ and $F^{\left(1\right)}$ can be computed using (35) and (36).

$$\frac{\mathrm{d}p}{\mathrm{d}z}=\frac{1}{d_{27}}\left(Q-\left(1+\frac{{\mathsf{\phi }}^2}{2}\right)+r_1^2-d_{25}-d_{26}\right)$$

(50)

3.3.2. Stream Function

Stream function for this case is

$$\mathsf{\Psi }=d_{16}h\left(r\right)+d_{18}{h}_1\left(r\right)+\frac{\mathrm{d}p}{\mathrm{d}z}\left(h_{{}_2}\left(r\right)+h_{{}_1}\left(r\right)d_{19}-h\left(r\right) d_{17}\right)$$

(51)

The constants appearing in the above equations are defined in Appendix A.

4. Results and Discussion

The objective of the current analysis is to present the closed form solutions of MHD Newtonian fluid with variable viscosity. The expression for pressure rise per wavelength and frictional forces are difficult to integrate analytically; therefore, numerical integration is used to evaluate the integrals. Figure 2, Figure 3 and Figure 4 are plotted for pressure rise and friction force against flow rate $Q$ when viscosity is constant. In Figure 2, it is observed that pressure rise increases with an increase of $M$ up to $Q<1.7$, after which the curves intersect each other and, finally, it gives an opposite behavior. The effects $M$ on $F^{\left(0\right)}$(for outer tube) and $F^{\left(1\right)}$ (for inner tube) are presented in Figure 3 and Figure 4. It is depicted from Figure 3 and Figure 4 that with an increase in $M$, both $F^{\left(0\right)}$ and $F^{\left(1\right)}$ decrease $M$ for small $Q$ and, finally, the behavior is reversed at the end. A comparison of the velocity field for constant viscosity case is made between the Adomian decomposition solution and perturbation solutions obtained by [6]. (see Figure 5). Figure 6, Figure 7, Figure 8 and Figure 9 are prepared when (viscosity) $\mathsf{\mu }=r$. It is observed from Figure 6 that in the retrograde $\left(\Delta p>0, Q<0\right)$ and peristaltic pumping $\left(\Delta p>0, Q>0\right)$ regions, the pressure rise decreases with an increase in amplitude ratio $\mathsf{\phi }$. Figure 7 and Figure 8 show that $F^{\left(0\right)}$ and $F^{\left(1\right)}$ give an opposite behavior as compared with $\Delta p$. The velocity field increases with the increase in $M$ and the maximum value of the velocity is at the center (see Figure 9). Figure 10, Figure 11, Figure 12 and Figure 13 are prepared when the viscosity $\mathsf{\mu }=\frac{1}{r}.$ It is observed from Figure 10 that with an increase in $r_1$, the pressure rise decreases in the retrograde $\left(\Delta p>0, Q<0\right)$, peristaltic pumping $\left(\Delta p>0, Q>0\right)$, and copuming $\left(\Delta p<0, Q>0\right)$ regions. It is depicted from Figure 11 and Figure 12 that with an increase in $r_1$, both $F^{\left(0\right)}$ and $F^{\left(1\right)}$ decrease for small $Q$ and, finally, the behavior is reversed at the end. The velocity profile for different values of $M$ for the case when viscosity is $\mathsf{\mu }=\frac{1}{r}$ is shown in Figure 13. It is observed from Figure 13 that the magnitude value of the velocity profile decreases with an increase in $M$.

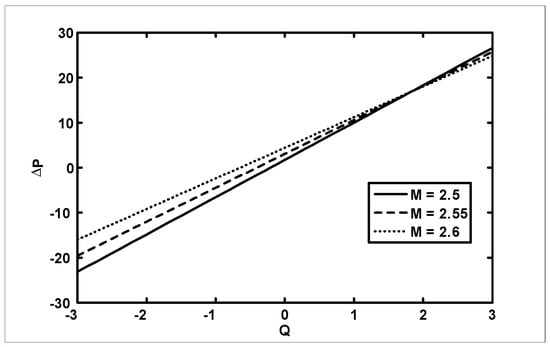
Figure 2. The variation of $\Delta p$ with $Q$ for different values of $M$ at $r_1=0.4, \mathsf{\phi }=0.4,$ when $\mathsf{\mu }=1.$

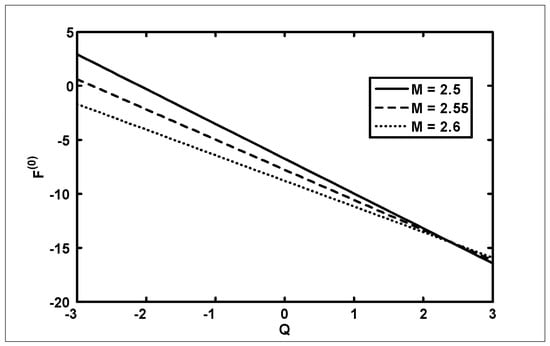
Figure 3. The variation of friction force $F^{(0)}$ (outer tube) with $Q$ for different values of $M$ at $r_1=0.4, \mathsf{\phi }=0.4,$ when $\mathsf{\mu }=1.$

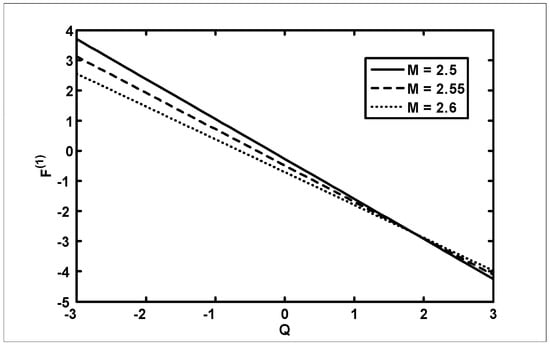
Figure 4. The variation of friction force $F^{(1)}$ (inner tube) with $Q$ for different values of $M$ at $r_1=0.4, \varphi =0.4,$ when $\mathsf{\mu }=1.$

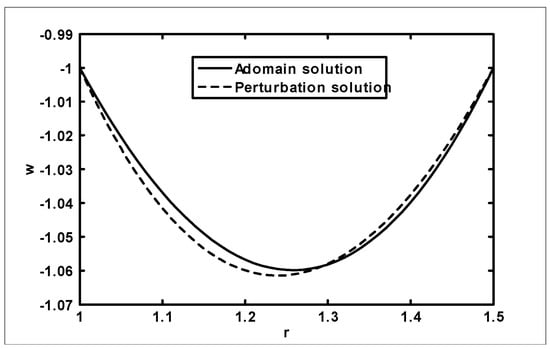
Figure 5. Comparison with the existing literature.

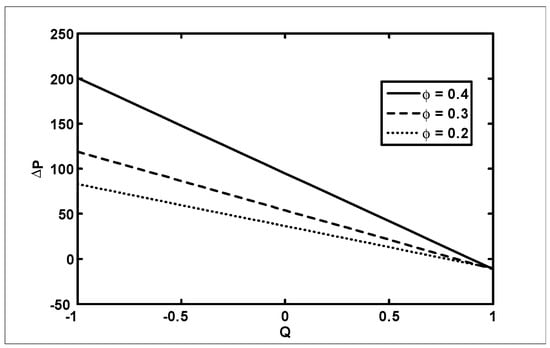
Figure 6. The variation of $\Delta p$ with $Q$ for different values of $\mathsf{\phi }$ at $M=3, r_1=0.1,$ when $\mathsf{\mu }=r.$

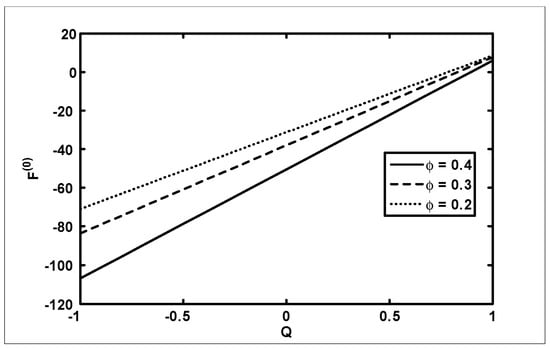
Figure 7. The variation of friction force $F^{(0)}$ (outer tube) with $Q$ for different values of ϕ at $r_1=0.1, M=3,$ when $\mathsf{\mu }=r.$

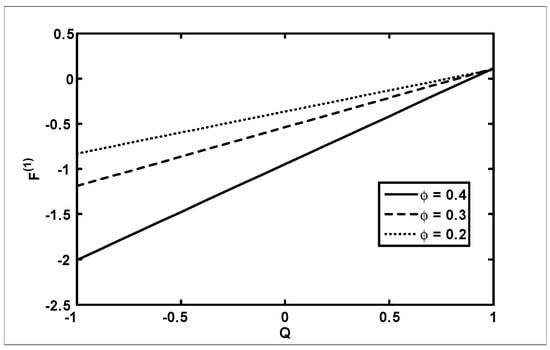
Figure 8. The variation of friction force $F^{(1)}$ (inner tube) with $Q$ for different values of $\mathsf{\phi }$ at $r_1=0.1, M=3,$ when $\mathsf{\mu }=r.$

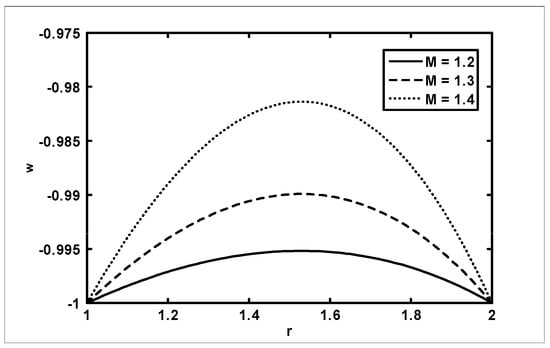
Figure 9. Velocity profiles for different values of $M$ at $t=1, z=1, \mathsf{\phi }=1,$ when $\mathsf{\mu }=r$.

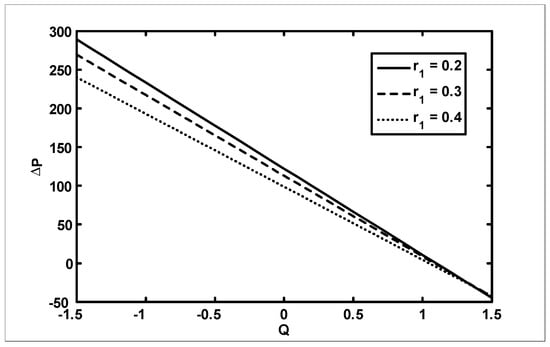
Figure 10. The variation of $\Delta p$ with $Q$ for different values of $r_1$ at $M=3, \mathsf{\phi }=0.4,$ when $\mathsf{\mu }=\frac{1}{r}.$

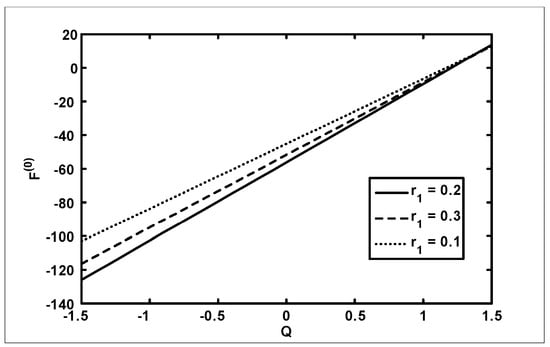
Figure 11. The variation of friction force $F^{(0)}$ (outer tube) with $Q$ for different values of $r_1$ at $\mathsf{\phi }=0.4, M=3,$ when $\mathsf{\mu }=\frac{1}{r}.$

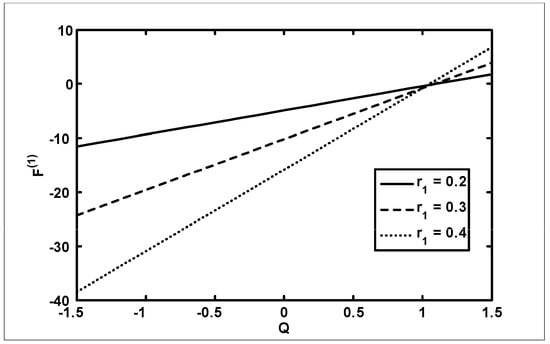
Figure 12. The variation of friction force $F^{(1)}$ (inner tube) with $Q$ for different values of $r_1$ at $\mathsf{\phi }=0.4, M=3,$ when $\mathsf{\mu }=\frac{1}{r}.$

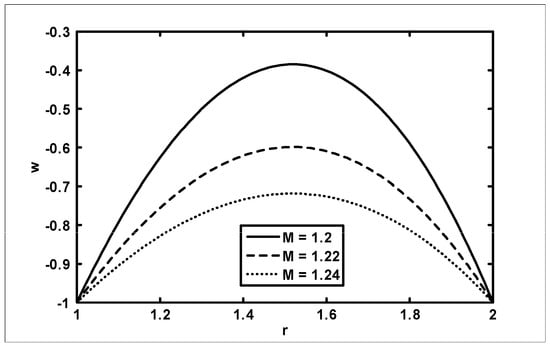
Figure 13. Velocity profiles for different values of $M$ at $t=1, z=1, \mathsf{\phi }=1,$ when $\mathsf{\mu }=\frac{1}{r}$.

Trapping Phenomenon

The trapping phenomenon is an interesting phenomenon in peristaltic motion, which is discussed in Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 for the case when $\mathsf{\mu }=1,$ $\mathsf{\mu }=r$, and $\mathsf{\mu }=\frac{1}{r}.$ Stream lines for different values of $\mathsf{\phi }$ for the case when $\mathsf{\mu }=1$ are shown in Figure 14. It is observed from Figure 6 that with an increase in amplitude ratio $\mathsf{\phi }$, the size of the trapping bolus increases. Stream lines for different values of $M$ and $\mathsf{\phi }$ for the case when $\mathsf{\mu }=r$ are shown in Figure 15 and Figure 16. It is observed from Figure 15 that the size of the trapping bolus decreases with an increase in Hartmann number $M$. The size of the trapping bolus increases with an increase in amplitude ratio $\mathsf{\phi }$ (see Figure 16). Stream lines for different values of $M$ and $\mathsf{\phi }$ for the case when $\mathsf{\mu }=\frac{1}{r}$ are shown in Figure 17 and Figure 18. It is observed from the Figures that the size of the trapping bolus increases with an increase in Hartmann number $M$ and amplitude ratio $\mathsf{\phi }.$

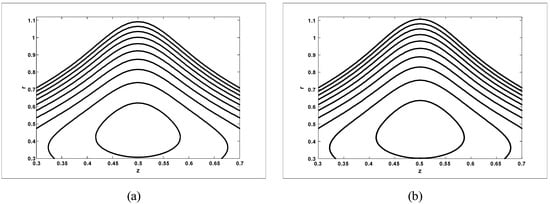
Figure 14. Streamlines for two different values of $\mathsf{\phi }$ for (a) $\mathsf{\phi }=0.1$ and (b) $\mathsf{\phi }=0.101.$ The other parameters are chosen as $M=2,$ $Q=0.41,$ $r_1=0.65$ when $\mathsf{\mu }=1.$

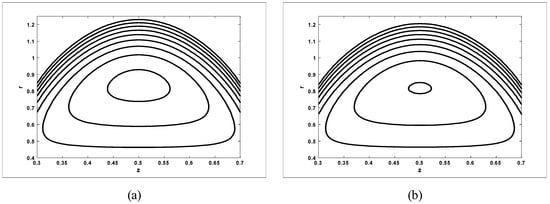
Figure 15. Streamlines for two different values of $M$ for (a) $M=1$ and (b) $M=0.6.$ The other parameters are chosen as $\mathsf{\phi }=0.2,$ $Q=0.45,$ $r_1=1$ when $\mathsf{\mu }=r.$

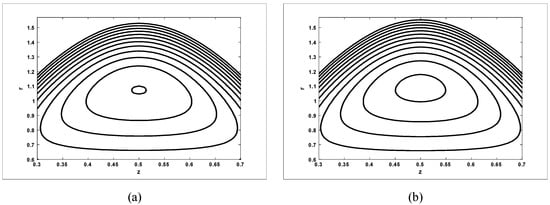
Figure 16. Streamlines for two different values of $\mathsf{\phi }$ for (a) $\mathsf{\phi }=0.29$ and (b) $\mathsf{\phi }=0.3.$ The other parameters are chosen as $M=1,$ $Q=0.45,$ $r_1=1.1$ when $\mathsf{\mu }=r$.

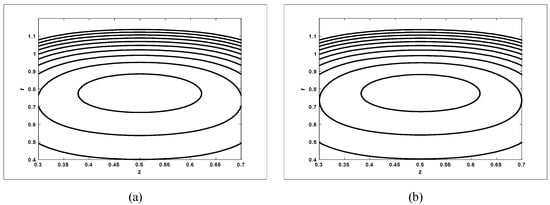
Figure 17. Streamlines for two different values of $M$ for (a) $M=0.2$ and (b) $M=0.1.$ The other parameters are chosen as $\mathsf{\phi }=0.1,$ $Q=0.4,$ $r_1=1.1$ when $\mathsf{\mu }=\frac{1}{r}.$

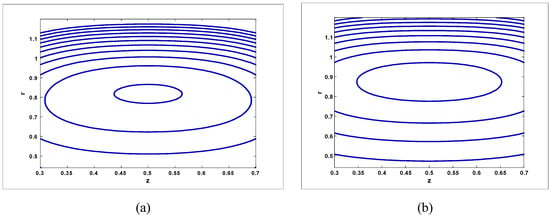
Figure 18. Streamlines for two different values of $r_1$ for (a) $r_1=1.11$ and (b) $r_1=1.13.$ The other parameters are chosen as $M=0.2,$ $Q=0.4,$ $\mathsf{\phi }=0.1$ when $\mathsf{\mu }=\frac{1}{r}.$

5. Conclusions

In the present analysis, peristaltic flow was discussed for MHD Newtonian fluid through the gap between two coaxial tubes, where the fluid viscosity was treated as variable. In addition, the inner tube was considered to be at rest, while the outer tube has the sinusoidal wave travelling down its motion. Further, the governing equations are simplified under the assumptions of long wavelength and low Reynolds number. The solution of the problem under discussion is computed analytically using the Adomian decomposition method. The results of the proposed problem are discussed through graphs. The main findings are summarized as follows:

• It was found that the pressure rise increases with an increase in Hartmann number $M$ and frictional forces for the outer $F^{\left(0\right)}$ and inner tube $F^{\left(1\right)}$ decreases with an increase in $M$ when viscosity $\mathsf{\mu }=1.$
• It was also found that the pressure rise decreases with an increase in amplitude ratio $\mathsf{\phi }$ in the retrograde $\left(\Delta p>0, Q<0\right)$ and peristaltic pumping $\left(\Delta p>0, Q>0\right)$ regions and frictional forces give opposite behavior as compared with pressure rise when viscosity $\mathsf{\mu }=r.$
• The pressure rise decreases in the retrograde $\left(\Delta p>0, Q<0\right)$, peristaltic pumping $\left(\Delta p>0, Q>0\right)$ and copuming $\left(\Delta p<0, Q>0\right)$ regions with an increase in $r_1$, and frictional forces decrease for small values of volume flow rate $Q$ with an increase in $r_1$ when viscosity $\mathsf{\mu }=\frac{1}{r}.$
• It was also noticed that the size of the trapping bolus increases with an increase in amplitude ratio $\mathsf{\phi }$ when viscosity $\mathsf{\mu }=1,$ while it increases with an increase in Hartmann number $M$ and amplitude ratio $\mathsf{\phi }$ when viscosity $\mathsf{\mu }=\frac{1}{r}.$ However, it decreases with an increase in Hartmann number $M$ and increases with an increase in amplitude ratio $\mathsf{\phi }$ when viscosity $\mathsf{\mu }=r.$