Abstract
The metal thickness uniformity of the micro-electroforming process determines the structural accuracy, surface finish, and functional characteristics, which directly affect the quality, performance, and reliability of the final parts. However, due to the non-uniformity of the electric field distribution, the problem of thickness non-uniformity in the micro-electroforming process has always been one of the key challenges limiting its application and development. The auxiliary cathode structure can improve the uniformity of electroforming thickness by regulating the cathode electrodeposition rate and electric field distribution and is widely used in the micro-electroforming process. In this study, with the micro-array metal die core as the research object, based on finite element simulations, the effect of the geometrical parameters of the auxiliary cathode on the thickness uniformity of electroforming is analyzed in depth. This study introduces the optimization method of the BP neural network and the NSWOA (Non-dominated Sorting Whale Optimization Algorithm) and achieves a significant improvement in the unevenness of electroforming thickness by designing and adjusting the parameters of the position, width, and shape of the auxiliary cathode. The unevenness of the microarray metal mold core is reduced to 4% from 475% without the auxiliary cathode, using the auxiliary cathode structure designed with this method.
1. Introduction
Micro-electroforming is a high-precision manufacturing technology based on the principle of electrolytic deposition. This technology uses electric current to make the metal ions in the electrolyte carry out a reduction reaction and deposit on the surface of the mold or substrate after many cycles of deposition, gradually forming complex and tiny metal parts. Because of its excellent dimensional accuracy and surface quality, micro-electroforming is widely used in various fields such as microelectronics manufacturing, optics, and medical care [1,2]. In microelectronics manufacturing, micro-electroforming technology is suitable for the production of micro-sensors, integrated circuit packages, micro-batteries and other high-precision devices [3,4,5], all of which have extremely stringent requirements for size and structural complexity. At the same time, micro-electroforming also shows great potential in the optical field, such as the production of high-precision micro-optical lenses, mirrors, and photoconductive elements [6,7,8]. In the medical field, the technology is widely used in the manufacture of miniature medical devices, such as cardiac stents, surgical instruments, and microlenses [9,10,11]; its high precision and good biocompatibility make it a key technology in the medical industry. In addition, micro-electroforming has important applications in the aerospace and military fields, such as the fabrication of miniature navigation devices, sensors, and radar components [12,13].
However, due to the extremely small scale and high precision requirements of micro-electroforming processing, the uniformity of the thickness of the electroforming layer is difficult to control during its process [14]. This inhomogeneity is mainly reflected in the difference between the deposition rate of the middle and edge regions of the cathode surface, leading to its inconsistent thickness, which in turn affects the performance and service life of the metal micro-devices [15]. To solve the above problem, the application of an auxiliary cathode has been well-proven as an effective optimization method. By rationally designing the auxiliary cathode, the current density distribution can be improved, which in turn improves the thickness uniformity of the electroforming layer (Figure 1). For example, Xiang et al. [16] investigated the application of auxiliary cathodes in copper plating circuits and found that increasing the width of the auxiliary cathode can significantly improve the plating uniformity. Wang et al. [17] compared four auxiliary cathode shapes—namely, circular, square, square triangle and square hexagon—and examined the improvement effect of different shapes of auxiliary cathodes on the thickness uniformity. Zhao et al. [18] proposed a method of co-cast layer thickness uniformity similar to the coplanar auxiliary cathode design that resembles the local microstructure of the mold, which improved the thickness uniformity of the electroforming mold by 49.1%. In addition, Zhan et al. [19] explored the effect of auxiliary cathode dimensions on the thickness uniformity of micropillar elements, and their study showed that the optimal auxiliary cathode parameters were closely related to the cathode surface area. Wang et al. [20] observed that the uniformity of electroformed gears improves with increasing thickness of the surrounding photoresist layer.
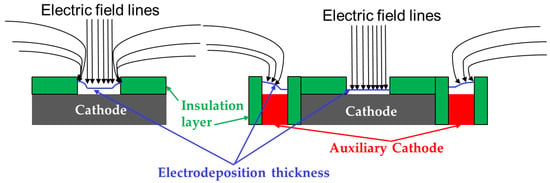
Figure 1.
Schematic of cathode deposition with and without an auxiliary cathode.
Although existing studies have optimized the auxiliary cathode structures, there is no accepted optimal solution when responding to the diverse micro-electroforming structure processing demands. Currently, the widely used auxiliary cathode structures are usually simple, such as metal rings or rectangular frames, whose shapes and sizes are difficult to quantify. When confronted with miniature parts with complex features, traditional design methods have difficulty meeting their diverse demands. Therefore, the key challenge for the current research is how to optimize the auxiliary cathode structures through innovative design strategies to adapt to different microstructural features.
A neural network is a computational model that simulates the neural system of the human brain that is widely used in the modelling and optimization of complex systems due to its powerful nonlinear mapping ability [21]. Its core mechanism is to adjust the connection weights and biases between the input, hidden, and output layers, and then gradually learn the potential relationship between inputs and outputs. The adaptive learning ability of neural networks can automatically extract complex features and potential patterns without the need for explicit mathematical formula descriptions, making it a powerful tool for solving nonlinear problems.
In recent years, the application of neural networks in micro-electroforming technology has gradually emerged. Some studies have focused on the prediction and optimization of electroforming process parameters. For example, Feng et al. [22] constructed a neural network model and successfully established the relationship between the electroforming copper process conditions and the target properties, achieving the high-precision prediction of the microhardness and tensile strength of the electroformed layer. Sassi et al. [23] optimized the structural stability of the casting layer by using a neural network and determined the optimal combination of the casting layer thickness, the PH value of the electrolyte, and the temperature. Subramanian et al. [24] constructed a prediction model for the electrodeposition rate of copper-tin alloys based on experimental data, verifying the advantages of neural networks in modelling complex deposition behavior. In this study, neural networks were used to capture the complex nonlinear relationship between auxiliary cathode parameters and electroforming thickness uniformity. By inputting multidimensional parameters, such as the shape, size, and position of the auxiliary cathode, the model can predict the corresponding thickness uniformity metrics.
Current auxiliary cathode designs are mainly limited to geometric factors, such as the similarity in shape to the main cathode, the distance between the auxiliary and main cathodes, and the width of the auxiliary cathode. However, there is a lack of systematic structural optimization analysis regarding their impact on thickness uniformity, and some critical geometric parameters may remain unidentified. This study aims to address these limitations by employing machine learning methods to optimize the design of the auxiliary cathode structure, thereby effectively improving the uniformity of the electroformed layer thickness. To address the deficiencies of existing auxiliary cathode designs in terms of generalization and diversity, this paper constructs an optimization framework that combines neural networks and genetic algorithms. The framework utilizes a neural network model to quickly predict the performance of the auxiliary cathode, and these prediction results are used as the basis for the adaptation evaluation of the genetic algorithm. Through continuous evolutionary optimization, the structural design of the auxiliary cathode with high electroforming uniformity in a large parameter space is explored. Compared with traditional methods, this joint framework can not only significantly improve the optimization efficiency but can also cope with the challenges of electroforming microstructure design with complex geometrical features. The study’s numerical simulation method, machine learning model, and optimization algorithm of the framework are described in detail in Section 2 of this paper. In Section 3, the optimization results and their analysis are presented to provide theoretical support and practical guidance for subsequent research.
2. Methods
2.1. Electroforming Model
Electroforming inhomogeneity mainly originates from the differences in deposition rates in various regions of the cathode surface. According to Faraday’s law, the local deposition rate v of the metal casting layer at the cathode can be expressed as [25]
where is the molar mass of nickel (kg/mol), is the density of nickel (kg/m3), is the deposition reaction rate (mol/(m2·s)), and the deposition reaction rate N is related to the local current density , which is satisfied by [17]
where is the stoichiometric coefficient, n is the number of electrons reacting, and F is the Faraday constant (96,485 C/mol). is the local current density of the cathode nickel plate. From the local current density, it is possible to calculate the deposition rate by Equations (1) and (2). The local current density can be described by the Bulter-Volmer equation:
where is the nickel exchange current density, is the anodic transfer coefficient, is the cathodic transfer coefficient, is the gas constant (J/(mol·K)), is the temperature (K), and is the overpotential, which is determined by the electrode potentials, the electrolyte interface potential, and the equilibrium potential:
where is the electrode potential (V), is the electrolyte potential (V), and is the equilibrium potential (V). The initial values of and are 0 V, and the initial potential of the electrolyte is from Equation (4).
Considering only the secondary current distribution, assuming that the composition of the electroforming liquid is uniformly distributed in the electroforming tank, without considering the double electric layer effect, and with no external flow field while ignoring the effect on the flow term, the electroforming liquid voltage and current distribution obey Ohm’s law:
where is the current density of the electrolyte and electrode surface (A/m2) and is the conductivity of the electrolyte (S/m). The potential distribution between the electrode and electrolyte can be calculated by Equations (5) and (6), which in turn solves the overpotential . The following boundary conditions are satisfied at the cathode interface:
where is the total externally applied current and S is the cathodic deposition area.
2.2. Geometric Model
To investigate in detail the influence of the shape of the auxiliary cathode on the electroforming uniformity, the study was carried out for a typical microfluidic chip mold preparation with an array of micropillars. The simulation model is shown in Figure 2a, including the anode (Ni plate), the electrolyte domain, the cathode surface, and the photoresist microstructure sidewall. The anode is configured as a planar plate structure measuring 0.1 cm × 0.1 cm. The cathode features a 0.1 cm × 0.1 cm square array of 7 × 7 photoresist micropillars (49 in total), with each pillar having 20 μm diameter and 300 μm pitch (Figure 2b). The cathode surface is an electroforming region enclosed within the square, defined by the vertical structure of the photoresist wall. To balance the computational efficiency and accuracy, a subarea optimization strategy was adopted for the meshing: encrypted meshes were used for the cathode and auxiliary cathode surfaces, and sparser meshes were used for the anode and photoresist regions.
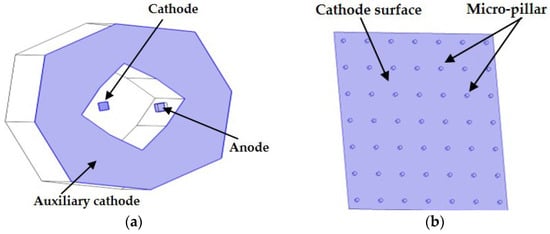
Figure 2.
The simulation model. (a) Geometric model. (b) Cathode surface structure.
The layer-to-layer thickness uniformity was quantitatively assessed through the thickness non-uniformity index α [15], expressed as
where is the thickness inhomogeneity of the cast layer and and represent the maximum and minimum thickness of the cast layer, respectively.
In this paper, finite element simulation was carried out using COMSOL Multiphysics software (version 6.2) to simulate the electroforming rate and metal deposition thickness, the simulation parameters for which are tabulated as shown in Table 1.

Table 1.
Simulation parameters [17,18].
The simulation results show that under the condition of an unassisted cathode (electroforming thickness of hmin = 20 μm), there is a significant edge effect on the cathode surface (Figure 3). The simulation results are consistent with those in reference [17], where the plating thickness is thin in the center of the electrode and thick at the edges, indicating the validity of our simulation methods and results. The thickness gradually increases from the center to the periphery, and the four endpoints of the edge have the largest inhomogeneity, α = 475%. The overall thickness of the cathode profile shows a symmetric parabolic distribution, and the thickness of the endpoints, hmax = 115 μm, is significantly higher than that of the center region. The presence of this edge thickening effect seriously affects the uniformity of the electroforming layer, further emphasizing the importance of assisted cathode design.
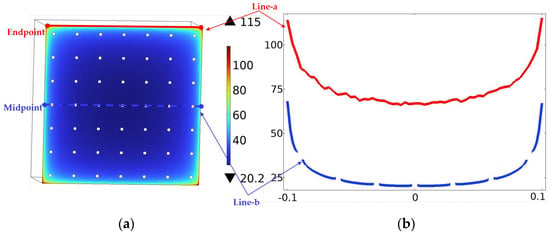
Figure 3.
The cathode deposition thickness under hmin = 20 um. (a) Simulation results of overall cathode thickness distribution; (b) Simulation results of cathode thickness distribution.
To reduce the computational complexity, appropriate simplifications are made in designing the auxiliary cathode to maximize the relative relationship between the auxiliary cathode and the cathode while saving computational resources. Combined with the case of Figure 3b, the thickness of the outer contour of the cathode is symmetric at the midpoint, and it gradually increases from the midpoint to the endpoint. The geometric parameters of the auxiliary cathode are defined through the schematic diagram shown in Figure 4. The position and shape of the auxiliary cathode (blue region) are precisely controlled by the following parameters: Considering symmetry, the endpoints of the auxiliary cathode (P1, P2, P3, P4) are positioned on the diagonal of the square cathode or on a line perpendicular to the boundary. Specifically, for the endpoints on the diagonal (P1 and P3), the perpendicular distance to the cathode boundary is defined as a1, while the perpendicular distance to the opposite boundary is a1 + a3, where a3 represents the additional offset extending outward from the initial distance a1. For the endpoints on a line passing through the cathode center and perpendicular to the boundary (P2 and P4), the perpendicular distance to the boundary is defined as a2, and the perpendicular distance to the opposite boundary is a2 + a4, where a4 represents the additional offset distance. By adjusting the values of a1, a2, a3, and a4, the shape and width of the auxiliary cathode can be flexibly controlled, thereby optimizing its impact on the electric field distribution. Furthermore, since the distance between the anode and cathode significantly affects the uniformity of electroforming thickness—where an excessively large or small distance can lead to uneven electric field line distribution [26]—the parameter a5 is introduced to represent the height difference between the auxiliary cathode and the cathode surface, and a6 is introduced to represent the thickness of the photoresist (non-conductive layer). These parameters are used to regulate the uniformity of the electric field lines and influence the current density distribution during the electrodeposition process, respectively, ensuring that the auxiliary cathode effectively improves thickness uniformity in the electroforming process.
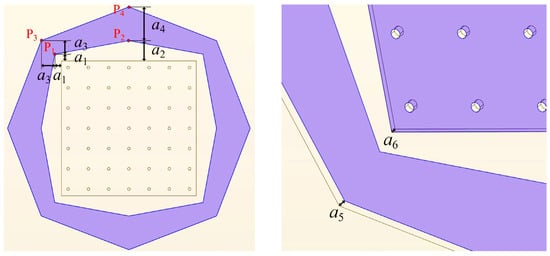
Figure 4.
Schematic design of the geometric parameters of the auxiliary cathode.
To investigate the influence of different parameter combinations on the deposition thickness of the cathode surface, numerical simulations were conducted. The simulation was terminated when the minimum deposition thickness on the cathode surface, hmin, reached 20 µm. By randomly generating values for a1 to a6 (within specified ranges), 1180 distinct auxiliary cathode configurations were simulated, providing robust data for machine learning model training; the specific value ranges are shown in Table 2:

Table 2.
Range of values of geometric parameters (unit: m).
To verify the effect of gridding on the calculation results, a set of auxiliary cathode parameters (a1 = 1 × 10−4, a2 = 3 × 10−4, a3 = 2 × 10−4, a4 = 5 × 10−4, a5 = 3 × 10−5, a6 = 5 × 10−5, unit: m) is selected to simulate the unevenness of electroforming thickness α and plating time t under different grid numbers with of 20 um. The relevant results are summarized in Table 3 and plotted in Figure 5.

Table 3.
Effect of mesh parameters on the inhomogeneity of the electroforming layer and plating time.
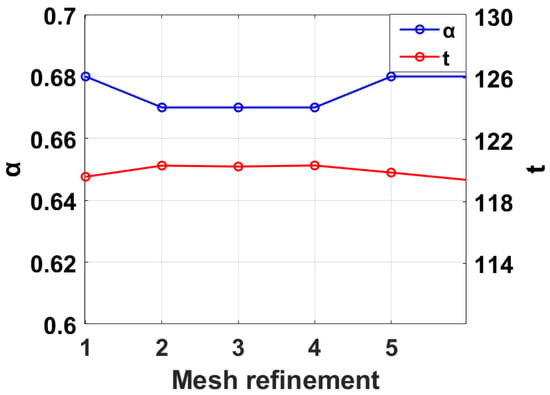
Figure 5.
The effect of the number of meshes on the inhomogeneity of the electroforming layer and plating time.
The calculation result of the initial mesh is α = 0.68, and the plating time is t = 119.6 min. After the third mesh refinement, α = 0.67 and t = 120.33 min. Compared with the initial mesh, the calculation result of the first refinement is closer to the stable solution, From the third refinement, the calculation results tend to be stable, and the changes of α and t are no longer significant. The α parameter (initial value: 0.68) and the t parameter (initial value: 119.6 min) stabilized at 0.67 and 120 min, respectively, after the first optimization. Subsequent mesh refinement (levels 1 to 5) did not significantly alter these values. This indicates that the optimized α and t are already close to the true physical solution, and further mesh refinement has negligible effects on these parameters, the observed stability validates the robustness of our optimization approach. To take into account the computational efficiency and accuracy, this study chooses the grid form with the maximum cell size of 0.018 cm as the final program. The specific setup parameters are shown in Table 4:

Table 4.
Grid parameters.
2.3. Establishment of Artificial Neural Networks
The neural network model used in this study is based on the classical BP (Back Propagation) neural network architecture, which is structurally designed to analyze the complex nonlinear relationships between parameters in the electroforming process.
Specifically, the input layer of the network contains six geometric dimensional parameters (a1, a2, a3, a4, a5, a6) to characterize the geometrical properties of the auxiliary cathode, while the output layer contains two output parameters: the inhomogeneity of the electroforming layer, α, and the plating time, t, as shown in Figure 6. The model is mainly used to predict the time at which the minimum electroforming thickness, hmin, will reach 20 µm, and the relationship between these parameters. The loss function is chosen as the mean absolute percentage error (), which is given by
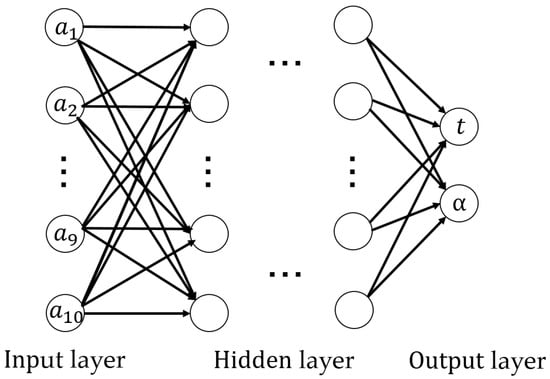
Figure 6.
Schematic diagram of the artificial neural network.
The study data are for the minimum electroforming thickness condition (20 µm), and 1180 sets of sample data were accumulated, of which 80% (944 sets) were used for training and 20% (236 sets) were used for testing to ensure the model’s generalization ability. The following steps were taken for data preprocessing to enhance training efficiency and improve model performance:
Input parameters were normalized before training to scale the data to the standard range of [0, 1]:
where and are the maximum and minimum values of the six parameters, respectively. Normalization helps to avoid the problem of vanishing gradients caused by too large a range of values and accelerates model convergence. To facilitate the interpretation of the results and subsequent analysis, the model outputs were inverse normalized back to the original scale:
where is the normalized time, and are the maximum and minimum values of the original time, and and are the maximum and minimum values of the normalized time, respectively.
To further improve the prediction accuracy, this study combines the CPO (Crested Porcupine Optimizer) to optimally adjust the initial weights and bias of the BP neural network. The CPO algorithm is known for its fast convergence and global search ability, which can effectively avoid the problem of traditional BP neural network training of easily falling into local optimum. As shown in Figure S1, the BP neural network optimized by CPO (CPOBP) demonstrates significantly improved prediction accuracy under both electroforming thickness conditions. Compared to the standard BP model (tMAPE: 0.020%; tα: 0.087%), CPOBP achieves a remarkable reduction in error, with tMAPE decreasing to 0.0024% (an 88% improvement) and tα decreasing to 0.0096% (an 89% improvement).
2.4. Multi-Objective Optimization
In this paper, multi-objective optimization is accomplished based on NSWOA. The optimization solution to the problem is found by simulating the foraging behavior of the whale population, while non-dominated sorting is used to deal with the multi-objective problem. The optimization process includes generating the population, evaluating individual fitness, non-dominated sorting, and updating the population; finally, the optimized Pareto front is obtained through multi-generation iterations, to minimize α and t. The population size is set to 150, and the maximum number of generations is 30. After each optimization, a few points of the Pareto front are selected for validation, the simulated values are added to the training set, and multiple rounds of training and optimization are performed to make the final solution set as close as possible to the real Pareto front; uniformity is maintained in the distribution of the solution set.
3. Results
3.1. Effect of Auxiliary Cathode on Thickness Uniformity
After the artificial neural network-based analysis and multi-objective optimization, all optimized data points and simulated values are shown in Figure 6. The data points demonstrate the electroforming characteristics under multiple parameter combinations. By analyzing the Pareto front, it can be divided into two parts according to the electroforming time t: the low-t section (<120 min) and high-t section (120 min).
From Equations (12) and (13), under the condition of fixed total current , t is mainly affected by the electroforming area, and the larger the total electroforming area is, the smaller the average current density is, and the longer the time consumed to deposit to the target thickness . As shown in Figure 7, in the low-t zone, the auxiliary cathode area is smaller and the average current density is larger, and the electroforming inhomogeneity α decreases rapidly with a slow increase in t. The average current density is higher in the low-t zone than in the high-t zone. This indicates that in this interval, the influence of the auxiliary cathode shape on the uniformity of the electroforming layer is greater than that of its area. By reasonably optimizing the auxiliary cathode parameters, the electroforming uniformity can be significantly improved while guaranteeing the electroforming efficiency. In the high-t region of the Pareto front, the decrease in α gradually slows down as t continues to increase. At this time, the auxiliary cathode area is large, the electroforming deposition rate is relatively low, and the auxiliary cathode area becomes the dominant factor affecting the thickness uniformity. At this stage, increasing the auxiliary cathode area can further improve the thickness uniformity, but it will significantly prolong the electroforming time, sacrificing the electroforming efficiency; from the overall trend, the low t region is suitable for seeking efficient improvement of thickness uniformity in limited space, while the high t region is suitable in the situation that the thickness uniformity is required to be extremely high in large space. The optimization results can provide important guidance for the design of the auxiliary cathode and parameter adjustment of the electroforming process.
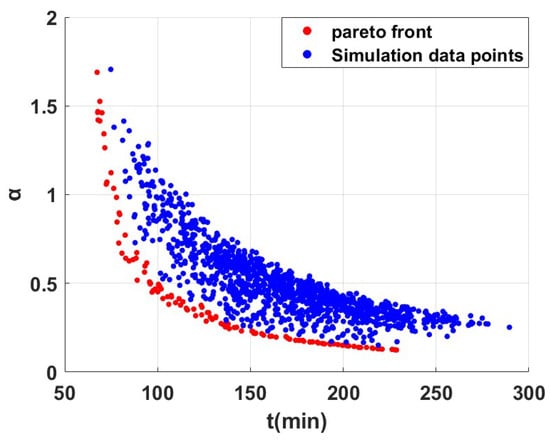
Figure 7.
Distribution of all simulated data points and optimized values.
When the inhomogeneity α is the smallest, it can be seen in Figure 8 that the shape of the optimized auxiliary cathode stays similar to that of the cathode. According to Table 2 and Table 5, it is found that, when the maximum current is fixed, in order to maximize the improvement of the electroforming homogeneity, the following is allowed by the fabrication conditions: the widths of the auxiliary cathode, a3 and a4, should be as large as possible, which will significantly increase the area of the auxiliary cathode and reduce the surface current density of the cathode, and thus the average electroforming rate of the cathode is reduced and the electroforming uniformity is improved; a5 and a6 should also be as large as possible, and they can have a certain effect on the uniformity by changing the diffusion conditions near the deposition interface; the auxiliary cathode should be as close as possible to the cathode, as this arrangement can more effectively disperse the local electric field of the cathode to the auxiliary cathode, shorten the path of ion diffusion, and improve the electroforming efficiency.
Figure 8.
Diagram of the optimal shape of the auxiliary cathode (unit: μm).

Table 5.
Optimized parameter results.
However, the increase in size will also bring about an increase in cost and a rise in manufacturing difficulty. The increase in the area of the auxiliary cathode will directly lead to a rise in the amount of substrate, mask plate, and photoresist used in the fabrication process, which will in turn increase the material cost. Fixing other parameters and adjusting the widths of the auxiliary cathode a3 and a4, when it exceeds a certain threshold (as shown in Figure 9, a3 = a4 > 0.4 cm), the main cathode current density distribution has levelled off, and further increasing the area does not have much effect on the uniformity. However, the required electroforming time t grows exponentially because too large an auxiliary cathode may divert too much current and reduce the current efficiency of the main cathode. This nonlinear growth significantly reduces productivity and restricts the practical application of the process. To address this situation, the allowable inhomogeneity α threshold can be set first, and an optimized solution that meets the target uniformity requirement with acceptable time can be predicted based on the model to achieve a balance between efficiency and uniformity.
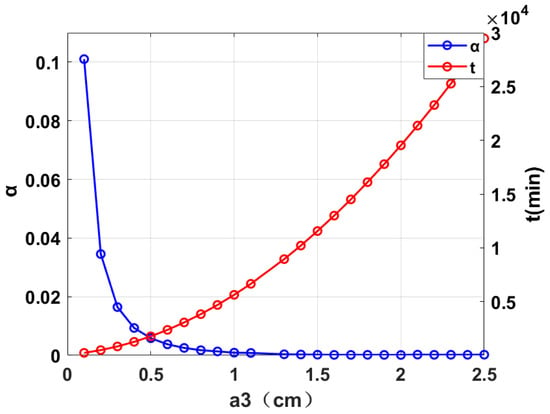
Figure 9.
Relationship between auxiliary cathode width a3 and α and t.
3.2. Effect of Auxiliary Cathode Shape on Thickness Uniformity
In the previous section, the influence of the auxiliary cathode on cathode electroforming uniformity under the condition of constant total current Itotal was discussed; however, the thickness uniformity in the high-t zone is mainly affected by the area of the auxiliary cathode. To avoid the reduction of current efficiency that is easily caused by too large an area, and to further determine the influence of shape on thickness uniformity to weaken the interference of the area factor, this subsection fixes the average current density iavg and performs the fine adjustment of the local current density by adjusting the boundary condition of the cathode surface potential distribution in Equation (7) through the shape. The electroforming model is consistent with 2.2 and iavg = 55.79 A/m2 is obtained according to Equation (13) and Table 5.
3.2.1. Optimization of Auxiliary Cathode Shape Parameters
Many cathodes are not completely symmetrical at the endpoints, and the endpoints tend to have concentrated electric fields and the most uneven thicknesses. To make the auxiliary cathode shape more universal and able to adapt to a variety of complex cathode shapes, P1P2 and P3P4 in Figure 4 are split into two segments at the endpoint position, to increase the diversity of shapes at the endpoints, and the photoresist and auxiliary cathode height parameters are retained; the design of the auxiliary cathode shape is shown in the schematic diagram in Figure 10, as follows.
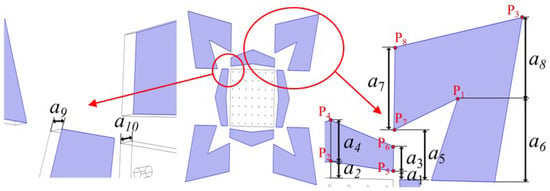
Figure 10.
Schematic diagram of the optimized design of the auxiliary cathode (local enlargement shows the position of the auxiliary cathode parameters).
All parameter values are randomly generated within the specified range, as shown in Table 6:

Table 6.
Range of values of geometric parameters (unit: m).
3.2.2. Multi-Objective Optimization Result
A neural network is built for multi-objective optimization, also following the methodology of Section 2.2 and Section 2.3 of the paper. The input layer of the network contains 10 geometrical dimensions (a1~a10), which are used to characterize the geometrical properties of the auxiliary cathode, and the output layer continues to be the inhomogeneity α of the electroforming layer and the plating time t. The relationship between these parameters is predicted for a minimum electroforming thickness hmin of 20 µm. Due to the increase in parameters and to ensure the generalization ability of the model, the sample data was increased to 3000 sets, of which 70% (2100 sets) were used for training and 30% (900 sets) were used for testing. The model prediction accuracy is very high, as shown in Figure S2; two cases of average current densities were considered (iavg = 55.79 A/m2 and 200 A/m2) to determine whether different current densities affect the parameters of the auxiliary cathode shape.
As seen in Figure S3, when the average current density is constant, the trend of electroforming time and electroforming uniformity is the same as that shown in Figure 6, and the inhomogeneity gradually decreases with the prolongation of electroforming time. This indicates that under the condition of fixed area, the shape of the auxiliary cathode also affects the thickness uniformity and electroforming time. By regulating the shape parameters, the thickness uniformity can be further optimized and the electroforming efficiency can be improved. When the current density increases, the inhomogeneity increases significantly, while the electroforming time is shortened. Notably, Figure S3 shows that when the current density was increased from 55.79 A/m2 to 200 A/m2, the ratio of the maximum and minimum inhomogeneities measured under the two current density conditions (αa/αb ≈ 3.58) was close to the corresponding current density ratio (iavg,b/iavg,a ≈ 3.58). This result indicates that the thickness inhomogeneity has a positive scaling property with the current density under fixed geometrical parameters and that the improvement effect of geometry optimization on the uniformity is limited by the current density constraint.
3.3. Parameter Importance
To explore the degree of influence of each parameter on the target value, for the simulated data, a regression analysis was performed using Random Forest to rank the characteristic importance of the input parameters. To improve accuracy, 100 sets of data were randomly selected for each characteristic importance, and the test was repeated 50 times to calculate its average value to reduce the effect of randomness.
3.3.1. Electroforming Time
As can be seen from Figure 11, the weights of the geometrical parameters of the auxiliary cathode on the electroforming time remain the same under different current density conditions. Among them, the width parameters a3, a4, a7, and a8 are the core variables affecting the electroforming time, and their importance is much higher than other parameters. This is because the width of the auxiliary cathode directly affects the distribution of current density in the electroforming process, which in turn has a decisive effect on the overall electroforming rate. Specifically, the larger their values, the more dispersed the current density distribution, resulting in a lower electroforming rate, thus prolonging the electroforming time. Secondly, the parameters a5 and a6 of the distance from the cathode endpoint also have a significant effect on the electroforming time, although their importance is lower than the width parameter, still a key auxiliary factor; this is because the current density at the cathode endpoint is the largest, and the sensitivity to the auxiliary cathode regulation is the highest. a1 is also a distance parameter of the endpoint, but compared to the joint effect of a5 and a6, its effect on the time is weaker. In contrast, a2, although also a parameter of distance from the cathode, has a lower electric field strength relative to the endpoints and the current density in that direction can be regulated by a4, so its effect on the results is almost none. The height of the auxiliary cathode and the photoresist thickness parameters (a9 and a10) also have a negligible effect on the electroforming time. The reason for this is that the range of values for these parameters is only a few tens of micrometers, and their variations have almost no significant effect on the overall ion diffusion process and electric field distribution, respectively.
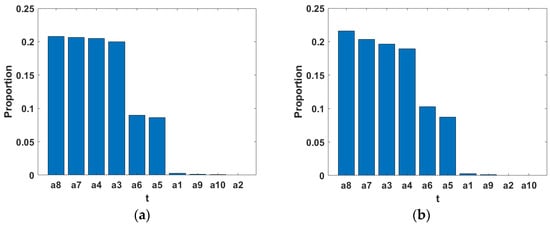
Figure 11.
Order of importance of temporal features. (a) t (iavg = 55.79 A/m2), (b) t (iavg = 200 A/m2).
3.3.2. Thickness Uniformity
As can be seen in Figure 12, the influence weights of the auxiliary cathode geometry parameters on the electroforming uniformity remain the same under different current density conditions. Among them, the width parameters a3, a4, a7, and a8 are again confirmed to be the core variables affecting the electroforming uniformity, with much higher importance than other parameters. This phenomenon suggests that the current density distribution is the main factor determining the uniformity of micro-electroforming. By optimally controlling the size of a3, a4, a7, and a8, the current density can be spread more evenly, thus reducing the difference in local deposition rate, significantly improving the electroforming uniformity, and reducing the volatility of thickness distribution. Secondly, the parameters a1, a5, and a6 also have a more obvious effect on the electroforming uniformity. This is because the local current density at the endpoint is large, and their three joint effects can make the local current density distribution more uniform compared with a2, which has a smaller effect on the electroforming uniformity. This is because a2 is the distance between the auxiliary cathode and the cathode edge where the current density is lowest, and it has a weaker effect on the overall current density distribution and the deposition rate. The size range of a9 is too small, and it has a limited effect on the current density distribution. However, it should be noted that a2 and a9 are still used as considerations when optimizing the design because the micro-electroforming process requires very high precision, and even smaller effects may be visible under specific conditions. a10 has almost no effect on the thickness uniformity and can be ignored.
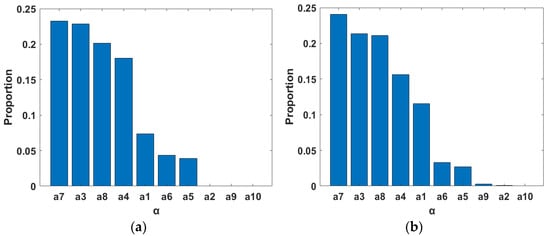
Figure 12.
Ranking of importance of homogeneity features (a) α (5.97 A/m2), (b) α (00 A/m2).
As can be seen in Table 5 and Table 7, when the current density is 55.79 A/m2, α is further reduced from 0.12 to 0.04 after shape optimization, indicating that the matched auxiliary cathode geometry contributes to the improvement of the current density distribution on the surface of the cathode, which in turn improves the uniformity of the electroforming thickness.

Table 7.
Thickness uniformity optimal auxiliary cathode parameters (unit: m).
The optimum shape of the auxiliary cathode is the same under both current densities—see Figure 13, which shows that the optimum auxiliary cathode can be determined once the cathode and current density are fixed. To obtain a better thickness uniformity, the endpoint diagonal is as close to the cathode as possible in the case of easy processing, i.e., a6 is taken to be the minimum, while a3, a4, a5, a7, and a8 should be taken to be the maximum and a1 and a2 are taken to be the appropriate position near the cathode. It is worth noting that the auxiliary cathode under the optimal shape is not completely parallel to the cathode contour, but rather there exists a proper inclination angle, and such a row of arrangement may help to eliminate the edge effect of the cathode.
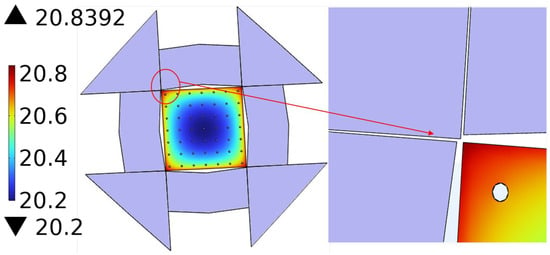
Figure 13.
Thickness uniformity optimized auxiliary cathode diagram (unit: μm).
4. Conclusions
In this paper, the effect of auxiliary cathode shape on cathode thickness uniformity in the micro-electroforming process has been investigated. This study shows that the proper design of shape parameters of the auxiliary cathode in micro-electroforming is crucial for high-precision fabrication based on micro-electroforming. The following four important conclusions can be drawn:
- In the case of fixed total current, the area of the auxiliary cathode is crucial for cathode uniformity; the larger the area, the better the thickness uniformity, while the influence of the shape parameter will be weakened.
- In the case of fixed average current density, the influence of the shape parameter is obvious, and the thickness uniformity can be further improved under a suitable shape parameter, but the optimization effect is still limited by the current density.
- The optimal auxiliary cathode parameter does not change with the change in average current density; it is not parallel to the cathode profile, but there is a certain angle.
- A method to find the shape of the auxiliary cathode is proposed, which can efficiently find the optimal auxiliary cathode parameters and shorten the electroforming time at the same time by establishing a neural network and multi-objective optimization.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/coatings15060652/s1, Figure S1. Plot of predicted versus true values for BP and CPOBP models (hmin = 20 um). Figure S2. Plot of predicted versus true values for BP and CPOBP models. a. t (iavg = 55.79 A/m2), b. α (iavg = 55.79 A/m2), c. t (iavg = 200 A/m2), d. α (iavg = 200 A/m2). Figure S3. Results of distribution of all simulated data points and optimized values. a. iavg = 55.79 A/m2, b. iavg = 200 A/m2.
Author Contributions
C.C.: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing—original draft, Writing—review & editing, Visualization, Supervision. S.L.: Methodology, and Investigation. M.Z.: Conceptualization, Methodology, and Writing—review & editing. J.Z.: Software and Data curation. K.S.: Writing—review & editing, Resources, Supervision, Project administration, and Funding acquisition. J.L.: Writing—review & editing, Resources, Supervision, and Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (2023YFC3008802), National Natural Science Foundation of China (52075465, 12172320), Hunan Provincial Natural Science Foundation of China (2021J50110), Key Products of Hunan Province’s Manufacturing Industry “Unveiled and Leading” Project (2023GXGG018), Hunan Innovative Province Construction Project (2023GK1030), and Hunan Provincial Innovation Foundation For Postgraduate (LXBZZ2024121).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article and Supplementary Materials.
Conflicts of Interest
The authors declare no competing financial interests.
References
- Rai, P.K.; Gupta, A. Review—Electroforming Process for Microsystems Fabrication. J. Electrochem. Soc. 2023, 170, 123510. [Google Scholar] [CrossRef]
- Min, S.-K.; Lee, S.-N.; Kim, M.; Kim, K.-B. Development of Electroforming Technology for Flexible Metal Substrates for High-Efficiency Double-Sided Electronic Devices. Mater. Today Commun. 2024, 39, 108784. [Google Scholar] [CrossRef]
- Soergel, T. Innovative Battery Electrodes Via Composite Electroforming. ECS Meeting Abstr. 2022, MA2022-01, 2358. [Google Scholar] [CrossRef]
- Wu, K.; Ding, F.; Yang, Y.; Li, D.; Qiao, Z.; Qiang, P.; Wang, B. Influence on Imaging Performance and Evaluation of Wolter-I Type Mandrel Fabrication Errors. Appl. Opt. 2022, 61, 6617. [Google Scholar] [CrossRef] [PubMed]
- Yang, X.; Zhang, X.; Ming, P.; Li, Y.; Wang, W.; Zhang, Y.; Li, Z.; Li, L.; Xiao, Y.; Guo, X.; et al. Fabricating Ultra-Narrow Precision Slit Structures with Periodically Reducing Current Over-Growth Electroforming. Micromachines 2023, 15, 76. [Google Scholar] [CrossRef]
- Yanagishita, T.; Hidaka, T.; Suzuki, M.; Masuda, H. Polymer Lenses with Antireflection Structures Prepared Using Anodic Porous Alumina Molds. J. Vac. Sci. Technol. B Nanotechnol. Microelectron. Mater. Process. Meas. Phenom. 2016, 34, 021804. [Google Scholar] [CrossRef]
- Wang, L.; Jiao, L.; Pang, S.; Yan, P.; Wang, X.; Qiu, T. The Development of Design and Manufacture Techniques for Bioresorbable Coronary Artery Stents. Micromachines 2021, 12, 990. [Google Scholar] [CrossRef]
- Sun, H.; Wang, X.; Xiong, Y.; Liu, G.; Wang, K. Fabrication of Microlens Based on Overplating in Electroforming. J. Micromech. Microeng. 2016, 26, 055007. [Google Scholar] [CrossRef]
- Xu, L.; Liu, Y. A Microresonant Gas Sensor by Micro-Electroforming. J. Micro Nano-Manuf. 2015, 4, 014501. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, N.; Gilchrist, M.; Fang, F. Advances in Precision Micro/Nano-Electroforming: A State-of-the-Art Review. J. Micromech. Microeng. 2020, 30, 103002. [Google Scholar] [CrossRef]
- Chen, X.; Liu, L.; He, J.; Zuo, F.; Guo, Z. Fabrication of a Metal Micro Mold by Using Pulse Micro Electroforming. Micromachines 2018, 9, 203. [Google Scholar] [CrossRef]
- Qiang, L.; Weiping, L.; Huicong, L.; Liqun, Z. Fabrication of Nanostructured Electroforming Copper Layer by Means of an Ultrasonic-Assisted Mechanical Treatment. Chin. J. Aeronaut. 2010, 23, 599–603. [Google Scholar] [CrossRef]
- Wang, R.; Lv, H.; Zhai, J.; Shen, T. Research and Exploration of Terahertz Feeder Manufacturing Technology Based on Micro-Precision Machining. J. Phys. Conf. Ser. 2023, 2459, 012133. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, N.; Fang, F. Investigation of Mass Transfer inside Micro Structures and Its Effect on Replication Accuracy in Precision Microelectroforming. Int. J. Mach. Tools Manuf. 2021, 165, 103717. [Google Scholar] [CrossRef]
- Du, L.; Yang, T.; Zhao, M.; Tao, Y.; Luo, L.; Wang, L.; Liu, C. Study on Improving Thickness Uniformity of Microfluidic Chip Mold in the Electroforming Process. Micromachines 2016, 7, 7. [Google Scholar] [CrossRef]
- Xiang, J.; Chen, P.; Wang, Y.; Zeng, C.; Yang, W.; Li, J.; Xu, Y. Numerical Simulation of Optimizing Plating Uniformity of Interconnect Circuits on Printed Circuit Boards. J. Phys. Conf. Ser. 2021, 1986, 012135. [Google Scholar] [CrossRef]
- Wang, H.; Xing, J.; Fan, T.; Liu, J.; Xie, J.; Li, C. An Effect of Layered Auxiliary Cathode on Thickness Uniformity in Micro Electroforming Process. Micromachines 2023, 14, 1307. [Google Scholar] [CrossRef]
- Zhao, M.; Du, L.; Wei, Z.; Du, C.; Liu, X.; Ji, X. Fabrication of Metal Microfluidic Chip Mold with Coplanar Auxiliary Cathode in the Electroforming Process. J. Micromech. Microeng. 2018, 29, 025002. [Google Scholar] [CrossRef]
- Zhan, X.; Shen, C.; Zhu, Z.; Zhu, D. New Precision Electroforming Process for the Simultaneous Improvement of Thickness Uniformity and Microstructure Homogeneity of Wafer-Scale Nanotwinned Copper Arrays. Int. J. Mach. Tools Manuf. 2023, 187, 104006. [Google Scholar] [CrossRef]
- Wang, H.; Xie, J.; Fan, T.; Sun, D.; Li, C. Improving the Thickness Uniformity of Micro Gear by Multi-Step, Self-Aligned Lithography and Electroforming. Micromachines 2023, 14, 775. [Google Scholar] [CrossRef]
- Foukalas, F. A Survey of Artificial Neural Network Computing Systems. Cogn. Comput. 2024, 17, 4. [Google Scholar] [CrossRef]
- Ji, F.; Chen, C.; Zhao, Y.; Min, B. Optimization of Copper Electroforming Process Parameters Based on Double Hidden Layer BP Neural Network. Micromachines 2021, 12, 1157. [Google Scholar] [CrossRef] [PubMed]
- Sassi, W.; Mrad, M.; Behera, D.; Ammar, S.; Hihn, J.Y. Prediction and Optimization of Electroplated Ni-Based Coating Composition and Thickness Using Central Composite Design and Artificial Neural Network. J. Appl. Electrochem. 2021, 51, 1591–1604. [Google Scholar] [CrossRef]
- Subramanian, K.; Periasamy, V.M.; Pushpavanam, M.; Ramasamy, K. Predictive Modeling of Deposition Rate in Electro-Deposition of Copper–Tin Using Regression and Artificial Neural Network. J. Electroanal. Chem. 2009, 636, 30–35. [Google Scholar] [CrossRef]
- Haghdoost, A.; Pitchumani, R. Numerical Analysis of Electrodeposition in Microcavities. Electrochim. Acta 2011, 56, 8260–8271. [Google Scholar] [CrossRef]
- Jiang, B.; Weng, C.; Zhou, M.; Lv, H.; Drummer, D. Improvement of Thickness Deposition Uniformity in Nickel Electroforming for Micro Mold Inserts. J. Cent. South Univ. 2016, 23, 2536–2541. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).