Investigation and Modelling of the Wear Resistance of Diamond Roller Dressers Made of Synthetic Diamonds with Mixed Grit Size

Abstract

The wear resistance of diamond dressing rolls depends on the manufacturing technology used and the characteristics of the working diamond layer, such as the type and grain size of the diamond grains, the type of bond, and the concentration and distribution of the diamonds. To optimise the lifetime of diamond rolls made of synthetic diamonds using the electroplating method, this paper proposes an innovative approach to compacting the intergranular spaces by treating them with diamond grains finer than the main fraction. To implement this approach, analytical dependencies were derived for the distance between the diamond grains. Intensive wear of the diamond roller bond was observed when the distance was exceeded as a result of contact with the abrasive grains of the grinding wheel. A ratio between the grain sizes of the main and additional diamond fractions is also recommended. Diamond roller dressers made of synthetic diamonds with a medium or high strength and a mixed grit size were created and their wear resistance was studied during the uni-directional and counter-directional dressing of electrocorundum grinding wheels using the plunge-grinding method. Theoretical and experimental models were constructed to predict the lifetime and the wear of diamond rolls in relation to the radial feed rate, the dressing speed ratio, the dress-out time, and the grit size ratio. Multi-objective optimisation based on a genetic algorithm was used to determine the optimal dressing conditions, ensuring the best combination of the maximum lifetime and minimum wear of the diamond rolls. The results obtained confirm the validity and correctness of the proposed approach for increasing the wear resistance of diamond roller dressers.

1. Introduction

The grinding process is a high-performance finishing process for the production of components with a high precision and surface quality. This complex process depends on both the grinding conditions and the relief of the grinding wheel cutting surface [1,2]. The surface topography is determined not only by the characteristics of the grinding wheels, but also—and more importantly—by the dressing process [3,4]. In this regard, the selection of the dressing tool and the optimal dressing system parameters is an important issue, on which the economic efficiency (production rate and manufacturing net cost) of the grinding process and the quality of the ground surfaces depend.

The dressing process changes the working behaviour (profile, topography, and effective hardness of the grinding layer) of the grinding tool. It impacts the grinding forces, power consumption, cutting zone temperatures, and wear behaviour of the grinding wheel and, as a result, the grinding process’s efficiency and accuracy [5,6].

Many studies have been conducted to understand the influence of the dressing conditions on grinding wheels and the surface finish. Normally, the objective of the grinding process is to achieve a better surface finish (roughness, flatness tolerance, etc.) or a high material removal rate of the workpiece. It has been established that an adequately designed dressing process ensures a consistent grinding process to achieve the intended workpiece surface quality as well as a small amount of grinding wheel wear [3]. Klocke et al. [3] also presented a quantitative analytical–empirical model of grinding wheel wear depending on the dressing condition. The new model allows for the prediction of the wear of the grinding wheel as a function of the geometric–kinematic engagement in dressing processes using the mean dressing chip cross-section. Linke [4] found that the performance of ultraprecision grinding is primarily dependent on the dressing of the grinding wheel, as the excellent cutting ability and the desired profile accuracy of the grinding wheel can be restored in the dressing process. The dressing process is considered a tribological system for improving the profile accuracy and optimising the surface morphology of the grinding wheel. Based on this, a holistic machining process model for glass-bonded grinding wheels was developed to predict the grinding wheel topography, the dressing forces, and the thermal dressing process load.

In [7], an in-depth analysis of modern technologies for dressing grinding wheels, including the rotary dressing process, was conducted. This work shows that a considerable amount of research has focused on the influence of the dressing conditions on the grinding wheel performance, including the influence of the radial feed and dressing speed ratio on the grinding wheel surface roughness, the influence of the dressing speed ratio on the radial dressing force, and the influence of the depth of dressing on the specific normal grinding force. Kloke and Linke [8] established that the surface morphology of the grinding wheel affects the machined surface roughness and damage layer through the number, shape, sharpness, porosity, and protruding height of the abrasive particles, while the profile accuracy of the grinding wheel mainly affects the shape accuracy of the ground parts. This was also confirmed in research conducted by Ding et al. [9]. Daneshi et al. [10] found that, through the dressing operation, the grinding process can be controlled in terms of the grinding forces, the grinding wheel wear, and the workpiece surface roughness. Three types of diamond rollers, including an electroplated roller, a vitrified bond form roller, and a cup dresser, with four different grinding wheels, two CBN and two corundum wheels, were examined. By applying an analysis of variance, Krajnik et al. [11] proved that the grinding wheel dressing condition most significantly affects the ground surface roughness in conventional centreless grinding. The surface roughness was additionally affected by the geometrical grinding gap set-up factor and the control wheel speed.

In [12], an analytical framework for evaluating the grinding wheel performance was developed that takes into account the effects of grain properties and dressing conditions on the wheel topography and, in turn, on the grinding performance. The proposed framework was experimentally verified and demonstrated via grinding tests using wheels with different grit types and under various dressing conditions. The framework and experiments quantified how the wheel wear influences the sliding component and how the grit protrusion influences the intrinsic specific grinding energy. This framework provides a rational basis for evaluating the grinding wheel performance and abrasive grit selection.

The scientific literature was focused on the phenomena involved in dressing tool wear. Godino et al. [13] found that one of the problematic issues of dressing tools is the wear they suffer, which affects the micro- and macro-geometry of the grinding wheel and its cutting ability. To investigate the impact of wear on diamond roller dressers, the authors developed a systematic methodology for analysing and characterising wear, including the design of specific software (in Python) to measure the rotary diamond tool wear, the proposal of a parameter to measure such wear, and an analysis of the grinding wheel behaviour, paying particular attention to the consumed power and surface roughness. They characterised the wear of two rotary dressers by analysing the wear behaviour depending on the pit radius of the dressers while studying the influence of the wear on ground surfaces. The results showed that the rotary dresser with a higher pit radius presented with wear that was approximately 28% higher than the dresser with a half pit radius.

In their study, Pombo et al. [5] focused on the relationship between dressing temperatures and dressing tool wear. According to them, the high temperatures and contact forces present in dressing lead to the wear of the diamond dressing tool, which in turn damages the topography of the wheel surface. The research conducted by Linke and Klocke [14] revealed some of the active processes for vitrified bonded grinding wheels by analysing the dressing temperatures and the dresser grit wear. They found that, as a result of the high dressing temperature, the inevitable wear of the dressing diamonds on a microscopic scale adds up to the profile wear of the entire dressing tool. As a consequence, both the accuracy of the profile and the surface roughness of the grinding wheel were affected by the wear of the dressing tool.

Several studies have been conducted to determine the optimal dressing condition for cylindrical grinding, surface grinding, and internal grinding using various optimisation methods [15]. For example, Baseri [16] used a feed-forward back-propagation neural network and a simulated annealing algorithm for the simultaneous minimisation of the tangential grinding force and the surface roughness. The dressing parameters that were considered during the experiments were the dressing speed ratio, dressing depth, and dressing cross-feed. Kalilpourazari and Khalilpourazary [17] proposed a novel meta-heuristic algorithm for optimising the grinding process. Pareto-optimal non-dominated solutions were obtained for the simultaneous optimisation of the surface quality, grinding cost, and total process time. Tran et al. [18] presented the optimisation of the grinding cost to determine the optimal exchanged grinding wheel. The optimal diameter value was determined by minimising the cost function. Tung et al. [1] optimised six dressing parameters, including the dressing feed rate, coarse dressing depth, coarse dressing times, fine dressing depth, fine dressing times, and non-feeding dressing to grind 9CrSi alloy steel to minimise the surface roughness and flatness tolerance using the Taguchi method and a grey relational analysis. The results showed that the coarse dressing depth, the coarse dressing times, the fine dressing depth, the fine dressing times, and the non-feed dressing were significant factors, while the feed rate was not an important factor. In [19,20], the optimal dressing system parameters (radial feed rate of diamond roller dresser, dressing speed ratio, dress-out time, diamond roller dresser grit size/grinding wheel grit size ratio, type of synthetic diamonds, and direction of dressing) were determined using the generalised utility function method. Pareto-optimal solutions were found that guarantee the best combination between the roughness and the deviation from cylindricity of the ground surface; between the grinding wheel lifetime and the manufacturing net costs of the fine grinding operation; and among the lifetime and cutting ability of the abrasive wheels, the tangential cutting force magnitude, and the production rate of the rough grinding process.

The analysis showed that, in recent years, many scholars have conducted a lot of research and exploration on the dressing methods of grinding wheels, which mainly include mechanical dressing, electrical discharge dressing, laser dressing, etc. [21,22]. Diamond grinding wheel dressing techniques have been discussed in detail with respect to their basic working principles and advantages/disadvantages, as well as their suitable applications and machining characteristics [9,23]. These include the grain protrusion of the dressed wheels, dressing forces, dressing tool wear, and so on. It has been established that dressing with diamond roller dressers using the plunge-grinding method ensures the high productivity of the dressing process, combined with a high quality of the machined surfaces [21,24].

Diamond roller dressers (DRs) have a high wear resistance exceeding that of single-crystal dressing tools several times over. The lifetime of DRs depends on a number of factors related to the tool-manufacturing technology and the characteristics of the working diamond layer (type and grain size of the diamond grains, type of bond, concentration and placement of the diamonds in the working layer) [7,21].

Both natural and synthetic diamonds are used in the production of diamond rolls, with an increasing trend towards the use of synthetic diamonds [25,26]. It has been established that, as the strength of the diamonds increases, so does the lifetime of the DR, as a result of which it is recommended to use medium-strength and high-strength synthetic diamonds for the manufacture of diamond rolls. The strength of synthetic diamonds under normal conditions is always greater than that of natural diamonds. However, when heated, the strength of synthetic diamonds decreases sharply, while the strength of natural diamonds remains virtually unchanged [27,28]. The dynamics of change in the strength of synthetic diamonds when heated depends on their grain size and the quantity of impurities they contain [24]. Their sensitivity increases with the size of the grains and the impurities in them. In view of this, synthetic diamonds with a grain size smaller than D601 (630/500) should be used in the manufacture of DRs. On the other hand, the use of synthetic diamonds with a grain size smaller than D107 (100/80) results in a high density of diamond grains in the working layer. As a result, the cutting forces and temperatures increase, the energy costs rise, and the lifetime of the diamond rolls decreases [28,29]. The selection of the appropriate grain size is the key to improving the truing profile accuracy of the grinding wheels. This was confirmed in the study by Wang et al. [30], which showed that a dressing wheel with a grain size of D213 μm successfully reduced the radial run-out error and section arc profile error of the hybrid-bonded arc-shaped diamond wheel to 1.9 μm and 10 μm. When the grain size of the electroplated diamond dressing wheel is too large, the abrasive layer on the surface of the arc-shaped diamond wheel is removed in the form of large pieces of fracture and falling off, and the profile accuracy of the trued arc-shaped diamond grinding wheel will be reduced.

Regardless of the method used to manufacture diamond rolls (powder metallurgy, metallisation filling, electrochemistry), the structure of their diamond-bearing layer can be represented by three schemes: with a relatively uniform distribution of diamond grains in the volume of the diamond-bearing layer; with the tips of the diamond grains oriented along a surface equidistant from the profile of the tool; or with the diamond grains oriented along a surface immediately forming the profile of the dressing tool [28,30].

Unlike multi-crystal dressing tools made of natural diamonds, where a grain size ranging from 0.8 mm to 2.5 mm ensures a good grip and retention in the working layer, the wear resistance of diamond rolls made of synthetic diamonds, whose maximum grain size is smaller than 0.6–0.55 mm, is mainly determined by the ability of the bond to retain the diamond grains and its resistance to abrasive wear [28,31].

In diamond rollers, where the diamond grains are fixed with a less wear-resistant bond, the lifetime of the tool depends on the structure of its working surface. It is mainly characterised by two parameters—the differences in the height and the density of the diamond grains, which must ensure high cutting properties of the tool and prevent contact between the bond and the abrasive, both in a free and fixed state. A possible way to increase the lifetime of diamond dressing rollers made of synthetic diamonds is presented in [31]. Spampinato et al. proposed a new type of rotary diamond dresser, characterised by abrasive features with controlled geometries and spatial arrangements.

By summarising and analysing the accumulated experience in the production of diamond roller dressers from synthetic diamonds, it has been concluded that the electroforming method is the most suitable and effective method that meets the requirements for the accuracy of the shape and dimensions of the dressing tool. The produced diamond rolls have a stable dimensional stability and ensure a high quality of the ground surface. Controlling the density of the diamond grains by applying mixed grain sizes eliminates the main disadvantage of diamond rolls—the low cutting ability of the grinding wheel after dressing. However, there are a number of problems, both in the production of diamond rolls using the electroplating method and in their use for dressing grinding wheels. They are related to a lack of information on the optimal combination of grain sizes of the main and additional fractions when using mixed grain sizes; a lack of recommendations for selecting the grain size of diamond rolls, especially those with a working layer of high-strength synthetic diamonds, depending on the grain size of the grinding wheel being dressed; and a lack of research to determine the optimal dressing conditions that ensure the maximum wear resistance of the diamond roller dressers.

In this regard, and to increase the wear resistance of diamond rollers manufactured using the electroplating method, this article proposes an approach for compacting the intergranular spaces in the working layer of the tools by treating them with diamond grains with a finer grain size than that of the main fraction. This approach was implemented in three stages: (i) the analytical determination of the maximum distance between diamond grains, beyond which contact between the diamond roller bond and the abrasive grains of the grinding disc was observed, leading to intensive wear, depending on the dressing conditions; (ii) theoretical and experimental modelling of the lifetime and wear of diamond rollers made of medium- and high-strength synthetic diamonds with a mixed grain size using a design of experiments and statistical regression; and (iii) multi-objective compromise optimisation, based on a genetic algorithm, for determining the optimal dressing system parameters that ensure the best compromise between the maximum lifetime of the diamond roller dresser, assessed by the number of dressing cycles, and minimal tool wear.

2. Theoretical Research of the Structure of the Working Layer of Diamond Rollers

When manufacturing diamond rollers using the electroforming method, the structure of their working layer is characterised by the orientation of the diamond grains on the surface that directly forms their profile. For the theoretical determination of the maximum distance between diamond grains $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$, beyond which contact is observed between the diamond roller bond and the abrasive grains of the grinding wheel, the scheme of dressing with a diamond roller using the plunge-grinding method with the parallel arrangement of the axes of the diamond roller and the grinding wheel was considered (Figure 1). This achieved both the counter-directional and uni-directional dressing of the grinding wheel. The dressing of the grinding wheel is considered a cutting process, taking into account the analogy between the dressing and grinding processes.

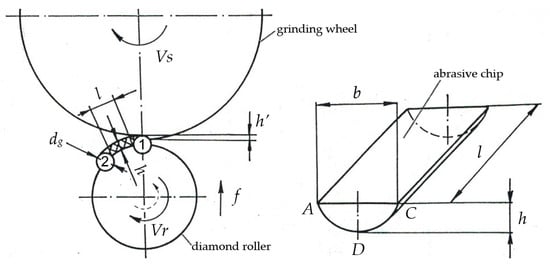
Figure 1. Diagram of the dressing process using a diamond roller dresser by the plunge-grinding method.

An idealised model of the diamond roller dresser was adopted. It was assumed that the diamond grains were spherical in shape and were evenly distributed in the working surface layer of the diamond roller along a circle, with their size being determined by the average reduced diameter $d_g$. The difference in the heights of the diamond grains was practically zero, since the working surface of the diamond roller was treated to form flat areas at the tips of the diamond grains. Diamond grains that were more than half cut after finishing were unusable, as their retention by the bond was compromised.

To prevent contact between the diamond roller connection and the abrasive grains, the volume of chips removed by diamond grain 1 must be smaller than the volume of the area between grains 1 and 2 (Figure 1).

The volume of the chip $W_{\mathrm{c}h} \left({\mathrm{m}\mathrm{m}}^3\right)$, whose shape is shown in Figure 1, is determined depending on the area $S_{\mathrm{c}h}$ $\left({\mathrm{m}\mathrm{m}}^2\right)$ of the cross-section of the chip:

$$W_{\mathrm{c}h}=S_{\mathrm{c}h}.I= 0.5\left({\displaystyle \frac{\pi ·d_g^2}{4}}-b\left({\displaystyle \frac{d_g}{2}}-h\right)\right).l=0.5\left(L{\displaystyle \frac{d_g}{2}}-b\left({\displaystyle \frac{d_g}{2}}-h\right)\right).l,$$

(1)

where $d_g \left(\mathrm{m}\mathrm{m}\right)$ is the average diameter of the diamond grains; $h$ (mm), $l$ (mm), and $b$ (mm) are the abrasive chip dimensions; and $L$ = 2${\displaystyle \frac{d_g}{2}}\mathsf{\Psi }$ $\left(\mathrm{m}\mathrm{m}\right)$ is the arc length $\widehat{ADC}$ of the segment ($\mathsf{\Psi }$—contact angle between the diamond grain and the grinding wheel).

Considering that the magnitude of the contact angle $\mathsf{\Psi }$ tends to zero ($\mathsf{\Psi }=\tan \mathsf{\Psi }={\displaystyle \frac{b}{d_g-2h}}$) and the value $b=2\sqrt{h\left(d_g-h\right)}$, the following correlation for determining the chip volume is obtained:

$$W_{ch}=2lh\sqrt{h\left(d_g-h\right)} {\displaystyle \frac{d_g-h}{d_g-2h}}.$$

(2)

Since the entire area between diamond grains 1 and 2 is filled with abrasive material, including the two side sections with triangular cross-sections, the total volume of the chips is

$$W_{ch}^t=2lh\sqrt{h\left(d_g-h\right)} {\displaystyle \frac{d_g-h}{d_g-2h}}+h^2\left(d_g-h\right)l.$$

(3)

Assuming that the shape of the cut abrasive layer of a single diamond grain is segmented, the average volume $W_m \left({\mathrm{m}\mathrm{m}}^3\right)$ of the maximum possible cut layer is determined by the following correlation:

$$W_m=L_k{S}_m={2L}_{k}h\prime \sqrt{h\prime \left(d_g-h\prime \right)}{\displaystyle \frac{d_g-h^{\prime }}{d_g-2h^{\prime }}}$$

(4)

where $L_k$ (mm) is the length of the contact arc between the diamond grain and the grinding wheel;$S_m$ $\left({\mathrm{m}\mathrm{m}}^2\right)$ is the cross-sectional area of the cut abrasive layer of a single abrasive grain; and $h^{\prime }$ (mm) is the cutting depth of a single diamond grain, which is determined by the following correlation: $h^{\prime }={\displaystyle \frac{h_w}{2}}+f/n_s$ [32,33] ($h_w=\left(0-0.5\right)d_g$—indicator characterising the working surface layer of the diamond roller, which determines the minimum amount of indentation in the grinding wheel when all grains are in operation; $n_s$ (${\mathrm{m}\mathrm{i}\mathrm{n}}^{-1}$)—rotational frequency of the grinding wheel; f (mm/min)—radial feed rate).

When dressing grinding wheels with diamond rolls using the plunge-grinding method, $L_k$ depends on the dressing speed ratio $q_v=V_r/V_s$ ($V_r$ (m/s)—speed of the diamond roll; $V_s$ (m/s)—grinding wheel speed) and the radial feed rate f (mm/min) in accordance with the following correlation [34]:

$$L_k={\displaystyle \frac{{\left(V_s^2 {\left(1\pm q_v\right)}^2+f^2\right)}^{\frac{3}{2}}-{\left(V_s^2{\left(1\pm q_v\right)}^2+f^2-4f{V}_s^2\frac{q_v^2{D}_s+d_r}{D_s{d}_r}{\tau }_g\right)}^{\frac{3}{2}}}{6f{V}_s^2\frac{q_v^2{D}_s+d_r}{D_s{d}_r}}}$$

(5)

where $d_r$ (mm)—diameter of the diamond roller; $D_s$ (mm)—diameter of the grinding wheel; $\pm q_v$—for uni-directional and counter-directional grinding wheel dressing, respectively; and ${\tau }_g=D_s{d}_r/\left(d_{r}f+q_v^2{V}_s^2\left(D_s+d_r\right)\right)-$ working time of the diamond grain for forming the contact arc $L_k$.

After equating Expressions (3) and (4), the distance ${ l}_k$ (mm) between the diamond grains is determined, at which there is no wear on the diamond roller bond under the action of the abrasive grains of the grinding wheel:

$${ l}_k=l={\displaystyle \frac{{2L}_k{h}^{\prime }\sqrt{h^{\prime }\left(d_g-h^{\prime }\right) }\frac{d_g-h^{\prime }}{d_g-2h^{\prime }}}{2h\sqrt{h\left(d_g-h\right)} \frac{d_g-h}{d_g-2h}+h^2\left(d_g-h\right)}}.$$

(6)

The minimum size protrusion of the diamond grains above the bond is ensured by the technological process of manufacturing the diamond roller. In the limiting case, it can be assumed to be equal to the cutting depth of a single diamond grain: $h=h\prime$. Taking into account that the cut abrasive layer is distributed both on the front surface of the diamond grain and on its side surfaces, Equation (6) takes the following form:

$${ l}_{\mathrm{m}\mathrm{a}\mathrm{x}}= {\displaystyle \frac{2}{3}}{\displaystyle \frac{L_k{h}^{\prime }\sqrt{h^{\prime }\left(d_g-h^{\prime }\right)}}{2h^{\prime }\sqrt{h^{\prime }\left(d_g-h^{\prime }\right)} +{h^{\prime }}^2\left(d_g-2h^{\prime }\right)}}.$$

(7)

By applying the single-factor regression analysis method and using the QstatLab (version 6.1.1.3) software product [35], regression models were constructed for the maximum permissible distance $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$ between diamond grains, depending on the radial feed rate, dressing speed ratio, and grain size of the diamond roll (Table 1). The models were constructed based on the theoretically determined values for $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$ in accordance with Equation (7) for diamond rolls with a diameter of $d_r=92 \mathrm{m}\mathrm{m}$ and grain sizes D107 (100/80) and D461 (400/315), grinding wheels with a diameter of $D_s=350 \mathrm{m}\mathrm{m}$, and a grinding wheel speed $V_s=30 \mathrm{m}/\mathrm{s}$. A graphical interpretation of the constructed regression models is shown in Figure 2.

Table 1. Regression models for the maximum permissible distance $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$ between diamond grains.

Grit Size of Synthetic Diamonds	Dressing Method	Radial Feed Rate (mm/min)	Models
D107	Uni-directional	0.2	${ l}_{\mathrm{m}\mathrm{a}\mathrm{x}11}=0.4033-0.384q_v-0.01639q_v^2-0.135q_v^3+0.1551q_v^4$
		1.4	${ l}_{\mathrm{m}\mathrm{a}\mathrm{x}12}=0.4733-1.094q_v+2.063q_v^2-2.452q_v^3+1.016q_v^4$
	Counter-directional	0.2	${ l}_{\mathrm{m}\mathrm{a}\mathrm{x}13}=0.4806+0.008738q_v+0.8233q_v^2-0.7022q_v^3+0.2076q_v^4$
		1.4	${ l}_{\mathrm{m}\mathrm{a}\mathrm{x}14}=0.3928+0.4867q_v-0.2163q_v^2+0.1973q_v^3-0.06057q_v^4$
D426	Uni-directional	0.2	${ l}_{\mathrm{m}\mathrm{a}\mathrm{x}21}=0.421-0.652q_v+0.8081q_v^2-1.092q_v^3+0.5355q_v^4$
		1.4	${\mathrm{l}}_{\mathrm{m}\mathrm{a}\mathrm{x}22}=0.4595-1.07q_v+2.029q_v^2-2.0406q_v^3+0.9942q_v^4$
	Counter-directional	0.2	${ l}_{\mathrm{m}\mathrm{a}\mathrm{x}23}=0.4652+0.01347q_v+0.7742q_v^2-0.6515q_v^3+0.1906q_v^4$
		1.4	${ l}_{\mathrm{m}\mathrm{a}\mathrm{x}24}=0.3839+0.435q_v-0.1182q_v^2+0.1045q_v^3-0.03125q_v^4$

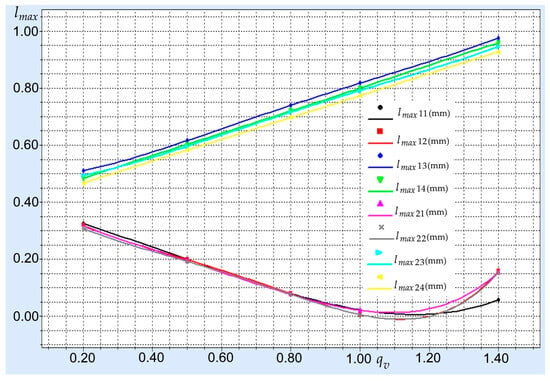
Figure 2. Maximum permissible distance $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$ between diamond grains depending on radial feed rate, dressing speed ratio, and diamond roller grain size.

The analysis of the regression models created for the maximum permissible distance $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$(Table 1) and the graphical dependencies constructed on their basis (Figure 2) showed that $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$ depends mainly on the dressing direction and the dressing speed ratio. Moreover, the theoretically determined values for $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$ are comparable and, under certain dressing conditions, even greater than the size of the diamond grains. This confirms the possibility of the additional saturation of the intergranular spaces with a diamond fraction whose grain size is smaller than that of the main fraction.

The conducted theoretical study shows that, when the grain size of the diamond rollers is greater than or equal to D126 (125/100), the additional saturation of the intergranular spaces is necessary to ensure a higher wear resistance of the tools. Moreover, the greater the difference in grain sizes, the greater the probability of diamond grains falling into the intergranular spaces and creating a working layer with a small difference in the heights of the diamond grains and a high degree of saturation. In accordance with this requirement, the working layer of diamond rollers with a grain size of D461 (400/315) and D251 (250/200) of the main fraction must be additionally saturated with a diamond fraction with a grain size of D107 (100/80).

3. Research and Modelling of the Wear Resistance of Diamond Roller Dressers

3.1. Equipment, Materials, and Methods

The aim of this study was to establish the correlation between the lifetime $T_{ph}$ and the wear ${\delta }_{ph}$ of the diamond rollers created with a working layer of medium- and high-strength synthetic diamonds with a mixed grain size on the one hand (ph—code for the combination “brand of synthetic diamonds, dressing method”—Table 2), and the conditions for the uni-directional and counter-directional dressing of grinding wheels on the other. The dressing speed ratio $q_v$, the radial feed rate f (mm/min), the dress-out time t (s), and the ratio $q_g$ between the grit sizes of the diamond roller dresser and grinding wheel (the grit size ratio) were selected as control factors.

Table 2. Code of the following combination: “brand of the synthetic diamonds, dressing method” [19].

Dressing Method—h	Type of Synthetic Diamonds—p
	AC32 (p = 1)	AC80 (p = 2)
Uni-directional (h = 1)	11	21
Counter-directional (h = 2)	12	22

The experimental studies were conducted on a KUF 250/500 cylindrical grinding machine. A special attachment was created to implement the dressing process with diamond rollers using the plunge-grinding method [34]. It was installed on the grinding saddle of the cylindrical grinding machine (Figure 3). The fixture control system allowed for the implementation of uni-directional and counter-directional dressing, as well as the modification of the control factors (speed ratio $q_v$, radial feed rate f, dress-out time t) within the following limits: $f=0.2-1.4 \mathrm{m}\mathrm{m}/\mathrm{m}\mathrm{i}\mathrm{n}$; $q_v=0.2-0.8$; $t=1-9 \mathrm{s}$. The coolant lubricant used was an emulsion of brand Lubrica Frezol with the following characteristics [36]: kinematic viscosity at 40—22 mm²/s; flash point in closed cup—130 °C; flash point in open cup—170 °C; pour point—(−15) °C; TBN, mgKOH/g—9.0; anti-seizure properties: welding load—2500 N. It was supplied as a free-falling jet through an open nozzle at a consumption rate of approximately 9 l/min. The technical designation of the emulsion used was in accordance with the standard ISO 6743/7 [37]. This is a metalworking fluid that is produced on the basis of a refined low-viscosity base oil and a combination of additives that improve its lubricating, anti-wear, and anti-seizure properties.

Figure 3. Experimental setup; 1—cylindrical grinder KUF 250/500; 2—special attachment; 3—grinding wheel; 4—diamond roller dresser; 5—workpiece [19].

The selected dressing conditions ensured the performance of the diamond rollers and the quality of the machined surfaces of the grinding wheels, which were established in the conducted research and the optimisation of the fine and rough grinding processes, depending on the speed ratio, radial feed rate, dress-out time, and grit size ratio presented in [19,20].

The dressed grinding discs made of electrocorundum, manufactured by the Abrasive Tools Factory—Berkovitsa, Bulgaria [38], had the following dimensions and characteristics: 1-350 × 125 × 22.5 95A80K8V38, 95A60K8V38, 1A46K8V38 (designation according to ISO 525 [39]). They were dressed with diamond rollers with a diameter of 92 mm and manufactured using the electroplating method, with a working layer of medium- and high-strength synthetic diamonds of grades AC32 and AC80 (this designation is in accordance with GOST 9206-80 and DSTU 3292-95 [40,41]) with a grain size of D426, D251, and D107 and an electrodeposited nickel bond (Table 3) [42]. The diamond rollers with grain sizes of D426 and D251 were additionally treated with grain sizes of D251 and D107, respectively, in order to compact the intergranular spaces, reducing the possibility of partial contact between the bond and the abrasive grains. AC32 and AC80 are brands of synthetic diamond grinding powders with different strengths, produced by the V. Bakul Institute for Superhard Materials. The different grain sizes of the diamond rollers and grinding wheels provide values of the control factor of $q_g=1.2-2.56$.

Table 3. Diamond grit properties [40,41,42].

Synthetic Diamonds		Static Compressive Strength (N)	Arithmetic Mean of the Compressive Strength for All Grit Sizes (N)	Micro-Hardness (GPa)	Heat Resistance (°C)
Brand	Grit Size
AC32	D107 (110/80)	18.4	32	86–101	700–900
	D251 (250/200)	23.5
	D426 (400/315)	49.6
AC80	D107 (110/80)	40.0	80
	D251 (250/200)	78.0
	D426 (400/315)	109.0

The lifetime of the diamond rollers $T_{ph}$ was assessed by the number of working cycles performed until reaching the permissible deviation of the grinding wheel profile after dressing ${\Delta }_s=0.02 \mathrm{m}\mathrm{m}$ of the shape of the ground surface $-{\Delta }_w=0.02 \mathrm{m}\mathrm{m}$. The number of working cycles was recorded using a counter included in the control system of the dressing device. The accuracy of the shape of the ground surface was assessed using the complex indicator of deviation from cylindricity, by using a device for measuring the deviation from roundness and cylindricity Roundtest RA-114/116. The grinding conditions were as follows: processed material—hardened steel 150Cr14 with a hardness of 64 HRC in the form of cylindrical blanks with a diameter $d_w=30\hspace{0.33em}\mathrm{m}\mathrm{m}$ and a length $L_w=150\hspace{0.33em}\mathrm{m}\mathrm{m}$; cutting depth—$a_e=0.1\hspace{0.33em}\mathrm{m}\mathrm{m}$; speed ratio—$q=60$; and radial feed—$f_r=0.01\hspace{0.33em}\mathrm{m}\mathrm{m}/\mathrm{s}\mathrm{t}\mathrm{r}$.

The wear of the diamond rollers ${\delta }_{ph}$ (mg/g) was estimated by the relative diamond consumption of the diamond-bearing layer (mg), used to remove a unit weight of abrasive material (g). The change in the weight of the diamond roller was determined using an electronic scale with an accuracy of $\pm 0.001 \mathrm{g}.$ The change in the weight of the grinding disc was determined by considering the volume of the disc before and after the specific test and the specific mass of the electrocorundum.

Based on preliminary experimental studies of the performance of diamond rollers made of AC32 and AC80 synthetic diamonds [19,20] it was assumed that the general form of the model describing the correlation between the target parameters studied (lifetime $T_{ih}$ and wear ${\delta }_{ph}$) and the group of independent variables—the control factors $f$ $\left(X_1\right)$, $q_v$ $\left(X_2\right),$ $t$ $\left(X_3\right)$, and $q_g$ $\left(X_4\right)$—is as follows:

$$Y_w=A_0+{\sum }_{i=1}^k{A}_i{X}_i+{\sum }_{i=1}^k{A}_{ii}{X}_i^2+{\sum }_{\begin{array}{c}i=1\\ i<j\end{array}}^k{A}_{ij}{X}_i{X}_j+{\sum }_{\begin{array}{c}i=1\\ i<j<l\end{array}}^k{A}_{ijl}{X}_i{X}_j{X}_l,$$

(8)

where Y₁ = $T_{ph}$ and Y₂ = ${\delta }_{ph}$.

To build the regression models (8), an optimal central composite design with $N=2^k+2.k+1=25$ trials was applied (k = 4—number of control factors, whose levels in coded and natural form are presented in Table 4). The models for the lifetime $T_{ph}$ and wear ${\delta }_{ph}$ of the diamond roller dresser made of AC32 and AC80 synthetic diamonds were created based on actual measured values of the target parameters during uni-directional and counter-directional dressing. The statistical processing of the experimental results was performed by applying a multifactorial regression analysis using the QstatLab software product [35], and included determining the regression coefficients of Model (8), testing their significance using Student’s t-test, and verifying the adequacy of the regression model by calculating the coefficient of determination and verifying its significance using Fisher’s F-test.

Table 4. Factor levels in the design of experiments.

Factors		Factor Levels
		−1	0	+1
X1	f (mm/min)	0.2	0.8	1.4
X2	$q_v$	0.2	0.5	0.8
X3	t (s)	1	5	9
X4	$q_g$	1.2	1.88	1.56

3.2. Results and Modelling

3.2.1. Experimental Results

The plans for the experiments with the values of the response variables studied (lifetime $T_{ph}$ and wear ${\delta }_{ph}$ of diamond rollers with a working layer of AC32 and AC80 synthetic diamonds) during the uni-directional and counter-directional dressing of grinding wheels are presented in Table 5.

Table 5. Design of the experiments and response variables of the dressing process.

Control Factors				Response Variables
				Number of Dressing Cycles				Wear of Diamond Roller Dresser
$\mathit{f}$	${\mathit{q}}_{\mathit{v}}$	t	${\mathit{q}}_{\mathit{g}}$	${\mathit{T}}_{11}$	${\mathit{T}}_{21}$	${\mathit{T}}_{12}$	${\mathit{T}}_{22}$	${\mathit{\delta }}_{11}$	${\mathit{\delta }}_{21}$	${\mathit{\delta }}_{12}$	${\mathit{\delta }}_{22}$
(mm/min)		(s)						(mg/g)	(mg/g)	(mg/g)	(mg/g)
0.2	0.2	1	1.2	60,452	66,769	69,369	83,944	0.171	0.124	0.172	0.108
1.4	0.2	1	1.2	45,465	50,691	53,750	63,895	0.343	0.249	0.315	0.237
0.2	0.8	1	1.2	14,542	17,158	80,797	102,897	0.793	0.649	0.145	0.083
1.4	0.8	1	1.2	9382	10,638	62,611	78,331	1.142	0.852	0.265	0.182
0.2	0.2	9	1.2	45,338	55,587	56,608	68,865	0.224	0.179	0.221	0.140
1.4	0.2	9	1.2	34,098	42,201	43,866	52,423	0.450	0.361	0.405	0.304
0.2	0.8	9	1.2	10,906	14,284	65,940	84,415	1.042	0.941	0.187	0.107
1.4	0.8	9	1.2	7037	8856	51,098	64,260	1.499	1.235	0.342	0.234
0.2	0.2	1	2.56	514,371	772,896	577,290	764,900	0.011	0.009	0.009	0.008
1.4	0.2	1	2.56	386,853	586,777	447,352	582,276	0.016	0.013	0.012	0.0097
0.2	0.8	1	2.56	84,339	138,566	672,461	937,620	0.114	0.076	0.007	0.006
1.4	0.8	1	2.56	54,421	85,914	521,101	713,759	0.230	0.153	0.010	0.0074
0.2	0.2	9	2.56	385,771	644,555	426,599	627,501	0.013	0.011	0.011	0.0098
1.4	0.2	9	2.56	290,135	488,503	330,546	477,682	0.025	0.021	0.015	0.012
0.2	0.8	9	2.56	63,253	115,359	496,878	769,195	0.150	0.110	0.009	0.0075
1.4	0.8	9	2.56	40,815	71,525	385,039	585,546	0.302	0.220	0.013	0.0096
0.2	0.5	5	1.88	138,435	234,139	222,254	307,634	0.102	0.119	0.031	0.023
1.4	0.5	5	1.88	113,714	192,532	172,222	234,186	0.261	0.196	0.048	0.036
0.8	0.2	5	1.88	186,137	316,744	167,549	221,405	0.055	0.042	0.048	0.038
0.8	0.8	5	1.88	36,427	61,796	195,168	271,400	0.559	0.448	0.040	0.029
0.8	0.5	1	1.88	154,790	261,307	224,554	292,834	0.183	0.129	0.035	0.027
0.8	0.5	9	1.88	112,092	190,694	172,779	240,230	0.240	0.188	0.045	0.034
0.8	0.5	5	1.2	21,501	35,765	55,130	68,398	0.790	0.653	0.284	0.191
0.8	0.5	5	2.56	195,774	331,099	426,624	623,219	0.192	0.157	0.011	0.0091
0.8	0.5	5	1.88	136,379	231,845	185,328	253,298	0.223	0.210	0.042	0.032

3.2.2. Statistical Modelling

After the statistical analysis of the experimental results using a regression analysis and the QstatLab software product [35], theoretical–experimental models were developed for the lifetime and the wear of AC32 and AC80 diamond rolls during the uni-directional and counter-directional dressing of the studied wheels (Table 6 and Table 7).

Table 6. Theoretical–experimental models for the lifetime of diamond roller dresser and statistical characteristics of the models.

Models	Student Criterion	Fisher Criterion		Determination Coefficient
		Calculated	Tabular
	${\mathit{t}}_{\mathit{\alpha }/2,\mathit{\nu }}$	$\widehat{\mathit{F}}$	${\mathit{F}}_{\mathit{\alpha },{\mathit{\nu }}_1,{\mathit{\nu }}_2}$	${\widehat{\mathit{R}}}^2$	${\mathit{R}}_{\mathit{p}\mathit{r}\mathit{e}\mathit{d}}^2$
$$\begin{gathered} T_{11}=-399445.65+38127.185f+426624.24q_v+ \\ 422735.84q_g+848.52844t^2-56692.811f{q}_g\hspace{0.33em}- \\ 8425.2189q_{v}t-10120.256t{q}_g-449870.45q_v{q}_g+ \\ 39778.392f{q}_v{q}_g+10642.88q_{v}t{q}_g \end{gathered}$$	2.1448	241.0093	2.6022	0.9942	0.9799
$$\begin{gathered} T_{21}=-801593.15+66099.332f+641107.02q_v+ \\ 833281.48q_g+642.69055t^2-48479.581q_g^2- \\ 665208.62q_v{q}_g\hspace{0.33em}-9283.7974t{q}_g- \\ 89085.693f{q}_g+56466.423f{q}_v{q}_g+6540.4907q_{v}t{q}_g \end{gathered}$$	2.1448	323.6017	2.6022	0.9926	0.9926
$$\begin{gathered} T_{12}=-54725.783-76080.101q_v+45013.304f^2 \\ +1367.105t^2+102194.94q_g^2\hspace{0.33em} \\ -12300.354t{q}_g-67767.101f{q}_g \\ +75748.281q_v{q}_g \end{gathered}$$	2.1098	688.7448	2.6143	0.9950	0.9925
$$\begin{gathered} T_{22}=119945.97-160888.21q_v+235769.31q_g \\ +63692.163f^2+1099.0426t^2 \\ +195444.45q_g^2\hspace{0.33em}-10688.828t{q}_g \\ -98542.366f{q}_g+151037.07q_v{q}_g \end{gathered}$$	2.11991	903.4419	2.5911	0.9967	0.9945

Table 7. Theoretical–experimental models for the wear of diamond roller dressers and statistical characteristics of the models.

Models	Student Criterion	Fisher Criterion		Determination Coefficient
		Calculated	Tabular
	${\mathit{t}}_{\mathit{\alpha }/2,\mathit{\nu }}$	$\widehat{\mathit{F}}$	${\mathit{F}}_{\mathit{\alpha },{\mathit{\nu }}_1,{\mathit{\nu }}_2}$	${\widehat{\mathit{R}}}^2$	${\mathit{R}}_{\mathit{p}\mathit{r}\mathit{e}\mathit{d}}^2$
$$\begin{gathered} {\delta }_{11}=1.38426+0.64786f+1.18197q_v+0.02871t \\ -1.82241q_g-0.21563f^2\hspace{0.33em}+0.53192q_v^2 \\ +0.00298t^2+0.50146q_g^2+0.22882f{q}_v \\ +0.08269q_{v}t-0.6387q_v{q}_g-0.02894q_{v}t{q}_g \\ -0.14078f{q}_g \end{gathered}$$	2.2010	373.5344	2.7614	0.9951	0.9863
$$\begin{gathered} {\delta }_{21}=1.134497+0.43501f+1.06233q_v+0.02889t \\ -1.5033194q_g-0.15534f^2\hspace{0.33em}+0.35088q_v^2 \\ +0.00343t^2+0.41431q_g^2+0.12604f{q}_v \\ +0.09353q_{v}t+0.00487ft-0.09237f{q}_g \\ -0.52631q_v{q}_g-0.03316q_v{tq}_g \end{gathered}$$	2.2281	489.5465	2.8647	0.9965	0.9908
$$\begin{gathered} {\delta }_{12}=0.93197+0.22794f+0.01457t-0.92312q_g \\ -0.12225q_v^2+0.21738q_g^2\hspace{0.33em}-0.005698t{q}_g \\ -0.09007f{q}_g+0.04678q_v{q}_g \end{gathered}$$	2.1199	2.5911	202.9674	0.9854	0.9785
$$\begin{gathered} {\delta }_{22}=0.57285+0.1762f-0.55823q_g+0.13239q_g^2\hspace{0.33em}- \\ 0.14201f{q}_v+0.01013ft-0.08619f{q}_g+ \\ 0.05489f{q}_v{q}_g-0.00393ft{q}_g \end{gathered}$$	2.1199	2.5911	151.1764	0.9804	0.9741

They included only the significant regression coefficients determined in accordance with the condition $\widehat{t}>t_{\alpha /2,\nu }$, where $\widehat{t}$ and $t_{\alpha /2,\nu }$ are the empirical and tabulated values of Student’s t-criterion for each of the regression coefficients (α = 0.05—significance level; ν = N − n—degrees of freedom; N—number of trials; n—number of coefficients in the model), presented for each model in Table 6 and Table 7.

The models presented were adequate, since the condition $\widehat{F}>F_{\alpha ,{\nu }_1,{\nu }_2}$ was fulfilled with a 95% confidence probability. The empirical $\widehat{F}$ and tabulated $F_{\alpha ,{\nu }_1,{\nu }_2}$ values of Fisher’s criterion (α = 0.05; ν₁ = n − 1 and ν₂ = N − n—degrees of freedom) for each of the regression models are presented in Table 6 and Table 7.

The theoretical–experimental models describe, with a high accuracy, the dependencies between the studied response variables and the controlling factors. The values of the coefficients of determination were ${\widehat{R}}^2=0.9804-0.9967$ (Table 6 and Table 7).

The coefficients included in the models ensured the minimisation of the residue values ($Y_w$−$\widehat{Y_w}$) ($Y_w$ and $\widehat{Y_w}$ were respectively experimentally measured and determined by models (Table 6 and Table 7)) of the lifetime $T_{ph}$ and the wear ${\delta }_{ph}$ of the diamond roller. A careful analysis of the residuals using a graphical method allowed for an assessment of the adequacy of the models (Figure 4 and Figure 5).

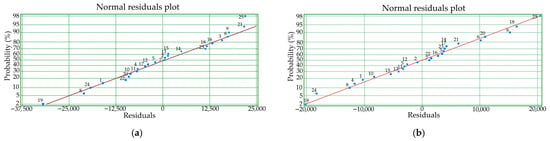
Figure 4. Normal residuals plot for the lifetime of diamond roller dressers made of AC80 (a) and AC32 (b) synthetic diamonds during the uni-directional dressing of the grinding wheel.

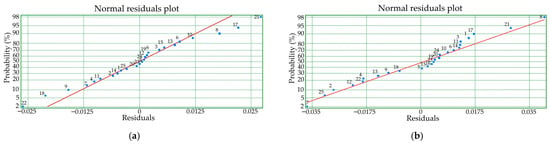
Figure 5. Normal residuals plot for the wear of diamond roller dressers made of AC80 (a) and AC32 (b) synthetic diamonds during the uni-directional dressing of the grinding wheel.

To assess the ability of the constructed regression models to predict responses to new, unseen observations, the predicted R-squared ${(R}_{pred}^2$) values were determined for each of the models (Table 6 and Table 7). A high predicted $R_{pred}^2$ (from 0.9741 to 0.9945) indicated a good ability of all the created models to predict new, unseen data.

Graphical interpretations of the constructed regression models (Table 6 and Table 7) for the lifetime and wear of the studied diamond rollers under the conditions of uni-directional and counter-directional dressing are shown in Figure 6 and Figure 7. To assess the degree of influence of the controlling factors (dressing speed ratio $q_v$, radial feed rate f, dress-out time t, and grit size ratio $q_g$) on the studied response variables during uni-directional and counter-directional dressing with AC32 and AC80 diamond rollers, an analysis of variance (ANOVA) was performed using the QStatLab software product. The ANOVA main effects plot for the studied response variables is presented in Figure 8 and Figure 9.

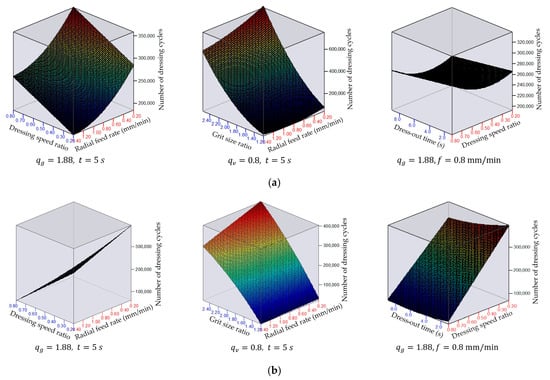
Figure 6. Lifetime of diamond roller dresser made of AC80 synthetic diamonds: (a) counter-directional dressing and (b) uni-directional dressing of grinding wheel.

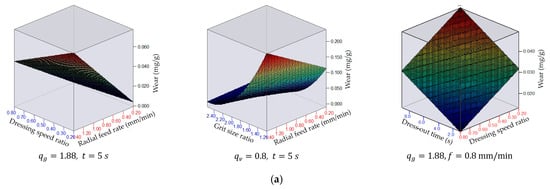
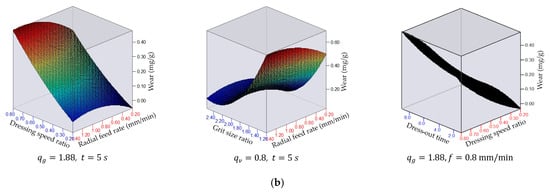
Figure 7. Wear of diamond roller dresser made of AC80 synthetic diamonds: (a) counter-directional dressing and (b) uni-directional dressing of grinding wheel.

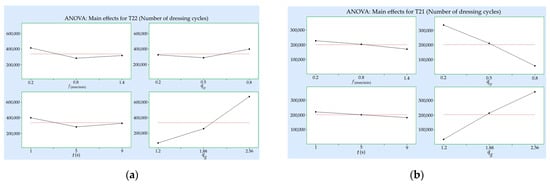
Figure 8. Main effects plot for the diamond roller dresser lifetime: (a) counter-directional dressing and (b) uni-directional dressing.

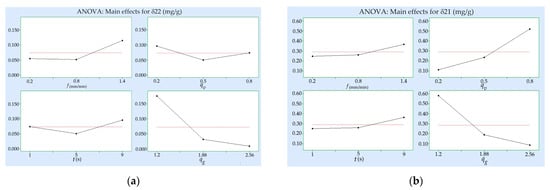
Figure 9. Main effects plot for the diamond roller dresser wear: (a) counter-directional dressing and (b) uni-directional dressing.

3.2.3. Analysis of the Experimental Results

The analysis of the theoretical–experimental models created (Table 6 and Table 7) and the graphical dependencies constructed (Figure 6 and Figure 7), as well as the results of the ANOVA (Figure 8 and Figure 9), showed the following:

• Of all the factors studied, the grit size ratio had the greatest influence on the lifetime and the wear of diamond rollers; as the $q_g$ increased, the lifetime increased from 5.8 to 11.6 times, and the wear decreased from 5 to 26 times. This trend remained the same for both uni-directional and counter-directional dressing with AC32 and AC80 DRs. The influence of $q_g$ on the lifetime of dressing tools was more pronounced for uni-directional dressing with diamond rollers made of high-strength synthetic diamonds, and increased with a decreasing dressing speed ratio. The wear of the diamond rollers, depending on the grit size ratio, changed most significantly during counter-directional dressing with AC32 DRs. The influence of the grit size ratio on the wear increased with an increasing radial feed rate during counter-directional dressing and with a decreasing dressing speed ratio during uni-directional dressing. The increase in the lifetime and decrease in the wear of the DRs, depending on the $q_g$, were related to the reduction in the normal $F_p$ and tangential $F_c$ forces during dressing [19,20]. At a constant grain size of the grinding wheel, an increase in $q_g$ led to a decrease in the number of simultaneously cutting diamond grains. As a result, although the force acting on individual diamond grains during dressing with a coarser diamond roller increased, the total cutting force decreased. The dressing forces were significantly lower than those in grinding and were within the following ranges: $F_p=(5 - 80) \mathrm{N}$ and $F_c=\left(2 - 20\right) \mathrm{N}$ [43].
• The dressing conditions had a varying nature and degree of influence on the lifetime and wear of diamond rollers, which depended on the direction of dressing and the type of synthetic diamonds in the working layer of the diamond rollers. This was related to the change in force and heat load. The greatest influence was exerted by the dressing speed ratio, followed by the radial feed and the dress-out time.
• When dressing in the uni-direction, an increase in $q_v$ led to increased wear and a corresponding decrease in the lifetime of the DR, while when dressing in the counter-direction, these trends were reversed. This was related to the nature of the change in the length of the contact arc between the dressing and the dressed tools, the number of diamond grains simultaneously participating in the cutting, and the total cutting force [44,45]—they decreased with an increase in the dressing speed ratio during counter-directional dressing and increased during uni-directional dressing. Malkin and Murray [44] found that the components of the dressing force reached their maximum (approximately 14–16 N/mm) during uni-directional dressing when the dressing speed ratio was at unity, while during counter-directional dressing with $q_v=-0.4$, the normal force was minimal (approximately 3–8 N/mm). As a result, for uni-directional dressing with an increase in the $q_v$, in the studied range, the lifetime of diamond rollers decreased by up to 7 times and the wear increased by up to 14 times, while for counter-directional dressing, an increase in the $q_v$ led to a maximum increase in the lifetime of the DR by 22% and a maximum decrease in the wear by 25%. The effect of $q_v$ was more pronounced for uni-directional dressing with diamond rollers made of AC32 synthetic diamonds, and increased with an increase in the radial feed rate and the grit size ratio.
• An increase in the radial feed rate led to a decrease in the lifetime of the diamond rollers by up to 38% and an increase in the wear by 2.2 times. This change in the studied parameters was related to an increase in the normal and tangential forces during dressing as a result of the increase in the cross-sectional area of the cut abrasive layer per revolution of the DR. At the same time, however, the specific dressing energy decreased when increasing the feed rate (from 15 J/mm³ to 2.5 J/mm³ at $q_v=0.9$ and from 2 J/m³ to 0.5 J/m³ at $q_v=-0.4$) [44,45]. In this regard, the effect of the radial feed rate on the lifetime of the DR was more pronounced for uni-directional dressing with AC80 diamond rollers and increased with an increasing dressing speed ratio. The effect of the feed rate on the wear increased with a decreasing grit size ratio and was most pronounced for counter-directional dressing with AC80 DRs.
• With an increase in the dress-out time in the studied range, the lifetime of the diamond rollers decreased by a maximum of 26%, with the greatest impact on uni-directional dressing with AC32 synthetic diamond rollers. Increasing the dress-out time led to an increase in the wear by 23% to 61% and was most pronounced for uni-directional dressing with AC 32 and AC80 DRs with a high radial feed rate and dressing speed ratio values. This nature of change in the studied parameters was related to the greater friction forces arising between the DR and the grinding wheel during dressing with levelling.
• The lifetime of diamond rollers for counter-directional dressing was greater (up to 9.5 times) than the lifetime for uni-directional dressing, which was associated with less wear (up to 23 times) on the tools. This was due to the smaller number of simultaneously cutting diamond grains in the contact zone of the DR with the grinding wheel and the lower total cutting force. The difference in the lifetime and the wear of the DR was greater when dressing with diamond rollers made of AC32 synthetic diamonds, and increased with an increase in the grit size ratio, the dressing speed ratio, and the radial feed rate.
• At a grit size ratio $q_g>1$, the lifetime of the diamond rollers made of high-strength synthetic diamonds was greater (up to 82%) than that of diamond rollers made of medium-strength diamond structures, and their wear was less (up to 27%). The difference in the lifetime and the wear was greater during uni-directional dressing and increased with an increasing dress-out time and an increasing grit size ratio.

4. Multi-Objective Optimisation of the Dressing System Parameters

In order to increase the wear resistance of the diamond roller dressers with a working layer of AC32 and AC80 synthetic diamonds and a mixed grain size, multi-objective compromise optimisation was performed to determine the optimal dressing conditions that provide the best balance between the maximum lifetime and minimum wear of the dressing tool. The concept of Pareto efficiency was applied.

Solving the optimisation problem is reduced to determining the combinations of the dressing method, dressing conditions (radial feed rate $f^{*}$, dressing speed ratio $q_v^{*}$, dress-out time $t^{*}$), synthetic diamond grade, and grit size ratio $q_g^{*}$, for which the following conditions are met:

$$\left|\begin{array}{c}{T}_{ph}\left(f^{*},q_v^{*},t^{*},q_g^{*}\right)=T_{{ph}_{\mathrm{m}\mathrm{a}\mathrm{x}}}>T_{ph}\left(f,\hspace{0.33em}{q}_v, t,q_g\right)\\ {\delta }_{ph}\left(f^{*},q_v^{*},t^{*},q_g^{*}\right)={\delta }_{{ph}_{\mathrm{m}\mathrm{i}\mathrm{n}}}<{\delta }_{ph}\left(f,\hspace{0.33em}{q}_v, t,q_g\right)\\ 0.2\mathrm{mm}/\min \le f\le 1.4 \mathrm{mm}/\min \\ 0.2\le q_v\le 0.8\\ 1 s\le t\le 9 s\\ 1.2\le q_g\le 2.56\end{array}\right.,$$

(9)

where $T_{ph}\left(f,\hspace{0.33em}{q}_v, t,q_g\right)$ and ${\delta }_{ph}\left(f,\hspace{0.33em}{q}_v, t,q_g\right)$ are determined in accordance with the developed models for the lifetime and wear of AC32 and AC80 during uni-directional and counter-directional dressing (Table 6 and Table 7).

By applying the NSGA-II genetic algorithm and using the QstatLab software product [35], the Pareto-optimal solutions were determined for the two objective functions—the lifetime and wear of the diamond rollers—the maximum and minimum of which were at different points in the researched factor space (Figure 10 and Figure 11). The NSGA-II parameters used in multi-objective optimisation were the following: population size—50; number of iterations—2500; number of generations—50; mutation probability—0.9; crossover probability—0.9; convergence criteria: mutation distribution—100; and crossover distribution—10.

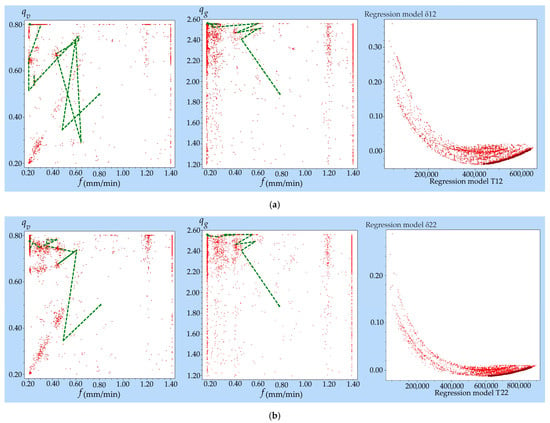
Figure 10. Optimal dressing system parameters during counter-directional dressing with AC32 (a) and AC80 (b) DRs.

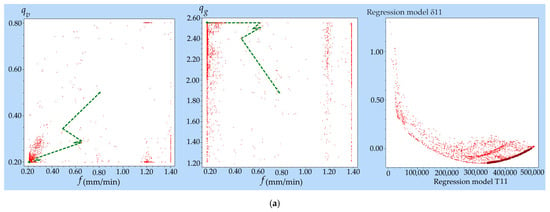
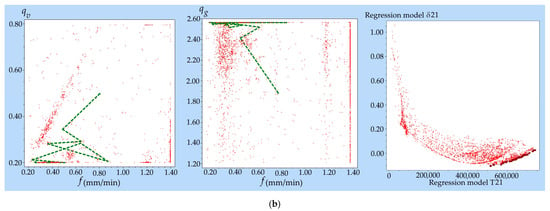
Figure 11. Optimal dressing system parameters during uni-directional dressing with AC32 (a) and AC80 (b) DRs.

From the found Pareto-optimal areas, the best compromise solutions for the control factors ($f^{*}$, $q_v^{*}$, $t^{*}, q_g^{*}$) were selected for uni-directional and counter-directional dressing with AC 32 and AC80 (Table 8).

Table 8. Pareto-optimal solutions for the dressing system parameters.

Synthetic Diamonds	Dressing Method	Control Factors				Number of Dressing Cycles		Wear of Diamond Roller Dresser
		${\mathit{f}}^{\mathit{*}}$ (mm/min)	${\mathit{q}}_{\mathit{v}}^{\mathit{*}}$	${\mathit{t}}^{\mathit{*}}$ (s)	${\mathit{q}}_{\mathit{g}}^{\mathit{*}}$	${\mathit{T}}_{\mathit{p}\mathit{h}}$		${\mathsf{\delta }}_{\mathit{p}\mathit{h}}(\mathbf{m}\mathbf{g}/\mathbf{g})$
						PV	EV	PV	EV
AC32	Uni-directional	0.2	0.2	1.0	2.56	499,073	514,371	0.0213	0.021
	Counter-directional	0.2094	0.8	1.0087	2.56	644,445	672,200	0.0104	0.01
AC80	Uni-directional	0.2541	0.2002	1.0	2.56	740,401	762,690	0.0253	0.026
	Counter-directional	0.2002	0.7733	1.0599	2.56	894,208	925,605	0.0104	0.01

EV—experimental value; PV—predicted value.

Confirmation run experiments were conducted to validate the results for the predicted dressing system parameters. The experimental values determined for the number of dressing cycles and for the wear of the diamond rollers for each combination of control factors ($f^{*}$, $q_v^{*}$, $t^{*}, q_g^{*}$) for uni-directional and counter-directional dressing with AC32 and AC80 diamond rollers are presented in Table 8. The comparison between the experimental values and those determined by the models in Table 6 and Table 7 showed that the error percentage was within the acceptable limits (≤5%) and was as follows: 2.97% to 4.12% for the lifetime of the diamond rollers; 1.4% to 3.8% for the wear of the diamond rollers. These results prove that the recommended dressing system parameters are optimal and correct.

5. Conclusions

As a result of the theoretical and experimental studies conducted, the modelling, and the multi-objective compromise optimisation—which aimed to increase the wear resistance of synthetic diamond roller dressers—the following results were achieved:

• An approach was proposed for increasing the wear resistance of synthetic diamond rollers manufactured using the electroplating method by additionally treating the intergranular spaces of the diamond grains finer than those of the main fraction. For its application, analytical dependencies were derived for the maximum distance between the diamond grains; when this was exceeded, intensive wear of the diamond roller dresser bond was observed as a result of its contact with the abrasive grains of the grinding wheels. A ratio between the grain sizes of the main and additional diamond fractions is recommended depending on the dressing conditions.
• Diamond roller dressers with a working layer of synthetic diamonds of a medium and high strength and mixed grain sizes were created, and their lifetime and wear were studied during the dressing of electrocorundum grinding wheels using the plunge-grinding method. Theoretical–experimental models were constructed for the studied response variables, depending on the dressing direction, radial feed rate, dressing speed ratio, dressing out-time, and grit size ratio. The models were constructed using the planned experimental approach and the method of a multifactor regression analysis.
• Based on the analysis of the developed theoretical and experimental models and through the application of an ANOVA, the significant effect of the working conditions of the dressing process on the wear resistance of diamond rollers with a working layer of synthetic diamonds was demonstrated. It was proven that the grit size ratio has the greatest effect on the lifetime and wear of diamond rollers, with an increase in $q_g$ increasing the lifetime by up to 11.6 times and reducing the wear by up to 26 times as a result of the decrease in normal and tangential forces during dressing.
• Through multi-objective compromise optimisation and the application of a genetic algorithm, the Pareto-optimal dressing system parameters were determined, valid for uni-directional and counter-directional dressing with diamond rollers made of medium- and high-strength synthetic diamonds, as follows: radial feed rate $f^{*}=0.2036 \mathrm{m}\mathrm{m}/\mathrm{m}\mathrm{i}\mathrm{n}$; dressing speed ratio $q_v^{*}=0.4052$; dress-out time $t^{*}=1.2 \mathrm{s}$; and grit size ratio $q_g^{*}=2.54$. They provide the best combination between the maximum lifetime ($T\ge 351,021$ dressing cycles) and minimum wear ($\delta \le 0.0182 \mathrm{m}\mathrm{g}/\mathrm{g}$) of the tested diamond roller dressers.

The theoretical and experimental results obtained confirm the validity and correctness of the proposed approach for increasing the wear resistance of diamond roller dressers made of synthetic diamonds using the electroplating method, and they prove the good combination of the grain sizes of the main and additional diamond fractions. They also show that increasing the wear resistance of diamond rollers is directly related to the selection of optimal working conditions, tailored to the specifics of the given process, and they provide opportunities for the effective control of the dressing process in all machine-building companies.