Stefan Blowing Impacts on Unsteady MHD Flow of Nanofluid over a Stretching Sheet with Electric Field, Thermal Radiation and Activation Energy

Abstract

In this paper, a mathematical model is established to examine the impacts of Stefan blowing on the unsteady magnetohydrodynamic (MHD) flow of an electrically conducting nanofluid over a stretching sheet in the existence of thermal radiation, Arrhenius activation energy and chemical reaction. It is proposed to use the Buongiorno nanofluid model to synchronize the effects of magnetic and electric fields on the velocity and temperature fields to enhance the thermal conductivity. We utilized suitable transformation to simplify the governing partial differential equation (PDEs) into a set of nonlinear ordinary differential equations (ODEs). The obtained equations were solved numerically with the help of the Runge–Kutta 4th order using the shooting technique in a MATLAB environment. The impact of the developing flow parameters on the flow characteristics is analyzed appropriately through graphs and tables. The velocity, temperature, and nanoparticle concentration profiles decrease for various values of involved parameters, such as hydrodynamic slip, thermal slip and solutal slip. The nanoparticle concentration profile declines in the manifestation of the chemical reaction rate, whereas a reverse demeanor is noted for the activation energy. The validation was conducted using earlier works published in the literature, and the results were found to be incredibly consistent.

1. Introduction

Nanofluids contain suspended nanoparticles with a size less than a hundred nm, which are used for improving thermal conductivity. The nanofluids have wide applications in the fields of coolants [1], reactors [2], bubble absorption technologies [3], pharmaceutical processes [4], refrigerator chiller systems [5], aggregate manufacturers [6], heat exchangers [7] and solar collectors [8]. Nowadays, nanofluids are developed for medical applications in treating brain tumors, heart surgery, cancer therapy and safe surgery by cooling. Masuda et al. [9] performed spearheading research on ultrafine scattered particles that were steadily suspended in a base fluid. Afterward, Choi et al. [10] named the mixture suspension of the ultrafine particles in the base fluid as nanofluids. The work of nanofluids in the scope of the boundary layer was started by Buongiorno [11], who emphasized the mechanisms of Brownian diffusion, which afterward was known as the Buongiorno model. The main component of nanofluids is its ability to improve the heat transfer apparatus’ efficiency, as recorded by Phillpot et al. [12]. Khairul et al. [13] examined the results regarding the magnificent thermal assets of the nanofluids. Numerous noteworthy works have investigated the nanofluid boundary layer flow. Bagh et al. [14] examined the significance of nanoparticles on the dynamics of the boundary layer rotating flow and found that Brownian motion is responsible for enhancing the heat transfer of the base fluid. Bagherzadeh et al. [15] studied the dispersion of nanoparticles and boundary layer flow in a microchannel subject to magnetic field. Ali et al. [16] conducted an analysis of the magnetic dipole influence on single and multi-wall carbon nanotubes to examine the dynamics of the micropolar boundary layer flow. Irfan et al. [17] discussed the result of activation energy and binary chemical reaction on the dual nature structure of the time-dependent flow of Carreau magnetite nanofluid over stretching /shrinking sheet. He demonstrated that Brownian motion and the thermophoresis of nanoparticles both escalate with the growing values in the lower solution over the temperature distribution. On the other hand, they show the opposite behavior in the upper solution. Maleki et al. [18] studied the Brownian motion impacts on the transportation of heat. Pordanjani et al. [19] discussed the thermal radiation and Brownian motion inside a cavity using nanoparticles. Kashif et al. [20] studied the significance of radiation and Soret on hybrid-based nanoparticles along the upright channel flow.

The past examinations neglected the electrically conducting character of the liquid. A lot of liquids mixed with salts transfer electrical charges. The Swedish physicist Hannes Alfven (1942) discovered the new field of physics, magnetohydrodynamics (MHD). Nowadays, MHD is a noteworthy nuclear designing scheme. Similarly, with the imposition of a magnetic field, it is possible to deal with the heat transfer rates in waterways, tubes, etc., adequately. The driving force of MHD is essentially the electromagnetic force, which can also be used to energize the transport of charged particles [21]. Magnetohydrodynamic flow with all its characteristics is still complex in the field of atomic coolant pumping [22] and tokamak liquid metal structures [23]. Maleki et al. [24] analyzed the influence of the slip condition on the heat transfer and dynamics of nanofluids over a porous plate. Gireesha et al. [25] conducted an analysis of the magnetohydrodynamic boundary layer flow and the heat transfer of nanofluids over a flat stretching sheet. Several numerical studies have been reported to predict the characteristics of magnetized fluids, such as MHD mixed convection flows [26], MHD non-Newtonian fluid flows [27], MHD impact on nanofluid flows [28] and the magnetic dipole effects on micropolar fluid flows [29,30].

The characteristic of activation energy is the minimum energy required to begin a specific chemical reaction. Generally, the relationship between a chemical reaction and mass transfer is complicated. It can be checked by the digestion of reactant species and fabrication at different rates in the mass transfer process and liquid flow. Arrhenius et al. [31] proposed the use of species chemical reactions along with arrhenius activation energy for the first time ever. He said that the threshold energy is required to make the molecules or atoms in the chemical system work to initiate a chemical reaction. The value of activation energy also imposes a great influence on nanoparticles’ movement in basic carrier fluids. Recently, valuable works have been targeting the activation energy effects on nanofluids. A binary chemical reaction and activation energy effects on the dynamics of the tangent hyperbolic nanofluid flow is considered by Ali et al. [32]; the Eyring-Powell nanofluid subjected to activation energy is studied by Reddy et al. [33]; the chemical reaction and thermodiffusion effects on Casson nanofluid dynamics is analyzed by Faraz et al. [34]; and the Maxwell nanofluid along with activation energy is examined by Ali et al. [35].

Far-field and wall conditions are significant in the problem of the convective transport of nanofluids. Fang and Jing [36] investigated the impacts of the Stefan blowing on species transfer in the transport of nanofluids, and then Fang [37] further extended Ref. [36] to the time-dependent analysis. It was found that the blowing of nanoparticles results in the enhancement of the blowing velocity and mass gradient. Hamid et al. [38] mentioned the potential application of Stefan blowing in the paper drying processes and studied the impacts of Stefan blowing on the mass transfer near the stagnation surface. Lund et al. [39] analyzed the significance of the Stefan blowing in the dynamics of Casson nanofluids subject to a stretching sheet. The species transfer was found to fluctuate over the flow field affected by the mass blowing at the wall. Uddin et al. [40] took the Stefan blowing into consideration and investigated the effects of multiple-slip by using the MATLAB nonlinear equation solver fsolve and ODE solver ode15s.

The above literature review suggests the Stefan blowing effects are of practical significance in various settings. Motivated by this fact, we intend to investigate the Stefan blowing effects on the unsteady magnetohydrodynamic flow of nanofluid over a stretching surface under the joint action of the electric field, activation energy and thermal radiation. The investigated problem has a configuration similar to the work of Daniel et al. [41], but Daniel et al. did not consider the Stefan blowing effects, activation energy and chemical reaction in their investigation. We used the appropriate similarities transformation to change the system of nonlinear governing equations to a system of nonlinear ordinary differential equations (ODEs). We also solved the nonlinear ODEs numerically with the Runge–Kutta 4th order with the shooting technique. The influences of the inserted parameters on the local Nusselt number $-{\theta }^{\prime }\left(0\right)$, skin friction $-f^{″}\left(0\right)$ and Sherwood numbers $-{\varphi }^{\prime }\left(0\right)$ are differentiable with the help of numerical solutions attained by the Runge–Kutta shooting technique. Some of the applications in industrial use of the current study have been found in paper manufacturing, the extrusion of a plastic sheet and glass blowing. The comparison between recently distributed information in the literature and the information revealed in this work suggests that the conclusions from this study constitute a magnificent improvement in the understanding of the Stefan blowing effects.

2. Physical Model and Mathematical Formulation

We consider the time-dependent magnetohydrodynamic (MHD) mixed convection, $2D$ incompressible electrically conducting, laminar and viscous flow of nano-sized nanoparticles over a stretching sheet, which has been examined in the presence of chemical reaction, Arrhenius activation energy and viscous dissipation. The flow is subjected to the transverse magnetic and electric field strength B and E, which are assumed to be applied in the direction $y>0$ and normal to the surface (see Figure 1). The magnetic and electric fields follow the law of Ohm’s $J=\sigma (E+V\times B)$, where V, J and $\sigma$ represent the velocity of fluid, Joule current and the electrical conductivity, respectively. The Joule (current) effect mentioned also plays roles in the transport of a charged particle in the electromagnetic field [42]. Since the magnetic Reynolds number is small, the induced magnetic field and Hall current effects are ignored [43]. The impacts of Stefan blowing has also been considered. Assuming the velocity of the linearly stretching sheet is $u_w(x,t)$, the velocity of mass transfer is $v_w(x,t)$, where $x-$axis and $y-$axis are assumed along the stretched sheet and (t) its time. Suppose that the values of the ambient concentration and temperature are symbolized by (${\zeta }_{\infty }$ and $T_{\infty }$), respectively. It is also assumed that the temperature and concentration at the surface has a constant value of $T_w$ and ${\zeta }_w$. Using these assumptions, the boundary layer equations governing the conservation of mass, linear momentums, thermal energy and nanoparticles volume friction in the vector form are as follows:

$$\begin{array}{c}\frac{\partial {\rho }_f}{\partial t}+\nabla ·\left({\rho }_f\overrightarrow{V}\right)=0,\end{array}$$

(1)

$$\begin{array}{c}{\rho }_f\left[\frac{\partial \overrightarrow{V}}{\partial t}+(\overrightarrow{V}·\nabla )\overrightarrow{V}\right]=\mu {\nabla }^2\overrightarrow{V}+F^{*}+\left[(1-{\zeta }_{\infty }){\rho }_{f\infty }{\beta }_t{g}^{*}(T-T_{\infty })-({\rho }_p-{\rho }_{f\infty }){\beta }_c{g}^{*}(\zeta -{\zeta }_{\infty })\right],\end{array}$$

(2)

$$\begin{array}{c}{\left(\rho c\right)}_f\left[\frac{\partial T}{\partial t}+(\overrightarrow{V}·\nabla )T\right]=-\nabla \overrightarrow{q}+{\left(\rho c\right)}_p\left\{D_B\nabla ·C+\frac{D_T}{T_{\infty }}(\nabla T·\nabla T)\right\}+\phi ,\end{array}$$

(3)

$$\begin{array}{c}\frac{\partial C}{\partial t}+(\overrightarrow{V}·\nabla )C=D_B{\nabla }^{2}C-k_r^2(C-C_{\infty }){\left(\frac{T}{T_{\infty }}\right)}^{n}exp\left(\frac{-E_a}{k_{B}T}\right).\end{array}$$

(4)

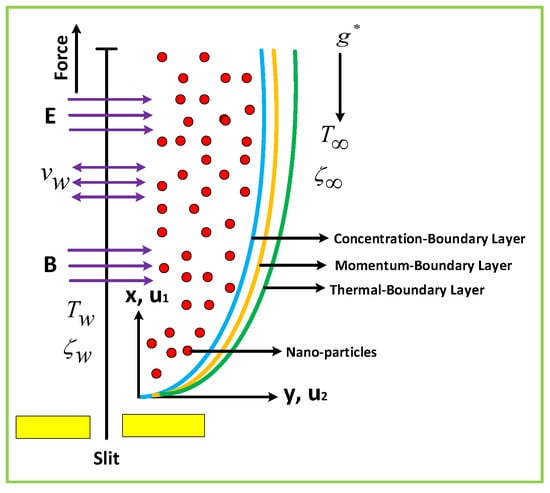
Figure 1. A schematic configuration with coordinate system.

Here, $\overrightarrow{V}=v(x,y,t$) are the velocity component in $(x,y)$ directions, respectively; ($C,T$) are the volume fraction of nanoparticle and fluid temperature, respectively; ($D_T,D_B$) are the thermophoretic and Brownian diffusion coefficients; ($F^{*},\nu ,{\rho }_f,c_p,{\left(\rho c\right)}_p,g^{*},{\beta }_t,{\beta }_c,\phi$) are, respectively, the external mechanical body forces, dynamic viscosity, density of the nanofluid, specific heat, heat capacity of the nanoparticle, gravitational acceleration, volumetric thermal, solutal expansion coefficients and the function of viscous dissipation, respectively. In the right-hand side of Equation (4), $k_r^2(C-C_{\infty }){\left(T/T_{\infty }\right)}^{n}exp\left(\frac{-E_a}{k_{B}T}\right)$ represents the modified Arrhenius function, where $kr$ is the chemical reaction rate and n the fitted rate constant.

In light of above-mentioned assumptions, the governing equations are written as [11,44,45]:

$$\begin{array}{c}{\partial }_x{u}_1+{\partial }_y{u}_2=0,\\ {\partial }_t{u}_1+u_1{\partial }_x{u}_1+u_2{\partial }_y{u}_1=\nu {\partial }_{yy}{u}_1-\left(\frac{\sigma }{{\rho }_f}\right)(B^2{u}_1-EB)\end{array}$$

(5)

$$\begin{array}{c}+\left(\frac{1}{{\rho }_f}\right)\left[(1-{\zeta }_{\infty }){\rho }_{f\infty }{\beta }_t{g}^{*}(T-T_{\infty })-({\rho }_p-{\rho }_{f\infty }){\beta }_c{g}^{*}(\zeta -{\zeta }_{\infty })\right],\\ {\partial }_{t}T+u_1{\partial }_{x}T+u_2{\partial }_{y}T=\left(\frac{\kappa }{{\left(\rho c\right)}_f}\right){\partial }_{yy}T+\left(\frac{\sigma }{{\left(\rho c\right)}_f}\right){(E-u_{1}B)}^2+\left(\frac{1}{{\left(\rho c\right)}_f}\right)\left(\frac{16T_{\infty }^3{\sigma }^{*}}{3K^{*}}{\partial }_{yy}T\right)\end{array}$$

(6)

$$\begin{array}{c}+\left(\frac{\mu }{{\left(\rho c\right)}_f}\right){\left({\partial }_y{u}_1\right)}^2+\tau \left[D_B\left({\partial }_y\zeta \right)\left({\partial }_{y}T\right)+\frac{D_T}{T_{\infty }}\left({\partial }_y{T)}^2\right)\right],\end{array}$$

(7)

$$\begin{array}{c}{\partial }_t\zeta +u_1{\partial }_x\zeta +u_2{\partial }_y\zeta =D_B{\partial }_{yy}\zeta +\frac{D_T}{T_{\infty }}{\partial }_{yy}T-K_r^2\left(\zeta -{\zeta }_{\infty }\right){\left(\frac{T}{T_{\infty }}\right)}^n{exp}^{\frac{-E_a}{K_{B}T}},\end{array}$$

(8)

The boundary conditions are expressed as [46,47]:

$$\begin{array}{c}{u}_1=u_w(x,t)+l_1{\partial }_y{u}_1,u_2=-\frac{D_B}{1-{\zeta }_w}\left({\partial }_y\zeta \right),T=T_w+l_2{\partial }_{y}T,\end{array}$$

$$\begin{array}{c}\zeta ={\zeta }_w+l_3{\partial }_y\zeta asy=0,\end{array}$$

(9)

$$\begin{array}{c}{u}_1\to 0,T\to T_{\infty },\zeta \to {\zeta }_{\infty }asy\to \infty .\end{array}$$

(10)

where $u_1=u_w(x,t)=\frac{bx}{1-at}$ and $u_2=-\frac{D_B}{1-{\zeta }_w}\left({\partial }_y\zeta \right)$ represent the velocity of linear stretching sheet and the blowing velocity at the wall, respectively, and $a,b$ are the positive constants with $at<1$. The components of velocity along the x-direction and y-direction are represented by $u_1$ and $u_2$, respectively. The magnetic field strength $B=\frac{B_0}{\sqrt{1-at}}$, the chemical reaction rate $K_r=\frac{K_0}{\sqrt{1-at}}$ and the electric field strength $E=\frac{E_0}{\sqrt{1-at}}$ are applied on the direction of the positive y-axis and $\alpha =\frac{\kappa }{{\left(\rho c\right)}_f}$, ${\sigma }^{*}$, $K^{*}$ and ${\left(\rho c\right)}_f$ stands for thermal diffusivity, the Stefan–Boltzmann constant, the mean absorption co-efficient and the heat capacity of the liquid, respectively. We also have $l_2=l_2^{\prime }\sqrt{1-at}$, $l_1=l_1^{\prime }\sqrt{1-at}$, $l_3=l_3^{\prime }\sqrt{1-at}$, $\tau =\frac{{\left(\rho c\right)}_p}{{\left(\rho c\right)}_f}$, and $E_a$ signifies the slip factor of temperature, slip factor of velocity, slip factor of concentration, capacity ratio and the activation energy, respectively. Now, we transform the flow problem into a dimensionless form by using the following dimensionless quantities [48,49].

$$\begin{array}{c}\hfill \psi =\sqrt{\frac{b\nu }{1-at}}x.f\left(\eta \right),\eta =y\sqrt{\frac{b}{\nu (1-at)}},\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }},\varphi \left(\eta \right)=\frac{\zeta -{\zeta }_{\infty }}{{\zeta }_w-{\zeta }_{\infty }}.\end{array}$$

(11)

The stream function $\psi$ is described as: $u_1={\partial }_y\psi$ and $u_2=-{\partial }_x\psi$, so Equation (5) is fulfilled. In view of Equation (11), the system of following nonlinear ODEs from Equations (6)–(8) are obtained:

$$\begin{array}{c}\hfill f^{‴}+f{f}^{″}-{f^{\prime }}^2-{\sigma }_t\left[\frac{\eta }{2}{f}^{″}+f^{\prime }\right]+M\left[E_I-f^{\prime }\right]+\lambda \left[\theta -N_r\varphi \right]=0,\end{array}$$

(12)

$$\begin{array}{c}\hfill \frac{1}{Pr}\left[1+\frac{4}{3}Rd\right]{\theta }^{″}+f{\theta }^{\prime }-{\sigma }_t\frac{\eta }{2}{\theta }^{\prime }+Ec{f^{″}}^2+Nb{\theta }^{\prime }{\varphi }^{\prime }+Nt{{\theta }^{\prime }}^2+MEc{\left[f^{\prime }-E_I\right]}^2=0,\end{array}$$

(13)

$$\begin{array}{c}\hfill {\varphi }^{″}-Sc\left[\Omega \varphi {(1+\Gamma \theta )}^n{exp}^{-\frac{A_e}{1+\Gamma \theta }}+{\sigma }_t\frac{\eta }{2}{\varphi }^{\prime }-f{\varphi }^{\prime }\right]+\frac{Nt}{Nb}{\theta }^{″}=0.\end{array}$$

(14)

The transformed boundary conditions of Equations (9) and (10) are as follows:

$$\begin{array}{c}f\left(0\right)=\frac{S_B}{Sc}{\varphi }^{\prime }\left(0\right),f^{\prime }\left(0\right)=1+L_f{f}^{″}\left(0\right),\theta \left(0\right)=1+L_{\theta }{\theta }^{\prime }\left(0\right),\varphi \left(0\right)=1+L_{\varphi }{\varphi }^{\prime }\left(0\right)at\eta =0\end{array}$$

(15)

$$\begin{array}{c}{f}^{\prime }(\infty )\to 0,\theta (\infty )\to 0,\varphi (\infty )\to 0at\eta \to \infty .\end{array}$$

(16)

where the dimensionless velocity, temperature and concentration are $f^{\prime }$, $\theta$ and $\varphi$, respectively. The unsteadiness parameter is denoted by ${\sigma }_t=\frac{a}{b}$. Additionally, $L_f=l_1^{\prime }\sqrt{\frac{b}{\nu }}$ is the slip parameter of velocity; $L_{\theta }=l_2^{\prime }\sqrt{\frac{b}{\nu }}$ is the slip parameter of thermal; $L_{\varphi }=l_3^{\prime }\sqrt{\frac{b}{\nu }}$ is the slip parameter of the solutal concentration, $\lambda =\frac{Gr}{R{e}^2}$ is the mixed convection parameter; the Grashof number is $Gr=\frac{g^{*}(1-{\zeta }_{\infty }){\rho }_{f\infty }{\beta }_t(T_w-T_{\infty })x^3}{\left({\rho }_f\right){\nu }^2}$; $N_r=\frac{({\rho }_p-{\rho }_{f\infty }){\beta }_c({\zeta }_w-{\zeta }_{\infty })}{(1-{\zeta }_{\infty }){\rho }_f{\beta }_t(T_w-T_{\infty })}$ represents the buoyancy ratio parameter; the Reynolds number is $Re=\frac{u_{w}x}{\nu }$, the Prandtl number is $Pr=\frac{\nu }{\alpha }$; the parameter of Brownian motion is $Nb=\frac{{\left(\rho c\right)}_p{D}_B({\zeta }_w-{\zeta }_{\infty })}{\nu {\left(\rho c\right)}_f}$; the parameter of thermophoresis is $Nt=\frac{{\left(\rho c\right)}_p{D}_T(T_w-T_{\infty })}{T_{\infty }\nu {\left(\rho c\right)}_f}$; the Eckert number is $Ec=\frac{u_w^2}{c_f(T_w-T_{\infty })}$; the parameter of magnetic field is $M=\frac{\sigma B_0^2}{\left({\rho }_f\right)b}$; the electric field parameter is $E_I=\frac{E_0}{u_w{B}_0}$; the Stefan blowing (mass blowing/suction) parameter is $S_B=\frac{{\zeta }_w-{\zeta }_{\infty }}{1-{\zeta }_w}$; the Schmidt number is $Sc=\frac{\nu }{D_B}$; the radiation parameter is $Rd=\frac{4T_{\infty }^3{\sigma }^{*}}{K^{*}\kappa }$; the chemical reaction rate is $\Omega =\frac{K_r^2}{b}$; the activation energy is $A_e=\frac{E_a}{K_B{T}_{\infty }}$; and the temperature relative parameter is $\Gamma =\frac{T_w-T_{\infty }}{T_{\infty }}$.

3. Physical Quantities

The most important relationships for the practical concern in the present exploration are the local skin friction coefficient $c_f=\frac{{\tau }_w}{\rho u_w^2(x,t)}$, the local nusselt number $Nu=\frac{x{q}_w}{\kappa (T_w-T_{\infty })}$ and the sherwood number $Sh=\frac{x{q}_m}{D_B({\zeta }_w-{\zeta }_{\infty })}$, with expressions of ${\tau }_w$, $q_w$ and $q_m$ given as ${\tau }_w=\mu {\left({\partial }_y{u}_1\right)}_{y=0}$, $q_w=-{\left((\kappa +\frac{16{\sigma }^{*}{T}_{\infty }^3}{3K^{*}}){\partial }_{y}T\right)}_{y=0}$ and $q_m=-D_B{\left({\partial }_y\zeta \right)}_{y=0}$, respectively. In non-dimensional variables, we have $\sqrt{Re}{C}_f=f^{″}\left(0\right)$, $\frac{Nu}{\sqrt{Re}}=-\left(1+\frac{4}{3}Rd\right){\theta }^{\prime }\left(0\right)$ and $\frac{Sh}{\sqrt{Re}}=-{\varphi }^{\prime }\left(0\right)$.

4. Execution of Method

The numerical solution of ordinary differential Equations (12)–(14) with the boundary conditions shown in Equations (15) and (16) has been obtained by using the Runge–Kutta 4th order with the shooting technique (see Figure 2). However, different analytical and numerical methods have been implemented to examine the nonlinearity in the flow process. The most commonly used approximate analysis methods for flow problems include HAM (homotopy analysis method), VPM (variation of parameter method), ADM (Adomain decomposition method), VIM (variational iteration method), etc. However, the Runge–Kutta 4th order is more effective. This method with the shooting technique is a powerful scheme for solving ODEs. The short Runge–Kutta 4th order solves boundary value problems precisely, adequately and rapidly. The Runge–Kutta strategy has been utilized via commercial software, for example, ADINA, ANSYS, ABAQUS, MATLAB and so on. We transformed Equations (12)–(14) into a set of first-order ordinary differential equations (ODEs). For this purpose, we introduced the following variables,

$$\begin{array}{c}{y}_1^{\prime }=y_2,\end{array}$$

(17)

$$\begin{array}{c}{y}_2^{\prime }=y_3,\end{array}$$

(18)

$$\begin{array}{c}{y}_3^{\prime }=y_2^2-y_1{y}_3+{\sigma }_t(\frac{\eta }{2}{y}_3+y_2)-M(E_I-y_2)-\lambda (y_4-N_r{y}_6),\end{array}$$

(19)

$$\begin{array}{c}{y}_4^{\prime }=y_5,\end{array}$$

(20)

$$\begin{array}{c}{y}_5^{\prime }=\frac{-Pr}{1+\frac{4}{3}Rd}\left[Ec{y}_3^2+MEc{(y_2-E_I)}^2+Nb{y}_5{y}_7+Nt{y}_5^2-{\sigma }_t\frac{\eta }{2}{y}_5+y_1{y}_5\right],\end{array}$$

(21)

$$\begin{array}{c}{y}_6^{\prime }=y_7,\end{array}$$

(22)

$$\begin{array}{c}{y}_7^{\prime }=Sc\left[\Omega y_6{(1+\Gamma y_4)}^n{e}^{\frac{-A_e}{(1+\Gamma y_4)}}+{\sigma }_t\frac{\eta }{2}{y}_7-y_1{y}_7\right]-\frac{Nt}{Nb}{y}_5^{\prime }.\end{array}$$

(23)

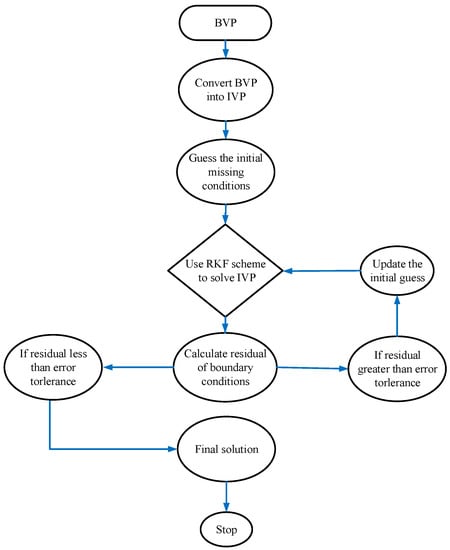
Figure 2. The algorithm of the numerical method.

To clarify the arrangement of the first-order initial values problem via the shooting technique, seven initial conditions are needed. Consequently, we estimated three unknown conditions $y_3\left(0\right)=a_1$, $y_5\left(0\right)=b_1$ and $y_7\left(0\right)=c_1$. The reasonable suppositions for these three unknown missing conditions are selected such that the three boundary conditions are known to be closely fulfilled for $\eta \to \infty$. In order to improve the missing initial conditions, Newton’s iterative structure will be applied until the desired approximation is seen. For several developed parameters and a right bounded domain $[0,{\eta }_{max}]$ in place of $[0,\infty )$, the calculation has been completed, where ${\eta }_{max}$ is a positive real number, and the value is chosen so that the resulting value does not change significantly greater than ${\eta }_{max}$. The criterion for stopping the iterative process is

$$max\left(|y_2\left({\eta }_{max}\right)-0|,|y_4\left({\eta }_{max}\right)-0|,|y_6\left({\eta }_{max}\right)-0|\right)\le {\zeta }_1,$$

where ${\zeta }_1$ is a very small positive real number.

5. Results and Discussion

In this article, we will discuss the numerical results of the dimensionless concentration, velocity and temperature profiles for different flow parameters, such as the Stefan blowing parameter $S_B$, the hydrodynamic slip parameter $L_f$, the electric current $E_I$, the solutal buoyancy ratio parameter $N_r$, the unsteady parameter ${\sigma }_t$, the magnetic parameter M, the thermal buoyancy $\lambda$, the radiation parameter $Rd$, the thermal slip parameter $L_{\theta }$, the Eckert number $Ec$, the solutal slip parameter $L_{\varphi }$, the Brownian motion parameter $Nb$, the activation energy $A_e$, thermophoresis $Nt$, the Schmidth number $Sc$, the chemical reaction rate $\Omega$ and the Prandtl number $Pr$. We have verified our results with the existing literature listed in (Table 1 and Table 2) before presenting the final results. In Table 1, we compared our results of the skin friction $-f^{″}\left(0\right)$ for different values of parameters ${\sigma }_t$ and M with the works of Ali et al. [50] and Liaqat et al. [51]. An excellent relationship has been achieved. An excellent agreement among the previous articles has been accomplished for the heat transfer rate (see Table 2). The physical parameters of choice are varied, while all the remaining parameters are fixed to constant values as: $M=0.2$, $\lambda =1.0$, $N_r=0.3$, $E_I=0.02,$ $Pr=6.2$, $Nb=Nt=0.1$, $Sc=12.0$, $Ec=0.3$, ${\sigma }_t=0.1$, $Rd=0.3$, $A_e=0.3$, $n=0.5$, $L_f=0.3$, $L_{\theta }=0.5$, $L_{\varphi }=0.4$, $\Omega =0.1$ and $\Gamma =0.1$.

Table 1. A comparison of $-f^{″}\left(0\right)$ for various values of ${\sigma }_t$ and M, when $\lambda =N_r=E_I=S_B=L_f=0$ with Refs. [50,51].

${\mathit{\sigma }}_{\mathit{t}}$	M	Ali et al. [50]	Liaqat et al. [51]	(Present Results)
0.2	0.0	1.06803	1.068027	1.068029
0.6		1.19912	1.199118	1.199115
1.0		1.32052	1.320522	1.320518
1.4		1.43284	1.432836	1.432839
0.0	0.0	−1.00001	−1.000000	−1.000006
	1.0	1.41421	1.414214	1.414208
	5.0	2.44949	2.449489	2.449481
	10.0	3.31662	3.316625	3.316617

Table 2. A comparison of $-{\theta }^{\prime }\left(0\right)$ for various values of P_r when $M=\lambda =N_r=E_I=S_B={\sigma }_t=L_f=L_{\theta }=Ec=Rd=0$, and $Nb=Nt={10}^{-6}$, $Sc=10.0$ with Refs. [52,53].

Pr	Wang [52]	Gorla and Sidawi [53]	(Present Results)
0.70	0.4539	0.5349	0.454909
2.00	0.9114	0.9114	0.911354
7.00	1.8954	1.8905	1.895386
20.0	3.3539	3.3539	3.353866

Figure 3a,b describes the effects of the magnetic parameter M, the thermal buoyancy parameter $\lambda$, and the Stefan blowing $S_B$ on the non-dimensional velocity profile. Figure 3a indicates that the component of velocity reduces with the increasing magnetic field strength. Exposing an electrically conducting nanofluid to a transverse magnetic field causes a surge in a resistance force recognized as a Lorentz force. This force tends to inhibit fluid velocity, and from Figure 3b, it is clear that the momentum of the boundary layer rises with an increase in the $\lambda$. Physically, the given detail is elaborated as to why the velocity profiles rise as more forces are added with these increases in buoyancy parameters $\lambda$. The $f^{\prime }\left(\eta \right)$ shows a rising trend against a higher input of $S_B$. From this figure, the fluid velocity is intensified for Stefan blowing $(S_B=1.0)$ as compared with mass suction $(S_b=-1.0)$. The injection of tiny particles (nanoparticles) through the boundary energizes species diffusion, while the evacuation of tiny particles inhibit diffusion, so growing values of blowing increase the fluid velocity. To observe the buoyancy ratio parameter influence and the unsteadiness parameter with the Stefan blowing effects on the dimensionless velocity profile demonstrated in Figure 4a,b. The result shows in Figure 4a that the increasing value of the buoyancy ratio caused to decline fluid velocity, and Figure 4b shows the similar trend against growing strength of unsteadiness parameters. The distribution shows that the thermal diffusion from the sheet surface to the ambient condition prominent over mass buoyancy forces of tiny particles, so the strength of the convection current decrease the fluid velocity.

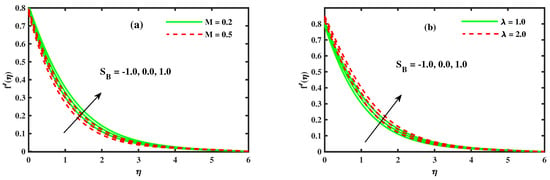
Figure 3. The impact of $f^{\prime }\left(\eta \right)$ for (a) Magnetic M and (b) thermal buoyancy $\lambda$.

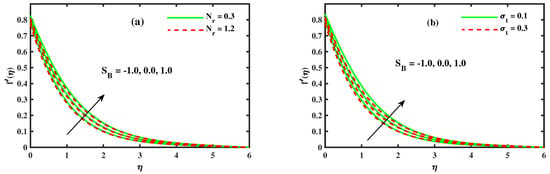
Figure 4. The impact of $f^{\prime }\left(\eta \right)$ for (a) Solutal buoyancy N_r and (b) unsteady parameter ${\sigma }_t$.

Figure 5a,b shows the impact of the electric field parameter $E_I$ and hydrodynamic slip parameter $L_f$ with Stefan blowing $S_B$ on the non-dimensional velocity profile. The effect of the $E_I$ has been demonstrated in Figure 5a. As the estimations of electric field parameter increments, the momentum boundary layer increases significantly above the sheet expressively. The electric field associated with Lorentz force, in general, prompt nanomaterial particles stress exchanging the effective viscosity of scattering as well as yield improvement because of energy transformations. Figure 5b shows that the escalation of the slip parameter of velocity causes a reduction in the velocity profile. Figure 6a,b show the results of the nanofluid temperature profile $\theta \left(\eta \right)$ with distinct values of the $Rd$, M and $S_B$. The temperature distribution increases with an increase in M, $Rd$ and $S_B$. Since the intensity of M increments in an electrically conducting nanofluid, it starts to create a resistive power (Lorentz power) and nanoparticle dissolves the vitality as heat; therefore, the boundary layer gets thicker (see Figure 6a). The effect of conduction increases against the growing value of radiation, and the fluid temperature raises at each point away from the surface, which intensifies the temperature (see Figure 6b).

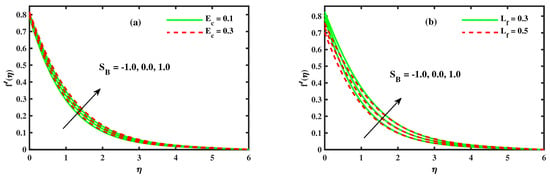
Figure 5. The impact of $f^{\prime }\left(\eta \right)$ for (a) Electric current $E_I$ and (b) hydrodynamic slip $L_f$.

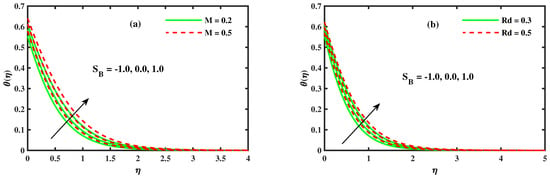
Figure 6. The impact of $\theta \left(\eta \right)$ for (a) Magnetic field M and (b) radiation $Rd$.

Figure 7a,b represent the results of the nanofluid temperature profile with distinct values of the Eckert number $Ec$, thermal slip parameter $L_{\theta }$, and Stefan blowing parameter $S_B$. The impact of the Eckert number is exposed in Figure 7a. The Eckert number effects include expanding the temperature due to frictional heating. Normally, the heat transfer ascends in the manners of electronic chips, power generation systems, fluid metal liquids, just as cooling of nuclear reactors. The ratio between the flow kinetic energy and enthalpy of the boundary layer difference is called the Eckert number. Physically, the temperature can be increased due to the multiplication of the Joule heating effect from the product of the magnetic and Eckert number. Figure 7b uncovers the physical attributes of the thermal slip boundary $L_{\theta }$ on $\theta \left(\eta \right)$. The impact is identical to the velocity profile (see Figure 5b). Basically, the temperature is represented by a nonlinear connection between the foothold and slip in the polymer dissolve. The temperature decreases radically under permeable circumstances. Figure 8a,b present the behavior of the nanofluid temperature profile with different values of the unsteady parameter ${\sigma }_t$ and thermal buoyancy $\lambda$. The impact of unsteadiness ${\sigma }_t$ on the dimensionless temperature distribution $\theta \left(\eta \right)$ (see Figure 8a) is identical to the effect of the velocity profile (see Figure 4b). The performance of the thermal buoyancy parameter $\lambda$ on $\theta \left(\eta \right)$ is presented in Figure 8b. The temperature of the nanofluid along the extending sheet is generous at the force convection stream location $(\lambda =1.0)$, which results in different values of Stefan blowing. For the heated extending surface location ($\lambda >1.0$), the convection current diminishes the temperature profile.

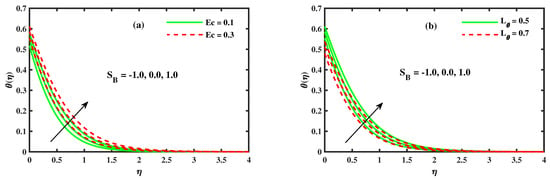
Figure 7. The impact of $\theta \left(\eta \right)$ for (a) Eckert number $Ec$ and (b) thermal slip $L_{\theta }$.

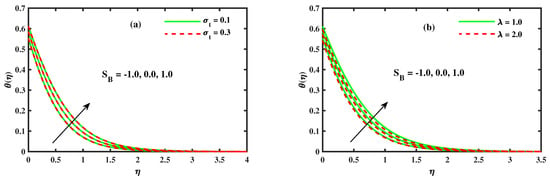
Figure 8. The impact of $\theta \left(\eta \right)$ for (a) unsteady parameter ${\sigma }_t$ and (b) thermal buoyancy $\lambda$.

Figure 9a,b demonstrated the distribution of the temperature of distinct values of the Brownian motion parameter $Nb$, thermophoresis parameter $Nt$ and with the suction/blowing parameter $S_B$. The impact of the Brownian motion parameter has been displayed in Figure 9a. Basically, Brownian motion supports heating the fluid in the boundary layer and immediately reduces particle deposition away from the fluid on the surface. Therefore, as $Nb$ rises, the temperature increases. Figure 9b summarizes the effect of changes in thermophoresis parameters $Nt$ on the temperature profile. Figure 9b outlines the influence of the variation of the $Nt$ on the temperature profile. As the thermophoresis parameter surges, the thickness of the thermal boundary layer grows as $Nt$ increments. In reality, nanoparticles have moved from a hot surface to a cold ambient liquid, so the temperature of the boundary layer rises. This impacts the development of the thermal boundary layer thickness. Figure 10a,b present the behavior of the nanoparticles concentration profile with different values of the thermophoresis parameter $Nt$, Brownian motion parameter $Nb$ and Stefan blowing parameter $S_B$. The impression of the thermophoresis parameter $Nt$ on the concentration profile (see Figure 10a) is identical to that of the temperature profile $\theta \left(\eta \right)$ (see Figure 9b). The impact of $Nb$ on the distribution of the concentration exists in Figure 10b. The concentration profile was diminished because of changes in the uneven development of the nanoparticles in the framework. This reinforces the thermal exhibition as vitality changes hugely, prompting a decrease in the layer thickness.

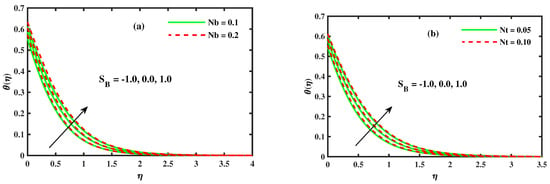
Figure 9. The impact of $\theta \left(\eta \right)$ for (a) Brownian motion $Nb$ and (b) thermophoresis $Nt$.

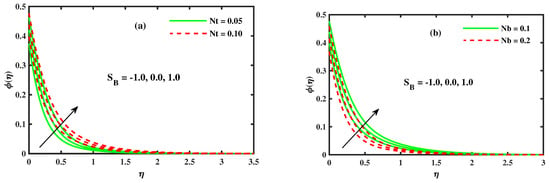
Figure 10. The impact of $\varphi \left(\eta \right)$ for (a) thermophoresis $Nt$ and (b) Brownian motion $Nb$.

Figure 11a,b show the results of the concentration distribution with dissimilar values of the unsteady parameter ${\sigma }_t$ and solutal slip parameter $L_{\varphi }$. The influence of unsteadiness ${\sigma }_t$ on the concentration profile $\varphi \left(\eta \right)$ (see Figure 11a) is the same as the velocity profile (see Figure 4b). Figure 11b indicates the justification of the behavior of $L_{\varphi }$ on the concentration distribution. This indicates that the liquid particles have a stream conduct influenced by the solid boundary. The thickness of the solutal layer and concentration decrease radically underneath the linear permeable surface. Figure 12a,b display the impact of the activation energy parameter $A_e$ and chemical reaction parameter $\Omega$ on the nanoparticle’s concentration profile. Figure 12a emphasizes the graphical potential of activation energy $A_e$ on concentration $\varphi \left(\eta \right)$. The result depicted by the activation energy parameter $A_e$ asserted an expanding concentration distribution. The activation energy indicates a major effect in numerous interesting manners. It assumes an important job to improve the reaction phenomenon, and Figure 12b manifest that more grounded $\Omega$ leads to a decrease in the nanoparticle concentration. The clarification for this conduct is that the destructive chemical rate upgrades the mass transfer rate and results in a decrease in the nanoparticle concentration. These factors influence the dampness and temperature destruction fields, causing the obliteration of yields due to freezing, vitality generally move to the drizzly cooling tower, and so on.

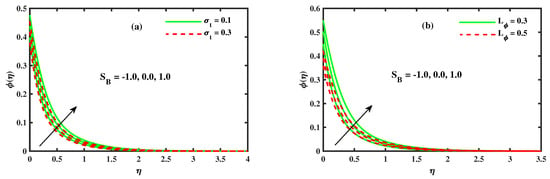
Figure 11. The impact of $\varphi \left(\eta \right)$ for (a) unsteady ${\sigma }_t$ and (b) solutal slip $L_{\varphi }$.

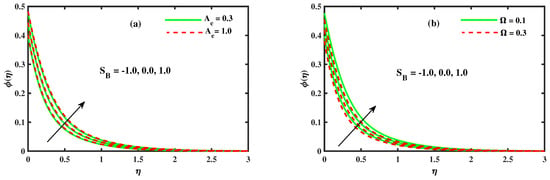
Figure 12. The impact of $\varphi \left(\eta \right)$ for (a) activation energy $A_e$ and (b) chemical reaction rate $\Omega$.

Figure 13a,b demonstrate the behavior of the nanoparticles concentration profile with different values of the Schmidt number Sc, Buoyancy ratio parameter $N_r$ and Stefan blowing parameter $S_B$. The Schmidt number Sc impact on the nanoparticle concentration diagram is portrayed in Figure 13a. Expanding the Schmidt number relates to a low Brownian dispersion coefficient, which prompts short entrance profundity for the concentration profile. Subsequently, the concentration at the surface abates with the expanding impact of the Schmidt number. Figure 13b illustrates the result of $N_r$ on $\varphi \left(\eta \right)$. The concentration profile boots up by increasing $N_r$.

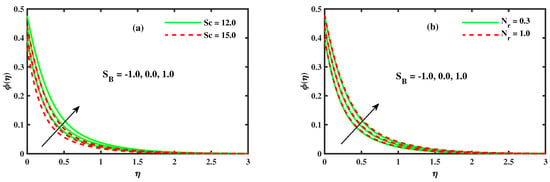
Figure 13. The impact of $\varphi \left(\eta \right)$ for (a) Schmidth number $Sc$ and (b) Buoyancy ratio parameter $N_r$.

6. Conclusions

In this study, we studied the unsteady electrical MHD mixed convection flow and heat transfer of nanofluid on the linear stretching sheet in the existence of thermal radiation, magnetic and electric fields, chemical reaction, activation energy and the Stefan blowing effects. The current work outcomes are confirmed as:

• The growing values of magnetic field, solutal buoyancy $N_r$ and hydrodynamic slip parameter $L_f$ slow down the fluid velocity, but the velocity profile rises against growing values of thermal buoyancy $\lambda$ and electric current parameters.
• The temperature profile $\theta \left(\eta \right)$ rises with rising values of Brownian motion $Nb$, magnetic field M, Eckert number $Ec$, thermophoresis $Nt$ and thermal radiation $Rd$.
• The fluid velocity, temperature and nanoparticle concentration profile are observed to have deteriorated with augmentation in the unsteadiness parameter ${\sigma }_t$.
• The temperature of the fluid declines with increasing values of the thermal slip $L_{\theta }$ and thermal buoyancy $\lambda$ parameters.
• Due to an enhancement in the activation energy $A_e$, thermophoresis $Nt$ and buoyancy ratio $N_r$ parameters, the nanoparticle concentration profile $\varphi \left(\eta \right)$ increases.
• With the increasing values of Brownian motion $Nb$, $L_{\varphi }$, $\Omega$ and $Sc$, the nanoparticle concentration profile $\varphi \left(\eta \right)$ decreases.
• The nanoparticle volume fraction, temperature and velocity function are decreased against wall suction $S_B=-1.0$ and enhanced against wall injection $S_B=1.0$.