Abstract
The MA2Z4 family represents a class of two-dimensional materials renowned for their outstanding mechanical properties and excellent environmental stability. By means of elemental substitution, we designed two novel phases of ScSi2N4, namely β1 and β2. Their dynamical, thermal, and mechanical stabilities were thoroughly verified through phonon dispersion analysis, ab initio molecular dynamics (AIMD) simulations, and calculations of mechanical parameters such as Young’s modulus and Poisson’s ratio. Electronic structure analysis using both PBE and HSE06 methods further revealed that both the β1 and β2 phases exhibit metallic behavior, highlighting their potential for battery-related applications. Based on these outstanding properties, the climbing image nudged elastic band (CI-NEB) method was employed to investigate the diffusion behavior of Li, Na, and K ions on the material surfaces. Both structures demonstrate extremely low diffusion energy barriers (Li: 0.38 eV, Na: 0.22 eV, K: 0.12 eV), indicating rapid ion migration—especially for K—and excellent rate performance. The lowest barrier for K ions (0.12 eV) suggests the fastest diffusion kinetics, making it particularly suitable for high-power potassium-ion batteries. The significantly lower barrier for Na ions (0.22 eV) compared with Li (0.38 eV) implies that both β1 and β2 phases may be more favorable for fast-charging/discharging sodium-ion battery applications. First-principles calculations were applied to determine the open-circuit voltage (OCV) of the battery materials. The β2 phase exhibits a higher OCV in Li/Na systems, while the β1 phase shows more prominent voltage for K. The results demonstrate that both phases possess high theoretical capacities and suitable OCVs.
1. Introduction
Since the isolation of graphene in 2004, two-dimensional (2D) materials have attracted extensive research interest due to their unique structural, electronic, and mechanical properties [1]. Recent years have witnessed a surge in the exploration of novel 2D systems beyond conventional materials such as MoS2 [2], WS2 [3], and [4]. These materials are now widely studied for applications in electronics, optoelectronics, sensing, and energy storage. The emergence of atomically thin materials with tailored compositions has greatly enriched the 2D material family. Among them, the MA2Z4 (M = transition metal, A = group IV element, Z = N or other pnictogens/chalcogens) system represents a new frontier [5,6]. Notably, MoSi2N4 was synthesized experimentally via chemical vapor deposition (CVD) in 2020, marking the first realization of this class with high environmental stability and potential for integration in flexible electronic devices [7]. Although the majority of research to date remains theoretical, recent advances suggest that MA2Z4 materials could serve in real-world applications such as field-effect transistors, piezoelectric devices, and possibly as electrode materials in batteries [8], though experimental demonstrations remain limited.
The MA2Z4 family [9], including the archetypal MoSi2N4, has garnered increasing attention for its structural tunability via isoelectronic substitution. By systematically varying M (e.g., Mo, W, Cr, V, Sc), A (Si, Ge), and Z (N, P, As), researchers have predicted a wide range of stable configurations, each with distinct electronic, magnetic, or optoelectronic properties [10,11,12]. In particular, MSi2N4 [13,14] systems have shown promising potential, with members from early transition metals (e.g., groups III–VI) offering diverse physical behaviors due to d-orbital contributions. However, many of these studies are based solely on first-principles calculations, and caution must be exercised when extrapolating potential applications without experimental validation. Properties such as carrier mobility, band gap modulation, and magnetic ordering have been predicted, yet only a limited number of MA2Z4 structures have been synthesized and characterized to date. Among these, MoSi2N4 remains the most well-studied [15,16], underscoring the need to explore other group and period combinations experimentally to fully assess the potential of this materials platform.
Recent theoretical investigations have expanded the MA2Z4 family to include the ScSi2N4 system, a previously unexplored compound that exhibits promising characteristics for energy storage applications. To date, the known studies on ScSi2N4 include [17,18]. In this work, two structurally stable polymorphs—β1-ScSi2N4 and β2-ScSi2N4—were designed and evaluated using density functional theory (DFT). This study focused on their viability as anode materials for Li-, Na-, and K-ion batteries. The diffusion energy barriers for alkali metal ions were found to be exceptionally low: 0.38 eV (Li), 0.22 eV (Na), and 0.12 eV (K) for both β1 and β2 phases, indicating excellent ion mobility. These values are competitive with or superior to those of conventional 2D anode materials such as phosphorene or Ti3C2 MXenes [19]. The relevance of these low barriers underscores the potential of ScSi2N4-based materials in next-generation rechargeable battery technologies, especially considering their favorable open-circuit voltages and theoretical capacities. As such, the exploration of Sc-based MA2N4 systems could significantly broaden the applicability of this emerging materials family.
2. Computational Details
First-principles calculations were carried out within the framework of density functional theory (DFT) [20] using the Vienna Ab initio Simulation Package (VASP 5.4) [21]. The interaction between ions and electrons was treated using the projector augmented-wave (PAW) [22] method, and the exchange–correlation energy was described by the generalized gradient approximation (GGA) [23] in the form proposed by Perdew, Burke, and Ernzerhof (PBE) [24]. The HSE06 hybrid functional (Heyd–Scuseria–Ernzerhof) [25] was employed to achieve accurate bandgap predictions by mixing exact exchange with PBE exchange–correlation energy. To ensure computational accuracy, the plane-wave energy cutoff was set to 520 eV, and the energy convergence criterion was set to 10−6 eV. During structural optimization, all atomic positions were relaxed until the residual force on each atom was less than 10−3 eV/Å. A supercell with a vacuum layer of approximately 30 Å was constructed to eliminate spurious interactions between periodic images along the out-of-plane direction. For the analysis of dynamical stability, phonon dispersion relations were calculated using the Phonopy package (2.22.1) [26] based on the supercell approach. In addition, ab initio molecular dynamics (AIMD) simulations were conducted under the canonical (NVT) ensemble to evaluate thermal stability at various temperatures. Each simulation lasted for 10 ps with a time step of 2.0 fs, and temperature control was achieved using the Nosé–Hoover thermostat [27]. The elastic constants C11, C22, and C66 for the 2D β1-ScSi2N4 and β2-ScSi2N4 structures were obtained by applying a series of small strains to the fully relaxed structures using the Vienna Ab initio Simulation Package (VASP) and calculating the resulting stress tensors. The elastic constants were then extracted from the linear stress–strain relationships using the VASPKIT package (1.5.1) [28]. The diffusion behavior of Li, Na, and K ions on the material surface was investigated using the climbing image nudged elastic band (CI-NEB) method to determine the migration pathways and corresponding energy barriers, revealing their potential for energy storage applications. To calculate the open-circuit voltage (OCV) of battery materials, we adopted a thermodynamic approach, first computing the Gibbs free energy change (ΔG) during Li/Na/K intercalation in the electrode material, then deriving the voltage via the Nernst equation. For consistency, all compared data were obtained using the PBE-GGA functional unless otherwise noted. Previous studies [25] have shown that while hybrid functionals such as HSE06 can affect the predicted band gap of MA2Z4 compounds, the differences in adsorption energy and ion diffusion barriers between PBE and HSE06 remain minor. Thus, our comparisons are considered valid within the accepted computational accuracy for battery material screening. To evaluate the practical competitiveness of ScSi2N4 as an anode material, we compared its theoretical electrochemical performance with several extensively studied two-dimensional materials reported in the literature [29,30]. Although these materials differ in structure and composition, they serve as valid references for assessing electrochemical performance. To further evaluate the electrochemical performance of ScSi2N4-based electrodes, we compared our calculated results with those reported for other two-dimensional anode materials. These references were selected because they provide relevant performance benchmarks. We note that the reported values for these materials were obtained using different DFT methods (e.g., PBE, PBE + U, HSE06), which can lead to quantitative differences in properties such as adsorption energies, diffusion barriers, and voltages. Therefore, these comparisons are intended as qualitative indicators of relative performance rather than exact numerical matches. This approach highlights the competitive advantages of the ScSi2N4 phase, particularly in terms of ion mobility and capacity, while also acknowledging the differences between the different research methods. The formulas for Young’s modulus and Poisson’s ratio are as follows: and ; , .
3. Results and Discussion
3.1. Structural Information and Stability of 2D β1-ScSi2N4 and β2-ScSi2N4
Both β1-ScSi2N4 and β2-ScSi2N4 have a hexagonal lattice structure consisting of seven atomic layers, as shown in Figure 1. It can be regarded as the insertion of a layer of MoS2-type ScN2 into a layer of InSe-type Si2N2 monolayer; that is, sandwiching the ScN2 layer between two SiN layers to form a hexagonal ScSi2N4 monolayer structure, which belongs to the P6m1 space group. The optimized lattice constant of β1-ScSi2N4 is a = b = 3.00 Å, and the optimized lattice constant of β2-ScSi2N4 is a = b = 2.98 Å. Both unit cells contain one Sc atom, two Si atoms, and four N atoms, and each Sc atom and Si atom are surrounded by six and four adjacent N atoms, respectively. β1-ScSi2N4 belongs to the P-3m1 (164) space group, and β2-ScSi2N4 belongs to the P3m1 (156) space group.
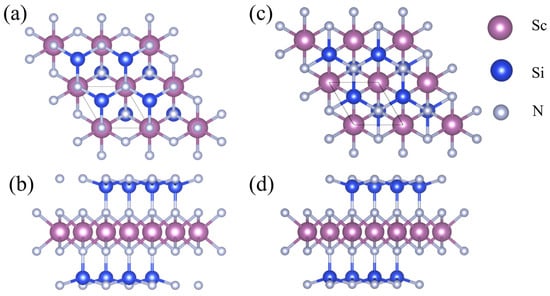
Figure 1.
(a) Front view and (b) side view of β1-ScSi2N4; (c) front view and (d) side view of β2-ScSi2N4. Pink, blue, and gray balls represent Sc, Si, and N atoms, respectively.
The stability calculation of two-dimensional materials is the bridge between theoretical predictions and experimental applications, and directly determines whether the material can be synthesized, whether it can be used in practice, and whether it has unique physical and chemical properties. In the phonon calculation, the phonon dispersion of β1-ScSi2N4 and β2-ScSi2N4 does not exhibit any imaginary frequency, confirming their dynamic stability, as shown in Figure 2a,b. The maximum frequency of 2D β1-ScSi2N4 is 27.7 THz (925 cm−1), while 2D β2-ScSi2N4 is 28.6 THz (954 cm−1), which is slightly lower than for VSi2N4 (992 cm−1) [14] but sufficiently higher than MoS2 (473 cm−1) [31], showing the high stability of 2D β1-ScSi2N4 and β2-ScSi2N4. Ab initio molecular dynamics (AIMD) simulations were performed using a 3 × 3 × 1 supercell for the β1-ScSi2N4 and β2-ScSi2N4 monolayers at 300 K. Within 10 ps, there is no obvious displacement of the atomic positions in the structure, no obvious breakage of the chemical bonds, and the structure remains intact, indicating good thermal stability, as shown in Figure 2c,d. Cohesive energy is a physical quantity that describes the binding strength between atoms or molecules in a material. It reflects the material’s stability: the more negative the value, the stronger the atomic bonding and the more stable the material. The cohesive energy of β1-ScSi2N4 is −7.78 eV/atom. The cohesive energy of β2-ScSi2N4 is −7.79 eV/atom. The cohesive energies of β1-ScSi2N4 and β2-ScSi2N4 are more negative than those of YSi2N4 [32] (−4.294 eV/atom), Cr2BN [33] (−4.06 eV/atom), and Fe2Si [34] (−4.10 eV/atom). The negative cohesive energies indicate structural stability, demonstrating the experimental feasibility of synthesizing β1-ScSi2N4 and β2-ScSi2N4.
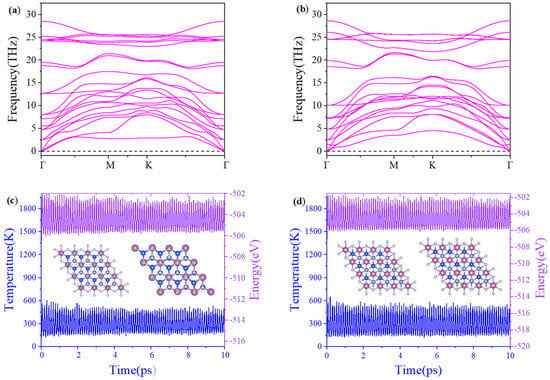
Figure 2.
Phonon spectra of (a) β1-ScSi2N4 and (b) β2-ScSi2N4, molecular dynamics of (c) β1-ScSi2N4 and (d) β2-ScSi2N4 at 300K for 10ps. The letters “Γ”, “M”, and “K” correspond to the high-symmetry points.
In β1-ScSi2N4, the elastic constants are C11 = 325.96 N/m, C22 = 121.65 N/m, and C66 = (C11 − C12)/2 = 102.16 N/m. For β2-ScSi2N4, these values are C11 = 381.83 N/m, C22 = 137.80 N/m, and C66 = (C11 − C12)/2 = 122.01 N/m. These elastic constants satisfy the Born criteria for hexagonal systems [35,36] (C11 > 0 and C11 > |C12|), confirming their mechanical stability. Figure 3 demonstrates that the angle-dependent Young’s modulus and Poisson’s ratio exhibit remarkable isotropy, indicating consistent mechanical properties in all directions, which facilitates practical applications of these materials. The magnitude of Young’s modulus reflects material stiffness—higher values correspond to greater resistance to deformation. The β1-ScSi2N4 monolayer shows a Young’s modulus of 281 N m−1, while β2-ScSi2N4 exhibits a higher value of 332 N m−1. These values surpass those of Ti2C (130 N m−1) [37] and MoS2 (119 N m−1) [38]. The Poisson’s ratio, describing the transverse strain response to longitudinal stress, is 0.37 for β1-ScSi2N4 and 0.36 for β2-ScSi2N4, comparable to CrAsS4 (0.34) [39] and MoS2 (0.31) monolayers. These results confirm that both β1-ScSi2N4 and β2-ScSi2N4 possess excellent tensile/compressive resistance within their elastic limits.
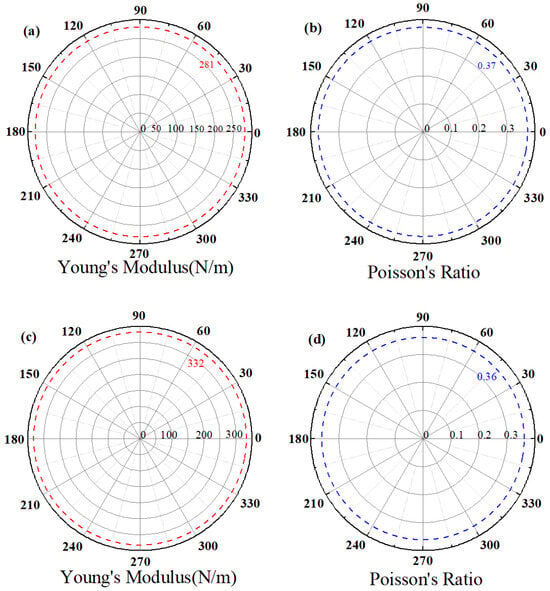
Figure 3.
Young’s modulus and Poisson’s ratio of (a,b) β1-ScSi2N4 and (c,d) β2-ScSi2N4.
3.2. Electronic Properties of 2D β1-ScSi2N4 and β2-ScSi2N4
Next, the spin-polarized band structures were calculated using the PBE and HSE06 methods to explore the electronic properties of the β1-ScSi2N4 and β2-ScSi2N4 monolayers (Figure 4). In the PBE calculations, we found that the spin-up and spin-down channels of β1-ScSi2N4 and β2-ScSi2N4 cross the Fermi level, indicating their intrinsic metallic nature. However, the PBE functional typically underestimates band gaps. Therefore, we further calculated the band structures of the β1-ScSi2N4 and β2-ScSi2N4 monolayers using the HSE06 method.
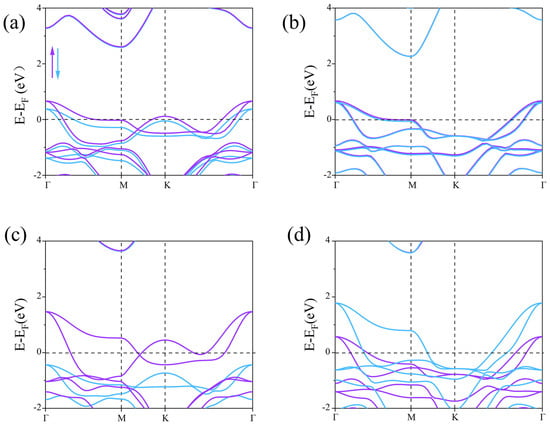
Figure 4.
Electronic band structure of ((a,b), the upside line) β1-ScSi2N4 and β2-ScSi2N4 calculated from GGA + PBE methods; ((c,d), the downside line) β1-ScSi2N4 and β2-ScSi2N4 calculated from HSE06 methods. Purple represents the spin-up energy band, blue represents the spin-down energy band, and the black dotted line marks the Fermi level position.
With the inclusion of HSE06 (Figure 4c,d) we observed that the spin-down band of β1-ScSi2N4 crosses the Fermi level, exhibiting metallic behavior, while the spin-up band lies below the Fermi level. The valence band at the Γ point is primarily contributed by N atoms, whereas the conduction band at the M point is mainly dominated by Sc atoms. A band gap of approximately 4.0 eV exists between the conduction and valence bands, resulting in an overall half-metallic character. The presence of half-metallicity implies vacant states in the band structure, leading to spin asymmetry and partially filled valence electron arrangements. Due to the significantly higher electronegativity of N compared with Sc and Si, its ability to attract electrons is much stronger. Based on the Bader charge [40] analysis shown in Table S1, we calculated the charge distribution of Sc, Si, and N atoms. The results show that N atoms are negatively charged, indicating their strong electron-withdrawing ability, while Sc and Si atoms are positively charged, indicating that electrons are mainly transferred to N atoms, supporting their strong electronegativity. Additionally, through orbital-projected band structure analysis, we demonstrated that the half-metallic nature primarily originates from the N atoms, as illustrated in Figure 5.
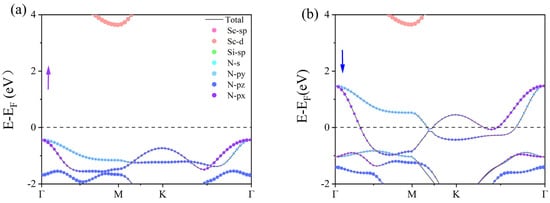
Figure 5.
Orbital projection band structure and spin projection density of β2-ScSi2N4 ((a) represents spin-up, while (b) represents spin-down). Purple represents the spin-up energy band, blue represents the spin-down energy band, and the black dotted line marks the Fermi level position.
PBE notoriously underestimates bandgaps, while HSE06 shows excellent agreement with experimental values, justifying its use for electronic structure analysis. Consequently, β1-ScSi2N4 holds promising potential for applications in magnetism, optics, and related fields. In the HSE06 calculations, the spin-up and spin-down bands of β2-ScSi2N4 both cross the Fermi level, maintaining their metallic nature. However, while the spin-up and spin-down states were initially degenerate, the inclusion of HSE06 leads to band splitting, with the spin-down valence band shifting to higher energies. Based on the HSE06 results, β1-ScSi2N4 exhibits a half-metallic character, whereas β2-ScSi2N4 remains metallic, thereby expanding the potential applications of the MA2Z4 family. COHP (crystal orbital Hamilton population) analysis helps to distinguish bonding, anti-bonding, and non-bonding interactions by evaluating the energy-resolved overlap of electronic states between atom pairs. The ionic bonding character is confirmed as the near-zero ICOHP values (≈0) observed in the COHP curves near the Fermi level (−2 to 2 eV) indicate negligible electronic state overlap in the Sc-N/Si-N bonding (Figure 6c,d). Furthermore, differential charge density and crystal orbital Hamiltonian population (COHP) analyses confirm that the Sc-N and Si-N bonds in both β1-ScSi2N4 and β2-ScSi2N4 exhibit ionic characteristics, as illustrated in Figure 6.
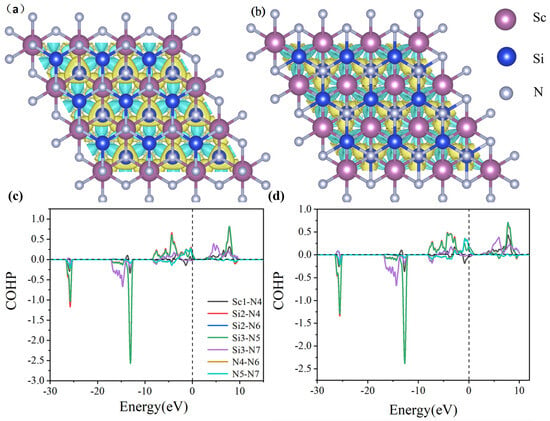
Figure 6.
Difference charge density of (a) β1-ScSi2N4 and (b) β2-ScSi2N4. Blue represents electron loss, while yellow indicates electron gain; COHP diagrams of (c) β1-ScSi2N4 and (d) β2-ScSi2N4. Pink, blue, and gray balls represent Sc, Si, and N atoms, respectively.
3.3. β1-ScSi2N4 and β2-ScSi2N4 Performance as Anode Materials
The evaluation of binding energies for Li/Na/K atoms on substrate materials is crucial for assessing the performance of ion batteries. In this study, to investigate the surface adsorption behavior on β1-ScSi2N4, we selected four typical adsorption sites on the outermost AZ layer: the top site of the N atom (S1), the top site of the Si atom (S2), the bridge midpoint between N and Si atoms (S3), and the center site of the honeycomb ring (S4). Similarly, for the surface adsorption study on β2-ScSi2N4, four characteristic sites on the outermost AZ layer the adsorption points are: the top site of the Sc atom (S1), the top site of the Si atom (S2), the bridge midpoint between Sc and Si atoms (S3), and the center site of the honeycomb ring (S4) (as shown in Figure S1).
The binding energy can be calculated using the following formula:
In the binding energy calculations, represents the total energy of the pristine structure without adsorbed atoms, denotes the total energy of the system after Li/Na/K atom adsorption, and corresponds to the total energy of an isolated Li/Na/K atom (show in Table S2). The research results demonstrate that for the β1-ScSi2N4 material, Li/Na/K atoms initially positioned at the S3 site spontaneously migrate to the S2 site. In contrast, for the β2-ScSi2N4 material, Li/Na/K atoms at the S3 site relax to the S1 site. This indicates that the S1, S2, and S4 sites can serve as effective adsorption sites for Li/Na/K atoms in both materials. The binding energy data presented in Table S1 show that a larger value corresponds to a stronger interaction between the ScSi2N4 material and Li/Na/K atoms (take Li as an example). Consequently, in the β1-ScSi2N4 material, the S4 site exhibits the most stable adsorption for Li/Na/K atoms, while in the β2-ScSi2N4 material, the S1 site demonstrates optimal adsorption stability.
To gain deeper insights into the adsorption mechanism of Li, Na, and K atoms on the surface of MA2Z4 monolayer materials, a quantitative evaluation of the charge transfer between the metal atoms and the two-dimensional ScSi2N4 was carried out based on Bader charge analysis. The results indicate that Li acts as a typical electron donor during adsorption, transferring approximately 0.85 e and 0.9 e of charge to the β1-ScSi2N4 and β2-ScSi2N4 monolayers, respectively. For Na and K atoms, the amount of charge transferred to the β1 configuration is approximately 0.88 e and 0.84 e, respectively, and the same values are observed for the β2 configuration. These substantial charge transfers suggest that the adsorption of Li/Na/K atoms on the MA2Z4 surface is primarily governed by electron transfer from the metal atoms to the substrate, effectively filling the lowest unoccupied molecular orbitals (LUMO) of the ScSi2N4 monolayer. This process enhances both the adsorption stability and interfacial coupling strength.
To further elucidate the spatial distribution of the electronic structure during adsorption, the differential charge density (Δ) was calculated for Li, Na, and K atoms adsorbed at the S4 site of β1-ScSi2N4 and the S1 site of β2-ScSi2N4. The results reveal evident regions of charge accumulation and depletion in the vicinity of the adsorption sites, indicating strong electronic coupling and electrostatic interactions between the adsorbed metal atoms and the ScSi2N4 substrate. These differential charge density maps not only corroborate the dominant role of electron transfer in the adsorption mechanism but also provide critical theoretical insight into the interfacial charge behavior of MA2Z4-based two-dimensional materials for applications in energy storage and related electrochemical systems.
Here, and ) represent the electronic charge densities of the two-dimensional ScSi2N4 system with and without the adsorbed Li, Na, or K atoms, respectively. At the same time, denotes the charge density of an isolated Li, Na, or K atom. In the differential charge density plots shown in Figure 7, the yellow and blue regions correspond to electron accumulation and depletion, respectively. A clear charge transfer from the Li, Na, and K atoms to the ScSi2N4 monolayer is observed, indicating significant electron redistribution upon adsorption. This charge transfer leads to the formation of stable chemical bonds (M–Sc) between the adsorbed metal atoms and the substrate. Such bonding interactions are beneficial for suppressing the aggregation of metal atoms into clusters, thereby enhancing the stability of single-atom dispersion and offering theoretical support for their application in energy storage and related fields.
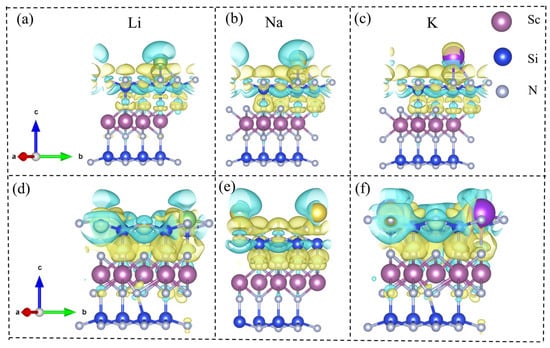
Figure 7.
Charge density difference (CDD) of (a) Li, (b) Na, and (c) K atoms adsorbed at the S2 site of 2D β1-ScSi2N4, and (d) Li, (e) Na, and (f) K atoms adsorbed at the S1 site of 2D β2-ScSi2N4. Figures (a–c) correspond to β1-ScSi2N4, and figures (d–f) correspond to β2-ScSi2N4. Units: e/Å3 electrons per cubic angstrom. Regions of electron accumulation and depletion are shown in light yellow and blue, respectively. Pink, blue, and gray balls represent Sc, Si, and N atoms, respectively, while green, yellow, and purple balls represent Li, Na, and K atoms, respectively.
To determine the maximum monolayer adsorption capacity of lithium and sodium atoms on two-dimensional ScSi2N4, structural optimizations were performed using a 2 × 2 × 1 supercell (as shown in Figure S1). Li and Na ions were incrementally added in pairs to the energetically favorable adsorption sites on the ScSi2N4 surface, followed by full geometric relaxation of each configuration. The final stable structures correspond to the fully adsorbed states of Li and Na. The results indicate that up to four Li or Na atoms can be stably adsorbed on each side (top and bottom) of both β1-ScSi2N4 and β2-ScSi2N4, resulting in a total of eight Li or Na atoms per supercell. This corresponds to a maximum stoichiometry of ScSi2N4-Li2 and ScSi2N4-Na2.
Similarly, the maximum adsorption capacity for potassium atoms was found to be two atoms per side, yielding a total of four K atoms per 2 × 2 × 1 supercell. This corresponds to a stoichiometry of ScSi2N4-K1.5. These findings provide important theoretical insights into the alkali metal storage capability of ScSi2N4 monolayers, which is crucial for evaluating their potential as electrode materials in alkali-ion batteries.
The calculation formula for the sequential binding energy is as follows:
Here, , , and represent the total energies of the ScSi2N4 system with x adsorbed Li, Na, or K atoms, the pristine ScSi2N4 monolayer, and a single isolated Li, Na, or K atom, respectively. A decreasing trend in the sequential binding energy indicates that the adsorption becomes progressively less stable with increasing metal ion concentration. This can be attributed to the enhanced electrostatic repulsion between neighboring Li, Na, or K ions at higher coverages. The calculated sequential binding energies () for Li and Na adsorption on both β1- and β2-ScSi2N4 phases remain positive across the full range of x values (1–8), confirming that these phases can stably host up to eight Li or Na atoms without reaching adsorption saturation. In contrast, potassium adsorption shows a marked drop in binding energy at = 8 (0.18 eV for β1 and 0.38 eV for β2), indicating that K approaches its saturation limit at high coverage and is less favorably accommodated than Li or Na. (show in Table S3) Overall, Li and Na exhibit strong and stable interactions with both ScSi2N4 polymorphs, whereas K shows limited adsorption capacity at high loading. At the same time, these results suggest that, throughout the entire adsorption process, Li, Na, and K atoms energetically prefer to bind to the 2D ScSi2N4 surface rather than aggregating into bulk metallic clusters, highlighting their favorable dispersion and potential for energy storage applications.
According to the maximum number of Li, Na, and K atoms stably adsorbed on 2D β1-ScSi2N4 and β2-ScSi2N4, the capacity is defined as follows:
where represents the maximum number of intercalated ions, is Faraday’s constant (26,801 mAh/mol), and denotes the molecular weight. By first principles calculation we calculated the theoretical storage capacities of the β1 and β2 phases of ScSi2N4. For lithium and sodium intercalation with Li (X = 8), the capacity reaches 343.45 mA h/g, while for potassium with K, it is 171.12 mA h/g. The calculated theoretical capacities surpass those of several typical anode materials, such as TiS2 (240 mA h g−1 for Li) [41], Ta2CO2 (132.1 mA h g−1 for Li) [42], and YS2 (350 mA h g−1 for Na) [43]. These values are comparable to those of conventional anode materials, with the lithium and sodium capacities exhibiting excellent application potential.
The open-circuit voltage was also calculated to estimate the voltage output. The open-circuit voltage formula is:
Here, , , and denote the total energies of , and a single Li, Na, or K atom, respectively. The calculated open-circuit voltages (OCVs) for both β1- and β2-ScSi2N4 exhibit a monotonic decrease with increasing alkali-metal concentration for all three ions (Li, Na, K), as illustrated in Figure 8. Throughout the entire insertion range, all OCV values remain positive, indicating thermodynamically favorable adsorption without spontaneous metal release. Notably, the final OCVs at the maximum insertion concentration are still within the practical voltage window for anode applications. These results collectively suggest that both β1- and β2-ScSi2N4 possess the key electrochemical characteristics required for high-performance Li-, Na-, and K-ion battery anodes.
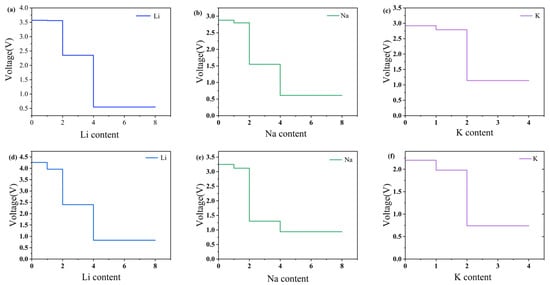
Figure 8.
Open-circuit voltage (OCV) profiles for (a) Li, (b) Na, and (c) K atoms adsorbed at the S4 site of 2D β1-ScSi2N4, and (d) Li, (e) Na, and (f) K atoms adsorbed at the S1 site of 2D β2-ScSi2N4. Figure (a–c) correspond to β1-ScSi2N4, and figure (d–f) correspond to β2-ScSi2N4.
Another critical feature of high-performance anode materials for rechargeable batteries is their rate capability, which originates from the mobility of the intercalated ions. To further evaluate the charge/discharge performance of ion batteries, the diffusion behavior of ScSi2N4 was investigated using the climbing image nudged elastic band (CI-NEB) method. S4 and S1 sites were chosen for simulation based on the adsorption energy analysis. One of the most favorable diffusion pathways at this site is illustrated in Figure 9a,b. The migration path of β1-ScSi2N4 follows S4 → S2 → S4, while that of β2-ScSi2N4 follows S1 → S2 → S1. The calculated diffusion energy barriers for Li, Na, and K ions in both β1- and β2-ScSi2N4 are notably low (Figure 9c,d), indicating favorable ion mobility. For comparison, these diffusion barriers are lower than or comparable to several reported anode materials, such as GeP3 (0.50 eV) [44] and T-graphene (0.44 eV) [29]. The diffusion barriers for Na and K are comparable to those of MoS2 (0.28 eV) [30] and Ti3C (0.18 eV) [45], respectively.
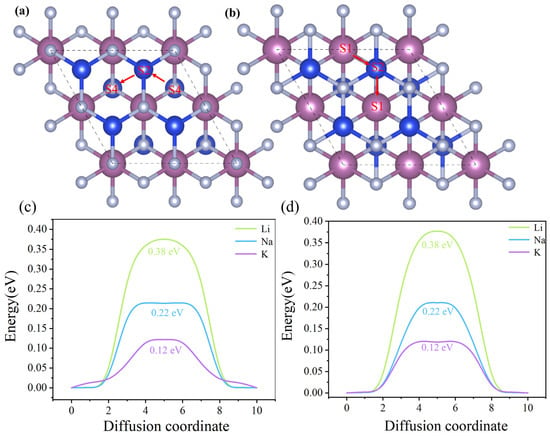
Figure 9.
(a,b) Top view of the diffusion paths of metal ions (Li, Na, and K) on monolayers of β1-ScSi2N4 and β2-ScSi2N4, S1, S2, and S4 denote different adsorption sites, the locations along the red arrows represent the migration paths, the dashed box represents the 2 × 2 × 1 supercell used for adsorption capacity calculation. and (c,d) diffusion energy barrier profiles of Li, Na, and K ions on β1-ScSi2N4 and β2-ScSi2N4 monolayers.
These results suggest that the 2D ScSi2N4 electrode offers excellent rate performance for rechargeable Li-, Na-, and K-ion batteries. In particular, Na ions exhibit faster diffusion than Li ions due to their larger atomic radius, which leads to a greater distance from the substrate and reduced repulsive interactions. Similarly, K ions diffuse even more rapidly than Na ions for the same reason.
To further clarify the influence of structural anisotropy on ion migration, three possible diffusion pathways were evaluated, and the lowest-barrier Path 1 was chosen as the reference. The migration energy barriers of Li+, Na+, and K+ along Path 2 and Path 3 in both configurations (see Figure S2 and Table S4) reveal that in β1, the barriers differ significantly between directions, demonstrating distinct anisotropic behavior—Li+ migrates more easily along Path 2, while Na+ and K+ prefer Path 3. This directional preference originates from variations in channel width and local potential fields. In contrast, β2 exhibits overall higher migration barriers and reduced directional differences, approaching isotropic diffusion. These findings demonstrate that the inherently low migration barriers of ScSi2N4 not only ensure excellent ion transport kinetics, but also highlight that the asymmetric channels in β1 can further enhance diffusion along specific directions, while the high-symmetry β2 suppresses such directional selectivity.
4. Conclusions
This study systematically investigates the structural stability, electronic properties, and potential applications of two-dimensional β1-ScSi2N4 and β2-ScSi2N4 as anode materials for rechargeable Li-, Na-, and K-ion batteries. Our first-principles calculations demonstrate that both phases possess low diffusion energy barriers for the considered alkali ions, indicating excellent ion mobility and suggesting potential for fast charge/discharge cycles. The materials also exhibit high theoretical capacities, reflecting their ability to accommodate a significant number of ions without structural degradation. Moreover, the predicted average open-circuit voltages lie within suitable ranges that align well with typical metal-ion battery operating voltages, indicating good compatibility with existing battery technologies. Taken together, these favorable structural and electrochemical properties highlight two-dimensional ScSi2N4 as a promising candidate for next-generation anode materials in diverse alkali-ion battery systems.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/nano15161268/s1, Figure S1: Schematic diagram of the four favorable adsorption sites on (a) β1-ScSi2N4 and (b) β2-ScSi2N4. In β1-ScSi2N4, S1, S2, S3, and S4 correspond to the top N atom above the Sc atom, the top of Si, the top of the bridge site between Si and N, and the N atom above the Si atom, respectively. In β2-ScSi2N4, S1, S2, S3, and S4 correspond to the top of Sc, the top of Si, the top of the bridge site between Si and Sc, and the N atom above the Si atom, respectively; Figure S2: (a–c) Maximum adsorption configurations of Li, Na, and K atoms on the β1-ScSi2N4 monolayer, and (d–f) on the β2-ScSi2N4 monolayer, in the order of Li, Na, and K; Figure S3: Ion diffusion paths and corresponding migration barrier curves for β1 and β2 configurations. (a) and (b) are schematic diagrams of the structures and path annotations. Red arrows indicate the diffusion direction, and blue and pink balls represent different atomic species, respectively. (c) and (d) are migration barrier curves for Li+, Na+, and K+ along paths 2 and 3. Curves of different colors correspond to different ion species. Barrier values are shown in Table S3; Table S1 shows the Bader charge analysis results for Sc, Si, and N atoms. The table lists the average Bader electron number, the corresponding valence electron number (ZVAL), and the calculated net charge (net charge = valence electron number - Bader electron number) for each atom; Table S2: Binding energies for metal (Li, Na) atoms at the S1, S2, S3, and S4 sites on 2D β1-ScSi2N4 and β2-ScSi2N4; Table S3: Sequential Binding Energies () for Li, Na, and K adsorption on β1- and β2-ScSi2N4; Table S4: Migration energy barriers of Li+, Na+, and K+ along different diffusion paths in the β1 and β2 configurations.
Author Contributions
Methodology, Y.L., H.F. and W.H.; Validation R.M.; Writing, Y.L., L.Y. and X.Q.; Review and Editing, Y.L., L.Y. and X.Q.; Visualization; Y.L.; Funding Acquisition, X.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 12204194), and the Program for the Development of Science and Technology of Jilin Province (No. 20250101059JJ).
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no competing financial interest.
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric Field Effect in Atomically Thin Carbon Films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Lee, G.H.; Yu, Y.J.; Cui, X.; Petrone, N.; Lee, C.H.; Choi, M.S.; Lee, D.Y.; Lee, C.; Yoo, W.J.; Watanabe, K.; et al. Flexible and Transparent MoS2 Field-Effect Transistors on Hexagonal Boron Nitride-Graphene Heterostructures. ACS Nano 2013, 7, 7931–7936. [Google Scholar] [CrossRef]
- Ji, H.G.; Solís-Fernández, P.; Erklllç, U.; Ago, H. Stacking Orientation-Dependent Photoluminescence Pathways in Artificially Stacked Bilayer WS2Nanosheets Grown by Chemical Vapor Deposition: Implications for Spintronics and Valleytronics. ACS Appl. Nano Mater. 2021, 4, 3717–3724. [Google Scholar] [CrossRef]
- Wang, X.; Jones, A.M.; Seyler, K.L.; Tran, V.; Jia, Y.; Zhao, H.; Wang, H.; Yang, L.; Xu, X.; Xia, F. Highly Anisotropic and Robust Excitons in Monolayer Black Phosphorus. Nat. Nanotechnol. 2015, 10, 517–521. [Google Scholar] [CrossRef] [PubMed]
- Tho, C.C.; Guo, S.-D.; Liang, S.-J.; Ong, W.-L.; Lau, C.S.; Cao, L.; Wang, G.; Ang, Y.S. MA2Z4 Family Heteorstructures: Promises and Prospects. arXiv 2023, arXiv:2304.02802. [Google Scholar] [CrossRef]
- Yin, Y.; Gong, Q.; Yi, M.; Guo, W. Emerging Versatile Two-Dimensional MoSi2N4 Family. Adv. Funct. Mater. 2023, 33, 2214050. [Google Scholar] [CrossRef]
- Hong, Y.-L.; Liu, Z.; Wang, L.; Zhou, T.; Ma, W.; Xu, C.; Feng, S.; Chen, L.; Chen, M.-L.; Sun, D.-M.; et al. Chemical Vapor Deposition of Layered Two-Dimensional MoSi2N4 Materials. Science 2020, 369, 670–674. [Google Scholar] [CrossRef] [PubMed]
- Wei, F.; Gao, S.; Jia, B.; Hao, J.; Chen, C.; Abduryim, E.; Guo, S.; Gao, L.; Lu, P. First-Principles Computational Study of Janus van Der Waals Layered VSiGeN4 as Anode Material for Li-Ion Battery. Colloids Surf. A Physicochem. Eng. Asp. 2024, 681, 132777. [Google Scholar] [CrossRef]
- Wang, L.; Shi, Y.; Liu, M.; Zhang, A.; Hong, Y.-L.; Li, R.; Gao, Q.; Chen, M.; Ren, W.; Cheng, H.-M.; et al. Intercalated Architecture of MA2Z4 Family Layered van Der Waals Materials with Emerging Topological, Magnetic and Superconducting Properties. Nat. Commun. 2021, 12, 2361. [Google Scholar] [CrossRef]
- Piquemal-Banci, M.; Galceran, R.; Godel, F.; Caneva, S.; Martin, M.B.; Weatherup, R.S.; Kidambi, P.R.; Bouzehouane, K.; Xavier, S.; Anane, A.; et al. Insulator-to-Metallic Spin-Filtering in 2D-Magnetic Tunnel Junctions Based on Hexagonal Boron Nitride. ACS Nano 2018, 12, 4712–4718. [Google Scholar] [CrossRef]
- Sivadas, N.; Okamoto, S.; Xu, X.; Fennie, C.J.; Xiao, D. Stacking-Dependent Magnetism in Bilayer CrI3. Nano Lett. 2018, 18, 7658–7664. [Google Scholar] [CrossRef]
- Fei, Z.; Huang, B.; Malinowski, P.; Wang, W.; Song, T.; Sanchez, J.; Yao, W.; Xiao, D.; Zhu, X.; May, A.F.; et al. Two-Dimensional Itinerant Ferromagnetism in Atomically Thin Fe3GeTe2. Nat. Mater. 2018, 17, 778–782. [Google Scholar] [CrossRef]
- Zhao, Z.; Duan, X.; Fang, X.; Wang, X.; Mi, W. Prediction of Electronic Structure and Magnetic Anisotropy of Two-Dimensional MSi2N4 (M = 3d Transition-Metal) Monolayers. Appl. Surf. Sci. 2023, 611, 155693. [Google Scholar] [CrossRef]
- Gao, S.; Wei, F.; Jia, B.; Chen, C.; Wu, G.; Hao, J.; Chen, W.; Wu, L.; Zou, W.; Lu, P. Two-Dimensional van Der Waals Layered VSi2N4 as Anode Materials for Alkali Metal (Li, Na and K) Ion Batteries. J. Phys. Chem. Solids 2023, 178, 111339. [Google Scholar] [CrossRef]
- Cui, Z.; Yang, K.; Ren, K.; Zhang, S.; Wang, L. Adsorption of Metal Atoms on MoSi2N4 Monolayer: A First Principles Study. Mater. Sci. Semicond. Process. 2022, 152, 107072. [Google Scholar] [CrossRef]
- Xu, J.; Wu, Q.; Sun, Z.; Mwankemwa, N.; Zhang, W.-B.; Yang, W.-X. First-Principles Investigations of Electronic, Optical, and Photocatalytic Properties of Au-Adsorbed MoSi2N4 Monolayer. J. Phys. Chem. Solids 2022, 162, 110494. [Google Scholar] [CrossRef]
- Huang, H.; Zhao, W.; Yang, M.; Xue, S.; He, Z.; Laref, A. Half-Metallic Behavior and Anisotropy of Two-Dimensional MoSi2N4/ScSi2N4 Heterojunction. J. Magn. Magn. Mater. 2024, 610, 172592. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, X.; Mi, W. Ferroelectric Polarization Tailored Spin Polarized Electronic Structure and Magnetic Anisotropy in Two-Dimensional ScSi2N4/CuInP2S6 Multiferroic Heterostructures. J. Phys. D Appl. Phys. 2023, 56, 505001. [Google Scholar] [CrossRef]
- Shepelin, N.A.; Sherrell, P.C.; Skountzos, E.N.; Goudeli, E.; Zhang, J.; Lussini, V.C.; Imtiaz, B.; Usman, K.A.S.; Dicinoski, G.W.; Shapter, J.G.; et al. Interfacial Piezoelectric Polarization Locking in Printable Ti3C2Tx MXene-Fluoropolymer Composites. Nat. Commun. 2021, 12, 3171. [Google Scholar] [CrossRef]
- Cohen, A.J.; Mori-Sánchez, P.; Yang, W. Challenges for Density Functional Theory. Chem. Rev. 2012, 112, 289–320. [Google Scholar] [CrossRef]
- Allouche, A.R. Gabedita—A Graphical User Interface for Computational Chemistry Softwares. J. Comput. Chem. 2011, 32, 174–182. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Paier, J.; Hirschl, R.; Marsman, M.; Kresse, G. The Perdew-Burke-Ernzerhof Exchange-Correlation Functional Applied to the G2-1 Test Set Using a Plane-Wave Basis Set. J. Chem. Phys. 2005, 122, 234102. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid Functionals Based on a Screened Coulomb Potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Togo, A.; Tanaka, I. First Principles Phonon Calculations in Materials Science. Scr. Mater. 2015, 108, 1–5. [Google Scholar] [CrossRef]
- Martyna, G.J.; Klein, M.L.; Tuckerman, M. Nosé-Hoover Chains: The Canonical Ensemble via Continuous Dynamics. J. Chem. Phys. 1992, 97, 2635–2643. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.-C.; Tang, G.; Geng, W.-T. VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, L.; Dai, X.; Chen, G.; Liu, G. A Record-High Ion Storage Capacity of T-Graphene as Two-Dimensional Anode Material for Li-Ion and Na-Ion Batteries. Appl. Surf. Sci. 2020, 527, 146849. [Google Scholar] [CrossRef]
- Jing, Y.; Zhou, Z.; Cabrera, C.R.; Chen, Z. Metallic VS2 Monolayer: A Promising 2D Anode Material for Lithium Ion Batteries. J. Phys. Chem. C 2013, 117, 25409–25413. [Google Scholar] [CrossRef]
- Molina-Sánchez, A.; Wirtz, L. Phonons in Single-Layer and Few-Layer MoS2 and WS2. Phys. Rev. B 2011, 84, 155413. [Google Scholar] [CrossRef]
- Yu, Q.; Huang, H.; Zhao, W.; Xue, S.; Tong, R.; Chen, J.; Hu, Y.; Laref, A.; Luo, S. Electronic and Half-Metallic Properties of Novel Two-Dimensional YSi2N4 Monolayer by Theoretical Exploration. Mater. Sci. Semicond. Process. 2024, 169, 107862. [Google Scholar] [CrossRef]
- Yan, X.; Han, F.; Yao, Y.; Zhang, X.; Liu, Y.; Yang, G. Semiconducting Cr2BN Monolayer with Antiferromagnetic Order. Phys. Rev. B 2023, 108, 174402. [Google Scholar] [CrossRef]
- Sun, Y.; Zhuo, Z.; Wu, X.; Yang, J. Room-Temperature Ferromagnetism in Two-Dimensional Fe2Si Nanosheet with Enhanced Spin-Polarization Ratio. Nano Lett. 2017, 17, 2771–2777. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, J.; Wang, Q.; Chen, X.; Kawazoe, Y.; Jena, P. Penta-Graphene: A New Carbon Allotrope. Proc. Natl. Acad. Sci. USA 2015, 112, 2372–2377. [Google Scholar] [CrossRef]
- Waller, I. Dynamical Theory of Crystal Lattices by M. Born and K. Huang. Acta Crystallogr. 1956, 9, 837–838. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.X.; Du, Y.L.; Cui, C. First-Principles Study on Structural, Electronic and Elastic Properties of Graphene-like Hexagonal Ti2C Monolayer. Comput. Mater. Sci. 2014, 83, 290–293. [Google Scholar] [CrossRef]
- Cooper, R.C.; Lee, C.; Marianetti, C.A.; Wei, X.; Hone, J.; Kysar, J.W. Nonlinear Elastic Behavior of Two-Dimensional Molybdenum Disulfide. Phys. Rev. B 2013, 87, 035423. [Google Scholar] [CrossRef]
- Hu, T.; Wan, W.; Ge, Y.; Liu, Y. Strain-Tunable Magnetic Order and Electronic Structure in 2D CrAsS4. J. Magn. Magn. Mater. 2020, 497, 165941. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A Fast and Robust Algorithm for Bader Decomposition of Charge Density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Huang, S.Y.; Kavan, L.; Exnar, I.; Grätzel, M. Rocking Chair Lithium Battery Based on Nanocrystalline TiO2 (Anatase). J. Electrochem. Soc. 1995, 142, L142–L144. [Google Scholar] [CrossRef]
- Chen, Z.; Huang, S.; Yuan, X.; Gan, X.; Zhou, N. A Comparative Study of M2CS2 and M2CO2 MXenes as Anode Materials for Lithium Ion Batteries. Appl. Surf. Sci. 2021, 544, 148861. [Google Scholar] [CrossRef]
- Guo, Y.; Bo, T.; Wu, Y.; Zhang, J.; Lu, Z.; Li, W.; Li, X.; Zhang, P.; Wang, B. YS2 Monolayer as a High-Efficient Anode Material for Rechargeable Li-Ion and Na-Ion Batteries. Solid. State Ion. 2020, 345, 115187. [Google Scholar] [CrossRef]
- Zhang, C.; Jiao, Y.; He, T.; Ma, F.; Kou, L.; Liao, T.; Bottle, S.; Du, A. Two-Dimensional GeP3 as a High Capacity Electrode Material for Li-Ion Batteries. Phys. Chem. Chem. Phys. 2017, 19, 25886–25890. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Zhao, Z.; Liu, L.; Zhang, S.; Xu, H.; Yang, G. TiC3 Monolayer with High Specific Capacity for Sodium-Ion Batteries. J. Am. Chem. Soc. 2018, 140, 5962–5968. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).