Abstract
Nickel(II) complexes of mono-functionalized pyridine-tetraazamacrocycles (PyMACs) are a new class of catalysts that possess promising activity similar to biological peroxidases. Experimental studies with ABTS (2,2′-azino-bis(3-ethylbenzothiazoline-6-sulfonic acid), substrate) and H2O2 (oxidant) proposed that hydrogen-bonding and proton-transfer reactions facilitated by their pendant arm were responsible for their catalytic activity. In this work, density functional theory calculations were performed to unravel the influence of pendant arm functionalization on the catalytic performance of Ni(II)–PyMACs. Generated frontier orbitals suggested that Ni(II)–PyMACs activate H2O2 by satisfying two requirements: (1) the deprotonation of H2O2 to form the highly nucleophilic HOO−, and (2) the generation of low-spin, singlet state Ni(II)–PyMACs to allow the binding of HOO−. COSMO solvation-based energies revealed that the O–O Ni(II)–hydroperoxo bond, regardless of pendant arm type, ruptures favorably via heterolysis to produce high-spin (S = 1) [(L)Ni3+–O·]2+ and HO−. Aqueous solvation was found crucial in the stabilization of charged species, thereby favoring the heterolytic process over homolytic. The redox reaction of [(L)Ni3+–O·]2+ with ABTS obeyed a 1:2 stoichiometric ratio, followed by proton transfer to produce the final intermediate. The regeneration of Ni(II)–PyMACs at the final step involved the liberation of HO−, which was highly favorable when protons were readily available or when the pKa of the pendant arm was low.
1. Introduction
Oxidation reactions involving electron transfer are customary in the study of biological processes, in organic synthesis, and in the production of novel energy sources, among others [1]. While reactions of this type are essentially fast, the rate of electron transfer between two redox species may be hastened if a more favorable reaction pathway is conceived in the presence of a catalyst. For reactions involving hydrogen peroxide (H2O2) as an oxidant, typical catalysts usually involve transition metals (e.g., Fenton reagent: Fe2+ + H2O2) [2,3,4,5]. From the studies reported to date, two general types of mechanisms for H2O2 activation have been proposed: (1) the radical mechanism that involves HO· and HOO· that both create a redox cycle with the metal species [6]; and (2) the peroxide complex mechanism, which causes a two-electron oxidation of the metal, leading to the heterolytic cleavage of the peroxide O–O bond [7]. The activation of H2O2 commences when the oxidant coordinates to the metal center of the catalyst via nucleophilic addition [8,9]. Its rate of binding to the complex is affected by the nature of the metal, the ligands, and the solution matrix [10]. Once the oxidant is bound, those complexes that contain metals with a single stable non-zero oxidation state (e.g., Al, Be, Mg, Ca, Zn, Cd, etc.) will not participate in the electron transfer reaction, although they function as Lewis acids. In contrast, complexes of transition metals that have at least two relatively stable oxidation states (e.g., Fe, Ni, Co, Cu, Mn, etc.) are typical for the Fenton-type chemistry and will serve as a source and sink of electrons during the reaction [11].
Peroxidases are among the natural enzymes that have high efficiency and specificity for H2O2-driven oxidation of substrates [12,13,14]. However, similar to other enzymes, peroxidases are expensive and are prone to denaturation in response to extreme conditions [15,16,17]. With such a disadvantage comes the initiative to design cheap metal-based biomimetics with improved catalytic sustainability over a wide range of pH and temperatures [18]. The most prominent of which are iron-based complexes, yet many other compounds containing metals such as Mn, Cu, Co, Ru, V, and Ti have also been reported [9,19,20,21,22,23]. In 2009, Organo and colleagues synthesized novel Ni(II) complexes of monofunctionalized pyridine-tetraazamacrocycles (PyMACs) (Figure 1), which exhibited catalytic activity toward the one-electron oxidation of 2,2′-azino-bis(3-ethylbenzo thiazoline-6-sulfonic acid) (ABTS) with H2O2 as the oxidant [24]. These catalysts, bearing different pendant arms, displayed remarkable reaction kinetics where they accelerated the production of ABTS+· at varying rates. Ni(II)–PyMACs of acidic (pKa < 7) pendant arms were observed to possess higher activity than Ni(II)–PyMACs with a basic functional group. Parallel findings were also published for copper complexes of analogous macrocycle structures, where the pentadentate carboxylic acid complex demonstrated mild peroxidase-like activity, while the unfunctionalized one showed no activity at all [25]. So far, among the assumptions highlighted in the mechanism were the possible interactions between the coordinated peroxide and the pendant arm via hydrogen bonding and intramolecular proton transfer. This scenario has already been implicated in carboxyl-appended “hangman” metalloporphyrins in which H2O2 is activated through proton-coupled electron transfer that facilitates the cleavage of its O–O bond [26]. While the study on Ni(II)–PyMACs provided preliminary evidence of the influence of functionalization on their catalytic activity, no succeeding reports have ever investigated the reaction mechanism by which the pendant arm group facilitates the oxidation of the substrate in the presence of H2O2.
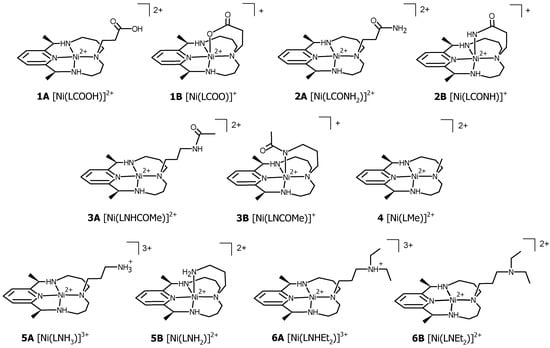
Figure 1.
Molecular structures of Ni(II)–PyMAC (pyridine-tetraazamacrocycle) complex ions 1–6. A and B denote protonated and deprotonated forms, respectively (except structure 4).
In the present work, insights into the role of Ni(II)–PyMAC pendant arm in the oxidation of ABTS by H2O2 are presented. Density functional theory (DFT) calculations were employed to model the reaction systems [27,28,29,30,31,32]. The nature, energy, and reactivity of Ni(II)–PyMACs were examined together with the potential intermediates and transition states suggested by the collective information reported in the literature [8,13,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47]. The selection of the most plausible reaction mechanism was based primarily on the frontier orbitals of the involved structures, their relative stabilities, the estimated O–O bond dissociation energies, and the ease of electron transfer from ABTS to active oxidative species using energy levels of highest occupied molecular orbitals (HOMO) and lowest unoccupied molecular orbitals (LUMO). The general pendant arm (L) of all hypothetical structures presented in this paper was treated neutral in charge unless stated otherwise.
Proposed Reaction Pathways
The mediated one-electron oxidation of ABTS by Ni(II)–PyMAC catalysts in the presence of H2O2 was initially hypothesized to follow either of the two reaction pathways (A and B) shown in Scheme 1 and Scheme 2, respectively. The pendant arm of the catalyst is proposed to undergo a reversible proton dissociation to form the acid–base pair. The key primary step of the catalytic cycle, regardless of the form of the catalyst, is the binding of H2O2 to the nickel complex either as is or in the form of the highly nucleophilic HOO− species made possible by the presence of an abstracting base. Either way, the O–O bond of the first intermediate undergoes cleavage (either homolytic or heterolytic) to generate the active nickel-oxo species. The four spin multiplicities (i.e., S = 0, 1/2, 1, and 3/2) of nickel-oxo are all accepted as candidate forms of the active intermediate as necessary. Regardless of the spin state, ABTS undergoes one-electron oxidation via electron transfer to the nickel-oxo species, which may or may not be coupled with a proton, depending on the pathway followed. This step subsequently leads to the formation of ABTS+ and nickel(II)-hydroxo complexes. The terminal OH of the final intermediate then leaves the complex through a proton, either free or from the pendant arm, to give back the resting state of the catalyst.
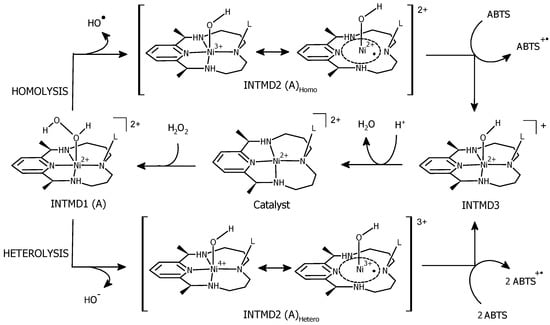
Scheme 1.
Proposed pathway A for Ni(II)–PyMAC-mediated one-electron oxidation of ABTS using H2O2 as the oxidant. INTMD1, INTMD2, and INTMD3 refer to the first, second, and third intermediates. ABTS: 2,2′-azino-bis(3-ethylbenzothiazoline-6-sulfonic acid).
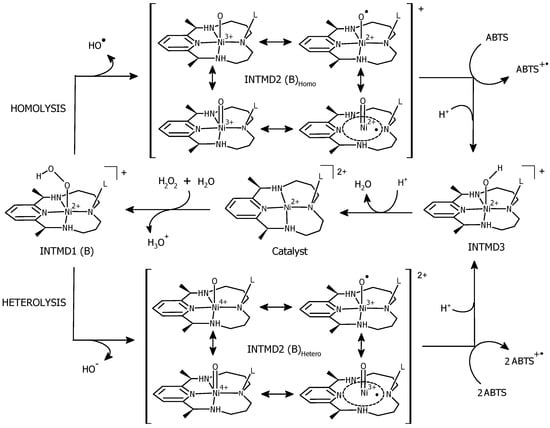
Scheme 2.
Proposed pathway B for Ni(II)–PyMAC-mediated one-electron oxidation of ABTS using H2O2 as the oxidant. INTMD1, INTMD2, and INTMD3 refer to the first, second, and third intermediates.
2. Computational Methods
All density functional theory calculations were carried out using a generalized gradient approximation (GGA) of Becke’s exchange with Lee Yang and Parr (BLYP) correlation functional [48,49], as employed in the Amsterdam Density Functional program (ADF 2014) [50,51,52,53,54,55,56,57,58,59,60]. The selection of BLYP as the functional was based on its years of widespread application in DFT-based studies [61,62,63,64] and its relatively cheap computational cost with respect to other methods. At this level of theory, the Slater-type triple-ζ basis sets extended with a single polarization function (TZP) were used to describe all the atoms (H, N, C, O, and Ni), and the 1s electrons of N, C, and O, as well as 1s–2p electrons of Ni, were treated as frozen cores. The modeled molecules in the study included all Ni(II)–PyMAC-L (where L = LCOOH, LCOO−, LCONH2, LCONH−, LNHCOMe, LNCOMe−, LMe, LNH3+, LNH2, LNHEt2+, or LNEt2), ABTS, ABTS+·, H2O2, H2O, H3O+, HO−, and HO·. The Ni metal in the macrocycles was considered free from coordination of the counterion, ClO4−, but not from nucleophilic pendant arms, which served as axial ligands in some complexes. The starting geometries of all catalysts were constructed similarly to how they were previously described [24].
To capture the intrinsic properties and the possible electronic variations of structures in response to solvation, separate calculations were performed in the gas phase and in solution. The Conductor-like Screening Model (COSMO) [65,66,67], as implemented in ADF, was utilized to calculate energies in solution where each solute structure was embedded in a molecule-shaped cavity of the chosen dielectric medium. The dielectric constant and radius of the rigid sphere were set to 78.39 and 1.93 Å, respectively to describe water as the solvent.
The initial geometries of all molecular models, except for the transition states, were fully optimized using the default integration accuracy and convergence criteria of the software. For systems with hard-to-converge SCF, corresponding occupation numbers were specified in the input to make sure Aufbau solutions were obtained. SCF convergence criterion was also tightened to 1 × 10−5 from the default of 1 × 10−3. The optimized spin states of the structures with the lower electronic energies were taken as their electronic ground states, although all spin multiplicities were considered for the succeeding vibrational frequency calculations. To verify predicted ground states of structures with closely lying states, single-point calculations using BLYP-related hybrid functionals (B3LYP and B3LYP*) were performed on the optimized geometries.
For the transition states, linear transit (LT) calculations were first carried out, where one or a combination of the three LT parameters (i.e., distance, angle, dihedral angle) were set and defined in the input, getting initial and final values. All coordinates were frozen to run a sequence of single-point calculations at equidistant steps along the LT path. The one with the highest energy among all geometries was selected to undergo the final and true transition state search. The same convergence criteria for both the geometry and SCF cycles were applied in the transition state search as those defined in geometry optimization runs. The nature of all the stationary points generated was verified through vibrational frequency calculation.
After obtaining all the optimized structures from geometry optimization and transition state search, the generated Hessian matrices were calculated analytically by doing vibrational frequency. One-point numerical differentiation, symmetric displacements, and medium integration accuracy were applied purposely to minimize the computational time. Imaginary frequencies were checked for all optimized structures to confirm whether the stationary points are local minima (equilibrium geometries) or first-order saddle points (transition states). Statistical thermal analysis (i.e., to calculate for nuclear internal energy and entropy) was carried out at a constant temperature and pressure of 298.15 K and 1 atm, respectively. The corresponding zero-point vibrational energies (ZPE) were derived automatically from the measured frequencies and were included in all quoted energies.
3. Results and Discussion
3.1. Structural Characterization of Ni(II)–PyMAC Complexes
Fully optimized structures of mono-functionalized Ni(II)–PyMAC complexes are shown in Figure 2, where both the acid and base forms of each catalyst were studied separately, except complex 4. The decision to investigate both forms of the catalysts was influenced by previous findings that the protonation of 5B to 5A reduced the catalytic strength of the original complex during the first few seconds of the reaction but made it acquire a much longer shelf-life [24]. These notable differences between this acid–base pair prompted us to consider that the functional state of the pendant arm affects the catalytic action of these complexes. Both forms must be treated separately to be able to elucidate several possible mechanisms of action for these catalysts.
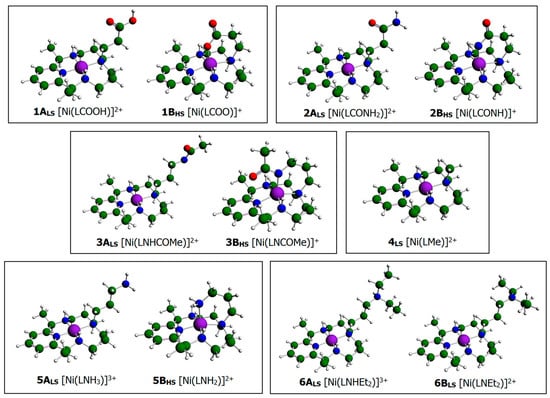
Figure 2.
Density functional theory (DFT)-optimized electronic ground states of Ni(II)–PyMAC complex cations 1–6 using BLYP functional [where: green—carbon, blue—nitrogen, red—oxygen, white—hydrogen, and purple—nickel]. A and B denote protonated and deprotonated forms, respectively (except model 4). Corresponding spin states are indicated as subscripts, LS or HS. BLYP: Becke-Lee-Yang-Parr.
The optimized structures of complexes 1 to 6 supported the idea that pendant arms have different binding modes toward the nickel metal. The lowest energy conformation of the three basic complexes, 1B, 2B, and 3B, adopted a five-coordinate square pyramidal geometry, while their protonated counterparts favored the slightly distorted, four-coordinate square planar conformation. Deprotonation of the pendant arms increased their nucleophilic character and allowed them to coordinate readily to the Lewis acidic metal at the axial position. In fact, with the strong sigma-donor interaction in these three complexes, specifically between the orbital of the axial ligand and the orbital of the nickel metal, the separation gap between their respective HOMOs and LUMOs was small, which allowed them to achieve a high-spin (S = 1) electronic ground state. In contrast, optimization of the structures without available axial ligands, such as 4, all the protonated forms, and 6B, only led to their low-spin (S = 0) states, as expected. These results regarding the ground state of the complexes were in agreement to what was previously reported [24], except for 5B, which after optimization in both spin states emerged to be more stable in the singlet rather than in the triplet form by a small free energy difference of 0.19 kcal mol−1. We can account for such nonconformity to the fairly weak Ni-Naxial interaction in 5B brought by a lesser nucleophilic character of neutral amine relative to other basic pendant arms. As a result, the energy gap between the low-spin and high-spin states is small, to which the BLYP functional incorrectly predicted the ground state. This incongruity with experimental findings is not peculiar in most GGA functionals where the low-spin multiplicity is often over-stabilized when calculating weak-field complexes [68,69,70]. Fouqueau et al. (2004) believed that such a phenomenon is caused by the underestimation of the Fermi correlation and is normally resolvable by the inclusion of the Hartree–Fock (HF) exchange parameter into hybrid functionals [71]. The energy splitting was shown to depend linearly on the coefficient of exact exchange admixture and that hybrid functionals provided much more reasonable values [72,73]. Thus, at this point, we were prompted to calculate the bonding energy of 5B at multiple spin states using BLYP and two hybrid functionals —B3LYP and B3LYP* to check for possible discrepancies in the resulting ground state. Based on the obtained values (Table 1), high-spin/low-spin state separation is more pronounced when employing functionals with a higher percentage of HF. B3LYP (with 20% exact exchange) resulted in a triplet state that is 11.5 kcal mol−1 more stable than its corresponding singlet pair. Similarly, B3LYP* also correctly predicted the ground state of 5B with a 7.7 kcal mol−1 energy gap between the two spin multiplicities. Recognizing this as a limitation of GGA BLYP, we eventually accepted the high-spin (S = 1) to be the ground state of 5B consistent with the previous experiment. All calculated energies from the statistical thermal analysis of fully optimized Ni(II)–PyMAC catalysts (in both spin states) are summarized in Table 2.

Table 1.
High-spin/Low-spin bond energy splitting (kcal mol−1) in 5B complex as derived from single-point calculations at selected exchange-correlation (XC) functionals. A positive value in energy splitting indicates that the predicted ground state is high-spin.

Table 2.
Calculated energies in the gas phase of optimized Ni(II)–PyMAC structures in their low-spin (S = 0) and high-spin (S = 1) states at 298.15 K and 1 atm. U, H, S, and G are the internal energy, enthalpy, entropy, and Gibbs free energy, respectively, corrected with ZPE (zero-point vibrational energy).
In comparison to the experimentally determined crystal structures by Herrera et al. (2003) and Organo et al. (2009), the computed geometric parameters of the catalysts (Table 3) were not much different [24,74] (refer to Figure 3 for the atomic labels). There were only slight elongations in Ni–Ni bond lengths ranging from 0.039 to 0.083 Å for 1A, 0.050 to 0.068 Å for 6B, 0.032 to 0.138 Å for 6A, and 0.035 to 0.086 Å for 5BHS, and bond length shortening between 0.047 and 0.101 Å for 2A. The Ni metals in the optimized models were also slightly undisplaced from the ring except only for 2A, which showed a 0.90° constriction of the N1–Ni–N3 bond angle due to the considerable protrusion of Ni above the equatorial plane. Nonetheless, the results of the optimization were consistent throughout all types of Ni(II)–PyMAC complex, where the four Ni–Nequatorial bonds were longer in the deprotonated forms than in their conjugate acid counterparts. The pendant arms in these forms could favorably act as axial ligands and slightly draw the nickel metal out of the plane.

Table 3.
Bond lengths (Å) and angles (°) for the optimized electronic ground states of protonated and deprotonated forms of Ni(II)–PyMAC complex cations. Experimental pKas are also shown.
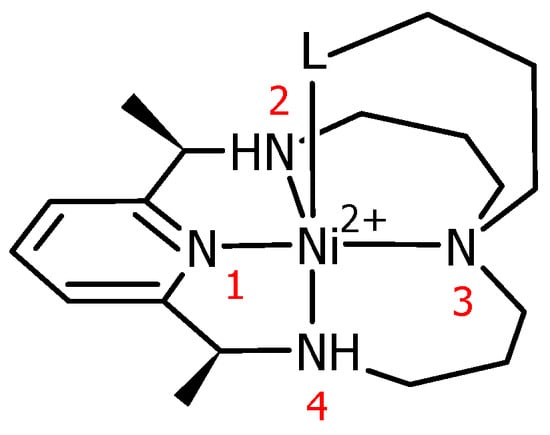
Figure 3.
General representation of Ni(II)–PyMAC complex. Nitrogen atoms are numbered accordingly. L stands for the part of the pendant arm that coordinates axially to the Ni metal center.
3.2. H2O2 Activation and Reactivity with Ni(II)–PyMACs
The binding of H2O2 to the complex is a crucial step in the catalytic process of Ni(II)–PyMACs. Two possible fates of H2O2 (Scheme 3) were investigated: (a) straightforward coordination to Ni via linkage to one of its two oxygen atoms to form [(L)Ni2+–HOOH]2+; and (b1/2) deprotonation by a base to generate HOO−, which will eventually bind to the complex to form [(L)Ni2+–OOH]+. To determine the more plausible form of the first intermediate (INTMD1), complex 4 was studied as the model catalyst. The optimization of high-spin (S = 1) [(LMe)Ni2+–HOOH]2+ and [(LMe)Ni2+–OOH]+ revealed that pathway (a) is less likely to be the first reaction step regardless if it is in the gas phase or in solution. For [(LMe)Ni2+–HOOH]2+, the coordinate covalent bond between Oaxial and Ni elongated to the extent that it eventually disappeared during optimization. The presence of the unabstracted proton made the terminal oxygen of H2O2 weak to coordinate axially to Ni. In fact, its energy level diagram consistently showed an unoccupied orbital below HOMO, which suggested that the structure was not in the ground state when calculated in high-spin. In contrast, geometry optimization of high-spin [(LMe)Ni2+–OOH]+ resulted in a distinct binding of hydroperoxo with Ni and followed Aufbau occupations in its energy-level diagram.
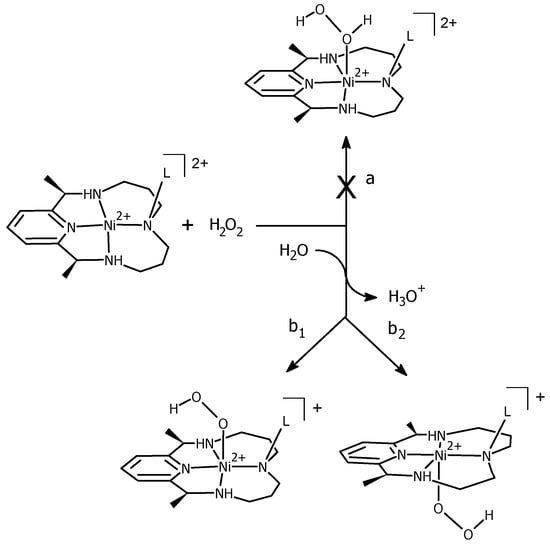
Scheme 3.
Proposed reaction pathways for the formation of the first intermediate (INTMD1).
While Ni(II)–PyMACs can take on a slightly distorted square planar geometry, it can be assumed that HOO− can coordinate axially to Ni either above (b1) or below (b2) the equatorial plane of the macrocycle. To determine which side is more susceptible to binding, we optimized [(LMe)Ni2+–OOH]+ with HOO− positioned below and compared its energy with that of the overhead-coordinated HOO−. Based on the bonding energies in the gas phase, the nucleophilic attack of hydroperoxo ion to Ni is more favorable above than below the plane by approximately 2.6 kcal mol−1. These close energies between the two forms suggest that HOO− can attack the nickel metal either way. However, the top-axial coordination is preferred, since Ni tends to protrude above the plane due to the presence of the pendant arm. As Ni gets more exposed above than below, the preference of HOO− to bind at this location also increases. With this result, we took the “overhead” [(L)Ni2+–OOH]+ as the most plausible form of INTMD1 across all catalysts, and the attempt to bind HOO− anti to the axially bound pendant arm at this point was no longer made.
HOMO orbitals of optimized Ni(II)–PyMACs in the gas phase (Figure 4) display the portions of the complexes that are likely to interact with H2O2 before it binds to Ni. Note that for complexes with coordinated pendant arms, HOMO for both the high-spin and low-spin structures are shown. Based on the shape and location of these orbitals, we can group the 11 catalysts into four: (G1) 1A, 4, 5A, and 6A; (G2) 2A, 3A, and 6B; (G3) 1B and 5B; and (G4) 2B and 3B. G1 catalysts are those that have HOMO localized on the nickel center, specifically of the orbital type , which is in contrast to G2 catalysts that have lobes mainly confined in the pendant arm. On the other hand, low-spin G3 and G4 catalysts have their highest-energy electrons occupy the orbitals, but they differ in their high-spin states where G3 HOMO is of the type , while that of G4 is . Using this classification (Table 4), the catalysts of the same group will follow the same mechanism in activating H2O2 toward binding to the complex. There are two requirements for this step to proceed: (1) H2O2 should first be deprotonated by a base to produce the more nucleophilic HOO−, as discussed earlier; and (2) the top-axial position of Ni in the complex should first be free and available for the consequent binding of HOO−. The first requirement renders G2, G3, and G4 catalysts the advantage over G1 in forming INTMD1, since they can abstract a proton from H2O2 using the electrons (HOMO) of their pendant arms. In terms of this ability, G4 catalysts are the strongest since they are the most basic, followed by G3 and then G2. G1 catalysts, in contrast, would require the presence of any other base just to deprotonate H2O2 before binding to them. Meanwhile, the second requirement implies that high-spin complexes specifically G3 and G4 should have their pendant arms “off” of Ni before the oxidant can bind either below or above. G3 catalysts in their high-spin cannot favorably react with H2O2 due to the absence of proper symmetry and shape of HOMO, which requires them to turn to low-spin states before they can deprotonate H2O2 by a significant overlap of their orbitals. High-spin G4 catalysts in comparison to G3 can meet the first condition but not the second. The pendant arms of G4 hardly dissociate from Ni and thus, HOO− cannot bind easily on top. In fact, high-spin G4 HOMO can overlap sufficiently with LUMO of H2O2 so that they do not need to detach their amide pendant arms from Ni to deprotonate the oxidant. This makes them the least effective catalysts among the four groups being classified. The prerequisite to change from high-spin to low-spin before HOO− can coordinate to the complex is further supported by the HOMO () orbitals of the catalysts, in which all of them provide the same molecular platform only when they are in low-spin. Although coordination to Ni below the plane is also possible, it cannot render any of the catalysts better than the rest as they are all capable of the same. Thus, it can be inferred that at the first reaction step of the mechanism, G3 complexes may be the most effective, followed by G2, then G1, and lastly, G4.
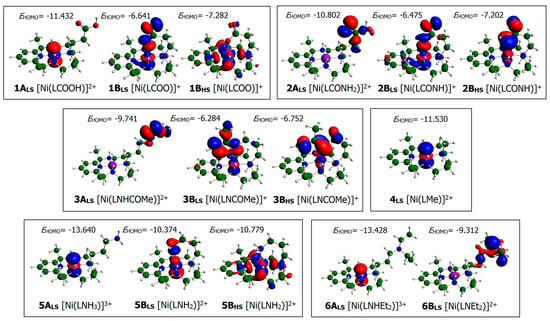
Figure 4.
Highest occupied molecular orbitals (HOMO) of optimized Ni(II)–PyMAC complexes (gas phase) in their allowed spin states: low-spin (S = 0) and high-spin (S = 1). EHOMO values are the corresponding orbital energies in eV. Red and blue orbitals denote opposite signs. Note that structures with no axial ligand coordinated to the Ni metal exist only as singlet structures. Complexes are labeled in the same way as in Figure 1.

Table 4.
Classification of Ni(II)–PyMAC complexes based on their reactivity with H2O2 as predicted using BLYP-generated frontier orbitals.
Interestingly, calculations of Ni(II)–PyMACs carried out with solvation effects resulted in a slightly different view of possible catalyst–H2O2 interaction. By orbital shape, all four-coordinate complexes except 6B (i.e., 1A, 2A, 3A, 4, 5A, and 6A) fell under the same group, and the rest (i.e., 1B, 2B, 3B, and 5B), which all have axially coordinated pendant arms, formed another. Solvation with water stabilizes the high energy electrons located along the pendant arms of 2A, 2B, 3A, and 3B. Carbonyl atoms (O, N, and H) form hydrogen bonding with the concentric shell of water molecules. In effect, four-coordinate complexes rather achieve HOMO similar to G1 of the previous classification, and five-coordinate complexes acquire similar to G3. 6B is a special case given that hydrogen bonding with N is forbidden due to the steric hindrance and electron-donating abilities of two ethyl groups. The HOMO of 6B is the same for both cases. Nonetheless, the addition of a water cavity generally masks the ability of some pendant arms to possibly react with H2O2. For this step, gas-phase calculations were better at differentiating the pendant arms in terms of their reactivity with H2O2.
3.3. Structure and Energetics of Nickel-Hydroperoxo Species
Nickel-hydroperoxo intermediates were found identical for complexes that form an acid–base pair, such as in 1A/1B, 5A/5B, and 6A/6B. However, for those with amide pendant arms (e.g., 2A/2B and 3A/3B), the pairs did not immediately produce identical nickel-hydroperoxo species right after the first reaction step. The LUMO of the first intermediate of 2A and 3A displayed an orbital type different from those of other catalysts’ INTMD1s. Orbital lobes of their LUMO were strictly confined in the carbonyl-amide functional group of their pendant arms (Scheme 4). By shape and symmetry, these orbitals were in nature. Their pendant arms rather formed a protonated Schiff base as a result of nitrogen’s lone pair forming a pi-bond with carbonyl carbon. This can shuttle the oxygen to abstract a proton either from H2O or H2O2. The positive charge of Schiff base rendered it susceptible to deprotonation by free basic species, leading to new intermediates that were identical to INTMD1 of 2B and 3B. Such a case would turn out different if calculations were made in aqueous solution. Water molecules will stabilize the iminium group by electrostatic attraction and hydrogen bonding. This is supported by the fact that after applying solvation effects, the intermediate generated LUMO, which exactly matches those of other Ni-OOH. However, neutralization by proton-transfer is still favorable, since it would reduce the energy of the intermediate by −19.4 kcal mol−1. This additional step before forming INTMD1 renders 2A and 3A the disadvantage similar to G1 catalysts (1A, 4, 5A, and 6A), whose reactivity also requires the assistance of H2O or any free base. Nonetheless, the 2A and 3A reaction mechanism still passes through the formation of INTMD1, which is a prerequisite step in forming the active intermediate. For consistency, we considered the Ni–OOH complex with neutral imine as the INTMD1 of 2A and 3A while naming the intermediate with protonated Schiff base as INTMD0. With the LUMO of all the catalysts’ INTMD1 now being the same (), it is likely that they follow the same pathway in O–O bond breaking. Optimized INTMD1 structures for all catalysts had only slight differences in their O–O and Ni–OOH bond lengths, with values ranging from 1.487–1.503 Å and 1.973–2.000 Å, respectively.
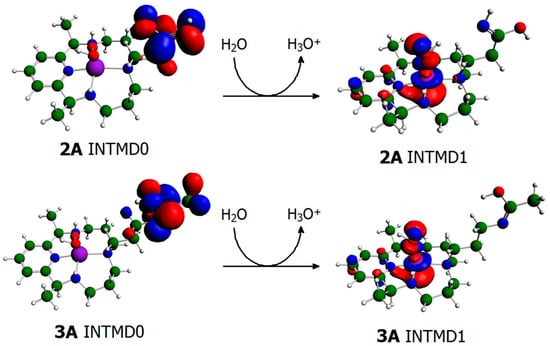
Scheme 4.
Lowest unoccupied molecular orbital (LUMO) of the pseudo-first (INTMD0) and pseudo-second (INTMD1) intermediates of amide-containing Ni(II)–PyMACs calculated in the gas phase.
3.4. O–O Bond Cleavage: Heterolytic vs. Homolytic
Following the coordination of HOO− to the complex, the O–O bond of the generated nickel-hydroperoxo complex is proposed to undergo cleavage via either of the two pathways shown in Scheme 5. Many studies about oxidation catalysts similar to Ni(II)–PyMACs have reported contrasting evidence regarding which process is more favored [8,38,40,41,42,43]. In this study, we first identified the possible intermediates arising from each of the two pathways. Heterolytic cleavage of the O–O bond generates HO−, leaving the complex behind in either of the four forms: [(L)Ni4+=O]2+, [(L)Ni3+–O·]2+, [(L)Ni4+–O]2+, and [(L·)Ni3+=O]2+. On the other hand, homolysis results in free HO· radical species with four possible reactive intermediates, [(L·)Ni2+=O]+, [(L)Ni3+–O]+, [(L)Ni2+–O·]+, and [(L)Ni3+=O]+. Across all catalysts, the optimization of nickel-oxo geometries both in the gas phase and in solution only led to [(L)Ni3+–O·]2+ for the heterolytic pathway, while both [(L)Ni2+–O·]+ and [(L)Ni3+–O]+ species were produced for the homolytic pathway. These forms were supported by the calculated spin density distribution of Ni and Oaxial in these structures (Table 5). Note that regardless of catalyst type, [(L)NiO]2+ was optimized only in high-spin (S = 1), while both the high-spin (S = 3/2) and low-spin (S = 1/2) were allowed for [(L)NiO]+. For the heterolytic pathway, the [(L)Ni3+–O·]2+ radical species were favored based on the two unpaired electrons predicted to be located separately in Ni and Oaxial. For the homolytic pathway, the (Ni) and (O) values of quartet [(L)NiO]+ indicated the presence of two unpaired electrons in Ni and one unpaired electron in Oaxial, supporting the formation of [(L)Ni2+–O·]+. In its low-spin state, the unpaired electron had no uniform location across all catalysts. It predominantly resided either in Oaxial for some catalysts supporting the existence of [(L)Ni2+–O·]+, or in Ni metal suggesting [(L)Ni3+–O]+ species as the other homolytic intermediate. However, we believe that oxygen is singly bonded to Ni, since the optimized Ni–O bond lengths (1.8–1.9 Å) lie within the typical range of nickel-oxo single bonds [75], ruling out the formation of [(L)Ni3+=O]+. The energy of the high-spin (S = 3/2) structure was also calculated to be approximately 8 kcal mol−1 less than that of the low-spin (S = 1/2) structure. This prediction was consistent across all types of pendant arm and irrespective of whether calculations were made in the gas phase or in solution.
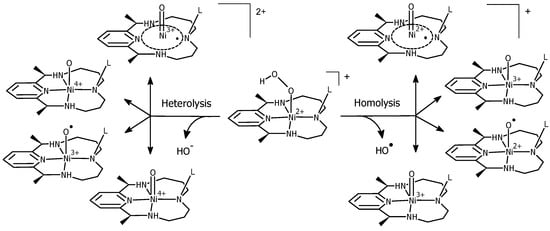
Scheme 5.
Proposed reaction pathways (homolysis vs. heterolysis) for the O–O bond cleavage of nickel-hydroperoxo intermediates.

Table 5.
Mulliken spin population of Ni and Oaxial in the three possible active nickel-oxo intermediates calculated both in the gas phase and in solution. Values enclosed in brackets refer to solvated structures. Heterolytic cleavage of the O–O bond only led to high-spin triplet intermediate.
The gas-phase energies of nickel-oxo species (with consideration of HO·/HO− energies) showed that the heterolytic pathway leading to [(L)Ni3+–O·]2+ is thermodynamically forbidden by over 171 kcal mol−1 relative to the homolytic pathway that produces high-spin [(L)Ni2+–O·]+. This inference is synonymous with the findings of Sankaralingam et al. (2014), who also investigated the Ni(II)-catalyzed alkane hydroxylation with m-CPBA using similar DFT methods [76]. They reported [Ni2+–O·]+ species to be the active intermediate of their catalysts, being more energetically stable than [Ni4+=O]2+ by at least 900 kJ mol−1 (or approximately 215 kcal mol−1). This looked acceptable at first and supportive of our initial findings, but our calculations with solvation effects suggested otherwise. Due to solvation, the heterolytic pathway emerged to be more favorable with energy splitting of the resulting species (considering HO·/HO− energies) falling within 3 to 9 kcal mol−1 depending on the pendant arm. Hydration stabilized both homolytic and heterolytic intermediates, but the change in energy was more significant in the latter (e.g., ΔEHeterolytic = −131 kcal mol−1 versus ΔEHomolytic = −39 kcal mol−1 for complex 4). Overall, we conclude that depending on where the reaction takes place, the O–O bond cleavage of nickel-hydroperoxo intermediate either undergoes homolysis (if in the gas phase) or heterolysis (if in solution). Yet since the previous experiment studied the peroxidase activity of Ni(II)–PyMAC catalysts in an aqueous medium, it is warranted to select triplet [(L)Ni3+–O·]2+ as the most plausible active intermediate.
The calculated singly-occupied molecular orbitals (SOMO) of high-spin [(L)Ni3+–O·]2+ indicated that the two unpaired electrons (in order of decreasing energy) individually reside in Ni– (Ni–Oaxial interaction) and O– (Ni-Oaxial interaction). This implies that after O–O bond heterolytic cleavage, Oaxial received an electron from Ni, causing the metal to achieve a +3 oxidation state. Specifically, the unpaired electron of Ni occupying the orbital (Ni–Nequatiorial interactions) was utilized for this process. This is supported by the decrease in the total spin density of Ni + 4Nequatorial atoms by 0.94. Regardless of the pendant arm, [(L)Ni3+–O·]2+ showed the same type and order of SOMOs in terms of energy, none of which is the highest lying orbital. Therefore, further oxidation by electron removal is highly unfavorable in these intermediates. Instead, [(L)Ni3+–O·]2+ appear to be good oxidizing agents. They can readily accept two electrons from substrates given that they have two lowest-lying unoccupied orbitals that are nearly degenerate. The two SOMOs with corresponding energies (in eV) of the active (S = 1) [(L)Ni3+–O·]2+ intermediates are shown in Figure 5.
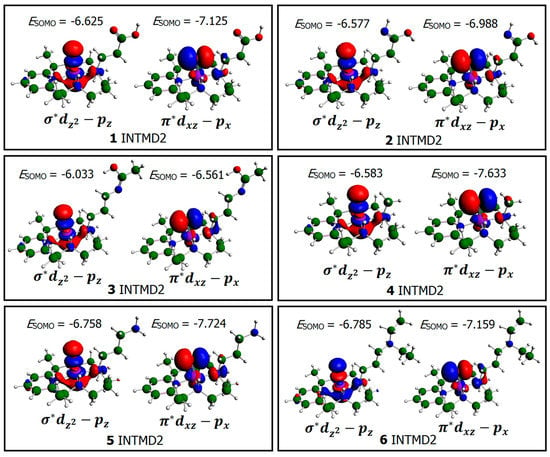
Figure 5.
Singly occupied molecular orbitals (SOMO) of the active high-spin (S = 1) [(L)Ni3+–O·]2+ intermediates calculated with solvation effects. ESOMO values are the corresponding orbital energies in eV. Molecular orbitals are named based on the computed spin density distributions in Ni and Oaxial (see Table 5) and their interaction. The x, y, and z axes point along N(1)–N(3), N(4)–N(2), and Ni–Oaxial directions, respectively (numbering of nitrogen atoms is similar to that in Figure 3).
3.5. Dissociation Energy of Nickel-Hydroxo O–O Bond
The ease in breaking the O–O bond is a factor that affects the degree of reactivity of H2O2 as oxidant. In the absence of any catalytic influence, the rate of peroxide bond dissociation may be very slow under mild conditions. From our calculations (Table 6), it would require 53.0 kcal mol−1 of energy in aqueous solution to produce two HO· radicals from H2O2. The transition state for this process verified by a single imaginary frequency (vi) of −254 cm−1 was also determined to lie 11.2 kcal mol−1 downhill of the resulting radical pair. These results agree well with the published report of Sandhiya and Zipse in 2017 [77]. Compared to that of [(L)Ni2+–OOH] intermediates, the H2O2 peroxo bond appeared to be the strongest. The energy barrier associated with the heterolytic breaking of the [(L)Ni2+O–OH] peroxo bond was only 26 to 27 kcal mol−1. The energies of the resulting intermediates were also 21.6 to 28.3 kcal mol−1 lower than their corresponding INTMD1s. Thus, we can ascribe the catalytic activity of Ni(II)–PyMACs to their potential role of lowering the bond strength of the attached peroxo group to generate the active intermediate that will serve as the actual oxidant of ABTS. Based on calculated energy barriers, the ease of O–O bond breaking in [(L)Ni2+–OOH] follows the trend: 4 > 3A/3B > 2A/2B > 5A/5B > 6A/6B > 1A/1B. Unexpectedly, 1A/1B appears to be the poorest pair of catalysts in this step, while in the previous experimental study, it was shown to be the most effective [24]. Apparently, the energy difference between 1A/1B and 4 is not significantly large (approximately 1.8 kcal mol−1), and to treat the catalytic strength of the complexes this way may not be the most ideal.

Table 6.
Selected structural data of transition states (TS2) and active intermediates (INTMD2) for the O–O bond heterolytic cleavage of [(L)Ni2+–OOH]+ (INTMD1) calculated in solution. Energy change (ΔE) values of structures relative to INTMD1s are shown, together with other data describing the uncatalyzed homolytic dissociation of H2O2 to two HO radicals.
Therefore, we also looked into each catalyst’s degree of partitioning between heterolysis and homolysis. Although homolytic intermediates are less stable in aqueous solution, it does not guarantee that the [(L)Ni2+–O–OH]+ bond may not break evenly, forming a hydroxyl radical and [(L)Ni2+–O·]+. Nam et al. (2000) had previously pointed out that both pathways occur in iron porphyrin complexes, and the preference of the complex is affected by its electronic nature [42]. It was emphasized that electron-deficient iron porphyrin showed a tendency to cleave the hydroperoxide O–O bond heterolytically, whereas electron-rich ones cleave the same bond homolytically. As shown in Figure 6, all catalysts will favor the homolytic pathway if reactions are carried out in the absence of any solvent. However, the opposite is true for catalysis occurring in aqueous solution. Heterolysis is more preferred since water will contribute to the stabilization of charged species that are produced after bond cleavage. Among the six types, 5A/5B and 6A/6B showed the smallest partitioning between the two pathways in aqueous solution, followed by 4, 1A/1B, 2A/2B, and 3A/3B of relatively the same disparity. The pendant arms in 1A/1B, 2A/2B, and 3A/3B are all electron-withdrawing due to the presence of a carbonyl group. As a result, the nickel metal in these complexes is more electron-deficient compared to that in 5A/5B and 6A/6B. Then, this greatly weakens the O–O bond in [(L)Ni2+–OOH]+, thus increasing its chance to break heterolytically. Although for all catalysts the homolytic cleavage may still proceed regardless of pendant arm type, a partition gap between the two processes would indicate that preferably more of [(L)Ni3+–O·]2+ and the HO− pair are produced after O–O bond cleavage rather than [(L)Ni2+–O·]+ and HO·.
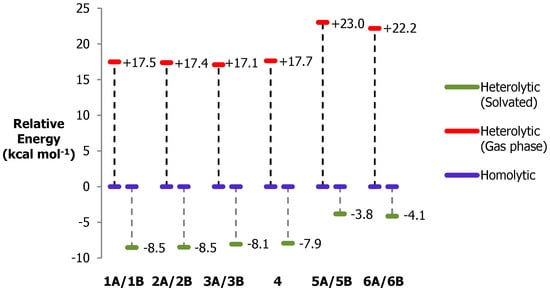
Figure 6.
Relative stabilities of [(L)Ni2+–O·]+HS (homolytic) and [(L)Ni3+–O·]2+HS (heterolytic) intermediates. Calculated energies in the gas phase are reflected in × 10 kcal mol−1 units.
3.6. ABTS Oxidation by [(L)Ni3+–O·]2+ Active Intermediates
ABTS in its fully deprotonated di-anionic form (HABTS+ pKa = 2.2) [78] was optimized in solution and was verified to have a singlet electronic ground state (E = −6865.0 kcal mol−1). Its highest energy electrons were found occupying the antibonding molecular orbital delocalized around the aromatic rings up to the bridge nitrogens. From this, it can be expected that in the presence of an oxidizing species (e.g., [(L)Ni3+–O·]2+ or HO·), the first electron that will be removed from ABTS will come from this region (Figure 7). The computed ground state (S = 1/2) of ABTS+· (E = −6762.5 kcal mol−1), the one-electron oxidized form of the substrate supports this assumption. It was noted that the HOMO and LUMO obtained from this structure were the same in shape, although each has a different energy (HOMO = −4.979 eV and LUMO = −4.650 eV). In addition, the obtained spin density values indicate that the unpaired electron of ABTS+· is distributed along the two central nitrogens (Ncenter = 0.198) and the two other ring nitrogens (Nring = 0.111).
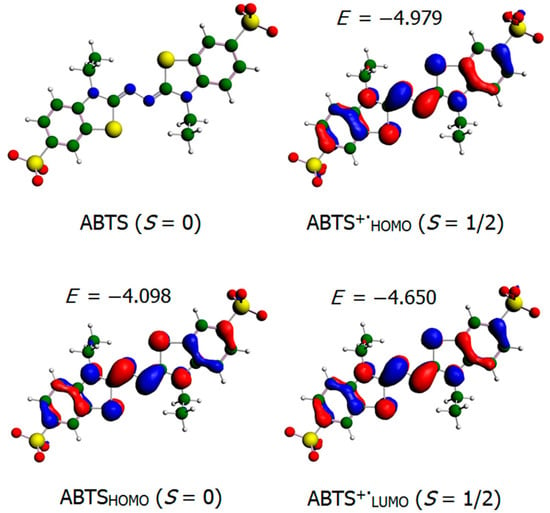
Figure 7.
Optimized structure of singlet ABTS together with the three selected frontier orbitals (HOMOABTS, HOMOABTS+· and HOMOABTS+·). Energy values in eV. Parent ABTS and ABTS+· were assigned an overall charge of −2 and −1, respectively.
The energy difference between the HOMO of ABTS and the LUMO of each oxidant was calculated in solution to compare the oxidizing power of [(L)Ni3+–O·]2+ intermediates in inducing electron transfer from ABTS. Since in general, electron transfer reactions do not involve the formation of transition states, it is not possible using the proposed method to estimate the energy barrier associated with this step of the reaction. However, we may rationalize the electron transfer by treating the reaction system as a Lewis acid–base pair wherein, based on frontier orbital combinations, an electron transfer from HOMO to LUMO is highly permissible when the energies of the involved orbitals are more disparate [79]. The electron is shuttled completely to a more electronegative atom rather than being shared as in the case of adduct formation that involves covalent bonding. Applying the same concept, it is safe to assume that if the oxidant provides an unoccupied orbital that is significantly lower in energy than that of the source, electron transfer between the two redox species would be favorable. In Figure 8, all the intermediates have two low-lying unoccupied orbitals that are nearly degenerate and are both significantly lower in energy than HOMO of ABTS. They can accommodate two electrons, which we think will come either from ABTS or ABTS+·. Apparently, HOMO of the radical form is also high at −4.98 eV considering the energy of the LUMOs in subject. However, the further oxidation of ABTS+· to ABTS2+ with λmax at 513–520 nm has been reported to be very slow, roughly three times that of the first oxidation [80]. Hence, we considered the parent ABTS as the principal electron donor for this redox process.
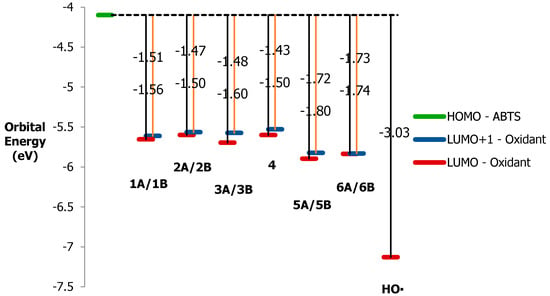
Figure 8.
Energy difference between HOMO of ABTS and the LUMO and LUMO+1 of [(L)Ni3+-O·]2+ intermediates. LUMO of HO· was also incorporated for comparison.
Among the six types, 5A/5B and 6A/6B INTMD2s are the two with the lowest LUMO energies each at 1.7 to 1.8 eV lower than the HOMO energy of ABTS. We believe they are the strongest oxidants in the group, since they offer empty orbitals where the two electrons will be the most stable. The low energies of their LUMO and LUMO+1 can be attributed to the very weak antibonding interactions along their Ni-Oaxial bond and Ni-Nequatorial bonds. Their oxidizing power is followed by those of other catalysts in the order: 3A/3B > 1A/1B > 2A/2B > 4.
3.7. Formation of [(L)Ni2+–OH] and Regeneration of the Resting State
Upon transfer of two electrons from ABTS to [(L)Ni3+–O·]2+, a proton eventually comes over and stabilizes the thermodynamically unstable [(L)Ni2+–O] by the formation of a high-spin (S = 1) nickel–hydroxo complex. The two channeled electrons each occupy the SOMO () of terminal oxygen to couple the unpaired electron and the SOMO () of Ni to reduce the metal back to its 2+ oxidation state. Then, the resulting lone pair of O easily invites a proton to share its orbital, forming an MO that is much lower in energy. In fact, for 1A/1B INTMD3 as an example, the calculated energy of the newly occupied orbital decreased from −2.03 to −4.99 eV upon protonation of the terminal oxygen. The solvent-corrected energy of the intermediate (with HO−) was also lowered by about 32 kcal mol−1 considering proton transfer from H2O to unprotonated INTMD3.
Nickel–hydroxo species were believed to be the final intermediates of the catalytic cycle before the whole process gets back to the resting state of the catalyst. Based on the generated frontier orbitals, the spin-conversion of INTMD3 from high-spin (S = 1) to low-spin (S = 0) is expected by the time the terminal HO− dissociates from the nickel metal, similar to the reversible coordination of HOO− at the initial step. The ease of the axial HO− to leave the complex is influenced by the nature of the surrounding ligands, which in the case of Ni(II)–PyMACs is determined by the functional group of the pendant arm being the only one unique for each catalyst. It can be assumed that HO− dissociation is slower in complexes containing an electron-withdrawing pendant arm than those that have an electron-donating pendant arm. In the presence of an electron-withdrawing group such as that in 1A/1B, 2A/2B, and 3A/3B, the metal is made more electron-deficient, thereby increasing both its Lewis acid character and its propensity toward nucleophilic binding. However, 1A/1B may also appear as having the greatest tendency to liberate HO− as it can easily stabilize the free ion with its very low pKa. 1A/1B INTMD3 has a pendant arm that can provide ionizable H+ to neutralize HO− ion to form H2O. Taking all these into consideration, basic complexes, 2A/2B and 3A/3B, tend to have the lowest turnover number compared to the rest of the catalysts. In this particular step, HO− dissociation from the complex likely follows the trend: 1A/1B > 5A/5B > 4 > 6A/6B > 2A/2B > 3A/3B.
3.8. Reaction Energy Profile of Ni(II)–PyMAC Catalysis
The functional state of the pendant arm dictates the reaction pathway of the catalytic action. In the first part of the discussion, we introduced the concept of acid–base equilibria of the pendant arm and how it can affect the reaction rate. Synonymous with experimental findings, the basic form B of each catalyst will boost the reaction kinetics of ABTS oxidation during the initial reaction timeframe. Based on the energy diagram (Figure 9), B will proceed on a two-step, minimal energy process, leading to the formation of INTMD1. B undergoes spin-transition (S = 0→S = 1), and the originally coordinated pendant arm will serve as hydrogen-abstracting moiety to transform H2O2 to HOO−. Such a process is more thermodynamically favorable compared to that of its conjugate counterpart A (e.g., +36.9 kcal mol−1 from 1A to INTMD1). A depends solely on the availability of free basic species to deprotonate the oxidant. However, since A and B coexist in solution, it is likely that apart from H2O and HO−, B may also assist A in generating HOO− prior to INTMD1 formation. Note that due to computational limitation and the complexity of the modeled system, we were unable to locate the first-order saddle point (transition state) associated with this reaction step. We merely relied on the thermodynamic stabilities, frontier orbitals, and spin density distribution of equilibrium structures as a fair start to orchestrate the overall mechanism of the reaction. Remarkably, the results obtained so far were suggestive of the most plausible pathway undertaken by each form of the catalyst. Starting from INTMD1 toward catalyst regeneration in the form of triplet BHS, both forms proceed along the same reaction scheme. In fact, the relative energies that correspond to INTMD1, TS2, and INTMD2 are equal for both functional states. They only deviate when INTMD2 is converted to INTMD3, where it is thermodynamically forbidden for B while thermodynamically favorable for A. This result is surprisingly noteworthy. The high energy requirement for complex B can be attributed to the limited protons that can stabilize the reduced form of INTMD2 after accepting an electron from ABTS. The formation of INTMD3 will only proceed when the system can sustain the proton requirement of the proton-coupled electron transfer without disrupting the equilibrium among participating species. Such a criterion is fulfilled by the reaction environment of A, being more acidic. For complex 1A, the stabilization energy associated with the formation of INTMD3 measures −18.6 kcal mol−1. While this is not the case for complex B, we still believe that regardless of whether protons are sufficient, electron transfer from ABTS should still irreversibly proceed given the much lower energy of the accepting orbital of INTMD2. However, the major implication of the high-energy formation of INTMD3 in B is the likely low turnover of the complex after going through successful catalysis. B is practically consumed after INTMD2 formation, and little of it will undergo another round of catalysis after serving as an electron repository for ABTS oxidation. Similarly, A may not be regenerated also because it needs to overcome a considerably high energy to convert from BHS (e.g., 22.0 kcal mol−1 from 1BHS to 1A). Such a conversion is thermodynamically restricted, as the liberated HO− from INTMD3 will instead favor the formation of B to maintain equilibrium. Yet, this allows complex A to go another round of reaction catalysis, but this time following the pathway of the basic form, B.
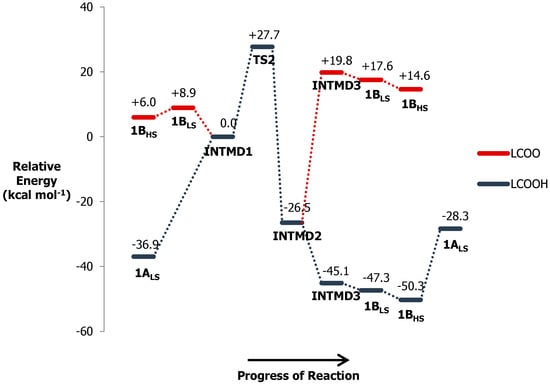
Figure 9.
Reaction energy diagram of ABTS oxidation with H2O2 catalyzed by Ni(II)–PyMACs. 1A/1B was chosen as the model catalyst pair. Individual energies of participating species (H2O2, ABTS, ABTS+·, HO·, HO−, H3O+, and H2O) have been incorporated accordingly in all quoted relative energies.
Overall, the calculated reaction energies provide a theoretical explanation as to why in the previous experiment [24], 5B reaction rate was observed to be superior during the first few seconds of the reaction but had gone constant toward the end. Practically, 5B was only able to catalyze up to a certain extent, and that was limited both by the starting concentration of the complex and the actual pH of the solution. In contrast, 5A catalysis was fair throughout as it acted twice in the redox reaction −first as 5A and second as 5B.
4. Conclusions and Recommendation
The reaction mechanism of ABTS oxidation with H2O2 over Ni(II)–PyMAC catalysts has been investigated using density functional theory. By frontier orbital inspection, the catalysts were grouped in terms of their ability to deprotonate H2O2 and bind to HOO−. Some catalysts would require a free base (e.g., H2O, HO−) in forming the first intermediate, [(L)Ni2+–OOH]+. The calculated energies in solution suggested that the heterolytic cleavage of the O–O bond, which produces [(L)Ni3+–O·]2+ and HO−, is more favorable thermodynamically compared to the homolytic cleavage. The resulting charged species in heterolysis were stabilized significantly and preferentially by the surrounding aqueous solvent. High-spin (S = 1) [(L)Ni3+–O·]2+ was the active intermediate in the catalytic process, oxidizing ABTS in a 1:2 stoichiometric ratio followed by proton transfer. The acid dissociation constant of the pendant arm influenced the liberation of the terminal OH from Ni. The more ionizable the protons, the easier it was for the dissociated hydroxyl ion to be stabilized by neutralization. Lastly, Ni(II)–PyMAC catalysts in their basic form were more difficult to regenerate compared to their conjugate acid counterparts because of the high energy formation of (S = 1) [(L)Ni2+–OH]+ due to proton requirement. Overall, deprotonated Ni(II)–PyMACs were verified to be superior catalysts during the first few seconds of the reaction, and their protonated pairs were better toward the end.
The present study will serve as a theoretical framework for future use of Ni(II)–PyMACs as peroxidase-like catalysts. Given the experimental studies available in the literature, prospective computational works may focus on studying the variations in bonding MOs of mononuclear PyMAC complexes with different types of metal center (e.g., Ni, Fe, Co, Cu). Doing so will shed light on the distinctive catalytic strength displayed by each catalyst. In addition, the influence of other solvents on the preferred degradation pathway of the oxidant may have to be studied as well in order to expand the application of these novel catalysts to other reaction systems.
Author Contributions
Conceptualization, writing—review and editing, V.G.O.; software and computational results validation, J.B.B.; methodology, data curation, analysis, writing—original draft preparation, J.J.E.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare that there is no conflict of interest.
References
- Houmam, A. Electron transfer initiated reactions: Bond formation and bond dissociation. Chem. Rev. 2008, 108, 2180–2237. [Google Scholar] [CrossRef] [PubMed]
- Legros, J.; Bolm, C. Iron-catalyzed asymmetric sulfide oxidation with aqueous hydrogen peroxide. Angew. Chem. Int. Ed. 2003, 42, 5487–5489. [Google Scholar] [CrossRef] [PubMed]
- Neumann, R.; Khenkin, A.M.; Juwiler, D.; Miller, H.; Gara, M. Catalytic oxidation with hydrogen peroxide catalyzed by ‘sandwich’ type transition metal substituted polyoxometalates. J. Mol. Catal. A Chem. 1997, 117, 169–183. [Google Scholar] [CrossRef]
- Prasad, R.V.; Thakkar, N.V. Study of cobalt complexes as catalysts in the decomposition of hydrogen peroxide. J. Mol. Catal. 1994, 92, 9–20. [Google Scholar] [CrossRef]
- Shivankar, V.S.; Thakkar, N.V. Decomposition of hydrogen peroxide in presence of mixed ligand cobalt (II) and nickel (II) complexes as catalysts. J. Sci. Ind. Res. (India) 2005, 64, 496–503. [Google Scholar]
- Haber, F.; Weiss, J. Uber die Katalyse des Hydroperoxydes. Die Nat. 1932, 20, 948–950. [Google Scholar] [CrossRef]
- Kremer, M.L. Oxidation reduction step in catalytic decomposition of hydrogen peroxide by ferric ions. Trans. Faraday Soc. 1963, 59, 2535. [Google Scholar] [CrossRef]
- Stephenson, N.A.; Bell, A.T. Mechanistic insights into iron porphyrin-catalyzed olefin epoxidation by hydrogen peroxide: Factors controlling activity and selectivity. J. Mol. Catal. A Chem. 2007, 275, 54–62. [Google Scholar] [CrossRef]
- Tanaka, M.; Matsuura, K.; Yoshioka, S.; Takahashi, S.; Ishimori, K.; Hori, H.; Morishima, I. Activation of hydrogen peroxide in horseradish peroxidase occurs within ~200 μs observed by a new freeze-quench device. Biophys. J. 2003, 84, 1998–2004. [Google Scholar] [CrossRef]
- Salem, I.A.; El-maazawi, M.; Zaki, A.B. Kinetics and mechanisms of decomposition reaction of hydrogen peroxide in presence of metal complexes. Int. J. Chem. Kinet. 2000, 32, 643–666. [Google Scholar] [CrossRef]
- Kuznetsov, M.L.; Teixeira, F.A.; Bokach, N.A.; Pombeiro, A.J.L.; Shul’pin, G.B. Radical decomposition of hydrogen peroxide catalyzed by aqua complexes [M(H2O)n]2+ (M=Be, Zn, Cd). J. Catal. 2014, 313, 135–148. [Google Scholar] [CrossRef]
- Aebi, H. Peroxidase. The properties and uses of a versatile enzyme and of some related catalysts. Angew. Chemie. 1965, 77, 1144. [Google Scholar] [CrossRef]
- Veitch, N.C.; Smith, A.T. Horseradish peroxidase. Adv. Inorg. Chem. 2000, 107–162. [Google Scholar] [CrossRef]
- English, A.M.; Tsaprailis, G. Catalytic structure–function relationships in heme peroxidases. Adv. Inorg. Chem. 1995, 79–125. [Google Scholar] [CrossRef]
- Pappa, H.S.; Cass, A.E.G. A step towards understanding the folding mechanism of horseradish peroxidase Tryptophan fluorescence and circular dichroism equilibrium studies. Eur. J. Biochem. 1993, 212, 227–235. [Google Scholar] [CrossRef] [PubMed]
- Tams, J.W.; Welinder, K.G. Deglycosylation without anisole. Anal. Biochem. 1995, 228, 48–55. [Google Scholar] [CrossRef]
- Tams, J.W.; Welinder, K.G. Glycosylation and thermodynamic versus kinetic stability of horseradish peroxidase. Fed. Eur. Biochem. Soc. Lett. 1998, 421, 234–236. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, Y.; Li, H.; Zhu, R.; Shao, Q.; Yang, S.; Xu, J. NiO nanoparticles modified with 5,10,15,20-tetrakis(4-carboxyl pheyl)-porphyrin: Promising peroxidase mimetics for H2O2 and glucose detection. Biosens. Bioelectron. 2014, 64, 147–153. [Google Scholar] [CrossRef]
- Kitamura, Y.; Mori, K.; Yamamoto, M.; Nozaki, A.; Saito, M.; Tsukamoto, I.; Mifune, M.; Saito, Y. Peroxidase-like catalytic activity of aqueous- and immobilized-Mn3+-octabromo-porphyrins on ion-exchange resin supplied as mimetic of horseradish peroxidase. Chem. Pharm. Bull. (Tokyo) 2008, 56, 1364–1366. [Google Scholar] [CrossRef][Green Version]
- Shu, J.; Qiu, Z.; Wei, Q.; Zhuang, J.; Tang, D. Cobalt-porphyrin-platinum-functionalized reduced graphene oxide hybrid nanostructures: A novel peroxidase mimetic system for improved electrochemical immunoassay. Sci. Rep. 2015, 5, 15113. [Google Scholar] [CrossRef]
- Lousada, C.M.; Yang, M.; Nilsson, K.; Jonsson, M. Catalytic decomposition of hydrogen peroxide on transition metal and lanthanide oxides. J. Mol. Catal. A Chem. 2013, 379, 178–184. [Google Scholar] [CrossRef]
- Wei, H.; Wang, E. Fe3O4 Magnetic nanoparticles as peroxidase mimetics and their applications in H2O2 and glucose detection. Anal. Chem. 2008, 80, 2250–2254. [Google Scholar] [CrossRef]
- McAteer, B.; Beattie, N.; Richens, D.T. Catalytic oxidation of cyclohexene by aqueous Iron(III)/H2O2 in mildly acidic solution: Epoxidation versus allylic oxidation. Inorg. Chem. Commun. 2013, 35, 284–289. [Google Scholar] [CrossRef]
- Organo, V.G.; Filatov, A.S.; Quartararo, J.S.; Friedman, Z.M.; Rybak-Akimova, E.V. Nickel(II) complexes of monofunctionalized pyridine-azamacrocycles: Synthesis, structures, pendant arm “on-off” coordination equilibria, and peroxidase-like activity. Inorg. Chem. 2009, 48, 8456–8468. [Google Scholar] [CrossRef]
- McKenzie, S.G.; Pallucio, T.D.; Patterson, J.D.; Rybak-Akimova, E.V. Synthesis, characterization, and oxidation catalysis studies of a monofunctionalized copper pyridine-aza macrocycle. Inorg. Chim. Acta 2018, 482, 732–737. [Google Scholar] [CrossRef]
- Chng, L.L.; Chang, C.J.; Nocera, D.G. Catalytic O−O activation chemistry mediated by iron hangman porphyrins with a wide range of proton-donating abilities. Am. Chem. Soc. 2003, 5, 1403–1406. [Google Scholar] [CrossRef]
- Aniagyei, A.; Tia, R.; Adei, E. A density functional theory study of the mechanisms of oxidation of ethylene by technetium oxo complexes. Comput. Theor. Chem. 2013, 1009, 70–80. [Google Scholar] [CrossRef]
- Hou, L.-J.; Wu, B.-W.; Han, Y.-X.; Kong, C.; Chen, D.-P.; Gao, L.-G. Density functional theoretical study on the reaction mechanism of HNCS with SiHF radical. Comput. Theor. Chem. 2015, 1051, 57–61. [Google Scholar] [CrossRef]
- Lundberg, M.; Borowski, T. Oxoferryl species in mononuclear non-heme iron enzymes: Biosynthesis, properties and reactivity from a theoretical perspective. Coord. Chem. Rev. 2013, 257, 277–289. [Google Scholar] [CrossRef]
- Luo, Y.; Maeda, S.; Ohno, K. Decomposition of alkyl hydroperoxide by a copper(I) complex: Insights from density functional theory. Tetrahedron Lett. 2008, 49, 6841–6845. [Google Scholar] [CrossRef]
- Mothana, B.; Boyd, R.J. A density functional theory study of the mechanism of the Paal-Knorr pyrrole synthesis. J. Mol. Struct. THEOCHEM. 2007, 811, 97–107. [Google Scholar] [CrossRef]
- Vafaeezadeh, M.; Fattahi, A. DFT investigations for “Fischer” esterification mechanism over silica-propyl-SO3H catalyst: Is the reaction reversible? Comput. Theor. Chem. 2015, 1071, 27–32. [Google Scholar] [CrossRef]
- Hynninen, P.H.; Kaartinen, V.; Kolehmainen, E. Horseradish peroxidase-catalyzed oxidation of chlorophyll a with hydrogen peroxide Characterization of the products and mechanism of the reaction. Biochim. Biophys. Acta Bioenerg. 2010, 1797, 531–542. [Google Scholar] [CrossRef]
- Keilin, D.; Hartree, E.F. Purification of horse-radish peroxidase and comparison of its properties with those of catalase and methaemoglobin. Biochem. J. 1951, 49, 88–106. [Google Scholar] [CrossRef]
- Gajhede, M.; Schuller, D.J.; Henriksen, A.; Smith, A.T.; Poulos, T.L. Crystal structure of horseradish peroxidase C at 2.15 Å resolution. Nat. Struct. Biol. 1997, 4, 1032–1038. [Google Scholar] [CrossRef]
- Poulos, T.; Kraut, J. A hypothetical model of the cytochrome c peroxidase. Cytochrome c electron transfer complex. J. Biol. Chem. 1980, 255, 10322–10330. [Google Scholar]
- Henriksen, A.; Smith, A.T.; Gajhede, M. The structures of the horseradish peroxidase c-ferulic acid complex and the ternary complex with cyanide suggest how peroxidases oxidize small phenolic substrates. J. Biol. Chem. 1999, 274, 35005–35011. [Google Scholar] [CrossRef]
- Stephenson, N.A.; Bell, A.T. Effects of porphyrin composition on the activity and selectivity of the iron(III) porphyrin catalysts for the epoxidation of cyclooctene by hydrogen peroxide. J. Mol. Catal. A Chem. 2007, 272, 108–117. [Google Scholar] [CrossRef]
- Song, W.J.; Ryu, Y.O.; Song, R.; Nam, W. Oxoiron(IV) porphyrin π-cation radical complexes with a chameleon behavior in cytochrome P450 model reactions. J. Biol. Inorg. Chem. 2005, 10, 294–304. [Google Scholar] [CrossRef]
- Almarsson, O.; Bruice, T.C. A homolytic mechanism of O-O bond scission prevails in the reactions of alkyl hydroperoxides with an octacationic tetraphenylporphinato-iron(III) complex in aqueous solution. J. Am. Chem. Soc. 1995, 117, 4533–4544. [Google Scholar] [CrossRef]
- Traylor, T.G.; Kim, C.; Richards, J.L.; Xu, F.; Perrin, C.L. Reactions of iron(III) porphyrins with oxidants. Structure-reactivity studies. J. Am. Chem. Soc. 1995, 117, 3468–3474. [Google Scholar] [CrossRef]
- Nam, W.; Han, H.J.; Oh, S.-Y.; Lee, Y.J.; Choi, M.-H.; Han, S.-Y.; Kim, C.; Woo, S.K.; Shin, W. New insights into the mechanisms of O−O bond cleavage of hydrogen peroxide and tert -alkyl hydroperoxides by iron(III) porphyrin complexes. J. Am. Chem. Soc. 2000, 122, 8677–8684. [Google Scholar] [CrossRef]
- Nagataki, T.; Ishii, K.; Tachi, Y.; Itoh, S. Ligand effects on NiII-catalysed alkane-hydroxylation with m-CPBA. Dalt. Trans. 2007, 1120. [Google Scholar] [CrossRef]
- Pfaff, F.F.; Heims, F.; Kundu, S.; Mebs, S.; Ray, K. Spectroscopic capture and reactivity of S = 1/2 nickel(III)–oxygen intermediates in the reaction of a Ni(II)-salt with mCPBA. Chem. Commun. 2012, 48, 3730. [Google Scholar] [CrossRef]
- Nagataki, T.; Tachi, Y.; Itoh, S. NiII(TPA) as an efficient catalyst for alkane hydroxylation with m-CPBA. Chem. Commun. 2006, 4016. [Google Scholar] [CrossRef]
- Schröder, D.; Schwarz, H. C-H and C-C bond activation by bare transition-metal oxide cations in the gas phase. Angew. Chemie Int. Ed. English. 1995, 34, 1973–1995. [Google Scholar] [CrossRef]
- Fenton, H.J.H. Oxidation of tartaric acid in presence of iron. J. Chem. Soc. Trans. 1894, 65, 899–910. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; Van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Boerrigter, P.M.; Te Velde, G.; Baerends, J.E. Three-dimensional numerical integration for electronic structure calculations. Int. J. Quantum Chem. 1988, 33, 87–113. [Google Scholar] [CrossRef]
- Fonseca Guerra, C.; Snijders, J.G.; Te Velde, G.; Baerends, E.J. Towards an order- N DFT method. Theor. Chem. Acc. 1998, 99, 391–403. [Google Scholar] [CrossRef]
- Schreckenbach, G.; Ziegler, T. The calculation of NMR shielding tensors based on density functional theory and the frozen-core approximation. Int. J. Quantum Chem. 1996, 60, 753–766. [Google Scholar] [CrossRef]
- Versluis, L.; Ziegler, T. The determination of molecular structures by density functional theory. The evaluation of analytical energy gradients by numerical integration. J. Chem. Phys. 1988, 88, 322. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Ehlers, A.; Baerends, E.-J. Geometry optimizations in the zero order regular approximation for relativistic effects. J. Chem. Phys. 1999, 110, 8943. [Google Scholar] [CrossRef]
- Head, J.D.; Zerner, M.C. A Broyden-Fletcher-Goldfarb-Shanno optimization procedure for molecular geometries. Chem. Phys. Lett. 1985, 122, 264–270. [Google Scholar] [CrossRef]
- Fan, L.; Ziegler, T. Nonlocal density functional theory as a practical tool in calculations on transition states and activation energies. Applications to elementary reaction steps in organic chemistry. J. Am. Chem. Soc. 1992, 114, 10890–10897. [Google Scholar] [CrossRef]
- Fan, L.; Ziegler, T. Application of density functional theory to infrared absorption intensity calculations on main group molecules. J. Chem. Phys. 1992, 96, 9005. [Google Scholar] [CrossRef]
- Bérces, A.; Dickson, R.M.; Fan, L.; Jacobsen, H.; Swerhone, D.; Ziegler, T. An implementation of the coupled perturbed Kohn-Sham equations: Perturbation due to nuclear displacements. Comput. Phys. Commun. 1997, 100, 247–262. [Google Scholar] [CrossRef]
- Jacobsen, H.; Bérces, A.; Swerhone, D.P.; Ziegler, T. Analytic second derivatives of molecular energies: A density functional implementation. Comput. Phys. Commun. 1997, 100, 263–276. [Google Scholar] [CrossRef]
- Alexiadis, A.; Kassinos, S. On the use of the BLYP functional for the DFT calculation of graphite-hydrogen systems. J. Nuc. Mat. 2010, 396, 307–308. [Google Scholar] [CrossRef]
- Yankov, E.P.; Bakalska, R.I.; Horkel, E.; Svatunek, D.; Delchev, V.B. Experimental and theoretical study of the excited-state tautomerism of 6-azauracil in water surroundings. Chem. Phys. 2018, 515, 663–671. [Google Scholar] [CrossRef]
- de Oliveira, A.Z.; Jorge, F.E. Structural, electronic, electrical, and magnetic properties of Rhn (1≤ n ≤13) clusters. Comput. Theo. Chem. 2020, 1177, 112765. [Google Scholar] [CrossRef]
- Delchev, V.B.; Horkel, E.; Svatunek, D. Excited-state photocyclodimerization of 6-azauracil to oxazetidine cyclodimer: A mechanism elucidation in water surroundings. J. Mol. Struc. 2020, 1205, 127571. [Google Scholar] [CrossRef]
- Klamt, A.; Schuurmann, G. COSMO: A new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J. Chem. Soc. Perkin Trans. 2 1993, 799–805. [Google Scholar] [CrossRef]
- Klamt, A. Conductor-like Screening Model for real solvents: A new approach to the quantitative calculation of solvation phenomena. J. Phys. Chem. 1995, 99, 2224. [Google Scholar] [CrossRef]
- Klamt, A.; Jones, V. Treatment of the outlying charge in continuum solvation models. J. Chem. Phys. 1996, 105, 9972. [Google Scholar] [CrossRef]
- Ye, S.; Neese, F. Accurate Modeling of Spin-State Energetics in Spin-Crossover Systems with Modern Density Functional Theory. Inorg. Chem. 2010, 49, 772–774. [Google Scholar] [CrossRef]
- Boguslawski, K.; Jacob, C.R.; Reiher, M. Can DFT accurately predict spin densities? Analysis of discrepancies in iron nitrosyl complexes. J. Chem. Theory Comput. 2011, 7, 2740–2752. [Google Scholar] [CrossRef]
- Kepp, K.P. Consistent descriptions of metal–ligand bonds and spin-crossover in inorganic chemistry. Coord. Chem. Rev. 2013, 257, 196–209. [Google Scholar] [CrossRef]
- Fouqueau, A.; Mer, S.; Casida, M.E. Comparison of density functionals for energy and structural differences between the high- [5T2g: (t2g)4(eg)2] and low- [1A1g: (t2g)6(eg)0] spin states of the hexaquoferrous cation [Fe(H2O)6]2+. J. Chem. Phys. 2004, 120, 9473–9486. [Google Scholar] [CrossRef] [PubMed]
- Reiher, M.; Salomon, O.; Hess, B.A. Reparameterization of hybrid functionals based on energy differences of states of different multiplicity. Theor. Chem. Acc. 2001, 107, 48–55. [Google Scholar] [CrossRef]
- Lawson Daku, L.M.; Vargas, A.; Hauser, A.; Fouqueau, A.; Casida, M.E. Assessment of Density Functionals for the High-Spin/Low-Spin Energy Difference in the Low-Spin Iron(II) Tris(2,2′-bipyridine) Complex. Chem. Phys. Chem. 2005, 6, 1393–1410. [Google Scholar] [CrossRef] [PubMed]
- Herrera, A.M.; Staples, R.J.; Kryatov, S.V.; Nazarenko, A.Y.; Rybak-Akimova, E.V. Nickel(II) and copper(II) complexes with pyridine-containing macrocycles bearing an aminopropyl pendant arm: Synthesis, characterization, and modifications of the pendant amino group. Dalton Trans. 2003, 846–856. [Google Scholar] [CrossRef]
- Shiren, K.; Ogo, S.; Fujinami, S.; Hayashi, H.; Suzuki, M.; Uehara, A.; Watanabe, Y.; Moro-oka, Y. Synthesis, structures, and properties of bis(μ-oxo)nickel(III) and bis(μ-superoxo)nickel(II) complexes: An unusual conversion of a NiIII2(μ-O)2 core into a NiII2(μ-OO)2 core by H2O2 and oxygenation of ligand. J. Am. Chem. Soc. 2000, 122, 254–262. [Google Scholar] [CrossRef]
- Sankaralingam, M.; Balamurugan, M.; Palaniandavar, M.; Vadivelu, P.; Suresh, C.H. Nickel(II) complexes of pentadentate N5 ligands as catalysts for alkane hydroxylation by using m-CPBA as oxidant: A combined experimental and computational study. Chem.-A Eur. J. 2014, 20, 11346–11361. [Google Scholar] [CrossRef]
- Sandhiya, L.; Zipse, H. O-O Bond Homolysis in Hydrogen Peroxide. J. Comput. Chem. 2017, 38, 2186–2192. [Google Scholar] [CrossRef]
- Scott, S.L.; Wen-Jang, C.; Bakac, A.; Espenson, J.H. Spectroscopic Parameters, Electrode Potentials, Acid Ionization Constants, and Electron Exchange Rates of the 2,2′-Azinobis(3-ethylbenzothiazoline-6-sulfonate) Radicals and Ions. J. Phys. Chem. 1993, 97, 6710–6714. [Google Scholar] [CrossRef]
- Miessler, G.L.; Fischer, P.J.; Tarr, D.A. Inorganic Chemistry, 5th ed.; Pearson Education, Inc.: Upper Saddle River, NJ, USA, 2014; pp. 185–188. [Google Scholar]
- Ilyasov, I.R.; Beloborodov, V.L.; Selivanova, I.A.; Terekhov, R.P. ABTS/PP Decolorization Assay of Antioxidant Capacity Reaction Pathways. Int. J. Mol. Sci. 2020, 21, 1131. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).