Abstract
This paper proposes a new definition of fractional derivative with non-singular kernel in the sense of Caputo which generalizes various forms existing in the literature. Furthermore, the version in the sense of Riemann–Liouville is defined. Moreover, fundamental properties of the new generalized fractional derivatives in the sense of Caputo and Riemann–Liouville are rigorously studied. Finally, an application in epidemiology as well as in virology is presented.
1. Introduction
Fractional derivative is the generalization of the classical derivative of integer order. It has been recently used to study the impact of memory on the dynamics of various systems from different fields such as epidemiology [1,2], virology [3,4,5], ecology [6,7,8] and economics [9]. On the other hand, it has been shown that the membranes of cells of biological systems have a fractional-order electrical conductance [10]. Furthermore, the fractance is an electrical circuit with non-integer order impedance [11]. Additionally, fractional differential equations are currently used to model and solve a variety of biological and engineering problems [12,13,14,15,16,17].
In recent years, the definition of fractional derivative has drawn attention several researchers. In 2015, Caputo and Fabrizio [18] presented a new fractional derivative with non-singular kernel. In 2016, Atangana and Baleanu [19] remarked that the fractional derivative proposed in [18] cannot produce the original function when the order of derivative is equal to zero. To solve this problem, they proposed a new definition of fractional derivative based on Mittag–Lefler function. In 2020, Al-Refai [20] defined the weighted Atangana–Baleanu fractional derivative in a Caputo sense and he used the Laplace transform to solve an associated linear fractional differential equation.
The main purpose of this study is to propose a new definition of fractional derivative that generalizes the above mentioned fractional derivatives with non-singular kernel for both Caputo and Riemann–Liouville types. To do this, Section 2 is devoted to the definition for both types and some fundamental properties. The Laplace transform and fractional integral corresponding to new generalized derivative are given in Section 3 and Section 4. Finally, an application is presented in the last section.
2. The New Fractional Derivative
In this section, we define our new fractional derivative and establish their properties.
Let be the Sobolev space of order one defined as follows:
Definition 1.
Let , , and .
The new generalized fractional derivative of order α of Caputo sense of the function with respect to the weight function is defined as follows:
where , on [a,b], is a normalization function obeying , and is the Mittag-Leffler function of parameter β.
It is very important to note that the above definition includes many special cases existing in the literature. For example,
- When , , we obtain the Caputo–Fabrizio fractional derivative [18] given by
- When , , we get the Atangana–Baleanu fractional derivative [19] given by
- When , we obtain the weighted Atangana–Baleanu fractional derivative that recently defined in [20], and it is given by
On the other hand, it is not hard to show that the new generalized fractional derivative of Caputo sense has the following properties:
- (i)
- holds for all scalars and functions . This implies that the new generalized fractional derivative is a linear operator.
- (ii)
- , for all constant function .
- (iii)
- .
From the last property, we observe that when the derivative order is equal to zero, we do not recover the original function, unless is null. To avoid this problem, we present the following new definition.
Definition 2.
Let , , and .
The new generalized fractional derivative of order α of Riemann–Liouville sense of the function with respect to the weight function is given by
Equation (2) shows that the new generalized fractional derivative of Riemann–Liouville sense of zero order recovers the original function. Indeed,
Furthermore, the new generalized fractional derivative in the sense of Riemann–Liouville is a linear operator. In fact, for all scalars and functions , we have
Theorem 1.
Let be an analytic function. Then
Proof.
Since is an analytic function, we have and
This completes the proof. □
3. Laplace Transform of the New Derivative
In this section, we determine the Laplace transform of the generalized fractional derivative of both types, Caputo and Riemann–Liouville.
Lemma 1.
The Laplace transform of is given by
In particular, when , we have
Proof.
We have
□
According to Lemma 1, we can easily get the following result.
Theorem 2.
The Laplace transform of is given by
In particular, we have
Further, the Laplace transform of is given by
In particular, we have
Obviously, we have the following remark.
Remark 1.
When and , we obtain the Laplace transform of the Atangana–Baleanu fractional derivatives in the sense of Caputo and Riemann–Liouville calculated in [19].
4. Fractional Integral Associated to the New Derivative
This section focuses on the definition of fractional integral corresponding to the new generalized derivative.
Theorem 3.
The following fractional differential equation:
has a unique solution given by
Proof.
We have
By passage to Laplace transform and applying Theorem 2, we find
The passage to the inverse Laplace leads to
Thus, . □
Definition 3.
When , we define the generalized fractional integral corresponding to new fractional derivative as follows
This generalized fractional integral coincides with the Atangana–Baleanu fractional integral when and , and with the weighted Atangana–Baleanu fractional integral defined by Al-Refai [20] when . Additionally, we recover the original function when and also the ordinary integral when .
On the other hand, we have
Hence,
where
which denotes the weighted Riemann–Liouville fractional integral of order . Consequently, the generalized derivative in the sense of Riemann–Liouville can be represented by an infinite series whose general term contains the weighted Riemann–Liouville integral.
5. Application
Mathematical modeling in epidemiology has become an effective tool for understanding and describing the dynamics of infectious diseases. It currently used to predict the evolution of coronavirus disease 2019 (COVID-19) in many countries. The first epidemiological model was introduced by Ross [21,22] to study transmission of Malaria in early 1900. Based on Ross’ ideas, Kermack and Mckendrick [23] presented a susceptible-infected-recovered (SIR) compartmental model in order to explain the evolution of the plague in island of Bombay over the period 17 December 1905 to 21 July 1906. This classical SIR model was extended by many researchers to describe other infectious diseases (see for example [24,25]). In this section, we consider the following model:
where , and are the number of susceptible, infected, and removed individuals at time t, respectively. The parameters A, , and r represent the recruitment rate, the natural death rate, the infection rate and the removal rate, respectively.
Let be the total population. Then and
Clearly, the solution of (16) is given by
For simplicity, we denote by . When a disease spreads within a community, individuals acquire knowledge about this disease. It is more reasonable to replace the classical derivative by . Then (16) becomes
In the following, we are interested to solve this last fractional differential equation which plays a significant role in epidemiology as well as in virology. In particular for human immunodeficiency virus (HIV) infection, can represent the concentration of healthy CD4+ T cells that are produced at rate A and die at rate .
Applying Laplace transform to (18), we obtain
From Theorem 2, we have
Let . Then
The passage to the inverse Laplace leads to
By using integration by parts, we have
Therefore,
Now, we study numerically the impact of the order of new fractional derivative on the dynamics behavior of the solution given by (20). For the case of HIV infection, we choose cells L−1 day−1, day−1 and T(0) = 600 cells L−1. For simplicity, we take .
Figure 1 shows that when the graph of (20) coincides with that of the ordinary differential equation given by (17). In addition, when the order of fractional derivative increases the solution given by (20) converges rapidly to the steady state .
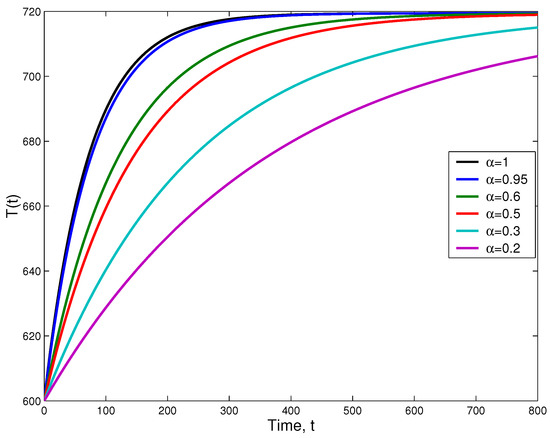
Figure 1.
Graph of (20) for different values of and .
6. Conclusions
In this work, we have proposed a new fractional derivative with non-singular kernel which includes the Caputo–Fabrizio fractional derivative, the Atangana–Baleanu fractional derivative and the recent weighted Atangana–Baleanu fractional derivative presented [20]. We have derived some fundamental properties of this new generalized derivative and applied it to a model in epidemiology as well as in virology. In addition, we have studied numerically the impact of the order on the dynamical behavior of the biological model.
Modeling other biological systems with memory or having hereditary properties using the new fractional derivative, and also the determination of other important properties of this new derivative, will be the subject of our future works.
Funding
This research received no external funding.
Acknowledgments
The author would like to thank the editor and anonymous reviewers for their constructive comments and valuable suggestions to improve the quality of this study.
Conflicts of Interest
The author declares no conflict of interest.
References
- Mouaouine, A.; Boukhouima, A.; Hattaf, K.; Yousfi, N. A fractional order SIR epidemic model with nonlinear incidence rate. Adv. Differ. Equ. 2018, 160. [Google Scholar] [CrossRef]
- Sene, N. SIR epidemic model with Mittag-Leffler fractional derivative. Chaos Solitons Fractals 2020, 137, 109833. [Google Scholar] [CrossRef]
- Bachraoui, M.; Hattaf, K.; Yousfi, N. Dynamics of a fractional order HBV infection model with capsids and CTL immune response. Commun. Math. Biol. Neurosci. 2019, 2016, 6. [Google Scholar]
- Boukhouima, A.; Hattaf, K.; Yousfi, N. Modeling the Memory and Adaptive Immunity in Viral Infection. In Trends in Biomathematics: Mathematical Modeling for Health, Harvesting, and Population Dynamics; Springer: Cham, Switzerland, 2019; pp. 271–297. [Google Scholar]
- Boukhouima, A.; Hattaf, K.; Yousfi, N. Dynamics of a fractional order HIV infection model with specific functional response and cure rate. Int. J. Differ. Equ. 2017, 2017, 8372140. [Google Scholar] [CrossRef]
- Ghanbari, B.; Djilali, S. Mathematical and numerical analysis of a three-species predator-prey model with herd behavior and time fractional-order derivative. Math. Methods Appl. Sci. 2020, 43, 1736–1752. [Google Scholar] [CrossRef]
- Ghanbari, R.; Kumar, D. Numerical solution of predator-prey model with Beddington-DeAngelis functional response and fractional derivatives with Mittag-Leffler kernel. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 063103. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Kumar, R.; Cattani, C.; Samet, B. Chaotic behaviour of fractional predator-prey dynamical system. Chaos Solitons Fractals 2020, 135, 109811. [Google Scholar] [CrossRef]
- Acay, B.; Bas, E.; Abdeljawad, T. Fractional economic models based on market equilibrium in the frame of different type kernels. Chaos Solitons Fractals 2020, 130, 109438. [Google Scholar] [CrossRef]
- Cole, K.S. Electric conductance of biological systems. Cold Spring Harb. Symp. Quant. Biol. 1933, 1, 107–116. [Google Scholar] [CrossRef]
- Le Mehaute, A.; Crepy, G. Introduction to transfer and motion in fractal media: The geometry of kinetics. Solid State Ionics 1983, 9, 17–30. [Google Scholar] [CrossRef]
- Goufo, E.F.D.; Kumar, S.; Mugisha, S.B. Similarities in a fifth-order evolution equation with and with no singular kernel. Chaos Solitons Fractals 2020, 130, 109467. [Google Scholar] [CrossRef]
- Ghanbari, B.; Kumar, S.; Kumar, R. A study of behaviour for immune and tumor cells in immunogenetic tumour model with non-singular fractional derivative. Chaos Solitons Fractals 2020, 133, 109619. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.; Singh, J.; Nisar, K.S.; Kumar, D. An efficient numerical scheme for fractional model of HIV-1 infection of CD4+ T-cells with the effect of antiviral drug therapy. Alex. Eng. J. 2020. [Google Scholar] [CrossRef]
- Alshabanat, A.; Jleli, M.; Kumar, S.; Samet, B. Generalization of Caputo-Fabrizio Fractional Derivative and Applications to Electrical Circuits. Front. Phys. 2020. [Google Scholar] [CrossRef]
- Khan, Y.; Wu, Q.; Faraz, N.; Yildirim, A.; Madani, M. A new fractional analytical approach via a modified Riemann–Liouville derivative. Appl. Math. Lett. 2012, 25, 1340–1346. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Saad, K.M.; Agarwal, P.; Aly, S.; Jain, S. Certain new models of the multi space-fractional Gardner equation. Phys. A Stat. Mech. Appl. 2020, 545, 123806. [Google Scholar] [CrossRef]
- Caputo, A.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Al-Refai, M. On weighted Atangana–Baleanu fractional operators. Adv. Differ. Equ. 2020, 2020, 3. [Google Scholar] [CrossRef]
- Ross, R. The Prevention of Malaria, 2nd ed.; Murray: London, UK, 1911. [Google Scholar]
- Ross, R. Some a priori pathometric equations. Br. Med. J. 1915, 1, 546–547. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. Lond. 1927, 115, 700–721. [Google Scholar]
- Hattaf, K.; Yousfi, N. Mathematical model of the influenza A (H1N1) infection. Adv. Stud. Biol. 2009, 1, 383–390. [Google Scholar]
- Hattaf, K.; Lashari, A.A.; Louartassi, Y.; Yousfi, N. A delayed SIR epidemic model with general incidence rate. Electron. J. Qual. Theory Differ. Equ. 2013, 3, 1–9. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).