Three-Dimensional and Multiple Image Encryption Algorithm Using a Fractional-Order Chaotic System
Abstract
1. Introduction
2. Fractional-Based Hybrid Chaotic System
2.1. 4D Fractional Chaotic System
2.2. Hybrid Chaotic System
- Step 1. Consider and as input values.
- Step 2. Define and run the following algorithm.
|
- Step 3. Consider .
- Step 4. If , stop, orelse go to Step 2.
3. 3D and Multiple Image Encryption Algorithm
3.1. The Key of Encryption Algorithm
- Step 1. In this step, in order to reduce the volume of calculations, we reduce the size of the image used in the calculations by wavelet transformation. For , derive as the low–low pass filter of the Daubechies wavelet transform at level 5 (db5) for .
- Step 2. Obtain the sequence by using the following formulae.
- Step 3. Define and .
- Step 4. Calculate the and using the following algorithm.
|
3.2. Proposed Shift and Rearrange
| Algorithm 1 PermutationMatrix |
Input: A permutation Output: A permutation matrix
|
| Algorithm 2 Shift |
Input: Matrices and permutations Output: Matrices
|
| Algorithm 3 RowCol |
Input: Natural umbers Output: Natural numbers
|
| Algorithm 4 Rearrange |
Input: A matrix and a permutation Output: A matrix
|
| Algorithm 5 Rearrange3D |
Input: A multilayer matrix and a permutation Output: A matrix
|
3.3. Proposed Encryption Algorithm
- Step 1. By using the input keys and hybrid chaotic system, obtain the vector with as follows:
- Step 2. Obtain the sequence aswhere
- Step 3.
- (a) By using input keys and obtain with as
- (b) Calculate as follows:
- (c) Consider and as input values for shift Algorithm 2 and obtain as output of this function.
- (a) Obtain as
- (b) Define asand reshape the into an n-by-k matrix, denoted as .
- (c) Define as
- (d) Define a multilayer matrix , and then consider and A as input values for Rearrange3D Algorithm 5 and obtain final encrypted images .
4. Simulation Results and Security Analysis
4.1. Simulation Infrastructure
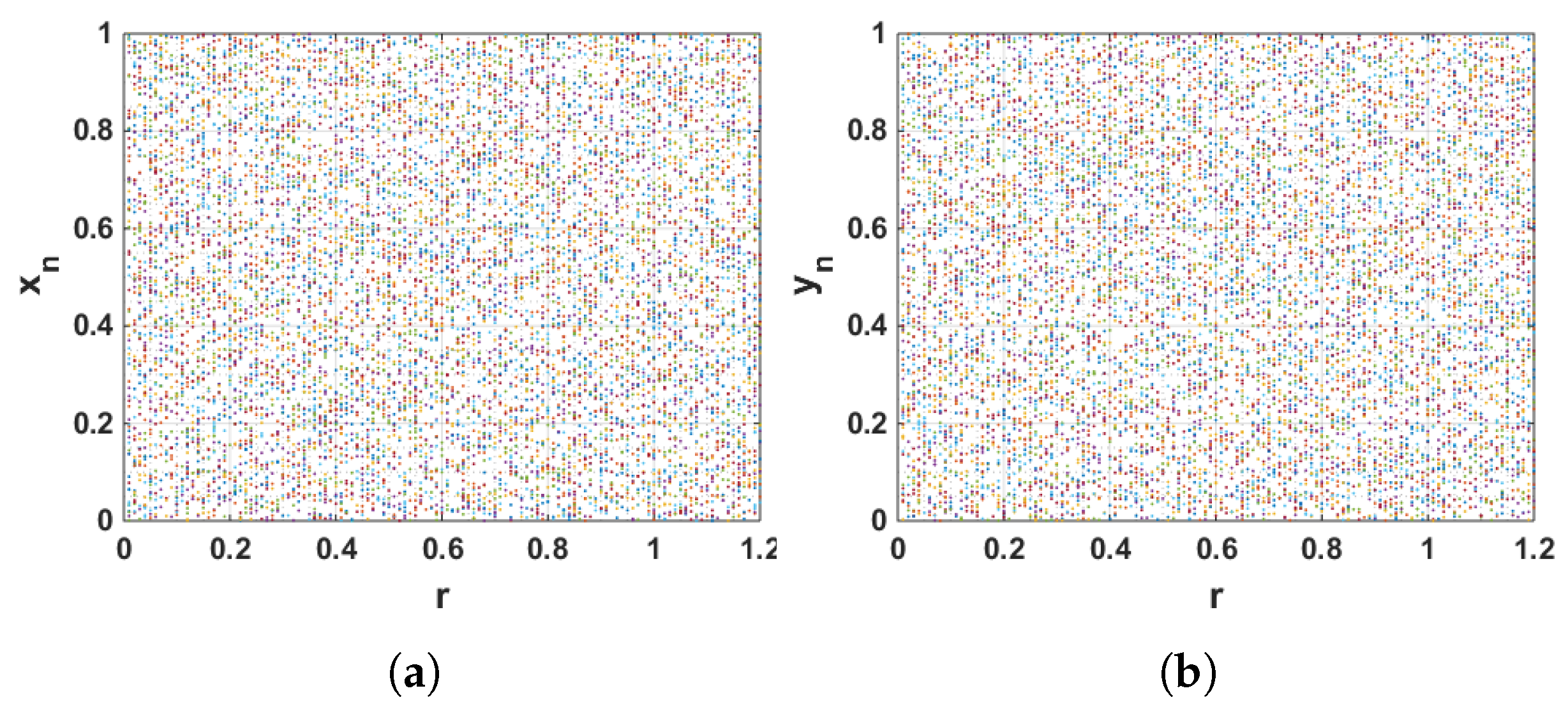
4.2. Analysis of the Proposed Systems
- .
- .
- .
- , , .
- , , , , , , , .
- , , .
4.3. Key Space Analysis
- Aerial 5.1.10(256 × 256), Airplane 5.1.11(256 × 256), Chemical plant 5.1.14(256 × 256), Clock 5.1.12(256 × 256)}.
- Female 4.1.02(256 × 256 × 3), Female 4.1.03(256 × 256 × 3), Jelly beans 4.1.08(256 × 256 × 3), House 4.1.05(256 × 256 × 3)}.
- Airplane 5.1.11(256 × 256), Clock 5.1.12(256 × 256), Jelly Jellybeans 4.1.08(256 × 256 × 3), House 4.1.05(256 × 256 × 3)}.
- Watch(512 × 512), Lena(512 × 512), Peppers(512 × 512), Fishing Boat(512 × 512)}.
- Case i.
- Without changing the input data.
- Case ii.
- The following changes have been applied to images and : and .
- Case iii.
- has been changed to .
- Case iv.
- The value of r has been updated to .
- Case v.
- The new value assigned to h is .
4.4. Analysis of Program Execution Time
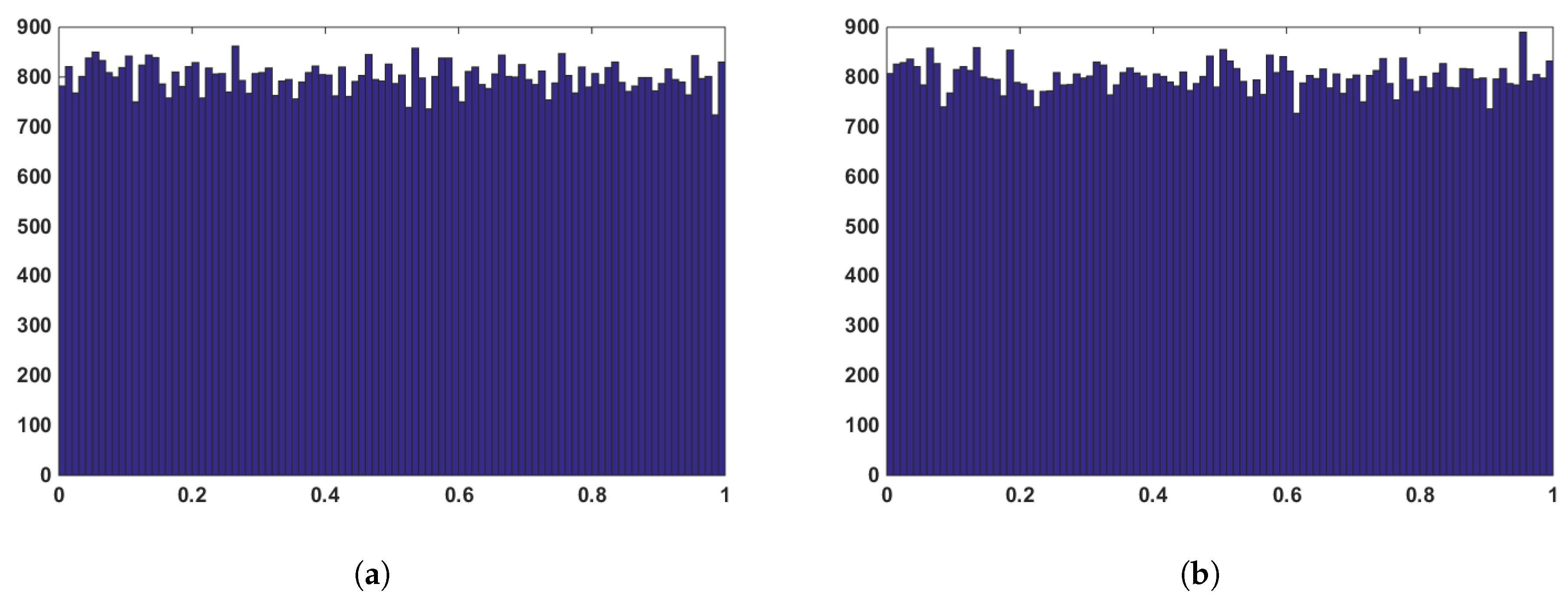
4.5. Histogram and Correlation Coefficients Analysis
4.6. NPCR, UACI and Information Entropy Analysis
4.7. Data Loss and Noise Attacks
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Liu, H. Cross-plane multi-image encryption using chaos and blurred pixels. Chaos Solitons Fractals 2022, 164, 112586. [Google Scholar] [CrossRef]
- Sangavi, V.; Thangavel, P. An exquisite multiple image encryption harnessing multi-scroll Lu–Chen and Chua chaotic systems employing domino strategy. J. Inf. Secur. Appl. 2023, 72, 103408. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Y.; Zhang, D. Research on multiple-image encryption mechanism based on Radon transform and ghost imaging. Opt. Commun. 2022, 504, 127494. [Google Scholar] [CrossRef]
- Zhou, N.R.; Tong, L.J.; Zou, W.P. Multi-image encryption scheme with quaternion discrete fractional Tchebyshev moment transform and cross-coupling operation. Signal Process. 2023, 211, 109107. [Google Scholar] [CrossRef]
- Pham, D.H.; Huynh, T.T.; Lin, C.M.; Giap, V.N.; Vu, V.P. Secure transmission of medical image using a wavelet interval type-2 TSK fuzzy brain-imitated neural network. Soft Comput. 2025, 29, 2311–2329. [Google Scholar] [CrossRef]
- Chang, H.; Wang, E.; Liu, J. Research on image encryption based on fractional seed chaos generator and fractal theory. Fractal Fract. 2023, 7, 221. [Google Scholar] [CrossRef]
- Setiadi, D.R.; Rijati, N. An image encryption scheme combining 2D cascaded logistic map and permutation-substitution operations. Computation 2023, 11, 178. [Google Scholar] [CrossRef]
- Liu, X.; Tong, X.; Wang, Z.; Zhang, M. A new n-dimensional conservative chaos based on Generalized Hamiltonian System and its’ applications in image encryption. Chaos Solitons Fractals 2022, 154, 111693. [Google Scholar] [CrossRef]
- Liu, X.; Tong, X.; Zhang, M.; Wang, Z. A highly secure image encryption algorithm based on conservative hyperchaotic system and dynamic biogenetic gene algorithms. Chaos Solitons Fractals 2023, 171, 113450. [Google Scholar] [CrossRef]
- Liu, X.; Tong, X.; Wang, Z.; Zhang, M. A novel hyperchaotic encryption algorithm for color image utilizing DNA dynamic encoding and self-adapting permutation. Multimed. Tools Appl. 2022, 81, 21779–21810. [Google Scholar] [CrossRef]
- Dutta, H.; Akdemir, A.O.; Atangana, A. (Eds.) Fractional Order Analysis: Theory, Methods and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Zarebnia, M.; Parvaz, R. Image encryption algorithm by fractional based chaotic system and framelet transform. Chaos Solitons Fractals 2021, 152, 111402. [Google Scholar] [CrossRef]
- Gomez-Aguilar, J.F.; Atangana, A. (Eds.) Applications of Fractional Calculus to Modeling in Dynamics AND Chaos; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Anastassiou, G.A. Abstract Fractional Monotone Approximation, Theory and Applications; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Gómez, J.F.; Torres, L.; Escobar, R.F. Fractional Derivatives with Mittag-Leffler Kernel; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Parvaz, R.; Yengejeh, Y.K.; Behroo, Y. A new 4D chaos system with an encryption algorithm for color and grayscale images. Int. J. Bifurc. Chaos 2022, 32, 2250214. [Google Scholar] [CrossRef]
- Agarwal, R.P.; El-Sayed, A.M.; Salman, S.M. Fractional-order Chua’s system: Discretization, bifurcation and chaos. Adv. Differ. Equations 2013, 2013, 320. [Google Scholar] [CrossRef]
- Falcioni, M.; Palatella, L.; Pigolotti, S.; Vulpiani, A. Properties making a chaotic system a good pseudo random number generator. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2005, 72, 016220. [Google Scholar] [CrossRef]
- Wu, Y.; Hua, Z.; Zhou, Y. n-dimensional discrete cat map generation using Laplace Expansions. IEEE Trans. Cybern. 2015, 46, 2622–2633. [Google Scholar] [CrossRef]
- Bao, J.; Yang, Q. Period of the discrete Arnold cat map and general cat map. Nonlinear Dyn. 2012, 70, 1365–1375. [Google Scholar] [CrossRef]
- Van Opstall, M. Quantifying chaos in dynamical systems with Lyapunov exponents. Furman Univ. Electron. J. Undergrad. Math. 1998, 4, 1–8. [Google Scholar]
- Rana, S.M. Bifurcation Analysis and 0–1 Chaos Test of a Discrete T System. Chaos Theory Appl. 2023, 5, 90–104. [Google Scholar] [CrossRef]
- Bernardini, D.; Litak, G. An overview of 0–1 test for chaos. J. Braz. Soc. Mech. Sci. Eng. 2016, 38, 1433–1450. [Google Scholar] [CrossRef]
- Alvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 16, 2129–2151. [Google Scholar] [CrossRef]
- Shao, Z.; Liu, X.; Yao, Q.; Qi, N.; Shang, Y.; Zhang, J. Multiple-image encryption based on chaotic phase mask and equal modulus decomposition in quaternion gyrator domain. Signal Process. Image Commun. 2020, 80, 115662. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X. Multiple-image encryption algorithm based on mixed image element and permutation. Opt. Lasers Eng. 2017, 92, 6–16. [Google Scholar] [CrossRef]
- Yu, C.; Li, J.; Li, X.; Ren, X.; Gupta, B.B. Four-image encryption scheme based on quaternion Fresnel transform, chaos and computer generated hologram. Multimed. Tools Appl. 2018, 77, 4585–4608. [Google Scholar] [CrossRef]
- Patel, A.; Parikh, M. Multiple image encryption using chaotic map and DNA computing. Int. J. Sci. Res. Sci. Eng. Technol. 2018, 4, 1395–1400. [Google Scholar]
- Zhang, X.; Wang, X. Multiple-image encryption algorithm based on mixed image element and chaos. Comput. Electr. Eng. 2017, 62, 401–413. [Google Scholar] [CrossRef]
- Tang, Z.; Song, J.; Zhang, X.; Sun, R. Multiple-image encryption with bit-plane decomposition and chaotic maps. Opt. Lasers Eng. 2016, 80, 1–11. [Google Scholar] [CrossRef]
- Patro, K.A.; Soni, A.; Netam, P.K.; Acharya, B. Multiple grayscale image encryption using cross-coupled chaotic maps. J. Inf. Secur. Appl. 2020, 52, 102470. [Google Scholar] [CrossRef]
- Hanif, M.; Naqvi, R.A.; Abbas, S.; Khan, M.A.; Iqbal, N. A novel and efficient 3D multiple images encryption scheme based on chaotic systems and swapping operations. IEEE Access 2020, 8, 123536–123555. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X. Multiple-image encryption algorithm based on DNA encoding and chaotic system. Multimed. Tools Appl. 2019, 78, 7841–7869. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, Y. Multiple-image encryption algorithm based on the 3D scrambling model and dynamic DNA coding. Opt. Laser Technol. 2021, 141, 107073. [Google Scholar] [CrossRef]
- Sahasrabuddhe, A.; Laiphrakpam, D.S. Multiple images encryption based on 3D scrambling and hyper-chaotic system. Inf. Sci. 2021, 550, 252–267. [Google Scholar] [CrossRef]
- Hasheminejad, A.; Rostami, M.J. A novel bit level multiphase algorithm for image encryption based on PWLCM chaotic map. Optik 2019, 184, 205–213. [Google Scholar] [CrossRef]
- Ye, H.S.; Zhou, N.R.; Gong, L.H. Multi-image compression-encryption scheme based on quaternion discrete fractional Hartley transform and improved pixel adaptive diffusion. Signal Process. 2020, 175, 107652. [Google Scholar] [CrossRef]
- Zhang, X.; Liao, J. Multiple-image encryption algorithm based on 3D-LWT and dynamic stereo S-box. Multimed. Tools Appl. 2024, 83, 16337–16362. [Google Scholar] [CrossRef]
- Tian, Y.; Lu, Z. Novel permutation-diffusion image encryption algorithm with chaotic dynamic S-box and DNA sequence operation. AIP Adv. 2017, 7, 085008. [Google Scholar] [CrossRef]
- Zhang, X.; Liao, J. Multiple-image encryption algorithm based on the dice-rotation model and improved chaos. J. Electron. Imaging 2022, 31, 043047. [Google Scholar] [CrossRef]
- Zhu, H.; Dai, L.; Liu, Y.; Wu, L. A three-dimensional bit-level image encryption algorithm with Rubik’s cube method. Math. Comput. Simul. 2021, 185, 754–770. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. Cyber J. Multidiscip. J. Sci. Technol. J. Sel. Areas Telecommun. (JSAT) 2011, 1, 31–38. [Google Scholar]
- Naseer, Y.; Shah, T.; Javeed, A. Advance image encryption technique utilizing compression, dynamical system and S-boxes. Math. Comput. Simul. 2020, 178, 207–217. [Google Scholar] [CrossRef]




















| Images | Key | Case i | Case ii | Case iii | Case iv | Case v |
|---|---|---|---|---|---|---|
| 0.3699 | 0.3607 | 0.0053 | 0.2009 | 0.1936 | ||
| 0.3302 | 0.3437 | 0.2468 | 0.2260 | 0.3965 | ||
| 0.3310 | 0.1241 | 0.5127 | 0.3521 | 0.2145 | ||
| 0.3041 | 0.3462 | 0.4062 | 0.1765 | 0.1814 | ||
| 0.4680 | 0.1866 | 0.1718 | 0.1439 | 0.1860 | ||
| 0.3314 | 0.3966 | 0.1107 | 0.3376 | 0.3431 | ||
| 0.3057 | 0.4664 | 0.2168 | 0.1822 | 0.3739 | ||
| 0.2933 | 0.1508 | 0.4643 | 0.1746 | 0.3616 | ||
| 0.2307 | 0.1978 | 0.4691 | 0.4069 | 0.2901 | ||
| 0.1547 | 0.1771 | 0.1116 | 0.3248 | 0.3889 | ||
| 0.4242 | 0.2972 | 0.3734 | 0.3846 | 0.2588 | ||
| 0.4377 | 0.5214 | 0.2964 | 0.3770 | 0.3176 | ||
| 0.2633 | 0.2028 | 0.2784 | 0.2385 | 0.3297 | ||
| 0.0873 | 0.3831 | 0.3515 | 0.1748 | 0.0777 | ||
| 0.1848 | 0.3284 | 0.5258 | 0.2342 | 0.2752 | ||
| 0.2583 | 0.3127 | 0.4522 | 0.2607 | 0.2202 | ||
| Engine | 0.5381 | 0.3147 | 0.3814 | 0.2705 | 0.0153 | |
| 0.2818 | 0.5031 | 0.3812 | 0.2064 | 0.1799 | ||
| 0.2737 | 0.1674 | 0.2143 | 0.0793 | 0.2559 | ||
| 0.1766 | 0.4007 | 0.0623 | 0.0133 | 0.5334 |
| Algorithm | Proposed | Ref. [25] | Ref. [26] | Ref. [27] | Ref. [28] |
| Key size | |||||
| Algorithm | Ref. [29] | Ref. [30] | Ref. [31] | Ref. [32] | Ref. [33] |
| Key size |
| Images | Key Generation | Encryption | Decryption |
|---|---|---|---|
| 0.2084 | 3.7334 | 3.8196 | |
| 0.2677 | 6.6504 | 6.4169 | |
| 0.2648 | 5.1215 | 5.0604 | |
| 0.3203 | 14.1428 | 14.1293 |
| Input images | Proposed | Ref. [34] | |
| Horizontal | |||
| Vertical | |||
| Diagonal | |||
| Ref. [35] | Ref. [36] | Ref. [37] | |
| Horizontal | |||
| Vertical | |||
| Diagonal |
| Input images | Proposed | Ref. [38] | |
| Horizontal | |||
| Vertical | |||
| Diagonal | |||
| Ref. [39] | Ref. [40] | Ref. [41] | |
| Horizontal | |||
| Vertical | |||
| Diagonal |
| UACI Critical Values [42] | NPCR Critical Values [42] | |||||||
|---|---|---|---|---|---|---|---|---|
| = 33.2824 | = 33.2255 | = 33.1594 | ||||||
| Image | UACI | = 33.6447 | = 33.7016 | = 33.7677 | NPCR | 99.5693 | 99.5527 | 99.5341 |
| 33.3277 | Pass | Pass | Pass | 99.6063 | Pass | Pass | Pass | |
| 33.4920 | Pass | Pass | Pass | 99.6190 | Pass | Pass | Pass | |
| 33.4685 | Pass | Pass | Pass | 99.6002 | Pass | Pass | Pass | |
| Engine | 33.4090 | Pass | Pass | Pass | 99.6107 | Pass | Pass | Pass |
| Proposed | Ref. [34] | Ref. [37] | Ref. [43] | |
|---|---|---|---|---|
| NPCR | ||||
| UACI | ||||
| Information entropy |
| Engine | ||||
|---|---|---|---|---|
| Information entropy |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghasemi, G.; Parvaz, R.; Khedmati Yengejeh, Y. Three-Dimensional and Multiple Image Encryption Algorithm Using a Fractional-Order Chaotic System. Computation 2025, 13, 115. https://doi.org/10.3390/computation13050115
Ghasemi G, Parvaz R, Khedmati Yengejeh Y. Three-Dimensional and Multiple Image Encryption Algorithm Using a Fractional-Order Chaotic System. Computation. 2025; 13(5):115. https://doi.org/10.3390/computation13050115
Chicago/Turabian StyleGhasemi, Ghader, Reza Parvaz, and Yavar Khedmati Yengejeh. 2025. "Three-Dimensional and Multiple Image Encryption Algorithm Using a Fractional-Order Chaotic System" Computation 13, no. 5: 115. https://doi.org/10.3390/computation13050115
APA StyleGhasemi, G., Parvaz, R., & Khedmati Yengejeh, Y. (2025). Three-Dimensional and Multiple Image Encryption Algorithm Using a Fractional-Order Chaotic System. Computation, 13(5), 115. https://doi.org/10.3390/computation13050115





