Battery Sizing Method for Microgrids—A Colombian Application Case
Abstract
1. Introduction
2. Microgrids in the Colombian Context
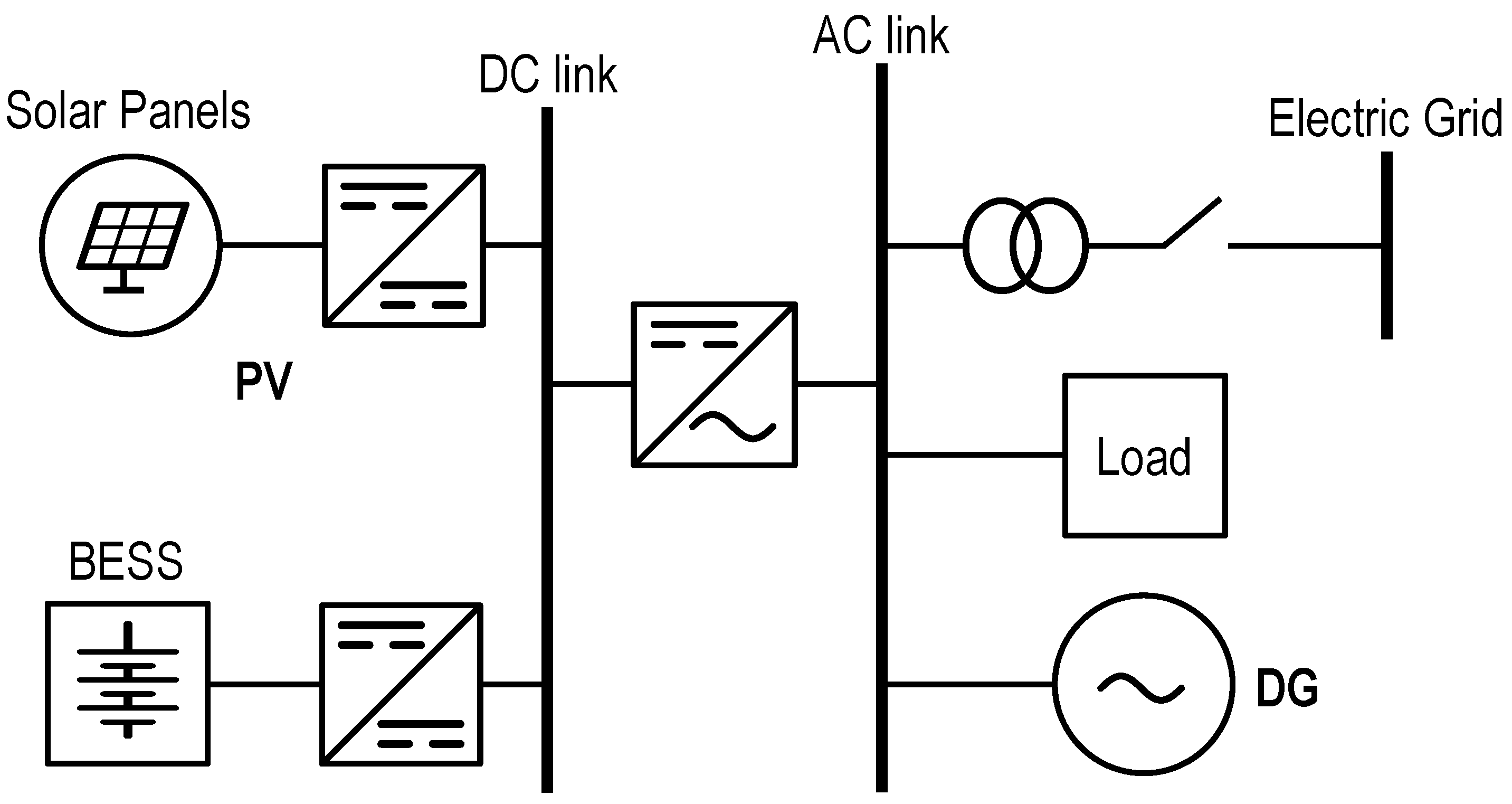
3. Model of the Optimization Problem
3.1. Decision Variables
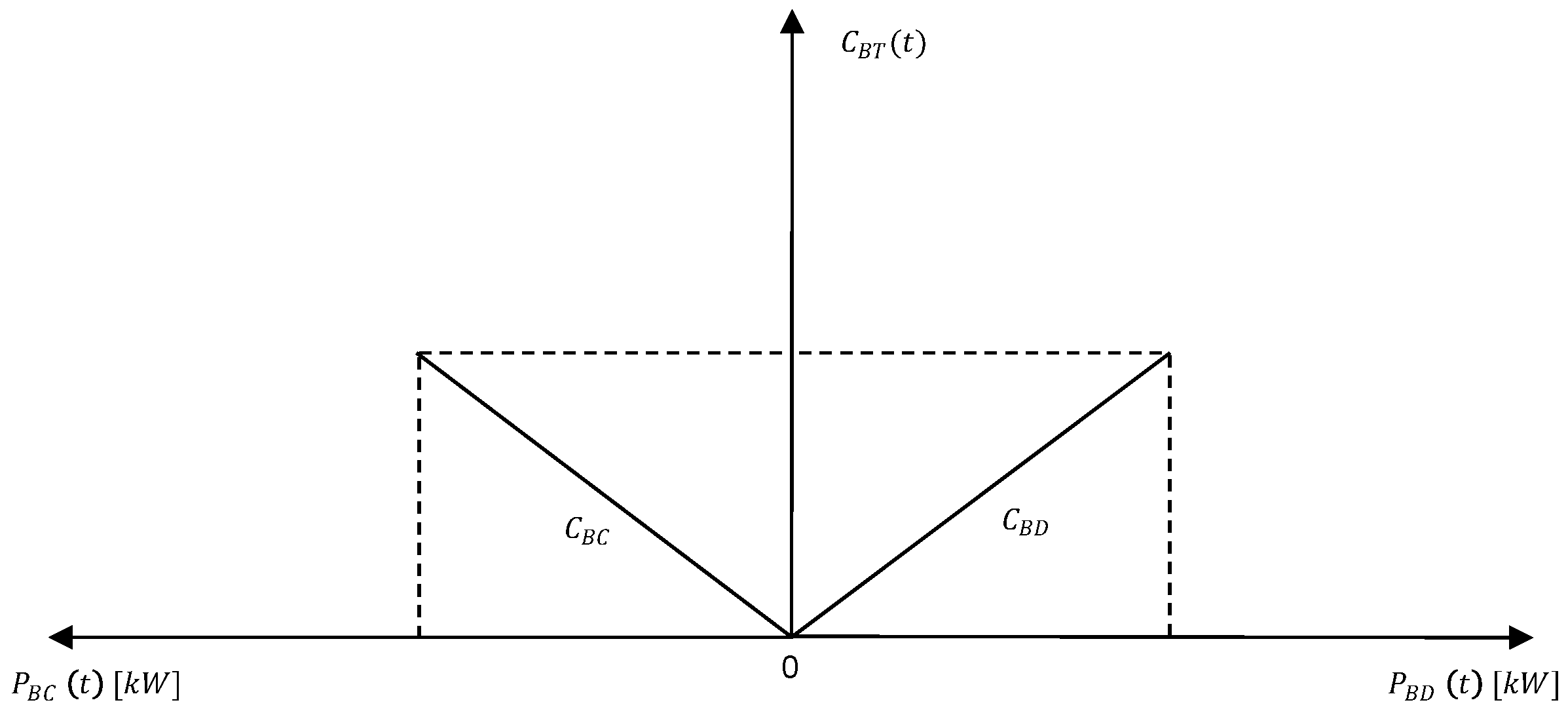
3.2. Objective Function
3.3. Constraints
4. Proposed Method for BESS Sizing
- Define search criteria: Establish the search criteria of exiting microgrid projects. Information on microgrid projects should exist in document or digital forms. In Colombia, the IPSE is the institution that gathers information about the microgrids in ZNIs. For example, the search criteria of microgrid projects may include areas with renewable energy potential, a heavy dependence on DGs, favorable government policies, high populations or energy consumption, and conflict-stricken areas, among others.
- Conduct database query: Investigate relevant data from existing electrical system projects in ZNIs to find suitable locations for including or optimizing BESSs. Relevant data include load and power source profiles.
- Select the case study: Select cases that satisfy the requirements of the defined search criteria.
- Characterize the case study: Elaborate the consumption profile and energy potential of the location regarding loads and the energy matrix.
- Parameterize the optimization problem: Identify the parameters of the models and cost function established in the optimization problem; this is based on the MILP algorithm.
- Analysis of results: BESS sizing is analyzed using the resulting data. Decision makers should provide a recommendation about the inclusion of a BESS in the microgrid of the case study.
5. Application of the Proposed Method for BESS Sizing in a Colombian Case
5.1. Define Search Criteria
5.2. Conduct Database Query
5.3. Select a Case Study
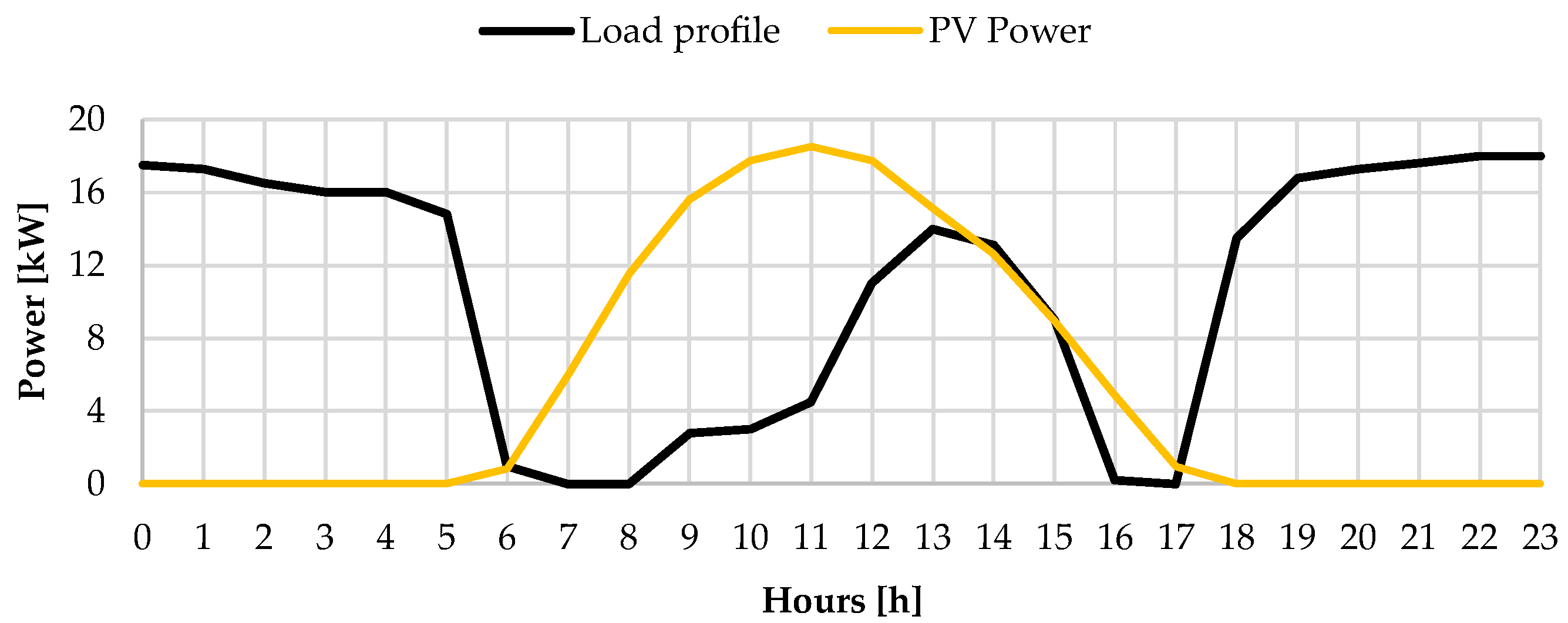
5.4. Characterize the Case Study
5.5. Parameterization of the Solution Model
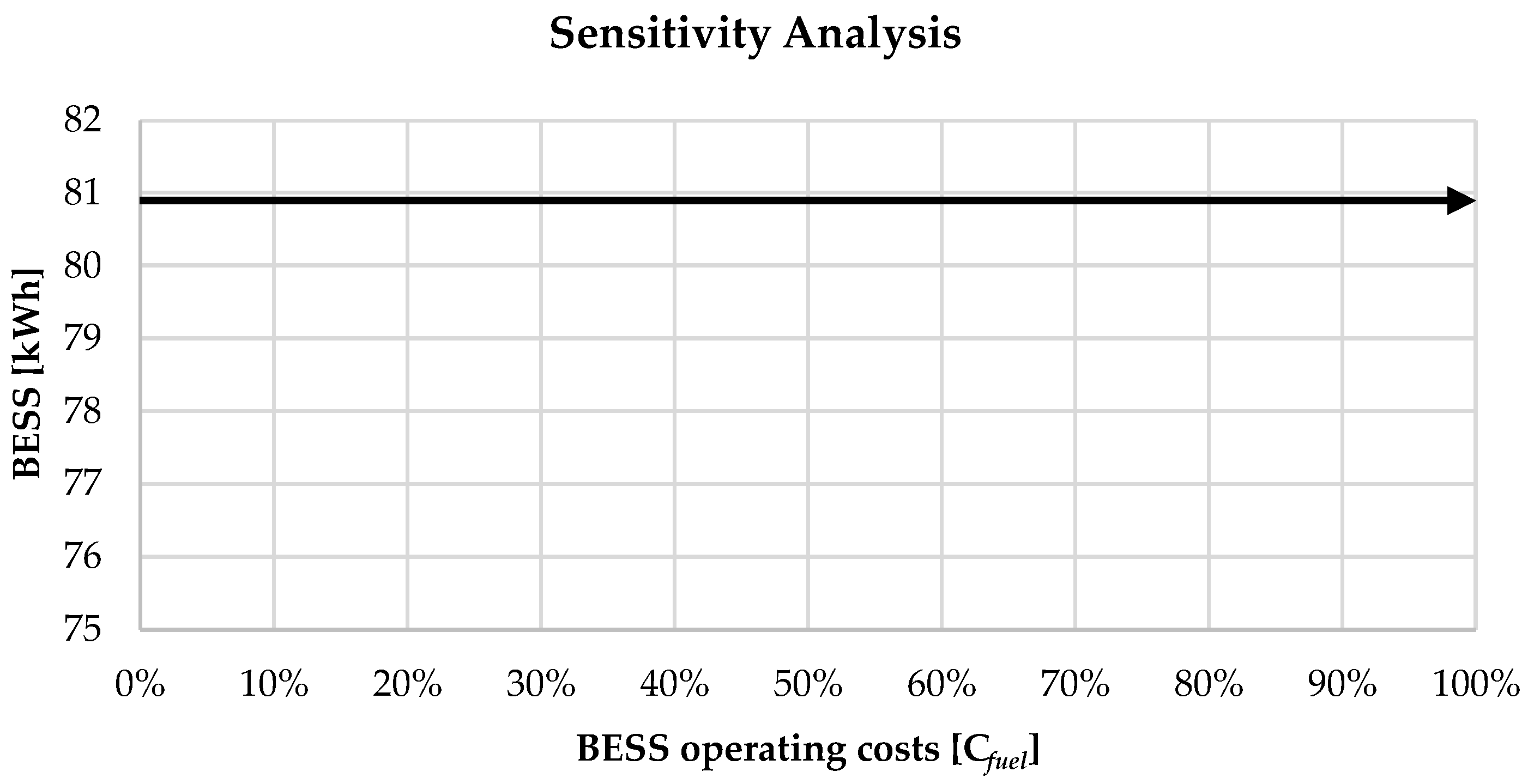
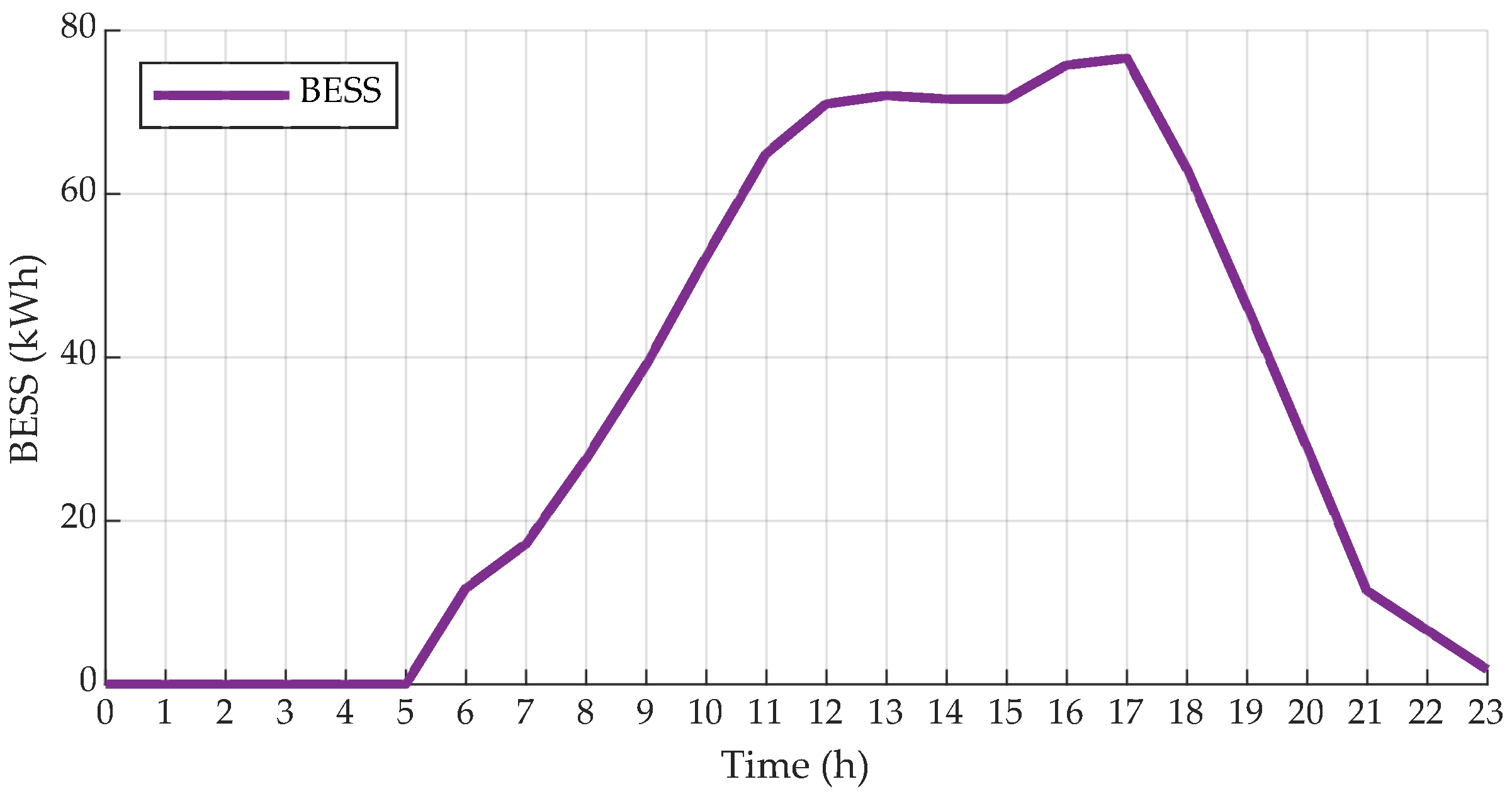
5.6. Analysis of Results for the Case Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| Objective function cost | |
| Cost of diesel fuel | |
| Cost of starting the diesel generator | |
| Cost of using the battery | |
| Power delivered by the diesel generator | |
| Binary variable for the diesel generator | |
| Binary variable for the diesel generator at a previous time step | |
| Diesel fuel consumption | |
| v | Linear segment in the diesel fuel consumption function |
| Number of linear segments in the diesel fuel consumption function | |
| Slope of the diesel fuel consumption function | |
| Intercept of the diesel fuel consumption function | |
| Cost of diesel fuel in Colombian Pesos per liter | |
| Cost of starting the diesel generator | |
| Battery discharge cost function | |
| Battery charge cost function | |
| Power delivered by the battery | |
| Power absorbed by the battery | |
| Binary variable for battery discharge | |
| Binary variable for battery charge | |
| Unitary factor for battery discharge cost | |
| Unitary factor for battery charge cost | |
| Intercept for battery discharge cost | |
| Intercept for battery charge cost | |
| Battery discharge cost | |
| Battery charge cost | |
| Power delivered by the photovoltaic array | |
| Power demand by the load | |
| Minimum power of diesel generator | |
| Maximum power of diesel generator | |
| Minimum discharge power of the battery | |
| Maximum discharge power of the battery | |
| Minimum charge power of the battery | |
| Maximum charge power of the battery | |
| Energy stored in the battery | |
| Energy stored in the battery at previous time step | |
| Discharge efficiency of battery | |
| Charge efficiency of battery | |
| Abbreviations | |
| BESS | Battery energy storage system |
| ZNI | Non-interconnected zones |
| DERs | Distributed energy resources |
| DG | Diesel generator |
| PV | Photovoltaic |
| IPSE | Institute for the Planning and Promotion of Energy Solutions |
| MILP | Mixed integer linear programming |
References
- Chen, S.X.; Gooi, H.B.; Wang, M.Q. Sizing of Energy Storage for Microgrids. IEEE Trans. Smart Grid 2012, 3, 142–151. [Google Scholar] [CrossRef]
- Li, X.; Hu, C.; Luo, S.; Lu, H.; Piao, Z.; Jing, L. Distributed Hybrid-Triggered Observer-Based Secondary Control of Multi-Bus DC Microgrids Over Directed Networks. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 72, 2467–2480. [Google Scholar] [CrossRef]
- Li, W.; Zou, Y.; Yang, H.; Fu, X.; Xiang, S.; Li, Z. Two-Stage Stochastic Energy Scheduling for Multi-Energy Rural Microgrids With Irrigation Systems and Biomass Fermentation. IEEE Trans. Smart Grid 2025, 16, 1075–1087. [Google Scholar] [CrossRef]
- Bahramirad, S.; Reder, W.; Khodaei, A. Reliability-Constrained Optimal Sizing of Energy Storage System in a Microgrid. IEEE Trans. Smart Grid 2012, 3, 2056–2062. [Google Scholar] [CrossRef]
- Alsaidan, I.; Khodaei, A.; Gao, W. A Comprehensive Battery Energy Storage Optimal Sizing Model for Microgrid Applications. IEEE Trans. Power Syst. 2018, 33, 3968–3980. [Google Scholar] [CrossRef]
- Amini, M.; Khorsandi, A.; Vahidi, B.; Hosseinian, S.H.; Malakmahmoudi, A. Optimal sizing of battery energy storage in a microgrid considering capacity degradation and replacement year. Electr. Power Syst. Res. 2021, 195, 107170. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Crow, M.L.; Elmore, A.C. Optimal Sizing of a Vanadium Redox Battery System for Microgrid Systems. IEEE Trans. Sustain. Energy 2015, 6, 729–737. [Google Scholar] [CrossRef]
- Mozafari, B.; Mohammadi, S. Optimal sizing of energy storage system for microgrids. Sadhana 2014, 39, 819–841. [Google Scholar] [CrossRef]
- Takano, H.; Hayashi, R.; Asano, H.; Goda, T. Optimal Sizing of Battery Energy Storage Systems Considering Cooperative Operation with Microgrid Components. Energies 2021, 14, 7442. [Google Scholar] [CrossRef]
- Fossati, J.P.; Galarza, A.; Martín-Villate, A.; Fontán, L. A method for optimal sizing energy storage systems for microgrids. Renew. Energy 2015, 77, 539–549. [Google Scholar] [CrossRef]
- Bahmani-Firouzi, B.; Azizipanah-Abarghooee, R. Optimal sizing of battery energy storage for micro-grid operation management using a new improved bat algorithm. Int. J. Electr. Power Energy Syst. 2014, 56, 42–54. [Google Scholar] [CrossRef]
- Sharma, S.; Bhattacharjee, S.; Bhattacharya, A. Grey wolf optimisation for optimal sizing of battery energy storage device to minimise operation cost of microgrid. IET Gener. Transm. Distrib. 2016, 10, 625–637. [Google Scholar] [CrossRef]
- Zolfaghari, M.; Ghaffarzadeh, N.; Ardakani, A.J. Optimal sizing of battery energy storage systems in off-grid micro grids using convex optimization. J. Energy Storage 2019, 23, 44–56. [Google Scholar] [CrossRef]
- Quynh, N.V.; Ali, Z.M.; Alhaider, M.M.; Rezvani, A.; Suzuki, K. Optimal energy management strategy for a renewable-based microgrid considering sizing of battery energy storage with control policies. Int. J. Energy Res. 2021, 45, 5766–5780. [Google Scholar] [CrossRef]
- Vaka, S.S.K.R.; Matam, S.K. Optimal Sizing and Management of Battery Energy Storage Systems in Microgrids for Operating Cost Minimization. Electr. Power Compon. Syst. 2021, 49, 1319–1332. [Google Scholar] [CrossRef]
- Tejero-Gómez, J.A.; Bayod-Rújula, Á.A. Analysis of Grid-Scale Photovoltaic Plants Incorporating Battery Storage with Daily Constant Setpoints. Energies 2024, 17, 6117. [Google Scholar] [CrossRef]
- Bade, S.O.; Tomomewo, O.S.; Meenakshisundaram, A.; Dey, M.; Alamooti, M.; Halwany, N. Multi-Criteria Optimization of a Hybrid Renewable Energy System Using Particle Swarm Optimization for Optimal Sizing and Performance Evaluation. Clean Technol. 2025, 7, 23. [Google Scholar] [CrossRef]
- Alshamri, H.; Cockerill, T.; Tomlin, A.S.; Al-Damook, M.; Al Qubeissi, M. On–off-Grid Optimal Hybrid Renewable Energy Systems for House Units in Iraq. Clean Technol. 2024, 6, 602–624. [Google Scholar] [CrossRef]
- Trivić, B.; Savić, A. Optimal Allocation and Sizing of BESS in a Distribution Network with High PV Production Using NSGA-II and LP Optimization Methods. Energies 2025, 18, 1076. [Google Scholar] [CrossRef]
- Saleeb, H.; El-Rifaie, A.M.; Sayed, K.; Accouche, O.; Mohamed, S.A.; Kassem, R. Optimal Sizing and Techno-Economic Feasibility of Hybrid Microgrid. Processes 2025, 13, 1209. [Google Scholar] [CrossRef]
- Rus-Casas, C.; Gilabert-Torres, C.; Fernández-Carrasco, J.I. Optimizing Energy Management and Sizing of Photovoltaic Batteries for a Household in Granada, Spain: A Novel Approach Considering Time Resolution. Batteries 2024, 10, 358. [Google Scholar] [CrossRef]
- Amin, S.M.M.; Hossain, N.; Lipu, M.S.H.; Urooj, S.; Akter, A. Development of a PV/Battery Micro-Grid for a Data Center in Bangladesh: Resilience and Sustainability Analysis. Sustainability 2023, 15, 15691. [Google Scholar] [CrossRef]
- Jarso, A.K.; Jin, G.; Ahn, J. Hybrid Genetic Algorithm-Based Optimal Sizing of a PV–Wind–Diesel–Battery Microgrid: A Case Study for the ICT Center, Ethiopia. Mathematics 2025, 13, 985. [Google Scholar] [CrossRef]
- Guamán-Molina, J.; Pesantez, P.; Chavez-Fuentez, C.; Ríos, A. Industrial Application of Photovoltaic Systems with Storage for Peak Shaving: Ecuador Case Study. Eng. Proc. 2023, 47, 15. [Google Scholar] [CrossRef]
- La Bella, A.; Cominesi, S.R.; Sandroni, C.; Scattolini, R. Hierarchical predictive control of microgrids in islanded operation. IEEE Trans. Autom. Sci. Eng. 2016, 14, 536–546. [Google Scholar] [CrossRef]
- Hannan, M.; Faisal, M.; Ker, P.J.; Begum, R.; Dong, Z.; Zhang, C. Review of optimal methods and algorithms for sizing energy storage systems to achieve decarbonization in microgrid applications. Renew. Sustain. Energy Rev. 2020, 131, 110022. [Google Scholar] [CrossRef]
- Ton, D.T.; Smith, M.A. The U.S. Department of Energy’s Microgrid Initiative. Electr. J. 2012, 25, 84–94. [Google Scholar] [CrossRef]
- UPME. Plan Indicativo de Expansión de Cobertura de Energía Eléctrica—PIEC 2019–2023. Available online: https://www1.upme.gov.co/siel/Pages/Plan-indicativo-expansion-cobertura-EE-PIEC.aspx (accessed on 20 April 2024).
- IPSE. Centro Nacional de Monitoreo. Available online: https://ipse.gov.co/cnm/ (accessed on 20 April 2024).
- Linderoth, J.T.; Lodi, A. MILP software. Wiley Encycl. Oper. Res. Manag. Sci. 2010, 5, 3239–3248. [Google Scholar]
- Palma-Behnke, R.; Benavides, C.; Lanas, F.; Severino, B.; Reyes, L.; Llanos, J.; Sáez, D. A Microgrid Energy Management System Based on the Rolling Horizon Strategy. IEEE Trans. Smart Grid 2013, 4, 996–1006. [Google Scholar] [CrossRef]
- IPSE. Guía Practica de Estructuración de Proyectos. Available online: https://ipse.gov.co/guia-practica-de-estructuracion-de-proyectos/ (accessed on 20 April 2024).
- Renewables.ninja. Solar Photovoltaic Power. Available online: https://www.renewables.ninja/ (accessed on 20 April 2024).
- GlobalPetrolPrices. Colombia Precios del Diesel. Available online: https://es.globalpetrolprices.com/Colombia/diesel_prices/ (accessed on 20 April 2024).
- Distribuidora, G.G. Catalogo Plantas Eléctricas. Available online: https://gedisa.com.ve/recientes_aun/catalogos/electricos/libreria_planta/ConjuntoMarco_01.html (accessed on 20 April 2024).
- Hu, C.; Luo, S.; Li, Z.; Wang, X.; Sun, L. Energy Coordinative Optimization of Wind-Storage-Load Microgrids Based on Short-Term Prediction. Energies 2015, 8, 1505–1528. [Google Scholar] [CrossRef]
- Megger. Battery Testing Guide. Available online: https://megger.widen.net/s/cdtz6qcgg5/batterytesting-guide_en_v02 (accessed on 24 April 2025).
- Made in China. Batería Solar de Plomo-ácido Sellada SMF de 2V 2500ah Cspower. Available online: https://es.made-in-china.com/co_cspower/product_Cspower-2V-2500ah-SMF-Sealed-Lead-Acid-Battery-Solar-Battery_rnoinnuug.html (accessed on 24 April 2025).
- HITACHI. ¿Cómo Calcular la Potencia de Aire Acondicionado para una Superficie Determinada? Available online: https://www.hitachiaircon.com/es/noticias/descubre-como-calcular-la-potencia-de-aire-acondicionado-que-necesitas-para-tu-casa (accessed on 24 April 2025).




| Ref. | Advantages | Disadvantages | Application Cases |
|---|---|---|---|
| [5] | Determine the size of the BESS considering different technologies, degradation, and discharge depth. | Require annual hourly demand profiles, energy flow models, and financial parameters. | Projects of energy expansion in non-interconnect zones, systems with advanced monitoring and historical data. |
| [10] | Integrate an energy management system with a BESS sizing strategy. | Focused on energy systems with high wind generation penetration. Require annual hourly demand, generation, and financial data. | Interconnected microgrids able to work in isolated mode. |
| [16] | Determine the BESS size to improve the reliability in PV systems. | Focused on large-scale photovoltaic plants; hence, it is limited to small-scale rural applications. | Grid-connected solar plants to ensure reliable power for participating in intraday markets. |
| [22] | Integrate resilient cost and renewable energy penetration indicators in a BESS and PV size method. | Focused on data centers in urban areas; hence, it has limited application on ZNI or rural zones with reduced data available. | Critical infrastructure in urban areas with vulnerable or unstable electrical grids. |
| [24] | Evaluate self-consumption and peak-shaving strategies through technical–economic analysis, comparing investment, energy savings, and financial viability. | Limited to interconnected systems. Low robustness in front of multiple constraints. | Grid-connected industries facing peak usage penalties, where regulations allow peak-shaving strategies. |
| [19] | Simultaneous multi-objective optimization of costs and technical indicators such as energy losses and voltage deviation. | Require data infrastructure, such as demand distribution and solar production by node, limiting its practical application to grid-connected networks with monitoring systems. | Medium-voltage distribution networks with high PV penetration, in which technical performance and efficiency are improved through energy storage. |
| [13] | Guarantee globally optimal solutions, minimizing operational costs and achieving rapid convergence compared to heuristic algorithms. | Require dynamic restrictions for the diesel generator; thus, monitoring is required. Due to some restrictions, there is a reduced fidelity in startups and switching operating modes. | Isolated microgrids formed by different sources, with high monitoring capacity. |
| [7] | Size power and capacity in systems with vanadium redox batteries. Optimize the daily operation through dynamic programming to maximize efficiency and minimize operating costs. | Require specific parameters of the vanadium redox battery system, such as temperature, electrolyte voltage, and absorption curve. | Critical and high-budget facilities. Advanced system instrumentation for the vanadium redox batteries is required. |
| [6] | Consider degradation and optimal replacement cycle for multiple technologies, enabling long-term technical and economic selection of the BESS. | Grid-connected operation with occasional island operation. Require annual hourly demand and generation profiles. | Urban or industrial areas with high data availability, in which long-term strategic planning and economic analysis of the BESS are required. |
| [20] | Integrate batteries for short-term storage and hydrogen generators for long-term storage, improving energy resilience in front of solar variability. | Focused on grid-connected systems with occasional island operation mode. | Grid-connected regions with high solar irradiance, green hydrogen potential, and unstable power grids. |
| [9] | Bi-level optimization model that simultaneously determines the optimal size of BESS and optimal operating schedule of the controllable resources. | Focused on grid-connected microgrids. Minimize penalties for power imbalance and consider controllable loads, which is uncommon in ZNI. | Urban or industrial microgrids with controllable loads. |
| [8] | Optimize the economic return by maximizing the net present value considering hourly prices, operation, and costs of the BESS. | Focused on grid-connected microgrids, limiting its applicability in isolated areas. | Microgrids connected to the power grid focused on maximize economic returns through energy arbitrage. |
| [21] | High sizing accuracy by considering nonlinear degradation and a 5-minute time resolution in consumption and generation data, improving the profitability and useful life of a BESS. | Require real-time and high-frequency monitoring, which is not feasible in rural communities. | Grid-connected urban homes with advanced metering systems. |
| [11,12,14,15] | Satisfactory reduction in operating costs, convergence times, and standard deviations compared to some heuristic methods. | Formulation focused on microgrids interconnected to the electrical grid, which limits its applicability in isolated operating contexts. | Interconnected microgrids with differentiated tariffs, energy exchange taxes, and reserve requirements supported by the main grid. |
| [17,18,23] | Multi-objective optimization, including metrics such as annualized cost, and probability of supply interruption. | Optimize the sizing of all components without in-depth technical and economic analysis of the BESS. This requires high-resolution hourly data for a full year, both for resources and the load profile. | Microgrids in the planning stage where no pre-installed resources exist, requiring an optimal configuration design of the entire system. |
| Localities | Users | DG [kW] | PV [kW] | BESS |
|---|---|---|---|---|
| Isla fuerte (Cartagena-Bolívar) | 431 | 800 | 175 | 432 batteries 3.850 Ah/2 V |
| Isla Múcura (Cartagena-Bolívar) | 43 | 125 | 30 | 96 batteries 2.500 Ah/2 V |
| Santa cruz del islote (Cartagena-Bolívar) | 127 | 100 | 68 | 144 batteries 4.800 Ah/2 V |
| San Francisco (Acandí-Choco) | 279 | 224 | 120 | No |
| San Roque (Medio Atrato (Beté)-Choco) | 208 | 224 | 120 | No |
| Unguía (Unguía-Choco) | 2.536 | 1.540 | 779 | 116 kWp 24.800 Ah/2 V |
| Barranco Minas (Barranco Minas-Guainía) | 355 | 225 | 121 | No |
| Inírida (Inírida-Guainía) | 6.159 | 9.250 | 1.300 | No |
| Nazareth (Uribia-La Guajira) | 146 | 600 | 430 | 576 batteries 3.350 Ah/2 V |
| DG | BESS | ||
|---|---|---|---|
| [COP/l] | 2382.00 | 1.00 | |
| [l/kW] | 0.24 | −1.00 | |
| [l] | 3.00 | [COP] | 0.00 |
| [l/kW] | 0.21 | [COP] | 0.00 |
| [l] | 4.00 | [kW] | 18.00 |
| [l/kW] | 0.24 | [kW] | −18.83 |
| [l] | 2.00 | [%] | 100.00 |
| [kW] | 132.00 | [%] | 90.00 |
| and [kW] | 66.00 | [kWh] | 0.00 |
| and [kW] | 33.00 | [kWh] | |
| [kW] | 13.20 | ||
| [COP] | 14,006.16 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zamora-Muñoz, A.F.; Orozco-Gutierrez, M.L.; Lopez-Santiago, D.M.; Montenegro-Oviedo, J.A.; Ramos-Paja, C.A. Battery Sizing Method for Microgrids—A Colombian Application Case. Computation 2025, 13, 114. https://doi.org/10.3390/computation13050114
Zamora-Muñoz AF, Orozco-Gutierrez ML, Lopez-Santiago DM, Montenegro-Oviedo JA, Ramos-Paja CA. Battery Sizing Method for Microgrids—A Colombian Application Case. Computation. 2025; 13(5):114. https://doi.org/10.3390/computation13050114
Chicago/Turabian StyleZamora-Muñoz, Andres Felipe, Martha Lucia Orozco-Gutierrez, Dany Mauricio Lopez-Santiago, Jhoan Alejandro Montenegro-Oviedo, and Carlos Andres Ramos-Paja. 2025. "Battery Sizing Method for Microgrids—A Colombian Application Case" Computation 13, no. 5: 114. https://doi.org/10.3390/computation13050114
APA StyleZamora-Muñoz, A. F., Orozco-Gutierrez, M. L., Lopez-Santiago, D. M., Montenegro-Oviedo, J. A., & Ramos-Paja, C. A. (2025). Battery Sizing Method for Microgrids—A Colombian Application Case. Computation, 13(5), 114. https://doi.org/10.3390/computation13050114






