Group Buying-Based Data Transmission in Flying Ad-Hoc Networks: A Coalition Game Approach
Abstract
1. Introduction
- A resource allocation optimization method based on distributed data content is proposed, where different data content is considered to transmit to UAVs which have corresponding data requirements. The designed utility function based on data transmission probability can reflect both link qualities and the efficiency of resource transmission. This provides theoretical support for the UAVs’ coalition selections and the formation of internal stable structures.
- We propose a coalition game framework to solve resource allocation and data transmission problems. In the framework, coalitional graph game characterizes the inner coalition structure (transmission mechanism). Data resource allocation of UAVs is analyzed in coalition formation game (CFG). Both games are proven to have stable solutions, indicating the effectiveness of our proposed model.
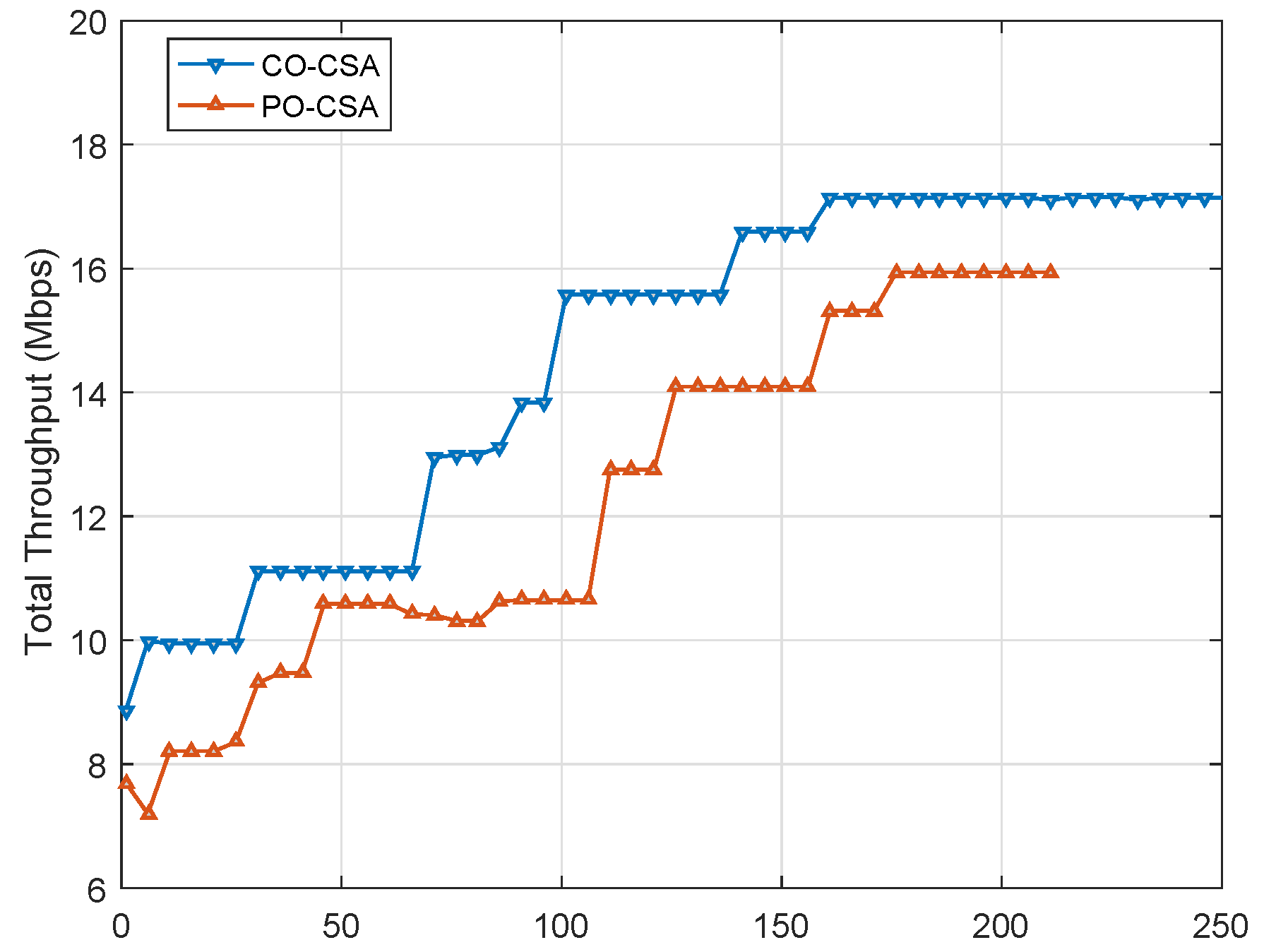
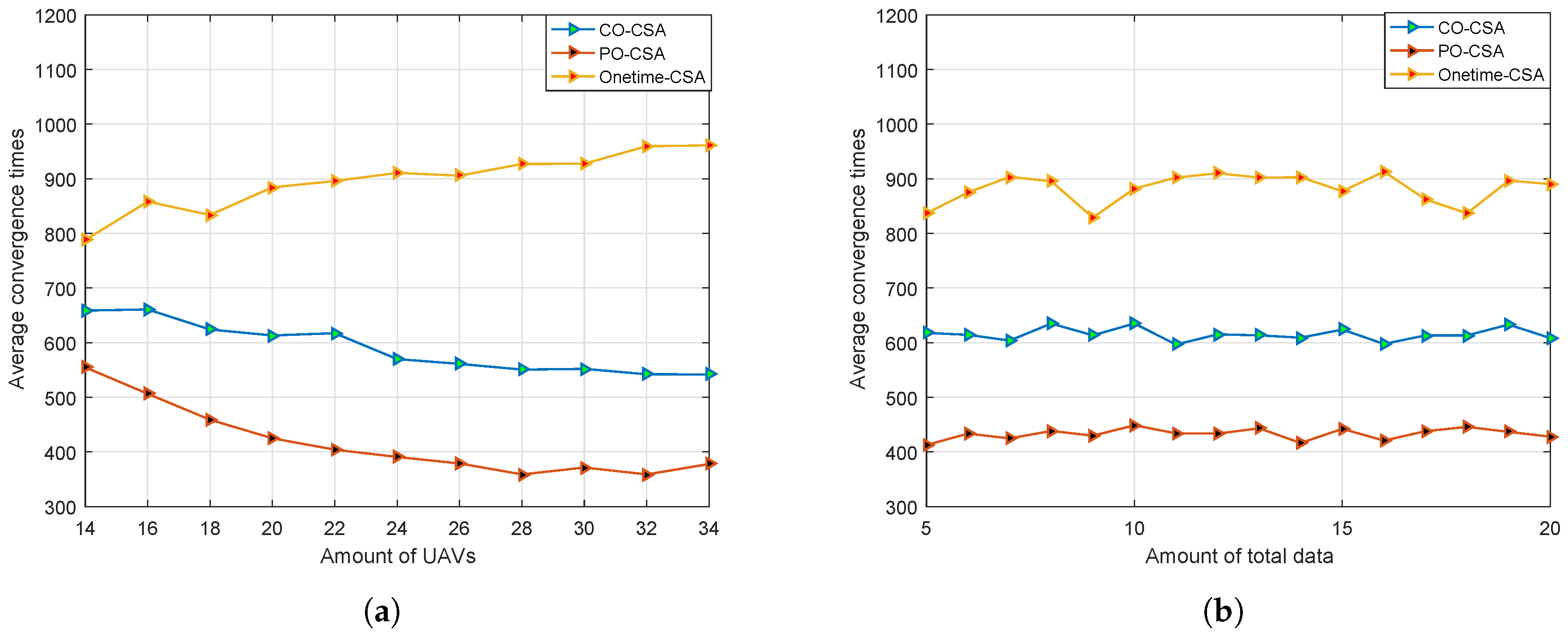
- A cooperative coalition selection mechanism is proposed to improve the performance of system model. CO-CSA and PO-CSA are designed to execute cooperative exchange mechanism. Simulation results show that both CO-CSA and PO-CSA achieve better performance than Onetime-CSA. In addition, the performance of CO-CSA is better than PO-CSA, while PO-CSA converges in less time.
2. System Model and Problem Formulation
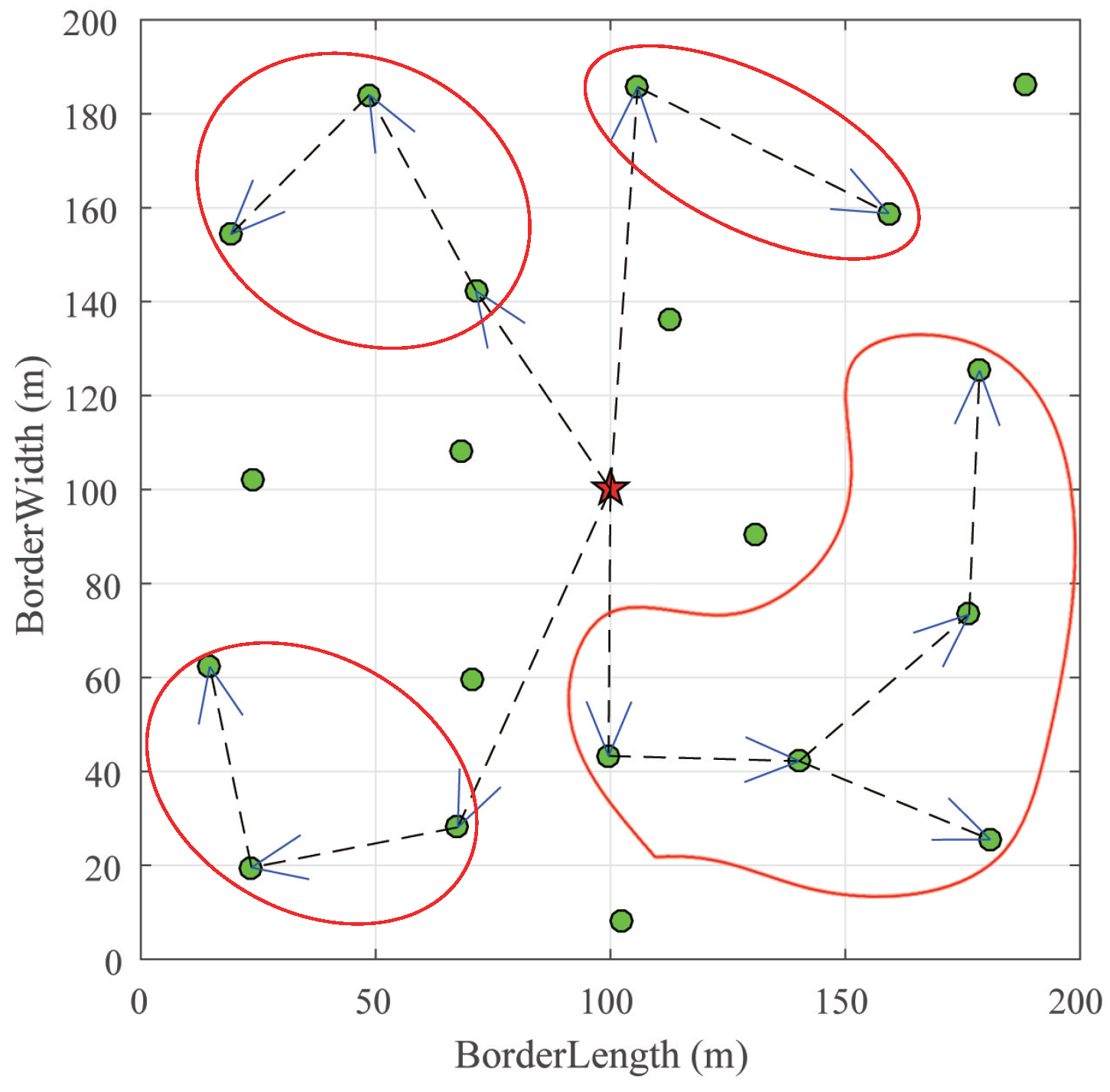
2.1. System Model
2.2. Problem Formulation
3. Coalitional Graph Game for Data Transmission
- is a set of all nodes (including central UAV).
- ε is the set of all edges (UAV-to-UAV links). For any , we say the link from i to j exists, if .
- is the available coalition selections for each , let denote the coalition selection for n.
- represents the utility function of UAV n while playing its strategy.
| Algorithm 1 Throughput maximization network formation algorithm. |
(1) Input , set . (2) while: All UAVs in coalition are connected considering data content s, i.e., . 1: Find , , UAV , where . 2: Find UAV m if where . 3: Offer UAV i and UAV m a new link . Add i and to and , respectively. End (3) Output routing link and UAV n’s current coalition ’s throughput . |
4. Coalition Formation Game for Resources Allocation based on Group Buying
4.1. Game Model
4.2. Analysis of the Stable Coalition Partition
4.3. Algorithm Design
| Algorithm 2 Coalition order/(Pareto order) based coalition selection algorithm, CO-CSA/(PO-CSA) |
Step 1: Initialize UAVs’ state strategies considering data content s. Loop: IterationMax Step 2: Select one UAV randomly, say i. . Step 3: Input into Algorithm 1 and obtain . Calculate according to Equation (8). Step 4: UAV i generate a new strategy . . Step 5: Input into Algorithm 1 and obtain . Calculate according to Equation (8). Step 6: UAV i update strategy with coalition order/ (Pareto order) according to Equation (10)/(Equation (9)), and the update probability is given as follows: Step 7: Update . End loop: |
5. Simulation Results and Discussion
5.1. Basic Performance
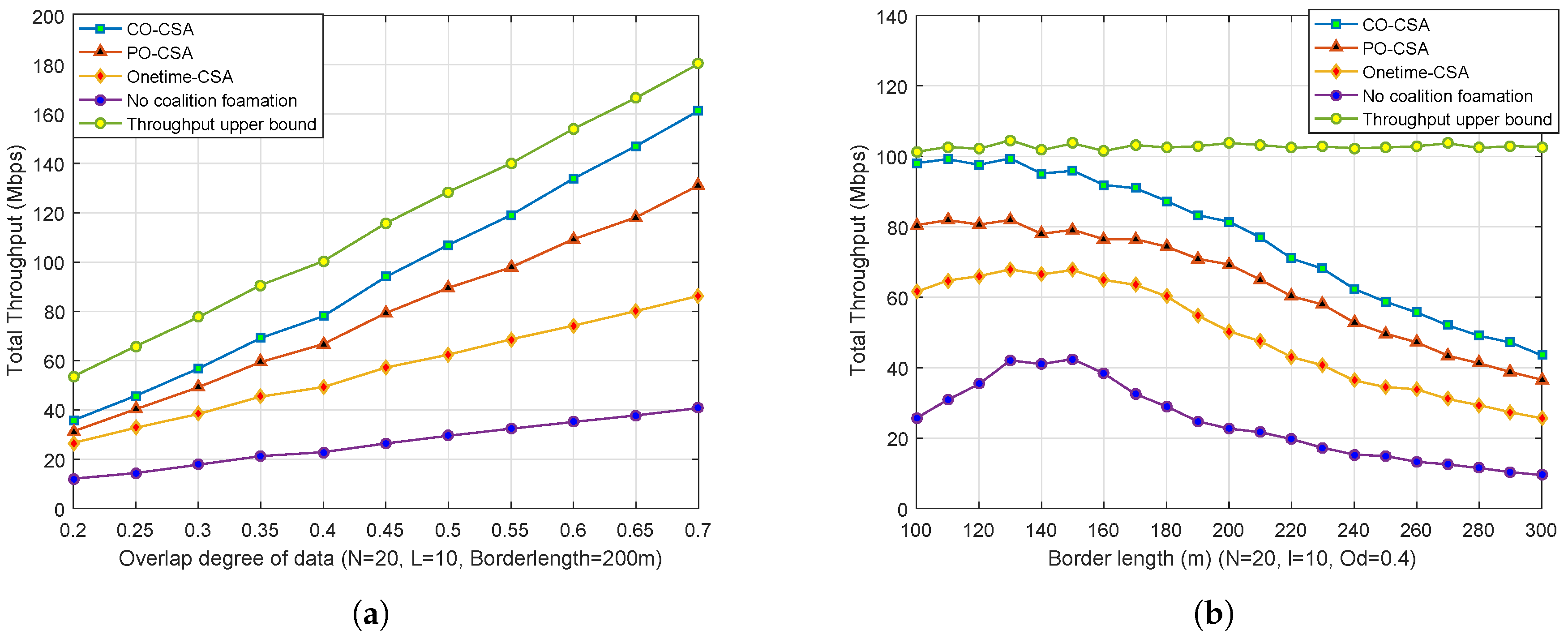
5.2. Different Orders and Contrast Algorithms
5.3. Convergence Performance
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zeng, Y.; Zhang, R.; Teng, J.L. Wireless communications with unmanned aerial vehicles: Opportunities and challenges. IEEE Commun. Mag. 2016, 54, 36–42. [Google Scholar] [CrossRef]
- Liu, D.; Xu, Y.; Wang, J.; Xu, Y.; Anpalagan, A.; Wu, Q.; Wang, H.; Shen, L. Self-organizing relay selection in UAV communication networks: A matching game perspective. IEEE Wirel. Commun. 2018, arXiv:1805.09257v1. [Google Scholar]
- Bekmezci, İ.; Sahingoz, O.K.; Temel, Ş. Flying ad-hoc networks (FANETs): A survey. Ad Hoc Netw. 2013, 11, 1254–1270. [Google Scholar] [CrossRef]
- Ruan, L.; Wang, J.; Chen, J.; Xu, Y.; Yang, Y.; Jiang, H.; Zhang, Y.; Xu, Y. Energy-efficient multi-UAV coverage deployment in UAV networks: A game-theoretic framework. China Commun. 2018, 15, 194–209. [Google Scholar] [CrossRef]
- Xu, Y.; Ren, G.; Chen, J.; Luo, Y.; Jia, L.; Liu, X.; Yang, Y.; Xu, Y. A one-leader multi-follower bayesian-Stackelberg game for anti-jamming transmission in UAV communication networks. IEEE Access 2018, 6, 21697–21709. [Google Scholar] [CrossRef]
- Zou, Y.; Jiang, X.; Yan, P.; Zhu, J. Next-generation unmanned aerial vehicle (UAV) cooperative communications. J. Nanjing Univ. Posts Telecommun. Nat. Sci. Ed. 2017, 37, 43–51. [Google Scholar] [CrossRef]
- Fang, T.; Tian, H.; Zhang, X.; Yang, Y.; Zhang, Y.; Xu, Y. Location-aware emergency content delivery in UAV-assisted networks: A game-theoretic approach. IEEE Access. under major revision.
- Thammawichai, M.; Baliyarasimhuni, S.P.; Kerrigan, E.C.; Sousa, J. Optimizing communication and computation for multi-UAV information gathering applications. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 601–615. [Google Scholar] [CrossRef]
- Fan, R.; Cui, J.; Jin, S.; Yang, K.; An, J. Optimal node placement and resource allocation for UAV relaying network. IEEE Commun. Lett. 2018, 22, 808–811. [Google Scholar] [CrossRef]
- Lyu, J.; Zeng, Y.; Zhang, R.; Teng, J.L. Placement optimization of UAV-mounted mobile base stations. IEEE Commun. Lett. 2017, 21, 604–607. [Google Scholar] [CrossRef]
- Say, S.; Inata, H.; Liu, J.; Shimamoto, S. Priority-based data gathering framework in UAV-assisted wireless sensor networks. IEEE Sens. J. 2016, 16, 5785–5794. [Google Scholar] [CrossRef]
- Ruan, L.; Chen, J.; Guo, Q.; Jiang, H.; Zhang, Y.; Liu, D. A coalition formation game approach for efficient cooperative multi-UAV deployment. Preprints 2018. [Google Scholar] [CrossRef]
- Yang, D.; Xue, G.; Zhang, X. Group buying spectrum auctions in cognitive radio networks. IEEE Trans. Veh. Technol. 2017, 66, 810–817. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Anpalagan, A. Context-aware group buying in ultra-dense small cell networks: Unity is strength. arXiv, 2018; arXiv:1807.08426v1. [Google Scholar]
- Saad, W.; Han, Z.; Debbah, M.; Hjørungnes, A.; Başar, T. Coalitional game theory for communication network. IEEE Signal Process. Mag. Spec. Issue Game Theory 2009, 26, 77–97. [Google Scholar] [CrossRef]
- Ruan, L.; Chen, J.; Qiu, Y.; Liu, X.; Zhang, Y.; Zhu, X.; Xu, Y. Context-aware group buying in D2D networks: An overlapping coalition formation game approach. In Proceedings of the 2017 IEEE 17th International Conference on Communication Technology (ICCT), Chengdu, China, 27–30 October 2017; pp. 142–149. [Google Scholar]
- Pinto, L.R.; Moreira, A.; Almeida, L.; Rowe, A. Characterizing multihop aerial networks of COTS multirotors. IEEE Trans. Ind. Inform. 2017, 13, 898–906. [Google Scholar] [CrossRef]
- Parrot, A.R. Drone 2. Available online: http://ardrone2.parrot.com (accessed on 21 January 2016).
- Wang, T.; Song, L.; Han, Z. Coalitional graph games for popular content distribution in cognitive radio VANETs. IEEE Trans. Veh. Technol. 2013, 62, 4010–4019. [Google Scholar] [CrossRef]
- Arcaute, E.; Johari, R.; Mannor, S. Local dynamics for network formation games. In Proceedings of the 2008 46th Annual Allerton Conference on Communication, Control, and Computing, Urbana-Champaign, IL, USA, 23–26 September 2008. [Google Scholar]
- Wang, T.; Song, L.; Han, Z.; Saad, W. Overlapping coalition formation games for emerging communication networks. IEEE Netw. 2013, 2016, 46–53. [Google Scholar] [CrossRef]
- Hamilton, J. Game Theory: Analysis of Conflict. by R. B. Myerson. Managerial Decis. Econ. 2010, 13, 369. [Google Scholar] [CrossRef]
- Bogomolnaia, A.; Jackson, M.O. The stability of hedonic coalition structures. Games Econ. Behav. 2002, 38, 201–230. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, Y.; Wu, Q. Context awareness group buying in D2D networks: A coalition formation game-theoretic approach. IEEE Trans. Veh. Techn. Unpublished work. [CrossRef]
- Bala, V.; Goyal, S. Noncooperative model of network formation. Econometrica 2000, 68, 1181–1230. [Google Scholar] [CrossRef]
- Apt, K.R.; Witzel, A. A generic approach to coalition formation. Int. Game Theory Rev. 2009, arXiv:0709.0435v3 [cs.GT]11, 347–367. [Google Scholar] [CrossRef]
- Monderer, D.; Shapley, L.S. Potential games. Games Econ. Behav. 1996, 14, 124–143. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, J.; Wu, Q.; Anpalagan, A.; Yao, Y.D. Opportunistic spectrum access in cognitive radio networks: Global optimization using local interaction games. IEEE J. Sel. Top. Signal Process. 2012, 6, 180–194. [Google Scholar] [CrossRef]
- Vcking, B. Congestion games: Optimization in competition. In Proceedings of the Second ACiD Workshop, Durham, UK, 18–20 September 2006; pp. 9–20. [Google Scholar]
- Xu, Y.; Wang, J.; Wu, Q.; Anpalagan, A.; Yao, Y.D. Opportunistic spectrum access in unknown dynamic environment: A game-theoretic stochastic learning solution. IEEE Trans. Wirel. Commun. 2012, 11, 1380–1391. [Google Scholar] [CrossRef]
- Li, P.; Duan, H. A potential game approach to multiple UAV cooperative search and surveillance. Aerosp. Sci. Technol. 2017, 68, 403–415. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, J.; Wu, Q.; Zheng, J.; Shen, L.; Anpalagan, A. Dynamic spectrum access in time-varying environment: Distributed learning beyond expectation optimization. IEEE Trans. Commun. 2017, 65, 5305–5318. [Google Scholar] [CrossRef]
- Feng, Z.; Qiu, C.; Feng, Z.; Wei, Z.; Li, W.; Zhang, P. An effective approach to 5G: Wireless network virtualization. IEEE Commun. Mag. 2015, 53, 53–59. [Google Scholar] [CrossRef]
- Liu, X.; Xu, Y.; Jia, L.; Wu, Q.; Anpalagan, A. Anti-jamming Communications Using Spectrum Waterfall: A Deep Reinforcement Learning Approach. IEEE Commun. Lett. 2018, 22, 998–1001. [Google Scholar] [CrossRef]

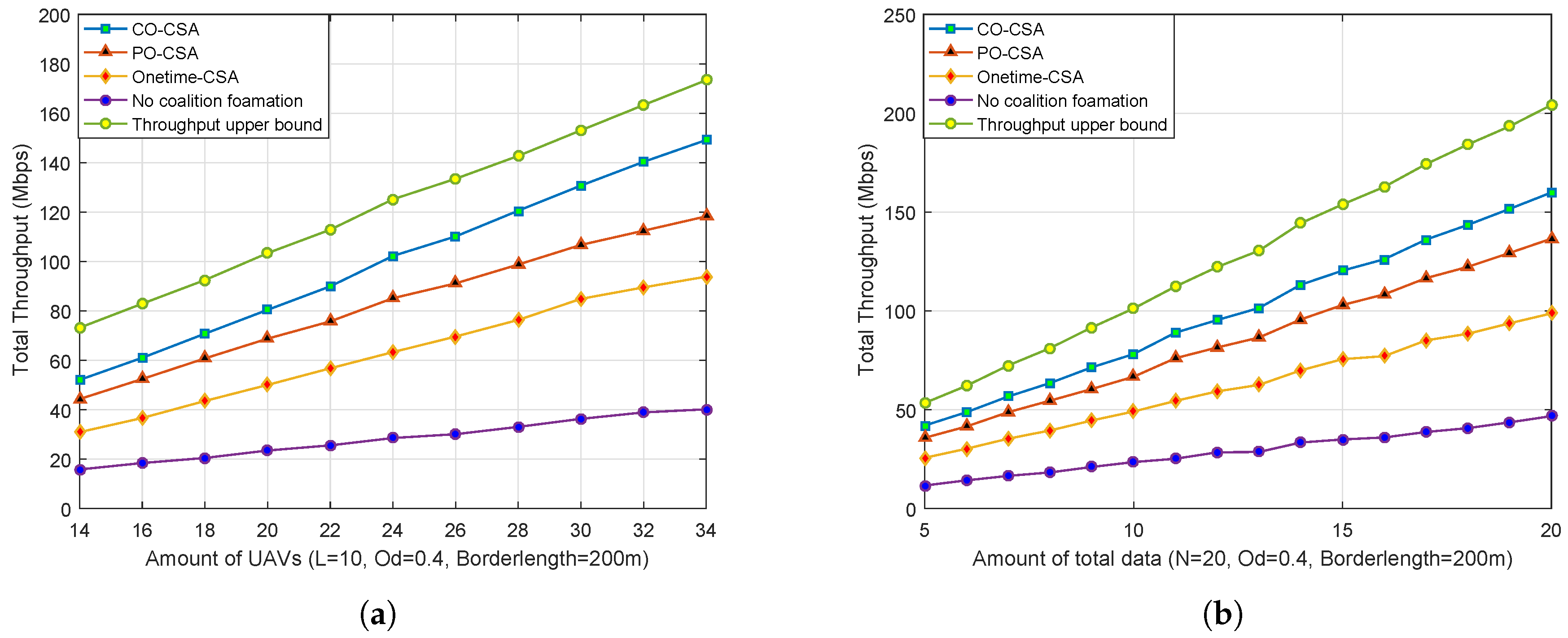
| Number of UAVs (N) | Mean (Mbps) | Variance (Mbps) | Confidence Interval (Mbps) |
|---|---|---|---|
| 14 | 52.07 | 8.74 | (50.33, 53.80) |
| 16 | 61.02 | 8.30 | (59.38, 62.67) |
| 18 | 70.77 | 8.99 | (68.98, 72.55) |
| 20 | 70.77 | 9.96 | (78.45, 82.40) |
| 22 | 89.93 | 10.16 | (87.92, 91.95) |
| 24 | 102.23 | 11.23 | (100.00, 104.46) |
| 26 | 110.14 | 11.32 | (107.90, 112.39) |
| 28 | 120.55 | 11.65 | (118.24, 122.87) |
| 30 | 130.73 | 12.35 | (128.28, 133.18) |
| 32 | 140.32 | 12.29 | (137.88, 142.76) |
| 34 | 149.16 | 12.70 | (146.64, 151.68) |
| Overlap Degree () | Mean (Mbps) | Variance (Mbps) | Confidence Interval (Mbps) |
|---|---|---|---|
| 0.3 | 35.81 | 6.78 | (34.46, 37.15) |
| 0.35 | 45.75 | 8.52 | (44.06, 47.44) |
| 0.4 | 56.79 | 9.82 | (54.84, 58.74) |
| 0.45 | 69.18 | 9.10 | (67.37, 70.99) |
| 0.5 | 78.04 | 9.71 | (76.11, 79.97) |
| 0.55 | 93.99 | 10.12 | (91.98, 96.00) |
| 0.6 | 106.93 | 9.50 | (105.05, 108.82) |
| 0.65 | 119.03 | 10.51 | (116.94, 121.12) |
| 0.7 | 133.84 | 11.03 | (131.65, 136.03) |
| 0.75 | 147.02 | 10.84 | (144.87, 149.17) |
| 0.8 | 161.34 | 10.28 | (159.30, 163.38) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, L.; Chen, J.; Guo, Q.; Zhang, X.; Zhang, Y.; Liu, D. Group Buying-Based Data Transmission in Flying Ad-Hoc Networks: A Coalition Game Approach. Information 2018, 9, 253. https://doi.org/10.3390/info9100253
Ruan L, Chen J, Guo Q, Zhang X, Zhang Y, Liu D. Group Buying-Based Data Transmission in Flying Ad-Hoc Networks: A Coalition Game Approach. Information. 2018; 9(10):253. https://doi.org/10.3390/info9100253
Chicago/Turabian StyleRuan, Lang, Jin Chen, Qiuju Guo, Xiaobo Zhang, Yuli Zhang, and Dianxiong Liu. 2018. "Group Buying-Based Data Transmission in Flying Ad-Hoc Networks: A Coalition Game Approach" Information 9, no. 10: 253. https://doi.org/10.3390/info9100253
APA StyleRuan, L., Chen, J., Guo, Q., Zhang, X., Zhang, Y., & Liu, D. (2018). Group Buying-Based Data Transmission in Flying Ad-Hoc Networks: A Coalition Game Approach. Information, 9(10), 253. https://doi.org/10.3390/info9100253





