Improvement of Fast Simplified Successive-Cancellation Decoder for Polar Codes

Abstract

This paper presents a new latency reduction method for successive-cancellation (SC) decoding of polar codes that performs a frozen-bit checking on the rate-other (R-other) nodes of the Fast Simplified SC (Fast-SSC) pruning tree. The proposed method integrates the Fast-SSC algorithm and the Improved SSC method (frozen-bit checking of the R-other nodes). We apply a recognition-based method to search for as many constituent codes as possible in the decoding tree offline. During decoding, the current node can be decoded directly, if it is a special constituent code; otherwise, the frozen-bit check is executed. If the frozen-bit check condition is satisfied, the operation of the R-other node is the same as that of the rate-one node. In this paper, we prove that the frame error rate (FER) performance of the proposed algorithm is consistent with that of the original SC algorithm. Simulation results show that the proportion of R-other nodes that satisfy the frozen-bit check condition increases with the signal-to-noise-ratio (SNR). Importantly, our proposed method yields a significant reduction in latency compared to those given by existing latency reduction methods. The proposed method solves the problem of high latency for the Improved-SSC method at a high code rate and low SNR, simultaneously.

1. Introduction

Polar codes [1] have been proven to achieve the symmetric capacity of memoryless channels with a successive-cancellation (SC) decoder. They have low implementation complexity and a very low error-floor [2]. However, the SC decoding speed is limited by the serial process, resulting in a high decoding latency. To decode a length-N polar code, the basic SC decoder should require $2(N-1)$ clock cycles [3]. In [4], a simplified SC (SSC) decoder is reported, for which the latency is reduced by classifying three types of constituent code nodes in the decoding tree. These are rate-zero (R-0), rate-one (R-1), and rate-other (R-other) nodes, the leaves of which are all frozen bits, all information bits, and partially frozen and information bits, respectively. The local decoder of an R-1 node uses threshold detection. Further, an R-0 node is a zero vector at any time. An R-other node retains the SC decoding rules and contributes the most latency. Two methods to improve the parallelism of the R-other node have been developed: the recognition-based method [5,6,7,8] and the check-based method [9,10,11].

The recognition-based method recognizes the constituent codes offline before decoding. The Fast Simplified SC (Fast-SSC) decoder has been introduced [5] to recognize the two other constituent code types (apart from R-0, R-1, and R-other); thus, the repetition (Rep) codes and single parity-check (SPC) codes can be decoded in parallel with low-complexity algorithms without traversing their corresponding sub-trees. Both the SSC decoder and Fast-SSC decoder provide significant latency reduction in comparison with that obtained from the SC decoder, while exhibiting the same performance as the SC decoder [5]. Further, some software decoders explore the implementation of the Fast-SSC algorithm [6,7,8]. However, the decoding latencies of the SSC and Fast-SSC decoders are constant without the influence of the channel condition.

The check-based method is designed to convert the R-other nodes to the constituent codes online, when a specific condition or check is satisfied [9,10,11]. To decrease the latency, resource constrained maximum-likelihood (ML) decoding on R-other nodes has been proposed [9]. To obtain the Improved Modified SC(IMSC) Decoder, the frozen-bit check (FC) has been applied to the SSC decoder [10] (Note that a similar method has been studied in [11]). Assuming that an R-other node follows the R-1 node rule of the SSC decoder, the bit estimates of the current code and its leaf node are decoded directly. If the bit estimates of all frozen leaf nodes are zero following checking, the FC condition is satisfied. Then, the bit estimate of the R-other node obtained in the previous step is valid, and there is no need to traverse the corresponding sub-trees. Otherwise, the R-other node still follows the original SC decoding rules. With this method, latency and complexity are reduced without loss of error-correction performance [10]. Note that the percentage of R-other nodes satisfying the FC condition increases with the signal-to-noise ratio (SNR), which introduces dynamic features in the decoding process. However, the decoding latency of the high-rate IMSC decoder is extremely high in the low-SNR range.

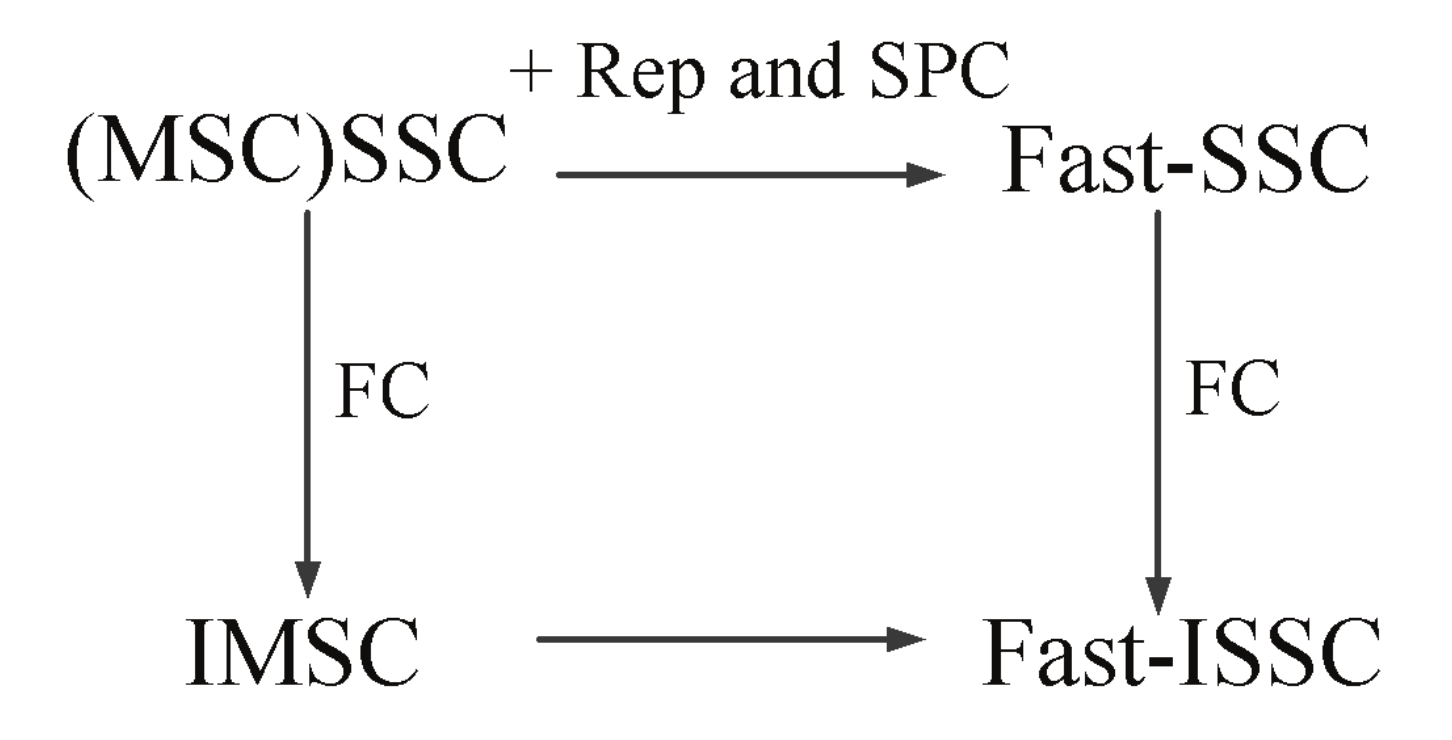
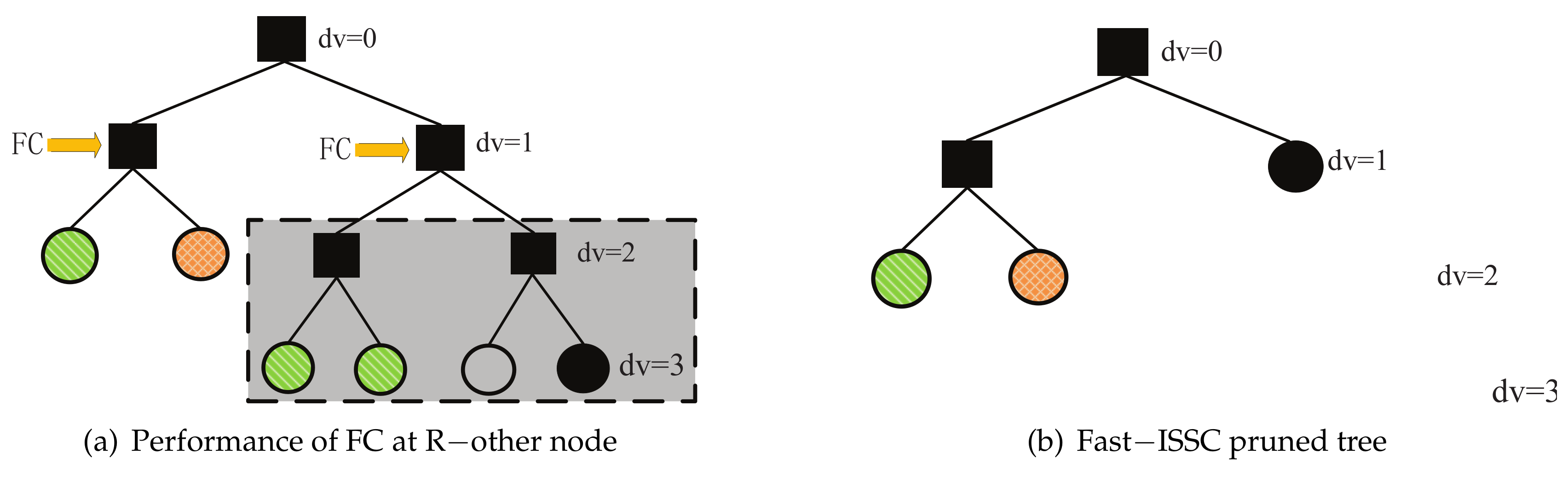
In this study, we propose a new type of latency reduction method called the Fast-ISSC algorithm, which performs the FC on the R-other nodes of the Fast-SSC pruning tree. Before decoding, the decoding tree becomes a Fast-SSC pruning tree through the recognition-based method. During decoding, the specific constituent codes follow the specific decoding rules. The R-other nodes are converted to R-1 nodes when the FC condition is satisfied. The Fast-ISSC decoder integrates the Fast-SSC algorithm and the FC method. The relationships between the various SC decoding latency reduction methods are shown in Figure 1.

The proposed Fast-ISSC algorithm is the first technique that integrates the stability of the recognition-based method and the dynamics of the check-based method. The main contribution of this study is as follows.

(1)

This approach realizes the lowest latency compared to the existing methods without error-correction performance loss.

(2)

The approach is highly adaptable to different rates and different channel conditions.

(3)

Our method facilitates further study of latency reduction for polar decoding. Future advances in recognition-based methods and check-based methods can be integrated together to implement a faster SC decoder.

We begin this paper by reviewing the SSC and Fast-SSC decoding algorithms in Section 2. We then present our improved decoding algorithm (Fast-ISSC) and analyze its latency and decoding performance in Section 3. In Section 4, we present simulation results obtained using the proposed algorithm. Finally, conclusions are presented in Section 5.

2. Background

A polar code is defined by three parameters, $(N,R,\mathcal{A})$, where the code length $N=2^m$, cardinality of information set $\mathcal{A}$ is K, and rate $R=K/N$. The set of the frozen bits indices are denoted by ${\mathcal{A}}^c$, and all frozen bits $u_{{\mathcal{A}}_c}$ are set to zero. For simplicity, we denote $(u_1,u_2,\dots ,u_N)$ as $u_1^N$.

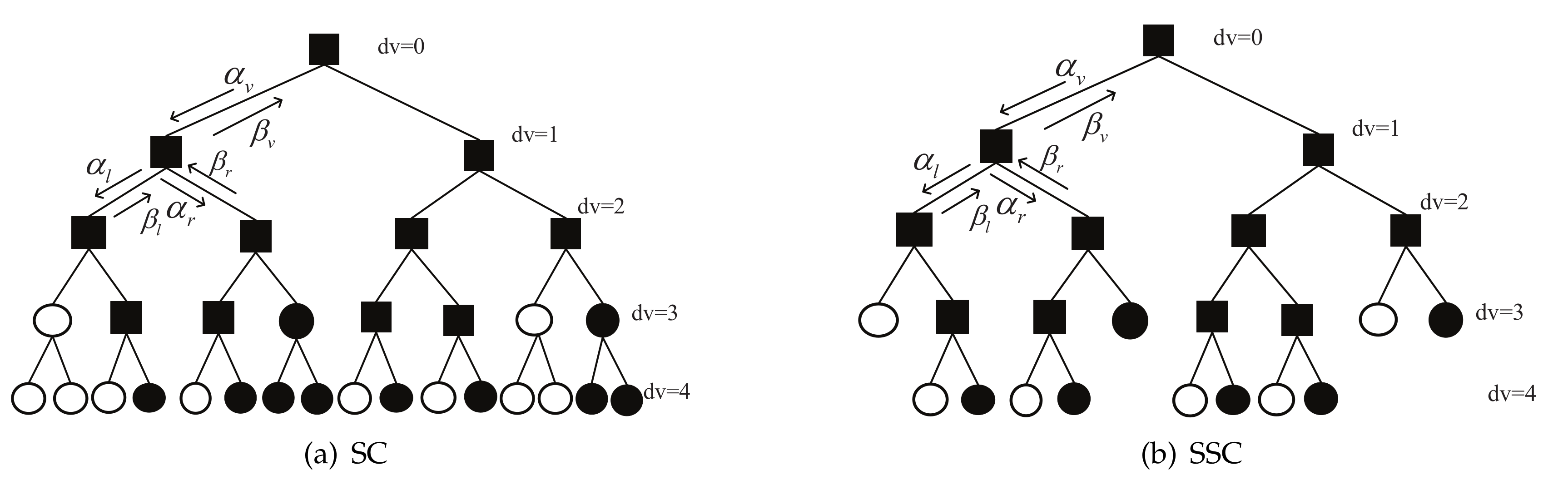
The original SC decoding graph can be converted to a message-passing algorithm executed on a full binary tree. The SC decoding process is executed sequentially and each leaf node is activated. The SC decoding tree for an (16, 8) polar code (P(16, 8)) is shown in Figure 2a. The R-0 and R-1 nodes are shown as white and black circles, respectively, and the R-other nodes are represented by squares. The messages passed to child nodes are log-likelihood ratios (LLRs) denoted ${\mathit{\alpha }}_v$, while those passed to parent nodes are bit estimates denoted ${\mathit{\beta }}_v$. Messages to a left child node are calculated using the sum-product update rules [12]:

$$\begin{array}{cc}\hfill {\mathit{\alpha }}_{v_l}\left[i\right]& =2{tanh}^{-1}(tanh(\frac{{\mathit{\alpha }}_v[2i-1]}{2})tanh(\frac{{\mathit{\alpha }}_v\left[2i\right]}{2})),fori=1:2^{m-d_v-1}\hfill \end{array}$$

(1)

where $d_v$ is the depth of the current constituent code.

Messages to a right child node are calculated using the formula

$$\begin{array}{cc}\hfill {\mathit{\alpha }}_{v_r}\left[i\right]& ={\mathit{\alpha }}_v[2i-1](1-2{\mathit{\beta }}_{v_l}\left[i\right])+{\mathit{\alpha }}_v\left[2i\right],fori=1:2^{m-d_v-1}\hfill \end{array}$$

(2)

where ${\mathit{\beta }}_{v_l}$ is the bit estimate from the left child.

The locations of some frozen bits indices are special, and these can be utilized to reduce the decoding latency. This concept was first employed by the SSC decoder to reduce the latency. For a sub-tree rooted at node v, $I_v$ denotes the set of all leaf nodes indices. A node v is a R-1 (R-0) node if $I_v\subset \mathcal{A}$($I_v\subset \left[N\right]\setminus \mathcal{A}$). A sub-tree corresponding to the R-0 and R-1 nodes can be cut, removing the need to traverse the sub-tree [4]. The R-other nodes still follow the original SC decoder rule. The SSC pruned tree is shown in Figure 2b, corresponding to the same code as for Figure 2a. The SSC decoder reduces the latency and number of calculations for the real value vector ${\mathit{\alpha }}_v$. As the gains of the latency reduction are obviously large, many studies have been conducted to improve the SSC decoder [5,6,7,8,9,10,11].

The Fast-SSC decoder recognizes the other two constituent codes, namely, the Rep codes, for which only the last leaf is not a frozen bit, and the SPC codes, for which only the first leaf is a frozen bit [5]. A node v, corresponding to a constituent code of length $N_v$, receives the soft-message vector ${\mathit{\alpha }}_v$ to the constituent decoder; the Rep and SPC codes can provide an codeword estimate ${\mathit{\beta }}_v$ in parallel using low-complexity algorithms [5]. The output for a Rep code is

$${\mathit{\beta }}_v\left[i\right]=\left\{\begin{array}{cc}0,\hfill & {\sum }_i{\mathit{\alpha }}_v\left[i\right]\ge 0,\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(3)

The output of the SPC code is

$${\mathit{\beta }}_v\left[i\right]=\left\{\begin{array}{cc}{\mathit{\beta }}_v\left[i\right]\oplus \mathrm{parity},\hfill & i=\arg \underset{\mathrm{i}}{min}\left|{\mathit{\alpha }}_v\left[i\right]\right|,\hfill \\ {\mathit{\beta }}_v\left[i\right],\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(4)

The parity of a SPC code is calculated as

$$\mathrm{parity}=\begin{array}{c}\hfill \underset{i=0}{\overset{N_v-1}{⨁}}{\mathit{\beta }}_v\left[i\right],\end{array}$$

(5)

$$\begin{array}{c}\hfill {\mathit{\beta }}_v\left[i\right]=\mathrm{h}({\mathit{\alpha }}_v\left[i\right])=\left\{\begin{array}{cc}0,\hfill & {\mathit{\alpha }}_v\left[i\right]\ge 0,\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(6)

where h$({\mathit{\alpha }}_v\left[i\right])$ is the hard-decision function based on ${\mathit{\alpha }}_v\left[i\right]$.

The Fast-SSC decoder provides a significant latency reduction compared to the SC decoder. However, the decoding latency of the Fast-SSC decoder is constant without the influence of the channel condition.

3. Proposed Method

By taking advantage of the special positions of the frozen bits, the Rep and SPC nodes are identified from the R-other nodes of the SSC pruned tree. Because the frozen leaf bits have no particular location, there is no corresponding low-complexity decoding algorithm for the remaining R-other nodes, which causes additional latency. To further reduce the decoding latency and adapt to the different rates and different channel conditions, we propose an approach that combines the stability of the recognition-based method and the dynamics of the check-based method, as described in this section.

The proposed method is called Fast-ISSC. First, the different constituent codes are identified on the decoding tree offline. During decoding, the current node can be decoded directly if it is a special constituent code; otherwise, the FC is performed at the R-other nodes, reducing the decoding latency of those nodes. Simultaneously, the problem of high latency for the check method in the case of a high code rate and low SNR can be solved. The overall procedure of the Fast-ISSC decoder is described in Algorithms 1–4. First, the main function is summarized in Algorithm 1. The receiver calculates an LLRs vector $\mathit{L}$ = ${(l_1,\dots ,l_N)}^{\mathrm{T}}$ with $l_i=\ln (W(y_i|1)/W(y_i|0))$, and feeds it into the Fast-ISSC decoder. Then, the node state initialization is outlined in Algorithm 2. The FC and ${\beta }_v$ procedures are summarized in Algorithms 3 and 4, respectively.

3.1. Detailed Description

Node state initialization: The constituent codes, i.e., the R-0, R-1, Rep, SPC, and R-other nodes, are identified on the decoding tree, offline. Let $\mathit{F}={[f_1,f_2,\dots ,f_N]}^{\mathrm{T}}$ denote the frozen bit vector; if the i corresponds to a frozen bit index, $f_i=1$, otherwise $f_i=0$. The leaf node types correspond to the values of $\mathit{F}$. Apart from the leaf node level, recognition of the constituent code is based on the left and right child node types; the recognition is performed in order, from bottom to top, and left to right. Recognition using binary tree traversal alters the node flag until identifications are no longer obtained. The flag of each constituent node is set corresponding to the specialized processing at the root of the constituent codes. Algorithm 2 summarizes the initialization procedure of the node state in the decode tree. This step forms a Fast-SSC pruning tree. Figure 3a shows an example of a Fast-SSC pruned tree, which is transformed from Figure 2b. This tree has significantly fewer nodes to operate on and visit than that of the SSC decoder. The Rep and SPC nodes are indicated by green stripes and cross-hatched orange, respectively. In Figure 3a, the SPC and Rep nodes at $d_v=3$ are equivalent, and the code length is 2. Recognition of the Rep and SPC nodes with greater code length is based on the case in which the Rep node length is 2. Once the decoding tree structure has been established, depth-first tree traversal decoding begins.

For a code length of N = $2^m$, the data structure of a binary decoding tree T is first generated. The nodes of the tree are created using a structure type in C++ programming, and its members include $level,left,right,parent,index,length$, etc. The tree includes $m+1$ node levels, indexed from depth $d_v$ = m to $d_v$ = 0. Each level $d_v$ contains $2^{d_v}$ nodes, and each node of level $d_v$ contains $2^{m-d_v}$ LLRs, and ${\mathit{\alpha }}_v$ and $2^{m-d_v}$ binary values ${\mathit{\beta }}_v$. The details of the Fast-ISSC decoding algorithm are as follows.

Algorithm 1: Fast-ISSC decoder.

Input:  Channel LLRs $\mathit{L}$ Output:  Decoded codeword $\widehat{\mathit{C}}$ 1: Node state initialization( ) 2: $T_0\left[0\right].{\mathit{\alpha }}_v$ = $\mathit{L}$ 3: if$Flag$ == 1 then 4:   ${\mathit{\beta }}_v=0$ //R-0 nodes 5:   Beta_compute( ) 6: else if$Flag$ == 2 then 7:   ${\mathit{\alpha }}_v$ is calculated as in Equations (1) or (2) 8:   ${\mathit{\beta }}_v$ = h$({\mathit{\alpha }}_v)$ //R-1 nodes 9:   Beta_compute( ) 10: else if$Flag$ == 6 or $Flag$ == 4 then 11:   ${\mathit{\alpha }}_v$ is calculated as in Equations (1) or (2)//Rep nodes 12:   the decoder output is calculated as in Equation (3) 13:   Beta_compute( ) 14: else if$Flag$ == 5 then 15:   ${\mathit{\alpha }}_v$ is calculated as in Equations (1) or (2) //SPC nodes 16:   the decoder output is calculated as in Equations (4)–(6) 17:   Beta_compute( ) 18: else 19:   ${\mathit{\alpha }}_v$ is calculated as in Equations (1) or (2)//R-other nodes 20:   $Flag\_check$ = 0; 21:   FC( ) 22:   if $Flag\_check$ == 1 then 23:     ${\mathit{\beta }}_v$ = ${\widehat{\mathit{\beta }}}_v$ 24:     Beta_compute( ) 25:   else 26:     Travel toward the next level of the decode tree 27:   end if 28: end if 29: return The decoded codeword $\widehat{\mathit{C}}$ = $T_0\left[0\right]$.${\mathit{\beta }}_v$.

Decoding process: The soft information, i.e., ${\mathit{\alpha }}_v$, of the root node is the decoder input, which is calculated from the received channel values. The flag of the current node is first judged: if it corresponds to one of the R-0, R-1, Rep, or SPC codes, it follows the specialized decoding rule at the roots of these constituent codes; otherwise, the ${\mathit{\beta }}_v$ values of the R-other node and its leaf nodes are obtained via the R-1 node rule. Then, the FC is executed; this procedure is shown in Algorithm 3. If the ${\mathit{\beta }}_v$ values of all frozen leaf nodes are zero, the FC condition is satisfied. Then, the local process at this R-other node can be simplified to that of an R-1 node and the sub-tree surrounded by the grey box in Figure 3a can be pruned, forming a Fast-ISSC pruned tree. The result is shown in Figure 3b. Otherwise, the local process still follows the SC decoding rules.

Algorithm 2: Node state initialization.

Input:  T, $\mathit{F}$ 1: $m={log}_{2}N$ 2: $T_m\left[j\right].Flag$ = 1; // $f_j$ == 1 3: $T_m\left[j\right].Flag$ = 2; // $f_j$ == 0 4: for$i=m-1$ down to 0 do 5:  $K=2^i$ 6:  for $j=0$ to $K-1$ do 7:   l = $T_i\left[j\right].left$; r = $T_i\left[j\right].right$ 8:   if $T_{i+1}\left[l\right].Flag$ == 1 and $T_{i+1}\left[r\right].Flag$ == 1 then 9:    $T_i\left[j\right].Flag$ = 1 //R-0 code 10:   else if $T_{i+1}\left[l\right].Flag$ == 2 and $T_{i+1}\left[r\right].Flag$ == 2 then 11:    $T_i\left[j\right].Flag$ = 2 //R-1 code 12:   else if $T_{i+1}\left[l\right].Flag$ == 1 and $T_{i+1}\left[r\right].Flag$ == 2 and $K==N/2$ then 13:    $T_i\left[j\right].Flag$ = 4//Rep code, length = 2 14:   else if $T_{i+1}\left[l\right].Flag$ == 4 and $T_{i+1}\left[r\right].Flag$ == 2 then 15:    $T_i\left[j\right].Flag$ = 5 //SPC code, length = 4 16:   else if $T_{i+1}\left[l\right].Flag$ == 5 and $T_{i+1}\left[r\right].Flag$ == 2 then 17:    $T_i\left[j\right].Flag$ = 5 //SPC code, length > 4 18:   else if $T_{i+1}\left[l\right].Flag$ == 1 and $T_{i+1}\left[r\right].Flag$ == 4 then 19:    $T_i\left[j\right].Flag$ = 6 //Rep code, length = 4 20:   else if $T_{i+1}\left[l\right].Flag$ == 1 and $T_{i+1}\left[r\right].Flag$ == 6 then 21:    $T_i\left[j\right].Flag$ = 6 //Rep code, length > 4 22:   else 23:    $T_i\left[j\right].Flag$ = 3 //R-other node 24:   end if 25:  end for 26: end for

Algorithm 3: Frozen-bit check (FC).

Input:  ${\mathit{\alpha }}_v$, min$I_v$, max$I_v$, $\mathit{F}$ Output:  $Flag\_check$, ${\widehat{\mathit{\beta }}}_v$ 1: ${\widehat{\mathit{\beta }}}_v$ = h$({\mathit{\alpha }}_v)$; $\widehat{\widehat{\mathit{u}}}$ = ${\widehat{\mathit{\beta }}}_v{\mathit{G}}_{m-d_v}$ 2: $sum$ = 0 3: fori = min$I_v$ to max$I_v$ do 4:  if $f_i$ == 1 then 5:   if ${\widehat{\widehat{\mathit{u}}}}_i$≠ 0 then 6:    $sum$ = $sum$ + 1 7:   end if 8:  end if 9: end for 10: if$sum$ == 0 then 11:  $Flag\_check$ = 1 12: end if

Algorithm 3 summarizes the FC procedure implemented on the R-other nodes. The initialization value of Flag_check is set to zero, and indicates whether the FC is successful.

Bit estimates: If the current node is a right node, its ${\mathit{\beta }}_v$ is passed to its parent, where it is combined with the ${\mathit{\beta }}_v$ of the brother node and passed through the upper level until the root node is reached. The process for calculation of ${\mathit{\beta }}_v$ is given in Algorithm 4. The systematic polar code is adopted in this paper, as it is well suited to a fast decoder; the root node ${\mathit{\beta }}_v$ constitutes the decoder output. In the case of systematic polar codes, in addition to improvement of the bit error rate (BER), it is not necessary to apply an inverse transformation on ${\mathit{\beta }}_v$, unlike in the case of non-systematic polar codes.

Algorithm 4: Beta_compute $\left(T_{\lambda }\left[index\right]\right)$.

1: Data: current node $T_{\lambda }\left[index\right]$ 2: $parent=⌊\frac{index}{2}⌋$ 3: if$index$ is odd then 4:  if i is even then 5:   ${\mathit{\beta }}_v[2i-1]$ = ${\mathit{\beta }}_{v_l}\left[i\right]$⊕${\mathit{\beta }}_{v_r}\left[i\right]$ 6:  else 7:   ${\mathit{\beta }}_v\left[2i\right]$ = ${\mathit{\beta }}_{v_r}\left[i\right]$ 8:  end if 9: end if 10: if$parent$ is odd then 11:  Beta_Compute $\left(T_{\lambda -1}\left[parent\right]\right)$ 12: end if

3.2. Latency Analysis

The number of time steps for polar decoding is referred to as the latency. As in [3], the calculations of ${\mathit{\beta }}_v$ and the hard decision h$({\mathit{\alpha }}_v)$ can be performed instantaneously. For the Fast-SSC decoder discussed in [5], special hardware modules are required for Rep and SPC code decoding. The Rep code module mainly includes the adder tree structure and sign function. This adder tree can be implemented through combinational logical. The compare and select unit is the kernel of the SPC code. The short SPC code is decoded in one time step and the long SPC code requires $2^{m-d_v}/P+c$ time steps, where $c\ge$ 1, because some steps are necessary to correct the most unreliable bit estimate and pipelining [5].

We can ignore the computational cost of FC in the latency analysis, for the following reasons: (1) The main FC operation is matrix multiplication ${\widehat{\mathit{\beta }}}_v{\mathit{G}}_{m-d_v}$, and the generator matrix ${\mathit{G}}_{m-d_v}$ has a special structure; thus, it can be implemented using combinational logic; (2) It is generally considered that, if binary operation is not the main component of the all operation, the computational cost can be ignored; (3) If the R-other node satisfies the FC, the obtained ${\widehat{\mathit{\beta }}}_v$ can be used as the bit estimate ${\mathit{\beta }}_v$ of the current node.

Based on the above analysis, the decoding latency calculation in this paper is consistent with [10], for the sake of fair comparison of different low latency decoders. Here, the latency was determined under the constraint that only P processing elements(PEs) of a real value vector ${\mathit{\alpha }}_v$ can be calculated when evaluating Equations (1) and (2), and P was assumed to be a power of 2.

(1)

For an R-0 node, the time step for calculation was ignored.

(2)

For an R-1, Rep, SPC, or R-other node, if its length was $2^{m-d_v}\le P$, the time step for calculation was one; otherwise, it was calculated as $2^{m-d_v}/P$.

3.3. Performance Analysis

The Fast-ISSS algorithm includes the parallel process for the constituent code and bit process for the leaf node, and the parallel process is similar to the multi-bit parallel process with the Symbol-Decision SC Algorithm [13]. During decoding, the constituent code length of the Fast-ISSS algorithm with parallel process is not fixed; however, the symbol length with the parallel process of the Symbol-Decision SC Algorithm is fixed.

For the convenience of analysis, two assumptions are made: (1) A length-N polar code is unevenly divided into K segments, and the length $M_i$ of each segment can be changed, where $i=0,1,\dots ,K-1$, and $M_i$ is a power of 2 (i.e., $M_i$ can be 1). The bit-decision SC and Fast-ISSS algorithms are used to decode each segment. Both decoding schedules are the same from a segment to the next segment. (2) During the local decoding, the process length $M_i$ of the two algorithms is not fixed, and are changed simultaneously; further, the length $M_i$ for both algorithms is same. In terms of the FER performance, we have the following.

Proposition 1.

If the data sequence is independent and equally likely, for an $(N,K)$ polar code over the given channel, the FER of the Fast-ISSS algorithm ${\mathrm{P}}_{\mathrm{M}+\mathrm{B}}\left({\widehat{u}}_0^{N-1}\ne u_0^{N-1}\right)$ and the FER of the bit-decision SC algorithm ${\mathrm{P}}_{\mathrm{B}}$ $\left({\widehat{u}}_0^{N-1}\ne u_0^{N-1}\right)$ satisfy:

$$\begin{array}{c}\hfill {\mathrm{P}}_{\mathrm{M}+\mathrm{B}}\left({\widehat{u}}_0^{N-1}\ne u_0^{N-1}\right)={\mathrm{P}}_{\mathrm{B}}\left({\widehat{u}}_0^{N-1}\ne u_0^{N-1}\right)\end{array}$$

(7)

Proof. 

The FER of a polar code with the bit-decision SC algorithm is given in [14].

$$\begin{array}{c}\hfill {\mathrm{P}}_{\mathrm{B}}\left({\widehat{u}}_0^{N-1}\ne u_0^{N-1}\right)=1-\prod _{i=0}^{K-1}\left(1-p\left(C_i\right)\right)\end{array}$$

(8)

For the Fast-ISSS algorithm,

$$\begin{array}{c}\hfill {\mathrm{P}}_{\mathrm{M}+\mathrm{B}}\left({\widehat{u}}_0^{N-1}\ne u_0^{N-1}\right)=1-\prod _{i=0}^{K-1}\left(1-p\left(C_i^{\prime }\right)\right)\end{array}$$

(9)

Let $p\left(C_0\right)={\mathrm{P}}_{\mathrm{SC}}\left({\widehat{u}}_0^{M_0-1}\ne u_0^{M_0-1}\right)$ and $p\left(C_0^{\prime }\right)={\mathrm{P}}_{\text{Fast-ISSS}}\left({\widehat{u}}_0^{M_0-1}\ne u_0^{M_0-1}\right)$ represent the probability that the first segment is erroneously decoded by the SC and M-bit Fast-ISSS algorithms, respectively. For $i=1,2,\dots ,K-1$, let $p\left(C_i\right)={\mathrm{P}}_{\mathrm{SC}}\left({\widehat{u}}_{M_i}^{M_i+M_{i+1}-1}\ne u_{M_i}^{M_i+M_{i+1}-1}|{\widehat{u}}_0^{M_i-1}=u_0^{M_i-1}\right)$ and $p\left(C_i^{\prime }\right)={\mathrm{P}}_{\text{Fast-ISSS}}\left({\widehat{u}}_{M_i}^{M_i+M_{i+1}-1}\ne u_{M_i}^{M_i+M_{i+1}-1}|{\widehat{u}}_0^{M_i-1}=u_0^{M_i-1}\right)$ denote the segment error probabilities of the ith segment by the SC and M-bit Fast-ISSS decoding algorithms, provided that all previous segments are correctly decoded.

We need to analyze ${\mathrm{P}}_{\text{Fast-ISSS}}\left({\widehat{u}}_0^{M_0-1}\ne u_0^{M_0-1}\right)$ of the Fast-ISSS algorithm compared with ${\mathrm{P}}_{\mathrm{SC}}\left({\widehat{u}}_0^{M_0-1}\ne u_0^{M_0-1}\right)$ of the bit-decision SC decoding on the first segment in possible five cases: (a) For an R-0 node, it does not affect performance. (b) For an R-1 node, it shows that for any R-1 node v, the calculated ${\mathit{\beta }}_v$ of both methods has the same results, and that the decisions at leave nodes with index $i\subset I_v$ made by both methods also agree. These results are proved in [4]. (c) For an REP or SPC node, because the special positions of the frozen bits, the constituent code performs low complexity ML decoding in parallel based on hard decision, that is, the performance is no worse than the original SC decoding [5]. (d) If an R-other node v satisfies the FC, the output of the corresponding node v can be computed by hard decision, i.e., ${\mathit{\beta }}_v$ = h$({\mathit{\alpha }}_v)$, $\widehat{\mathit{u}}$ = ${\mathit{\beta }}_v{\mathit{G}}_{m-d_v}$, which is consistent with the node in the same case as the SSC decoding. This theorem has been proven in [10,11] using mathematical induction. (e) For an R-other node that does not satisfy the FC, the bit-decision SC decoding is performed at the leaf node.

If a constituent code is activated, the $M_i$ corresponds to the number of all leaf nodes of this constituent code. Due to the control of the Algorithm 2 node state initialization( ), $M_i\ge 2^1$ for the R-0, R-1, or REP code, and $M_i\ge 2^2$ for the SPC or the R-other node. When an R-other node does not satisfy the FC and its child node is not a constituent code, and the leaf node of the R-other node is activated, $M_i$ = $2^0$ corresponds to the bit process. The distribution and number of constituent codes are affected by the code length and code rate of the polar code. When the polar codes are constructed with the method in [15], the R-0 code is more likely to be the first segment, and $M_0\ge 2^1$.

Summarizing the above five cases, we can conclude that ${\mathrm{P}}_{\text{Fast-ISSS}}\left({\widehat{u}}_0^{M_0-1}\ne u_0^{M_0-1}\right)$ of Fast-ISSS decoding is no worse than ${\mathrm{P}}_{\mathrm{SC}}\left({\widehat{u}}_0^{M_0-1}\ne u_0^{M_0-1}\right)$ of the bit-decision SC decoding for the first segment. Therefore, we have

$$\begin{array}{c}\hfill p\left(C_0\right)=p\left(C_0^{\prime }\right)\end{array}$$

(10)

For $1\le i<K$, the segment error probability P$\left({\widehat{u}}_{M_i}^{M_i+M_{i+1}-1}\ne u_{M_i}^{M_i+M_{i+1}-1}|{\widehat{u}}_0^{M_i-1}=u_0^{M_i-1}\right)$ can be analyzed in a similar way as for Equation (10); we also have

$$\begin{array}{c}\hfill p\left(C_i\right)=p\left(C_i^{\prime }\right)for1\le i<K.\end{array}$$

(11)

According to Equations (10) and (11), we have

$$\begin{array}{c}\hfill {\mathrm{P}}_{\mathrm{M}+\mathrm{B}}\left({\widehat{u}}_0^{N-1}\ne u_0^{N-1}\right)={\mathrm{P}}_{\mathrm{B}}\left({\widehat{u}}_0^{N-1}\ne u_0^{N-1}\right)\end{array}$$

(12)

□

Therefore, the FER of the Fast-ISSS algorithm is not degraded compared to the original SC algorithm.

4. Simulation Results

In this section, we demonstrate the performance of the proposed method with binary phase shift keying (BPSK) over the additive white Gaussian noise (AWGN) channel. The Tal-Vardy algorithm [15] was used to find information set $\mathcal{A}$ (optimized at SNR = 0 dB for N = 256, and SNR = 2 dB for N = 1024, 2048, and 4096). The system polar encoding was implemented according to [16].

The identification of constituent codes on the decoding tree was performed offline. To calculate the ratio of the latency reduction, it was necessary to count the number of codes for each of the constituent code types. The decoding latency was the joint influence on these constituent codes, and the R-other node was the main cause of the latency.

Table 1. Various node types at (1024, R).

R	Node	Length
		2	4	8	16	32	64	128	256	512
$\frac{1}{4}$	R-other	0	4	15	15	12	9	6	3	2
	R-1	4	3	2	1	0	0	0	0	0
	R-0	4	3	3	3	3	2	0	0	0
	Rep	0	10	6	3	2	0	0	1	0
	SPC	0	10	4	2	1	1	0	0	0
$\frac{1}{2}$	R-other	0	6	20	20	16	10	6	4	2
	R-1	6	5	4	3	2	0	0	0	0
	R-0	6	5	4	3	2	0	0	0	0
	Rep	0	12	6	3	0	1	1	0	0
	SPC	0	12	6	3	0	1	1	0	0
$\frac{3}{4}$	R-other	0	5	15	15	12	9	6	3	2
	R-1	5	4	3	2	0	2	0	0	0
	R-0	5	4	4	3	3	0	0	0	0
	Rep	0	8	3	1	1	1	0	0	0
	SPC	0	9	5	3	2	0	0	1	0

lists the number of different nodes when $N=1024$. It was found that, as the code rate increased, the number of R-1 and SPC nodes of longer lengths increased, while the number of R-0 and Rep nodes of longer lengths decreased.

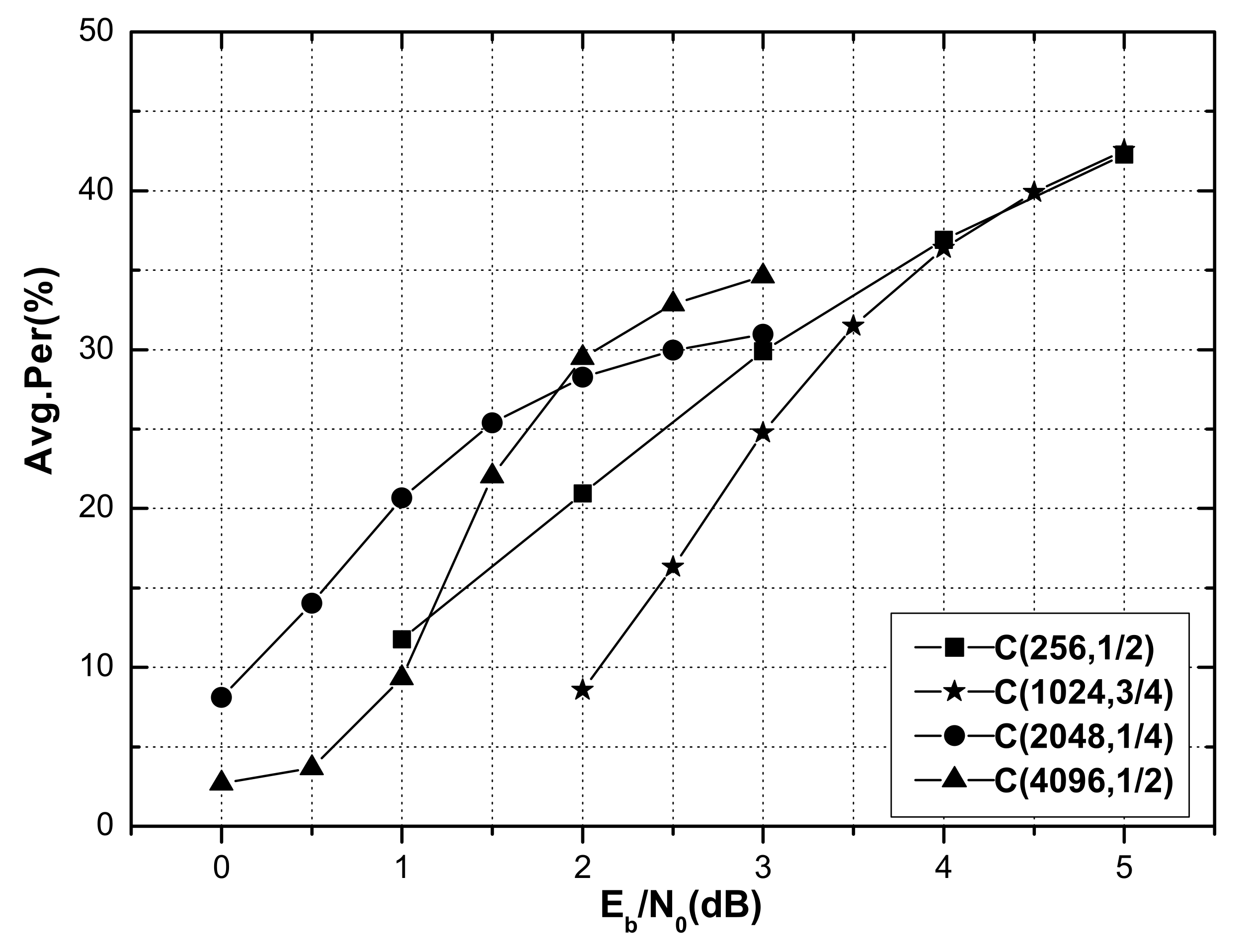
$C(N,R)$ was defined as the average percentage of R-other nodes satisfying the FC for a code of a certain length and rate. Figure 4 shows the average percentage of R-other nodes under the Fast-ISSC decoder for polar codes (256, 1/2), (1024, 3/4), (2048, 1/4), and (4096, 1/2) that satisfy the FC, along with the corresponding SNR. It is shown that the FC of the Fast-ISSC decoder remained valid, the proportion of R-other nodes that satisfied the FC increased with the SNR, and 30% of the R-other nodes satisfied the FC when the SNR was 3 dB. When the SNR was 4.5 dB, 40% of the R-other nodes of the polar codes (1024, 3/4) and (256, 1/2) satisfied the FC.

The average ratios of latency reduction compared to the SSC decoder for Fast-SSC, IMSC, and Fast-ISSC for polar codes (1024, 1/4), (1024, 1/2), and (1024, 3/4) with $P=256$ are compared in Figure 5. Here, $L(N,R)$ denotes the latency reduction of the Fast-ISSC decoder relative to the SSC decoder for a code of block length N and rate R, i.e., $L(N,R)$ = $\frac{\left(L_{SSC}(N,R)-L_{Fast-ISSC}(N,R)\right)}{L_{SSC}\left(N,R\right)}$. The $L(N,R)$ for the Fast-SSC and IMSC decoders are defined in a similar manner.

The latencies of both the Fast-ISSC and IMSC are affected by the channel conditions, both of which have the dynamics of the FC method, while the Fast-SSC is independent of the channel condition. The Fast-ISSC achieves the smallest decoding latency compared to the SSC, Fast-SSC, and IMSC decoder, at different code rates and different SNRs. When the SNR is 5 dB, the proposed Fast-ISSC decoder decreases the latency by almost 90% compared to the SSC decoder. In addition, the problem of high latency for the IMSC method at a high code rate and low SNR is solved.

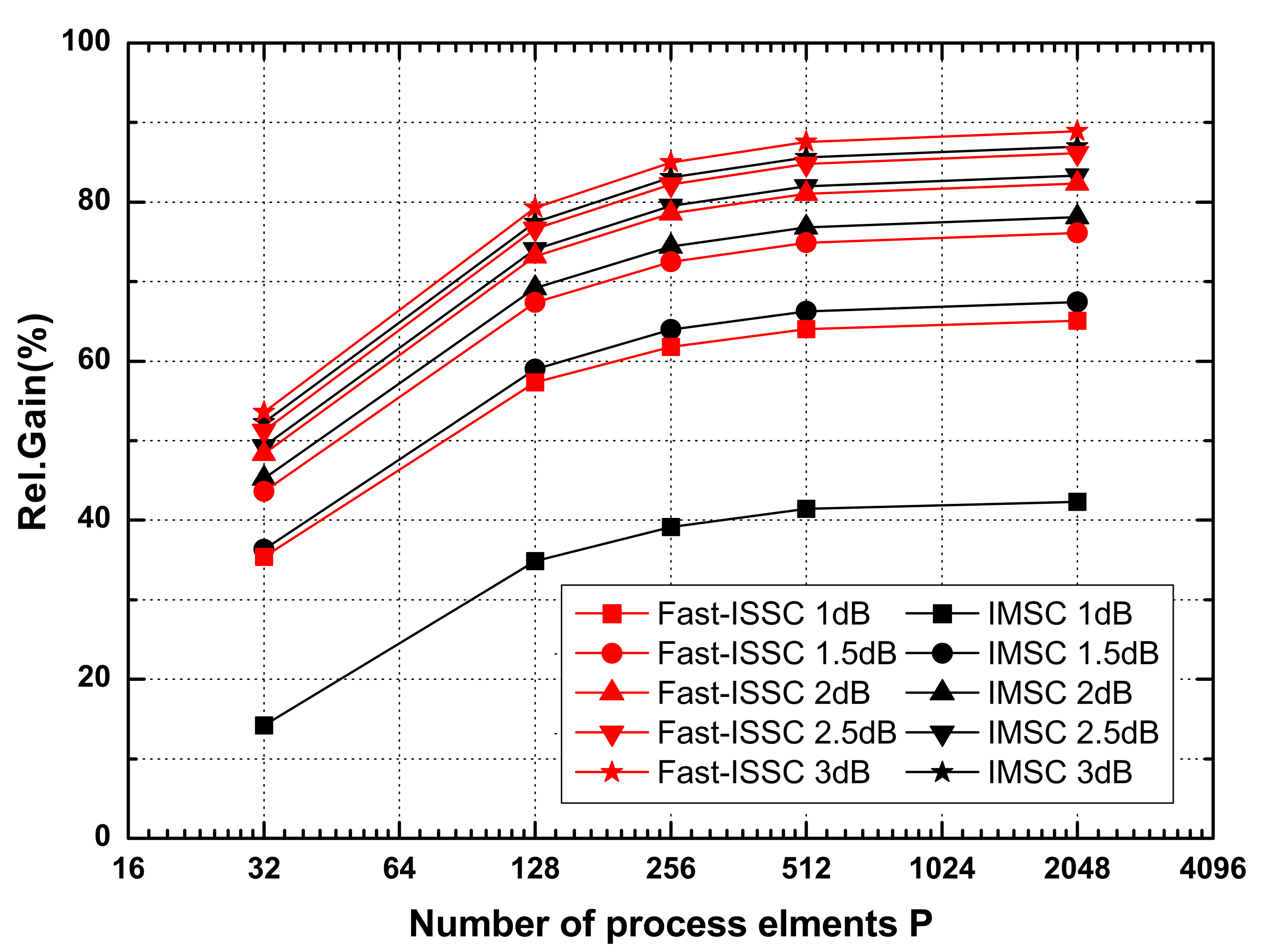
To investigate the relationship between the relative gain of the latency and P PEs, the effects of L(4096, 1/2) using the Fast-ISSC and IMSC for P varying from 16 to 4096 are shown in Figure 6. The trends of both the Fast-ISSC and IMSC are identical, and the relative gain of the former is greater than that of the latter at each P value, when the SNR is within the range of 1–2 dB. For SNR ≥ 2.5 dB, the gap between the two methods is gradually reduced. Further, when the value of P is greater than 256, the improvement in the latency reduction decreases.

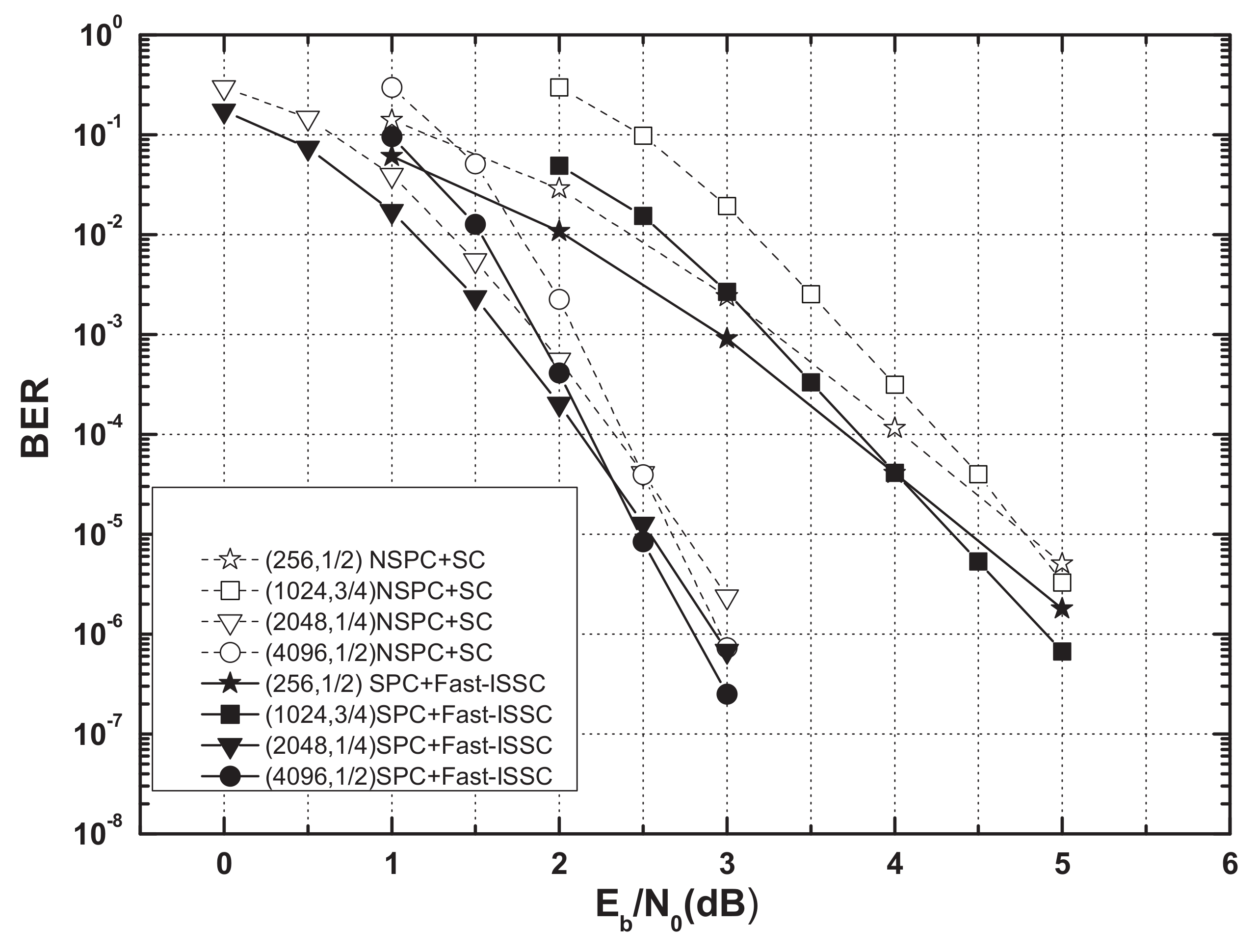
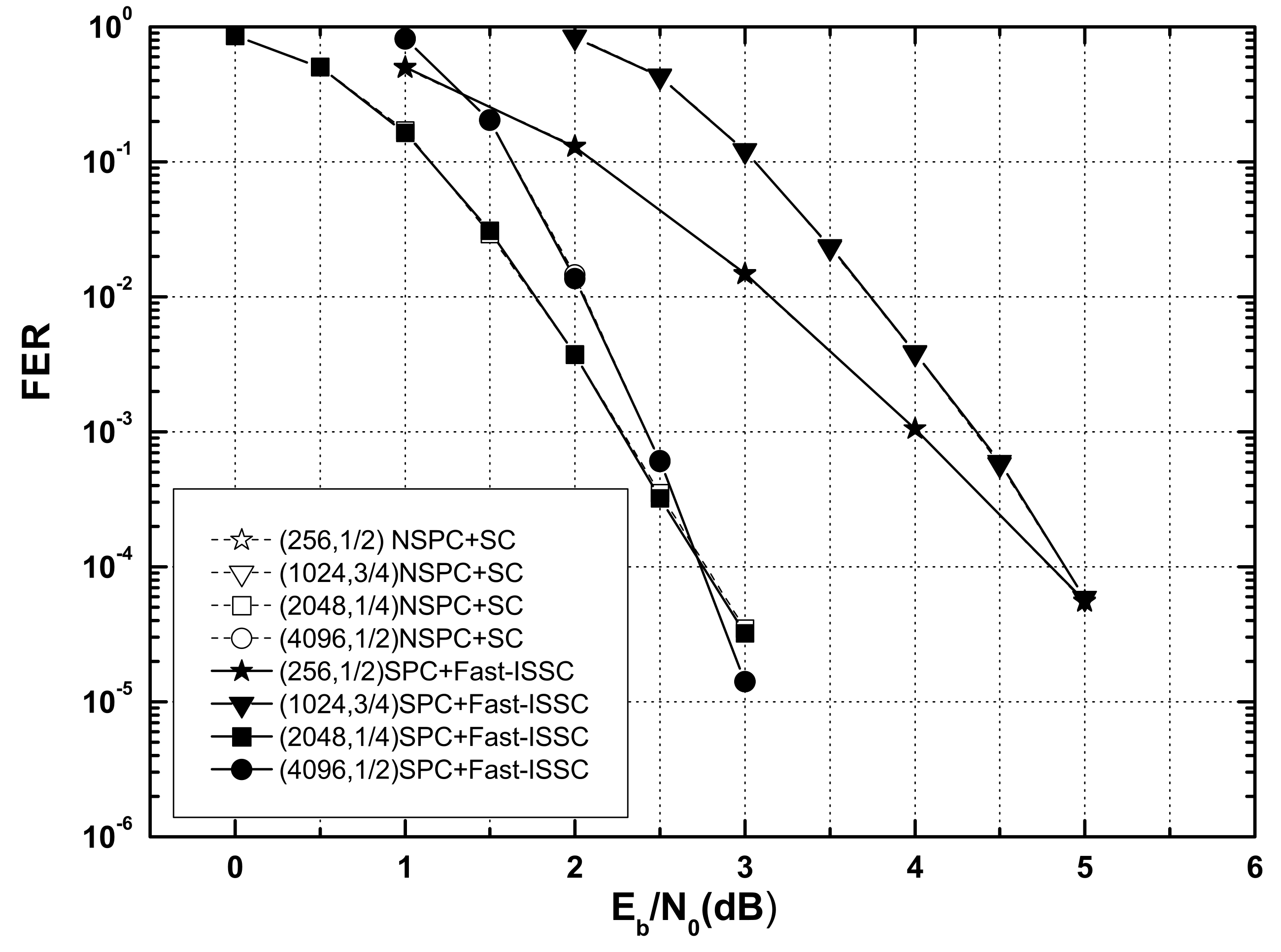
The polar codes (256, 1/2),(1024, 3/4),(2048, 1/4), and (4096, 1/2) were used for comparison of the error-correction performance. Figure 7 and Figure 8 show the BERs and frame error rates (FERs) of four systematic polar codes (SPC) under the Fast-ISSC decoder and the corresponding non-systematic polar codes (NSPC) under the SC decoder. Although we cannot offer a rigorous proof for the BER, we conjecture that the BER of the Fast-ISSC decoder is no worse than that of the original SC decoder. The simulation result in Figure 7 supports this conjecture. Since the SPC is used, the BERs of the Fast-ISSC decoder are improved, which is consistent with the result in [16]. The FERs of the Fast-ISSC decoder are the same as those of the SC decoder. These simulation results, in Figure 8, are consistent with Proposition 1.

5. Conclusions

We proposed an improved method for reduction of SC decoding latency. In this approach, the constituent codes were first identified offline on the decoding tree. Further, the frozen-bit check is conducted at the R-other nodes. It is shown that 30% of the R-other nodes on the pruning tree satisfy the FC when the SNR is 3 dB. Compared to the Fast-SSC and IMSC decoders, the proposed method yields the smallest decoding latency without affecting the error-correction performance. Moreover, the proposed method solves the problem of high latency for the Improved-SSC method at a high code rate and low SNR simultaneously. In the future, the method proposed in this work can be used for low-complexity successive cancellation list decoding.