Abstract
The use of ontological knowledge to improve classification results is a promising line of research. The availability of a probabilistic ontology raises the possibility of combining the probabilities coming from the ontology with the ones produced by a multi-class classifier that detects particular objects in an image. This combination not only provides the relations existing between the different segments, but can also improve the classification accuracy. In fact, it is known that the contextual information can often give information that suggests the correct class. This paper proposes a possible model that implements this integration, and the experimental assessment shows the effectiveness of the integration, especially when the classifier’s accuracy is relatively low. To assess the performance of the proposed model, we designed and implemented a simulated classifier that allows a priori decisions of its performance with sufficient precision.
1. Introduction
The topic of this paper is the problem of recognising the content of a digital image. This is a particularly important problem due to the very large number of images now available on the Internet, and the need to produce an automatic description of the content of the images. This research topic has received increasing attention, as shown by the references in Section 2, and well performing systems using deep networks have been proposed. In this paper, which extends what was presented in [1,2], we consider a method that exploits context information in the image to improve the performance of a classifier.
Classifiers for recognising the content of natural images are usually based on information extracted only from images and can be, in most general cases, prone to errors. The approach taken in this paper attempts to integrate some domain knowledge in the loop. The framework presented here aims to integrate the output—a classier/detector, considered as the probability that a particular object is present in a definite part of the input image with an encoded domain knowledge. The most commonly used tools for encoding a-priori information are standard ontologies; however, they do fail when dealing with real-world uncertainty. For this reason, we preferred to include a Probabilistic Ontology (henceforth, PO) [3] in our framework, which associates probabilities with the coded information, and then provides an adequate solution to the issue of coding the context information necessary to correctly understand the content of an image. Such information is then combined with the classifier output to correct possible classification errors on the basis of surrounding objects.
The aim of this work is to boost the performance of a system for the recognition/identification of classes of objects in natural images, introducing knowledge coming from the real world, expressed in terms of the probability of a set of spatial relations between the objects in the images, into the loop. A probabilistic ontology can be made available for the considered domain, but it could also be built or enriched by using entities and relations extracted from a document related to the image. For example, the picture could have been extracted from a technical report or a book where the text gives information that is related to the considered images. We wish to stress the fact that we are not thinking of a text that directly comments on or describes the image, but of a text which is completed and illustrated by the image. In this case, both classes of objects which can appear in the image and the relations connecting them could be mentioned in the text and could therefore be automatically extracted [4]. A probability can then be associated with them on the basis of the reliability of the extraction or the frequency of the item in the text.
The objective of the system discussed in this paper, which is depicted in Figure 1 and detailed in Section 3, is to obtain a set of keywords that can be used to describe the content of an image. The system takes an image as the input and produces a set of hypotheses on the presence of some objects in the image. Some of these hypotheses are likely to be wrong. As an example, let us consider the case of the reflection of a building on the water, beneath a boat; it is likely that a simple classifier will label that reflection as a building, while the boat can be labelled correctly. Our opinion that the spatial relation between the two image segments together with the external knowledge that an image segment beneath a boat and surrounded by water is more likely to be water than a building can be used to correct the misclassification. This world knowledge, formalised in a probabilistic ontology, together with the output of the classifier, is fed to a probabilistic model [5], with the goal of improving the performance of the single classifiers.
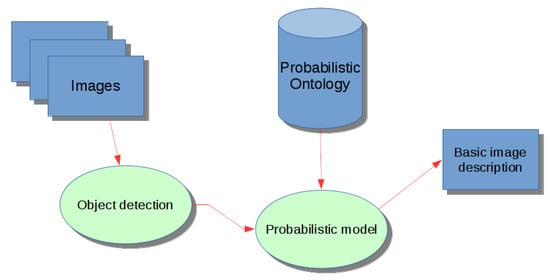
Figure 1.
Scheme of the proposed framework.
The framework described in this paper has two main aspects of novelty. The first one is that, to the best of our knowledge, a probabilistic ontology has never been proposed for a computer vision problem. The integration of a probabilistic model with a probabilistic ontology presents a second element of novelty.
This paper extends [1,2] by giving an experimental evaluation of the simulated classifier introduced in Section 4 and justifying the choice of the parameters used in the proposed probabilist model experimentally.
2. Related Work
Human beings express their knowledge and communicate using natural language, and, in fact, they usually find it easy to describe the content of images with simple and concise sentences. Because of this human skill, it is not difficult for a human user, when using an image search engine, to formulate a query by means of natural language.
Due to the large number of images available on the web, to answer textual image queries, the capability to describe the content of an image automatically would be very helpful. However, such a task is not easy at all for a machine, as it requires a visual understanding of the scene. This means that almost each object in the image must be recognised, and how the objects relate to each other in the scene must be understood [6]. This task is tackled in two different ways. The most classical one [7,8,9,10] attempts to solve the single sub-problems separately and combines the solutions to obtain a description of an image. A different approach [6,11,12] proposes a framework that incorporates all of the sub-problems in a single joint model. A method that tries to merge the two main approaches was proposed recently in [13] using a semantic attention model. The problem is, however, very far from being solved.
In the context of textual image queries, it can be enough to extract a less complex description from the images (image annotation [14]), such as a list of entities represented in the image and information about their positions and mutual spatial relations in the image. The work proposed in this document addresses this task that is also, as mentioned above, a necessary sub-task of the more general problem of generating a description in natural language.
The use of ontologies in the context of image recognition is not new [15]. For instance, in [16], a framework was proposed for an ontology based image retrieval for natural images, where a domain ontology was developed to model qualitative semantic image descriptions. An ontology of spatial relations was proposed in [17] in order to guide image interpretation and the recognition of the structures contained. In [18], low-level features, describing the colour, position, size, and shape of segmented regions, were extracted and mapped to descriptors; these descriptors were used to build a simple vocabulary termed object ontology. Probabilistic ontologies have been applied recently in various tasks. In [19], the authors described a PO which models a list of publications from the DBLP database; new interest for the authors was inferred using a Bayesian network. An activity recognition system integrating probabilistic inference with the represented domain ontology was introduced in [20]; this ontology based activity recognition system is augmented with probabilistic reasoning through a Markov Logic Network. An infrastructure for probabilistic reasoning with ontologies based on a Markov logic engine was recently presented in [21], and applied to different tasks including activity recognition and root cause analysis. In [22], the authors proposed a scheme that uses a PO capable of detecting potential violations of contracts between on-demand Cloud service providers and customers, and alerts the provider when a violation is detected. A probabilistic semantic model that enables reasoning over uncertainty without losing semantic information is the basis for a system providing reminders to elderly people in their home environment while they perform their daily activities [23]. To the best of our knowledge, a probabilistic ontology has never been used for the task of image recognition and annotation.
Contextual information has been used in image recognition for long time [24,25], and it has been already shown [26] that the use of spatial relations can decrease the response time and error rate, and that the presence of objects that have a unique interpretation improves the identification of ambiguous objects in the scene. Just to mention a few application domains, contextual information has been used for face recognition [27], medical image analysis [28], and analysis of group activity [29].
In the same way, the use of probabilistic models is not new in computer vision; in particular, a probabilistic model combining the statistics of local appearance and position of objects was proposed in [30] for the task of face recognition, and in [31] in an image retrieval task, showing that adding a probabilistic model in the loop can improve the recognition rate. In [32], a probabilistic semantic model was proposed in which the visual features and the textual words are connected via a hidden layer. More recently, in the context of 3D object recognition, a system that builds a probabilistic model for each object based on the distribution of its views was proposed in [33]. In [34], a hierarchical Bayesian network was introduced in a weakly supervised segmentation model; in particular, the system learns the semantic associations between sets of spatially neighbouring pixels, defined as the probability that these sets share the same semantic label. Finally, Ref. [35], in the context of action recognition, presented a generative model that allows the characterisation of joint distributions of regions of interest, local image features, and human actions.
3. Materials and Methods
The framework proposed in this paper (see Figure 1 for a graphical description) is a pipeline composed of several logical modules. The first module is a classifier, or a set of classifiers, the goal of which is detecting a set of predefined classes of objects in the image, therefore determining a set of regions of interest in the image. For each identified region of interestm the first module produces classifier scores for each one of the classes of objects considered, computed in terms of probability, and the spatial relations between all the regions of interest.
The hypotheses formulated for each segment in the image by a statistical classifier are then fed to a probabilistic model, that has been trained offline. This module is the core of our framework and has the objective of validating or correcting the hypotheses produced by the first module. The probabilistic model integrates the output of the classifier with the world knowledge coded in a probabilistic ontology that is expressed in terms of the probability of a spatial relationship between instances of two classes of image objects.
The class associated with each segment together with the relations existing between segment pairs constitute the output of the system and can be interpreted as a basic description of the image.
3.1. Probabilistic Ontology
This section discusses how a fragment of PO providing the information needed by our system can be constructed. Such a fragment is needed for the experimental assessment of the system.
Ontologies cannot cope properly with uncertain information when dealing with real-world problems. To overcome this problem, in previous years, some tools have been designed to add probabilities to the information contained in the ontologies. Among the tools proposed, one of the most important is probably PrOWL [36]. The POs obtained are capable of encoding a priori knowledge for real-world applications.
As a consequence, the research area concerning POs is very active and we expect that a number of POs in different domains will be available soon. However, a PO in the domain of the dataset used in our assessment is necessary for the experiments. Therefore, we designed and implemented an ad-hoc ontology. The scheme of the PO needed to contain the classes of objects and the spatial relations considered in our analysis. The probabilities were estimated from a training set of images where the objects had been manually labelled, and spatial relations were constructed between pairs of regions of interest. More in detail, we estimated the probability of two classes having a given relation by the frequency of the event in the dataset. No smoothing was applied.
Formally, D denotes the set of image segments used to compute the probabilities, and denotes the set of relations considered, with C being the set of classes of objects. The probability that has a relation with is computed as:
where is the number of times pairs of segments in D classes, respectively, and , satisfy the relation r. In general, it is , since the relations are not necessarily symmetric.
We are not aware of any available tool designed for constructing a PO directly; therefore, we used Protégé (freely available from http://protege.stanford.edu/) to formalise the schema of the ontology, and we used Pronto [37] as a reasoner for POs, because it adopts the standard OWL 1.1. The schema developed with Protégé was imported into Pronto simply by adding the probabilities into the corresponding XML files.
An example is given in Figure 2, where the element tagged pronto:certainty is added to the axiom produced with by Protégé. Although Pronto accepts probability ranges, simple values are used, the two extremes of the interval coincide ( in the example).

Figure 2.
Piece of the XML of the Probabilistic Ontology (PO) corresponding to an axiom with an associated probability.
3.2. Combination Models
In this section, we discuss the probabilistic model adopted to integrate the classifiers with the ontological knowledge.
The role of PO in the task considered in this work requires that probabilities describing the domain of interest are integrated with the probabilities coming from the classifier associated with each class of objects for each input region of interest.
The main goal of the system discussed here is the identification of some classes of objects in the input image. Our aim is to exploit the spatial relations between pairs of identified objects to improve the classification. In more formal terms, in every image, a set S of regions of interest is identified and there are a number of possible relations R between pairs of regions. The classifier associates a probability distribution to each region for all possible classes C. The classifier alone associates the region of interest with the class with the highest probability, that is, the image segment is classified by choosing the most probable class; this represents our baseline, as it only considers the classifier output without any information coming from the PO. However, the output of the classifier can be interpreted as a random variable with values in the set of classes C. The remainder of this section reports the method used to integrate this random variable with the ontological probabilities.
Given any triplet , where is any pair of classes, is any possible relation, the probability that two image instances of classes and , respectively, have a relation r is given in Equation (1). Our claim is that the classification performance can improve by integrating this last element of information with the probabilities returned by the classifier. It is worth pointing out that the solution produced by this integration procedure is likely to be consistent with the knowledge given by the ontology. This last one is a very important feature for systems where post-processing requires a set of properties on the considered candidates. In fact, if the relation holding between two regions of interest is unlikely for the classes assigned by the classifier, the corresponding ontological probability is very low, lowering the probability of the corresponding pair of classes.
Given a context , where and are the identified regions of interest and r is a relation holding between and and two classes and , we compute the following log-linear probability
where and , while is a normalisation factor that depends on x and on the classes assigned to the two segments. Note that the features are produced by the classifier, while depends on the probabilistic ontology. To summarise, in Equation (2), two families of parameters are taken into account: class parameters for each class c and relation parameters for each type of relation r and pair of classes . In total, the model has class parameters and relation parameters.
A training step is necessary for the estimation of the parameters defined above. The objective function of the training maximises the likelihood of the training set. For the implementation of this optimisation procedure, we used the Toolkit for Advanced Optimisation (TAO) library (that is part of the PETSc library [38], which includes a collection of optimisation algorithms for a variety of classes of problems (unconstrained, bound-constrained, and PDE-constrained minimisation, nonlinear least-squares, and complementarity). For this paper, we focused on unconstrained minimisation methods, which are very popular when minimising a function with many unconstrained variables. The method adopted was the Limited Memory Variable Metric, that is a quasi-Newton optimisation solver which solves the Newton step with an approximation factor composed using the BFGS update formula [39].
After the training step, once all the parameters , with and , have been estimated, the objective is to associate the correct class with each identified region of interest. Given a context x and two candidate classes and , we must assign a score expressing how the two classes fit the context. To this aim, two different models were considered. The former, referred to as M1, considers the score equal to the probability given in Equation (2), while the latter (M2) takes the logarithm of as the score. In fact, when adopting, as in our case, a log-linear expression, only considering exponents is much more efficient than directly summing probabilities. We used then two expressions, and , respectively corresponding to M1,and M2, given as
After this we needed to compute, for each context x, a score indicating how much a given class c is associated with a region of interest s in the context. This was done by summing up all the scores of the association of each class with each region, and the relations were assumed to include any of the possible relation types. We then associated the class which maximised such a score in all segment pairs including itself to the first region. Formally, this is expressed as
where stays for or , according to the model adopted between M1 and M2. It is worth pointing out that all the relations considered in this work were symmetrical; then, for each existing context , also the symmetrical was defined, producing the same scores as the first one; therefore, only the first of the two cases could be considered when computing the scores. If asymmetrical relations come into play, the score expressions can be easily generalised.
The last step is assigning the class which maximises the score of the class to each detected region of interest, that is
This final output of the classifier, together with the relations between the regions of interest can be used as a starting point for creating a simple textual description of the image.
4. Results
This section describes the quantitative assessment of the performance of the proposed method detailed in Section 3.
The main objective of the experiments described in this section was to assess whether the model proposed really improves the performance of the classifier. To this end, we measured the classification performance of our model against the classifier’s performance. The literature on object recognition is very rich [40], but in order to make this experiment as general as possible, we decided not to use an existing system for the detection/classification task, but preferred to design a simulated classifier for which we were able to set a desired accuracy. The use of a simulated classifier is not novel (see, for instance, [41]). In this way, it is possible to obtain an idea of the impact that the ontological information has on the performance, and to describe the dependence of the system performance on the classification accuracy.
What we needed was then a method to simulate the behaviour of a multi-class classifier with an assigned accuracy a. To this end, we designed a strategy that is detailed by the pseudo-code in Algorithm 1. In this strategy, given a region of interest in an image containing an object of a particular class c, a set of n random scores from the interval is extracted where n is the number of classes. After this, the maximum score is assigned to the gold class c, while the other scores are assigned to the other classes randomly. As a last step, the scores are normalised to get a probability distribution. In the end, since the simulated classifier assigns the class with the highest score to each image region of interest, the classifier has the desired accuracy a, as the highest score is assigned to the correct class with a probability of a.
| Algorithm 1: Pseudo-code for the simulated classifier. |
 |
The dataset selected for this experimental assessment is a subset of the MIT-Indoor [42] where interesting objects have been manually segmented and labelled; this gives us a reliable ground-truth for estimating the performance of our combination model. The dataset includes 1700 images that have been manually segmented. These images, see Figure 3 for few samples, were taken at common indoor locations, such as kitchens, bedrooms, libraries, gyms, and so on. The dataset is partitioned into three subsets: , and . The first two, each containing of the whole dataset, were used to train the probabilistic ontology () and the combination model () proposed in this work (see Section 3), and the remaining went into the subset that was used to assess the performance of the system. In our experiments, the three subsetss were selected randomly at each run of the algorithm. Each run was repeated several times (see below for details) in order to avoid experiment bias due to lucky or unlucky data splits. From our point of view, it is particularly important that the probabilistic ontology and the combination model are trained on different data, as this is what it is very likely to happen in real cases.

Figure 3.
Sample images from the dataset [42] used in the experiments.
The dataset contains a large set of object classes, some of them with very few objects. In order to avoid the impact that small classes might have on the construction of the probabilistic ontology, we preferred to take only the six with the largest number of items: the adopted classes and the number of times they occur in the data set are reported in Table 1. The final information necessary for building the probabilistic ontology was the definition of the spatial relations between the objects. We considered three different relations corresponding to the relative positions of two regions of interest in the same image: near, very near and intersecting. All the three relations were symmetrical. The near and very near relations between two region of interest were computed considering
where and are the two regions of interest, is the convex-hull [43] determined by the two regions and , is the area of the region passed as the argument; the parameter is set to for near and to for very near regions. The two relations are not exclusive, so two regions that are very near are also near.

Table 1.
Dataset statistics.
The simulated classifier played an important role in our experimental evaluation, so we decided to verify how close the accuracy of the classifier was to the one requested. The results are shown in Table 2. The experiment was run using the test set, and, due to the randomness of the simulator, the results were averaged over 10 trials, with a target accuracy increasing from to . It is clear from the table that the simulated classifier performed as expected.

Table 2.
Accuracy of the simulated classifier. The accuracies of the simulated classifier were averaged over 10 trials.
In Section 3.2, where the proposed model is explained, it is stated that the model depends, in our case, on 114 parameters: 6 for the classifier probabilities, one for each class, and 108 () for all possible relations between classes. This is the most general parametrisation of the model as it considers the maximal number of parameters. However, there are other possible parametrisations. For instance, we can consider the following alternatives: one single parameter for the classifier (all the six parameters are equal) and one for the relations (all the 108 are equal), adding to two parameters; six different parameters for the classifier and only one parameter for the ontological part of the model, giving seven parameters in total; 108 different parameters for the ontological part and a single parameter for the classifier, that is, only 108 parameters; 108 learnt parameters for the ontological part and a single parameter for the classifier, summing to 109 parameters.
We tested the performance of the system using all four alternative parametrisations, and the results are shown in Table 3. The results of models with two and seven parameters, presented in the first two lines of the table, were always below the classifier accuracy, except for the case. The case of 108 return accuracies showed a lack of regularity which makes this parametrisation unreliable. The behaviour when using 109 parameters was shown to be similar to the cases with two and seven parameters. The last model, using 108 parameters, behaved much better, as seen later in the next section, and therefore, is the one we chose to use in our system.

Table 3.
Different parametrisations for the combination model. Performance was measured on single runs with varied classifier accuracy levels (top row).
Having ruled out alternative parametrisations, we focused our attention on the model discussed later in the paper, for which we aimed to assess the improvement that could be obtained by introducing probabilistic ontological knowledge into the loop. To this end, we compared the system’s performance with a baseline consisting of the (simulated) classifier alone. The two approaches discussed in Section 3.2 were applied to combine the PO into the system: M1 and M2. The results, shown in Figure 4 and discussed in the next section, were obtained by averaging over 20 runs.
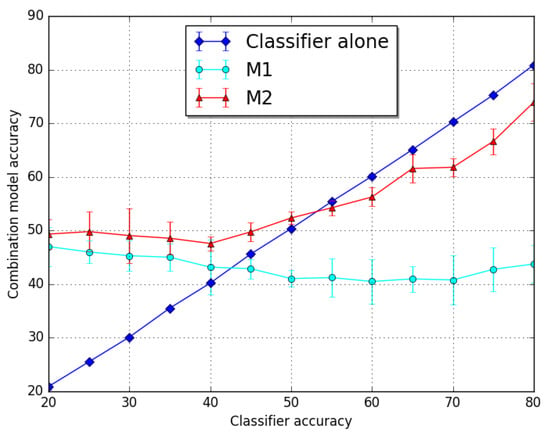
Figure 4.
Performance of the two systems compared with the baseline. The error bars give the confidence intervals. Results are the average of 20 runs.
5. Discussion
The system accuracy of the approaches proposed in this paper is depicted in Figure 4 and compared with the accuracy of the statistical classifier applied alone.
The experiment inspected the performance of our system by considering a wide range of accuracy levels for the simulated classifier; in fact, the values spanned from a lowest accuracy of to an accuracy of . It is clear from the graph in Figure 4 that the M2 model outperformed the M1 model, the performance of which slightly deteriorated as the classifier performance improved. A possible interpretation for this behaviour could be that too much confidence is given to the a priori score given by the probabilistic ontology with respect to the actual input data evidence.
On the other hand, the M2 model was shown to behave better than the classifier alone when performance of the latter was no more the which is a realistic experimental condition. We can also point out that this model performed better than the classifier alone when this was below than . A low performance of the classifier can indicate that the task is not particularly easy. Even for classifiers obtaining an accuracy between and , the adoption of an approach integrating PO knowledge was shown to be advantageous.
It is also worth pointing out that model M2 showed an almost constant accuracy when the classifier accuracy was no more than ; then, it started increasing, but at a slower rate than the classifier. The graph of the M2 model starts getting steeper soon after the classifier alone returns a better performance, so that the two graphs are almost parallel. A possible explanation for this behaviour is that, different from the M1 model where it seems that the model always gives the same level of trust to the classifier, the M2 model is always trying to adapt to the classifier performance. This could suggest that a better ontology design, resulting in a better PO, could help the system to overcome the performance obtained by the classifier alone.
6. Conclusions
This paper proposes two probabilistic models for integrating probabilities coming from a probabilistic ontology, representing a domain knowledge, with the probabilities produced by some sort of statistical classifier. The two models were experimentally evaluated and only one of them showed a level of performance that may encourage researchers to push forward its use in real systems.
In order to obtain a clear idea of the performance of the integration module, we removed the effects of most of the external factors. To this end, we conducted our experiments using images that had been manually segmented and labelled, and used a simulated classifier designed in such a way that we could control its accuracy. In future work, we plan to assess the performance of the proposed approach when coupled with state-of-the-art modules.
A prototype of a fragment of a probabilistic ontology was designed and populated using three binary relations which can be automatically detected in input images. The probabilities corresponding to each relation were estimated from their frequencies in the ontology training set. When more sophisticated ontologies containing information from large datasets are available, we expect the integration to give even better results.
Author Contributions
All authors contributed equally to this work.
Funding
The research presented in this paper was partially supported by the national project CHIS—Cultural Heritage Information System and Perception, and by the national project Perception, Performativity and Cognitive Sciences (PRIN Bando 2015, cod. 2015TM24JS_009).
Acknowledgments
We are grateful to M. Benerecetti e P. A. Bonatti for useful discussions about the most effective ways to represent knowledge.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PO | Probabilistic Ontology |
| PDE | Partial Differential Equation |
References
- Apicella, A.; Corazza, A.; Isgrò, F.; Vettigli, G. Integrating a priori probabilistic knowledge into classification for image description. In Proceedings of the 26th IEEE WETICE Conference, Poznan, Poland, 21–23 June 2017; pp. 197–199. [Google Scholar]
- Apicella, A.; Corazza, A.; Isgrò, F.; Vettigli, G. Exploiting context information for image description. In Proceedings of the International Conference on Image Analysis and Processing, Catania, Italy, 11–15 September 2017; pp. 320–331. [Google Scholar]
- Ding, Z.; Peng, Y. A Probabilistic Extension to Ontology Language OWL. In Proceedings of the 37th Annual Hawaii International Conference on System Sciences (HICSS’04)—Track 4, Big Island, HI, USA, 5–8 January 2004. [Google Scholar]
- Bach, N.; Badaskar, S. A Review of Relation Extraction; Technical Report; Language Technologies Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 2007. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Vinyals, O.; Toshev, A.; Bengio, S.; Erhan, D. Show and tell: A neural image caption generator. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3156–3164. [Google Scholar]
- Farhadi, A.; Hejrati, M.; Sadeghi, M.A.; Young, P.; Rashtchian, C.; Hockenmaier, J.; Forsyth, D. Every Picture Tells a Story: Generating Sentences from Images. In Proceedings of the 11th European Conference on Computer Vision: Part IV, Crete, Greece, 5–11 September 2010; pp. 15–29. [Google Scholar]
- Kulkarni, G.; Premraj, V.; Dhar, S.; Li, S.; Choi, Y.; Berg, A.C.; Berg, T.L. Baby Talk: Understanding and Generating Simple Image Descriptions. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 1601–1608. [Google Scholar]
- Elliott, D.; Keller, F. Image Description using Visual Dependency Representations. In Proceedings of the 2013 Conference on Empirical Methods in Natural Language Processing, Seattle, WA, USA, 18–21 October 2013; Volume 13, pp. 1292–1302. [Google Scholar]
- Fang, H.; Gupta, S.; Iandola, F.; Srivastava, R.K.; Deng, L.; Dollar, P.; Gao, J.; He, X.; Mitchell, M.; Platt, J.C.; et al. From Captions to Visual Concepts and Back. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1473–1482. [Google Scholar]
- Chen, X.; Zitnick, C.L. Mind’s eye: A recurrent visual representation for image caption generation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 2422–2431. [Google Scholar]
- Karpathy, A.; Fei-Fei, L. Deep Visual-Semantic Alignments for Generating Image Descriptions. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 664–676. [Google Scholar] [CrossRef] [PubMed]
- You, Q.; Jin, H.; Wang, Z.; Fang, C.; Luo, J. Image Captioning With Semantic Attention. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4651–4659. [Google Scholar]
- Wang, C.; Blei, D.M.; Fei-Fei, L. Simultaneous image classification and annotation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 1903–1910. [Google Scholar]
- Tousch, A.M.; Herbin, S.; Audibert, J.Y. Semantic Hierarchies for Image Annotation: A Survey. Pattern Recognit. 2012, 45, 333–345. [Google Scholar] [CrossRef]
- Sarwar, S.; Qayyum, Z.U.; Majeed, S. Ontology based Image Retrieval Framework Using Qualitative Semantic Image Descriptions. Procedia Comput. Sci. 2013, 22, 285–294. [Google Scholar] [CrossRef]
- Hudelot, C.; Atif, J.; Bloch, I. Fuzzy spatial relation ontology for image interpretation. Fuzzy Sets Syst. 2008, 159, 1929–1951. [Google Scholar] [CrossRef]
- Mezaris, V.; Kompatsiaris, I.; Strintzis, M.G. An ontology approach to object-based image retrieval. In Proceedings of the 2003 International Conference on Image Processing, Catalonia, Spain, 14–18 September 2003. [Google Scholar]
- Hlel, E.; Jamoussi, S.; Hamadou, A.B. A Probabilistic Ontology for the Prediction of Authorìs Interests. In Proceedings of the International Conference on Computational Collective Intelligence Technologies and Applications, Madrid, Spain, 21–23 September 2015; Lectures Notes in Computer Science. Volume 9330, pp. 492–501. [Google Scholar]
- Gayathri, K.S.; Easwarakumar, K.S.; Elias, S. Probabilistic ontology based activity recognition in smart homes using Markov Logic Network. Knowl. Based Syst. 2017, 121, 173–184. [Google Scholar] [CrossRef]
- Huber, J.; Niepert, M.; Noessner, J.; Schoenfisch, J.; Meilicke, C.; Stuckenschmidt, H. An infrastructure for probabilistic reasoning with web ontologies. Semant. Web 2017, 8, 255–269. [Google Scholar] [CrossRef]
- Jules, O.; Hafid, A.; Serhani, M.A. Bayesian network, and probabilistic ontology driven trust model for SLA management of Cloud services. In Proceedings of the IEEE International Conference on Cloud Networking, Luxembourg, 8–10 October 2014; pp. 77–83. [Google Scholar]
- Lunardi, G.M.; Machado, G.M.; Machot, F.A.; Maran, V.; Machado, A.; Mayr, H.C.; Shekhovtsov, V.A.; de Oliveira, J.P.M. Probabilistic Ontology Reasoning in Ambient Assistance: Predicting Human Actions. In Proceedings of the IEEE 32nd International Conference on Advanced Information Networking and Applications, Krakow, Poland, 16–18 May 2018; pp. 593–600. [Google Scholar]
- Toussaint, G. The use of context in pattern recognition. Pattern Recognit. 1978, 10, 189–204. [Google Scholar] [CrossRef]
- Oliva, A.; Torralba, A. The role of context in object recognition. Trends Cognit. Sci. 2007, 11, 520–527. [Google Scholar] [CrossRef] [PubMed]
- Bar, M.; Ullman, S. Spatial context in recognition. Perception 1996, 25, 343–352. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, J.W.; Sengco, J.A. Features and their configuration in face recognition. Mem. Cognit. 1997, 25, 583–592. [Google Scholar] [CrossRef] [PubMed]
- Bloch, I.; Colliot, O.; Camara, O.; Géraud, T. Fusion of spatial relationships for guiding recognition, example of brain structure recognition in 3D MRI. Pattern Recognit. Lett. 2005, 26, 449–457. [Google Scholar] [CrossRef]
- Choi, W.; Shahid, K.; Savarese, S. Learning context for collective activity recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 3273–3280. [Google Scholar]
- Schneiderman, H.; Kanade, T. Probabilistic Modeling of Local Appearance and Spatial Relationships for Object Recognition. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Santa Barbara, CA, USA, 23–25 June 1998; IEEE Computer Society: Washington, DC, USA, 1998; pp. 45–51. [Google Scholar]
- Schmid, C. A structured probabilistic model for recognition. In Proceedings of the 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Fort Collins, CO, USA, 23–25 June 1999; Volume 2, p. 490. [Google Scholar]
- Zhang, R.; Zhang, Z.; Li, M.; Ma, W.Y.; Zhang, H.J. A probabilistic semantic model for image annotation and multimodal image retrieval. In Proceedings of the ICCV 2005 Tenth IEEE International Conference on Computer Vision, Beijing, China, 17–20 October 2005; Volume 1, pp. 846–851. [Google Scholar]
- Wang, M.; Gao, Y.; Lu, K.; Rui, Y. View-Based Discriminative Probabilistic Modeling for 3D Object Retrieval and Recognition. Trans. Image Proc. 2013, 22, 1395–1407. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Yang, Y.; Gao, Y.; Yu, Y.; Wang, C.; Li, X. A Probabilistic Associative Model for Segmenting Weakly Supervised Images. IEEE Trans. Image Process. 2014, 23, 4150–4159. [Google Scholar] [CrossRef] [PubMed]
- Eweiwi, A.; Cheema, M.S.; Bauckhage, C. Action recognition in still images by learning spatial interest regions from videos. Pattern Recognit. Lett. 2015, 51, 8–15. [Google Scholar] [CrossRef]
- Costa, P.C.G.D. Bayesian Semantics for the Semantic Web. Ph.D. Thesis, George Mason University, Fairfax, VA, USA, 12 July 2005. [Google Scholar]
- Klinov, P.; Parsia, B. Uncertainty Reasoning for the Semantic Web II: International Workshops URSW 2008–2010 Held at ISWC and UniDL 2010 Held at FLoC, Revised Selected Papers; Chapter Pronto: A Practical Probabilistic Description Logic Reasoner; Springer: Berlin/Heidelberg, Germnay, 2013; pp. 59–79. [Google Scholar]
- Abhyankar, S.; Brown, J.; Constantinescu, E.M.; Ghosh, D.; Smith, B.F.; Zhang, H. PETSc/TS: A Modern Scalable ODE/DAE Solver Library. arXiv, 2018; arXiv:1806.01437. [Google Scholar]
- Fletcher, R. Practical Methods of Optimization, 2nd ed.; Jonh Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Szeliski, R. Computer Vision: Algorithms and Applications, 1st ed.; Springer Inc.: New York, NY, USA, 2010. [Google Scholar]
- Zouari, H.; Heutte, L.; Lecourtier, Y. Simulating classifier ensembles of fixed diversity for studying plurality voting performance. In Proceedings of the 17th International Conference on Pattern Recognition, Cambridge, UK, 23–26 August 2004; Volume 1, pp. 232–235. [Google Scholar]
- Quattoni, A.; Torralba, A. Recognizing indoor scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 413–420. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing; Pearson: London, UK, 2017. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).