Abstract
The Yellow River Delta is located at the junction of the Yellow River and Bohai. The impact function from the river and the dynamics of the ocean tides make the soil composition and distribution in this area substantially complicated. In order to test the distribution and variation of the soil layers in the Yellow River Delta, the soil layers in the test area were classified and the variation was calculated using the cone penetration test (CPT). The following conclusions were drawn: (1) the soil in the measured area is mainly composed of sensitive fine-grained soil, accounting for about 70% of all soil types, and the content of sensitive fine-grained soil in the far-sea position is higher than that in the offshore position in the direction perpendicular to the coastline. (2) It has a high vertical variability index (VVI) at the near-shore location, above 45%, and a low vertical variability at the far coast, generally below 20%. (3) The horizontal variability index (HVI) changes significantly near the coast, and it remains below 45% in the test area.
1. Introduction
A large number of cables and pipelines are distributed on the bottom of the Yellow River Delta, which is an important area for offshore oil and gas production [1]. Many international researchers have paid full attention to the investigations of the geological disasters in the Yellow River Delta [2,3,4,5], finding that the study area is characterized by complex topography and geological disasters. The shoreline boundary on either side of the estuary moves towards the sea at the average speed of 100 m/month [6]. The engineering characteristics of the sensitive fine-grained soil are relatively complicated, and may produce fluid mud to cause potential marine geological disasters [7,8]. The wave actions will directly lead to changes in the seabed topography at the mouth of the Yellow River, making the construction of the area, the engineering survey of the soil, and the prediction of geological disasters on the seabed difficult [9,10]. The Yellow River Delta is located at the intersection of the Yellow River and Bohai, which will cause sediment accumulation, and the effect of waves will cause the erosion of silt and sediment [11]. Changes in the erosion and deposition of the Yellow River Delta will seriously affect the development of ports [12]. Besides this, the deposition of the seabed results in frequent instability accidents, making it challenging to develop offshore projects on a large scale [13]. Therefore, the geological conditions in the Yellow River Delta are relatively complex, with an uneven distribution of soil layers, diverse soil composition, the influence of ocean tide dynamics, river erosion and accumulation on the coast, etc. Various conditions make the assessment of the strata of the Yellow River Delta region and exploration work very complicated. As a result, it is very important to investigate the variability of the entire test area. The variability is composed of the value and change of horizontal and vertical variability.
The cone penetration test (CPT) and its enhanced version (piezocone, CPTu) have seen extensive applications in many kinds of soils due to their continuity and repeatability [14]. Compared with traditional laboratory tests, CPT—with the advantages of fast, continuous, repeatable and reliable measurements—was often the preferred method for in-situ marine geological investigation, and abundant experience has been gained in the interpretation of CPT results for soil types [15], meaning that CPT is used in engineering geological monitoring widely. Due to the effect of ocean dynamics, sedimentary minerals will be transported and accumulated again [16], and the mineral composition of surface sediments in the modern Yellow River Delta is rather complicated [17]. These factors made the stratigraphic variability of the delta area relatively large. The soil classification information obtained by CPT can provide essential and useful information to geotechnical engineers [18,19,20]. The proposed soil classification charts by Robertson [21] have been popular and widely used [22,23]. Using the data obtained by the cone penetration test, it is convenient to investigate the changes of the soil layer and calculate the properties and parameters of various soil bodies. It can meet the simple operation and protect the nature of the original soil. Using the measured data to comprehensively investigate the variability values can draw more accurate results.
Due to the complex composition of the seabed soil in the Yellow River Delta, the study of the quantity and composition of the soil layers cannot provide the characteristics of the changes in the soil layers in detail. Therefore, it is necessary to continue to quantify the changes and calculate the changes in variability. Around the location of the area promoted by the Yellow River Delta, we established several points that can be used to investigate the horizontal and vertical changes, that is, the changes in the direction of the vertical coast of the Yellow River Delta near the coast and parallel to the coast.
Then, we used the variability calculation method summarized by previous scholars to investigate the characteristics of the soil variability in this area. Finally, we preliminarily summarized the change characteristics of the soil layer. Combined with the advantages of the cone penetration test, the composition of the soil layers in the Yellow River Delta region can be explored and the variation of the seabed soil can be quantified. The classification of the soil layers and the analysis of the site variability provide support for the Yellow River Delta underwater engineering construction, and make a preliminary exploration of the composition and variation of the underwater seabed soil.
2. In-Situ Survey
In order to determine accurate geological conditions and soil classification in the north of the Yellow River Subaquatic Delta, ten stations were arranged, of which one is perpendicular to the coastline, two others are parallel to it, as shown in Figure 1. The independently-developed Submarine Engineering Geological Environment Investigation System (SEGEIS) carried out a one-month CPT survey—as shown in Figure 2.
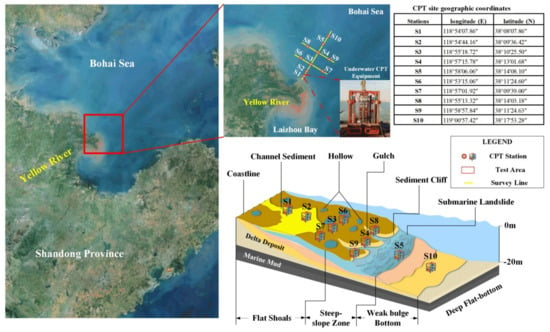
Figure 1.
The stations and survey lines.

Figure 2.
Underwater CPT system, developed independently.
The surface layer of the area consisted of yellow-brown silt with a thickness of 4.7 m and a medium density, of which parts were interspersed in the silty clay. The standard test shot number was 12–31, and the median diameter of the topsoil particles was about 0.03 mm, of which the saturation and density were 27.4–32.3%, and 19.4–20.1 kN/m3, respectively. The in-situ investigation system of the seabed engineering geological environment had many functions, such as in-situ observation, in-situ detection, static penetration, penetration, the extraction of sediment static sampling tubes, seabed environmental lighting, video shooting, and photography. The underwater CPT equipment, developed independently, was an in-situ investigation system for the subsea engineering geological environment. A high-quality pressure strain sensor was used to measure the cone tip resistance (range 0–50 MPa) and the sidewall friction resistance (range 0–1 MPa). The pore water pressure was measured by a piezoelectric element (range 0–2 MPa). The tilt angle was measured by an accelerometer (inclination angle in both the X and Y directions, range 0–15°). Finally, the sampling and penetration methods were static and hydraulic. The parameters of the underwater cone sounding test equipment are shown in Table 1.

Table 1.
The main parameters of the independently-developed underwater CPT system.
3. Soil Classification
Soil classification charts have been used widely to assess soil behavior based on CPT results [22,23]. The soil classification chart [21] is divided into twelve zones in order to represent the different grain size distributions, as well as the different soil states or behaviors coded by numbers. For example, Zone 1 indicates a soil type of sensitive fine grains, while the CPT data points of classical stiff fine-grained soil will fall in Zone 11, according to Figure 3, as given by Robertson [21].
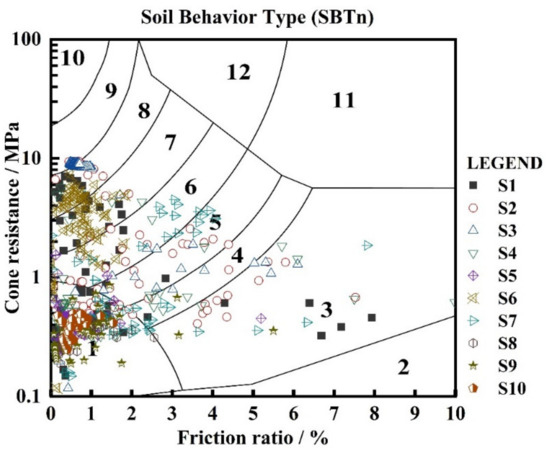
Figure 3.
Soil behavior type chart.
Fine-grained soil is widely distributed in the Yellow River Delta region, and some sandy soil with larger particle sizes also exists. As shown in Figure 4, there is an increase by 10 MPa sharply at depths of 1.5 m and 2 m, etc. The continuous accumulation of pore water pressure under the action of tides and waves in the sediments of the Yellow River Delta results in the continuous accumulation of the strength of the surface soil [24]. Typically, there is high cone resistance in sands but low resistance in clays, while the friction ratio is contrary, according to Robertson’s research [25].
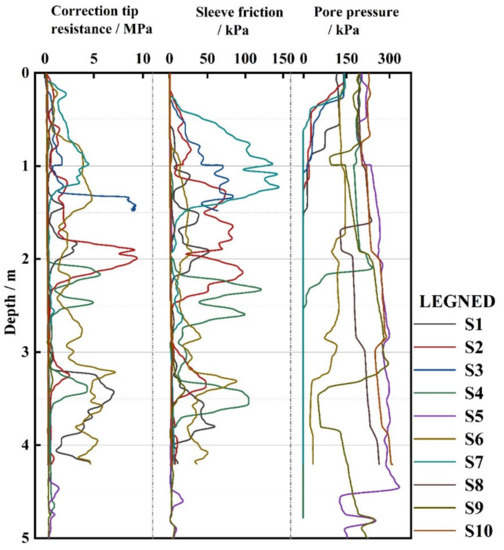
Figure 4.
The in-situ CPTu data.
The pore water pressure is distributed in 150 kPa–200 kPa, and the different sites vary significantly in depth. The pore water pressure will drop steeply at a certain depth. As such, the excess pore pressure shows a decreasing trend near 150 kPa–200 kPa in 0.5 m, at 3.4 m depth below from the surface for S9 and 2.1 m depth below for S4. At 4.5 m, it drops by about 140 kPa in S5. There is a high negative pore pressure in the case of high-density fine sands and dilative silts according Cai et al. [23]. Affected by the over-consolidation state, the pore water pressure may also become small or even negative [26].
The data for the locations of the 10 stations are arranged in the chart [21]. There is a clear distribution of 10 measuring points in area 1, and there no points in areas 11 and 12, revealing preliminarily that the soil composition in the area is mainly sensitive fine-grained soil, as shown in Figure 3. 50% of the points are in zone 1, which is mainly related to the sediment accumulation in the Yellow River Delta, according to the relevant research [27]. The sediment of the Yellow River is mainly from the Loess Plateau, and the sensitive fine-grained soil is mainly in the depth of 40 cm below the surface, while the deep layer is dominated by clay [28] where there is an obvious effect from the wave actions [27]. The method of soil layer classification in this area is shown in Table 2. By referring to the classification results in Figure 3 and Table 2, the soil layer results are obtained in the test area. As shown in Figure 5, there is very fine sand on the delta front, which is consistent with previous studies [4]. Sedimentation in the sedimentary area is slow when it is near the land in the west, and steep when it is far away from the land in the east. According to previous research [29], from the coast to the deep sea, the sediment composition shows a coarse-fine-coarse variation.

Table 2.
Non-normalized CPT soil behavior type (SBT) chart [21].
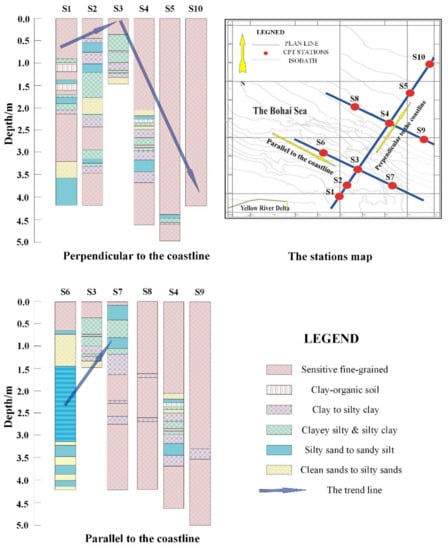
Figure 5.
The soil layers profile.
4. Site Variability Analysis Based on CPT
By calculating the site variability, the geological conditions of the measured area can be evaluated, and the civil engineering construction of the site can be guided. There are three main parts about the analysis on the site variability of the static penetration test. The first part is the calculation of the vertical variability, including the intra-layer variation index (VVIIL), log vertical variability index (VVIlog), and cone resistance vertical variability index (VVIqc). The second part is the calculation of the horizontal variability. The final part is a comprehensive analysis of the obtained data of the horizontal variability and vertical variability, as well as the variability of the site considering the geology and marine factors of the measured area.
When processing the CPT data, all of the abnormal data caused by instrument error, improper operation, and special geological phenomena should be correctly identified and interpreted reasonably.
4.1. Vertical Variability Index (VVI)
First, the depth and qc values measured by CPT are detrended. It is necessary to fit the data with functions. The polynomial function is used to fit the qc data and depth for the data detrending processing in this paper. The polynomial function used is denoted as f(x). After the fitting of the function is completed, the function is detrended, and the function used is as shown in the following Equation (1):
where f(x) is the qc value obtained after the polynomial function processing, y is the qc value in the original data, and ω is the qc value after the detrending. The relationship between the qc data and the depth after the detrend processing of S8 is shown as an example in Figure 6.
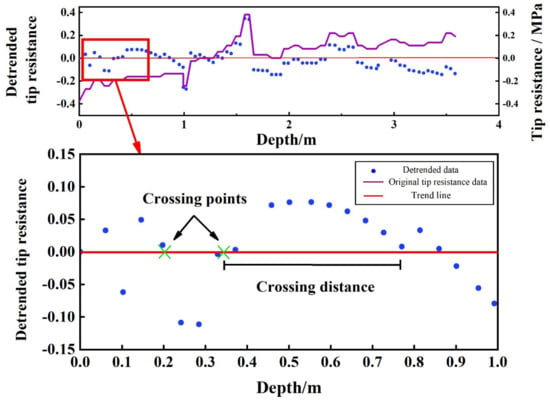
Figure 6.
CPT detrended data with the fitted trendline.
The value after detrending ranges from −1 to 1. The crossing point and crossing distance are shown in Figure 6; the scale of the fluctuation-normalized coefficient of coefficient variation (COV) is defined as SNC, which will indicate the variety of the soil layers. Furthermore, the area of one side of the trendline will indicate the value of the scale of fluctuation (SF), which represents the variety of the soil layers. Although the cone penetration test method suffers a measurement error [30] when the soil layer thickness is small, the influence of the layer thickness on the variability is not significant. Therefore, the error of the cone penetration test in the case of a minimal-thickness soil layer is ignored in this paper.
4.2. Intra-Layer Variation Index (VVIIL)
By considering that the intra-layer variability index is affected by COV and SF, a new parameter—SNC—is defined. The variation index of intra-layer size has a significant connection with the each-layer soil thickness and the number of soil layers in the entire soil section. First of all, the data obtained from the CPT is used in calculating each soil COV with soil layer maps and different soil type layer classification. Then, the relationship between the data after the detrending process with crossing points is established. The SF value used in this paper has been introduced [31], which relates to the model and the soil type used in the calculation. According to the research, many differences vary from 0.07 m to 4 m in marine or clay soil types regarding the SF value [32]. Finally, the SNC value is found with the formula proposed [33]. Figure 7 clearly illustrates the calculation process.
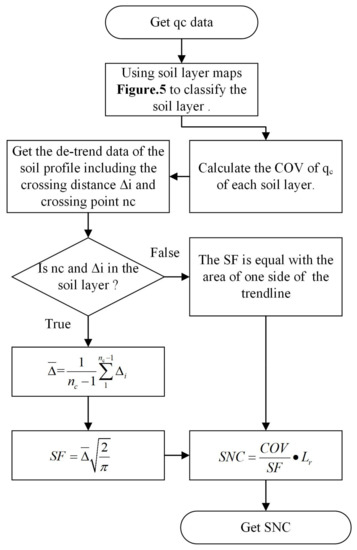
Figure 7.
The SNC calculation method (adopted by Salgado et al. 2019) [33].
Here, nc is the number of the crossing point, is the crossing distance, and the value of Lr is 1. ACF means the Autocorrelation Function, which is used to determine the distance of the correlation, which changes with the function type [34]. The twice-positive area formed by the fitting function and the trend line is regarded as the SF value in this paper. The main factor affecting the variability in the soil layer is qc; thus, only the SNC of qc needs calculating [33]. The SNC results are shown in Table 3.

Table 3.
The SNC.
The results are quite different, where S9 and S10 approach 90%; S3 and S6 are near 30%; S2, S5, and S8 are about 10%; and S1 and S7 are just about 3%. The soil stratification, SNC data, and the variability index of the intra-layer size are related to the thickness of the soil layer, the number of normalized qc crossing points in each layer, and the COV of each layer of the variation coefficient. Therefore, the SNC at S9 and S10 is bigger than those of the other stations. Furthermore, the thickness of a single layer and the COV is large, resulting in a large SNC. There is a prime feature within S4 and S5, given that both of them have a dominant thickness; even the thickness of S5 is over 4 m in a single layer between S4 and S5. However, there is clay or silty clay type in both S4 and S5, making the VVIIL in S4 and S5 small. All in all, the thickness of a single layer has a significant effect on the SNC.
4.3. Log Vertical Variability Index (VVIlog)
The logarithmic vertical variability index mainly calculates the diversity factors (DF) within a layer. Firstly, the soil layer is classified according to Table 4. The numbers of the sand, clay, and mixed soil obtained are respectively recorded as NS, NC, and NMS. Then, the proportions of the DS, DC, and DMS—of which the sum is 1—are calculated. The D* shown in Figure 8 represents the distance between the soil of any content of the three, and the three of them are 1/3, which is the degree of variation of the three. Theoretically, it fluctuates between 0 and 1, such that the DF ranges from 0 to 100. The lower the DF, the higher the dominance of the soil; therefore, the vertical variability will be smaller. Eventually, the final VVIlog value is obtained. The main steps in the DF and VVIlog are in Figure 9.

Table 4.
Soil group classification for the modified Robertson chart used to group soils for the calculation of dominance factor Di and diversity factor DF.
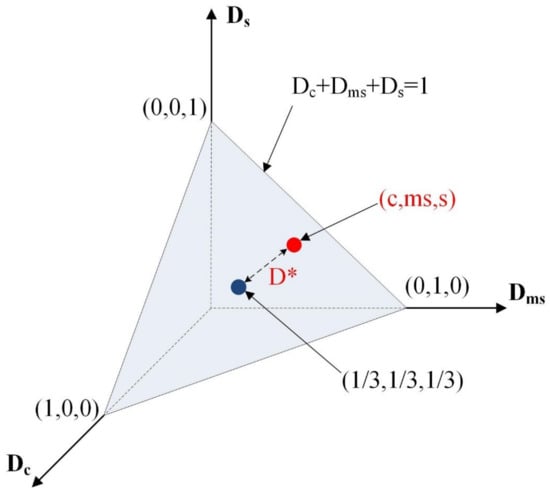
Figure 8.
D* schematic diagram (modified from Salgado et al., 2019) [33].
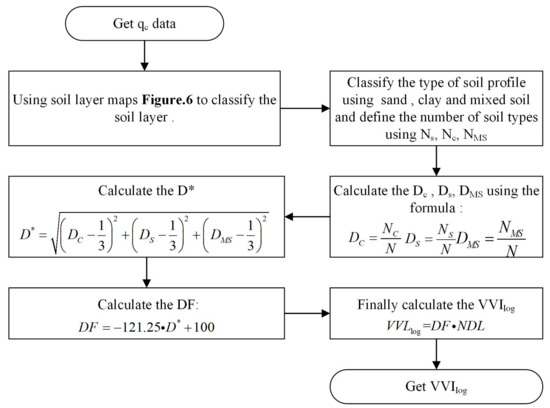
Figure 9.
The VVIlog calculation method (modified from Salgado et al., 2019) [33].
The NDL is the number of layers per unit length. In this test, various values of NDL were calculated, with a range of 1 to 5.7, revealing that there are complex and diverse soil types and layers in the Yellow River Delta. The calculated VVIlog value is normalized with the log10(x) function in order to keep the value obtained in the range of 0 to 1. As illustrated in Table 5, S1, S5, S8, S9, and S10 are below 90%, indicating that there is a dominant soil layer, or that the number of soil layers is small. Taking S4 as an example, there is a large proportion of sensitive fine-grained soil, but the number of soil layers at this point is 14, which is exceptionally numerous. Therefore, the VVIlog value of S4 is relatively large, resulting in a large vertical variability, which means that the value of VVIlog can intuitively show the influence of the number of soil layers and the thickness variation of the different soil layers.

Table 5.
The VVIlog.
4.4. Cone Resistance Vertical Variability Index (VVIqc)
VVIqc is a COV of qc, and the standardized COV of qc as the VVIqc value of the soil layer, because the VVIqc value is related to the soil layer profile and the composition of the soil type. We can calculate the COV from the obtained qc value, and we should normalize the result if it is between 0–1. In a soil layer comprising a single soil, especially a single clay or silty clay layer, the VVIqc value is below 10%, such as for S5, S8, S9 and S10, as listed in Table 6. On the contrary, if the profile consists of multiple soil types, the number of soil layers is plentiful, and the physical characteristics of the soil types are quite different, then the VVIqc is relatively large, just as for S1, S2, S4, and S7. Comparing S8 with S7, the number of layers is similar, and the main components of the soil are clay and silty clay, but the number of soil layers in S7 is five times as many as for S8, so the VVIqc of S7 is higher than that of S8.

Table 6.
The VVIqc.
Eventually, the vertical variability index can be calculated by Equation (2), and the VVI value is listed in Table 7.

Table 7.
The VVI.
The VVI is related to the soil layer content, number, and thickness. When the composition of the soil layer is single within three layers, the vertical variability is relatively single, which makes the value of VVI small, i.e., under about 40%. The vertical variability is various; meanwhile, when a single soil layer is thicker where there are five or more layers in one meter, and the number of soil layers is larger in one soil profile where the totally different layer numbers exceed ten, this will also cause more considerable vertical variability, and the value of VVI will even reach 50%. Therefore, the number of layers has a significant effect on the vertical variability.
4.5. Horizontal Variability Index (HVI)
When calculating the coefficient of the horizontal variation index, the size of the cone tip resistance and the depth of the sounding need to be considered as two factors affecting the horizontal variability, because they have a deficient level of variability to some extent if the changes in the two groups of qc data have a high correlation.
First, the influence factors of qc should be indicated. The differences between qc and the average of qc are calculated. The f0 is defined by dividing the previous maximum value qc with the absolute qc value |qc|. Secondly, the correlation coefficient ρxy between qc and the depth is calculated under the consideration of the depth effect. The parameters of f1 and f2 are figured with the Equations (3) and (4). The eventual HVI value can be calculated using Equation (6). The main calculation process is shown in Figure 10, where ρxy is the correlation coefficient, and s is the vertical distance between the two CPT data points [33].
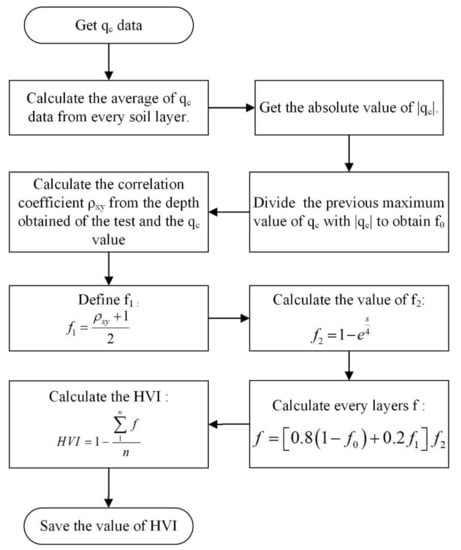
Figure 10.
The HVI calculation method (modified from Salgado et al., 2019) [33].
The result of HVI is shown in Table 8. The horizontal variability index is related to the content of hard clay. According to the previous research [33], the high content of hard clay or silt will make the horizontal variability index large; otherwise, the horizontal variability index will be small. Besides this, due to changes in the carrying capacity of the Yellow River and the carrying capacity when entering the sea, the particle size of the Yellow River Delta varies from the estuary to the sea. Therefore, the horizontal variability has a major change with the direction of the vertical coastline [35]. In terms of the soil stratification in the overall soil profile, the content of hard clay in S6 is higher. Therefore, the horizontal coefficient of variation of S6 is the largest, while the rest are medium.

Table 8.
The HVI.
5. Site Variability Rating
The site variability evaluation and analysis are performed after obtaining the above horizontal variability index and the vertical variability index. The values of the HVI and VVI are divided into three grades of L, M, and H depending on the three criteria of (0–33%), (33–66%), and (66–100%). For the analysis of the horizontal and vertical variability of the entire measurement station, the overall horizontal and vertical variability is high throughout the exploration area.
As shown in Figure 11 and Figure 12, the overall regularity of the vertical variability gradually decreases from the shore to the distance. As can be seen from Figure 13, the seabed soil in the Yellow River Delta region has complex geological conditions [36]. The maximum value of the near coast is about twice the minimum value of the far coast. Furthermore, the local law of vertical variability is roughly equivalent to the decrease of undulation. In a direction parallel to the coastline, the vertical variability of the measured area in the northwest direction is smaller than that in the southeast direction, as shown in Figure 12a. The horizontal variability in the direction perpendicular to the coastline gradually escalates, with an increase of about 20% according to Figure 12b. In the direction parallel to the coastline, the horizontal variability gradually decreases from northwest to southeast near the coast. Near the shore, the bottom of the stratum is mainly composed of relatively dense silt, and the fine-grained sand layer on the upper part of the soil layer far from the shore is relatively thick, which is related to the suspension of sand particles caused by the convergence of seawater and Yellow River water when the Yellow River enters the sea. These results are consistent with the previous studies [37,38]. The silty soil and cohesive soil of the Yellow River sediments were found on the sticky bed of the Yellow River Delta. Furthermore, because the Yellow River Delta belongs to the strong accumulation type estuary with a weak and sandy tide, the combination of runoff and tidal current causes the saltwater and freshwater to meet, leading a large amount of suspended sediment to flocculate and settle, which results to the development of the sand in the Yellow River Mouth. S1, S2, and S4 contain sand, clay, and silty soil, such that the vertical variability index is approximately similar, around 50%. However, compared with S6, the vertical variability index of S1, S2, and S4 are 25% higher than S6, although their number of soil layers are approximately equal. This is because S6 mainly contains stiff soil, while S1, S2, and S4 are more comprehensive, resulting in a smaller VVI of S6. It has been revealed that the entire soil section is dominant sensitive to fine-grained soil in the Yellow River Delta [39]. Therefore, the vertical variability is generally medium, around 40–50%. Considering all of the above factors and Figure 11a,b, in the direction perpendicular to the coastline, the VVI values are smaller than 33% far from the coastline, and generally above 50% near the coastline due to various components of soil layers. The HVI values hold at a medium level. Moreover, in the direction parallel to the coastline, the values of VVI far from the coast are smaller and more varied than those near the coast. On the contrary, the HVI values near the coast are more varied than those far from the coast. As shown in Figure 13, there are many complex geological hazards, such as gas-bearing soils, fault zones, eroded coasts, and slippery bodies in the Yellow River Delta. Besides this, the front geological body of the delta is also divided into smooth delta front and disturbing delta front. Combined with the calculated values of the horizontal and vertical variability of the measured points, the above comprehensive geological distribution and hazards also affect the distribution of the horizontal and vertical variability. It can be seen from Figure 12 and Figure 13, in the direction perpendicular to the coastline, that the vertical variability gradually decreases with the distance of the Yellow River Delta into the sea. In other words, the water depth has a substantial influence on the vertical variability but little effect on the horizontal variability. In the direction parallel to the coastline, the horizontal and vertical variability mainly change along the contour line. Far away from the coastline, the impact of the marine hydrodynamic environment on the seabed is weakened as the water depth increases, so that the position far away from the coastline has less horizontal and vertical variability. In conclusion, the VVI value and the HVI value have something to do with the number of soil layers in a profile, the soil thickness, and its composition, which is mainly determined by the characteristics of the sand carried by the Yellow River into the sea and the sedimentation characteristics of the estuary.
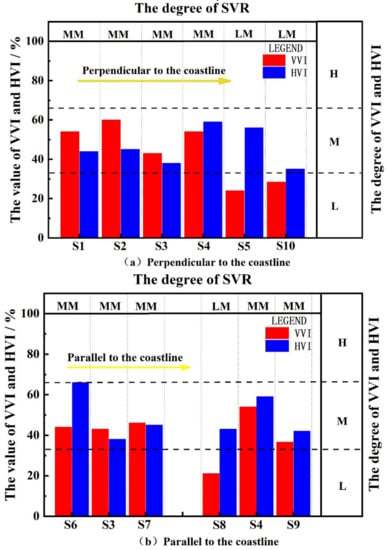
Figure 11.
The SVR data. (a) Perpendicular to the coastline; (b) Parallel to the coastline.
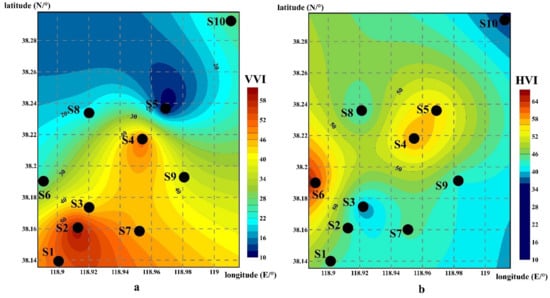
Figure 12.
VVI (a) and HVI (b) contour sketch maps.
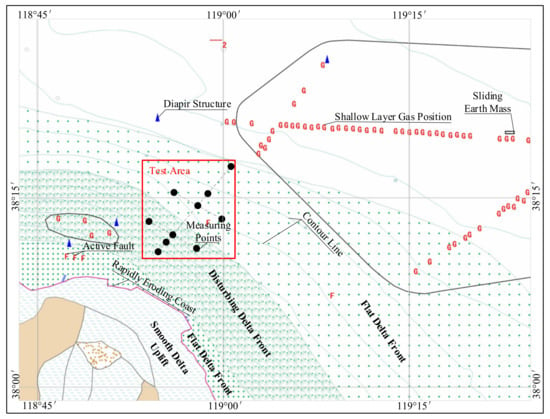
Figure 13.
Measuring points and the surrounding geological hazards map (modified from Zhou et al. 2003) [36].
6. Conclusions
In-situ tests were carried out on the Yellow River Delta using independently-designed submarine CPT equipment. The classification of the soil layers and the analysis of the site variability were performed based on the obtained data. The main conclusions are as follows:
- (1)
- Sensitive fine-grained soil is widely distributed in the Yellow River Delta. The classification results revealed that 70% of the soil layers in the test area are mainly sensitive fine-grained soil, and the soil composition type is distributed variously. There is an obvious change in the direction perpendicular to the coastline where the content of sensitive fine-grained soil in the near-coast is less than that in the far-coast.
- (2)
- Vertical to the coast, the water depth changes complexly and is obviously affected by hydrodynamic forces. The vertical variability index varies obviously in the direction perpendicular to the coastline. The vertical variability in the offshore areas is basically maintained in the range of more than 45%, which is much larger than the value in distant sea areas, which is less than 20%.
- (3)
- The soil layer changes are complex because of the shallow water depth and the obvious effect of the wave load near the shore. The diversification of the horizontal variability mainly occurs near the coast, and gradually decreases from the northwest direction to the southeast direction. There is no significant change of the horizontal variability distribution in the measured area, and its value is maintained at a moderate level of about 45% or less.
- (4)
- Based on the previously-available geological composition of the Yellow River Delta, the vertical variability and soil distribution are significantly different in the disturbing delta front and the flat delta front. In the distribution delta front, the soil composition is diverse, with high vertical variability basically exceeding 40%; in the flat delta front, the soil composition is homogeneous, with low variability, and is below 20%.
Author Contributions
Conceptualization, Z.Y. and L.G.; methodology, Z.Y.; software, X.L. (Xuesen Liu); validation, Y.C. and X.S.; formal analysis, X.L. (Xuesen Liu); investigation, L.G.; resources, Z.Y. and L.G.; data curation, Z.Y. and L.G.; writing—original draft preparation, X.L. (Xuesen Liu); writing—review and editing, X.L. (Xuesen Liu) and Z.Y.; visualization, X.L. (Xuesen Liu); supervision, Z.Y.; project administration, Z.Y.; funding acquisition, Z.Y., L.G. and X.L. (Xianzhang Ling). All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Shandong Province Focused Research and Development Program, grant number 2019GHY112075; the Special Project Fund of Taishan Scholars of Shandong Province, grant number 2015-212; the National Major Scientific Research Instrument Development Project, grant number 41627801; the Ministry of Science and Technology of the People’s Republic of China, Key R&D Program, grant number 2018YFB2000901.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Song, B.; Sun, Y.; Song, Y.; Dong, L.; Du, X.; Zhou, Q.; Zhao, X. Post-liquefaction re-compaction effect on the cyclic behavior of natural marine silty soil in the Yellow River delta. Ocean. Eng. 2020, 195, 106753. [Google Scholar] [CrossRef]
- Prior, D.B.; Yang, Z.-S.; Bornhold, B.D.; Keller, G.H.; Lu, N.Z.; Wiseman, W.J.; Wright, L.D.; Zhang, J. Active slope failure, sediment collapse, and silt flows on the modern subaqueous Huanghe (Yellow River) delta. Geo-Mar. Lett. 1986, 6, 85–95. [Google Scholar] [CrossRef]
- Xiuli, F.; Hongshuai, Q.; Teng, W.; Anlong, L.; Lin, L. Geomorphological evolution and geological disasters analysis in Chengdao sea area of the Yellow River Delt. Rock Soil Mech. 2004, 25, 17–20. [Google Scholar] [CrossRef]
- Yuling, Z.; Xiuli, F.; Sheng, S.; Donghui, T. Geochemical partition of surface sediments in the seas near the modern Yellow River Delta. Mar. Sci. 2016, 40, 98–104. [Google Scholar]
- Liangyong, Z.; Jian, L.; Xiqing, L.; Guangxue, L.; Zhengxin, C. Hazardous Geology in the Shallow Sea Area of Modern Yellow River Delta. Mar. Geol. Quat. Geol. 2004, 24, 19–27. [Google Scholar]
- Haoran, H.; Zhili, Z.; Chengshu, C. Numerical Simulation of Morphological Evolution Process of the Yellow River Mouth. Coast. Eng. 2018, 37, 1–14. [Google Scholar]
- Yang, Z.; Zhu, Y.; Liu, T.; Sun, Z.; Ling, X.; Yang, J. Pumping effect of wave-induced pore pressure on the development of fluid mud layer. Ocean. Eng. 2019, 189, 106391. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, Y.; Liu, T.; Sun, Z.; Ling, X.; Zheng, Y. Contribution of Pumping Action of Wave-Induced Pore-Pressure Response to Development of Fluid Mud Layer. J. Mar. Sci. Eng. 2019, 7, 317. [Google Scholar] [CrossRef]
- Jia, Y.; Zhang, L.; Zheng, J.; Liu, X.; Jeng, D.-S.; Shan, H. Effects of wave-induced seabed liquefaction on sediment re-suspension in the Yellow River Delta. Ocean. Eng. 2014, 89, 146–156. [Google Scholar] [CrossRef]
- Ren, Y.; Xu, G.; Xu, X.; Zhao, T.; Wang, X. The initial wave induced failure of silty seabed: Liquefaction or shear failure. Ocean. Eng. 2020, 200, 106990. [Google Scholar] [CrossRef]
- Zheng, J.-W.; Jia, Y.-G.; Liu, X.-L.; Shan, H.-X.; Zhang, M.-S. Experimental study of the variation of sediment erodibility under wave-loading conditions. Ocean. Eng. 2013, 68, 14–26. [Google Scholar] [CrossRef]
- Xiushan, G.; Qinian, Z.; Mingzuo, F.; Peiying, L.; Xiaoshi, X. Quantitative analysis and evaluation of scouring and silting in the Yellow River Estuary. Acta Oceanol. Sin. 1988, 10, 712–719. [Google Scholar]
- Anlong, L.; Guangxue, L.; Lihua, C.; Qingde, Z.; Shenggui, D. Coastal erosion and shoreline evolution of abandoned leaf petals in the Yellow River Delta. Acta Geogr. Sin. 2004, 59, 731–737. [Google Scholar] [CrossRef]
- Robertson, P.K. Evaluating Soil Liquefaction and Post-earthquake deformations using the CPT. In Proceedings of the Geotechnical and Geophysical Site Characterization, Porto, Portugal, 19–22 September 2004. [Google Scholar]
- Lakusic, S.; Librić, L.; Jurić-Kaćunić, D.; Kovačević, M.S. Application of cone penetration test (CPT) results for soil classification. J. Croat. Assoc. Civ. Eng. 2017, 69, 11–20. [Google Scholar] [CrossRef]
- Dong, D.; Wan, D. Preliminary Study on the Erosion of the Modern Yellow River Delta. Mar. Geol. Quat. Geol. 1988, 8, 53–60. [Google Scholar]
- Liuqi, W.; Zaixing, J. Mineralogical characteristics and sedimentary genesis of land surface sediments in the Yellow River Delta. J. Univ. Pet. China 1993, 17, 1–6. [Google Scholar]
- Eslami, A.; Fellenius, B.H. Pile capacity by direct CPT and CPTu methods applied to 102 case histories. Can. Geotech. J. 1997, 34, 886–904. [Google Scholar] [CrossRef]
- Guo, L.; Liu, X.; Yang, Z.; Jia, C.; Shi, W.; Ling, X. CPT-based analysis of structured soil characteristics and liquefaction failure of the Yellow River Subaquatic Delta. Mar. Georesour. Geotechnol. 2021, 1–20. [Google Scholar] [CrossRef]
- Cetin, K.O.; Ozan, C. CPT-Based Probabilistic Soil Characterization and Classification. J. Geotech. Geoenviron. Eng. 2009, 135, 84–107. [Google Scholar] [CrossRef]
- Robertson, P.K.; Campanella, R.G.; Gillespie, D.; Greig, J. Use of piezometer cone data. In Use of In Situ Tests in Geotechnical Engineering; ASCE: Blacksburg, VA, USA, 1986. [Google Scholar]
- Long, M. Key Note Lecture: Design parameters from in situ tests in soft ground—Recent developments. In Proceedings of the 3rd International Conference on Geotechnical and Geophysical Site Characterisation (ISC’3), Taipei, Taiwan, 1–4 April 2008. [Google Scholar]
- Cai, G.; Liu, S.; Puppala, A.J. Comparison of CPT charts for soil classification using PCPT data: Example from clay deposits in Jiangsu Province, China. Eng. Geol. 2011, 121, 89–96. [Google Scholar] [CrossRef]
- Robertson, P.K. Soil behavior type from the CPT: An updata. In Proceedings of the 2nd International Symposium on Cone penetration Testing, Huntington Beach, CA, USA, 9–11 May 2010. [Google Scholar]
- Jianmin, Z.; Hongxian, S.; Yonggang, J.; Hongjun, L.; Guohui, X. Experimental study on non-uniform consolidation of soil using fast-deposited seafloor in the Yellow River and estuary under wave tide. Rock Soil Mech. 2007, 7, 88–94. [Google Scholar] [CrossRef]
- Hongxian, S.; Jianmin, Z.; Yonggang, J.; Hongjun, L.; Guohui, X. Study on the Consolidation Process of Rapidly Deposited Seabed Soil in the Yellow River Estuary. Chin. J. Rock Mech. Eng. 2006, 25, 1676. [Google Scholar] [CrossRef]
- Xiaohua, W.; Hongjun, L.; Yonggang, J. Study on Mineral Composition Characteristics of Silty Soil in the Yellow River Estuary and Its Response to Hydrodynamic Conditions. Mar. Geol. Lett. 2004, 5, 34–39. [Google Scholar]
- Yonggang, J.; Hongxian, S.; Xiujuan, Y.; Xiangmei, M.; Fangqiang, C.; Jiewen, Z. Sediment Dynamics and Geologic Hazards in the Estuary of Yellow River, China; Science Press: Beijing, China, 2011. [Google Scholar]
- Xiaoying, C.; Shenliang, C.; Yongsheng, L. Characteristics and regularity of sediments in the coastal area of the Yellow River Delta. In Proceedings of the 9th National Symposium on Estuary and Coast, Xiamen, China, 6–9 September 2006. [Google Scholar]
- Ganju, E.; Prezzi, M.; Salgado, R. Algorithm for generation of stratigraphic profiles using cone penetration test data. Comput. Geotech. 2017, 90, 73–84. [Google Scholar] [CrossRef]
- Vanmarcke, E.H. Probabilistic Modeling of Soil Profiles. J. Geotech. Eng. Div. 1977, 103, 1227–1246. [Google Scholar] [CrossRef]
- Bombasaro, E.; Kasper, T. Evaluation of spatial soil variability in the Pearl River Estuary using CPTU data. Soils Found. 2016, 56, 496–505. [Google Scholar] [CrossRef]
- Salgado, R.; Ganju, E.; Prezzi, M. Site variability analysis using cone penetration test data. Comput. Geotech. 2019, 105, 37–50. [Google Scholar] [CrossRef]
- Jaksa, M.B.; Kaggwa, W.S.; Brooker, P.I. Experimental evaluation of the scale of fluctuation of a stiff clay. In Proceedings of the 8th International Conference on the Application of Statistics and Probability, Sydney, Australia, 12–15 December 1999. [Google Scholar]
- Ping, Y.; Naishuang, B.; Xiao, W.; Yong, Z.; Houjie, W. Spatial Distribution of Surface Sediments in the Modern Yellow River Delta. Mar. Geol. Quat. Geol. 2016, 36, 49–55. [Google Scholar]
- Liangyong, Z.; Jian, L.; Xiqing, L. Geo Cloud. 2003. Available online: http://geocloud.cgs.gov.cn/#/portal/geologicalDatabase/DetailsPage?child_id=v_cpgl_dzt_33302020520183866214&tableCode=v_cpgl_dzt&jddm=333 (accessed on 2 March 2021).
- Jianmin, Z. Super-Consolidation Characteristics of Sediments in Modern Yellow River Delta and Their Genesis; Ocean University of China: Qingdao, China, 2006. [Google Scholar]
- Guohui, X.; Ruifang, C.; Anlong, L.; Guanghai, H. Experimental study on the behavioral changes of sticky silty bed under wave action. Adv. Mar. Sci. 2020, 18, 19–26. [Google Scholar]
- Xiujuan, Y.; Yonggang, J.; Jie, L. Analysis of engineering geological characteristics of sediments in the Yellow River Delta. Yellow River 2010, 32, 201–202. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).