Abstract
Adverse conditions within specific offshore environments magnify the challenges faced by a vessel’s energy-efficiency optimization in the Industry 4.0 era. As the data rate and volume increase, the analysis of big data using analytical techniques might not be efficient, or might even be infeasible in some cases. The purpose of this study is the development of deep-learning models that can be utilized to predict the propulsion power of a vessel. Two models are discriminated: (1) a feed-forward neural network (FFNN) and (2) a recurrent neural network (RNN). Predictions provided by these models were compared with values measured onboard. Comparisons between the two types of networks were also performed. Emphasis was placed on the different data pre-processing phases, as well as on the optimal configuration decision process for each of the developed deep-learning models. Factors and parameters that played a significant role in the outcome, such as the number of layers in the neural network, were also evaluated.
1. Introduction
The need to integrate a ship into a wider ecosystem for the exchange of structured information, even between ships or between long-distance ports and low-coverage areas, is a difficult problem to solve. The aim of reducing environmental impacts, increasing maritime safety, optimizing ship performance, and assisting with new technologies (such as intelligent sensors, big data, the Internet of things, and cloud services) has made smart shipping a necessity in the field of navigation. Although data have long supported decision-making, the abundance of data streams and the migration toward a digital era tends to be overwhelming when it comes to shipping. As a result, the data are composed of user-generated content (e.g., traces of digital communication) and machine-generated content (e.g., data collected by sensors), complemented by structured data from external sources (e.g., weather/environmental data). The compilation, alignment, and integration of this heterogeneous and multi-modal data are critical steps that precede its analysis [1]. Data need to be transparently aligned at the schema level, but also at the level of units and for measurement precision. The development of new methods, tools, and technical capabilities for big-data analytics is highly dynamic, driven by academia and large companies. Currently, there are only a few examples of well-established models, such as the analytics underlying weather forecasting. While these models need to be adjusted as computational and sensing capabilities advance and the volume of processable data increases, applications do not have any reference models that have been proven to work reliably.
Data analysis for the development of a regression model based on artificial neural networks was employed in [2] to accurately predict fuel-oil consumption (FOC). Since the available dataset was not too large, comprising 4000 samples, 7 input variables, and 1 target feature, we shall not refer to it as big data, and the data preprocessing pipeline proposed is deemed appropriate for effectively manipulating and refining vessel-related data with large capacity. Also, [3] concerns the development of data-driven models for the prediction of ship main engine FOC. For this study case, two different strategies for the data acquisition endeavor were considered and compared, namely noon-reports and automated data logging and monitoring (ADLM) systems, each at different sampling rates. It was concluded that even though hyperparameter tuning is a means of affecting the output of the model and identifying the optimal configuration to yield optimal results, investigating a diverse set of different models, evaluating the performance of each one, and selecting the best is more significant. In [4], a data analysis was carried out on the fuel usage of vessels to render shipping operations more efficient. For this task, the analysis of continuous data pipelines obtained from monitoring systems must be executed. In [5], it was proposed to exploit the preeminence of the long short-term memory (LSTM) models in sequence, to recover or predict accurately missing information from datasets, drastically improving the already existent imputation techniques of filling the missing data points with the mean of each variable. This methodology was applied to predict and fill the missing values of three variables, namely the trajectory of the vessel, the FOC, and the speed over the ground of the vessel. The efficacy of the suggestion was evaluated against actual data acquired from monitoring systems of inland vessels. In [6], regression models to predict a ship’s speed were developed by utilizing high-frequency data spanning about three months. Modeling techniques such as k-folds, cross-validation, and ensemble methods were examined. In [7] a least absolute shrinkage and selection operator (LASSO) regression model was used to predict the fuel-oil consumption of a containership. A comparison of the results of the LASSO models with other typical models of machine-learning methods was presented, demonstrating an improvement in the accuracy of the predictions.
In [8], the authors presented a calculation framework based on machine-learning methods for handling big data. Three processes were presented: sensor-fault detection, data classification, and data compression. Specifically, principal component analysis and Gaussian mixture models were exploited to filter the data points and cluster them, respectively. In the same direction, in [9], three different modeling approaches were tested: physical or white-box, hybrid or gray-box, and black-box models. White-box models are physics-based, black-box models correspond to data-driven models, and hybrid combines both methods. It was found that hybrid models can incorporate the best of the two types of models. They achieve a high level of accuracy, like that of the black-box models, but require less data due to the transferred knowledge from the physical models. Moreover, the feature selection phase was thoroughly examined, including random-forest feature testing.
Going one step further, in the present study, we investigate how different deep-learning approaches can be employed to exploit a heterogeneous source of information coming from data collected onboard. The main focus was given to the testing of neural-network models that have been successfully tested in different industrial or engineering sectors. Based on its criticality to vessel operations, the power generated for propulsion by a ship’s main engine is the selected target feature. The paper is structured as follows: in Section 2, the methodology used in the current work for the data collection, pre-processing, and cleansing is presented. In Section 3 and Section 4, descriptions of the FFNN and RNN models are provided, respectively. Parameter calculation and critical decisions for the network construction are also provided for each model. Analysis of the results and accuracy estimation, by comparison with the measured values, are provided in Section 5, while a comparison of the FFNN and RNN models in terms of performance and computational cost is further provided in Section 6. Finally, the key results of the study are summarized in Section 7.
2. Data Collection and Preparation
2.1. Data Acquisition
The ship employed in the study is a 165,000-DWT tanker. Table 1 provides its basic characteristics. For this work, data was collected over approximately 19 months, and the acquisition frequency rate was set to 1 min.

Table 1.
Ship’s Particulars.
For the collection of the data, the LAROS system was used [10]. In more detail, smart collectors set up a secure wireless network inside the vessel to transmit the processed data to the gateway with a user-defined sampling rate and the ability to maintain and customize them remotely. The wireless protocol was based on IEEE 802.15.4 MESH, with additional layers and data format to cover the requirements of the vessel environment and increase the network’s Quality of Service, while different protocols will be examined to secure the scalability of the solution in the future. Pre-processed data from the collector network on each of the ship floors was further delivered to the next processing level: the gateways. Data from the gateways were further transferred to the onboard server. The onboard server periodically produced binary files and compressed them to reduce the size of the data to be sent via normal satellite broadband to the headquarters data center (cloud computing). The cloud collected the processed data from a wide range of vessels (fleet wise) and handled them for -fleet-level data analytics. For our work, parameters from the following signal sources were collected (Table 2).

Table 2.
Collected parameters.
2.2. Data Pre-Processing Pipeline
As shown in Figure 1, the first phase of this analysis is the acquisition of data, which is an essential step for any data-driven model-development endeavor. This step was described in the previous subsection. In this subsection, the second phase of the work needed is demonstrated. Having acquired the data from the server, data preprocessing is the next essential part of any data-science-related study. Data acquisition is the cornerstone for the creation of any data-driven model; however, its real value will emerge only after it undergoes proper refining, improving the overall performance of the deep-learning model. The data preprocessing pipeline applied in this case comprised three steps: (i) feature selection (or feature elimination), (ii) outlier removal, and (iii) data smoothing.

Figure 1.
Different phases and processing steps executed in the different edge of the network.
2.2.1. Feature Selection
The first part of the data preprocessing phase was the selection of the feature set that will be fed into the models. The 180 features related to vessel conditions that were provided by the acquisition phase were examined for their importance related to the main target, either through the application of statistical models, or through experience and domain insight. For this purpose, it is plausible to perform a preliminary selection, eliminating features by sheer intuition. In that way, features, which by no means affect the target values, are excluded from the dataset. Afterward, it is generally desirable to further refine the features, to train the neural network only on those regarded as the most important, thus reducing the time required for each model to train. In this context, a series of statistical analyses to determine the final set of features the dataset will comprise were implemented as follows:
- At first, a significance level was selected. In most cases, a 5% significance level is enough.
- Secondly, the model was fitted with all the features left from the intuitive feature exclusion.
- The feature with the highest p-value was identified.
- If the p-value of this feature is greater than the significance level selected in the first step, this feature was removed from the dataset. This procedure was repeated until the highest p-value of this specific subset was lower than the significance level. Once the highest p-value of this subset of features was less than the significance level, the feature-selection process ended.
Afterward, a Pearson correlation elimination was applied to remove highly intercorrelated features. This way, reduction in the dataset size was performed by the removal of redundant features. Features highly correlated with the target feature were accepted, since they contain information vital to our models, and their discarding would signify a major loss of information. For illustrational purposes, a correlation heatmap of the remaining features is presented in Figure 2.
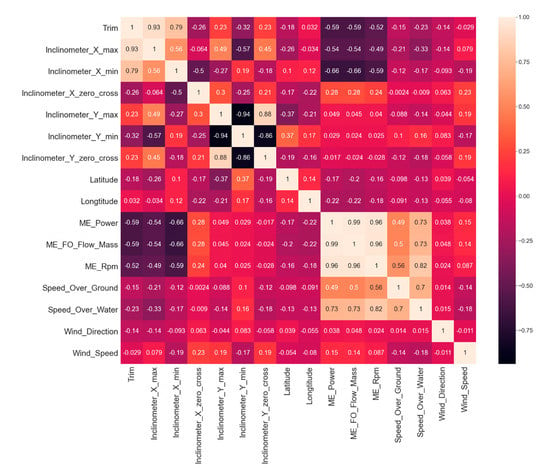
Figure 2.
A correlation heatmap (Pearson correlation) of the remaining selected features.
2.2.2. Outlier Removal
The next step in the pre-processing procedure was the identification and, subsequently, the removal of outliers. Outliers are extreme values that deviate from other observations on data. In other words, an outlier is an observation that diverges from an overall pattern in a sample. It is an abnormal observation that lies far away from other values. An outlier is an observation that diverges from otherwise well-structured data. In this study, three features were considered for the elimination of outlier entries: main engine rpm, main engine power, and speed over ground. After experimentation, we found that for specific intervals concerning the main engine rpm values, the other two variables would approximately follow a normal distribution, therefore main engine rpm was selected as the primary feature. As presented in [11], if we accept the hypothesis under a certain level of significance that the second parameter values follow a normal distribution, it can be used to eliminate values located towards the tail of the distribution. More explicitly:
- Select a feature of the dataset that is deemed to be of high significance to our study (for instance, the main engine RPM was chosen as our primary feature);
- The rest of the dataset is split into intervals based on the primary feature’s values within a specific range. Subsequently, each sample is assigned to the respective group. (i.e., intervals of 10 rpm are created);
- For any other given feature, the mean and the standard deviation in each cluster of data are calculated and let mean to be m and standard deviation to be s;
- The arbitrarily chosen factor k is multiplied by the standard deviation, setting an outlier threshold (in our case, a value of 3 was selected, which corresponds to a loose outlier-detection criterion);
- The inequality for each data point following Equation (1) determines if the given sample is an outlier.
The following indicative histograms (Figure 3) provide a better intuitive understanding of where the discarded values are (the ones located outside the range defined by the dashed vertical lines).

Figure 3.
Left: Histogram of the speed over ground for rpm values in the range (50,60). Right: Histogram of the power generated by the main engine for rpm values in the same range.
According to the procedure described above, the results of outlier detection regarding the main engine rpm as the primary parameter, and the vessel’s speed over ground and main engine power as the secondary parameters, are illustrated in Figure 4.
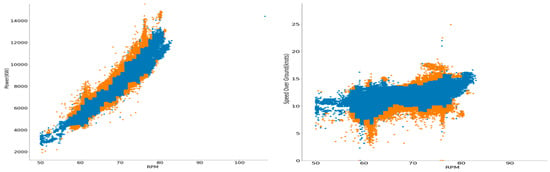
Figure 4.
Outlier removal with respect to main engine rpm; the left diagram corresponds to the power feature, and the right one to the speed over ground feature. Samples to be removed appear in orange, and the remainder of the data points appear in blue.
2.2.3. Data Smoothing
The final step of this pre-processing data scheme is the smoothing of data by applying a simple moving average (SMA) algorithm. The SMA is an unweighted average of the last n samples, and since the sampling frequency remains constant, the number of the last n samples coincides with the time window of the rolling mean. The purpose of implementing the moving average is to smooth out any short-term fluctuations while still capturing essential patterns, or concisely, to increase the signal-to-noise ratio. In the relevant literature, very frequent time windows of 10 to 15 min were used. In this case, to determine the best choice for a time window, we used numerous values and examined how well they canceled out the noise while still maintaining as much information from the original data as possible. It was observed that as the averaging time window increased, the standard deviation, hence the uncertainty, increased as well. This observation should be expected, since it is a known that a time-series analysis that increases the value of the order in a moving average model also increases bias. The plots of change of the standard deviation concerning the size of the averaging window for the selected feature of the studied vessel are shown in Figure 5.
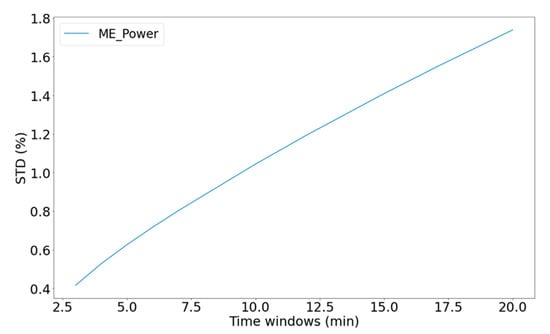
Figure 5.
The standard deviation of Main Engine power relative to the averaging time window.
As shown, the standard deviation increased significantly as time windows increased. To create a balance between computational cost and precision in our work, a time window of 5 min was selected. This way the STD remains below 1% while important information is not lost over averaging. To ensure that this assumption is valid, extensively graphs of selected features for 5- and 10-min time windows are shown in Figure 6.
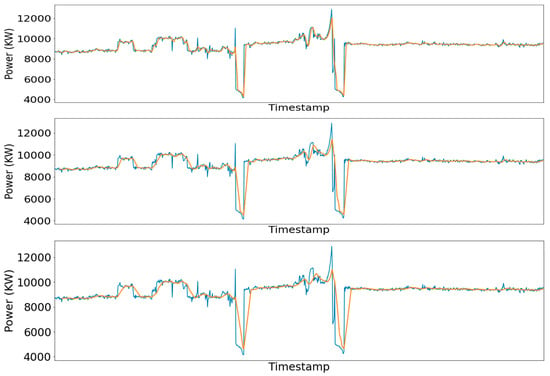
Figure 6.
Real (blue line) vs smoothed (red line) signal for a 5-min (up), 10-min (middle), and 15-min (down) averaging window.
3. Feed-Forward Neural Networks
3.1. Model Description
Artificial neural networks (ANNs), usually simply called neural networks (NNs), are computing systems modeled loosely after the biological neural networks that constitute animal brains. Neural nets are designed to simulate associative memory. Such systems “learn” to perform tasks by considering examples, generally without being programmed with task-specific rules. They are trained by processing examples, each of which contains a known input and result, and through this process, they learn to recognize patterns, either numerical or categorical, and form probability-weighted associations between the inputs and the target features. After being provided with enough examples, the model becomes capable of establishing causal relationships and correlations between events, hence its ability to estimate results from inputs.
Components of the ANNs
The neurons are typically organized into multiple layers. The connection is explicitly between neurons of consecutive layers. Each artificial neuron is connected to a single input and output. The inputs can be either the values of a sample row of external data or the outputs of other neurons. The layer that receives external data is called the input layer. The layer that produces the ultimate result is the output layer, while in between, there are the hidden layers.
Additionally, the weights of each neuron’s input are internal parameters of the model that occur through training so that the corresponding outputs emerge. Explicitly, the output of each neuron is calculated by the sum of all the inputs, weighted by the weights of the connections from the inputs to the neuron. This weighted sum is then passed through a (usually nonlinear) activation function to produce the output. Ultimately, the result of the output layer is subsequently the result of the whole model, and is compared with the actual values from the dataset to evaluate the model’s performance. This difference between the predicted and real values of the same parameter is the input of an error function. This part of the optimization algorithm is critical. Our objective was the minimization of the error function through weight update in each iteration to reduce the loss.
The choice of loss functions and evaluation metrics is a crucial part of the model-building endeavor for the assessment of the performance of the model. The loss function selection process is an equivocal undertaking. Following [11], both the loss function and the metric used to evaluate the model performance is the mean absolute percentage error (MAPE), which is defined as:
The training procedure of a deep-learning model involves parameters, besides those internal to the model, that need to be set in advance that are called hyperparameters. The hyperparameter selection process is not a straightforward endeavor, as it requires extensive experimentation through trial and error. Therefore, the task is to find the best configuration of these parameters. These parameters are: (1) activation function, (2) election of loss function, (3) weight initialization, (4) the number of epochs, (5) the batch sizes, (6) the number of hidden layers and the number of units in each layer, (7) the learning rate of the optimizer, and (8) the dropout rate.
The optimizer selection can also be viewed as a hyperparameter. However, weighing the advantages and disadvantages of each of the possible choices and aiming not to overwhelm the algorithm with additional hyperparameters further, the ADAM optimizer was preferred over the rest. The multitude of hyperparameters implies that a manual inquiry for the best configuration of hyperparameters is impracticable. Therefore, an automatizing algorithm for such an endeavor was implemented. Two very widely used algorithms were examined in this case: the grid search and the randomized search. The tradeoff is that we sacrificed the optimal arrangement of hyperparameters, acquired from implementing the examination against every combination of hyperparameters, with a less optimal, randomized selection in exchange for a less computationally costly algorithm. The process for the finalization of the model can be summarized in the following steps:
- Use specifically applicable: rules of thumb utilized in deep-learning models/applications to initialize the process with abstract values for the hyperparameters and insert these parameters to the neural network, given that tuning every hyperparameter is overwhelming not only for the computer, but also for the human behind it trying to interpret the results. Hyperparameters regarded as more significant than others whose values have been defined in this step will be reviewed in the next step.
- After experimentation, a grid search was deemed computationally affordable, hence it was preferred over the randomized search in the optimal configuration inquiry process. The hyperparameters being examined through the implementation of grid search algorithms are model-structure related, such as the number of layers, and the number of neurons per layer, and activation functions. Assess performance on the training and, more importantly, on the test set. Determine the network’s structure and activation function.
- Having determined the structure of the model and the selection of the activation function, the value of the learning rate is reviewed. It is reduced until the loss function ceases to fluctuate during the training process.
- After convergence of the loss function is observed, the batch size is also a hyperparameter that could further improve overall performance.
3.2. Model Application
In this part of the study, the FFNN approach is described in detail. Following the steps mentioned in the previous sub-section, the application of several rules of thumb from the broader machine-learning community helps determine which parameters should not be considered in the grid-search implementation, as well as the values assigned to these secondary hyperparameters. The secondary parameters not assessed by the hyperparameter tuning algorithm, for each of the models presented in the subsequent paragraphs of this study, are presented in Table 3.

Table 3.
Initial selection of secondary hyperparameters.
The reason behind the selection of the dropout rate’s value is that we implemented cross-validation and shuffling of the dataset during training to address overfitting. We will try adding dropout after the finalization of our architecture to see if it improves the performance of our model. The kernel weight initializer is rather insignificant since, given the small-batch relative to the number of samples on which our model was trained, in addition to the number of epochs, it results in the updating of the weights of the neurons numerous times before the end of the training process. Each power predictive model was implemented a total of four times. The next step toward the finalization of the configuration of the hyperparameters of the model was the implementation of the grid search algorithm. The hyperparameters being inspected were the number of layers in the model, the number of nodes per layer, and the activation function applied at each node. Table 4 presents the selected values.

Table 4.
Hyperparameters examination grid.
The two most common activation functions for regression are the rectified linear unit function (ReLU) and the linear function, which provide a linear combination of the inputs. Experimentation led us to conclude that, given our dataset’s high dimensionality, increasing the network’s width may play a catalytic role in improving model performance without delaying the training process significantly, as much as increasing the number of layers to model, and therefore explaining why we chose to inspect over such high values of nodes per layer.
This procedure took place four times since two different shapes of the structure of the model are scrutinized, and two different models are built being fed two different datasets. More specifically, two types of shapes of the structure of the model were inspected: a rectangular one and a trapezoidal one. In the case of the rectangular-shaped model, the number of nodes per layer remained constant, whereas in the case of the trapezoidal-shaped model, the number of nodes in each layer decreased for each layer closer to the output layer, starting with the same number of nodes in the first hidden layer, as in the rectangular-shaped case, and ended up with half of the nodes in the last hidden layer. This experimentation was carried out to see whether the calculation of fewer weights in the latter case would contribute to faster training time while yielding comparable results, or if the rectangular-shaped models were ultimately significantly more robust. One noteworthy comment about trapezoidal-shaped architectures is that since the number of nodes per layer was not constant, we shall refer to the maximum number of nodes in the first hidden layer to maintain cohesion with rectangular shaped models.
Additionally, two types of datasets were also examined. The first was the dataset as obtained at the end of the data preprocessing phase described earlier in this study. The second dataset was the same dataset after the application of the principal component analysis (PCA) algorithm. Principal component analysis is a statistical technique used widely to explain high-dimensional data in various fields in which it is mostly used as a tool in exploratory data analysis and for making predictive models. PCA tries to find maximum variance directions that are mutually orthogonal, and thus linearly independent of projecting the original data points. Dimension reduction is thereby accomplished in a smaller-dimensional subspace using a smaller number of variables, called the principal components, before running a machine-learning algorithm on the data. Principal components could be viewed as linear combinations of the original variables in the dataset. However, after applying PCA, the parameters relinquish their natural meaning, so their interpretation becomes more challenging, if not impossible. Dimensionality reduction was examined once again to examine whether it could manage to reduce the duration of the training process of the models while achieving comparable results to the model with the original dataset. In the comparative charts (Figure 7), the best accuracy and time needed for the implementation of the grid search are presented to distinguish the more-efficient model of the four that were examined.
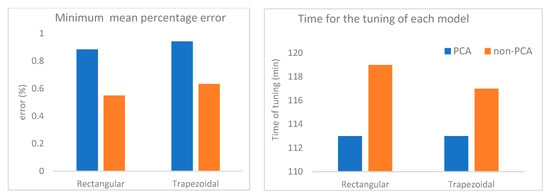
Figure 7.
Left: Comparison of the models concerning the mean percentage error each one achieved on the test set. Right: Comparison of the models concerning the time required for the hyperparameter tuning procedure.
As shown, whereas the implementation time was almost identical across all four examined models, with every model requiring a tuning time of approximately 4 h, the rectangular network that was fed the original dataset was deemed to have returned the lowest error in the test set. For the tuning procedure, each model had to be retrained 72 times with different layout structures and the results each one achieved on the test set were subsequently compared to distinguish the best-performing model, as well as the most efficient one. More explicitly, the fastest of the four models was the expected trapezoidal model into which the PCA dataset was fed; however, this model also seemed to be the worst-performing, whereas the difference in training time seemed to be marginal, as it required only 3 min less than the rectangular non-PCA network, which was the slowest of the four. Conclusively, the model deemed to be more efficient was the rectangular network with the non-PCA dataset inputted, as it was the most accurate, while requiring approximately the same amount of time for training. It is worth noting that having determined to use the non-PCA dataset, feature scaling to normalize the range of independent variables is an important step to ensure the proper functioning of the objective function. The selected scaling algorithm is min–max normalization:
where x’ is the new value and x is the old value of the feature, and min(X) and max(X) are the minimum and maximum value, respectively, of the particular feature.
Results yielded by the selected model are presented more thoroughly in Figure 8 and Figure 9. The curves illustrate the mean absolute percentage error and the standard deviation yielded on the test set, acquired by applying the ReLU and the linear activation function, along with a different configuration of the hyperparameters related to the layout of the model, namely the number of layers and the number of nodes per layer.
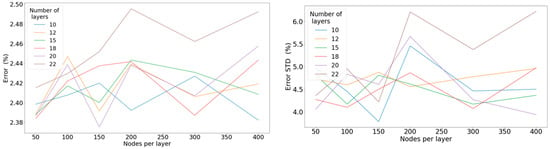
Figure 8.
Left: Mean percentage error concerning the number of nodes per layer for a different number of hidden layers when applying the linear activation function. Right: Standard deviation of the percentage error concerning the number of nodes per layer for a different number of hidden layers when applying the linear activation function.
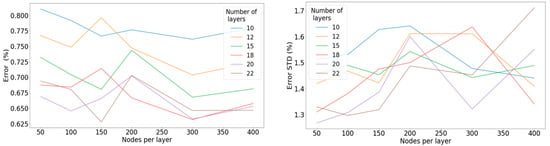
Figure 9.
Left: Mean percentage error concerning the number of nodes per layer for a different number of hidden layers when applying the ReLU activation function. Right: Standard deviation of the percentage error concerning the number of nodes per layer for a different number of hidden layers when applying the ReLU activation function.
We intend to examine the two activation functions with the structure of the networks inspected as the common denominator in the context of this comparison. It seems that in the case of the linear activation function, the results were counterintuitive, as deeper networks yielded more erroneous results, suggesting in the case of the linear activation function that deep structures are not required to observe the convergence of the results. In contrast, in the case of the ReLU activation, it was evident what intuitively seems reasonable: that as the structure was composed of more layers and more nodes, the loss between predicted and actual values diminished. Nevertheless, the aim was not necessarily optimum accuracy at any cost, rather than optimal efficiency. Therefore, we did not continue to further increase either the number of layers or the number of nodes per layer. Ultimately, the results led to the conclusion that the ReLU activation function profoundly outperformed the linear activation function, and thus it was selected for our finalized model.
One set of hyperparameters impacting our model’s performance profoundly, into which we have not delved yet, is related to the optimizer’s learning rate, namely the learning rate itself and its decay parameters. Their magnitude dictated the speed of convergence of the training procedure and, ultimately, the model’s loss on the test set. This approach reduced the learning rate and increased the learning decay parameters of the optimizer until any volatility to both training and validation error was removed, intending to determine the order of magnitude of the parameters. This concept is presented in Figure 10, which shows four curves with different learning rates; the one being trained with a greater learning rate appears to be volatile, while the one with the smaller one seems smoother.
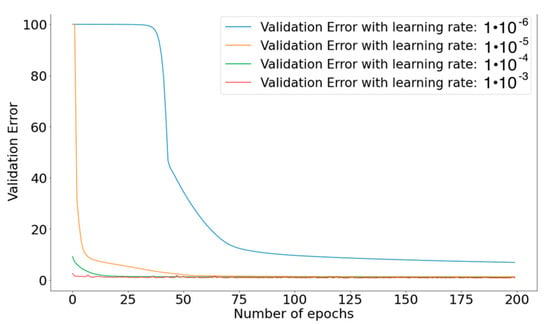
Figure 10.
Learning-rate order of magnitude and its effect on the model performance.
It is shown that the learning-rate curve starts to smoothen for values smaller than 10−3, leading us to claim that the optimal learning rate that should be used for this particular model is situated between 10−3 and 10−5. Errors and standard deviation of errors obtained from the implementation with different learning rates are illustrated in Figure 11.
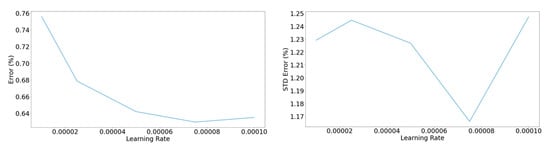
Figure 11.
Left: Mean percentage error concerning the learning rate of the optimizer. Right: Standard deviation of the percentage error concerning the learning rate of the optimizer.
Ultimately, our task was to minimize the error between predicted and actual values on the test set and keep the standard deviation low. Considering the points, 2.5 × 10−4 seemed to be an ideal value for our model’s learning rate. Once we determined the values of the learning parameters, the batch size and its effect on the error on the test set was scrutinized (Figure 12).
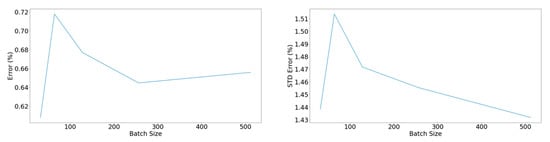
Figure 12.
Left: Mean percentage error concerning the batch size. Right: Standard deviation of the percentage error concerning the batch size.
Indeed, performance optimization was achieved by shrinking the batch size. In this case, the tradeoff was that smaller batch sizes invoked more weight updates during the training procedure; therefore, training required more time. Weighing this tradeoff, a batch size of 128 was selected. Ultimately, we determined a predictive model that generated a mean error of 0.608% on the test set and a standard deviation of 1.438%. Table 5 shows the model’s main characteristics.

Table 5.
Finalized configuration of the hyperparameters for the power-predicting model.
4. Recurrent Neural Networks
4.1. Model Description
Recurrent neural networks (RNN) are a class of neural networks in which connections between nodes allow better sequential data processing. Derived from feed-forward data, RNNs utilize their internal memory to process temporal dynamic behavior and input sequences. Given the fact that our dataset is a time sequence, RNN models were encouraged to be examined. Specifically, in the present study, the type of recurrent neural network that was examined was a long short-term memory neural network (LSTM). LSTM units possess feedback connections, which are beneficial characteristics rendering them appropriate to process and make predictions in time-series analyses. LSTM units seem to outclass traditional RNNs regarding long memory. The problem addressed was the vanishing gradient problem encountered when training on traditional RNNs. An RNN using LSTM units can be trained in a supervised fashion on a set of training sequences using an optimization algorithm, like gradient descent, combined with backpropagation through time to compute the gradients needed during the optimization process, to change each weight of the LSTM network in proportion to the derivative of the error concerning the corresponding weight. The problem with using gradient descent for standard RNNs is that error gradients vanish exponentially for increasing time lag. However, with LSTM units, when error values are backpropagated from the output layer, the error remains in the LSTM unit’s cell, continuously feeding the error back to each of the LSTM unit’s gates, until they learn to cut off the value.
Components of LSTM RNNs
A common LSTM architecture is composed of a cell and three regulators, which usually are called gates. The cell acts as the memory unit. LSTM neurons, or memory blocks, are composed of three types of gates:
- Forget Gate: conditionally decides what information to discard from the block.
- Input Gate: conditionally decides which values from the input to update the memory state.
- Output Gate: conditionally decides what to output based on input and the memory of the block.
The similarities of LSTM models and regression ANNs are emerging, and as we will see in the following section of the present study, both models share the same pitfalls, hyperparameters, and loss functions. Regarding the loss function, the error observed between the predicted and the actual values was monitored through the same regression loss functions mentioned above (MAPE).
Similarly, as in the case of the FFNNs, hyperparameters should be finalized before starting the training process. The model does not learn hyperparameters during the training process; however, they profoundly affect the model’s performance. Indicatively, in LSTM models, the hyperparameters required to carry out the training procedure are:
- The number of epochs: Increasing the number of epochs improves performance, since more iterations give the model the chance to learn better. However, this eventually results in overfitting.
- The batch size: This defines the frequency of weight updates. Increasing the batch size lowers the computational cost, enhances the algorithm’s efficiency, and intensifies the error function variance.
- The number of hidden layers and the number of units in each layer: Both of these enhance the model’s accuracy, but eventually lead to memorizing extravagantly intricate patterns in training, resulting in overfitting.
- Learning rate of the optimizer: This is a critical parameter that dictates the learning pace of the algorithm, but also entails the risk of utter learning failure if chosen to be too large in order to expedite the process.
- Dropout rate: This is responsible for dealing with the problem of overfitting; nevertheless, the pitfall of underfitting is imminent if chosen to be larger than the model would require.
- The number of samples inputted: LSTM models need to receive n number of samples each time to generate one outputted value. A large number of inputted samples provides a more holistic view of our model; however, there is a risk of overfitting.
The futility of manual searching for the best configuration of the hyperparameters due to their plenteousness is again underlined. A similar approach is followed for the LSTM models. Specifically, the steps for the consummation of the model are summarized in the following steps:
- Use specific applicable rules of thumb known in the deep-learning community to initialize the process with abstract values for the hyperparameters.
- Implement the grid or the randomized search repeatedly until hypermeters converge to a specific configuration.
- Insert these parameters into the neural network.
- Assess performance on the training, and more importantly, on the evaluation data.
- Manually carry out further refinements to the hyperparameters if deemed necessary.
4.2. Model Application
In this part of the study, in the same manner of implementation for the ANN models, an LSTM model was created to predict of the power of the main engine. After experimentation, it was discovered that profoundly better performance was achieved by creating a time-series model that only received the past values of the target parameters upon which the model aspired to predict. Models receiving as input all features of the dataset would fail to generalize, thus indicating overfitting patterns. This selection of a sole input feature to the model was enabled by two factors:
- The large inertia characterizing a tanker ship, resulting in slow rates of change among most features, and
- A large amount of data for both training and testing our algorithm.
The dataset was again split into two equal parts: the training and validation subsets. The concept behind the training set remained the same as in the FFNN case, and the validation set was used for evaluating the performance of each configuration of hyperparameters. We tracked the minimum validation error for each implementation below and the average mean absolute percentage error over the 10 best validation errors observed. The main difference, compared to the ANN implementation described in Section 3, was the utilization of the time-sequence trait of our initial dataset; hence, it was not plausible to shuffle the dataset, since this would disturb the sequential trait needed for the RNN. The values of the hyperparameters not tested in the grid search are listed in Table 6, while Table 7 presents the plausible values of the hyperparameters that underwent the tuning procedure.

Table 6.
Values of secondary less-significant hyperparameters.

Table 7.
Hyperparameter tuning values.
For the values of the number of input samples that the LSTM units received each time, the emphasis was placed on testing smaller windows. Because of the slow dynamics that characterize a vessel, it was deemed that larger windows would not provide anything valuable, but instead would increase the risk of overfitting. Moreover, the number of layers units in the model was selected equal to 1, since adding more layers would have delayed the training process significantly, and decreased our model’s ability to generalize. The default function of LSTM models was the sigmoid function, regardless of the nature of the problem, and this was the reason behind our choice to test it. The ReLU function was selected due to its outstanding performance in the ANN models presented in Section 3. Our initial chosen values for the learning rate and the batch size were 2 × 10−4 and 256, respectively. However, those two values were reviewed for each model to determine the learning-rate and batch-size values that would optimize our models’ performance.
Application of the ReLU activation function returned the results illustrated in Figure 13, which entails the minimum error on the validation set observed out of all the epochs during the training of the tuning phase, along with the average of the epochs with the 10 lowest errors returned on the validation set.
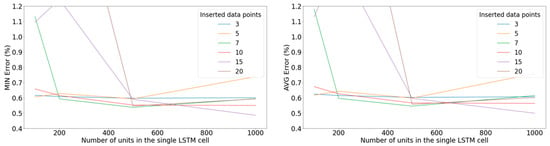
Figure 13.
Left: Minimum error on the validation set with respect to the number of units in the LSTM cell for various windows of inputted data points when applying the ReLU activation function. Right: Average error on the validation set among the 10 best-performing epochs with respect to the number of units in the LSTM cell for various windows of inputted data points when applying the ReLU activation function.
Execution of the same algorithm with the application of the sigmoid activation function on the LSTM units yielded significantly lower accuracy. Experimentation with the learning rate and other hyperparameters did not ameliorate anything. Indicatively, Figure 14 illustrates this exact underperformance.
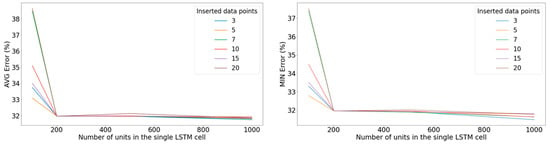
Figure 14.
Left: Minimum error on the validation set with respect to the number of units in the LSTM cell for various windows of inputted data points when applying the sigmoid activation function. Right: Average error on the validation set among the 10 best-performing epochs with respect to the number of units in the LSTM cell for various windows of inputted data points when applying the sigmoid activation function.
Based on these results, it was evident that the rectified linear unit should be selected as the activation function. Additionally, the results illustrated in Figure 14 prompted the selection of an LSTM cell with 1000 cells and an input window of 15 samples. Next, the order of magnitude of the optimizer’s learning rate was examined, in which the intention was to eliminate the volatility of the validation error curve. Figure 15 suggests that the range of values of the learning rate that accomplish the task was from 10−4 to 10−3, and despite the mild volatility in this range of values, convergence can be observed. Observing Figure 16, a learning rate of 5 × 10−4 was selected.
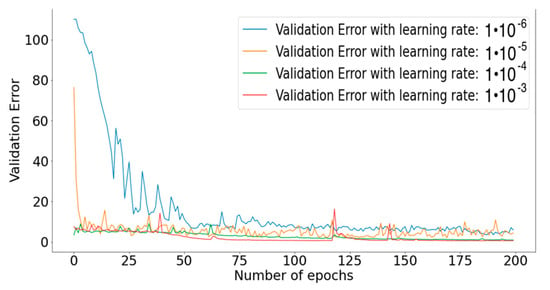
Figure 15.
Effect of the order of magnitude of the learning rate on the performance of the model.
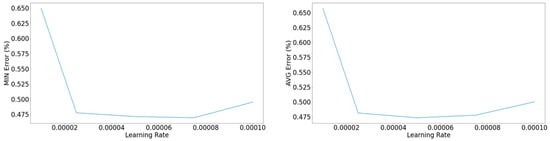
Figure 16.
Left: Minimum error on the validation set concerning the learning rate. Right: Average among the 10 epochs with the lower yielded error concerning the learning rate.
Finally, in a similar fashion to the approach followed in the FFNN models, an inspection of the batch size took place. Observation of Figure 17 shows minimization of the yielded error for a batch size of 128, thus finalizing the power-predicting LSTM model, as shown in Table 8.
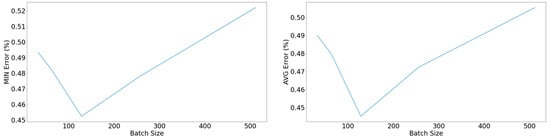
Figure 17.
Left: Minimum error of the validation set concerning the batch size. Right: Average among the 10 epochs with the lower yielded error concerning the batch size.

Table 8.
Finalized values of hyperparameters defining the LSTM power-predicting network.
5. Application of the Ship Power Prediction
Based on the same dataset as in the previous section, this part of the study focused on creating performance-optimized deep-learning models to estimate and predict the main engine delivered power (the target feature). Two fundamentally different approaches were presented, each implemented with a different deep-learning model type. First, the creation of ANN models was presented to tackle the feature estimation problem as a regression problem. RNN models, and more specifically, LSTM models were implemented, exploiting our dataset’s time-sequential behavior. It was found that both deep-learning model genres yielded comparable results, with both achieving both target features with accuracies greater than 99%. This fact satisfied one of this study’s aims: to provide trustworthy and reliable results for a vessel’s performance. In this part of the study, we present our efforts to simulate realistic conditions and the evaluation of our model’s performance under unseen data, incoming in real time. The model was trained using the inner part (80%—270,000 samples) of the dataset, while the remaining part (20%—74,600 samples) was kept for the out-of-sample predictions phase.
5.1. Power Prediction Using ANN
First, we present the performance of the regression-based feed-forward deep-learning model in feature prediction. Interestingly, FFNNs seemed to fail to handle many out-of-sample predictions, as they cannot predict with a high level of accuracy the steep fluctuations of the power signal, as shown in Figure 18. It appears that until the 20,000 sample, the model was performing satisfactorily, as the predicted values of the target feature matched real ones. However, for subset sizes larger than that, the divergence between predicted and real ones started to emerge. Additionally, the model could still estimate maintaining a constant error percentage when the signal of the target feature did not significantly vary in time. However, the FFNN model inadequacy was displayed by the steep error increase induced by data points that reflected the signal variation. Another illustration of the same observation is given in Figure 19 by the constant increase in the error mean.
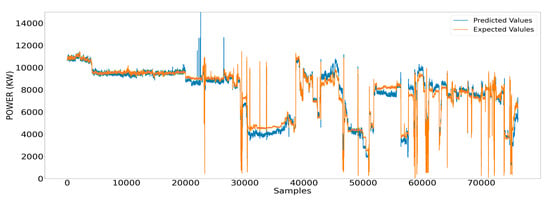
Figure 18.
Measured values of the shaft power and respective estimated ones using ANN.
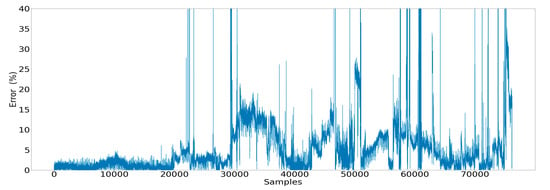
Figure 19.
Error observed for each data point estimated by the ANN model.
Figure 20 illustrates the steep error standard deviation increase around the 20,000 data point, expressing that the model certainty in its predicted values was significantly deteriorating; thus the error increase and the divergence between estimated and measured values when needed to predict more data points.
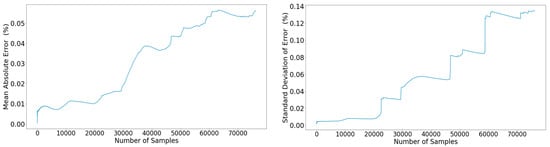
Figure 20.
Left: Propagation of the mean percentage error across the out-of-sample subset. Right: Propagation of the standard deviation of the error across the out-of-sample subset.
Figure 21 presents the measured values concerning the sample size of the subset surrounded by the 95% confidence interval. A pronounced expansion of the interval as the sample size grew is obvious; this is a natural consequence of the standard deviation increase.
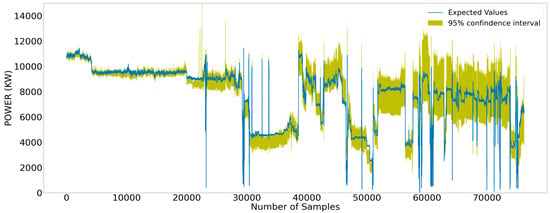
Figure 21.
Measured values surrounded by the respective 95% confidence interval that stemmed from the estimated values.
5.2. Power Prediction Using RNN
Time sequential models undertaking the same task seemed to perform significantly better. It is illustrated in Figure 22 that the LSTM power-predicting model could capture fluctuations and volatility appearing in the power signal with significant accuracy. We would expect that toward the end of a large sample size, the LSTM would find it troublesome to predict with such high levels of accuracy. However, it kept both the error and its standard deviation below 0.5% and 2%, respectively, across the whole out-of-sample subset (Figure 23).
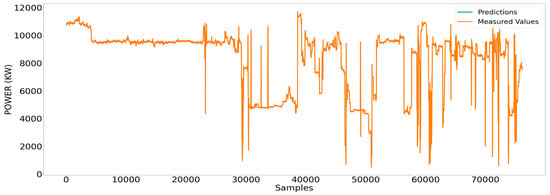
Figure 22.
Measured values of the shaft power and respective estimated ones using RNN models.
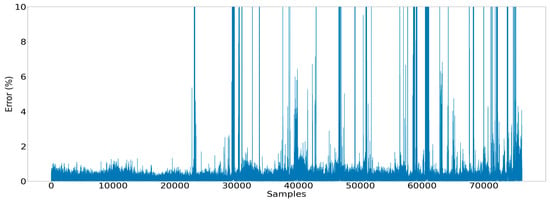
Figure 23.
Error observed for each data point estimated by the RNN models.
Similar to the FFNN model, the LSTM model demonstrated similar behavioral patterns; namely, the mean error propagation in this case was continuously increasing along with a steep rise of the error standard deviation (Figure 24). However, compared to the respective values yielded by the FFNNs, the profound performance change is evident.
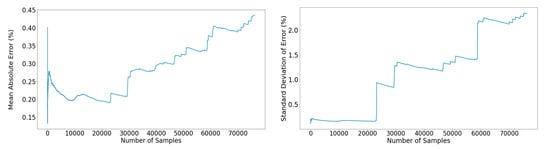
Figure 24.
Left: Propagation of the mean percentage error across the out-of-sample subset. Right: Propagation of the standard deviation of the error across the out-of-sample subset.
In contrast to the ANN models, the LSTM models predicted the real values of the generated power more accurately. This is shown in Figure 25, in which the 95% confidence interval remained relatively narrow around the measured values across the whole out-of-sample subset, with the corollary of the standard deviation of the error being kept in the moderate range.
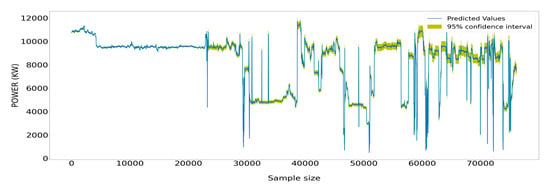
Figure 25.
Measured values of the power generated by the main engine surrounded by the respective 95% confidence interval that stemmed from the estimated values from the RNN models.
6. Model Comparison
In the previous section, it was concretely shown that the RNNs’ innate attribute of processing sequential data did manage to significantly outperform the FFNN counterparts, yielding more accurate predictions across the whole predictions subset.
In this section, the comparison between the two different types of neural networks shall be taken a step further, delving deeper into the statistical meaning behind the more accurate predictions of the RNN (Table 9). Implementation of the neural networks was executed with fuel-oil consumption considered as a target feature, along with the shaft power.

Table 9.
Performance comparison of the two types of networks (mean error–percentage error).
The gap in the performance between the two types of networks is evident. To analyze this significant difference more thoroughly, it was deemed worthwhile to divide the subset, where previously sample predictions were carried out, into segments of 10,000 samples. As demonstrated in Figure 26, in the case of the FFNN, the estimated and the actual values of the power seemed to agree more in the first portion of the out-of-sample predictions subset, but as the number of samples estimated increased, predicted values appeared to diverge from the measured ones, whereas the RNN seemed to be accurate throughout the whole subset. For the first 10,000 samples, predicted values stemming from each network were plotted against measured ones, forming two scatter plots, and linear regression subsequently was carried out in each one, returning the “best-fit” line, also called the trend line of the specific subset. Ideally, that line should approach the identity line, which expresses the theoretical instance of having perfectly accurate predictions across the whole subset, namely Pmeas = Ppr, for every sample.
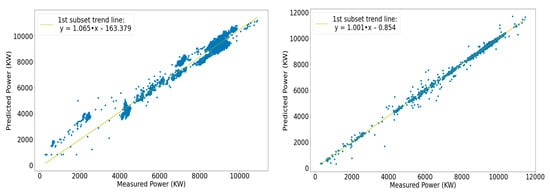
Figure 26.
Left: Scatter plot and optimal-fit line of the first segment of the FFNN model. Right: Scatter plot and optimal-fit line of the first segment of the RNN model.
Figure 27 demonstrates explicitly that the RNN models were consistently and explicitly more accurate than the FNNs, even when the latter seemed to be at their peak performance; namely, what appeared to be the case at the beginning of the out-of-sample predictions phase. Similarly, the process described above was implemented for the other segments consisting of 10,000 samples. In Figure 27 (right), the optimal-fit lines of each segment are presented, along with the identity line, to compare the acquired lines with the theoretically perfect predictive model.
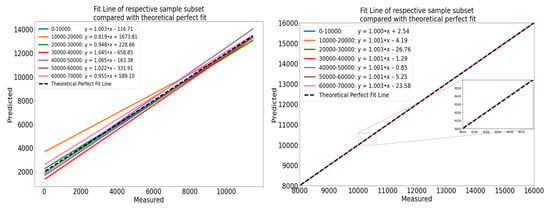
Figure 27.
Left: Optimal-fit lines for all segments of the FFNN model. Right: Optimal-fit line for all segments of the RNN model.
A comparison of the two legs of Figure 27 verifies the supremacy of the RNNs, as they converge with the identity line to the point that they almost coincide, verifying the claim that the accuracy was held throughout the whole subset. In Figure 27 (left), it is apparent that, except for the second segment, for the first four sectors of the subset, approximately up to the 40,000 sample, predictions seemed to be relatively good; however, lines referring to the next section appear to diverge more from the identity line. However, the goodness of the fit as described above is not always an objective means of comparison and can easily be misleading, especially when the results are more ambiguous. To quantify these results, the coefficient of determination, denoted as R2, was employed.
Supposedly, a dataset consisting of n samples forming a vector and the model’s predicted values are denoted with
Subsequently, the following quantities are defined:
- (i)
- The mean of the observed data:
- (ii)
- The sum of the squared difference of every sample to the mean (proportional to the variance):
- (iii)
- The sum of squares of residuals:
Having defined the above quantities, it is plausible to define the coefficient of determination as follows:
Figure 28 presents the R2 metric scores from both network types across all segments. The slope deviation from 1 of each line is also depicted. We defined slope deviation as:
where m is the slope of the respective line.
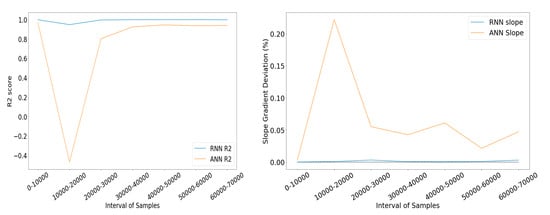
Figure 28.
Left: R2 score comparison between the types of networks. Right: Slope deviation comparison between the types of networks.
Finally, observation of the two graphs further solidifies the original claims made regarding the performance edge the RNNs possessed over the respective FFNNs.
This drastic drop in the accuracy percentage is justified by the fact that when power prediction was approached as a regression problem, the time sequence was discarded and data was shuffled to avoid overfitting, and there was an isolated portion of the data devoted to simulating out-of-sample predictions. Subsequently, that means that the training data points were spread throughout the whole dataset, thus enabling our model to predict against trends and fluctuations with a significantly smaller error. As demonstrated above, FFNNs can still estimate target feature values with an error smaller than 1% for a small number of predicted data points. The uncertainty, thus the error, grows as the number of samples asked to estimate increases. One way to counteract this phenomenon is by retraining the model, including new data points that occur. However, by doing so, this methodology renders the choice of artificial neural networks inefficient, as their computational cost and accumulated training time is dramatically increasing.
On the other hand, the LSTM models are trained for this exact purpose: to predict based on past values of the target feature, exploiting the time dependency of the data. Therefore, when asked to carry sequential out of sample predictions, they inherently perform significantly better.
Besides the performance-wise edge of the RNN-based models over the equivalent ANN ones, other significant advantages can be distinguished. For instance, as stated in Section 4, in the implementation of the RNNs, to predict either power or fuel-oil consumption values, no other feature was used other than the target feature itself, as they are solely based and trained on each respective target feature, which they attempt to estimate. Therefore, the monitoring of data gathering of other values is deemed redundant. That means that our data gathering was dependent on fewer monitoring devices, reducing the probability of measurement error situated in the data fed into our model, thus increasing the fidelity and reliability of both the data and the results.
However, this great accuracy comes at a cost. One drawback that can be spotted in the RNN model selection is the fact that they required more time to generate results than the FFNNs. More explicitly, when training all models on a cloud-computing instance comprised of a 2-core CPU and a 1-core GPU, recurrent neural networks required almost three more times to complete the training of a model over 200 epochs. The difference is even greater when prediction times are compared, as FFNNs required only a few seconds to complete more than 70,000 predictions, while the RNNs required approximately 40 min for the same task (Table 10).

Table 10.
Comparison of the training duration and the time * required for each network type to complete.
7. Discussion of Use-Case Applications
While the focus of the current work was the description of the pre-and post-processing techniques, as well as the comparison of the two models, in this section, we briefly discuss indicative applications of the results in a real situation. The aim is to provide a short glimpse of the applicability of the methodology through two real case studies from the maritime industry, mainly as working examples of the capabilities of the proposed methodology.
In the first example, the methodology was used for the construction of a key performance indicator (KPI), which was defined as the % difference between the measured and the predicted (RNN) power for a specific ship’s speed. This KPI (m-K3) was derived as a modified version of the K3 indicator presented in [1], which was defined as the % deviation of the difference between the measured and the designed (sea-trial) power for a specific ship’s speed. Both indicators target energy efficiency, as they entail hull and propeller degradation in time, which could result in a substantial increase in fuel consumption. Well-functioning ship behavior would be expressed by the power increase deviation with a constant value of 0. In Figure 29, the evolution in time for the two KPIs is presented. As shown the m-K3 indicator, a precipitous change of the curve indicates an anomaly that was artificially inserted in the dataset as an ME power-degradation factor. The analytical K3 indicator failed to detect the anomaly.
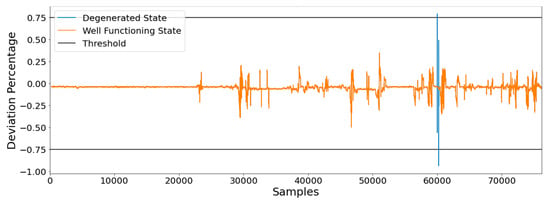
Figure 29.
Detecting the anomaly of degradation of the ship through the power increase deviation indicator.
By setting an alert condition of abnormality detection of 75%, we were able to provide an enhanced energy-efficiency monitoring tool. Additional oscillation around 0 was also observed as well; nevertheless, as depicted, their magnitude was satisfyingly below the threshold line. These oscillations were caused by slightly inaccurate predictions, and they were present in both states of the vessel’s functioning state. Results were presented in [12].
Going one step further, in [13], the same methodology was introduced as a data-processing tool in a hybrid multilayered data-acquisition technique demonstrated onboard an oil tanker. More specifically, in that occasion, data were collected and pre-processed in different computing levels ranging from the mist (very close to the sensor) to fog (onboard server) and cloud (headquarters). The RNN model was applied at the fog level, with an aim to fill data gaps.
8. Conclusions
The evolution of Industry 4.0 brought to the surface the necessity of the development of efficient data-analysis frameworks that are capable of handling an enormous amount of heterogeneous data, and thus provide enhanced decision support in terms of energy-efficiency optimization and optimal maintenance scheduling. As a result, the utilization of neural networks in marine engineering has been an emerging topic in the last decade. The specific genre of neural networks that are most studied and documented in this field is the ANNs, which are employed in the estimation of parameters such as power or fuel-oil consumption, approaching the problem in a regressive fashion in which the values of the other parameters in each moment enable the model to estimate the value of the target feature. Realizing, however, that the problem could be addressed as a time-series analysis, in the current work, RNNs with LSTM cells were suggested as an alternative method. Therefore, a comparative study between not only the two types of neural networks, but also between the two substantial approaching methods, was performed. Our main focus was on the identification of the different data pre-processing phases, as well as on the optimal-configuration decision process for each of the developed deep-learning models. The models were further compared to obtain their accuracy in predicting target features. We conclusively deduced that the time-series analysis course (RNN) produced more accurate predictions. This accuracy came at a cost of computational resources.
The main findings of this work are as follows:
- (1)
- LSTM models appeared to be suitable for propulsion power prediction, providing both great sensitivity and precision.
- (2)
- One of the main reasons of the accuracy decline of the FFNNs in the out-of-sample predictions was the stochasticity of the signal; namely, the sudden and steep changes. Therefore, applying more filters could smoothen the signal, resulting in performance and accuracy enhancement.
- (3)
- The method was tested through real case applications onboard, with an aim to determine the performance degradation of the vessel. It was shown that the suggested methodology incorporates diagnostic and prognostic features in a flexible framework, enabling technical and economic monitoring of past, current, and forecasted states.
The same endeavor could be undertaken by implementing other machine-learning algorithms as well, like support vector machines (SVM) or random forests, which are currently under development.
Author Contributions
Conceptualization, P.T., C.C.S., N.T. and S.F.; Data curation, P.T., C.C.S. and N.T.; Formal analysis, P.T., C.C.S. and N.T.; Funding acquisition, C.G.; Investigation, P.T.; Methodology, P.T., C.C.S. and N.T.; Project administration, C.G.; Resources, C.G.; Software, P.T. and C.C.S.; Supervision, C.C.S., N.T. and S.F.; Validation, C.C.S., N.T. and S.F.; Visualization, P.T., C.C.S. and N.T.; Writing—original draft, P.T. and C.C.S.; Writing—review & editing, C.C.S., N.T., C.G. and S.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Themelis, N.; Spandonidis, C.; Giordamlis, C. Data acquisition and processing techniques for a novel Integrated Ship Energy and Maintenance Management System. In Proceedings of the 17th International Congress of the International Maritime Association of the Mediterranean 2019 (IMAM-2019), Varna, Bulgaria, 9–11 September 2019; pp. 306–315. [Google Scholar]
- Jeon, M.; Noh, Y.; Shin, Y.; Lim, O.K.; Lee, I.; Cho, D. Prediction of ship fuel consumption by using an artificial neural network. J. Mech. Sci. Technol. 2018, 32, 5785–5796. [Google Scholar] [CrossRef]
- Gkerekos, C.; Lazakis, I.; Theotokatos, G. Machine learning models for predicting ship main engine Fuel Oil Consumption: A comparative study. Ocean Eng. 2019, 188, 106282. [Google Scholar] [CrossRef]
- Trodden, D.G.; Murphy, A.J.; Pazouki, K.; Sargeant, J. Fuel usage data analysis for efficient shipping operations. Ocean Eng. 2015, 110, 75–84. [Google Scholar] [CrossRef]
- Yuan, Z.; Liu, J.; Liu, Y.; Zhang, Q.; Liu, R.W. A multi-task analysis and modeling paradigm using LSTM for multi-source monitoring data of inland vessels. Ocean Eng. 2020, 213, 107604. [Google Scholar] [CrossRef]
- Brandsæter, A.; Vanem, E. Ship speed prediction based on full-scale sensor measurements of shaft thrust and environmental conditions. Ocean Eng. 2018, 162, 316–330. [Google Scholar] [CrossRef]
- Wang, S.; Ji, B.; Zhao, J.; Liu, W.; Xu, T. Predicting ship fuel consumption based on LASSO regression. Transp. Res. Part D Transp. Environ. 2018, 65, 817–824. [Google Scholar] [CrossRef]
- Perera, L.P.; Mo, B.; Soares, G. Machine intelligence for energy-efficient ships: A big data solution. In Maritime Engineering and Technology III; Soares, C.G., Santos, T.A., Eds.; CRC Press: Boca Raton, FL, USA, 2016; Volume 1, pp. 143–150. [Google Scholar]
- Coraddu, A.; Oneto, L.; Baldi, F.; Anguita, D. Vessels fuel consumption forecast and trim optimization: A data analytics perspective. Ocean Eng. 2017, 130, 351–370. [Google Scholar] [CrossRef]
- Spandonidis, C.; Giordamlis, C. Data-centric Operations in Oil & Gas Industry by the Use of 5G Mobile Networks and Industrial Internet of Things (IIoT). In Proceedings of the Thirteenth International Conference on Digital Telecommunications 2018 (ICDT 2018), Athens, Greece, 22–26 April 2018; pp. 1–5. [Google Scholar]
- Karagiannidis, P.; Themelis, N.; Zaraphonitis, G.; Spandonidis, C.; Giordamlis, C. Ship Fuel Consumption Prediction using Artificial Neural Networks. In Proceedings of the Annual meeting of marine technology conference proceedings, Athens, Greece, 26 November 2019; pp. 46–51. [Google Scholar]
- Theodoropoulos, P.; Spandonidis, C.C.; Themelis, N.; Giordamlis, C.; Fassois, S. Monitoring of a ship’s energy efficiency based on Artificial Neural Networks and Innovative KPIs. In Proceedings of the Annual Meeting of Marine Technology Conference Proceedings, Athens, Greece, 2 December 2020; pp. 87–103. [Google Scholar]
- Spandonidis, C.; Theodoropoulos, P.; Giordamlis, C. Combined multi-layered big data and responsible AI techniques for enhanced decision support in Shipping. In Proceedings of the 2020 International Conference on Decision Aid Sciences and Application (DASA), Sakheer, Bahrain, 8–9 November 2020; pp. 669–673. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).