Towards Least-CO2 Ferry Routes in the Adriatic Sea
Abstract
1. Introduction
2. Materials and Methods
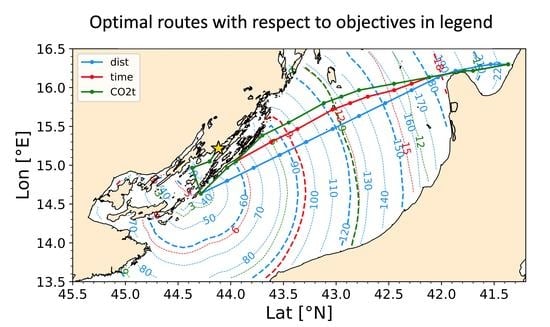
- Least-CO routes. VISIR can compute optimal routes by suggesting a spatial diversion which leads to avoidance of rough sea and related ship speed loss. Besides least-distance and least-time routes, we added a capacity to compute routes of least-total-CO emissions. This required a further generalisation of the time-dependent Dijkstra’s algorithm which is at the core of VISIR [15]. To this end, it is not enough to feed the routine with edge weights corresponding to the CO emissions along each edge. Indeed, the time for sailing through each edge (“edge delay”) should still be provided, in order to evaluate the position of the vessel and the environmental conditions encountered and the duration of the route. The related pseudocode will be published elsewhere;
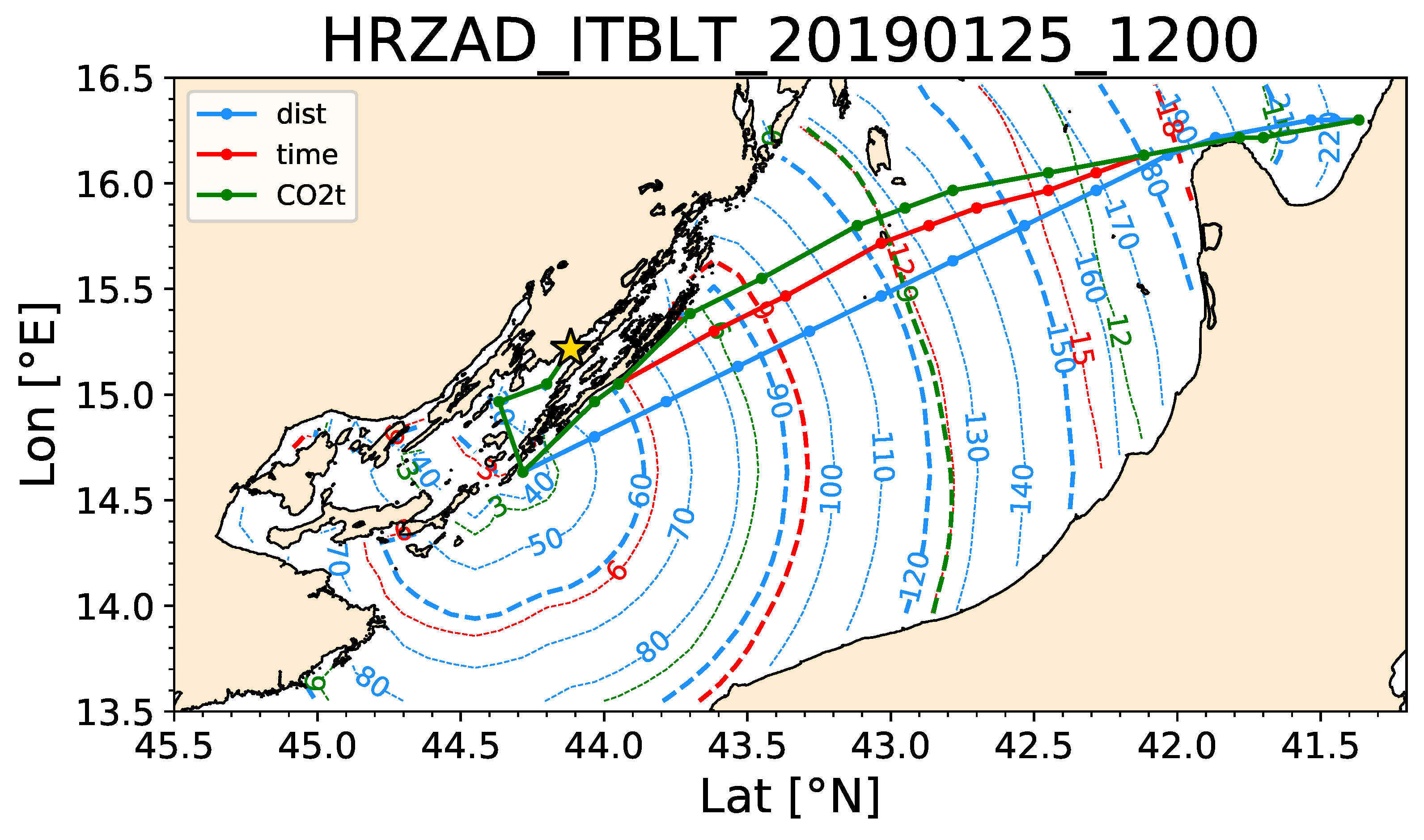
- Visualization. Mapping of the routes was improved by including the fronts of the locations reachable within a given time since departure (isochrones) and the environmental fields were sliced among isochrones. The latter were compared with lines of equal distance from route origin (or: “isometres”) and lines of equal amount of CO emissions (or: “isopones”), cf. Table 2. The name isopone is related to energy consumption (the greek word means “equal effort”), which is proportional to CO emissions;
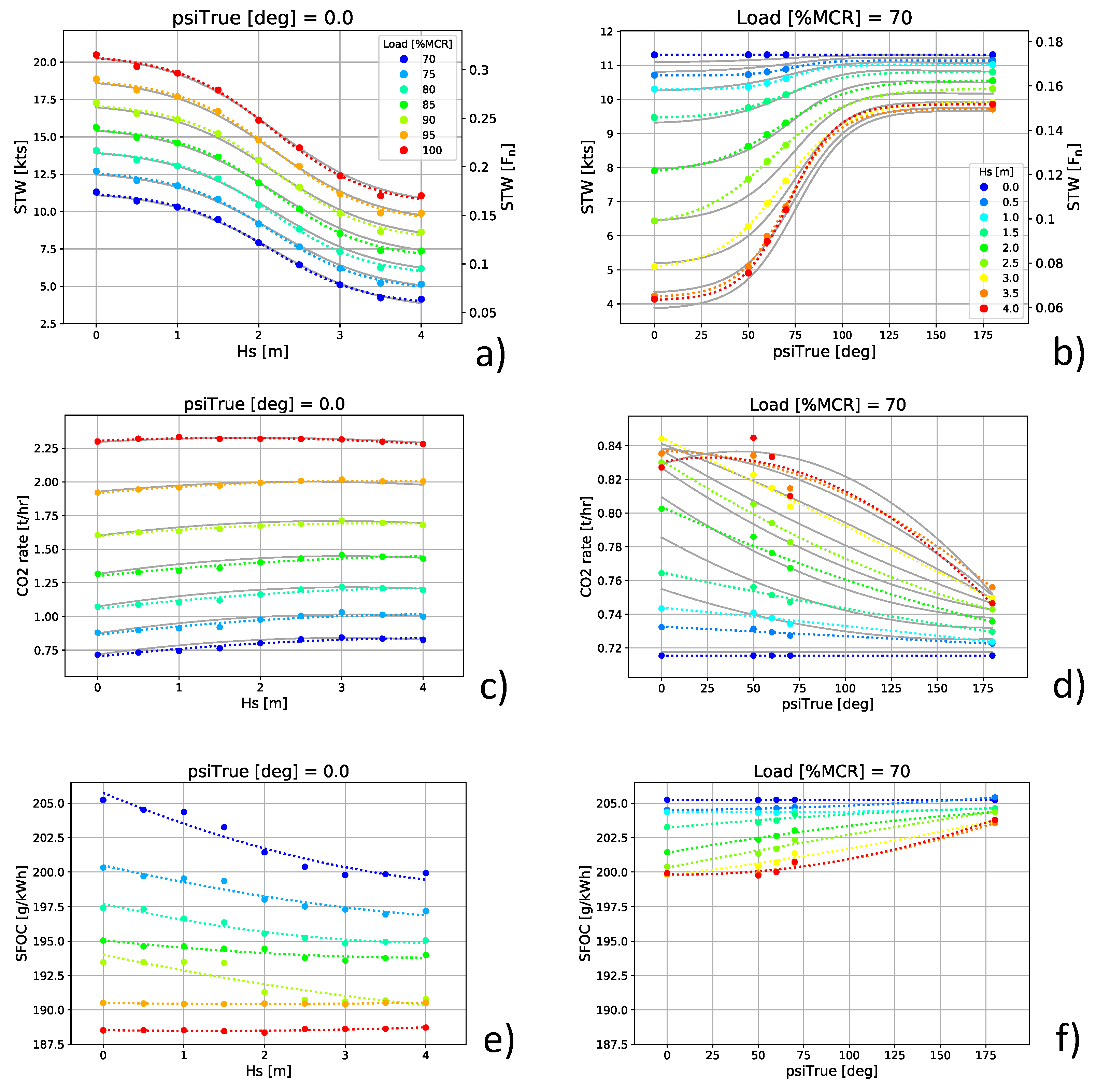
- Vessel performance modeling. In addition to the VISIR-1 model based on a dynamic balance at the propeller and parametrisation of calm water and wave-added resistance [15], an alternative vessel model was introduced in VISIR-2. It made use of the outcome of a ship simulator, from which the performance and emissions of a ferry were estimated in various sea conditions. This is described in more detail in Section 2.1. The Speed Through Water (STW) resulting from this approach can then be combined with the sea surface currents for computing the Speed Over Ground (SOG), along the way already demonstrated in [11].
2.1. Ship Simulator
2.2. Environmental Fields
- Bathymetry. The EMODnet bathymetric database6 was used for checking that navigation does not occur in shallow waters. Given its high spatial resolution (1/16 arc minute or about 120 m in the meridional direction), the bathymetry was also used to derive a pseudo-shoreline. It went this way: An under keel clearance map UKC = was computed from the bathymetry map (z) and the vessel draught (T). The contour line at UKC = 0 defined a pseudo-shoreline, which was then used for pruning graph edges crossing it;
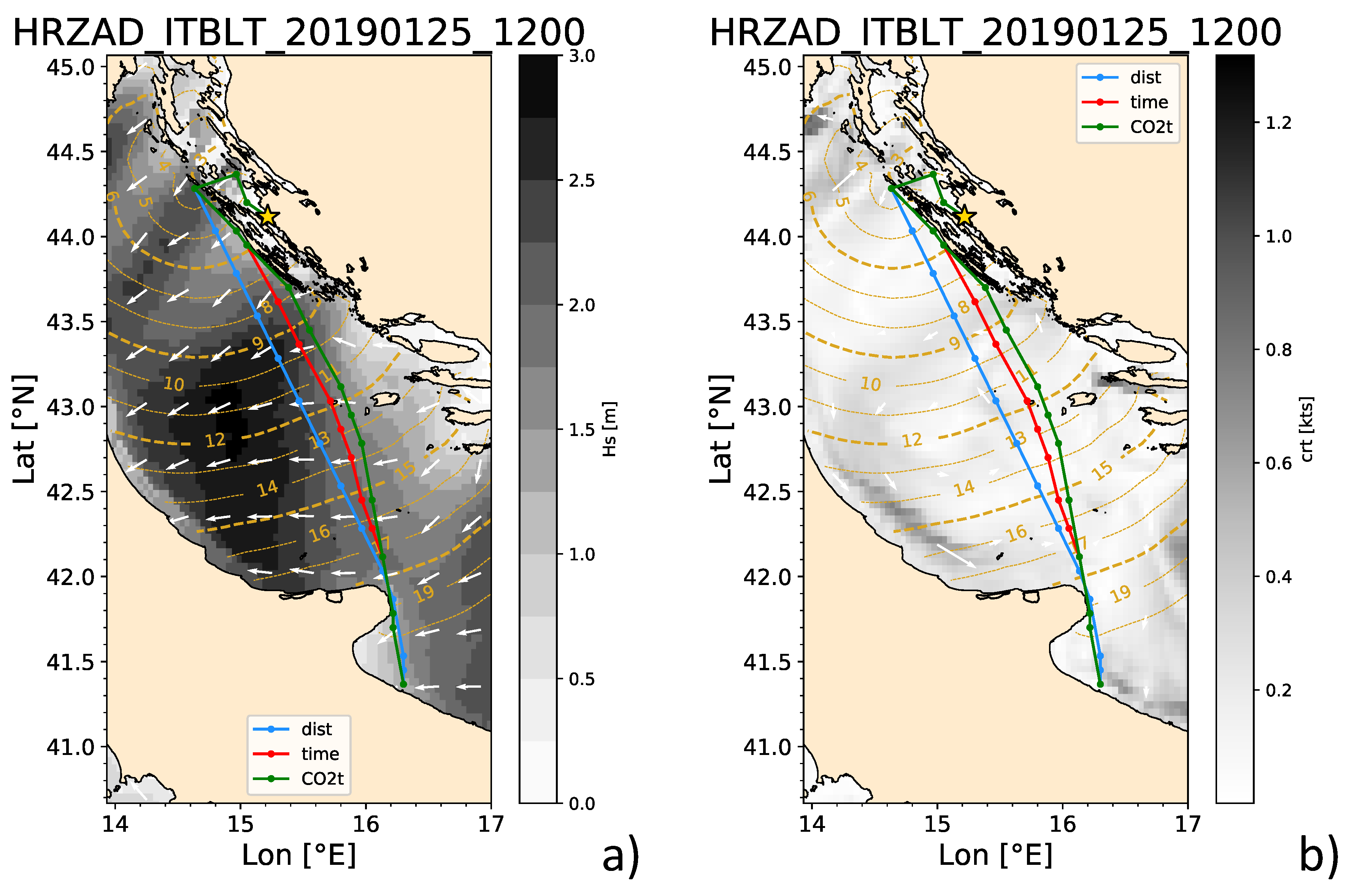
- Waves. Sea state analysis products were obtained through CMEMS (Copernicus-Marine Environment Monitoring Service)7 from the operational analysis and forecast system by HCMR (Hellenic Centre for Marine Research) for the Mediterranean Sea, based on wave model WAM Cycle 4.6.2. The dataset name was MEDSEA_ANALYSIS_ FORECAST_WAV_006_017. Significant wave height and direction fields were used. They had hourly time resolution and 1/24 degree (2.5 nmi8 in the meridional direction) horizontal resolution;
- Currents. Sea circulation analysis products were obtained through CMEMS from the operational analysis and forecast system by CMCC (Euro-Mediterranean Center on Climate Change) for the Mediterranean Sea, based on NEMO v3.6 coupled to wave model WW3 and making use of a 3DVAR data assimilation scheme. The dataset name was MEDSEA_ANALYSIS_FORECAST_PHY_006_013. Surface level meridional and zonal currents were used. They had hourly time resolution and 1/24 degree horizontal resolution.
3. Results
3.1. Vessel Performance
3.2. Isolines
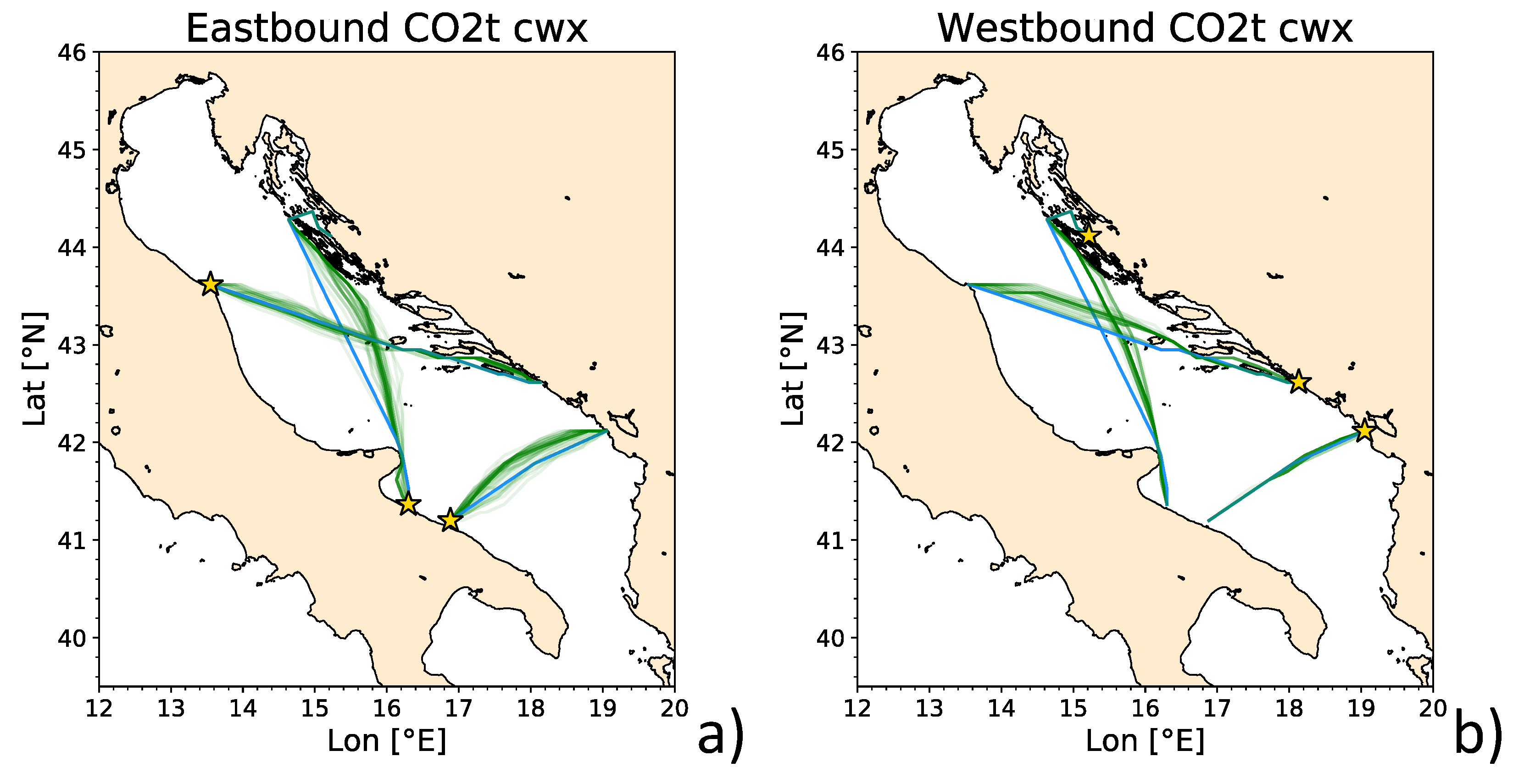
3.3. Spatial Diversions
3.4. Carbon Intensity Savings
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IMO. MEPC.304(72) Initial IMO Strategy on Reduction of GHG Emissions from Ships; Technical Report Annex 11; International Maritime Organization: London, UK, 2018. [Google Scholar]
- IMO. MEPC.1/Circ.684 Guidelines for Voluntary Use of the Ship Energy Efficiency Operational Indicator (EEOI); Technical Report; International Maritime Organization: London, UK, 2009. [Google Scholar]
- IMO. MEPC 75/WP1/Rev.1 Draft Report Of The Marine Environment Protection Committee On Its Seventy-Fifth Session; Technical Report; International Maritime Organization: London, UK, 2020. [Google Scholar]
- EU. Regulation 2015/757 of 29 April 2015 on the Monitoring, Reporting and Verification of Carbon Dioxide Emissions from Maritime Transport, and Amending Directive 2009/16/EC; Technical Report; European Parliament and the Council: Brussels, Belgium, 2015. [Google Scholar]
- Mannarini, G.; Carelli, L.; Salhi, A. EU-MRV: An analysis of 2018’s Ro-Pax CO2 data. In Proceedings of the 21st IEEE International Conference on Mobile Data Management (MDM), Versailles, France, 30 June–3 July 2020; pp. 287–292. [Google Scholar] [CrossRef]
- EP. Amendments Adopted by the European Parliament on 16 September 2020 on the Proposal for a Regulation of the European Parliament and of the Council Amending Regulation (EU) 2015/757 in Order to Take Appropriate Account of the Global Data Collection System for Ship Fuel Oil Consumption Data (COM(2019)0038–C8-0043/2019—2019/0017(COD)); Technical Report; European Parliament: Brussels, Belgium, 2020. [Google Scholar]
- Zis, T.P.; Psaraftis, H.N.; Tillig, F.; Ringsberg, J.W. Decarbonizing maritime transport: A Ro-Pax case study. Res. Transp. Bus. Manag. 2020, 37, 100565. [Google Scholar] [CrossRef]
- Panagakos, G.; Pessôa, T.d.S.; Dessypris, N.; Barfod, M.B.; Psaraftis, H.N. Monitoring the carbon footprint of dry bulk shipping in the EU: An early assessment of the MRV regulation. Sustainability 2019, 11, 5133. [Google Scholar] [CrossRef]
- Lu, R.; Turan, O.; Boulougouris, E.; Banks, C.; Incecik, A. A semi-empirical ship operational performance prediction model for voyage optimization towards energy efficient shipping. Ocean Eng. 2015, 110, 18–28. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, D.; Zhang, M.; Mao, W. Data-driven ship energy efficiency analysis and optimization model for route planning in ice-covered Arctic waters. Ocean Eng. 2019, 186, 106071. [Google Scholar] [CrossRef]
- Mannarini, G.; Carelli, L. VISIR-1.b: Ocean surface gravity waves and currents for energy-efficient navigation. Geosci. Model Dev. 2019, 12, 3449–3480. [Google Scholar] [CrossRef]
- Psaraftis, H.N.; Kontovas, C.A. Speed models for energy-efficient maritime transportation: A taxonomy and survey. Transp. Res. Part C Emerg. Technol. 2013, 26, 331–351. [Google Scholar] [CrossRef]
- Zis, T.P.; Psaraftis, H.N.; Ding, L. Ship weather routing: A taxonomy and survey. Ocean Eng. 2020, 213, 107697. [Google Scholar] [CrossRef]
- Farkas, A.; Parunov, J.; Katalinić, M. Wave statistics for the middle Adriatic Sea. Pomor. Zb. 2016, 52, 33–47. [Google Scholar] [CrossRef]
- Mannarini, G.; Pinardi, N.; Coppini, G.; Oddo, P.; Iafrati, A. VISIR-I: Small vessels – least-time nautical routes using wave forecasts. Geosci. Model Dev. 2016, 9, 1597–1625. [Google Scholar] [CrossRef]
- Mannarini, G.; Subramani, D.; Lermusiaux, P.; Pinardi, N. Graph-Search and Differential Equations for Time-Optimal Vessel Route Planning in Dynamic Ocean Waves. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3581–3593. [Google Scholar] [CrossRef]
- Hagiwara, H. Weather Routing of (Sail-Assisted) Motor Vessels. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 1989. [Google Scholar]
- Klompstra, M.B.; Olsder, G.J.; van Brunschot, P.K.G.M. The isopone method in optimal control. Dyn. Control 1992, 2, 281–301. [Google Scholar] [CrossRef]
- Bitner-Gregerse, E.M.; Guedes Soares, C.; Vantorre, M. Adverse weather conditions for ship manoeuvrability. Transp. Res. Procedia 2016, 14, 1631–1640. [Google Scholar] [CrossRef]
- Vitali, N.; Prpić-Oršić, J.; Guedes Soares, C. Coupling voyage and weather data to estimate speed loss of container ships in realistic conditions. Ocean Eng. 2020, 210, 106758. [Google Scholar] [CrossRef]
- Lang, X.; Mao, W. A semi-empirical model for ship speed loss prediction at head sea and its validation by full-scale measurements. Ocean Eng. 2020, 209, 107494. [Google Scholar] [CrossRef]
- Tsujimoto, M.; Kuroda, M.; Shibata, K.; Sogihara, N.; Takagi, K. On a calculation of decrease of ship speed in actual seas. J. Jpn. Soc. Nav. Archit. Ocean Eng. 2009, 9, 79–85. [Google Scholar] [CrossRef][Green Version]
- Lolla, T.; Lermusiaux, P.F.; Ueckermann, M.P.; Haley, P.J., Jr. Time-optimal path planning in dynamic flows using level set equations: Theory and schemes. Ocean Dyn. 2014, 64, 1373–1397. [Google Scholar] [CrossRef]
- Bertsekas, D. Network Optimization: Continuous and Discrete Models; Athena Scientific: Belmont, MA, USA, 1998. [Google Scholar]
- Artegiani, A.; Paschini, E.; Russo, A.; Bregant, D.; Raicich, F.; Pinardi, N. The Adriatic Sea general circulation. Part II: Baroclinic circulation structure. J. Phys. Oceanogr. 1997, 27, 1515–1532. [Google Scholar] [CrossRef]
- Taylor, J. Introduction to Error Analysis, the Study of Uncertainties in Physical Measurements; University Science Books: New York, NY, USA, 1997. [Google Scholar]
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. | 1 nmi = 1852 m. |
| 9. | |
| 10. | hhZ = hh:00 UTC. |


| Symbol | Name | ||
|---|---|---|---|
| EEOI | Energy Efficiency Operational Indicator | actual cargo mass | |
| EEOIpax | - | number of passengers | |
| AER | Annual Efficiency Ratio | DWT | capacity (maximum cargo mass) |
| LmDIST | - | lane meter | |
| ISPI | Individual Ship Performance Indicator | L | - |
| Name | Meaning | Shape | Bulging | Recessing |
|---|---|---|---|---|
| isometre | equal distance | arcs of circle | never | with obstructions |
| isochrone [17] | equal duration | any curve | along gradients of speed | with obstructions |
| isopone [18] | equal effort | any curve | against gradients of emissions | with obstructions |
| Name | Symbol | Value | Units | |
|---|---|---|---|---|
| Hull | Length overall | LOA | 125 | m |
| Length at waterline | 114 | m | ||
| Breadth | B | 23.4 | m | |
| Draft middle | T | 5.3 | m | |
| Hull coefficient | 0.54 | - | ||
| Deadweight | DWT | 4050 | t | |
| Gross tonnage * | GT | 14,000 | t | |
| Number of passengers * | 400 | - | ||
| Lane meters * | 1250 | m | ||
| Propulsion | Main engine power | 4000 | kW | |
| Main engine rated speed | 750 | rpm | ||
| Service speed | 19 | kts | ||
| Auxiliary engine power | 3 × 600 | kW |
| Variable | Bias | RMSE | Pearson’s R | |
|---|---|---|---|---|
| STW | all | −0.66% | 0.19 kts | 0.9987 |
| dCO/dt | all | +0.49% | 0.014 t/h | 0.9997 |
| STW | 70% | −1.40% | 0.22 kts | 0.9968 |
| dCO/dt | 70% | +1.16% | 0.014 t/h | 0.9644 |
| Optimization | L | T | CO | AER | EEOIpax | LmDIST |
|---|---|---|---|---|---|---|
| Length | 226.1 nmi 1. | 22.17 hr 1. | 16.88 t 1. | 18.44 g/(nmi·t) 1. | 186.7g/(nmi·pax) 1. | 59.73 g/(nmi·m) 1. |
| Duration | 227.8 nmi 1.008 | 21.55 hr 0.972 | 16.18 t 0.959 | 17.54 g/(nmi·t) | 177.6 g/(nmi·pax) 0.951 | 56.83 g/(nmi·m) |
| Emissions | 229.8 nmi 1.016 | 21.62 hr 0.975 | 16.18 t 0.956 | 17.39 g/(nmi·t) | 176.0 g/(nmi·pax) 0.943 | 56.33 g/(nmi·m) |
| Code | Name | Country | Latitude [N] | Longitude [E] |
|---|---|---|---|---|
| HRZAD | Zadar | Croatia | 44.1238 | 15.2174 |
| ITAOI | Ancona | Italy | 43.6162 | 13.4974 |
| HRDBV | Dubrovnik | Croatia | 42.6524 | 18.0939 |
| ITBLT | Barletta | Italy | 43.6162 | 13.4974 |
| MEBAR | Bar | Montenegro | 42.0928 | 19.0798 |
| ITBRI | Bari | Italy | 41.1358 | 16.8576 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mannarini, G.; Carelli, L.; Orović, J.; Martinkus, C.P.; Coppini, G. Towards Least-CO2 Ferry Routes in the Adriatic Sea. J. Mar. Sci. Eng. 2021, 9, 115. https://doi.org/10.3390/jmse9020115
Mannarini G, Carelli L, Orović J, Martinkus CP, Coppini G. Towards Least-CO2 Ferry Routes in the Adriatic Sea. Journal of Marine Science and Engineering. 2021; 9(2):115. https://doi.org/10.3390/jmse9020115
Chicago/Turabian StyleMannarini, Gianandrea, Lorenzo Carelli, Josip Orović, Charlotte P. Martinkus, and Giovanni Coppini. 2021. "Towards Least-CO2 Ferry Routes in the Adriatic Sea" Journal of Marine Science and Engineering 9, no. 2: 115. https://doi.org/10.3390/jmse9020115
APA StyleMannarini, G., Carelli, L., Orović, J., Martinkus, C. P., & Coppini, G. (2021). Towards Least-CO2 Ferry Routes in the Adriatic Sea. Journal of Marine Science and Engineering, 9(2), 115. https://doi.org/10.3390/jmse9020115