VIScous Vorticity Equation (VISVE) for Turbulent 2-D Flows with Variable Density and Viscosity

Abstract

The general vorticity equation for turbulent compressible 2-D flows with variable viscosity is derived, based on the Reynolds-Averaged Navier-Stokes (RANS) equations, and simplified versions of it are presented in the case of turbulent or cavitating flows around 2-D hydrofoils.

1. Introduction

The vorticity equation has been utilized by several authors in the past to analyze the viscous flow around bodies. Vortex element (or particle, or blub) and vortex-in-cell methods have been used for several decades for the analysis of 2-D or 3-D flows, as described in Chorin [1], Christiansen [2], Leonard [3], Koumoutsakos et al. [4], Ould-Salihi et al. [5], Ploumhans et al. [6], Cottet and Poncet [7], and Cottet and Poncet [8]. Those methods essentially decouple the vortex dynamics (convection and stretching) from the effects of viscosity.

In recent years, the VIScous Vorticity Equation (VISVE), has been solved by using a finite volume method, without decoupling the vorticity dynamics from the effects of viscosity. This method has been applied to 2-D and 3-D hydrofoils, cylinders, as well as propeller blades as described in Tian [9], Tian and Kinnas [10], Wu et al. [11], Wu and Kinnas [12], Wu et al. [13], Wu and Kinnas [14]. The major advantage of this approach is that it requires a significantly smaller computational domain than RANS over which VISVE must be solved, as shown in Figure 1, due to the fact that the vorticity vector vanishes much closer to the body surface (in the order of 1–3 maximum body thickness), as opposed to the velocity vector which vanishes much farther (in the order of 5–10 body lengths) from the body surface. Due to the significantly smaller domain, VISVE requires a much smaller number of cells (5–50 times smaller) than RANS for the same accuracy of the predictions, and subsequently, a significantly smaller CPU time, as reported in Wu et al. [11].

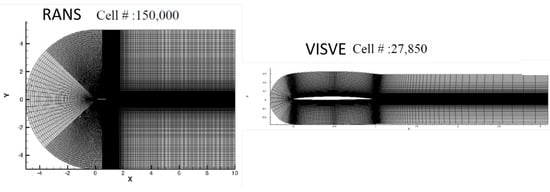
Figure 1. Typical domain and grids for flow around hydrofoil, from RANS with 150K cells (left) and from VISVE with 28K cells (right). Note the image on the right is drawn at a larger scale than that on the left.

All applications of VISVE mentioned above have addressed laminar flow of an incompressible fluid. However, in the case of incompressible turbulent flow the vorticity equation must be modified since the viscosity (molecular + turbulent) varies within the flow. In addition, in the case of cavitating flow, treated via a mixture model, both the density and the viscosity vary within the flow. In this work the general equation in terms of the mean vorticity is derived in the case of turbulent flows with variable density and viscosity, and then simplified in the case of turbulent or cavitating flows around 2-D hydrofoils.

2. Review of Reynolds-Averaged Navier-Stokes Equations

We consider flow of a fluid, where $\overrightarrow{q}=(u_1,u_2,u_3)$ is the mean velocity in a $x_1,x_2,x_3$ coordinate system. The Navier-Stokes equations are as follows:

$$\rho \frac{\partial \overrightarrow{q}}{\partial t}+\rho (\overrightarrow{q}·\overrightarrow{\nabla })\overrightarrow{q}=-\overrightarrow{\nabla }p+\overrightarrow{\nabla }·\mathbf{T}-\overrightarrow{\nabla }\Phi$$

(1)

where $\rho$ is the density of the fluid, p is the mean pressure, $\Phi$ is the potential of a conservative body force per unit volume ($\Phi =\rho gz$ in the case the body force is the gravity, with the gravity acceleration g pointing in the -z direction.), and $\mathbf{T}$ is the (symmetric) tensor of viscous stresses

$$\mathbf{T}=\left[\begin{array}{ccc}{\tau }_{11}& {\tau }_{12}& {\tau }_{13}\\ {\tau }_{21}& {\tau }_{22}& {\tau }_{23}\\ {\tau }_{31}& {\tau }_{32}& {\tau }_{33}\end{array}\right]\mathrm{and}\overrightarrow{\nabla }·\mathbf{T}=\left[\begin{array}{c}\frac{\partial {\tau }_{11}}{\partial x_1}+\frac{\partial {\tau }_{21}}{\partial x_2}+\frac{\partial {\tau }_{31}}{\partial x_3}\\ \frac{\partial {\tau }_{12}}{\partial x_1}+\frac{\partial {\tau }_{22}}{\partial x_2}+\frac{\partial {\tau }_{32}}{\partial x_3}\\ \frac{\partial {\tau }_{13}}{\partial x_1}+\frac{\partial {\tau }_{22}}{\partial x_2}+\frac{\partial {\tau }_{33}}{\partial x_3}\end{array}\right]=\left[\begin{array}{c}\frac{\partial {\tau }_{11}}{\partial x_1}+\frac{\partial {\tau }_{12}}{\partial x_2}+\frac{\partial {\tau }_{13}}{\partial x_3}\\ \frac{\partial {\tau }_{21}}{\partial x_1}+\frac{\partial {\tau }_{22}}{\partial x_2}+\frac{\partial {\tau }_{23}}{\partial x_3}\\ \frac{\partial {\tau }_{31}}{\partial x_1}+\frac{\partial {\tau }_{32}}{\partial x_2}+\frac{\partial {\tau }_{33}}{\partial x_3}\end{array}\right]$$

with

$${\tau }_{ij}=\mu \left[\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right]-{\delta }_{ij}\frac{2}{N}\left[\mu \overrightarrow{\nabla }·\overrightarrow{q}+\rho k\right]$$

(2)

where $\mu ={\mu }_m+{\mu }_t$ is the total dynamic viscosity, with ${\mu }_m$ being the molecular viscosity and ${\mu }_t$ being the turbulent viscosity of the fluid, under the Boussinesq approximation for the turbulent stresses; ${\delta }_{ij}$ is the Kronecker delta; k is the turbulent kinetic energy; $N=2$ for two-dimensional flows, and $N=3$ for three-dimensional flows. The second term in Equation (2) guarantees that ${\tau }_{ii}=-\rho \overline{u_i^{\prime }{u}_i^{\prime }}=-2\rho k$, where $u_i^{\prime }$ is the turbulent velocity in the $i^{th}$ direction.

Equation (1) can also be written as follows, as shown in the Appendix A:

$$\begin{array}{cc}\hfill \rho \frac{\partial \overrightarrow{q}}{\partial t}+\rho (\overrightarrow{q}·\overrightarrow{\nabla })\overrightarrow{q}=& -\overrightarrow{\nabla }p+2\overrightarrow{\nabla }·(\mu \overrightarrow{\nabla }\overrightarrow{q})+\overrightarrow{\nabla }\times (\mu \overrightarrow{\omega })\hfill \\ & -\frac{2}{N}\overrightarrow{\nabla }[\mu \overrightarrow{\nabla }·\overrightarrow{q}]-\frac{2}{N}\overrightarrow{\nabla }[\rho k]-\overrightarrow{\nabla }\Phi \hfill \end{array}$$

(3)

where $\overrightarrow{\omega }=({\omega }_1,{\omega }_2,{\omega }_3)=\overrightarrow{\nabla }\times \overrightarrow{q}$ is the vorticity of the flow, and the tensor $\overrightarrow{\nabla }\overrightarrow{q}$ is the gradient of $\overrightarrow{q}$, defined as follows

$$\overrightarrow{\nabla }\overrightarrow{q}=\left[\begin{array}{ccc}\frac{\partial u_1}{\partial x_1}& \frac{\partial u_2}{\partial x_1}& \frac{\partial u_3}{\partial x_1}\\ \frac{\partial u_1}{\partial x_2}& \frac{\partial u_2}{\partial x_2}& \frac{\partial u_3}{\partial x_2}\\ \frac{\partial u_1}{\partial x_3}& \frac{\partial u_2}{\partial x_3}& \frac{\partial u_3}{\partial x_3}\end{array}\right]$$

With the help of some identities of vector calculus, as shown in the Appendix A, Equation (3) becomes:

$$\begin{array}{cc}\hfill \rho \frac{\partial \overrightarrow{q}}{\partial t}+\rho (\overrightarrow{q}·\overrightarrow{\nabla })\overrightarrow{q}=& -\overrightarrow{\nabla }p+\mu {\nabla }^2\overrightarrow{q}+2(\overrightarrow{\nabla }\mu ·\overrightarrow{\nabla })\overrightarrow{q}+\mu \overrightarrow{\nabla }(\overrightarrow{\nabla }·\overrightarrow{q})+\overrightarrow{\nabla }\mu \times \overrightarrow{\omega }\hfill \\ & -\frac{2}{N}\overrightarrow{\nabla }[\mu \overrightarrow{\nabla }·\overrightarrow{q}]-\frac{2}{N}\overrightarrow{\nabla }[\rho k]-\overrightarrow{\nabla }\Phi \hfill \end{array}$$

(4)

Dividing Equation (4) by $\rho$ and rearranging will give us:

$$\begin{array}{cc}\hfill \frac{\partial \overrightarrow{q}}{\partial t}+(\overrightarrow{q}·\overrightarrow{\nabla })\overrightarrow{q}=& -\frac{\overrightarrow{\nabla }p}{\rho }+\nu {\nabla }^2\overrightarrow{q}+\nu \overrightarrow{\nabla }(\overrightarrow{\nabla }·\overrightarrow{q})+\frac{2}{\rho }(\overrightarrow{\nabla }\mu ·\overrightarrow{\nabla })\overrightarrow{q}+\frac{1}{\rho }\overrightarrow{\nabla }\mu \times \overrightarrow{\omega }\hfill \\ & -\frac{2}{N\rho }\overrightarrow{\nabla }[\mu \overrightarrow{\nabla }·\overrightarrow{q}]-\frac{2}{N\rho }\overrightarrow{\nabla }[\rho k]-\frac{\overrightarrow{\nabla }\Phi }{\rho }\hfill \end{array}$$

(5)

where $\nu =\frac{\mu }{\rho }$ is the kinematic (total) viscosity

Flow with Constant Density

In that case, since $\overrightarrow{\nabla }·\overrightarrow{q}=0$ and $\rho =constant$ (In this work we consider incompressible flow when $\rho =constant$, as opposed to the more general definition of incompressible flow when $\frac{D\rho }{Dt}=0$), Equation (5) becomes:

$$\frac{\partial \overrightarrow{q}}{\partial t}+(\overrightarrow{q}·\overrightarrow{\nabla })\overrightarrow{q}=-\frac{\overrightarrow{\nabla }p}{\rho }+\nu {\nabla }^2\overrightarrow{q}+2(\overrightarrow{\nabla }\nu ·\overrightarrow{\nabla })\overrightarrow{q}+\overrightarrow{\nabla }\nu \times \overrightarrow{\omega }-\frac{2}{N}\overrightarrow{\nabla }k-\frac{\overrightarrow{\nabla }\Phi }{\rho }$$

(6)

In the case of Newtonian fluid in laminar flow ($\mu ={\mu }_m=$ constant and $k=0$) and incompressible flow, in which case $\overrightarrow{\nabla }·\overrightarrow{q}=0$, Equation (4) reduces to its most common form:

$$\rho \frac{\partial \overrightarrow{q}}{\partial t}+\rho (\overrightarrow{q}·\overrightarrow{\nabla })\overrightarrow{q}=-\overrightarrow{\nabla }p+{\mu }_m{\nabla }^2\overrightarrow{q}-\overrightarrow{\nabla }\Phi$$

(7)

3. Vorticity Equation in 2D

We consider 2D flow, in which case $x_1=x$, $x_2=y$, $x_3=z$; $u_1=u$, $u_2=v$, $u_3=w$; $\frac{\partial }{\partial y}=0$ and $v=0$. The velocity has two components: $\overrightarrow{q}=(u,w)$, and the vorticity has only one component in the y direction ${\omega }_2=\omega =\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}$. As shown in the Appendix A the vorticity equation will become as follows:

$$\begin{array}{cc}\hfill \frac{\partial \omega }{\partial t}+\overrightarrow{\nabla }·\left(\omega \overrightarrow{q}\right)=& -\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)\times \overrightarrow{\nabla }p+\overrightarrow{\nabla }\nu \times {\nabla }^2\overrightarrow{q}+\nu {\nabla }^2\omega +\overrightarrow{\nabla }\nu \times \overrightarrow{\nabla }(\overrightarrow{\nabla }·\overrightarrow{q})\hfill \\ & -\omega {\nabla }^2\nu -\omega \overrightarrow{\nabla }·\left[\nu \frac{\overrightarrow{\nabla }\rho }{\rho }\right]+\overrightarrow{\nabla }\nu ·\overrightarrow{\nabla }\omega +\frac{\nu }{\rho }\overrightarrow{\nabla }\rho ·\overrightarrow{\nabla }\omega \hfill \\ & +2\left[\frac{\partial }{\partial z}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }u-\frac{\partial }{\partial x}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }w\right]\hfill \\ & -\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)\times \overrightarrow{\nabla }(\mu \overrightarrow{\nabla }·\overrightarrow{q})-\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)\times \overrightarrow{\nabla }\left(\rho k\right)-\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)\times \overrightarrow{\nabla }\Phi \hfill \end{array}$$

(8)

As shown in the Appendix A Equation (8) may also be written as follows:

$$\begin{array}{cc}\hfill \frac{\partial \omega }{\partial t}+\overrightarrow{\nabla }·\left(\omega \overrightarrow{q}\right)=& -\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)\times \overrightarrow{\nabla }p+{\nabla }^2\left(\nu \omega \right)-2\omega {\nabla }^2\nu \hfill \\ & +2\overrightarrow{\nabla }\nu \times \overrightarrow{\nabla }(\overrightarrow{\nabla }·\overrightarrow{q})-\omega \overrightarrow{\nabla }·\left[\nu \frac{\overrightarrow{\nabla }\rho }{\rho }\right]+\frac{\nu }{\rho }\overrightarrow{\nabla }\rho ·\overrightarrow{\nabla }\omega \hfill \\ & +2\left[\frac{\partial }{\partial z}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }u-\frac{\partial }{\partial x}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }w\right]\hfill \\ & -\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)\times \overrightarrow{\nabla }(\mu \overrightarrow{\nabla }·\overrightarrow{q})-\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)\times \overrightarrow{\nabla }\left(\rho k\right)-\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)\times \overrightarrow{\nabla }\Phi \hfill \end{array}$$

(9)

3.1. 2D Flow of Fluid with Constant Density

In that case $\rho =constant$, $\overrightarrow{\nabla }\rho =0$, $\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)=0$, and $\overrightarrow{\nabla }·\overrightarrow{q}=0$. Then Equation (9) reduces to:

$$\frac{\partial \omega }{\partial t}+\overrightarrow{\nabla }·\left(\omega \overrightarrow{q}\right)={\nabla }^2\left(\nu \omega \right)-2\omega {\nabla }^2\nu -2\frac{\partial \overrightarrow{\nabla }\nu }{\partial x}·\overrightarrow{\nabla }w+2\frac{\partial \overrightarrow{\nabla }\nu }{\partial z}·\overrightarrow{\nabla }u$$

(10)

or, by expressing $\omega =\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}$ in the second term on the RHS of Equation (10), and by making use of the continuity equation, $\frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}=0$, we get:

$$\frac{\partial \omega }{\partial t}+\overrightarrow{\nabla }·\left(\omega \overrightarrow{q}\right)={\nabla }^2\left(\nu \omega \right)+2\frac{{\partial }^2\nu }{\partial z^2}\frac{\partial w}{\partial x}-2\frac{{\partial }^2\nu }{\partial x^2}\frac{\partial u}{\partial z}+4\frac{{\partial }^2\nu }{\partial x\partial z}\frac{\partial u}{\partial x}$$

(11)

It is worth noting that Equation (10) is valid for turbulent flows (with the vorticity $\omega$ being the mean vorticity), but the turbulent kinetic energy k is not involved in the equation.

In the case of laminar flow of Newtonian fluid $\nu =\frac{{\mu }_m}{\rho }=constant$, Equation (10) becomes the vorticity equation in its most common diffusion equation form:

$$\frac{\partial \omega }{\partial t}+\overrightarrow{\nabla }·\left(\omega \overrightarrow{q}\right)=\nu {\nabla }^2\omega$$

(12)

or, since $\overrightarrow{\nabla }·\overrightarrow{q}=0$:

$$\frac{D\omega }{Dt}\equiv \frac{\partial \omega }{\partial t}+\overrightarrow{q}·\overrightarrow{\nabla }\omega =\nu {\nabla }^2\omega$$

(13)

3.2. 2D Flow around Hydrofoil

In that case we assume that the hydrofoil is placed along axis x, with the inflow also along x axis, and that $\frac{\partial }{\partial x}<<\frac{\partial }{\partial z}$, especially within the narrow region close to the hydrofoil and its wake where $\omega \ne 0$. Then, as shown in the Appendix A, Equation (9) reduces to:

$$\frac{\partial \omega }{\partial t}+\overrightarrow{\nabla }·\left(\omega \overrightarrow{q}\right)={\nabla }^2\left(\nu \omega \right)+\overrightarrow{\nabla }·\left[\nu \frac{\overrightarrow{\nabla }\rho }{\rho }\omega \right]$$

(14)

4. Conclusions and Future Work

The vorticity equation (in terms of the mean vorticity) is derived in the case of turbulent flows with variable density and viscosity, and its simplified version in the case of flows around 2-D hydrofoils has been provided. Equation (14) has already been implemented by Yao and Kinnas [15] to address the turbulent non-cavitating flow around 2-D hydrofoils and cylinders, as well as the cavitating laminar flow around 2-D hydrofoils, using the mixture model, by Xing et al. [16].

Representative results from the work of Yao and Kinnas [15] are shown in Figure 2, Figure 3 and Figure 4 together with results from RANS by using the commercial code ANSYS/Fluent (https://www.ansys.com/products/fluids/ansys-fluent). In this case Equation (14) was used where the turbulent viscosity was evaluated by synchronous coupling of VISVE with the open source RANS code OpenFOAM (https://www.openfoam.com/). As described in more detail in Yao and Kinnas [15], at every time step the velocities determined by VISVE were passed into the part of OpenFOAM which solved the k,$ϵ$ equations and then returned the turbulent kinematic viscosity back to VISVE, in order to solve Equation (14) with the updated values of the kinematic viscosity.

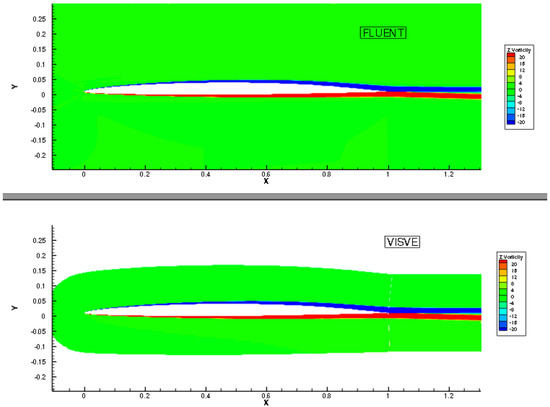
Figure 2. Vorticity contour plots from RANS (ANSYS/Fluent, top) and VISVE (bottom) for turbulent flow around hydrofoil. $Re=2\times {10}^6$.

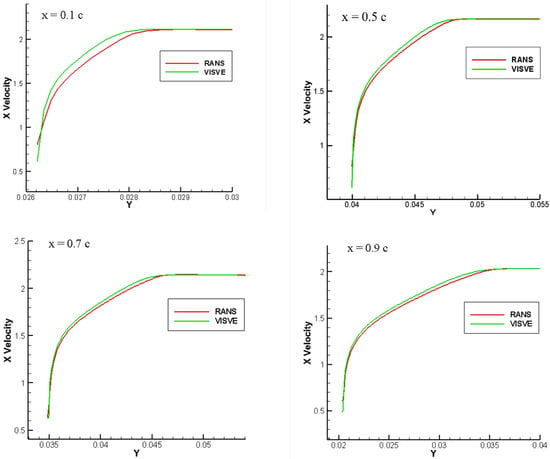
Figure 3. Velocity profiles of turbulent flow around hydrofoil, from RANS (ANSYS/Fluent) and from VISVE, at different locations along the chord, c, on the suction side. $Re=2\times {10}^6$.

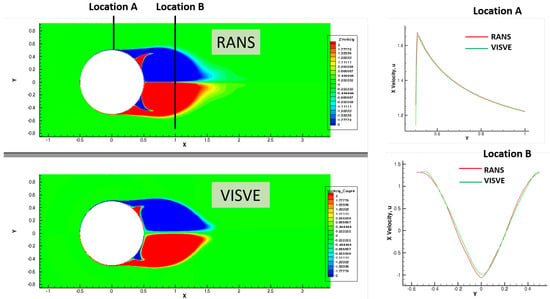
Figure 4. Vorticity contour plots and velocity profiles for turbulent flow over cylinder from RANS (ANSYS/Fluent) and from VISVE, at t = 4 s and $Re={10}^6$.

In the case of the hydrofoil the velocity profiles predicted by VISVE, shown in Figure 3, are in good agreement to those predicted by RANS. It should be noted that the hydrofoil assumption has also been used in the case of the cylinder, for which results are shown in Figure 4. The results from VISVE compare well with those from RANS, even though with somewhat larger differences downstream of the cylinder, up to the time shown in the figure, but deteriorate for later times as shown in Yao and Kinnas [15], once asymmetry appears between the top and bottom flow (not shown in this paper).

In the future, the author and his students intend to assess numerically the effect of the last three terms in the right-hand side of Equation (10), on the prediction. These terms are currently ignored, but they might affect the accuracy of predictions, especially in the case of a hydrofoil at high angles of attack where the hydrofoil assumptions, made in this paper, would not hold. The ultimate objective of this research is to extend VISVE in the case of turbulent flows around 3-D hydrofoils, and eventually propeller blades.

Appendix A.1. How to Get from Equation (1) to Equation (3)

We consider the $i^{th}$ component of Equation (1):

$$\rho \frac{\partial u_i}{\partial t}+\rho \overrightarrow{q}·\overrightarrow{\nabla }{u}_i=-\frac{\partial p}{\partial x_i}+\frac{\partial {\tau }_{ji}}{\partial x_j}-\frac{\partial \Phi }{\partial x_i}=-\frac{\partial p}{\partial x_i}+\frac{\partial {\tau }_{ij}}{\partial x_j}-\frac{\partial \Phi }{\partial x_i}$$

(A1)

with the $\frac{\partial {\tau }_{ji}}{\partial x_j}$ term meant in the Einstein notation with $j=1,2,3$

We then consider the rate of strain term of the expression for ${\tau }_{ij}$, as given by Equation (2):

$$\mu \left[\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right]=2\mu \frac{\partial u_i}{\partial x_j}+\mu \left[\frac{\partial u_j}{\partial x_i}-\frac{\partial u_i}{\partial x_j}\right]=2\mu \frac{\partial u_i}{\partial x_j}+{ϵ}_{kij}\mu {\omega }_k$$

(A2)

where ${ϵ}_{kij}$ is the Levi-Civita symbol.

Then for given i and with $j=1,2,3$, using the Einstein notation we have:

$$\begin{array}{cc}\hfill \frac{\partial }{\partial x_j}\left[\mu \left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right)\right]& =2\frac{\partial }{\partial x_j}\left(\mu \frac{\partial u_i}{\partial x_j}\right)+{ϵ}_{kij}\frac{\partial \left(\mu {\omega }_k\right)}{\partial x_j}\hfill \\ & =2\overrightarrow{\nabla }·\left(\mu \overrightarrow{\nabla }{u}_i\right)+{ϵ}_{ijk}\frac{\partial \left(\mu {\omega }_k\right)}{\partial x_j}\hfill \\ & =2\overrightarrow{\nabla }·\left(\mu \overrightarrow{\nabla }{u}_i\right)+{ϵ}_{i{j}^{\prime }{k}^{\prime }}\frac{\partial \left(\mu {\omega }_{k^{\prime }}\right)}{\partial x_{j^{\prime }}}+{ϵ}_{i{k}^{\prime }{j}^{\prime }}\frac{\partial \left(\mu {\omega }_{j^{\prime }}\right)}{\partial x_{k^{\prime }}}(i\ne k^{\prime }\ne j^{\prime }\ne i)\hfill \\ & =2\overrightarrow{\nabla }·\left(\mu \overrightarrow{\nabla }{u}_i\right)+{ϵ}_{i{j}^{\prime }{k}^{\prime }}\frac{\partial \left(\mu {\omega }_{k^{\prime }}\right)}{\partial x_{j^{\prime }}}-{ϵ}_{i{j}^{\prime }{k}^{\prime }}\frac{\partial \left(\mu {\omega }_{j^{\prime }}\right)}{\partial x_{k^{\prime }}}(i\ne k^{\prime }\ne j^{\prime }\ne i)\hfill \\ & =2\overrightarrow{\nabla }·\left(\mu \overrightarrow{\nabla }{u}_i\right)+{[\overrightarrow{\nabla }\times \left(\mu \overrightarrow{\omega }\right)]}_i\hfill \end{array}$$

(A3)

where ${[\overrightarrow{\nabla }\times \left(\mu \overrightarrow{\omega }\right)]}_i$ means the $i^{th}$ component of $\overrightarrow{\nabla }\times \left(\mu \overrightarrow{\omega }\right)$

Based on Equations (2) and (A3) we get:

$$\frac{\partial {\tau }_{ij}}{\partial x_j}=2\overrightarrow{\nabla }·\left(\mu \overrightarrow{\nabla }{u}_i\right)+{[\overrightarrow{\nabla }\times \left(\mu \overrightarrow{\omega }\right)]}_i-\frac{2}{N}\frac{\partial }{\partial x_i}\left[\mu \overrightarrow{\nabla }·\overrightarrow{q}+\rho k\right]$$

(A4)

which eventually leads to Equation (3).

Appendix A.2. How to Get from Equation (3) to Equation (4)

$$\overrightarrow{\nabla }·\left(\mu \overrightarrow{\nabla }\overrightarrow{q}\right)=\left[\begin{array}{c}\overrightarrow{\nabla }·\left(\mu \overrightarrow{\nabla }{u}_1\right)\\ \overrightarrow{\nabla }·\left(\mu \overrightarrow{\nabla }{u}_2\right)\\ \overrightarrow{\nabla }·\left(\mu \overrightarrow{\nabla }{u}_3\right)\end{array}\right]$$

(A5)

Using vector identities we get:

$$\overrightarrow{\nabla }·\left(\mu \overrightarrow{\nabla }{u}_i\right)=\overrightarrow{\nabla }\mu ·\overrightarrow{\nabla }{u}_i+\mu {\nabla }^2{u}_i$$

(A6)

or

$$\overrightarrow{\nabla }·\left(\mu \overrightarrow{\nabla }\overrightarrow{q}\right)=(\overrightarrow{\nabla }\mu ·\overrightarrow{\nabla })\overrightarrow{q}+\mu {\nabla }^2\overrightarrow{q}$$

(A7)

Then

$$\overrightarrow{\nabla }\times \left(\mu \overrightarrow{\omega }\right)=\mu \overrightarrow{\nabla }\times \overrightarrow{\omega }+\overrightarrow{\nabla }\mu \times \overrightarrow{\omega }$$

(A8)

$$\overrightarrow{\nabla }\times \overrightarrow{\omega }=\overrightarrow{\nabla }\times (\overrightarrow{\nabla }\times \overrightarrow{q})=\overrightarrow{\nabla }(\overrightarrow{\nabla }·\overrightarrow{q})-{\nabla }^2\overrightarrow{q}$$

(A9)

Using the equations above we get to Equation (4).

Appendix A.3. How to Get from Equation (5) to Equation (8)

We consider 2D flow, in which case $x_1=x$, $x_2=y$, $x_3=z$; $u_1=u$, $u_2=v$, $u_3=w$; $\frac{\partial }{\partial y}=0$ and $v=0$. The velocity has two components: $\overrightarrow{q}=(u,w)$, and the vorticity has only one component in the y direction ${\omega }_2=\omega =\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}$.

First:

$$\overrightarrow{\nabla }\times \left(\frac{\partial \overrightarrow{q}}{\partial t}\right)=\frac{\partial (\overrightarrow{\nabla }\times \overrightarrow{q})}{\partial t}=\frac{\partial \overrightarrow{\omega }}{\partial t}$$

(A10)

Then by using the identity:

$$(\overrightarrow{q}·\overrightarrow{\nabla })\overrightarrow{q}=(\overrightarrow{\nabla }\times \overrightarrow{q})\times \overrightarrow{q}+\overrightarrow{\nabla }\left(\frac{q^2}{2}\right)=\overrightarrow{\omega }\times \overrightarrow{q}+\overrightarrow{\nabla }\left(\frac{q^2}{2}\right)$$

(A11)

we get

$$\overrightarrow{\nabla }\times \left[(\overrightarrow{q}·\overrightarrow{\nabla })\overrightarrow{q}\right]=\overrightarrow{\nabla }\times (\overrightarrow{\omega }\times \overrightarrow{q})$$

(A12)

due to the identity:$\overrightarrow{\nabla }\times \overrightarrow{\nabla }f=0$

Then using the following identities:

$$\overrightarrow{\nabla }\times (\overrightarrow{\omega }\times \overrightarrow{q})=(\overrightarrow{q}·\overrightarrow{\nabla })\overrightarrow{\omega }-(\overrightarrow{\omega }·\overrightarrow{\nabla })\overrightarrow{q}+\overrightarrow{\omega }(\overrightarrow{\nabla }·\overrightarrow{q})-\overrightarrow{q}(\overrightarrow{\nabla }·\overrightarrow{\omega })$$

(A13)

$$\overrightarrow{\nabla }·\overrightarrow{\omega }=\overrightarrow{\nabla }·(\overrightarrow{\nabla }\times \overrightarrow{q})=0$$

(A14)

We get:

$$\overrightarrow{\nabla }\times \left[\mathrm{LHS}\mathrm{of}\mathrm{equation}\left(5\right)\right]=\frac{\partial \overrightarrow{\omega }}{\partial t}+(\overrightarrow{q}·\overrightarrow{\nabla })\overrightarrow{\omega }-(\overrightarrow{\omega }·\overrightarrow{\nabla })\overrightarrow{q}+\overrightarrow{\omega }(\overrightarrow{\nabla }·\overrightarrow{q})$$

(A15)

Now, in 2-D, since the vortex stretching term $(\overrightarrow{\omega }·\overrightarrow{\nabla })\overrightarrow{q}=0$, the above equation becomes:

$$\overrightarrow{\nabla }\times {\left[\mathrm{LHS}\mathrm{of}\mathrm{equation}\left(5\right)\right]}_{2D}=\frac{\partial \omega }{\partial t}+(\overrightarrow{q}·\overrightarrow{\nabla })\omega +\omega (\overrightarrow{\nabla }·\overrightarrow{q})=\frac{\partial \omega }{\partial t}+\overrightarrow{\nabla }·\left(\omega \overrightarrow{q}\right)$$

(A16)

We now take the $\overrightarrow{\nabla }\times$ of each term on the RHS of Equation (5):

• The $\overrightarrow{\nabla }\times$ of the 1st term on the RHS of (5):

  $$\overrightarrow{\nabla }\times \left(\frac{\overrightarrow{\nabla }p}{\rho }\right)=\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)\times \overrightarrow{\nabla }p+\left(\frac{1}{\rho }\right)\overrightarrow{\nabla }\times \overrightarrow{\nabla }p=\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)\times \overrightarrow{\nabla }p$$

  (A17)
  The $\overrightarrow{\nabla }\times$ of the last 3 terms of Equation (5) are treated in a similar manner as that of the first term, and the corresponding resulting terms are the last 3 terms of Equation (8). Please note the first and the last 3 terms in Equation (8) vanish in the case $\rho =constant$.
• The $\overrightarrow{\nabla }\times$ of the 2nd term on the RHS of (5):

  $$\overrightarrow{\nabla }\times \left(\nu {\nabla }^2\overrightarrow{q}\right)=\overrightarrow{\nabla }\nu \times {\nabla }^2\overrightarrow{q}+\nu {\nabla }^2(\overrightarrow{\nabla }\times \overrightarrow{q})=\overrightarrow{\nabla }\nu \times {\nabla }^2\overrightarrow{q}+\nu {\nabla }^2\omega$$

  (A18)
• The $\overrightarrow{\nabla }\times$ of the 3rd term on the RHS of (5):

  $$\overrightarrow{\nabla }\times \left[\nu \overrightarrow{\nabla }(\overrightarrow{\nabla }·\overrightarrow{q})\right]=\overrightarrow{\nabla }\nu \times \overrightarrow{\nabla }(\overrightarrow{\nabla }·\overrightarrow{q})+\nu \overrightarrow{\nabla }\times \left[\overrightarrow{\nabla }(\overrightarrow{\nabla }·\overrightarrow{q})\right]=\overrightarrow{\nabla }\nu \times \overrightarrow{\nabla }(\overrightarrow{\nabla }·\overrightarrow{q})$$

  (A19)
• The $\overrightarrow{\nabla }\times$ of the 4th term (divided by 2) on the RHS of (5):
  We only handle this term in 2D. In that case:

  $$\begin{array}{c}\hfill {\left\{\overrightarrow{\nabla }\times \left[\left(\frac{\overrightarrow{\nabla }\mu }{\rho }·\overrightarrow{\nabla }\right)\overrightarrow{q}\right]\right\}}_{2D}=\frac{\partial }{\partial z}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }·\overrightarrow{\nabla }u\right)-\frac{\partial }{\partial x}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }·\overrightarrow{\nabla }w\right)=\end{array}$$

  (A20)

  $$\begin{array}{c}\hfill =\frac{\partial }{\partial z}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }u+\frac{\overrightarrow{\nabla }\mu }{\rho }·\frac{\partial \overrightarrow{\nabla }u}{\partial z}-\frac{\partial }{\partial x}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }w-\frac{\overrightarrow{\nabla }\mu }{\rho }·\frac{\partial \overrightarrow{\nabla }w}{\partial x}=\end{array}$$

  (A21)

  $$\begin{array}{c}\hfill =\frac{\partial }{\partial z}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }u-\frac{\partial }{\partial x}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }w+\frac{\overrightarrow{\nabla }\mu }{\rho }·\overrightarrow{\nabla }\left(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}\right)=\end{array}$$

  (A22)

  $$\begin{array}{c}\hfill =\frac{\partial }{\partial z}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }u-\frac{\partial }{\partial x}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }w+\frac{\overrightarrow{\nabla }\mu }{\rho }·\overrightarrow{\nabla }\omega \end{array}$$

  (A23)
• The $\overrightarrow{\nabla }\times$ of the 5th term on the RHS of (5):

  $$\overrightarrow{\nabla }\times \left(\frac{1}{\rho }\overrightarrow{\nabla }\mu \times \overrightarrow{\omega }\right)=\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)\times (\overrightarrow{\nabla }\mu \times \overrightarrow{\omega })+\frac{1}{\rho }\overrightarrow{\nabla }\times (\overrightarrow{\nabla }\mu \times \overrightarrow{\omega })$$

  (A24)

  then

  $$\overrightarrow{\nabla }\times (\overrightarrow{\nabla }\mu \times \overrightarrow{\omega })=(\overrightarrow{\omega }·\overrightarrow{\nabla })\overrightarrow{\nabla }\mu -(\overrightarrow{\nabla }\mu ·\overrightarrow{\nabla })\overrightarrow{\omega }+\overrightarrow{\nabla }\mu (\overrightarrow{\nabla }·\overrightarrow{\omega })-\overrightarrow{\omega }(\overrightarrow{\nabla }·\overrightarrow{\nabla }\mu )$$

  (A25)

  with $\overrightarrow{\nabla }·\overrightarrow{\omega }=0$, and since $\overrightarrow{\omega }·\overrightarrow{\nabla }=0$ in 2D we get:

  $${[\overrightarrow{\nabla }\times (\overrightarrow{\nabla }\mu \times \overrightarrow{\omega })]}_{2D}=-\overrightarrow{\nabla }\mu ·\overrightarrow{\nabla }\omega -\omega {\nabla }^2\mu$$

  (A26)
  In addition, in 2D:

  $${(\overrightarrow{\nabla }\mu \times \overrightarrow{\omega })}_{2D}=\left(\frac{\partial \mu }{\partial x},0,\frac{\partial \mu }{\partial z}\right)\times (0,\omega ,0)=\left(-\omega \frac{\partial \mu }{\partial z},0,\omega \frac{\partial \mu }{\partial x}\right)$$

  (A27)

  and

  $$\begin{array}{c}\hfill {\left[\overrightarrow{\nabla }\left(\frac{1}{\rho }\right)\times (\overrightarrow{\nabla }\mu \times \overrightarrow{\omega })\right]}_{2D}=\left(\frac{\partial (1/\rho )}{\partial x},0,\frac{\partial (1/\rho )}{\partial z}\right)\times \left(-\omega \frac{\partial \mu }{\partial z},0,\omega \frac{\partial \mu }{\partial x}\right)=\end{array}$$

  (A28)

  $$\begin{array}{c}\hfill =-\omega \left[\frac{\partial (1/\rho )}{\partial x}\frac{\partial \mu }{\partial x}+\frac{\partial (1/\rho )}{\partial z}\frac{\partial \mu }{\partial z}\right]=-\omega \overrightarrow{\nabla }\left(\frac{1}{\rho }\right)·\overrightarrow{\nabla }\mu \end{array}$$

  (A29)
  Finally

  $$\begin{array}{ccc}\hfill {\left[\overrightarrow{\nabla }\times \left(\frac{1}{\rho }\overrightarrow{\nabla }\mu \times \overrightarrow{\omega }\right)\right]}_{2D}& =& -\omega \overrightarrow{\nabla }\left(\frac{1}{\rho }\right)·\overrightarrow{\nabla }\mu -\frac{\overrightarrow{\nabla }\mu ·\overrightarrow{\nabla }\omega }{\rho }-\frac{\omega {\nabla }^2\mu }{\rho }=\hfill \end{array}$$

  (A30)

  $$\begin{array}{cc}=& -\omega \overrightarrow{\nabla }\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)-\frac{\overrightarrow{\nabla }\mu ·\overrightarrow{\nabla }\omega }{\rho }\hfill \end{array}$$

  (A31)

The combination of the $\overrightarrow{\nabla }\times$ of the 4th and the 5th terms will give us:

$$\begin{array}{c}\hfill 2\frac{\partial }{\partial z}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }u-2\frac{\partial }{\partial x}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }w+\frac{\overrightarrow{\nabla }\mu ·\overrightarrow{\nabla }\omega }{\rho }-\omega \overrightarrow{\nabla }\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)\end{array}$$

(A32)

The last two terms above can also be rewritten by using $\mu =\nu \rho$ and $\overrightarrow{\nabla }\left(\nu \rho \right)=\nu \overrightarrow{\nabla }\rho +\rho \overrightarrow{\nabla }\nu$, which renders the RHS of Equation (8)

Appendix A.4. How to Get from Equation (8) to Equation (9)

In 2D $v=0$ and $\frac{\partial }{\partial y}=0$, and $\omega =\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}$

$$\begin{array}{cc}\hfill {[\overrightarrow{\nabla }\nu ·\overrightarrow{\nabla }\omega ]}_{2D}=& \frac{\partial \nu }{\partial x}\frac{\partial \omega }{\partial x}+\frac{\partial \nu }{\partial z}\frac{\partial \omega }{\partial z}=\frac{\partial \nu }{\partial x}\frac{\partial }{\partial x}\left(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}\right)+\frac{\partial \nu }{\partial z}\frac{\partial }{\partial z}\left(\frac{\partial u}{\partial z}-\frac{\partial w}{\partial x}\right)=\hfill \\ & \frac{\partial \nu }{\partial x}\frac{{\partial }^{2}u}{\partial x\partial z}-\frac{\partial \nu }{\partial x}\frac{{\partial }^{2}w}{\partial x^2}+\frac{\partial \nu }{\partial z}\frac{{\partial }^{2}u}{\partial z^2}-\frac{\partial \nu }{\partial z}\frac{{\partial }^{2}w}{\partial x\partial z}=\hfill \\ & \frac{\partial \nu }{\partial x}\frac{\partial }{\partial z}\left(-\frac{\partial w}{\partial z}+\overrightarrow{\nabla }·\overrightarrow{q}\right)-\frac{\partial \nu }{\partial x}\frac{{\partial }^{2}w}{\partial x^2}+\frac{\partial \nu }{\partial z}\frac{{\partial }^{2}u}{\partial z^2}-\frac{\partial \nu }{\partial z}\frac{\partial }{\partial z}\left(-\frac{\partial u}{\partial x}+\overrightarrow{\nabla }·\overrightarrow{q}\right)=\hfill \\ & -\frac{\partial \nu }{\partial x}{\nabla }^{2}w+\frac{\partial \nu }{\partial z}{\nabla }^{2}u+\frac{\partial \nu }{\partial x}\frac{\partial (\overrightarrow{\nabla }·\overrightarrow{q})}{\partial z}-\frac{\partial \nu }{\partial z}\frac{\partial (\overrightarrow{\nabla }·\overrightarrow{q})}{\partial x}=\hfill \\ & {\left[\overrightarrow{\nabla }\nu \times {\nabla }^2\overrightarrow{q}\right]}_{2D}-{[\overrightarrow{\nabla }\nu \times \overrightarrow{\nabla }(\overrightarrow{\nabla }·\overrightarrow{q})]}_{2D}\hfill \end{array}$$

(A33)

or

$${\left[\overrightarrow{\nabla }\nu \times {\nabla }^2\overrightarrow{q}\right]}_{2D}={[\overrightarrow{\nabla }\nu ·\overrightarrow{\nabla }\omega ]}_{2D}+{[\overrightarrow{\nabla }\nu \times \overrightarrow{\nabla }(\overrightarrow{\nabla }·\overrightarrow{q})]}_{2D}$$

(A34)

where we have made use of $\frac{\partial u}{\partial x}+\frac{\partial w}{\partial z}=\overrightarrow{\nabla }·\overrightarrow{q}$

We finally get to Equation (9) by considering the identity:

$${\nabla }^2\left(\nu \omega \right)=\nu {\nabla }^2\omega +\omega {\nabla }^2\nu +2\overrightarrow{\nabla }\nu ·\overrightarrow{\nabla }\omega$$

(A35)

Appendix A.5. How to Get from Equation (9) to Equation (14)

In that case we assume that the hydrofoil is placed along axis x, with the inflow also along x axis, and that $\frac{\partial }{\partial x}<<\frac{\partial }{\partial z}$, especially within the narrow region close to the hydrofoil and its wake where $\omega \ne 0$.

Then, since we ignore $\frac{\partial }{\partial x}$ then all $\overrightarrow{\nabla }F$ point in the z direction and thus $\overrightarrow{\nabla }F\times \overrightarrow{\nabla }G\approx 0$. In addition the following approximations can be made:

$$\begin{array}{ccc}\hfill -2\omega {\nabla }^2\nu & \approx & -2\omega \frac{{\partial }^2\nu }{\partial z^2}\hfill \end{array}$$

(A36)

$$\begin{array}{ccc}\hfill -\omega \overrightarrow{\nabla }\left(\nu \frac{\partial \overrightarrow{\nabla }\rho }{\rho }\right)& \approx & -\omega \frac{\partial }{\partial z}\left(\frac{\nu }{\rho }\frac{\partial \rho }{\partial z}\right)\hfill \end{array}$$

(A37)

$$\begin{array}{ccc}\hfill \frac{\nu }{\rho }\overrightarrow{\nabla }\rho ·\overrightarrow{\nabla }\omega & \approx & \frac{\nu }{\rho }\frac{\partial \rho }{\partial z}\frac{\partial \omega }{\partial z}\hfill \end{array}$$

(A38)

$$\begin{array}{ccc}\hfill 2\frac{\partial }{\partial z}\left(\frac{\overrightarrow{\nabla }\mu }{\rho }\right)·\overrightarrow{\nabla }u& \approx & 2\frac{\partial }{\partial z}\left(\frac{1}{\rho }\frac{\partial \mu }{\partial z}\right)\frac{\partial u}{\partial z}\approx 2\frac{\partial }{\partial z}\left(\frac{1}{\rho }\frac{\partial \mu }{\partial z}\right)\omega =\hfill \end{array}$$

(A39)

$$\begin{array}{c}2\frac{\partial }{\partial z}\left(\frac{\partial \nu }{\partial z}+\frac{\nu }{\rho }\frac{\partial \rho }{\partial z}\right)\omega =2\omega \frac{{\partial }^2\nu }{\partial z^2}+2\omega \frac{\partial }{\partial z}\left(\frac{\nu }{\rho }\frac{\partial \rho }{\partial z}\right)\hfill \end{array}$$

(A40)

By adding the approximate expressions for all the terms shown above we get

$$\frac{\nu }{\rho }\frac{\partial \rho }{\partial z}\frac{\partial \omega }{\partial z}+\omega \frac{\partial }{\partial z}\left(\frac{\nu }{\rho }\frac{\partial \rho }{\partial z}\right)=\frac{\partial }{\partial z}\left(\omega \frac{\nu }{\rho }\frac{\partial \rho }{\partial z}\right)$$

(A41)

Finally we get to Equation (14) by making the following approximation:

$$\frac{\partial }{\partial z}\left(\omega \frac{\nu }{\rho }\frac{\partial \rho }{\partial z}\right)\approx \overrightarrow{\nabla }·\left[\nu \frac{\overrightarrow{\nabla }\rho }{\rho }\omega \right]$$

(A42)