A Submersible Power Station: Part B Propulsion Systems

Abstract

Nuclear power continues to be a great promise in the green revolution, as it is a cost-effective, low-emission, and safer alternative to fossil fuels that is capable of continuous operation. A preliminary design evaluation is presented for a submersible nuclear power station capable of operating under its own power during emergencies and routine maintenance. Because it is stationed at sea, it offers a resilient solution to natural disasters such as earthquakes and tsunamis, giving it the capability to disengage and sail to deeper waters in less than a half of an hour. In the present evaluation, the hull dimensions of a very large existing submarine and the turbomachinery layout of a Pebble Bed Modular Reactor cycle were used as baselines. The conceptual design of the submersible nuclear power station includes reactor and turbomachinery integration, preliminary sizing (4 pressure hull design; total length of 57.74 m), and propulsion system analysis, demonstrating the technical viability of the proposed submersible power station.

1. Introduction

1.1. Nuclear Power

The increase in electricity demand has encouraged efficiency improvements in generation and transmission, increasing power plant cycle optimization and reducing distances between generation facilities and customers. This proximity to populated areas highlights the suitability of nuclear power for electricity generation. The contamination produced by these plants is restricted to the construction phase, keeping pollution levels at zero during operation due to the absence of a combustion process. The low carbon footprint and minimal fatality rate combined with high availability (continuous energy output 24 h a day) position this type of energy source as the most suitable candidate to replace fossil fuel-based power generation [1].

Moreover, most countries today are prioritizing transportation systems based on electric vehicles. A representative case is the UK, where electric vehicle utilization will expand rapidly, as government policies restricting internal combustion engine vehicles are said to be applied in 2030 [2]. Consequently, nuclear power emerges as a strategically suitable option for electrical power generation.

1.2. Research Scope—Objectives

The present study first addresses advanced thermodynamic cycle configurations, followed by the preliminary selection and assessment of the mechanical systems of a submersible nuclear power plant, including the integration of all components within the vessel to demonstrate its feasibility. The reactor type was selected based on previously implemented reactors in similar vessels. This implies a compact and modular design able to deliver power output comparable to a land-based power plant but with space restrictions. Once a feasible reactor type, total plant power output, and number of reactors were selected, different thermodynamic cycle configurations were analyzed. Plant thermal efficiency and overall power output were calculated and compared between different configurations [3]. To determine the dimensions of the submersible vessel, reactor size and helium working turbomachinery sizes were calculated. Auxiliary vessel systems, including the Reactor Shutdown System, RHR system, and vessel propulsion system, were designed.

In the past decades, Pebble Bed Modular Reactor (PBMR) cycles have been implemented for ship propulsion and power generation. As a result of technological progress in helium turbomachinery, intercooled–regenerated Brayton cycles have been developed and operated. This study was based on a previous [3] comparison of the performance, specific power output, and thermal efficiency of intercooled–recuperated Brayton cycles with a combined-cycle gas turbine configuration. Based on the possible location of the power plant and helium cooled reactor and turbomachinery limitations, the design basis key cycle input parameters were modified to maximize the performance and reduce the volume-to-power output ratio of the selected cycle. Based on previous PBMR reactor cycle turbomachinery dimensions, a preliminary sizing of the cycle equipment was performed, allowing an approximate estimation of the submersible vessel’s dimensions. The integration of the power plant within a submarine hull was analyzed as well. Once turbomachinery and reactor dimensions were defined and the optimal component layout was designed, preliminary submarine vessel sizing and mechanical design were carried out.

This study compares traditional submarine propulsion systems involving propellers with waterjets, giving the submarine the ability to reach deep waters within the available time window between the earthquake alarm and the tsunami reaching the coast. In the event of a natural catastrophe, the submersible power plant will be disconnected from the grid with all but one reactor shutting down. The remaining reactor will provide energy to the propulsion system to enable the vessel to move to deep water. The reactor shutdown times and the RHR system were studied to provide a safe shutdown process.

2. Helium Thermodynamic Cycles

Cycle Comparison and Selection

Helium nuclear cycles have traditionally been coupled with Brayton cycles incorporating intercooling, recuperation, and reheating. In order to improve power generation performance, two thermodynamic cycles were analyzed and compared based on thermal efficiency and specific work output. The Brayton cycle, being an intercooled, recuperated, and reheated Brayton cycle (working fluid: helium), was compared to a combined cycle configuration (Figure 1) [4] featuring a reheated topping Brayton cycle and a Rankine bottoming cycle with a heat recovery steam generator (working fluids: helium and steam), considering that CCGT configurations can achieve higher thermal efficiencies than most standalone Rankine or Brayton cycles.

A heat balance was performed for both cycles in order to determine their thermal efficiencies and specific work outputs [4]. Additionally, mass balance calculations were carried out for each cycle to define the mass flow rates required to achieve three total electric power outputs (150 MW(E), 200 MW(E), and 250 MW(E) per reactor). Based on the results shown in

Table 1. Comparison of power outputs.

Intercooled, Recuperated and Reheated Brayton Cycle	150 MW(E)	200 MW(E)	250 MW(E)
Helium turbine power [MW]	137.05	182.74	228.42
Helium compressors power [MW]	−137.68	−183.91	−229.41
Helium PT power [MW]	150.47	200.62	250.78
Useful power [MW]	149.84	199.45	249.79
Combined cycle (reheated Brayton)	150 MW(E)	200 MW(E)	250 MW(E)
Helium turbine power [MW]	115.94	154.58	193.22
Helium compressor power [MW]	−41.12	−54.08	−68.44
Helium PT power [MW]	74.48	99.3	124.12
Net helium power [MW]	149.3	199.8	248.9
Steam PT power [MW]	75.52	100.7	125.88
Steam pump power [MW]	−0.4	−0.4	−0.4
Net steam power [MW]	75.12	100.3	125.48
Useful power [MW]	224.42	300.1	374.38

, the combined cycle was selected to be implemented for the current study.

3. Double Pressure Hull Submarine and Power Plant

3.1. Typhoon-Class Submarine, HTR Technology, and Internal Pressure Hull Design

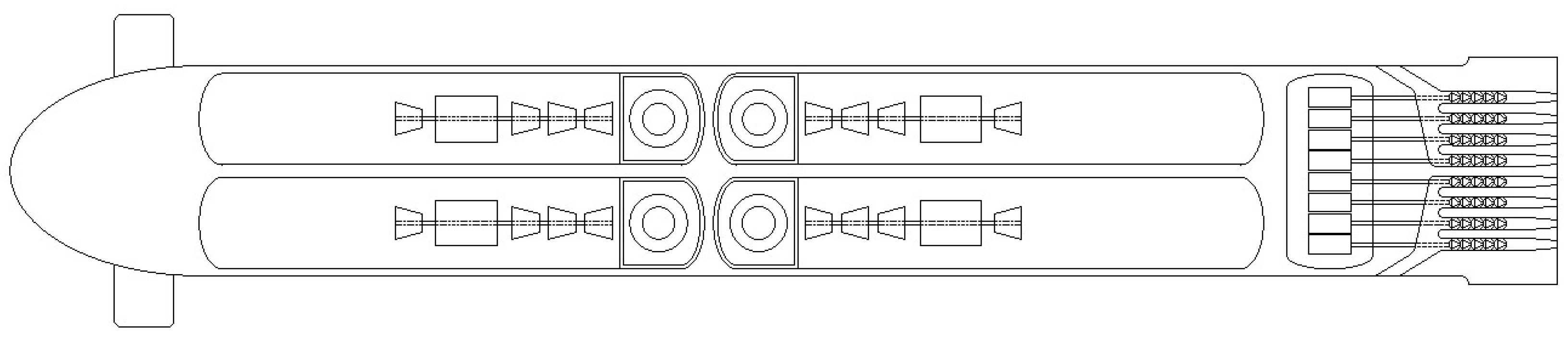
This study aims to modify the internal layout of a double pressure hull Typhoon-class submarine with a total length of 175 m, a beam of 23 m, and a draught of 12 m [5,6] and to propose a new design scenario capable of housing the machinery and propulsion systems under investigation.

The submarine featured a dual pressurized water reactor (PWR) design installed inside the two main internal hulls, delivering a combined thermal power output of 190 MW. Like most PWRs, each reactor was paired to a steam turbine generating 37.5 MW of shaft power per reactor. A total power of 75 MW was transmitted to two seven-bladed ducted propellers [7], providing a maximum cruise speed of 12 knots surfaced and 25 knots when submerged.

Pebble Bed Modular Reactors (PBMR) were proposed for the vessel due to their advantages over traditional water-cooled reactors, including lower meltdown risk, the capability of online refueling, and the ability to achieve high turbine entry temperatures (TET) [8].

The Typhoon-class internal hulls had diameters of up to 10 m for housing the reactor and turbomachinery, originally designed to accommodate two reactors. The internal hull design parameters in the present study were selected according to space availability of the submersible power plant, incorporating most features of land-based nuclear facilities in a compact design.

The design pressure was set at 1500 KPa, corresponding to an operating pressure of 1000 KPa with a safety factor of 1.5, representative of a 100 m operational depth. The design temperature was defined at 50 °C, close to the highest officially recorded temperature of 56.7 °C [9].

By removing the nuclear ballistic missiles and the torpedo silo of the Typhoon-class submarine, the internal hull could achieve an internal diameter (Di) of 10 m, an external diameter (Do) of 10.416 m, height of heads (h) of 2.604 m, and TL to TL length (TL) of 117 m.

The Typhoon’s internal hulls were made of titanium; however, to lower project costs and considering that the maximum operational depth of the submersible power plant is only one quarter that of the original vessel, SA-516 Gr. 60 carbon steel [10], a material widely used in the submarine industry, was proposed for constructing the internal hulls.

The following two internal pressure hull design scenarios were considered in the present study: the original two longitudinal pressure hull design with a constant internal diameter of 10 m, and a four pressure hull design.

3.2. Helium Turbomachinery Sizing

To evaluate the space availability for the helium turbomachinery (attached to each PBMR) at the design point, the compressor and power turbine power requirements were compared with the turbomachinery sizing study by C.F. McDonald for a 286 MW(E) GT-MHR power plant [11]. The power sizes of turbines for the CCGT are shown in Table 1.

Since the highest turbine power size in this study does not exceed 200 MW(E) and the maximum tip diameter for the 286 MW(E) turbo-compressor is under 2 m, it can be stated that the helium turbomachinery proposed could fit in a 10 m diameter internal pressure hull, providing available space for auxiliary units as well.

To obtain an approximate steam turbine diameter value for the current study, GE’s non-reheat STF-A100 steam turbine [12] was used as a reference. For an 80 MW(E) unit, an approximate exhaust area of 3.5 m² corresponds to a steam turbine diameter of around 2.2 m.

3.3. Reactor Sizing, Electrical–Thermal Power Outputs, and Shielding

The total electrical power output of the vessel relies on the maximum thermal power output that could be installed in a 10 m diameter internal pressure hull. Considering that a design employing four reactors was selected and a total electrical power output between 600 MW(E) and 1 GW(E) was investigated, three reactor electrical power outputs of 150 MW, 200 MW, and 250 MW were compared.

Installing a nuclear power plant of high-power density in a submarine requires a redesigning of the original reactor geometry into a shape that suits the internal hull cylindrical shape. This was achieved by changing the effective volume’s diameter-to-height ratio, usually approaching a value of 2:1. This process requires iteration loops until the space between the reactor and the internal hull shell is maximized. To determine the optimum geometrical ratio, three effective volume diameter-to-height ratio (h/D) configurations, 1/1, 0.8/1, and 0.6/1, were evaluated using AutoCAD 2019 software for three different thermal output values, 280 MW(TH), 375 MW(TH), and 470 MW(TH), assuming constant height-to-diameter ratios.

In a preliminary material property analysis, lead and tungsten reactor shield thickness values were obtained and compared. It was found that tungsten exhibits the most favorable properties, as it has the lowest required thickness compared to other materials [13]. However, lead’s mass attenuation coefficient is comparable with tungsten’s at a better price, and it has superior machining properties. Lead has a melting point of 600 K, presenting a 500 K margin below the reactor’s operating temperature of 1100 K. However, this difference between temperatures could be compensated for by cooling, making lead the most economical option for reactor shielding.

Based on the design considerations of the current study, a thermal output of 470 MW(TH) per reactor was selected, with an effective volume height-to-diameter ratio of 0.6:1.

3.4. Power Plant Arrangement

After the internal hull design, reactor sizing, shield thickness, and optimum geometrical ratios were calculated, they were integrated into the submersible vessel. The overall design of the vessel focused on space availability, maximum electrical power output installation, expected costs, and safety needed. Considering all these factors, the design configuration shown in Figure 2 was proposed [3].

The reactors were positioned in the center of the submarine for weight balancing and were isolated by the radiation shield. However, since helium is inert to radioactivity, the turbomachinery, piping, and auxiliary units were positioned outside the shielded area. Therefore, HTRs need less shielding material, reducing the parameter weight compared to water moderated reactors. Additionally, the four separate internal pressure hulls provide additional isolation in case of a reactor radiation leak.

An additional pressure hull at the vessel stern was required to house the propulsion system, and it was designed to comprise eight waterjets, electric motors driving the impellers, and propulsion auxiliary units.

The compressor, turbines, and generator were arranged on a single shaft towards the center length of the vessel for weight balancing. Via this arrangement, the torque being delivered to the generator can be transferred to the shaft to increase its speed and safely remove the decay heat produced after a shutdown. The generator would be located between the helium and steam turbine to enable the disengagement of the steam turbine when needed.

4. Submarine Propulsion Design

4.1. Propulsion Design Developments

Propellers offer high efficiencies at low vessel speeds with a relatively simple hydrofoil design connected to a driveshaft. However, this is not suitable for the submersible power plant being investigated, which requires maximum acceleration and high speeds. Water jets, commonly used in high-performance vessel propulsion, were considered as they offer high efficiencies at high speeds, avoiding issues such as cavitation at elevated propeller rotation rates [3].

Older submarines (in WWII) were propelled by diesel–electric engines connected by a shaft to a single propeller. Diesel engines could only operate while the vessel was surfaced. For submerged operations, batteries charged by a diesel-powered generator were used to feed an electric motor that drove the propeller. The new configuration type of submarines featured four diesel engines, each connected to individual generators [14].

After WWII, nuclear reactors (mainly PWRs) were introduced in submarines, and they were used as heat input to boil water and expand it in a steam turbine driving the propeller via a gear box. Research carried out by K. Phillips [15], where PBMR cycle optimization was analyzed for marine propulsion in the 1950s, showed better performance of high-temperature gas-cooled reactors compared to PWRs. This research showed technological improvements in the second half of the 20th century in vessels such as the Typhoon-class Russian submarine, where the propellers were ducted to guide the flow and to improve the cavitation performance of the propulsion system, while reducing the noise levels to avoid detection. The USS navy improved this design by implementing pump jets [16] into the USS Seawolf in the 1980s, reaching higher speeds and efficiencies while increasing the propeller blade number to achieve high frequencies in a ducted design, decreasing the probability of being detected.

4.2. Propellers

Several propeller designs have been investigated over the years, evolving from early designs searching for maximum efficiency to modern ones trying to reduce vibrations, minimizing noise levels and avoiding cavitation. Propeller efficiencies are mainly dependent on two factors. The firstly is the pitch angle of the blade. At a constant rotational speed, if the relative velocity between the fluid and the propeller increases, the angle of attack seen by the propeller blade will decrease, thereby reducing the propulsion efficiency. Hence, propellers designed for higher cruising speeds feature higher pitch angles to maintain the optimum angle of attack at higher vessel–fluid relative speeds.

The second factor determining propeller efficiency is the advance factor [17], which is dependent on the vessel velocity, shaft rotational speed, and impeller diameter. The envelope of maximum efficiency shows a decreasing tendency for high advance ratios, leading to cavitation problems. To avoid such problems in this scenario, supercavitating propellers have been developed, in which the entire blade section is designed to cavitate, creating a cavity that extends to the trailing edge of the blade [18].

In order to predict the flow direction in the propeller suction side, ducted propellers have been developed to guide the flow in the axial direction, forcing the flow to leave the blade parallel to the shaft axis. Moreover, ducting the propeller allows for changing the duct geometry to accommodate the flow pressure and velocity to the requirements of the propeller.

4.3. Waterjets

Waterjet propulsion units (Figure 3) were integrated into the hull, drawing water from beneath the vessel through an inlet screen and intake. Pressure was increased by an impeller and guided by stator vanes [3], which redirected the flow towards a nozzle where it was expanded and accelerated. In order to design a waterjet propulsion unit, a control volume was defined between the inlet screen and the nozzle, measuring the momentum change that the working fluid suffers throughout the system.

The impeller was driven by an engine at constant shaft rotational speed, and in contrast to propellers, the thrust was modulated by redirecting part of the flow with the aid of a reversing bucket, allowing the driving engine to operate in the best efficiency design point.

The waterjet control volume was defined between the inlet screen and the nozzle outlet, defining ${\mathbf{v}}_{\mathbf{1}}$ as the inlet flow velocity to the system and ${\mathbf{v}}_{\mathbf{2}}$ as the nozzle exit flow velocity. The reverse bucket was not considered in the study as it is primarily used for maneuvering and thrust modulation. The mass flow through the system can be determined by applying the conservation of mass principle between the inlet screen and the nozzle outlet, as follows:

$$\mathrm{ṁ}=\mathsf{\rho }·{\mathrm{A}}_1·{\mathrm{v}}_1=\mathsf{\rho }·{\mathrm{A}}_2·{\mathrm{v}}_2$$

(1)

Thrust produced by the system was defined as the rate of change in momentum suffered by the working fluid inside the control volume. For constant cruise speed, the required thrust to maintain that speed equals the drag force suffered by the vessel’s external hull. Thrust produced by the system and required thrust (equal to drag force) at certain cruise speed expressions are defined as follows:

$$\mathrm{T}=\mathrm{ṁ}·\left({\mathrm{v}}_2-{\mathrm{v}}_1\right)$$

(2)

$${\mathrm{T}}_{\mathrm{r}\mathrm{e}\mathrm{q}.}={\mathrm{F}}_{\mathrm{D}}={\displaystyle \frac{1}{2}}·{\mathrm{C}}_{\mathrm{d}}·\mathsf{\rho }·{\mathrm{A}}_{\mathrm{r}\mathrm{e}\mathrm{f}}·{{\mathrm{v}}_1}^2$$

(3)

Pump dynamic head (pressure differential between the suction and discharge side of the pump) expression was deducted from the conservation of mass principle (Bernoulli’s equation) applied to the control volume. This is shown as follows:

$${\displaystyle \frac{{\mathrm{p}}_1}{\mathsf{\rho }·\mathrm{g}}}+{\displaystyle \frac{{{\mathrm{v}}_1}^2}{2\mathrm{g}}}+{\mathrm{h}}_1+{\mathrm{H}}_{\mathrm{P}}={\displaystyle \frac{{\mathrm{p}}_2}{\mathsf{\rho }·\mathrm{g}}}+{\displaystyle \frac{{{\mathrm{v}}_2}^2}{2\mathrm{g}}}+{\mathrm{h}}_2+{\mathrm{h}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$$

(4)

Considering that the change in static pressure between the inlet and outlet of the control volume was negligible compared to the ambient pressure effect [3], pump dynamic head (${\mathrm{H}}_{\mathrm{P}}$) expression was defined as follows:

$${\mathrm{H}}_{\mathrm{P}}={\displaystyle \frac{{{\mathrm{v}}_2}^2-{{\mathrm{v}}_1}^2}{2\mathrm{g}}}+{\mathrm{h}}_2+{\mathrm{h}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$$

(5)

Pressure losses across the waterjet unit are divided into pump losses and internal losses. Internal losses account for friction and stall losses taking place in the inlet screen, intake duct, and convergent nozzle. In waterjet design procedures, when selecting the pump impeller from a manufacturer, pump losses are included in the dynamic head values provided in the impeller performance map. Therefore, these losses were not included in the h_loss term used to calculate the required pump head. Once these parameters are selected, pump type choice depends on the flowrate and dynamic pump head required to achieve certain thrust value. It is defined by the pump specific speed, as follows:

$${\mathrm{n}}_{\mathrm{s}}=\mathrm{n}·{\displaystyle \frac{\sqrt{\mathrm{Q}}}{\sqrt[4]{{\mathrm{H}}^3}}}$$

(6)

Depending on the pump specific speed value obtained, axial-flow, mixed-flow or centrifugal impellers can be selected. Centrifugal impellers deflect the flow 90° between the inlet and outlet of the impeller, while axial-flow impellers do not deflect the flow at all. Mixed-flow impellers accommodate deflection angles from 0° to 90°. However, jet efficiency can be expressed as a function of the velocity ratio of the working fluid between the inlet and outlet of the control volume, as well as an intake loss coefficient ζ_in. According to Faltinsen [19], the maximum efficiency occurs at a velocity ratio of 1.3 for highly optimized waterjet intakes. With the objective of preventing jet efficiency dropping drastically due to velocity ratio reduction, it is common practice to select a velocity ratio value above the maximum jet efficiency to ensure a wider operation range at relatively high jet efficiencies.

In order to calculate the shaft power required to drive a designed propulsion system, the power transferred to the working fluid as a function of the mass flow rate and the dynamic pump head must be defined, as follows:

$${\mathrm{P}}_{\mathrm{P}}=\mathrm{ṁ}·\mathrm{g}·{\mathrm{H}}_{\mathrm{P}}=\mathrm{ṁ}·\left[{\displaystyle \frac{{{\mathrm{v}}_2}^2-{{\mathrm{v}}_1}^2}{2}}+\mathrm{g}·({\mathrm{h}}_2+{\mathrm{h}}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}})\right]$$

(7)

The shaft power required is defined as the ratio between the power transferred to the fluid and the pump efficiency, as follows:

$${\mathrm{P}}_{\mathrm{M}}={\displaystyle \frac{{\mathrm{P}}_{\mathrm{P}}}{{\mathrm{ⴄ}}_{\mathrm{P}}}}$$

(8)

Waterjets compared to propellers offer better performance at higher vessel speeds, avoiding problems of cavitation and providing better maneuverability by installing a steering nozzle section. Rotating machinery is integrated into the hull and protected from impacts, and it also keeps impeller noise levels low.

4.4. Waterjet Design Initial Steps

Achieving high vessel speeds requires large amounts of shaft power to be delivered to propellers or impellers and a custom efficient design to transfer the maximum amount of power to the working fluid. Therefore, waterjet systems would be considered for the submersible power plant propulsion due to their potential. As shown in Figure 4, the waterjet design feasibility and performance analysis would rely on determining the maximum vessel speed achievable with a custom waterjet design and calculating the required shaft power. Defining the maximum vessel speed for a propulsion design requires assuming certain vessel specifications in order to calculate the thrust needed to overcome the drag force.

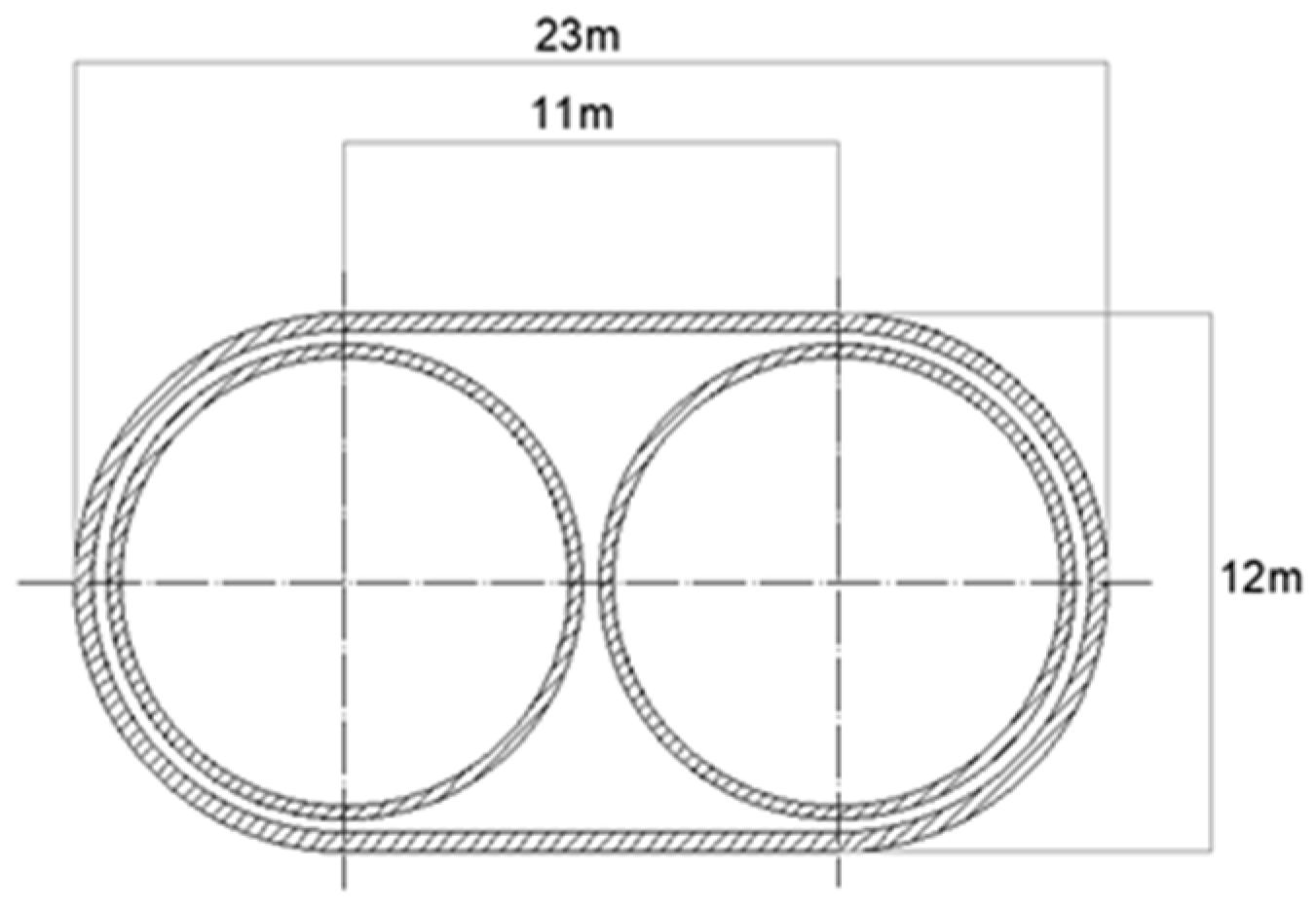
Without having the submersible power plant dimensions defined yet, Typhoon-class submarine external vessel dimensions were taken as reference. The area of reference A_ref was defined as the cross-sectional area of the vessel with the maximum value. The cross-section dimensions shown in Figure 5 were determined to contain a double internal pressure hull design and leave some space for the ballast tanks.

$${\mathrm{A}}_{\mathrm{r}\mathrm{e}\mathrm{f}}=\mathsf{\pi }·{\mathrm{r}}^2+\mathrm{w}·\mathrm{d}=\mathsf{\pi }·6^2+11·12=245.1 {\mathrm{m}}^2$$

(9)

The vessel density ρvessel was considered constant and equal to the saltwater density ρsaltwater (1027 kg/m³), assuming that the cruise conditions happen at a constant depth.

Vessel external hull drag coefficient varies with the geometry of the body analyzed, and it does not depend on the body size. Taking into consideration that the external hull design of the vessel was out of the scope of this study, the elemental figure drag coefficient was considered to assume a drag coefficient value [20].

A streamlined body is the geometric figure that best represents the submarine’s external hull geometry. By calculating the Reynolds number for the dimensions (characteristic length was considered the submarine’s total length), considering cruise conditions ${(\mathrm{v}}_{\mathrm{v}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{e}\mathrm{l} \mathrm{m}\mathrm{a}\mathrm{x}.}=17.75 \mathrm{m}/\mathrm{s}),$ and checking that it exceeded the 10⁵ values, a drag coefficient of 0.04 was assumed.

$$\mathrm{R}\mathrm{e}={\displaystyle \frac{\mathsf{\rho }·\mathrm{L}·\mathrm{v}}{\mathsf{\mu }}}={\displaystyle \frac{1027 \mathrm{k}\mathrm{g}/{\mathrm{m}}^3·175 \mathrm{m}·17.75 \mathrm{m}/\mathrm{s}}{8.9·{10}^{-4} \mathrm{P}\mathrm{a}·\mathrm{s}}}>{10}^5$$

(10)

Waterjet system losses could be divided into intake, pump, and nozzle losses. In order to calculate the dynamic head provided by the pump to compensate for the friction and stall losses in inlet and outlet ducts, a loss coefficient [21] was selected (K_{Inlet Diffuser} = 0.13 and K_Nozzle = 0.04). Pump losses are included in the manufacturer’s pump operation map.

The waterjet inlet duct would feature a 6° divergence angle to increase the static pressure at the suction side of the pump, therefore avoiding cavitation. The nozzle convergence angle was set to 30°, obtaining a relatively low pressure loss coefficient.

4.5. Propulsion Feasibility for Fukushima Accident Case

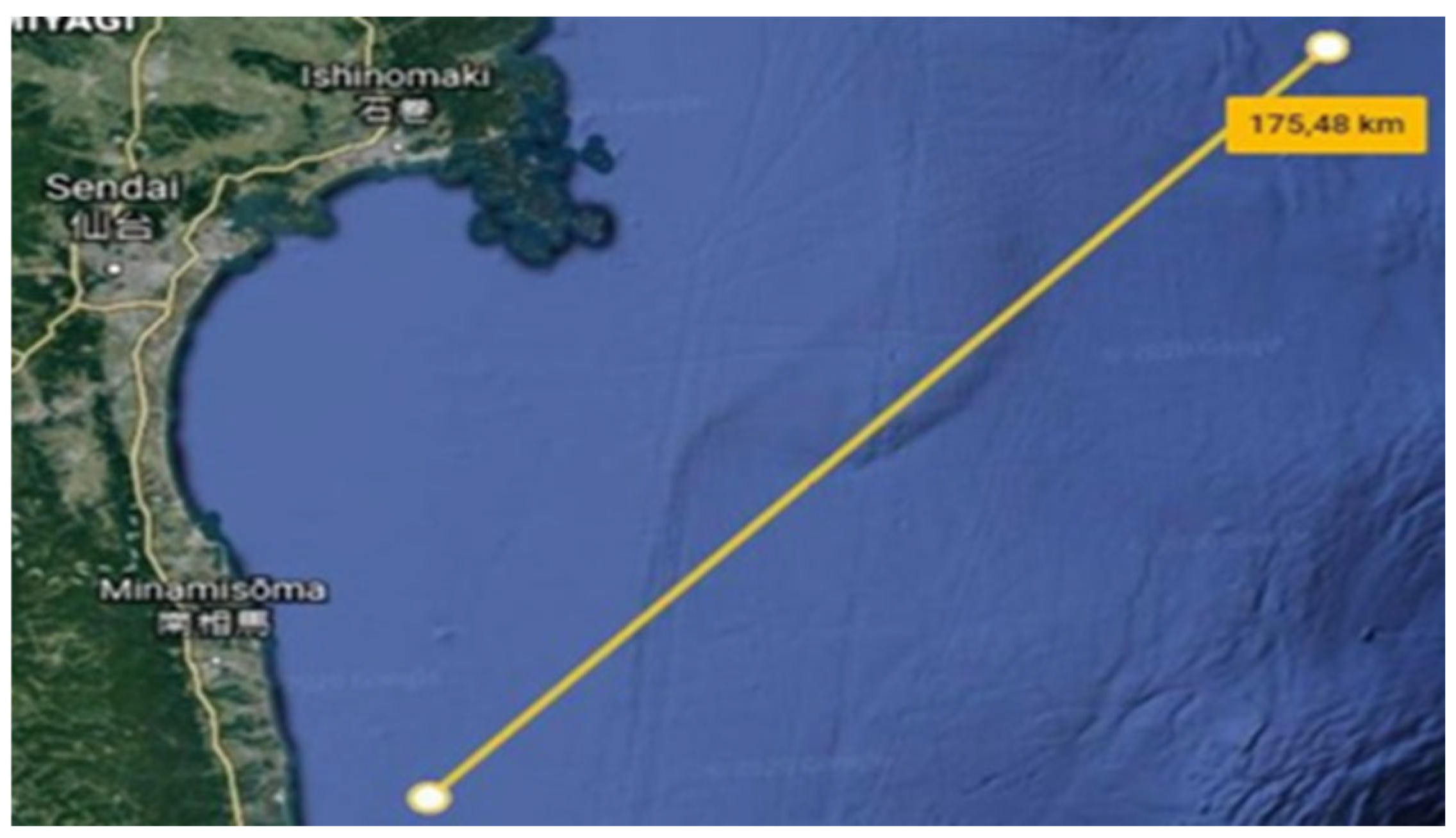
The concept of a submersible power plant was inspired by the Fukushima nuclear accident in 2011, with the objective of developing a power plant that could withstand earthquakes and tsunamis. Considering that the distance from the epicenter of the earthquake to the Fukushima Daiichi power plant was approximately 186.9 km [22], and the time between the first seismic aftershock and the tsunami hitting the power plant breakwaters was around 41.6 min, the tsunami spread speed was calculated to be 269.5 km/h. The time between the Tsunami Warning Centre (TWS) alerting the power plant and the tsunami reaching the safety emergency zone (defined as reaction time) is crucial. Hence, an emergency safety zone was selected at the minimum distance from the power plant with the required depth to ensure no damage is sustained by the submersible vessel. For the Fukushima Daiichi case, the safety minimum depth was selected at 150 m ocean bed depth (1.5 times the submersible vessel operation depth), 18 km away from the power plant. Google Earth was used to determine this distance.

Once the distance between the normal operation location and the earthquake epicenter (Figure 6) was defined (175 km), available reaction time to reach the safety zone was calculated using the tsunami spread speed.

$$\mathrm{R}\mathrm{T}={\displaystyle \frac{175 \mathrm{k}\mathrm{m}}{269.5 \mathrm{k}\mathrm{m}/\mathrm{h}}}=0.6494 \mathrm{h}\approx 39 \mathrm{m}\mathrm{i}\mathrm{n}$$

(11)

Considering a 5 min reduction in reaction time due to grid disconnection, reactor shutdown, and anchor system release, the reaction time would be set to 34 min, and hence, the vessel speed (V_{vessel min}) required to cover the safety distance of 18 km at this time interval would be 31.76 km/h.

In order to deliver the required propulsive power, it was estimated that one of the four reactors should remain in operation while the others would have to undergo a reactor shutdown process.

4.6. Propeller Propulsion Evaluation

By considering installing the propulsion system in a double pressure hull submarine similar to a Typhoon-class submarine, an extrapolation of the Typhoon-class propulsion system was carried out, considering that the submersible vessel hydraulic diameter, density, and propulsion efficiency remain constant. In order to account for these parameters, a correction factor had to be calculated for the original Typhoon-class shaft power and top speed. Hence, a reference propeller propulsion top speed was obtained for the three total plant power output configurations analyzed.

Typhoon-class submarine correction factor calculation for a shaft power of 75 MW and a top speed of 12.86 m/s (25 knots) was as follows:

$$\mathrm{P}=\mathrm{f}\left({\mathrm{v}}^3\right)⇨75·{10}^6 \mathrm{W}=\mathrm{C}\mathrm{F}·{(12.86 \mathrm{m}/\mathrm{s})}^3$$

(12)

$$\mathrm{C}\mathrm{F}=\mathrm{35,264.5}$$

Reference top speeds for the analyzed propulsive powers were obtained by using the correction factor and extrapolating the power vs vessel speed curve, as follows:

$$\mathrm{P}=\mathrm{C}\mathrm{F}·{{\mathrm{v}}_{\mathrm{v}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{e}\mathrm{l}}}^3$$

(13)

$${\mathrm{v}}_{300 \mathrm{M}\mathrm{W}}=\sqrt[3]{{\displaystyle \frac{300·{10}^6 \mathrm{W}}{\mathrm{35,264.5}}}}=20.41{\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}=73.48 \mathrm{k}\mathrm{m}/\mathrm{h}$$

(14)

Similarly, ${\mathrm{v}}_{400\mathrm{M}\mathrm{W}}$ was found to be 80.89 km/h, and ${\mathrm{v}}_{500\mathrm{M}\mathrm{W}}$ was 87.12 km/h. These reference speeds, along with the shaft power available for each case, were compared to the speeds and shaft powers required for a preliminary designed waterjet.

4.7. Waterjet Design

The present study did not account for transients; thus, the thrust value required was equal to the drag force suffered by the external hull at certain speed, as follows:

$${\mathrm{T}}_{\mathrm{r}\mathrm{e}\mathrm{q}.}={\mathrm{F}}_{\mathrm{D}}={\displaystyle \frac{1}{2}}·{\mathrm{C}}_{\mathrm{d}}·\mathsf{\rho }·{\mathrm{A}}_{\mathrm{r}\mathrm{e}\mathrm{f}}·{{\mathrm{v}}_1}^2=\mathrm{ṁ}·\left({\mathrm{v}}_2-{\mathrm{v}}_1\right)$$

(15)

In order to determine the maximum propulsion system size to be implemented to obtain the maximum vessel speed and the required propulsion shaft power, two variables were considered. Firstly, the maximum number of waterjet units was defined based on the beam value (23 m) considered for the external vessel. Secondly, the maximum number of pump stages per unit had to be established, and after the pump impeller was selected from a manufacturer, the maximum dynamic pump head was determined.

Taking into account the dimensions of the submersible vessel, large diameter pump impellers had to be selected to deal with the high mass flow values that would be required to propel the vessel. Pump selection was carried out by the “MWI pumps” manufacturer [23].

The MWI axial-flow impeller with the maximum diameter was selected [24] according to the maximum possible mass flow criterion, in order to reduce the velocity ratio between the inlet and outlet of the control volume to decrease the dynamic pump head required per waterjet unit. Impeller propulsion shafts would be operating at 190 rpm, with impellers offering an efficiency of 0.82 per unit compared to smaller impellers. Once the dynamic pump head per stage, impeller diameter, and mass flow per unit were known, the maximum number of waterjets that could be implemented was defined as follows:

$${\mathrm{N}}_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{j}\mathrm{e}\mathrm{t} \mathrm{m}\mathrm{a}\mathrm{x}.}=\mathrm{B}\mathrm{e}\mathrm{a}\mathrm{m}/\mathrm{I}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{l}\mathrm{l}\mathrm{e}\mathrm{r} \mathrm{D}={\displaystyle \frac{23 \mathrm{m}}{2.4384 \mathrm{m}}}=9.4$$

(16)

To achieve a symmetrical design and accounting for pump ducting, casing, and stern hydrofoils, eight waterjet units were defined as the max number of installable units. Pump stages per unit were defined at a max number of 5 (which admittedly complicates the system architecture).

The calculation of total mass flow and dynamic pump head per waterjet unit was carried out once the impeller had been specified, as follows:

$${\mathrm{Q}}_{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}=\mathrm{Q}/\mathrm{u}\mathrm{n}\mathrm{i}\mathrm{t}·{\mathrm{N}}_{\mathrm{u}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{s}}=15.3 {\mathrm{m}}^3/\mathrm{s}·8 \mathrm{u}\mathrm{n}\mathrm{i}\mathrm{t}\mathrm{s}=122.4 {\mathrm{m}}^3/\mathrm{s}$$

(17)

$${\mathrm{H}}_{\mathrm{P}}/\mathrm{u}\mathrm{n}\mathrm{i}\mathrm{t}={\mathrm{H}}_{\mathrm{P}}/\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}·{\mathrm{N}}_{\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{s}}=8 \mathrm{m}·5 \mathrm{s}\mathrm{t}\mathrm{a}\mathrm{g}\mathrm{e}\mathrm{s}=40 \mathrm{m}$$

(18)

Flow inlet velocity is required to obtain the nozzle outlet velocity and calculate the propulsion system thrust. Although inlet flow velocity values may vary with the overall waterjet design, it was assumed that the inlet flow velocity equals the vessel speed. For each vessel velocity value, the nozzle outlet flow velocity (${\mathrm{v}}_2$) was calculated in order to obtain the available thrust, as follows:

$${\mathrm{H}}_{\mathrm{P}}={\displaystyle \frac{{{\mathrm{v}}_2}^2{-{\mathrm{v}}_1}^2}{2 \mathrm{g}}}+{\mathrm{h}}_2+{\mathrm{h}}_{\mathrm{I}}={\displaystyle \frac{{{\mathrm{v}}_2}^2{-{\mathrm{v}}_1}^2}{2 \mathrm{g}}}+{\mathrm{h}}_2+{\mathrm{K}}_{\mathrm{I}}·{\displaystyle \frac{{\left({\mathrm{v}}_{\mathrm{s}}+\left({\mathrm{v}}_2-{\mathrm{v}}_1\right)\right)}^2}{2 \mathrm{g}}}$$

(19)

By substituting the known values in the above equation, the nozzle outlet flow velocity (${\mathrm{v}}_2$) was found to be 30.385 m/s.

Pump head losses were not included in the pump dynamic head calculations, as pump impeller would be selected directly from a manufacturer, and therefore, pump head losses are included in the provided maps.

Once the intake-to-nozzle velocity ratio was defined, available thrust (thrust produced by the system) and required thrust calculations for the selected vessel speed were carried out. If available thrust exceeds the required thrust, then the propulsion system would achieve speeds above the selected cruise velocity. Conversely, if required thrust exceeds the available thrust, then the vessel’s maximum speed for the chosen design and assumptions would fall below the target cruise velocity (as shown in the flow chart of Figure 4). The methodology employed an iterative process, and the results shown below correspond to the converged solution (maximum achievable velocity, ${({\mathrm{v}}_1=\mathrm{v}}_{\mathrm{v}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{e}\mathrm{l} \mathrm{m}\mathrm{a}\mathrm{x}.}=17.75 \mathrm{m}/\mathrm{s})$).

Based on Equations (2) and (3), the available and required thrust were obtained as follows:

$${\mathrm{T}}_{\mathrm{a}\mathrm{v}.}={\displaystyle \frac{125704.8 \mathrm{k}\mathrm{g}}{\mathrm{s}}}·\left({\displaystyle \frac{30.385 \mathrm{m}}{\mathrm{s}}}-{\displaystyle \frac{17.75 \mathrm{m}}{\mathrm{s}}}\right)=1588.35 \mathrm{k}\mathrm{N}$$

(20)

$${\mathrm{T}}_{\mathrm{r}\mathrm{e}\mathrm{q}.}={\displaystyle \frac{1}{2}}·0.04·\left(1027 {\displaystyle \frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^3}}\right)·245.1 {\mathrm{m}}^2·{\left(17.75 {\displaystyle \frac{\mathrm{m}}{\mathrm{s}}}\right)}^2=1586.14 \mathrm{k}\mathrm{N}$$

(21)

Nozzle area, diameter, and inlet screen area were defined as functions of the mass flow per waterjet unit and the inlet and outlet flow velocities as follows:

$${\mathrm{A}}_{\mathrm{I}\mathrm{n}\mathrm{l}\mathrm{e}\mathrm{t} \mathrm{S}\mathrm{c}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{n}}={\displaystyle \frac{\mathrm{Q}}{{\mathrm{v}}_1}}={\displaystyle \frac{15.3 {\mathrm{m}}^3/\mathrm{s}}{17.75 \mathrm{m}/\mathrm{s}}}=0.862 {\mathrm{m}}^2$$

(22)

$${\mathrm{A}}_{\mathrm{N}\mathrm{o}\mathrm{z}\mathrm{z}\mathrm{l}\mathrm{e}}={\displaystyle \frac{\mathrm{Q}}{{\mathrm{v}}_2}}={\displaystyle \frac{15.3 {\mathrm{m}}^3/\mathrm{s}}{30.385 \mathrm{m}/\mathrm{s}}}=0.5035 {\mathrm{m}}^2$$

(23)

$${\mathrm{D}}_{\mathrm{N}\mathrm{o}\mathrm{z}\mathrm{z}\mathrm{l}\mathrm{e}}=\sqrt{{\displaystyle \frac{4·{\mathrm{A}}_{\mathrm{N}\mathrm{o}\mathrm{z}\mathrm{z}\mathrm{l}\mathrm{e}}}{\mathsf{\pi }}}}=\sqrt{{\displaystyle \frac{4·0.5035 {\mathrm{m}}^2}{\mathsf{\pi }}}}=0.801 \mathrm{m}=80.1 \mathrm{c}\mathrm{m}$$

(24)

Once the propulsion system preliminary design was carried out, the required shaft power was determined to be 133.04 MW (

Table 2. Propulsion system specifications for design point.

Number of waterjet units	8
Pump stages per waterjet unit	5
Dynamic head per stage [m]	8
Pump efficiency per stage	0.82
Flow rate per waterjet [m3/s]	15.3
Shaft rotating speed [rpm]	190
Nozzle area [m2]	0.5035
Nozzle diameter [m]	0.801
Inlet screen area [m2]	0.862
Thrust [kN]	1588.35
Shaft power [MW]	133.04
Maximum vessel speed [m/s]	17.75

), calculated as the ratio of the power transferred to the working fluid and the pump efficiency, as per Equation (25).

$${\mathrm{P}}_{\mathrm{M}}={\displaystyle \frac{\mathrm{ṁ}·\mathrm{g}·{\mathrm{H}}_{\mathrm{P}}}{{\mathrm{ⴄ}}_{\mathrm{P}}}}={\displaystyle \frac{\mathrm{ṁ}·\left[\frac{{{\mathrm{v}}_2}^2-{{\mathrm{v}}_1}^2}{2}+\mathrm{g}·({\mathrm{h}}_2+{\mathrm{h}}_{\mathrm{I}})\right]}{{\mathrm{ⴄ}}_{\mathrm{P}}}}$$

(25)

4.8. Results Analysis

The submersible power plant would be installed in a double internal pressure hull vessel, with the Typhoon-class submarine dimensions and propulsive capabilities used as a baseline to meet the objectives of the current study. Although the study’s results did not accurately represent the propulsive performance of the Typhoon-class submarine for the power range being calculated (due to factors like high-speed cavitation problems not being considered), they were employed as reference to compare the feasibility of a custom designed waterjet propulsion system.

The propulsion results were obtained under the assumption that all the power provided by the shaft could be transferred to the working fluid, although, in practice, this is unlikely. Additionally, custom propeller design and optimization, along with cavitation analysis under design cruise conditions, should be conducted. A comparative assessment of alternative high-speed propulsion systems, such as surface-piercing propellers [25], variable-pitch propellers, electric rim thrusters, or outboard waterjet engines [26], could also be explored for performance evaluation.

5. Reactor Shutdown Process

The nuclear reactor shutdown process is critical for determining the time required to stop the reactor’s core chain reaction during an emergency and the duration of that reactor’s cooling pumps operation to avoid a core meltdown. In case of an earthquake happening near the submergible power station, the time between the earthquake alert and a possible tsunami reaching the coast (reaction time) will determine the time available for shutting down most reactors, disconnecting the power plant from the grid, releasing the submarine anchor systems, and reaching a safe distance from the coast.

In a PBMR power plant, reactor core cooling is achieved with helium, which is circulated through the system by a turbo-compressor. As the power generation turbine does produce electricity and no work extraction takes place, higher heat dissipation occurs in the pre-cooler to stabilize the reactor temperature. After the control rods are introduced to moderate the chain reaction, the shutdown process is not immediate. When a nuclear reactor has been shut down, and nuclear fission is not occurring at a large scale, the major source of heat production will be due to the delayed beta decay of the fission products. Due to this reason, at the moment of shutdown, decay heat will be about 6.5% of the previous core power if the reactor has had a long and steady power history. One hour after shutdown, the decay heat will be about 1.5% of the previous core power. After one day, the decay heat falls approximately to 0.4%, and after a week, it will be only around 0.2%. The decay heat production rate will continue to slowly decrease over time (almost 10 days) [27]. As a result, the remaining heat energy must be dissipated via the pre-cooler during the shutdown process, which can take up to 10 days.

DLOFC (depressurized loss of forced coolant) conditions in a PBMR reactor represent a lower threat compared to other water cooled reactors. Studies have shown that the core design of PBMRs allows rapid stabilization of core temperature, remaining below 1600 °C. This avoids any damage to the fuel pebbles, which are the primary contributors to reactor vessel meltdowns. These pebbles, constructed of graphite and silicon carbide, can withstand such high temperatures [28]. The safety shutdown process under DLOFC conditions was proven for the first time in the AVR German reactor after eliminating the reactor cooling flow and letting the reactor shut down passively without fuel damage. A rapid temperature increase occurred during the first few hours [28], as the ratio between the decay heat generated by the fuel and the passive cooling of the reactor pressure vessel (RPV) achieved the highest values. After 50 h from shutdown, this ratio tended to be near 1, stabilizing both the fuel and RPV temperatures. The reactor core rapid temperature stabilization is due to its high surface-area-to-volume ratios, which increase the conductive, convective, and radiative heat transfer. This allows the system to reach thermal equilibrium between the decay heat generated and the heat passively removed from the reactor.

After reactor shut down, the reactor thermal power reduces to less than 6.5% of its design value. At that moment, the electrical generator is disconnected from the grid, reducing the system’s torque resistance. During the first minutes, the power extracted from the fluid by the turbines will be delivered directly to the shaft, resulting in a transient process where turbine work exceeds compressor work, leading to positive shaft acceleration. The reduction of the reactor decay heat will continue over a period of approximately 10 days, resulting in the compressor work now exceeding the turbine work, resulting in deceleration.

Several solutions could be implemented for reactor cooling in case of insufficient mass flow rate to cool down the reactor core. External cooling systems could be implemented, such as the Reactor Cavity Cooling System (RCCS), used in the German HTR module [29]. Due to cooling water availability, RCCS implementation is considered in the current study. Seawater could be drawn into the submersible vessel into a double loop water cooling system with an intermediate heat exchanger between the saltwater and the reactor cooling freshwater loop. To optimize the space available for reactor installation, a cooling loop could be implemented using the reheat channel across the reactor. Pressure drop across the pre-cooler, valves, reactor, and piping would be compensated for by a blower (Figure 7) driven by an electric motor. In case of reactor emergency shutdown, the remaining operational reactors would supply the electrical power required to run the blowers.

PBMRs do not require redundant shutdown safety cooling systems. This was demonstrated by the German AVR PBMR, where the main circulators were intentionally stopped, forcing the reactor to shut down naturally by passive heat removal, via conduction and radiation, without core temperatures exceeding 1600 °C [29].

The disconnection of electric generators from the grid would cause a positive shaft acceleration transient that could damage the rotor. Therefore, the rotor should be designed to withstand the maximum expected torque and rotating speed. Once the operating shaft speed and the rotor’s mechanical and geometrical design were defined, the acceleration work (difference between turbine and compressor work) can be determined to calculate the turbomachinery transient behavior. The shaft positive angular acceleration following grid disconnection would increase the helium mass flow rate during the first minutes, helping to remove the decay heat generated in the reactor. After the mass flow rate falls below the mass flow provided by the blower, the four (4) three-way valves should be closed to the blower-loop position, enabling a constant helium flow through the reactor and into the pre-cooler, where the excess heat would be dissipated.

6. Conclusions

The feasibility of a submersible power plant was investigated in the present study. A thermodynamic cycle analysis was conducted, resulting in improved thermal efficiency compared to conventional cycles implemented with nuclear reactors. A CCGT configuration was selected with efficiencies above 53.5% [3]. This efficiency increase would reduce fissile fuel consumption and radioactive waste management costs.

In terms of technical feasibility, a double internal pressure hull design was selected, providing space for a total of four reactors and delivering a combined electrical power output of 1 GW(E). A preliminary mechanical design of the internal pressure hull was carried out to calculate the required hull thickness able to resist a design pressure of 15 bars, for both 2 and 4 pressure hull configurations. It has been demonstrated that the reactor and turbomachinery can be housed within the dimensions specified for the pressure hull.

An emergency scenario was also considered, in which a waterjet propulsion system was developed to propel the vessel up to 17.75 m/s (64 km/h) with electrical power provided by a single reactor. The effects of grid disconnection were also analyzed, identifying the main factors impacting the reactor and turbomachinery safety systems.