Retrofitted Gate Rudder System In Situ Performance Analysis Using Data-Driven Method

Abstract

The growing focus on enhancing ship performance over the past decades has driven the invention of various energy-saving devices. Conducting performance analyses of these devices is essential to substantiate the claimed energy savings. However, this process is complicated by the dynamic conditions experienced by ships, such as weather and loading conditions. These factors could significantly impact the results of comparisons made between pre- and post-retrofitting performance of new energy-saving devices. This paper presents a comprehensive investigation into the performance analysis process of a general cargo vessel equipped with a Gate Rudder system, which is a twin rudder system known for its thrust-producing and energy-saving properties. A multi-input, multi-output data-driven method, utilizing in situ and weather data, is developed and applied to account for the effects of weather and loading conditions. A performance analysis is then conducted by using the data-driven models to estimate three different indicators of ship performance in terms of propulsion efficiency. The results suggest that the Gate Rudder could potentially reduce torque requirements by up to 20.70%, shaft power requirements by up to 27.58%, and fuel consumption by up to 30.35%, with the same weather and loading conditions.

1. Introduction

The performance monitoring of seagoing vessels has become a critical aspect of the shipping industry. In recent years, rising fuel costs and stricter environmental rules on greenhouse gas emissions have put more pressure on the shipping industry to improve ship performance. Shipping operations significantly affect the global environment due to the emissions they produce [1]. In response, the International Maritime Organization (IMO) adopted the Initial GHG Strategy, setting ambitious reduction targets—cutting total GHG emissions from international shipping by at least 40% by 2030 relative to 2008 levels and reaching net-zero GHG emissions from international shipping close to 2050. To achieve these targets, IMO has introduced a series of short-term measures, including the Energy Efficiency Existing Ship Index (EEXI), enhanced Ship Energy Efficiency Management Plan (SEEMP), and Carbon Intensity Indicator (CII) rating scheme to improve ship energy efficiency and achieve the 2030 target [2]. The review process of the effectiveness of the short-term measures started from July 2023 [3]. The increasingly stringent regulatory framework established by the IMO acted as a key driver for the implementation of fuel-saving strategies and energy-efficient technologies [4]. The Gate Rudder (GR) concept, introduced by Sasaki [5], aims to recover part of the viscous resistance losses encountered by ships. The GR system illustrated in Figure 1 was installed on a ship. The GR is made up of a twin rudder setup with two asymmetric-section blades positioned on either side of the propeller. While it works like a conventional rudder, the GR also enhances the flow around the propeller by inducing axial velocity in the propeller plane, which generates additional thrust and helps recover viscous resistance losses by equalizing the ship’s wake, thus increasing the propulsive efficiency [6]. The GR operates based on similar principles to the accelerating nozzles in ducted propellers. Research and investigations of GR systems have been conducted by various institutions and researchers regarding their working principle [7], maneuverability characteristics [8], performance analysis [9,10], and even energy consumption in the retrofitting process [11]. The results of their research demonstrated the superior performance of a GR system in terms of maneuverability and energy saving, when compared with conventional rudders.

The performance analysis available today can be categorized based on its data analysis methods. Three major streams have emerged that are particularly associated with contemporary applications: deterministic [9,12], data-driven [13,14], and hybrid approaches [15,16,17].

The deterministic approach in ship performance modeling involves using physical models and causal relationships to represent ship behavior, similar to the principles used in sea trials [18]. This approach can employ Experimental Fluid Dynamics (EFD) or Computational Fluid Dynamics (CFD) to model parts of the ship’s total resistance. EFD might involve data from towing tanks, cavitation tunnels, and wind tunnels. However, both methods require significant resources for extensive testing. These techniques are typically used for assessing specific aspects like propeller open water characteristics and additional resistance components, such as added wave resistance in head seas. Semi-empirical methods may also be required for certain calculations, like wind resistance coefficients. A fundamental approach to extracting ship performance information involves controlling all other influential variables, such as weather and loading conditions, by filtering the dataset. This allows for the ship model to be distilled into a representation of ship power and fuel oil consumption (FOC) as a function of speed only. Such a model can be developed using data from sea trials, model tests, CFD analysis, or statistical regression analysis of operational data. An alternative method involves normalizing each influential variable to a baseline by utilizing a model that quantifies the ship’s power or fuel consumption across all environmental and operating conditions. The primary issue with normalization is that the model used for corrections may introduce uncertainties due to incorrect model functional forms or parameters. These uncertainties can appear in the integrity of the training or calibration dataset, the accuracy of the method used (such as sea trials or others), or from omitted variables and unknown effects [19]. Deterministic models are predominantly used in situations where voyage data are limited, such as estimating the ship performance on a specific route before a ship is launched, and are suitable for applications that do not necessitate high prediction accuracy and have constrained voyage data, such as ships in their preliminary stages of operation [20].

Data analysis is improving the understanding of complex phenomena much more rapidly than a priori physical models have accomplished in the past [21]. Today, there is a rising trend in adopting data-driven models, propelled by the affordable access to large volumes of operational data. This shift is motivated by the desire to improve the accuracy of empirical models while avoiding the high computational costs associated with CFD simulations and EFD facility limitations [22]. The black-box nature of data-driven models can help mitigate issues related to incorrect model parameters that may arise in normalization methods. The core concept of these models is to utilize data collected from a specific ship’s operations to develop a statistical model. This model can be trained to estimate the ship’s powering needs, forecast its fuel consumption, and monitor its performance. Data-driven methods can be highly accurate in predicting non-linear problems and are relatively cost-effective. However, their accuracy depends on the quality of the measured data used to develop the models. Thus, comprehensive data processing methods based on domain and statistical knowledge are required before model training and development processes take place [23]. Additionally, these methods usually require several months of onboard recorded data for effective implementation [24,25]. Nevertheless, the rapid advancement of ship sensor technologies, which offer high transmission rates, has created new opportunities for data collection and transmission onboard, thus applying the data-driven model in performance analysis.

Alternatively, hybrid models have been proposed to combine the deterministic and data-driven models, which implement the same machine learning or statistical method used by data-driven methods, while implementing some domain physical knowledge to foster the model development [16]. However, the so-called gray-box models usually combine physical and statistical modeling approaches, which can result in a complex model structure. This complexity can make the development and maintenance of these models challenging, particularly as system dynamics change over time. Additionally, despite the greater effort required to develop gray-box models, they often perform similarly to black-box models in most cases [20].

In the realm of performance analysis for the GR system, Tacar et al. conducted a rigorous investigation into its effectiveness as an innovative energy-saving and maneuvering device intended to enhance ship performance [9]. By comparing the performance of a container ship equipped with the GR system to its sister ship using a conventional rudder, the researchers identified significant improvements in both fuel efficiency and maneuverability. The study employed experimental model tests and CFD simulations to validate the performance benefits of the GR system under analogous operational conditions. The findings indicate that the GR system presents a promising solution for reducing fuel consumption and greenhouse gas emissions in maritime operations. However, despite the sister ship operating on the same route and pursuing similar missions along the northeast coast of Japan, variations in weather conditions over time can induce uncertainty in the performance comparison. Additionally, individual vessel characteristics may result in performance discrepancies even among sister ships. These factors may introduce bias when comparing the performance of a ship equipped with the GR system to that of a ship without it.

In this paper, a comprehensive investigation is conducted into the performance analysis of a general cargo vessel equipped with a GR system using data-driven methods. Two machine learning models are developed based on data collected from the same ship during voyages before and after installing the GR system. These models estimate ship performance under various operational, weather, and loading conditions by using these as the model inputs. Three performance indicators from previous research [16] are used as the model outputs in this case to evaluate and justify the energy savings and FOC reductions achieved by the GR system. Performance analysis is then conducted by comparing the output indicators of the two models given identical operational, weather, and loading conditions.

2. Methodology

The target ship investigated in this work is a multipurpose general cargo vessel that operates in the Black Sea, the Red Sea, and European coastal waters. The ship was originally operating with a Conventional Rudder System (CRS) before the installation of the GR system. To accommodate the retrofit, several key modifications have been implemented: the propeller diameter was increased by 5% while retaining the same number of blades (5 blades), the single flap rudder was replaced with two asymmetric gate rudder blades, and the single steering gear was replaced with twin units, each designed for 125 kNm torque. Additionally, the propeller shaft has been modified slightly longer than in the original CRS to suit the new arrangement. The main engine particulars for the target ship, including the engine type, rated power, rated engine speed, and gear box ratio, are illustrated in

Table 1. Main engine system particulars.

Parameter	Value
Main Engine Type	8L38/32A
Rated Power (kW)	1960
Gear Box Ratio	5.263:1
Rated Main Engine Speed (RPM)	775

.

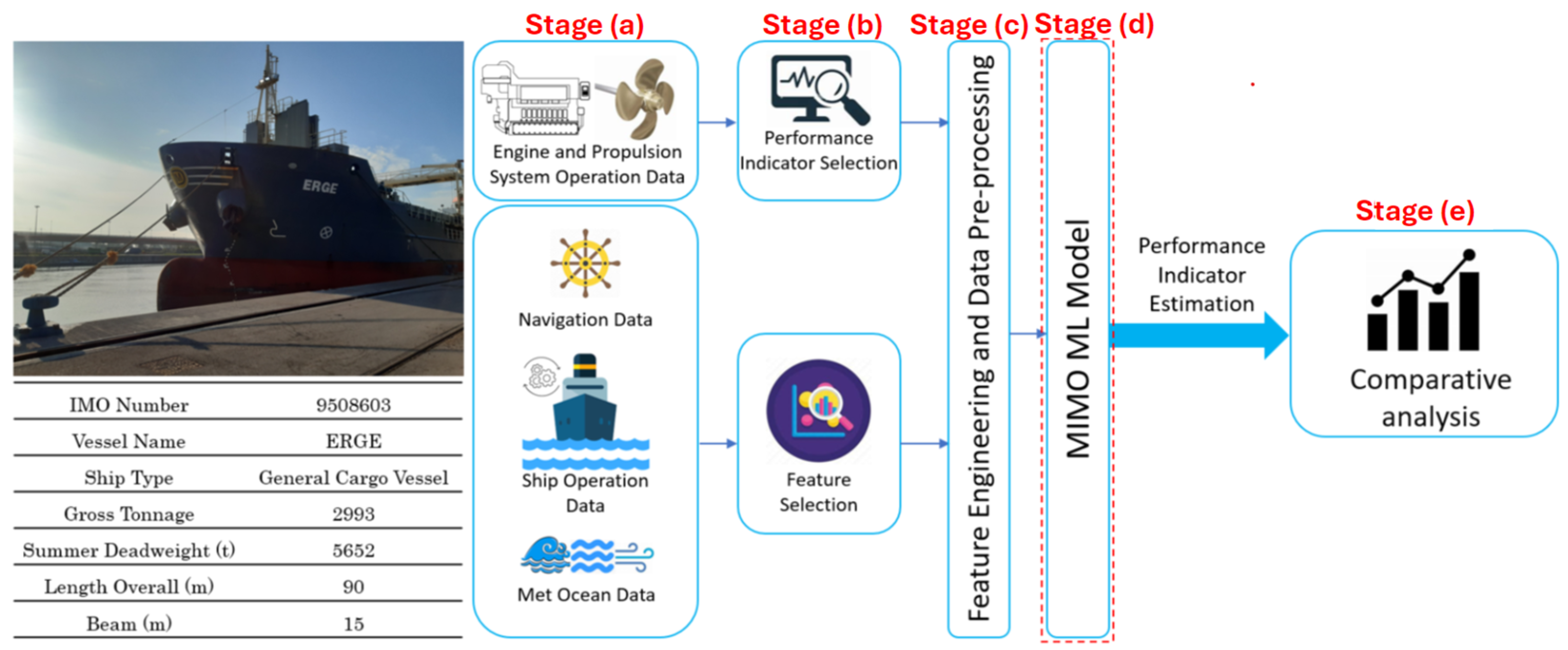
The methodology elaborated in this work can be visualized from Figure 2, which consists of: (a) data related to the engine, propulsion system, and ship operation from sensors installed on the ship, and weather data from an open source. (b) The process of feature selection and performance indicator identification, where domain knowledge is employed to select variables representing ship operating and loading conditions, as well as the surrounding weather conditions, which could impact the selected performance indicators; (c) During the feature engineering and preprocessing stage, data is meticulously prepared for model development. This stage involves implementing a comprehensive data cleaning process, where engine transients and recording anomalies are identified and excluded to ensure that only the steady-state operation is included. Additionally, the units of variables are standardized to maintain consistency, followed by feature standardization to facilitate faster convergence during model training. This preparation phase delivers the dataset in a format that is suitable for modeling; (d) Two multi-input, multi-output (MIMO) machine learning (ML) models are developed to evaluate ship performance before and after installing the GR system, respectively. Different modeling algorithms are applied to select the model that demonstrates the best predictive performance on validation and test datasets; (e) Following model development, comparative studies are conducted on performance indicators to evaluate ship performance before and after the GR system installation.

2.1. Data Acquisition

The data collected on board are from a CETENA Performance Monitoring system [26] at one-minute intervals. The system consists of one PC with dedicated software that records all available data on board and hardware to acquire in situ signals indicating propulsion efficiency, including torque, shaft power, and FOC. The monitoring system is connected to the integrated navigation system and other ship apparatus in order to acquire the ship navigation, propulsion, and metocean data. Additional data, such as displacement and draft forward and aft, are recorded by the ship deck officer.

Table 2. Main variables applied in this work.

Variable Name	Source	Unit
Date and Time	GPS	/
Ship Position	GPS	Degree
Speed Over Ground (SOG)	GPS	knots
Speed Through Water (STW)	Speed log	knots
Heading	Gyrocompass	Degrees
Relative Wind Direction	Anemometer	Degrees
Relative Wind Velocity	Anemometer	m/s
Wave Height	CMEMS database	m
Wave Direction	CMEMS database	Degrees
Displacement	Deck Officer Record	t
Draft Forward/After	Deck Officer Record	m
Shaft Torque	Shaft Sensor	kNm
Shaft Power	Shaft Sensor	kW
Main Engine FOC	Engine Flowmeter	kg/h

elaborates on the main variables applied in this work. In this research, wave data were collected from the Copernicus Marine Environment Monitoring Service (CMEMS). As the vessel was not equipped with wave sensors, the open-source datasets were used to estimate wave conditions. Specifically, the data were sourced from the short-term forecast products provided by the CMEMS Global Ocean Waves Analysis and Forecast (WAV) system [27]. The WAV product features a spatial resolution of 0.083° × 0.083° (equivalent to approximately 1/12 of a degree or 5 min), with a temporal resolution of every three hours. As noted, the wave data obtained from the CMEMS dataset have a lower temporal resolution compared to the 1 min onboard measurements. The lower temporal resolution may smooth short-term fluctuations, and the nearest-neighbor interpolation applied assumes a degree of spatio-temporal homogeneity that may not always hold.

2.2. Feature Selection and Performance Indicator Selection

In this research, ship STW is selected as one of the predictors of fuel consumption because it is a better proxy for the engine regime and a more reliable indicator of propulsion system performance than speed over ground (SOG) [28]. Ship course over ground (COG) is also selected as one of the model inputs, as it indicates the direction of movement. Additionally, ship displacement and draft (both forward and aft) are included as input features since they reflect the ship’s loading condition in terms of cargo. These variables have been employed in multiple previous studies on FOC modeling [29,30]. Domain knowledge and previous research findings [29,30,31] highlight the crucial role of metocean factors in FOC modeling. Key parameters include wave height, wind speed, and current speed, along with their respective absolute directional values, which are essential for accurately modeling the ship performance. Since STW tends to be less affected by sea current, only wave direction and height, and wind direction and speed are considered here as the inputs indicating the metocean conditions.

In assessing ship performance, shaft torque, shaft power, and engine FOC are selected as key indicators based on an earlier study [16]. These metrics provide valuable insights into the efficiency of the propulsion system and overall vessel operation. Changes in STW, weather conditions, and cargo loading conditions can significantly impact the vessel’s resistance. An increase in resistance requires additional power for propulsion, leading to higher FOC. Therefore, the comparison of these parameters before and after retrofitting is crucial for ship performance analysis.

2.3. Data Preprocessing and Feature Engineering

In Stage (c) of Figure 2, the initial step involves removing undesirable data samples resulting from sensor failures or monitoring system issues, such as NaN values and unrealistic readings. Additional filtering is applied to exclude data from engine idle or transient modes, as the performance analysis in this research focuses solely on steady-state periods of the ship’s operation. Furthermore, the retrieved weather data from CMEMS undergo further processing to prepare it for the subsequent modeling stage. This section will provide a detailed overview of these preprocessing steps.

2.3.1. Engine Steady-State Mode Identification

Steady-state operation is always referred to ship transit periods, where a vessel is moving on a relatively constant course and at a relatively steady speed. The main engine idle periods can be defined when shaft RPM < 70 and STW < 4 knots. The engine seldom operates below this threshold during active operations. Previous research by Castresana et al. identified engine speed and Fuel Oil Injection Pump Rack position (FORACK) as key parameters for classification [32]. However, in this study, direct readings of engine RPM and FORACK are unavailable. Instead, shaft RPM is utilized to identify engine steady-state operation. Although delays may occur due to gear ratios and shifting between engine RPM and shaft RPM, such delays are minimized in most well-designed marine propulsion systems. The study utilized the Relative Standard Deviation (RSD) over a 10-minute (min) window preceding each data point [33], which is applied to shaft RPM values. Equation (1) shows the expression used for the RSD calculation with standard deviations and moving averages calculated for the previous 10 min for each sample.

$${RSD}_{10\mathrm{m}\mathrm{i}\mathrm{n}}={\displaystyle \frac{{Sd}_{10\mathrm{m}\mathrm{i}\mathrm{n}}}{\overline{x_{10\mathrm{m}\mathrm{i}\mathrm{n}}}}}\times 100\%={\displaystyle \frac{\sqrt{\frac{{\sum }_{i=1}^n{\left(x_i-\overline{x_{10\mathrm{m}\mathrm{i}\mathrm{n}}}\right)}^2}{n-1}}}{\overline{x_{10\mathrm{m}\mathrm{i}\mathrm{n}}}}}\times 100\%$$

(1)

Here, ${Sd}_{10\mathrm{m}\mathrm{i}\mathrm{n}}$ represents the standard deviation of the last 10 min for each sample, while $\overline{x_{10\mathrm{m}\mathrm{i}\mathrm{n}}}$ denotes the moving average calculated over the same period. The variable $x_i$ indicates the $i^{th}$ sample observation, and $n$ is the number of samples of the 10 min considered before each sample. A threshold of ${RSD}_{10\mathrm{m}\mathrm{i}\mathrm{n},RPM}\le 5\%$ was established to ensure that each sample reflects a relatively steady state. Samples that exceed these thresholds are classified as non-steady-state engine activity and are subsequently filtered out in this study.

2.3.2. Copernicus Data Processing

CMEMS offers user interfaces for extracting data based on the vessels’ position and datetime indexes. To align data extraction with these indexes, the ship’s position and time data, provided every minute, must be matched with the three indexes from the environmental data sources. The Nearest Neighbors Imputation method, as proposed by Faisal and Tutz [34], is employed to identify the first nearest neighboring indexes for retrieving environmental data. The Nearest Neighbors method is based on the principle that data points that are close to each other in feature space are likely to have similar properties. In the context of data imputation, this means that missing values can be estimated by looking at the values of the nearest neighboring points. Matching environmental data to specific ship positions and times, for example, involves identifying the nearest data points in the source dataset to the target points in the query dataset.

2.3.3. Feature Engineering

In this study, data were sourced from two distinct datasets, which required the unification of units to enable effective interaction between them. For example, the ship’s position (latitude and longitude) is recorded in minutes by the onboard monitoring system, whereas the CMEMS dataset provides this information in degrees. To ensure consistency and accuracy in data analysis, onboard position data are converted to degrees. These conversions are particularly crucial for the successful application of the Nearest Neighbors Imputation method for retrieving wave data.

In addition, a standardization method is implemented before model training to enhance the convergence speed of the model algorithms, as noted by Ioffe and Szegedy [35]. In this study, z-score normalization is applied. The process involves calculating the mean, ${\mu }_i$, and standard deviation, ${\sigma }_i$, derived from the variable $x_i$. Then, the standardized variable, $x_{standardized}$, can be obtained from the equation below:

$$x_{standardized}={\displaystyle \frac{x_i-{\mu }_i}{{\sigma }_i}}$$

(2)

The above formula is applied to the training and validation datasets to obtain the scaler, which is then used to scale the testing datasets. This approach helps to prevent data leakage by ensuring that the testing data remain independent of the training data’s characteristics.

2.4. Modeling Algorithms

There are three key algorithms, which are frequently applied in ship performance modeling. The principles of these modeling algorithms will be introduced in this section.

2.4.1. Random Forest (RF)

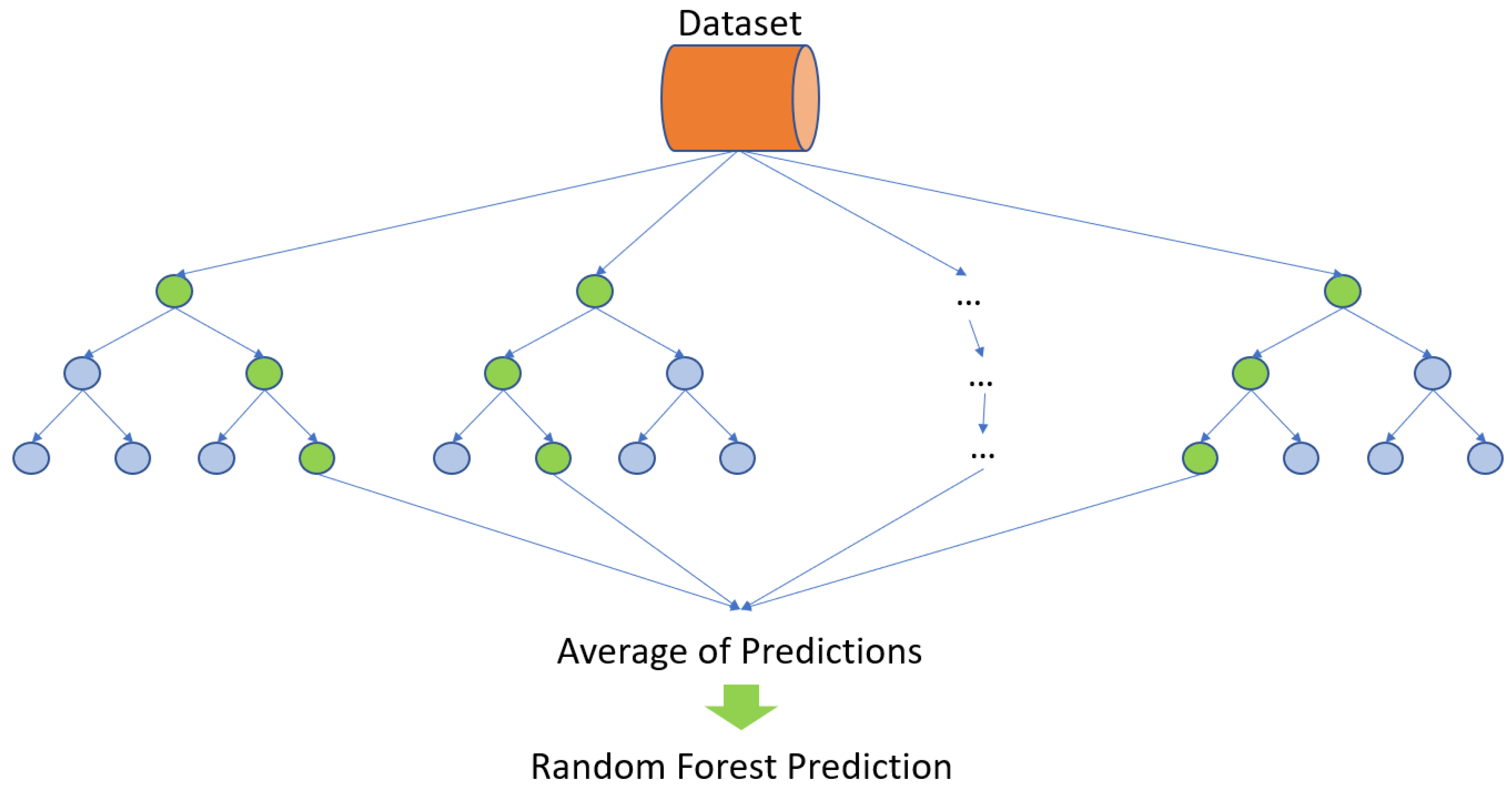
RF is an ensemble algorithm based on the bagging method that combines the performance of multiple decision tree algorithms to classify or predict the value of a variable. The trees in an RF grow in parallel and independently, each providing a prediction. For regression problems, the final prediction of the entire RF model is the average of the predictions from all the trees. The general structure of an RF is illustrated in Figure 3 [14]. The Python 3.10 Sklearn package provides convenient hyperparameter tuning for optimal model performance of RF. Key hyperparameters include the number of estimators (n_estimators), the number of features considered for the best split (max_features), the maximum depth of each tree (max_depth), the minimum number of samples required to split a node (min_samples_split), the minimum number of samples required to be at a leaf node (min_samples_leaf), and the option to apply bootstrapping. Adjusting these parameters allows the model to achieve the best predictive accuracy and generalization capabilities.

2.4.2. eXtreme Gradient Boosting (XGBoost)

XGBoost (XG) regression is a supervised ML technique that consists of multiple classification and regression trees. A more detailed overview of the algorithm is introduced in [36]. XG adds a regularization term on the basis of the Gradient Tree Boosting loss function, and the loss function of XG can be expressed as follows:

$$L_t={\sum }_{i=1}^{m}L(y_i, f_{t-1}\left(x_i\right)+h_t(x_i\left)\right)+\gamma J+{\displaystyle \frac{\lambda }{2}}{\sum }_{j=1}^J{\omega }_{tj}^2$$

(3)

where $L(y_i, f_{t-1}\left(x_i\right)+h_t(x_i\left)\right)$ represents the loss function, and $y_i$ is the true value for $i$-th sample. $f_{t-1}\left(x_i\right)$ is the prediction from the model at the previous iteration $t-1$, and $h_t\left(x_i\right)$ is the current model at iteration $t$. The loss function $L$ measures how well the predicted value $f_{t-1}\left(x_i\right)+h_t\left(x_i\right)$ matches the true value $y_i$.

A regularisation term $\gamma J$ penalizes the complexity of the model. The parameter $\gamma$ controls the weight of this penalty. In addition, the regularisation term ${\displaystyle \frac{\lambda }{2}}{\sum }_{j=1}^J{\omega }_{tj}^2$ for the weight ${\omega }_{tj}^2$ of the model $h_t$ encourages smaller weights, which helps prevent overfitting, where $\lambda$ controls the strength of this penalty.

Since XG does not natively support multi-output regression, the Python wrapper function ‘MultiOutputRegressor’ from scikit-learn is used to wrap XG models [37]. This allows training of one XG model per target variable. Each model predicts a single target.

2.4.3. Artificial Neural Networks (ANNs) and Deep Neural Networks (DNNs)

The fundamental working principle of an ANN method can be illustrated by considering an ANN model comprising an input layer $\mathit{x}$, a hidden layer Z consisting of Q nodes, and an output layer containing one or multiple targets. The transfer function at each node is given by the following expressions [38]:

$$Z_q={\sigma }_{NN}\left({\varphi }_{0q}+{\varphi }_q^T\mathit{x}\right)$$

(4)

$$Y=f\left(\mathit{x}\right)=g\left({ \mathrm{w}}_0+w^{T}Z\right)$$

(5)

where $Z=(Z_1,Z_2,\dots ,{ Z}_Q)$, with $q$ being the target node, ${\sigma }_{NN}\left(\right)$ denotes the activation function, and $g\left(\right)$ represents the output function in regression tasks. $\varphi$ and $w$ are the weight parameters of the ANN. This concept can be extended by incorporating multiple hidden layers and a larger number of neurons. The transfer function described above can be implemented in DNNs by passing the output of each layer to the subsequent one. $\varphi$ and $w$ are often optimized by adjusting the number of neurons in the hidden layers (hidden_layer_sizes) to achieve optimal model performance.

2.4.4. Multiple Linear Regression (MLR)

MLR is a parametric model frequently employed to describe the relationship between two or more independent variables and a single or multiple dependent variables. Given input variables $\mathit{x}$ = ${(x}_1$,…, $x_K)$, the target value $\mathit{y}$ = ${(y}_1$,…, $y_M)$ can be expressed as follows [39]:

$$y\left(\mathit{x}, \mathit{w}\right)=w_0+w_1{x}_1+\cdots +w_K{x}_K$$

(6)

The weight coefficients $\mathit{w}$ are estimated by using the Least Squares method:

$$\widehat{\mathit{w}}={argmin}_{\mathit{w}}\left\{\sum _{i=1}^N\sum _{m=1}^M{\left(y_{im}-w_{0m}-\sum _{j=1}^K\left(w_{jm}{x}_{ij}\right)\right)}^2\right\}$$

(7)

While MLR has demonstrated relatively poor performance compared to more advanced algorithms in many reviewed studies [29,31], it remains a valuable baseline for evaluating the performance of more complex models. The hyperparameters typically adjusted during optimization include ‘fit_intercept’ (which determines whether the intercept should be calculated), ‘normalize’ (which decides whether to apply normalization), and ‘positive’ (which constrains all coefficients to be non-negative). These hyperparameters are key factors in fine-tuning the model for optimal performance.

2.5. Model Development

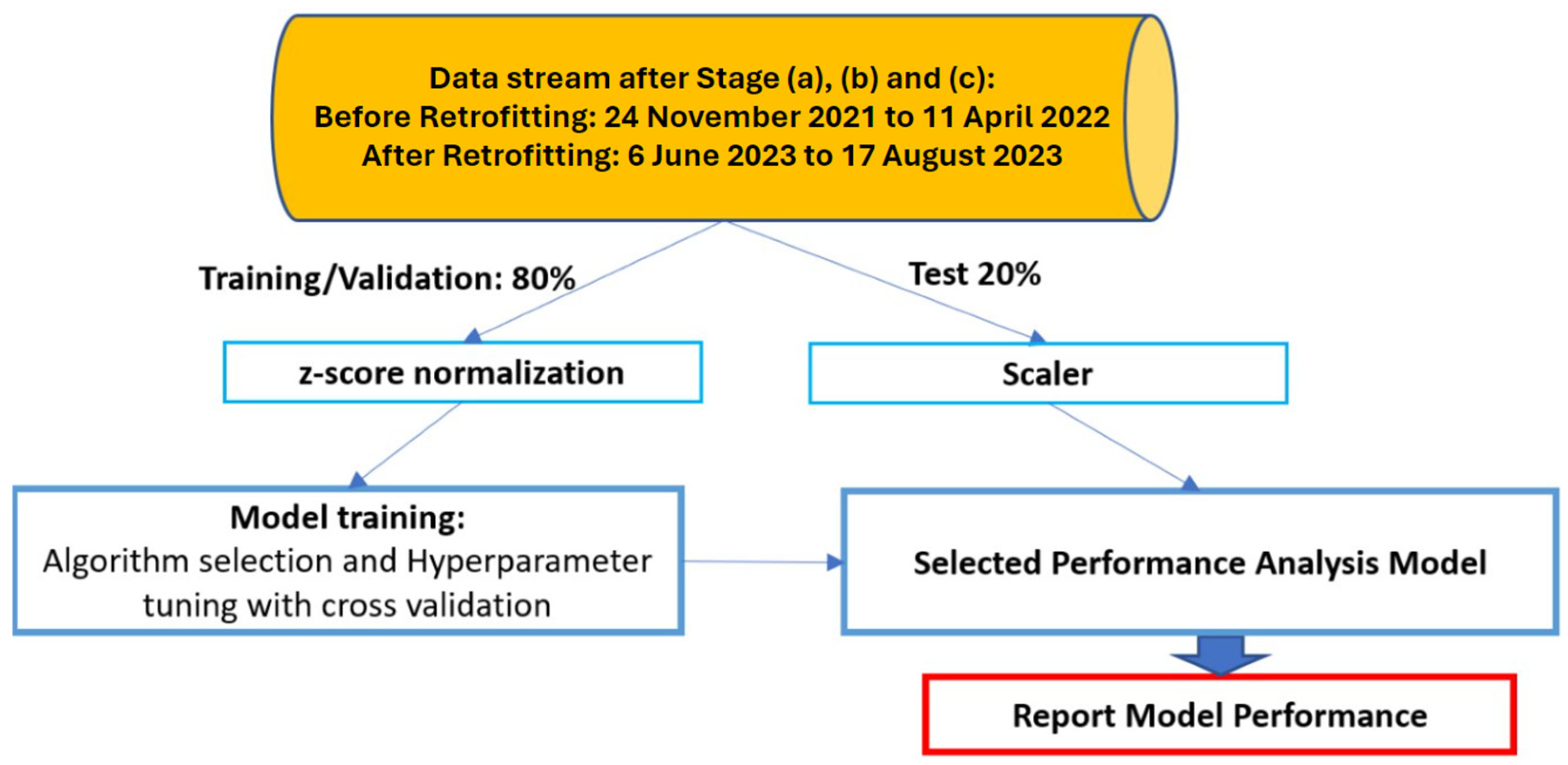
The GR system was installed on the target vessel in May 2023. As shown in Figure 4, data collected during the period 24 November 2021 to 11 April 2022 from the target ship are applied to train the performance model for the ship before retrofitting, while the data collected from 6 June 2023 to 17 August 2023 are applied to train the performance model for the ship after the retrofitting. After data acquisition, preprocessing, and feature engineering, the data stream for the performance model development before/after retrofitting is partitioned by randomly splitting the datasets into 80% for training/validation and 20% for testing, respectively. The z-score normalization method, discussed in Section 2.3.2, is developed based on the training and validation datasets to obtain the scaler, which is then later used to scale the testing datasets. During the model training phase, hyperparameter optimization was performed for both performance models using multiple modeling algorithms. This process identified the optimal hyperparameter sets for each algorithm-specific model. The performance of models developed using different algorithms was then evaluated on the test dataset. The final models for both pre- and post-retrofitting performance were selected based on their accuracy during cross-validation and testing phases.

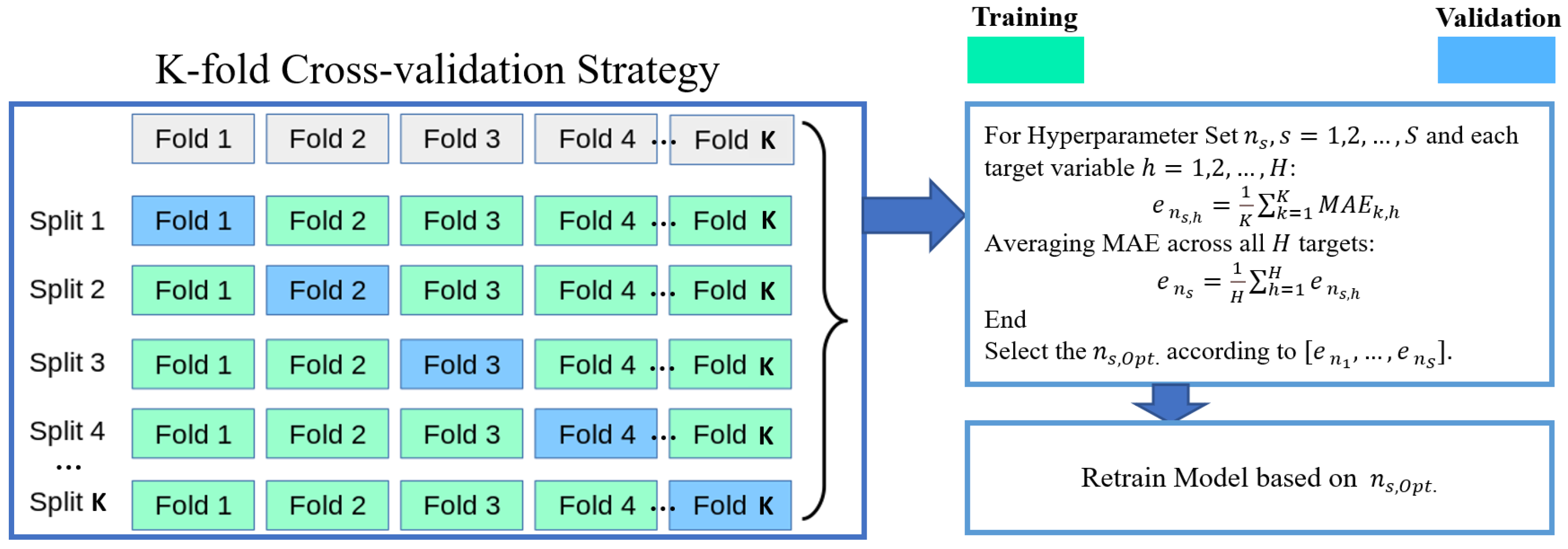
2.5.1. Cross-Validation Strategy and Model Hyperparameter Tuning

In this study, K-fold cross-validation is employed for model training and hyperparameter tuning to ensure that the selected hyperparameter sets approach optimality while mitigating the risk of overfitting [40]. Figure 5 illustrates the K-fold cross-validation strategy, where the dataset is divided into $K$ splits, each containing $K$ folds. During the cross-validation process, the training dataset is partitioned into $K$ equally sized folds, and $K$ iterations of training and validation are conducted. In each iteration, one segment $k$ serves as the validation set, while the remaining $K-1$ segments are utilized for model training. This strategy can be further refined to evaluate the performance of the model under various hyperparameter configurations. Specifically, a total of $K$ runs are performed for each of the $S$ hyperparameter sets during the cross-validation stage, facilitating a thorough assessment of model performance across different configurations. Since in this work MIMO models are required for multiple performance indicator estimation, firstly, the mean absolute error $e_{n_s,h}$ for each target variable $h$ is calculated by averaging the mean absolute error (MAE) values over $K$ folds. Then, the average error $e_{n_s}$ across all $h$ target variables is computed for each hyperparameter set $n_s$, and the optimal hyperparameter set $n_{s,opt}$ is selected based on the errors [$e_{n_1},\dots , e_{n_S}$]. Finally, the model is retrained on the full training dataset using the chosen hyperparameters.

2.5.2. Model Evaluation Metrics

The key indicator of model evaluation in this work, in cross-validation, is mean absolute error (MAE), which can be expressed as follows [25]:

$$MAE\left(y_i,{ \widehat{y}}_i\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|$$

(8)

where n is the number of samples in y, ${\widehat{y}}_i$ is the prediction by the model, and $y_i$ is the true value. $\left|y_i-{\widehat{y}}_i\right|$ is then the absolute error (AE) over n samples. This is applied as the performance metric in the validation stage.

In machine learning, $R^2$ is often used to evaluate the performance of a regression algorithm, which can be expressed as follows:

$$R^2=1-{\displaystyle \frac{\sum _i\left({\widehat{y_i} - y}_i\right)}{\sum _i\left({\overline{y_i} - y}_i\right)}}$$

(9)

where $\overline{y_i}$ represents the mean of the true values. An $R^2$ value closer to 1 indicates that the regression algorithm predicts the target variable with higher accuracy. The $R^2$ metric is key in evaluating the goodness of fit for a regression model, providing insight into the model’s performance. It is particularly useful for comparing the efficacy of multiple models, identifying the best-performing model, and determining which factors most significantly impact model performance during the optimization process, thereby guiding targeted improvements. $R^2$ is both informative and truthful, without the interpretability limitations associated with other metrics [41].

A variant of MAE is Mean Absolute Percentage Error (MAPE), expressed as follows:

$$MAPE\left(y_i, {\widehat{y}}_i\right)={\displaystyle \frac{1}{n}}\sum _{i=1}^n{\displaystyle \frac{\left|y_i - {\widehat{y}}_i\right|}{y_i}}\times 100\%$$

(10)

In practice, a major drawback of MAPE is that it becomes numerically unstable when there exists an i such that $y_i=0$ [29]. However, there are a few samples with target value close to 0 in this work, as engine idle periods are filtered out at the data pre-processing stage. Thus, this metric is adoptable in this case. $R^2$ and MAPE are therefore applied to evaluate the model performance in terms of precision on the test dataset.

3. Results and Discussion

In this section, the results of the model development, the model evaluation on test datasets, and the performance analysis stage will be elaborated and discussed.

3.1. Data Overview After Pre-Processing

The datasets after filtering and cleaning include 15,077 and 19,329 min-based samples for pre- and post-retrofitting, respectively. The model development and analysis in the following sections are carried out based on these datasets. The datasets can be visualized through histogram plots shown in Figure 6 (Model inputs) and Figure 7 (Model outputs). The horizontal axis of each plot denotes the number of points corresponding to each histogram bin.

The relationships between STW and the performance indicators are illustrated in Figure 8. As shown, despite filtering out non-steady-state data during the preprocessing stage, the relationships remain somewhat unclear due to the influence of varying weather and loading conditions. These factors can introduce bias when directly comparing the ship’s performance before and after the installation of the GR system using speed–performance indicator curves. Thus, data-driven models are required in this work to account for the effects of weather and loading conditions, ensuring that the comparisons are made under equivalent conditions.

3.2. Results of Cross-Validation and Hyperparameter Tuning

The results from the cross-validation stages mentioned in Section 2.5.1 are presented and discussed in this section. The three selected algorithms are used to develop the performance models based on validation loss.

The hyperparameter sets considered for the performance models and their range of values are presented in

Table 3. Model hyperparameters along with their range and validation results.

Model	Hyperparameters Tuned	Optimal Hyperparameters and Metrics
		Before Retrofit	After Retrofit
RF	n_estimators ∈ [500, 1500, step: 100], max_features ∈ [‘auto’, ‘sqrt’], max_depth ∈ [5, 20, step: 5], min_samples_split ∈ [2, 10, step: 1], min_samples_leaf ∈ [1, 4, step: 1], bootstrap ∈ [True, False]	‘bootstrap’: True, ‘max_depth’: 20, ‘max_features’: ‘auto’, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘n_estimators’: 500, MAE ± Std = 3.47 ± 0.06	‘bootstrap’: True, ‘max_depth’: 20, ‘max_features’: ‘auto’, ‘min_samples_leaf’: 2, ‘min_samples_split’: 10, ‘n_estimators’: 1000, MAE ± Std = 2.45 ± 0.07
XG	n_estimators ∈ [500, 1500, step: 100], max_depth ∈ [5, 20, step: 5], learning_rate ∈ [0.005, 0.01, step: 0.0001]	‘n_estimators’: 700, ‘max_depth’: 10, ‘learning_rate’: 0.01, MAE ± Std = 3.85 ± 0.10	‘n_estimators’: 500, ‘max_depth’: 20, ‘learning_rate’: 0.01, MAE ± Std = 2.46 ± 0.07
DNNs	hidden_layer_sizes ∈ [128, 1024, step: 128; 128, 1024, step: 128; 128, 1024, step: 128]	activation: ReLU hidden_layer_sizes: {‘neurons’: 1024, ‘neurons1’: 256, ‘neurons2’: 256} MAE ± Std = 5.01 ± 0.35	activation: ReLU hidden_layer_sizes: {‘neurons’: 256, ‘neurons1’: 512, ‘neurons2’: 1024} MAE ± Std = 4.06 ± 0.43
MLR	‘fit_intercept’: [True, False], ‘normalize’: [True, False], ‘positive’: [True, False]	‘fit_intercept’: True, ‘normalize’: True, ‘positive’: False MAE ± Std = 18.03 ± 0.29	‘fit_intercept’: True, ‘normalize’: True, ‘positive’: False MAE ± Std = 14.52 ± 0.30

along with the optimal hyperparameter sets and the optimized losses. It can be deduced that the best-performing model was the RF in both datasets. With hyperparameter optimization, it can achieve an average MAE ± Std of 3.47 ± 0.06 and 2.45 ± 0.07 for the performance models pre- and post-retrofitting, respectively, while the XG model yielded a comparable performance with errors of 3.85 ± 0.10 and 2.46 ± 0.07. The DNN (5.01 ± 0.35 and 4.06 ± 0.43) also provides acceptable performance for both models, while the MLR models demonstrated less accurate performance when compared with the first three algorithms.

3.3. Model Performance in Test Dataset

The results of the model performance on the test datasets are presented in

Table 4. Model performance on test datasets.

Model for Pre-Retrofitting
Indicator	Algorithm	MAE	R-Squared	MAPE (%)
Torque	RF	0.8092	0.9821	1.10
	XG	0.8256	0.9819	1.12
	DNN	1.0594	0.9754	1.42
	MLR	3.2859	0.8853	4.37
Shaft power	RF	10.6326	0.9860	1.25
	XG	10.8987	0.9850	1.27
	DNN	13.9621	0.9804	1.60
	MLR	55.5361	0.8878	6.45
FOC	RF	2.2140	0.9865	1.13
	XG	2.3246	0.9860	1.19
	DNN	3.1232	0.9803	1.54
	MLR	11.8871	0.8864	5.91
Model for Post-Retrofitting
Indicator	Algorithm	MAE	R-Squared	MAPE (%)
Torque	RF	0.5343	0.9812	0.72
	XG	0.5341	0.9812	0.72
	DNN	0.9091	0.9672	1.24
	MLR	2.6792	0.8030	3.70
Shaft power	RF	6.9842	0.9843	0.77
	XG	7.0069	0.9840	0.77
	DNN	11.2639	0.9556	1.27
	MLR	43.8444	0.8003	5.11
FOC	RF	1.9901	0.9839	0.95
	XG	1.9982	0.9838	0.96
	DNN	2.9280	0.9729	1.41
	MLR	10.7242	0.7815	5.39

, which demonstrates significant variations in performance across different indicators, as measured by MAE, R-squared, and MAPE.

For the pre-retrofitting models, the Random Forest algorithm outperforms the others in torque estimation with an MAE of 0.8092, an R-squared of 0.9821, and an MAPE of 1.10%. XG follows closely with slightly higher MAE and MAPE values. The DNN model performs less effectively, while MLR shows significantly higher errors, which indicates a poorer fit for the data. Again, RF shows the best performance in shaft power modeling with the lowest MAE (10.6326) and MAPE (1.25%) and a high R-squared value of 0.9860. XG is comparable but slightly less accurate. DNN has higher errors, while MLR exhibits the highest errors, particularly with a notably low R-squared value of 0.8878. In terms of FOC, RF provides the most accurate predictions with an MAE of 2.2140, R-squared of 0.9865, and MAPE of 1.13%. XG is slightly less accurate, while DNN again shows increased error. MLR performs poorly, with substantially higher error metrics compared to the other algorithms.

For the post-retrofitting models, RF and XG perform almost identically in torque estimation, with both achieving an MAE of approximately 0.534 and an MAPE of 0.72%. DNN shows a reduction in performance compared to RF and XG, while MLR again has the highest errors. The RF also outperforms the other models in the shaft power case with an MAE of 6.9842, an R-squared of 0.9843, and an MAPE of 0.77%. XG yields similar results, with slightly higher error metrics. DNN and MLR show lower accuracy, with MLR significantly lagging in performance. For the post-retrofitting FOC prediction, RF demonstrates the best performance, closely followed by XG. DNN, while better than MLR, still shows higher errors, and MLR continues to have the poorest performance with the highest MAE and MAPE.

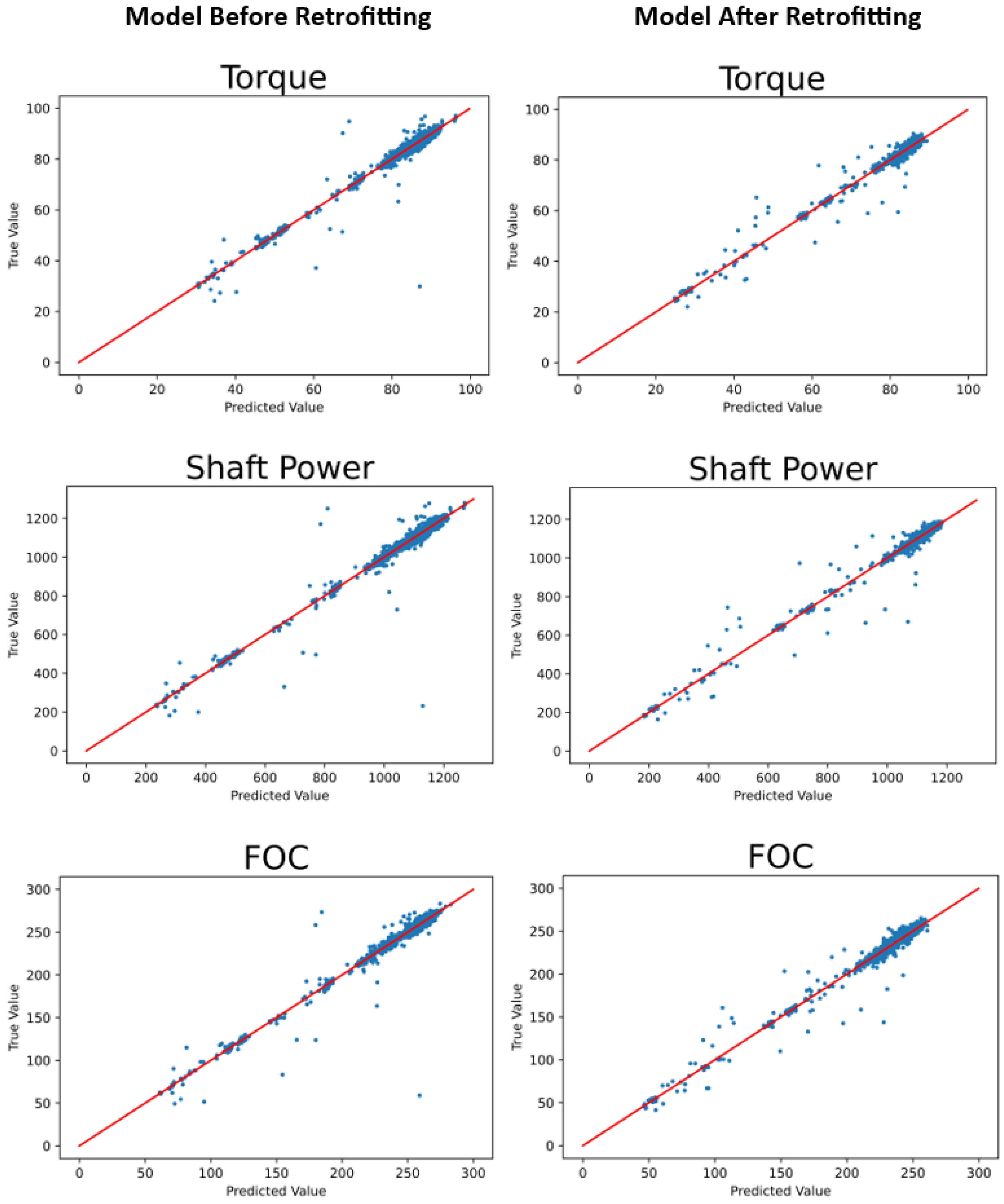
Across both the pre- and post-retrofitting models, Random Forest consistently provides the most accurate predictions across all indicators. Although followed closely by XG, RF models are selected as the performance indicator estimator for the next performance analysis and comparison stage. Figure 9 illustrates the indicator values estimated by RF models vs. their true values. The model shows a strong correlation between predicted and true values, although some discrepancies are evident, particularly at the higher end of the value ranges.

While the proposed method provides a precise estimation of overall performance indicators, they could potentially be further improved by incorporating additional variables related to seasonal effects into the model development stage, such as sea surface temperature and biofouling. This will be considered in the follow-up study.

3.4. Performance Analysis Through Comparative Studies

Having identified that RF models outperform other algorithms in both validation and test stages, the RF performance models developed for performance analysis are subsequently employed to estimate the performance indicators before and after retrofitting. Subsequently, the same input parameters, including ship loading conditions and environmental variables, were fed into both models. A comparative analysis (Figure 2 Stage (e)) of the resulting performance indicators was then conducted to quantify and substantiate savings associated with the GR system. Figure 10 illustrates the application of these models for performance analysis and comparison. To facilitate this analysis and ensure the models predict appropriately, the input ranges used in the comparative analysis fall within the datasets employed to train the models. This guarantees that the models were exposed to sufficient information during development and can offer reliable predictions in the comparative analysis and evaluation stage. Specifically, the relative wind direction and wave direction are standardized to a fixed value, representing head wind and wave scenarios.

This study explores three distinct scenarios to evaluate ship performance under varying conditions of speed, wind, and wave. In the first scenario, the ship STW is incrementally varied from 6.5 to 10 knots in 0.5-knot steps, while other parameters remain constant: wind speed at 20 knots, wave height at 0.16 m, displacement at 7465 tons, and a draft of 6.2 m forward and 6.7 m aft under full-load conditions. In the second scenario, the ship STW is fixed at a speed of 10 knots, with the wind speed varying between 0 and 20 knots, while other parameters are held constant as in the first scenario. The third scenario maintains the ship STW at 10 knots, varying the wave height from 0 to 2 m in 1 m increments, with all other settings consistent with those in the first scenario. The high-sea-state performance of the GR system was not investigated in this study because the vessel rarely encountered such conditions during the observation periods, which could result in insufficient data for reliable model development and validation.

The new artificial datasets were used to feed the developed models to predict shaft torque, power, and engine FOC. Figure 11 provides a comprehensive analysis of the ship’s performance before and after retrofitting, with a focus on key metrics such as torque, engine power, and FOC across varying operational scenarios, which include the changes in STW, wind speed, and wave height. The analysis reveals a consistent trend of improved performance following the retrofit, as indicated by lower values in torque, engine power, and FOC in all scenarios. Specifically, in the first scenario where ship speed is varied from 6.5 to 10 knots, the post-retrofit model exhibits a significant reduction (up to 20.70% at 9 knots) in torque and engine power requirements (up to 27.58% at 9 knots), along with a corresponding decrease in FOC (up to 30.35% at 9 knots) at all speed increments, which justifies the retrofit’s effectiveness in enhancing energy efficiency.

In the second scenario, which examines the impact of wind speeds ranging from 0 to 20 knots while maintaining a constant ship speed of 10 knots, the post-retrofit performance shows remarkable stability, with marginal increases in torque and engine power as wind speed increases. This observation aligns with the well-established principle that ship power requirements inevitably increase with greater added resistance from wind. Consistently, the post-retrofit model demonstrates a significant reduction (up to 13.69%) in torque and engine power requirements (up to 16.75%), as well as a decrease in FOC (up to 21.34%) at all wind speed settings. This suggests that the retrofitted ship is better equipped to handle various wind conditions with reduced power demand and fuel consumption.

The third scenario, which varies wave height from 0 to 2 m, further underscores the benefits of the retrofit. The results indicate that the GR system can reduce the torque and power requirements by up to 13.59% and 17.50%, respectively, which results in a reduction in FOC of up to 20.34% in the case of wave variation. The post-retrofit model displays a more gradual increase in torque and engine power as wave height increases, along with a significantly flatter FOC curve compared to the pre-retrofit condition. This indicates that the retrofit has not only improved the ship’s efficiency but also enhanced its ability to maintain performance consistency in maneuvering in rougher sea conditions. Overall, the analysis demonstrates that the retrofit has resulted in substantial improvements in the ship’s operational efficiency, particularly under conditions of increased speed, wind, and wave height, thereby enhancing both energy efficiency and the vessel’s resilience to environmental challenges.

4. Discussion

The findings from the performance analysis of the general cargo vessel equipped with the GR system demonstrate significant improvements in propulsion efficiency and energy savings. The data-driven models employed in this study have successfully accounted for the variable effects of weather and loading conditions, which is expected to provide a robust comparison between the pre- and post-retrofit scenarios.

The comparative analysis reveals a consistent reduction in torque, shaft power, and FOC across various operational scenarios following the installation of the GR system, with its effectiveness becoming noticeable at speeds starting from 6.5 knots. Specifically, the results indicate reductions of up to 20.70% in torque, 27.58% in shaft power, and 30.35% in FOC at a STW of 9 knots, as illustrated in Figure 11. These improvements are particularly distinct at relatively higher speeds for the ship, which suggests that the GR system is most effective during cruising periods. This aligns with the GR system’s design intent to enhance flow around the propeller, thereby reducing viscous resistance and improving thrust efficiency. Further analysis under varying wind speeds and wave heights supports the GR system’s effectiveness. The post-retrofit model consistently required less power and exhibited lower FOC across all wind speeds and wave heights tested. This suggests that the GR system not only improves fuel efficiency under calm conditions but also enhances the vessel’s resilience to adverse weather, maintaining efficiency even in challenging sea states.

Additionally, the results from this study indicate that a ship equipped with the GR system requires approximately 16% less power at STW of 10 knots—a relatively high operational speed for the vessel—compared to a ship fitted with a conventional rudder. Although this analysis involves a different vessel, the findings are consistent with those of [9], who applied a deterministic approach to analyze the GR system performance and reported a 17% reduction at the service speed of 15 knots. These aligned results from both data-driven and deterministic approaches underscore the GR system’s strong potential for improving energy efficiency across different vessels and operating conditions.

However, deterministic models, which rely on physical principles and predefined equations, often require extensive normalization techniques to account for environmental and operational variations. As discussed in Section 1, this process introduces uncertainties due to potential inaccuracies in model parameters or the exclusion of relevant variables. For example, deterministic models typically use sea trials, towing tank tests, or CFD simulations, which, while useful, may not fully capture the day-to-day operational variability that ships experience. In contrast, the data-driven models developed in this study directly leverage operational data collected during actual voyages, inherently incorporating real-time variations in weather and loading conditions. This approach minimizes the need for complex normalization processes, thereby reducing the associated uncertainties and enhancing the accuracy of performance predictions. By directly leveraging in situ operational and metocean data, the models account for real-time variations in environmental and operational conditions, which enables performance prediction and analysis in various operational and weather conditions.

Hybrid models attempt to combine the strengths of both deterministic and data-driven approaches by incorporating physical knowledge into machine learning algorithms. While this can offer improvements in model interpretability and performance, hybrid models often suffer from increased complexity, making them difficult to develop and maintain, especially as operational conditions change over time. Moreover, the results of hybrid models may not always justify the additional effort required for their development, as they often perform similarly to purely data-driven models [20]. In the context of this study, the results in unseen test datasets have suggested that data-driven models alone were sufficient to capture the effects of the GR system on vessel performance in this work.

In this work, the RF algorithm, in particular, demonstrated superior predictive performance, outperforming other models like XG and DNN in estimating torque, shaft power, and FOC. Moreover, the cross-validation and hyperparameter tuning processes employed during model development have ensured that the final models are not only accurate but also generalizable to unseen data. This is evidenced by the models’ high R-squared values and low MAE and MAPE on unseen test datasets. Despite the successes, the study also highlights certain limitations. The reliance on historical data limits the models’ ability to predict performance under novel or extreme conditions that were not encountered during the data collection periods. Additionally, while the GR system shows significant improvements in operational efficiency, the long-term effects on maintenance costs, hull fouling, and overall vessel durability were not considered in this analysis due to the lack of information regarding these factors.

5. Conclusions

As the marine industry continues to innovate with the development of new energy-saving devices, it is crucial that comprehensive and robust methods are established to accurately evaluate and justify the performance improvements claimed for these systems. The growing complexity and variability of maritime operations demand advanced analytical approaches that can provide reliable insights into the true energy savings and FOC reductions achieved. This study conducted a comprehensive performance analysis of a general cargo vessel equipped with a GR system, utilizing a data-driven methodology. The analysis demonstrated the potential of this advanced rudder system to significantly improve propulsion efficiency and reduce fuel consumption. The use of machine learning models, particularly Random Forest, provided accurate predictions of key performance indicators, which proves the efficacy of the data-driven approach in real-world maritime applications. Specifically, the results indicate that the installation of the GR system can reduce torque by up to 20.70%, shaft power by up to 27.58%, and FOC by up to 30.35%, depending on the ship’s speed and environmental conditions.

The findings highlight the practical benefits of incorporating data-driven models in ship performance analysis, particularly in assessing the impact of energy-saving technologies. The ability to account for real-time operational conditions makes these models a valuable tool for maritime operators seeking to optimize vessel performance and reduce operational costs.

While the study focused on a specific vessel and set of conditions, the methodology and insights gained are broadly applicable across different ship types and operational environments. Future research could expand on this work by exploring the long-term impacts of such retrofits and applying similar approaches to assess the performance of other energy-saving technologies in the maritime sector. By employing the proposed methodologies demonstrated in this study, stakeholders can gain a more precise understanding of how these innovations impact overall ship energy efficiency under real-world conditions. Further work will also explore integrating this framework with regulatory metrics, such as the EEXI and CII, which could enable a direct assessment of ship energy efficiency and emissions in line with IMO standards. Such rigorous evaluation frameworks are essential not only for validating the effectiveness of new technologies but also for guiding future advancements in sustainable maritime operations.

In addition, it is important to understand the energy consumption and capital costs associated with constructing and installing the GR system on a ship so that the industry and stakeholders can estimate the payback period. Some peer researchers have already investigated these aspects, and relevant outcomes have been published [11]. Building on this foundation, a more comprehensive lifecycle analysis of the GR system will be carried out in the near future, which will consider costs, energy use, and emissions during manufacturing and installation, alongside the energy and fuel savings realized in service following the installation of the GR system.