Abstract
As the demand for new sustainable solutions for harvesting energy increases, the offshore energy sector focuses on optimising well-established state-of-the-art solutions while striving for new innovative approaches. Hybrid foundation designs have introduced new challenges and raised questions regarding scour and effective countermeasures. To further improve the knowledge regarding scour prediction, this paper presents and analyses the results from an experimental study behaviour of a riprap protection system for a monopile that determines and characterises scour on a flexible arrangement of overlapping sub-areas. The study was complemented by a novel series of tests using a hybrid foundation, where an oscillating surge wave energy converter (OSWEC) type was coupled to the monopile. Despite being submitted to similar hydrodynamic conditions, distinct differences in the scour rate and damage number (S3D) were observed for both models. Although the OSWEC type contributed to local wave height attenuation (up to a 30% reduction on the leeward side of the hybrid monopile), its oscillatory motion severely aggravated scour, with measured damage rates two to three times higher than those observed in isolated monopiles. These results raise relevant questions about the applicability of existing design formulas for scour protection and underscore the necessity for revised criteria tailored to hybrid offshore foundations.
1. Introduction
1.1. Background
Offshore wind energy research has grown rapidly, becoming a key component of a global renewable energy strategies. The structural integrity and long-term stability of offshore wind turbine (OWT) foundations, predominantly using monopiles [1], are critical for ensuring economic feasibility and safety. A primary concern regarding the stability of the foundation, which entails around one-third of the overall investment [2,3], is scour, a common cause of interference in bearing capacity, the ultimate, and service limit states [4,5]. Various countermeasures, such as riprap protections, represent an essential part of that investment [6] and are commonly installed at the base of these structures to mitigate scour-related challenges. Implementing these countermeasures follows established empirical guidelines [7]. Existing design formulas and approaches are commonly monopile-related, creating a lack of a general understanding of scour development at more complex structures, such as jackets, gravity-based foundations (GBF), tripods, or even hybrid foundations [8]. The concept of hybrid energy solutions, i.e., the co-location of wave energy converters (WEC) with offshore wind foundations, has developed increasing interest from the scientific community and the private sector. Enhancing energy yield and optimising spatial utilisation of marine areas could help lower the levelised energy cost (LCoE). It remains unclear to what extent sediment mobilization and altered flow patterns caused by hybrid monopile structures impact the marine environment both near the foundation and in the far field. While WECs are designed to extract energy from waves, their presence can modify in-depth hydrodynamics, wave propagation, current patterns, turbulence levels, and scour mechanisms (downflow, horseshoe, and/or lee–wake vortices) around the foundation. Understanding the impact of these changes on the performance and stability of existing scour protections is crucial for a safe and efficient deployment of hybrid offshore energy systems.
Several authors have studied the effectiveness and behaviour of riprap protections, inspired by rubble-mound breakwaters. This type of countermeasure is widely used due to its low cost and material availability, although transport and installation costs may vary with the location, armour layer thickness, and required stone size [9,10], among other aspects.
1.2. Scour Protections: Design
The threshold of motion concept by [11], was one of the first studies providing insights into scour and scour protection design. This type of protection was later classified as static by [7,12] since the movement of the elements of the armour layer is not allowed. Hence, the median stone size (D50) should be determined so the shear stress induced by the offshore conditions is smaller than the critical shear stress (τcr) of the rock material—Equation (1), where ρs is the mass density of the material, ρw is the water mass density, θcr is the critical Shields parameter, which for non-cohesive soils is given by Equation (2), and is dependent on the dimensionless grain size (D*), Equation (3), where ν is the kinematic viscosity of water. For D* > 100 on non-cohesive soils, θcr has the asymptotic value of 0.056.
An amplification factor (α) for monopiles should reflect the foundation’s effect on enhancing the flow conditions and the associated shear stress [13,14]. An alternative way to obtain the maximum wave-and-current-induced shear stress for wide graded protections was provided by [15], but the formula uses the D67.5 value for a θcr = 0.035, instead of D50.
The conservative approach of static design led to expensive solutions, given the larger stone size applied, but it is the most common type of countermeasure used in commercial offshore wind projects [9,10]. An optimisation was introduced by [12] in the OPTI-PILE project, the concept of dynamic protection, which allowed for the controlled movement of the armour layer elements, thus reducing both the size, thickness, and volume of the material needed [2]. This new approach, [12], proposed a stability parameter (stab), Equation (4), where θmax is the maximum dimensionless wave–current-induced shear stress. The threshold of motion ceases to be the design criterion, and [12] defines failure when the filter layer is exposed to an area equivalent to 4—an area equivalent to a square of two-by-two stones of Dn50.
Nonetheless, the stab parameter was still dependent on the amplification factor, whose values differ from author to author and cannot be extrapolated to more complex structures [8,9]. Therefore, the three-dimensional damage number (S3D) for scour protection was introduced by [7,16], based on the concept of the two-dimensional number [17]. By performing an extensive physical model study, it was noted that the stab parameter failed to predict some of the motion caused under different hydrodynamic conditions. The advantage of the proposed S3D, Equation (5), was that it is not dependent on the critical shear stress or the amplification factor, leaving behind some of the limitations of the considerations presented by [11,12,15], allowing a classification of the protection into three different levels of damage: static (S3D < 0.25), dynamic (0.25 < S3D < 1.00), and failure (S3D ≥ 1.00):
where N is the number of waves, g is the gravitational acceleration, d is the water depth, Um is the orbital velocity, Tm−1,0 is the energy wave period, s is the ratio between ρs and ρw, Uc is the depth-average velocity, ws is the settling velocity, a0, a2, a3 and b0 are regression coefficients equal to 0.00076, −0.022, 0.0079, and 0.243, respectively, and a1 and a4 are coefficients for hydrodynamic conditions defined in [7,16].
Although the design concept of dynamic stability enables the optimisation of scour protections, testing conditions of the formula were extended by [18,19,20], concluding that:
- The design equation does not consider the thickness (ts) and pile diameter (Dp) variables.
- The limits established for stability showed that some overlapping situations arose; thus, the failure condition could occur for values above the limit of 1.00.
- Like in the static protections, the equation was obtained using only monopile foundations and a short variety of water depths and layer thicknesses.
- The failure criterion used by [7] was the same as in [12]. So, for the reference sub-area of 4, the maximum dynamic behaviour limit of S3D = 1.0 has the physical meaning of the scour protection decreasing in thickness by a distance equal to Dn50. For scour protections with thicknesses over nDn50 (n > 1), S3D = 1.0 may not be truly representative of failure.
- To quantify the S3D values, the scour protection was divided into fixed sub-areas with an equal area to the monopile cross-section, thus neglecting the damage occurring in the intersection of the sub-areas, the effect of damage in adjacent sub-areas, and not considering the cumulative impact.
An alternative methodology [21] discusses a different way to analyse the damage by creating a mesh of overlapping circles placed in concentric rings, centred at the foundation with an adaptable overlapping distance, angle, and resolution, offering a more detailed assessment of the extent and severity of scour. The concept prevents an excessive lowering of damage due to the averaging of the scour depth over larger sub-areas, reduces deceptive damage interpretations, can be adapted to more complex structures, and enables a much larger population of S3D values quantified over the scour protection’s area, thus allowing for the statistical analysis of damage, describing failure with additional parameters (standard deviation, 95th percentile, etc.) rather than only using the maximum damage number. However, this methodology still lacks a detailed definition of the limits to classify protections as dynamically or statically stable or failures. Hence, the literature shows a need for more physical modelling tests, such as the ones presented here, to address this gap.
The radius of the sub-area (Rcircle) is given by two parameters, Dn50 and a multiplication factor (p), Equation (7), which is chosen so that the area of the circle reflects a certain area (Asub), such as, for example, the failure criterion [12]. A percentage of the radius defines the overlapping distance. However, according to [21], the overlapping distance has a reduced influence. No considerable gains were obtained for overlapping distances different from 50%. The S3D is calculated by:
The sub-area arrangement and the mesh characteristics were analysed by [21] by comparing results for different grid ratios. The measurements revealed a strong dependency of the damage number on the size of the sub-area (Asub) and the S3D,max, which increases significantly with increasing grid ratio, thus revealing that the grid ratio selection can completely impact the damage calculation and the scour protection behaviour assessment. This ratio, ηS3D,grid, is given by:
An increase in the grid ratio for the same results in a decrease in the sub-area. Varying the grid ratio also implies a variation in the number of elements. Therefore, a higher value of ηS3D,grid indicates that the eroded volume pattern resembles more closely the digital terrain model (DTM). The conclusions derived from the variation of the ηS3D,grid highlight the necessity for a uniform and justified selection of a criterion of failure and size of the sub-area. Hence, a statistical analysis was performed by [21] to determine if a specific ηS3D,grid led to a convergence of the S3D values, concluding that the variation between ηS3D,grid = 0.25 (Asub = ) and ηS3D,grid = 0.5 (Asub = 2) seemed to be reasonably small, pointing to the failure criteria suggested by [12] to be a realistic limit to identify failure in scour protections. The research also concludes that, under this methodology, the acceptable damage number for dynamic scour protection needs to be defined, in opposition to the unit value formerly proposed. That implies larger datasets to analyse the influence of the armour layer thickness, the presence of a sand filter layer or geotextile, and the relation with parameters such as the Keulega–Carpenter (KC) and/or the Reynolds (Re) numbers.
1.3. Deformation and Mobility
More recently, ref. [22] performed an extensive database of 380 tests and claimed that the spatial deformation due to scour around a monopile is not unambiguous and that the classification and interpretation of scour protection’s behaviour into classes is not straightforward. It requires the precise definition of what constitutes failure, which can often be “case-specific”. It highlights that calculating the scour deformation depth could be more intuitive for design purposes. It points out that with only two parameters, it can quantitatively describe the deformation of a scour protection and presents a formula to predict it—Equation (9). These two parameters and their interpretable physical meaning are:
- MOBtop (relative mobility): measures the hydraulic loading at the top of the scour protection relative to the resistance of the armour layer material. In practical terms, this is the stab parameter presented by [12];
- KCtot (Total Keulegan–Carpenter number): measures and evaluates the contribution of the wave-orbital and steady-current velocities relative to the structure. It measures the wave stroke asymmetry and the bed shear stress amplification difference around the pile—Equation (10).
Equation (9) only considers two parameters to prevent overfitting. Still, the impact of the material grading width, the storm duration, the ratio of water depth vs. pile diameter, the wave–current velocity ratio (Ucw), and many others was assessed. However, none seemed to depend on the deformation, such as MOBtop and KCtot. Moreover, the results showed a weakly positive correlation between the two parameters, i.e., lower mobility numbers (relatively stable rocks) are associated with lower KC numbers (relatively large piles).
To measure deformations and to recognise the damage areas, a moving-disk filter algorithm was used [23], which separates scour deformation from sinking or sliding. However, the algorithm uses Asub = 2, an area equivalent to a circle with a diameter of 5D50. It is stated that the sub-area selected by [22] prevents recognition of spot deformation caused by the displacement of larger armour layer material, claiming that the failure criterion suggested by [12] does not eliminate spot deformation. By averaging a local spot deformation within a sub-area of 4 over a circular area of 4, it only represents approximately a weight of 20% within the moving average area—the local spot deformation is not neglected but instead weighted differently. Based on the average damage pattern from the 380 tests, it is suggested that according to the respective values of the MOBtop and KCtot the scour deformations occur in three distinct areas (upstream side of the pile, deposition area, and downstream side of the pile), which can be correlated to six different deformation pattern classes defined by [23]:
- Class 1: negligible deformation, small settlements, spot deformation, or slight local sinking (1.5 ≲ KCtot ≲ 4 and 0.20 ≲ MOBtop ≲ 0.50).
- Class 2: upstream deformation with negligible downstream deformation, associated with downflow pattern (1.75 ≲ KCtot ≲ 5 and 0.20 ≲ MOBtop ≲ 0.85).
- Class 3: evenly distributed upstream and downstream deformation. Increasing influence of lee–wake vortices (2 ≲ KCtot ≲ 5.5 and 0.35 ≲ MOBtop ≲ 0.85).
- Class 4: mainly downstream deformation. Higher prevalence of lee–wake vortices (3.5 ≲ KCtot ≲ 8 and 0.40 ≲ MOBtop ≲ 1.10).
- Class 5: deep upstream deformation combined with a single deep downstream deformation point. Can be difficult to distinguish from Class 4 but is highly related to the presence of a meaningful steady current (2.5 ≲ KCtot ≲ 9.5 and 0.35 ≲ MOBtop ≲ 0.95).
- Class 6: deformation mainly upstream with a single relatively shallow downstream deformation point. Associated with low current velocities or even only-wave conditions. Horseshoe vortices prevail over lee–wake vortices (3.5 ≲ KCtot ≲ 5 and 0.6 ≲ MOBtop ≲ 0.8);
By comparing tests with similar MOBtop and KCtot, but with different contributions from waves and currents (only waves, wave-dominant conditions, and current-dominant conditions), it was observed that the predicted scour depth was in the same order of magnitude of the measured values—Equation (9) had a 0.85 correlation between the measured and the predicted S/Dp values [22]. Nonetheless, the author also underlines that the formula can sometimes overestimate S/Dp for smaller values of KCtot, and underestimate for larger values of KCtot. Additionally, the deformation and scour pattern observed were significantly different, and sometimes some of the classes were difficult to distinguish, as evidenced by the overlapping range of values for both parameters. This observation was partially attributed to the asymmetry of the orbital wave motion when more intense current velocities exist. It emphasises that combining the hydrodynamic conditions is important to determine where the peak deformation will occur. In contrast, the values of the KCtot and MOBtop parameters will predict the possible range of scour depth and damage. Finally, it suggests and emphasises the need to develop a design formula combining scour depth, area, and volume, with guidelines on the volume–area–depth relation and requirements for what constitutes a universal, clear, and unambiguous definition of scour protection failure.
1.4. Hybrid Structures
Although dynamic scour protection systems for monopiles have been the focus of the scientific community, significant knowledge gaps persist, particular due to limited data, and limited experimental studies about structures with complex geometries, hybrid structures, or other marine harvesting technologies in general [8]. The oscillatory or rotational motion of these devices induces additional soil-fluid-structure interactions, potentially causing significant alterations to wave orbital motion, current velocity fields and overall flow patterns. Standard scour protection behaviour and expected scour patterns may no longer apply. Therefore, design guidelines and equations could be misadjusted as they do not consider certain characteristics imposed by these devices. New design equations should consider not only structural and environmental parameters regarding the foundation and the offshore conditions, respectively, but also consider cyclical variations of pressure, disturbance/enhancement of flow patterns, wave reflection/attenuation, impact on soil properties, and vibration increments and/or modifications on the natural frequency of the structure. A review study on cases of scour on WECs and tidal–current energy converters (TECs) only, on WECs used as a protective measure in front of pipelines and monopiles, and even on WECs or TECs incorporated into breakwaters and monopiles, respectively, was performed by [8]. None of those studies used scour protections, and different results were reported: from no scour detection to reductions in the scour rates in the vicinity of structures to detrimental cases where scour rates were enhanced.
Due to the lack of consensus on reports and the absence of scientific studies using scour protections for hybrid offshore foundations, the present work provides a comparative experimental study that applies a riprap scour protection to both a monopile and a hybrid monopile foundation. The hybrid configuration was obtained by an in-house adaptation of a WEC [24,25,26] to the specific dimensions of the experimental setup. The riprap scour protection was designed based on the configuration and methodology used by [7]. However, instead of determining the varying median stone diameter (Dn50) for the intended hydrodynamic conditions, the study estimated the damage number and the scour depth across a range of wave and current combinations for the same scour protection configuration. The approach allowed for predicting the protection’s behaviour regime (static, dynamic, or failure), thus enabling a comparison between the expected results and the experimentally measured outcomes. For the scour measurements, the overlapping methodology was used [21] to characterise scour damage in rubble mound scour protections and other marine structures, based on the statistical analysis of damage distribution in flexible meshes of overlapping circular sub-areas. Subsequently, a cautious and meticulous study of all relevant variables was conducted, drawing upon the insights from the literature. The aim was to encapsulate the existing knowledge and most recent research on offshore foundation scour protection, pointing out potential knowledge gaps and research synergies.
The findings reveal that despite the WEC-induced attenuation of the incident hydrodynamic conditions, its oscillatory motion induces complex flow patterns (including enhanced downflow, horseshoe vortices, and lee–wake vortices) that lead to irreversible damage to the riprap protection layer. Moreover, successfully applying the overlapping circles method to determine S3D for scour damage assessment provides a precise damage quantification. However, the obtained damage values raise significant questions regarding the applicability and conservatism of existing design criteria and formulas proposed for monopiles [7,15], and in the context of hybrid foundation systems. This research contributes to a deeper understanding of the hydrodynamic interactions within hybrid offshore energy farms. It provides critical insights for designing and maintaining scour protection measures in such complex environments. These results emphasise the need for new criteria and guidelines for designing protective measures for a broader spectrum of offshore and marine technologies and structures.
2. Experimental Setup
2.1. Wave–Current Flume
The experimental work was carried out in the wave-and-current flume of the Hydraulics Laboratory of the Hydraulics, Water Resources, and Environmental Division (LH-SHRHA) in the Faculty of Engineering of the University of Porto—FEUP (Portugal). The infrastructure is 29 m long, 1 m wide, and 1 m deep, fed by a constant head reservoir. The sediment pit in the middle of the flume has a length of 3.4 m, a width of 1 m, and a depth of 0.4 m. Wave reflections are reduced by a passive wave absorption system [27]. A singular piston-type wavemaker at the upstream side of the flume can reproduce regular, irregular, and solitary waves up to 0.25 m for a maximum water depth of 0.7 m. The experiments were conducted using a geometric scale of 1:50 with incident waves propagating in the direction of the currents [28]. Currents were generated using two intake pipelines with a combined maximum flow capacity of 255 m3/h, ensuring a depth-average mean flow velocity of up to 0.16 m/s for the target water depth d = 0.4 m. Tests also include regular/irregular “waves-only” conditions. Irregular waves were reproduced following JONSWAP spectra with a peak enhancement factor (ϒ) of 3.3, adopting a representation of North Sea conditions for all tests.
For the wave measurements, 4 wave gauges, sampled at 100 Hz, were placed along the flume to measure the water-free surface elevation at selected locations (Figure 1). Two gauges were placed on the seaside near the model to measure the local wave conditions, one on the leeward side to assess the effects of the oscillating surge WEC on the transmission coefficient, and one closer to the wavemaker. The gauge data allow the estimation of the wave-generated bottom orbital velocities (Um) using a MATLAB (v.R2022b) routine [29], which is necessary to predict S3D accurately. The reflection coefficients were determined for every test, using the incident and reflected wave heights, with values ranging from 0.10 to 0.17.
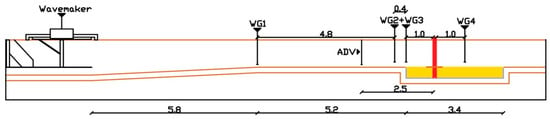
Figure 1.
Experimental setup and wave gauge (WG) placement (dimensions in meters).
Current-induced flow velocities were measured through an Acoustic Doppler Velocimeter (ADV)—Vectrino+, Nortek AS, Rud, Norway. The ADV was placed in line with the wave gauges, 2.5 m upstream from the model (Figure 1). The ADV was installed vertically at 0.16 m (0.4d) above the flume ground level, sampled at 100 Hz, with the x-axis pointing in the current direction. Measurements were not made closer to the bed due to the ripple migration and the minimum distance required for a good signal quality of the ADV. Preliminary tests were carried out to adjust the intended Uc values without the influence of waves.
2.2. Model Layout
A monopile foundation was simulated by acrylic glass with a diameter (Dp) of 110 mm. The pile was positioned around 1 m from the beginning of the sediment box at a 12 m distance from the wavemaker (Figure 1). A circular-shaped dynamic scour protection model was designed [7,16], with a uniform thickness of 2.5 times the nominal median grain size (Dn50) and an overall diameter of 5 times the pile diameter (Figure 2). The material yields a Dn50 = 3.696 mm for the armour layer, a density of ρs = 2.66 mg/m3, and a D85/D15 ratio of 3—very wide grading material [30]. Some stones were painted in different colours, creating mainly two concentric rings around the pile (Figure 3). The idea was to have an inner circle demarcating the amplification zone area and to allow a visual observation and distinction of the amount, direction, and displacement of the stones. A polypropylene geotextile with a surface density of 0.330 kg/m2 and the same diameter as the armour layer was applied as a filter layer to avoid the washing out of the fine material. As for the sediment box, the sand used had a median diameter of d50 = 0.215 mm, a density of ρs = 2.59 mg/m3, and a geometric standard deviation σs = √(d84/d16) = 1.8.
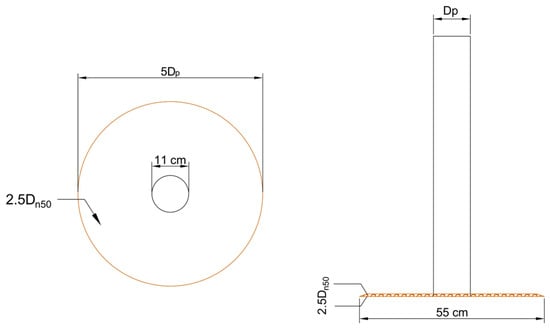
Figure 2.
Monopile physical model scheme (Geometric scale: 1:50).

Figure 3.
View of the scour protection (with demarcation of the amplification zone).
Regarding the WEC used to perform tests for a hybrid foundation, several devices could be suitable for testing. To assess and analyse the influence of a converter’s oscillatory movement, it was decided to adapt and scale down a FOSWEC (floating oscillating surge wave energy converter) device [24,25,26]. This 6-degrees-of-freedom (DOF) floating WEC was designed, built, and tested at Oregon State University in a geometric scale of 1:33 to develop open-access datasets for validating numerical model codes and create an in-house device suitable for future experimental campaigns regarding marine renewable energy. The device comprises two flaps hinged to a central platform, containing a power take-off (PTO) system and two belt drive systems that operate the flaps. It also has two lateral buoys and openings on the top and bottom of the device (Figure 4).
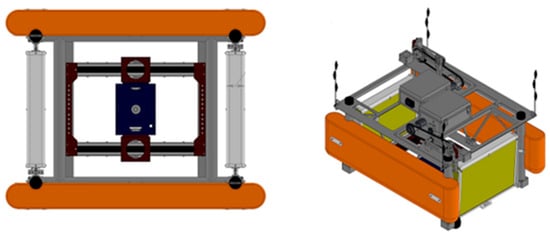
Figure 4.
Original FOSWEC scheme [25], adapted and reprinted with permission from© 2020 Elsevier Ltd. (Amsterdam, The Netherlands).
The adapted model built for this study was a simplified version fixed to the monopile 15 cm above the sediment bed through two small cantilever arm braces (Figure 5), locking all the converter’s body DOFs. Instead of a PTO system, a simplified system using springs was mounted, with a spring constant that limited the flaps’ pitch to a maximum motion angle of ±25°, Figure 6, the same angle motion of the FOSWEC device [24]. The simplification and substitution of a fully functional PTO system using springs was made, since the primary goal of this study was to assess the impact of the device on the amplification and enhancement of the flow patterns, instead of evaluating the performance and efficiency of the converter’s harvesting capacity under the proposed hydrodynamic conditions.

Figure 5.
Oscillating surge WEC model construction and installation.
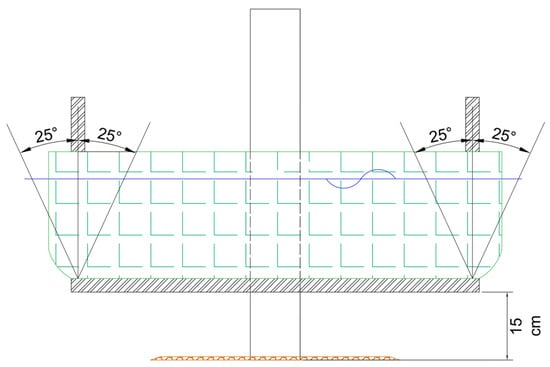
Figure 6.
Oscillating surge WEC scheme (Geometric scale: 1:50).
It is recommended to maintain the blockage ratio below the recommended threshold of 1/6 to minimise wall effects and avoid local acceleration of the flow in the contracted areas or excessive influence of the wall’s friction in the hydrodynamics [14]. In the present study, the inherent constraints imposed by both the flume spacing and the necessity to maintain the structural configurations and dimensions of the OSWEC led to a slight deviation of this ratio, as the device’s overall form could not be appropriately scaled without compromising its wave–device interaction or the experimental setup. However, the region for higher blocking is placed at the superficial part of the water depth. Excluding the submerged part of the OSWEC at the monopile foundation, the ratio remained way below 1/6, i.e., 1/9. The model was carefully implemented to optimise the balance between achieving a realistic Froude-scaled setup and mitigating the potential blockage effect closer to the seabed to avoid the flow blockage near the protection. Therefore, for the region directly between the OSWEC’s base and the sediment bed/scour protection, encompassing a 15 cm vertical distance, the blockage ratio was successfully maintained below the 1/6 mark. This ensured that the near-bed flow dynamics in this area, which are the most influential on the scour processes, were not influenced by the side wall effects. However, for the model’s upper region, the considerations mentioned above and scaling led to a higher blockage ratio. It is acknowledged that this represents a study limitation and may lead to a localised acceleration of the flow and enhancement of streamflow contractions. However, it is essential to contextualise its potential impact on these research objectives. Since the focus was to assess scour damage occurring at the protection due to the oscillating movement of the WEC’s paddles, which creates mainly a variation of upward/downward pressure right beneath the device in the scour protection region, enhancing downflow in an area where the blockage criterion was met. Therefore, while the hydrodynamics of the device’s upper structure might be subject to some influence, it can be stated that the results regarding the scour damage in the protection remain representative. Future research could benefit from testing in larger-scale facilities to further minimise wall effects across the entire model and validate these findings. Nevertheless, the present study aimed to provide novel and valuable insights into the scour behaviour around hybrid foundations, highlighting critical interactions essential for effective design and understanding scour protections.
2.3. Hydrodynamic Conditions and Scour Measurement Technique
The hydrodynamic conditions (Table 1) were selected to cover a specific range of wave–current ratios (Ucw) and KC numbers while considering other experimental campaigns found in the literature. Tests were run until 3000 waves, except in cases where the failure of the scour protection occurred prematurely. Three types of hydrodynamic conditions used for the monopile (M) and hybrid foundation (MH) were: irregular waves with currents in the same direction (WC), irregular waves only (WI), and regular waves only (WR). For the selected conditions and with the scour protection configuration, Table 2, it was expected to observe different behaviour from the scour protection (static, dynamic, or failure).

Table 1.
Physical model hydrodynamic conditions (geometric scale: 1:50).

Table 2.
Physical model foundation and scour protection configuration (model values).
To measure the seabed bathymetry and the scour of the protection, a FARO® focus laser scanner (2 million points/second, a 3D precision of 2 mm at 10 m, 1 mm standard deviation at 10 and 25 m) was used to obtain high-resolution 3D Digital Terrain Models (DTM). This technique allows the accurate representation of the erodible areas and the respective surroundings; thus, they were taken before and after each experimental test and wave train. The laser scan precision is smaller than the Dn50 used in the scour protection, hence enabling a high-precision identification of all the armour layer units’ movements, even spot deformations. The postprocessing of the DTMs was performed using the Autodesk ReCap and the CloudCompare software (v2.12.4). This resulted in precise point clouds of the seabed, scour protection, and hybrid structure profiles and contours. The DTMs were then used to assess scour depth and the S3D,measured values using a MATLAB routine [21] to employ the overlapping-circle technique. In addition, a visual observation and evaluation, plus a photographic register of all tests, were made to compare the results of the damage number obtained.
3. Experimental Results and Analysis
The experimental test campaign was planned so that the riprap protection and the controlled hydrodynamic conditions were aligned with the study performed by [7] for a more direct comparison of the results and to assess the impact and validation of using the overlapping-circle technique. A discussion of the measured results with the KCtot-MOBtop prediction formula [22] was also performed. The results for both formulations differed from the predicted values, opening a meaningful discussion regarding the failure criterion and how scour damage is measured and evaluated.
3.1. Scour Damage (S3D)
For all the tests, the overlapping-circle technique was applied by using a Asub = and an overlapping distance of 50% [21], allowing an objective quantification of the scour protection damage under each test condition. Table 3 summarises all the measured conditions. The Ucw values distinguish the three wave-dominated tests (Ucw < 0.44) from the current-dominated tests (Ucw > 0.44) [31]. The novel method provided high-resolution representations of the scour patterns and high accuracy of the S3D,measured values and distribution (see Figures in Appendix A). As expected, and generally, S3D correlates highly with the hydrodynamic load intensity. For low-energy conditions, the maximum S3D,measured values were lower and increased with higher wave heights. Also, when comparing the results of the wave-only tests (M_WI vs. M_WR and MH_WI vs. MH_WR), the S3D values were slightly higher when using regular waves, aligned with the findings of a study performed in rubble-mound structures [32], w attributed these difference to the fact that the root mean square (Hrms) value for irregular waves tends to be smaller than the wave height for regular waves.

Table 3.
Experimental measured conditions for scour protection tests—model values.
For the monopile tests (M_WC, M_WI, and M_WR), the scour protections exhibited lower damage rates across all the hydrodynamic conditions when compared to their hybrid structure counterparts (MH_WC, MH_WI, and MH_WR), as shown in Figure A1, Figure A2, Figure A3, Figure A4, Figure A5, Figure A6, Figure A7, Figure A8, Figure A9, Figure A10, Figure A11, Figure A12, Figure A13, Figure A14, Figure A15, Figure A16, Figure A17, Figure A18, Figure A19 and Figure A20 and Table 3, where very pronounced scour deformations were obtained for similar conditions. In some cases, nearly double or triple the damage number from the corresponding monopile test was obtained, consistent with the intense sediment erosion, the washout of the armour layer material, and the considerable sinking of the seabed under the filter layer (Figure 7).

Figure 7.
Damage comparison between the tests: (A) M_WR_14_1000 (monopile) and (B) MH_WR_14_1000 (hybrid monopile—test stopped due to large deformation of the armour layer and filter).
For most tests using a hybrid structure, failure occurred within the first 1000 waves. The only hybrid monopile test that provided scour protection support for some of the initial enhanced flow patterns was the MH_WC_7 test, which endured 2000 waves. The flow patterns responsible for the scour mechanism in monopiles are well documented [33]. However, with the results obtained for the hybrid structure, it is reasonable to assume that some of the main mechanisms responsible for scour were definitively enhanced. Due to the oscillatory movement of the paddles, on the front side of the foundation, the downflow was the flow pattern that caused most of the damage. Conversely, in the leeside, the movement of the downstream paddle enhanced the intensity of the lee–wake and counter-rotating vortices. Moreover, due to the dimensions of the WEC, the approaching flow conditions increase the streamline contractions around and beneath the device, which also adds to the overall result.
In contrast, monopiles retained integrity under mild conditions, M_WC_7 and M_WC_11, demonstrating dynamic behaviour unequivocally for the duration of the 3000 waves. For more intense conditions, the protection failed for M_WC_15.5 and M_WR_14 for the first 1000 waves. Although the regular wave-only test failed for the first wave train, the test was continued for comparison with the irregular wave test. The same was done for the hybrid test MH_WC_7, where failure occurred before the 3000-wave limit, but a final wave train was performed for comparison with the non-hybrid counterpart. Regarding the M_WI test, the high S3D value suggested that the scour protection had failed. Still, when visually assessing damage using Figure 8 and comparing it to Figure A10, no distinctive filter exposure was observed despite intense movement of the armour layer units. Therefore, the protection was deemed to be on the edge between the dynamic behaviour and failure.

Figure 8.
M_WI_14_3000 test scour protection.
A noteworthy capacity of dynamic scour protections is to reshape and recover from a specific damage degree due to the allowed movement of the armour layer units [12]. That capacity was empirically observed during the experimental tests, most notably by the tests M_WC_7_2000 to M_WC_7_3000. Furthermore, this characteristic was also manifested in a protection where failure occurred, from MH_WC_7_2000 to MH_WC_7_3000, where a partial recovery from a significant damage rate (quantified as an S3D reduction from 3.25 to 2.86) was observed. While both scenarios exhibit filter exposures, a subset of scour holes identified post-2000-wave train exposure was filled during the 3000-wave train. The backfilling originated from the armour layer units that had previously been displaced (Figure 9)—suggesting a potential for recovery under mild conditions. This observation raises a pertinent question regarding the potential for scour protections to recover and turn back to dynamic stability after failure.

Figure 9.
Scour holes (MH_WC_7_2000—left) and refilling (MH_WC_7_3000—right).
A discrepancy is visible when comparing the S3D,measured with those predicted by using Equation (5) formula (Table 3). It can be observed that, in general, the formula underestimates scour for the conditions tested. This is aggravated when dealing with a hybrid structure. The formula underestimates actual damage, suggesting that the formula needs to incorporate other non-linear factors that may occur in more complex or hybrid systems. However, this underestimation also stems from methodological differences in how damage is measured by the approaches developed by [7,21]. As previously mentioned, the methodology established by [7] makes use of fixed sub-areas equivalent to the monopile cross-section, which averages the scour depth over larger areas. Moreover, it does not consider the thickness of the scour protection.
Hence, if the damage number represents the number of protection layers lost to scour as a function of Dn50, as indicated by [7], for the model thickness (ts = 2.5Dn50), an S3D = 1.0 will not be a valid representation that physically failure occurs. Even dynamically stable scour protections were observed by [7,20], for S3D values larger than 1.0, up to 1.25, thus showing that the reference values proposed by [7] can be conservative. On the contrary, the approach developed by [21] allows the use of the criterion of failure suggested by [12], as the sub-area to be analysed over an overlapping mesh created over the protection. Thus, for a selected Asub, in this case , the filter layer exposure and failure should at least occur only when . Considering this, a comparison of S3D and thickness as a function of Dn50 could be more informative. Consequently, the failure limit should not be a fixed threshold value independent of the protection thickness, such as S3D = 1.0, as proposed by [7], but a range around S3D = ns for ts = ns·Dn50, accounting for a degree of uncertainty, being that ns is the number of rock stone size layers [18].
By adopting this perspective, comparing S3D,measured values to a starting point of S3D,failure = 2.5, determined by the ns value used during the experimental tests, allows for a clearer visual interpretation of the scour protection’s behaviour as a function of the damage number measured using the overlapping method and a more straightforward understanding of the physical meaning of the S3D—see Figure 10, Figure 11 and Figure 12. The static limit of S3D = 0.25 was maintained, as in the research carried out by [7]. It is worth reiterating that for the M_WI test, the values obtained for the damage number, in fact, point to failure for the totality of the 3000 waves, even for S3D,failure = 2.5. This reinforces the idea that the boundary between scour behaviour classification should be defined by a range that accounts for a certain degree of uncertainty instead of a single fixed threshold value.
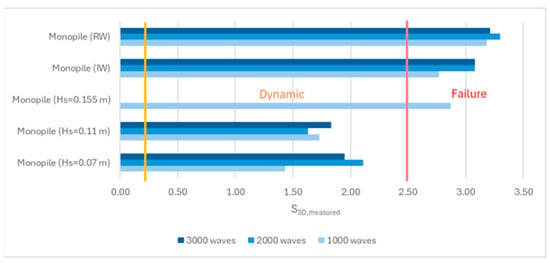
Figure 10.
S3D and damage classification for new limits based on the thickness of the scour protection—monopile tests.
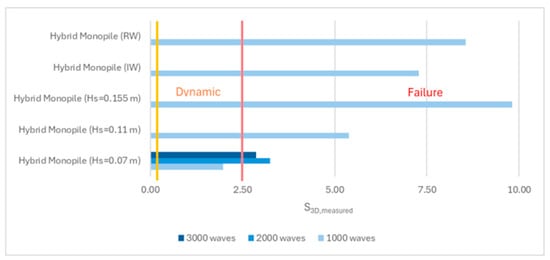
Figure 11.
S3D and damage classification for new limits based on the thickness of the scour protection—hybrid monopile tests.
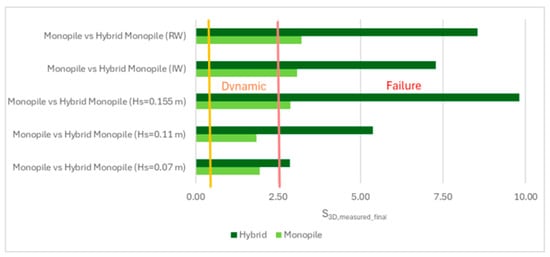
Figure 12.
Comparison of S3D values between the monopile and hybrid monopile for the same hydrodynamic conditions.
As a side note, it was detected that in some of the tests (M_WC_7, M_WR, and MH_WC_7), the damage number reached a peak value around 2000 waves and subsequently decreased slightly for 3000 waves or even remained constant in the M_WI test series. This observation highlights that most damage occurs in the first 1000 waves, as observed by [18]. Thereafter, scour holes begin to backfill with surrounding material, after 3000 or even 5000 waves, while other holes may appear, indicating an equilibrium state within this interval.
The development of a design formula combining scour depth, area, and volume, with guidelines on the volume–area–depth relationship, was raised by [22]. A generalisation of the scour volume–area–depth relation, assuming a S3D value for a Asub = ns, is given by applying the methodology by [21]:
Moreover, assessing the ratio S/Dp is a widespread practice in the literature when analysing scour rates for unprotected structures. Conversely, determining the deformation for riprap scour protections becomes expendable, since S/Dp becomes reduced, in some cases residual, and does not help the interpretation of the state of the protection. Taking this into consideration and due to the limitations of the fixed sub-areas approach [7], a new ratio was introduced by [18], the damage increase ratio (ΔS3D/ns), to express the variation of damage between each wave train, while considering the thickness of the scour protection layer by using the number of rock stone sizes. The experimental test results determined a specific range of values of the damage increase ratio for each scour protection behaviour (static, dynamic, failure) for three different durations (0 to 1000 waves, 1000 to 3000 waves, and 3000 to 5000 waves):
- From 0 to 1000 waves: = [0.05–0.09] (static), = [0.07–0.39] (dynamic), = [0.19–0.42] (failure).
- From 1000 to 3000 waves: = [0.00–0.03] (static), = [0.00–0.12] (dynamic), = [0.00–0.50] (failure).
- From 3000 to 5000 waves: = [−0.02–0.01] (static), = [−0.01–0.07] (dynamic), = [−0.04–0.17] (failure).
By comparing the values in Table 4, most damage occurs for the first 1000 waves, but at higher rates than the ones proposed by [18]. However, for the 1000 to 3000 wave duration, the values align with the suggested range. By looking strictly for the ratio values, it is possible to determine the speed and rate at which scour damage is developing, but it is hard to determine in which condition and/or behaviour the protection is. Therefore, instead of using the S/Dp and the ΔS3D/ns ratio, which do not have a clear physical meaning and can be unclear, and in the case of the ΔS3D/ns ratio has overlapping ranges for different behaviours, this study proposes a slight adaptation: S/Dp into S/ts and ΔS3D/ns into S3D/ns, both for a certain Asub (or Afailure).

Table 4.
Damage increase ratio results ΔS3D/ns.
These slight modifications convert both into more practical, intuitive ratios and are more representative of the scour protection deformation state and the relative amount of armour layer thickness loss. For these ratios, the authors suggest that the limits proposed by [7], 0.25 for static behaviour and 1.0 for failure, could make more sense as a good starting point than for the S3D:
- : failure–filter layer exposed, loss of filter layer and/or seabed lowering;
- : dynamic behaviour—loss of thickness in the armour layer and/or movement of the armour layer units;
- : static behaviour—no movement, or residual movement, of armour layer units;
- : accretion of sediments around the armour layer unit;
For most tests, a variable limit for the damage number and the S/ts ratio was used to fit the classification and assessment of the scour protection behaviour for the entire experimental campaign. The protections where failure was detected visually or with the overlapping-circle method correspond to values of S3D > 2.5 or S/ts > 1.0 (Table 5, Figure 10, Figure 11 and Figure 13). The same occurs for protections classified as dynamic, where S3D < 2.5 or S/ts < 1.0, with the only exception being the M_WI test, for the previously mentioned reasons. Therefore, it is worth mentioning that a failure criterion based on the S3D/ns or S/ts is defined by the scour protection properties and geometry and is independent of the foundation used. Possible higher values obtained for hybrid foundations are not an indicator to redefine the failure threshold criterion but an indicator of increased scour damage that eventually should lead to the necessity to upgrade the characteristics of the scour countermeasure. In the end, the overlapping method proved to be valuable in visualising, tracking, and identifying the scour patterns, holes, rate, and consequently the assessment and quantification of the damage and behaviour of each scour protection tested.

Table 5.
Scour depth, S3D/ns, S/ts, and scour damage comparison.
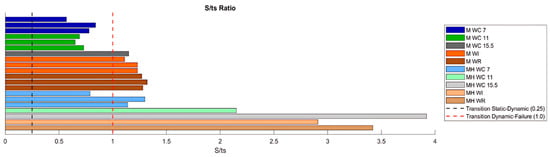
Figure 13.
S/ts ratio values and transition thresholds.
3.2. Overlapping Grid Ratio
It was proven by [21] that the damage number strongly depends on the grid ratio. However, the analysis of the volumetric damage concerning the grid ratio and the convergence between the two variables was made only for two large-scale cases. To expand and compare its dataset with the tests performed during this study, an analysis of the S3D,max results for each test for different ηS3D,grid was performed. Moreover, since the maximum damage number is valid only for a single value at the deepest point of the scour protection, a statistical study on the development of the standard deviation and the 95% percentile of the S3D was implemented to verify a possible convergence stage.
The grid ratios were selected to cover a variety of Asub values, including the monopile cross section [7], 25 (corresponding to five armour layer units), 4 as in [12], and many others equivalent to the arrangement of multiple or even single armour layer units (nDn50 × nDn50) (Figure 14).
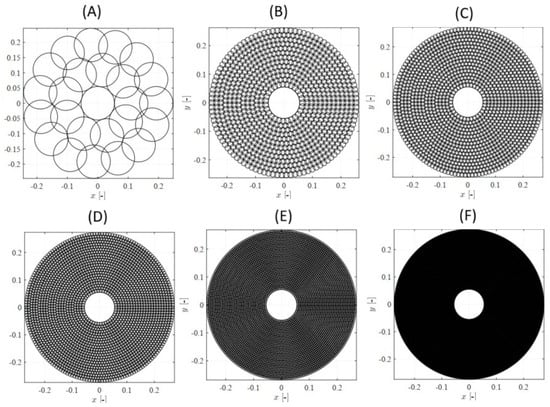
Figure 14.
Overlapping-circle arrangement for different ηS3D,grid and sub-areas: (A) ηS3D,grid = 1.43 × 10−3, Asub = Apile; (B) ηS3D,grid = 1/25, Asub = ; (C) ηS3D,grid = 1/16, Asub = 16; (D) ηS3D,grid = 1/9, Asub = 9; (E) ηS3D,grid = 1/4, Asub = 4; (F) ηS3D,grid = 1, Asub = .
Varying the grid ratio implies a variation in the number of elements, leading to a considerable variation in the maximum value of the damage number. Figure 15 illustrates the case for the M_WC_11_3000 tests. For higher grid ratios, i.e., lower Asub and more sub-areas, the scour pattern becomes closer to the DTM representation. The figure also illustrates the considerable variation of outcomes for different ratios, where for an Asub equal to the cross section of the monopile, the least amount of analysed elements, the maximum damage number detected was negative (accretion of sediments). Conversely, for an Asub equal to a single armour layer unit (), S3D was superior to the S3D,failure = 2.5 (representative of a meaningless spot deformation in depth).
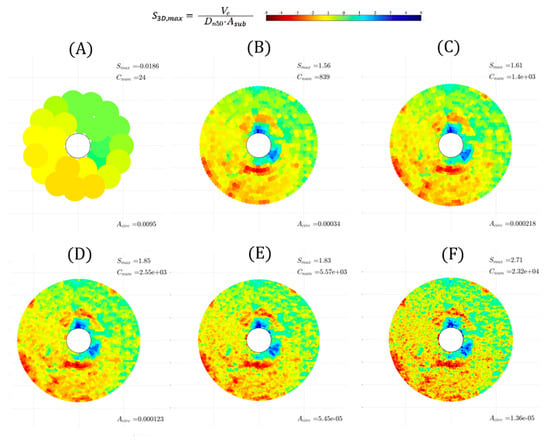
Figure 15.
Influence of ηS3D,grid on S3D,max value for test M_WC_11_3000: (A) ηS3D,grid = 1.43 × 10−3, Asub = Apile; (B) ηS3D,grid = 1/25, Asub = ; (C) ηS3D,grid = 1/16, Asub = 16; (D) ηS3D,grid = 1/9, Asub = 9; (E) ηS3D,grid = 1/4, Asub = 4; (F) ηS3D,grid = 1, Asub =.
The results obtained for the S3D,max vs. ηS3D,grid for all the tests in the study (Table A1 and Table A2) were plotted onto Figure 16 (monopile) and Figure 17 (hybrid monopile). Both plots show similar conclusions as in [21], a very strong dependency and positive correlation of the damage number with the grid ratio and/or size of the sub-area selected, demonstrating that different grid ratios lead to completely different results that would lead to entirely different interpretations of the scour protection behaviour. This is an argument for the necessity of considering a uniform criterion of failure to evaluate the performance of scour protections [21].
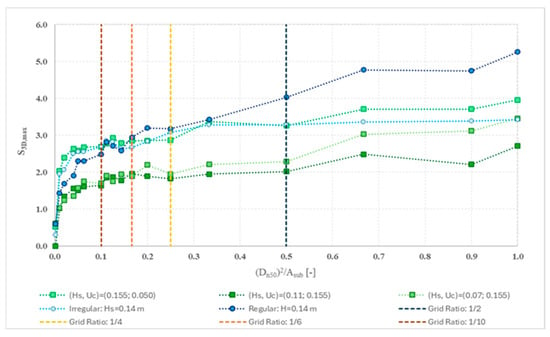
Figure 16.
Variation of S3D,max with ηS3D,grid—monopile tests.
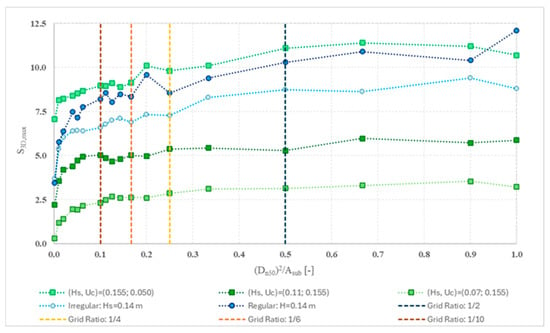
Figure 17.
Variation of S3D,max with ηS3D,grid—hybrid monopile tests.
By comparing the results and the plots, it is evident that the S3D,max exponentially grows until approximately ηS3D,grid = 1/10 (Asub = 10). The values seem to stabilise from that grid ratio value until ηS3D,grid = 1/4 (Asub = 4) and from that point forward starts to increase linearly for cases where the scour damage was quantitatively lower (monopiles), opposite to cases where the damage was significant (hybrid monopile), where the S3D,max value appears to remain almost the same independently form the Asub selected. Nevertheless, from the results obtained, the best range of grid ratios and sub-area to accurately assess the damage number value, for both cases, seems to be situated between ηS3D,grid = 1/6 (Asub = 6) and ηS3D,grid = 1/4 (Asub = 4), where residual or almost no differences were observed. These results indicate that the failure criterion 4, Ref. [12] is a reasonable limit to correctly identify failure in a scour protection and an accurate Asub to use on the overlapping method [21].
Since S3D,max seems to be fairly affected by the variation of the grid ratio and affected by minimal changes [21], the standard deviation (Figure 18) and the 95% percentile (Figure 19) of all S3D,sub values for each test were plotted to ensure if the convergence is given for the different grid ratios selected. For both statistical measures, S3D,max vs. ηS3D,grid for all the tests in the study (Table A1 and Table A2) were plotted onto Figure 16 (monopile) and Figure 17 (hybrid monopile). Both plots show similar conclusions as in the study performed by [21], a very strong dependency and positive correlation of the damage number with the grid ratio and /or size of the sub-area selected, demonstrating that different grid ratios lead to completely different results that would lead to entirely different interpretations of the scour protection behaviour. This is an argument for the necessity of considering a uniform criterion of failure to evaluate the performance of scour protections.
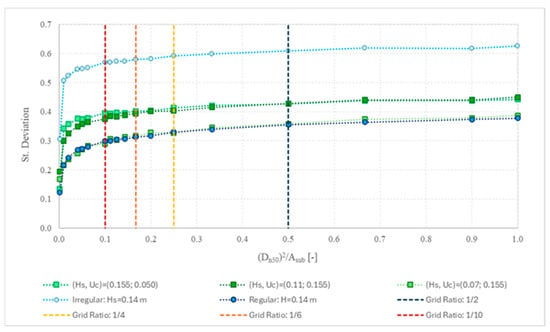
Figure 18.
Variation of the standard deviation of S3D,sub with ηS3D,grid—monopile tests.
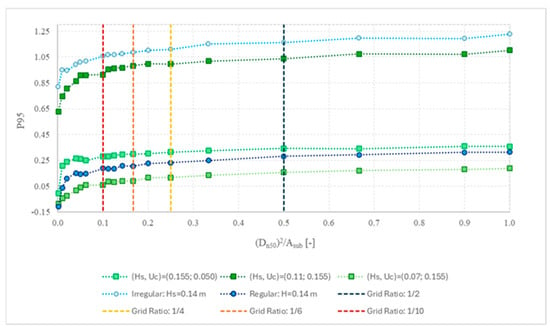
Figure 19.
Variation of the 95% percentile (P95) of S3D,sub with ηS3D,grid—monopile tests.
3.3. KCtot—MOBtop Effect and Ucw Analysis
In this section, the performance of the scour protection is evaluated using the dimensionless parameters MOBtop and KCtot, based on a predictive model developed by [22]. While the proposed formula has proven effective in characterising scour deformation in conventional monopile foundations, its application to hybrid structures was not considered. The MOBtop-KCtot framework was considered as having a higher correlation with scour depth and being the best absolute performance evaluator/predictor of a scour protection when compared to the stab parameter or the S3D [22]. However, the calculation of the absolute and dimensionless predicted scour depths (S and S/Dp, respectively) using Equation (9) showed a consistent underestimation for the monopile values measured 2 to 7 times higher than the predicted (Table 6). Similar trends were observed in the hybrid monopile tests, where actual scour depths exceeded the predictions by factors of 7 up to 11.

Table 6.
Scour measured vs. predicted values: KCtot—MOBtop design formula [22].
In a first analysis, these discrepancies may be attributed to the fact that the methodology proposed by [22] relied on a different algorithm [23] to detect deformations and measure scour depths, Asub = 20, that may dilute the localised scour effects when compared to the overlapping-circle method (Asub = 4). Additionally, the research developed by [22] used larger monopiles—Dp = 0.15 to 0.30 m vs. 0.11 m (model values)—different scour protection configurations—ts = [1,2] Dn50 vs. ts = 2.5Dn50, extent of 3Dp vs. 5Dp, ρs = [2650–3200] kg/m3 vs. ρs = 2666 kg/m3, and D85/D15 = [1,2,3] vs. D85/D15 = 3—and different model scales. Furthermore, the dataset (20 test points) in this experimental study was sparse when compared to the 380 tests performed by [22].
When a more detailed analysis was carried out, a crucial aspect was identified as a possible contribution to the discrepancy in the prediction values—the gradation width of the armour layer material. As Equation (2) was adopted by [22] to calculate the critical Shields parameter, the protection model in this study is considered a very wide-graded scour protection (D85/D15 = 3). For this type of scour protection, a lower value of θcr is recommended by [15] for calculating the stab parameter, which is the same parameter as the MOB [22]. For both foundations, improvements were detected by recalculating the Spredicted/Dp with the recommended value θcr = 0.035 (Table 7 and Figure 20).

Table 7.
Comparison of the predicted values using different critical Shields parameters.
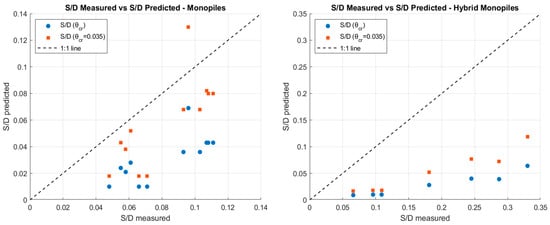
Figure 20.
Comparison between measured vs. predicted S/Dp, using different values for θcr.
For the monopile, despite most values still falling short of accurately predicting the measured results, a substantial improvement was identified—S/Dp values for the M_WC_11, M_WI, and M_WR tests were underpredicted by factors of less than 1.5, while the S/D value for the M_WC_15.5 test was even overpredicted—see Figure 21. Focusing on the results obtained for the hybrid monopiles, the differences between the predicted and the measured S/Dp decreased, but the prediction was still considerably far from the measured scour depths (Table 7, Figure 20 and Figure 21).
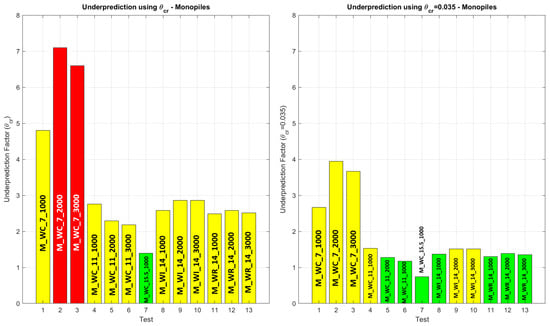
Figure 21.
Underprediction factor for monopiles, using different values for the θcr—green: under 1.5 times; yellow: between 1.5 and 5 times; red: over 5 times.
The pronounced underprediction values observed for the hybrid foundation (Table 7, Figure 20 and Figure 22), regardless of the θcr used to determine the MOBtop, cannot be solely attributed to the omission of the gradation width in the formula. Rather, it can be reasonably assigned to the presence of the WEC and its major influence on scour. Equation (8) was not developed to capture WEC-induced flow amplifications and associated shear stress increments generated by the paddles’ motion—effects absent from the conditions used to derive the formulation. As the MOBtop measures the hydraulic loading relative to the armour layer resistance, its variation depends not only on the stability of the protection but also on changes in the flow patterns. As the KCtot variable measures the contribution of wave-orbital and steady-current velocities relative to the structure, the WEC’s paddle motion, by enhancing the flow patterns acting on the foundations, is expected to exert a pronounced effect on both parameters, sufficient to substantially increase the bed shear stress acting on the scour protection to well above the θcr of the armour layer material. That contribution is not expressed in the formula by means of an amplification or safety factor, leading to a massive underestimation of the predicted scour depth.
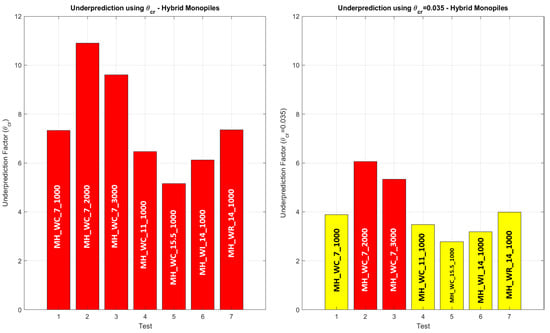
Figure 22.
Underprediction factor for hybrid monopiles, using different values for the θcr—yellow: between 1.5 and 5 times; red: over 5 times.
Nonetheless, the discrepancy between the measured vs. predicted scour depths for the hybrid monopile, in comparison to the monopile foundation, underlines the limitations and insufficiencies that current predictive models have in capturing the complexity that hybrid structures and WEC components and oscillatory movement integration induce in unsteady flow fields and offshore hydrodynamics. This reinforces the need for new predictive approaches tailored to multifunctional offshore structures that integrate in situ flow and seabed erosion measurements.
With the available metrics for assessing the scour protection condition, the parameter S/ts (scour depth relative to the protection thickness) or the S3D/ns (scour damage relative to the number of armour layer rock units) emerges as a more reliable damage indicator and/or predictor than the S/Dp. Unlike the S/Dp ratio, which lacks a clear physical correlation with the specific characteristics of the scour protection’s armour layer, such as Dn50 or overall thickness, both S/ts and S3D/ns directly reflect a direct and quantitative measure of the current state of the armour layer. For instance, a specific S/Dp value, even with known protection characteristics, offers limited insight into the protection’s behaviour, failing to illustrate whether failure occurred or if the scour countermeasure is in a dynamic/static state. While it quantitatively distinguishes different erosion magnitudes, it provides only a generalised appreciation of damage without offering significant qualitative information regarding the protection status or comparable information regarding the protection’s integrity. It provides greater utility in contexts where scour is measured without a scour protection, where the magnitude of the seabed erosion relative to the monopile offers a generalised sense of risk of ultimate and/or serviceability limit-state to the foundation. Conversely, S/ts and S3D/ns directly and unambiguously translate the percentage of protection in the evaluated area that has been eroded, offering a clear and actionable understanding of its condition. Furthermore, for hybrid foundations, where enhanced flow patterns due to the paddles’ movements and increased turbulence affect the erosion of the rubble-mound material, these parameters also offer sufficient credibility and a simpler visual representation and interpretation of the protection’s behaviour.
Although the classification of scour protections into deformation classes with the evaluation of MOBtop-KCtot is considered by [22] to be more useful than the standard behaviour classification (static, dynamic, and failure), it also acknowledges that the evaluation is not so straightforward and sometimes hard to determine. As shown in Figure 23 and Figure 24, most of the tests fall within the range of several deformation classes. An attempt to assess a specific deformation class for each test was made considering the description provided by [22] and the photographic record made during the tests, plus the DTMs and S3D distribution results in Figure A1, Figure A2, Figure A3, Figure A4, Figure A5, Figure A6, Figure A7, Figure A8, Figure A9, Figure A10, Figure A11, Figure A12, Figure A13, Figure A14, Figure A15, Figure A16, Figure A17, Figure A18, Figure A19 and Figure A20—see Table 8.
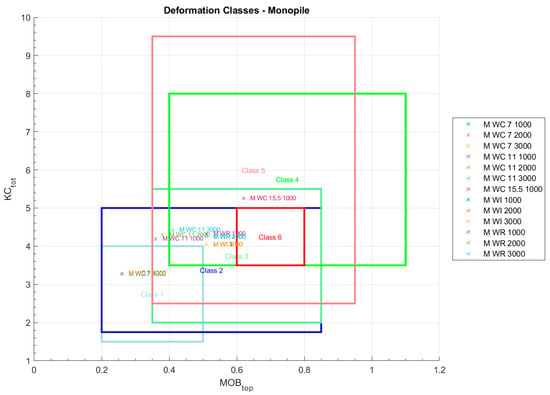
Figure 23.
Deformation classes for monopile tests.
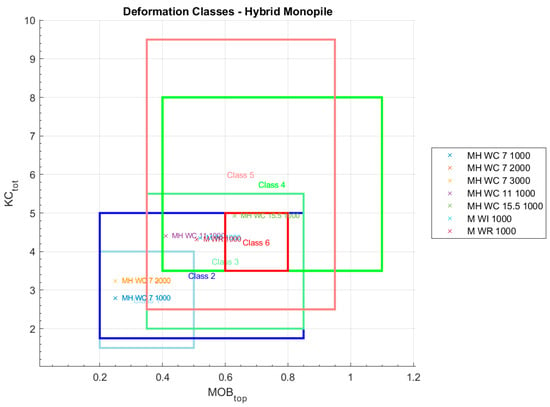
Figure 24.
Deformation classes for hybrid monopile tests.

Table 8.
Assessment of deformation class according to the criteria defined in [22].
Although the monopile tests were found to fall within one of the expected classes of deformation, a distinction was made in [22] based on whether the deformation occurred predominantly in the upstream or downstream area of the pile. When analysing the experimental tests in this study, it was observed that the damage occurred mainly within the vicinity of the pile, way inside the amplification area, mainly on the right and left sides. Moreover, in some cases, the deformation pattern was not evident in the photographic registration. It was only perceptible using the DTMs and the S3D results using the overlapping technique described in [21]. Additionally, according to the description of each class made by [22], the M_WC_15.5, M_WI, and M_WR tests should fall in class 6, since that class is associated with tests using low current velocities or cases with wave-only conditions. The tests M_WC_11_1000 and M_WC_11_2000 were classified as being in class 1, despite Figure 23 showing them outside of that class boundary. However, it was also reported in [22] that many tests expected to fall within a certain class may lie within the limits of other classes, or even outside of all defined class boundaries, due to significant overlaps.
Regarding the hybrid monopile tests, only the MH_WC_7 test sequence was in identifiable conditions to be placed within one of the described classes. For all the remaining tests, the scour damage was too excessive to identify a possible dominant location for the deformation in the protection or lack thereof. Therefore, considering the definition of each class presented in [22], each test was classified into the most appropriate class, considering the hydrodynamic conditions used in each test, and by adding a “+” sign in front of it, as a note of the extensive damage rates observed.
While categorising deformations by classes is deemed by [22] as a more useful classification, the fact is that it is not a linear, practical, or trivial task. From low to extreme scour deformations, distinguishing and classifying them could be challenging due to overlapping or even superposition of classes. Furthermore, it is possible to have deformation classes outside any boundary condition. This makes this classification system a highly subjective tool and less intuitive than the standard classification (static, dynamic, failure). However, directly comparing the MOBtop and KCtot to the damage number proved noteworthy.
Overall, S3D tends to increase with higher values of both variables (Figure 25), and regarding the monopile tests, it has a higher correlation with MOBtop number than the KCtot parameter (weak correlation). Since MOBtop measures the hydraulic loading relative to the resistance of the armour layer, essentially reflecting the potential for erosion/movement of the armour layer units, it provides high-quality information about the scour protection resistance to the loads and whether it might fail. Therefore, it directly captures the actual effects of the main scour mechanisms on scour, resulting in a higher correlation with the damage number. On the other hand, despite KCtot being a measure of the wave–current contribution relative to the structure, which is directly related to the shear stress amplification and vortex shedding around the monopile, primary causes of scour, in the end, it is a composite metric. Consequently, it may obscure the direct contribution of each hydrodynamic component to scour under varying flow conditions, as they may vary independently. Given that multiple wave–current regime combinations may yield identical KCtot values, relying on this parameter may result in less accurate interpretations regarding the primary scour driver. This could explain the observed low correlation with the damage number.
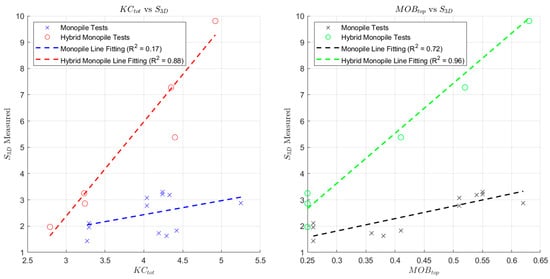
Figure 25.
Damage number comparison with KC number (left) and MOB parameter (right).
As for the hybrid monopile tests, since severe scour deformations were observed, a high correlation between both KCtot and MOBtop to S3D was expected. The interaction between the WEC paddles and the flow leads to a highly energetic near-bed environment. The resulting scour deformation is influenced by intensified oscillatory flow patterns (captured by KC number) and increased hydraulic stress acting on the seabed protection (captured by MOB parameter). As a result, the high correlation with damage number was confirmed, indicating that scour is governed jointly by enhanced shear stresses and the armour layer’s ability, or lack thereof, to resist them.
As the relation between the S3D and the MOBtop-KCtot model showed mixed results across the different structures, a more in-depth analysis was conducted. The analysis considers the influence of KCtot (wave–current contribution), the KC number (wave contribution), and the KCc (current contribution). Additionally, an evaluation of the Ucw ratio in relation to the S3D was also performed, since prior studies [31,34,35,36,37,38] have reported a general trend of increased scour depths for higher Ucw values under varying conditions. It is reported in the literature that for the same Ucw value, scour depths tend to increase for higher KC numbers [34]. That observation was considerably more pronounced in wave-dominant regimes. As Ucw increases, that correlation starts to weaken, and for Ucw > 0.65, scour depths remained almost constant and independent of KC number.
As previously mentioned, although the KCtot is directly associated with shear stress amplifications and scour, a clearer notion of the main scour drivers for each foundation emerges when its wave (KC) and current (KCc) components are considered separately (Table 9). For the hybrid monopile, the results exhibit strong positive correlations between the KCtot and KC, underscoring the predominant influence of wave-induced velocities enhanced by the WEC on the scour development (Figure 26). The moderate inverse correlation with the KCc, Figure 27, indicates a comparatively lower influence of currents on scour for this type of structure. Conversely, for the monopiles, a strong positive correlation with the KC and a strong negative correlation with KCc were identified—Figure 26 and Figure 27. This observation supports the earlier assertion that the combined parameter may mask the distinct influences of each individual hydrodynamic component to scour, since for the same KCtot value, multiple KC and KCc combinations are possible. In the end, the strong correlation of damage with KC and KCc, despite the weaker correlation observed with the KCtot, is an indicator that monopile scour is highly dependent on the complex interaction between the two main hydrodynamic loads, which may not be fully encapsulated by a single combined parameter.

Table 9.
S3D,measured, Ucw, KC, KCc, and KCtot comparison.
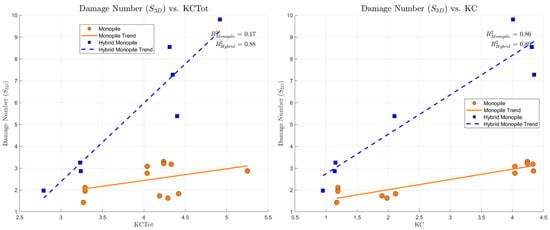
Figure 26.
S3D analysis for the KCtot and KC number.
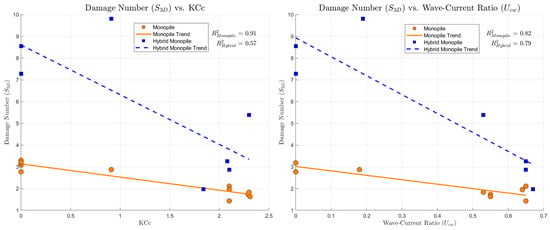
Figure 27.
S3D Analysis for the KCc and the Ucw ratio.
When interpreting the specific influence of the four parameters (KCtot, KC, KCc, and Ucw) on the damage number, any assessment should be made carefully. The apparent inverse correlation between the Ucw and S3D (Figure 27) reflects the hydrodynamic conditions selected for the tests, in which higher S3D values occurred for lower Ucw ratios as well as higher wave heights with lower current velocities (high KC and low KCc). In contrast, lower scour damage rates were recorded for tests with higher Ucw ratios, which corresponded to lower wave heights and higher current velocities (low KC and high KCc). However, when analysing tests with comparable KCtot values, e.g., M_WC_11 (Ucw = 0.55, KCtot ≈ 4.2 to 4.4, KC ≈ 1.9 to 2.1) vs. M_WR_14 (Ucw = 0, KCtot = KC ≈ 4.2 to 4.3), the test with the higher KC number (M_WR_14) presented almost a 60 to 90% increment on the S3D value. Furthermore, when comparing the wave-only tests (M_WI vs. M_WR), both with the same Ucw value, the test series with a higher KC number presented slightly higher scour damage, as reported by [34]. As for the tests with higher Ucw ratios, the ones with smaller KC numbers presented similar S3D values for the monopile tests, slightly higher for the Hs = 0.07 m and Ucw = 0.65 combination versus the Hs = 0.11 m and Ucw = 0.55 one—consistent with the observations reported by [31,34,35,36,37,38].
Overall, the results point to the fact that scour damage increases with increasing KC values, regardless of the prevailing regime.
When comparing the monopile test results with the hybrid monopile, it is evident that the influence previously observed for lower Ucw ratios was more pronounced for the hybrid monopile tests. That difference can be attributed to the unique hydrodynamic interactions generated by the oscillating paddle movement of the OSWEC. In wave-dominated regimes, that oscillatory motion induces substantial variations in the local flow velocities and conditions. These interactions enhance bed shear stresses, turbulence, and flow accelerations around the structure, acting as a supplementary source of scour-inducing force, thus promoting increased sediment transport when compared to conventional monopile foundations under similar conditions.
3.4. Wave Transmission (CTr) and Wave Reduction (CRed) Coefficients
The main goal of the experimental campaign was to assess damage to the scour protection of two different types of foundations. However, converting a standard monopile into a hybrid structure by incorporating a WEC revealed significant flow patterns and hydrodynamic differences. Since the focus was not on the performance of the WEC, the captured energy efficiency or the power per unit front was not calculated. Instead, straightforward metrics such as the wave transmission coefficient (CTr), which compares the seaside wave height to the leeside wave height in each test, and the wave reduction coefficient (CRed), which compares the wave heights between a monopile test and a hybrid monopile test for the same hydrodynamic condition, highlight how both foundations, including the device, influence wave attenuation.
For monopile-only tests, the CTr consistently remains near 100% (Table 10), indicating minimal interference with the incoming wave. The structure’s narrow cross-section contributes to this behaviour, allowing waves to propagate with negligible attenuation, reaffirming the limited wave sheltering capacity—deviations in the coefficient do not exceed ±5%. In contrast, for hybrid monopiles, the integrated WEC allows a significant reduction in the CTr, especially for higher wave heights, where almost 25% of wave reduction on the leeside was observed. These results were achieved using a simplified mechanical system to actuate the WEC paddles, suggesting that a fully functional PTO system could achieve even greater attenuation. The results support the premise that hybridisation effectively increases the dissipative capacity, enhancing wave absorption and reducing transmitted wave energy. On the other hand, as a negative impact, it increases the flow contraction and the wave–current velocities (not quantified in this study) between the WEC’s bottom and the scour protection.

Table 10.
Wave transmission coefficients (CTr).
While some seaside CRed values (Table 11) for the hybrid monopile show slight negative values, i.e., wave enhancement up to 9%, this was attributed to the intense scour that eroded out the protection and caused the lowering of the seabed, which increased the water depth, creating conditions for bigger waves to be registered without breaking. The leeside CRed values (Table 11) consistently reflect the substantial wave height reduction across all the hybrid tests, up to almost 30%. These results highlight the potential of WECs as promising components for integration into offshore structures. They may serve not only as a booster for renewable energy and power generation but also as a protective element that shields offshore structures and mitigates the effects of severe coastal erosion [8,9]. Nevertheless, the optimisation and strategic integration of PTO systems appear critical for addressing the scour enhancement associated with such devices. This phenomenon could otherwise undermine the overall efficiency of the hybrid structure.

Table 11.
Wave reduction coefficients (CRed).
Despite the presence of the WEC, a reduction in transmitted wave height was observed compared to the incident wave. However, the scour damage to the protection was concurrently enhanced. This suggests that the rotational angle of the converter’s paddle and its distance to the seabed must be considered a critical design criterion to mitigate excessive scour or damage in the protection. When using an OSWEC as a protective measure for a pipeline, it was concluded by [39] that scour was reduced by increasing the angle between the flap and the seabed, which translated to a reduction in the flap’s rotation relative to its vertical axis, thereby minimising its oscillatory movement and velocity.
Regarding the distance of a converter to the seabed, the influence of the tip clearance (defined as the vertical distance between a rotating blade and a stationary point) for tidal-current energy turbines was investigated by [40,41], with [40] specifically studying turbines attached to a monopile. Both studies demonstrated that scour was increased by the converter due to enhanced local velocities, downflow, and the occurrence of horseshoe vortices. A 10–20% increase in scour extent and a 30% increase in the scour depth were reported by [41]. Furthermore, it was observed that scour increased faster with lower distances to the bed profile. Nonetheless, it was also concluded that equilibrium scour is independent of tip clearance—a continuous decrease in the distance to the sediment bed, after a certain point, did not translate to a significant increase in the scour depth [41].
While this study maintained a fixed tip clearance, based on operational recommendations for the WEC, it is important to highlight that this parameter significantly influences scour development and could be critical to the future of hybrid foundations. Upcoming studies should consider a range of tip clearance distances and their interaction with other variables associated with the WEC and foundation geometry to quantify their impact under various hydrodynamic conditions. This would allow for a more comprehensive understanding of its influence on scour and ultimately support the development of tailored design criteria for scour protection of hybrid foundations incorporating WEC devices.
4. Conclusions
Experimental results revealed that, despite the WECS’s ability to attenuate incident hydrodynamic conditions, reducing leeward wave heights up to almost 30%, the oscillatory motion of the convergent paddles induced complex flow patterns. These patterns, which include downflow, horseshoe vortices, and lee–wake vortices, intensified scour mechanisms and led to severe scour on the armour layer unit, including the erosion and lowering of the seabed near the structure.
Applying the overlapping-circle methodology [21] to determine S3D number proved effective and precise in quantifying the damage rate, allowing for a detailed characterisation of its distribution. The analysis of the influence of the grid ratio (ηS3D,grid) on the quantification of S3D,max showed a strong dependency of this parameter on the selected circle sub-area size (Asub), reinforcing the need for a uniform failure criterion. The results suggest that a grid ratio between 1/6 and 1/4, corresponding to sub-areas of and , may be suitable for evaluating the damage number, validating, to some extent, the failure criterion suggested by [12] as a reasonable limit. However, the measured damage values raise significant questions about the applicability and conservatism of existing design criteria and formula [7].
The comparison between the monopile and hybrid monopile tests demonstrated a clear difference in the scour rate and the damage number (S3D). Riprap protections on hybrid foundations suffered significantly higher damage, resulting in pronounced deformations and, in many cases, premature failure (often within the first 1000 waves), unlike monopiles, which, under mild conditions, maintained integrity or exhibited dynamic behaviour. Although some protection configurations showed some capacity for reshaping and recovery, even after significant damage, in the case of the hybrid monopile, the intensity of the flow patterns induced by the WEC led to irreversible damage to the armour layer. These findings suggest that existing design criteria, particularly those developed for monopiles [7], are insufficient to comply with more complex and hybrid configurations. It can be argued that evaluating the S/ts or S3D/ns ratio emerges as a more reliable and representative damage indicator for riprap scour protections than the S/Dp ratio or S3D > 1.0 failure limit suggested by [7]. The proposed limits for S/ts or S3D/ns align better with the experimentally observed behaviour of the scour protections.
The scour prediction formula developed by [22], which relies on MOBtop and KCtot parameters, was found to consistently underestimate the scour deformation observed during the tests, mainly for the hybrid foundation ones. This discrepancy may be related to this study’s small dataset, differences in model scales, or even differences in the sub-areas of each measurement methodology. Hence, the methodology proposed by [22] also proved unsuitable for accommodating the increased complexity introduced by a WEC in a hybrid foundation system. However, a strong correlation was established between S3D and KCtot number, as naturally, the scour damage has a higher relation to the shear stress amplification and vortex shedding around the monopile. Moreover, although [22] reported no clear dependency on some parameters, such as gradation width, thickness, and extent, future studies could benefit from assessing the contribution of some of these parameters as they could exert a measurable influence on scour under combined wave–current and WEC-induced loading. Ideally, bridging the S3D with the MOBtop-KCtot model could be extremely valuable for developing a more robust approach to damage prediction for both monopiles and hybrid foundations.
This research also contributes to a deeper understanding of hydrodynamic interactions in hybrid offshore foundations, underlining the need to revise existing scour protection design frameworks. While based on a small dataset, the results point towards new design criteria, with guidelines that should incorporate structural complexities and dynamic load interactions to account for a broader spectrum of offshore and marine harvesting technologies, recognising the complexity introduced by hybrid structures and WEC motion.
In summary, the novel contributions and main takeaways are hereby highlighted:
- Application of a scour protection in a hybrid monopile-WEC system: comparative assessment of scour damage with a monopile foundation.
- ○
- Paddle-based WECs can intensify scour in hybrid foundations: although the used OSWEC device attenuated incoming wave heights by almost 30%, its oscillatory movement generates complex flow patterns and significantly increases the scour damage.
- Application and evaluation of the innovative overlapping-circle 3D method: demonstration of its effectiveness and high-resolution scour quantification capabilities of the method proposed by [21], while comparing it with two other different methods [7,22], making a sensitivity analysis to understand the need for a methodological standardisation.
- ○
- Overlapping method revealed limitations in existing design damage analysis methods: the overlapping method effectively quantified scour damage via S3D number, providing more insights into its behaviour, completing the information acquired from the studies performed by [7,22], mainly for hybrid configurations. However, its high sensitivity to the grid ratio indicates that the optimal value should fall within the 1/4 and 1/6 ratio interval, which aligns with the proposal made by [21].
- Identification of limitations in existing design standards and predictive formulas: the results lead to questioning the conservatism of existing design standards and their inability to capture WEC-induced enhanced flow complexities.
- ○
- Hybrid monopile riprap protections exhibited early failure: when compared to standard monopile tests, the scour countermeasures applied to hybrid structures showed markedly higher damage rates, often failing within the initial 1000 waves, thus indicating that the current design methods do not accommodate the dynamic loads induced by WECs.
- Proposal of alternative performance-aligned scour metrics: S/ts and/or S3D/ns ratios offer more accurate and straightforward indicators for quantifying and evaluating riprap scour protection performance in complex offshore environments by shifting the comparative/relative referential from the foundation to the protection itself.
- ○
- Alternative S/ts and S3D/ns indicators shown to be reliable: these two relative scour damage ratios better represent the actual riprap state and performance under hydrodynamic loading than the traditional S/Dp or S3D > 1.0 threshold, offering a more reliable basis for future design approaches.
- Framework for advancing design methodologies in hybrid offshore foundations: to update predictive tools that account for dynamic structural effects and vortex-induced shear amplifications of coupling (extra) devices, to promote safer, more adaptable infrastructures for marine harvesting technologies.
Future research should prioritise expanding the experimental test matrix to include a broader range of hydrodynamic scenarios, alternative scour protection configurations, and different WEC devices. It also should address secondary erosion behind riprap protections since it may become significant under long-term operational conditions. While the present study focused on the performance of scour protection under a maximum of 3000 waves, aligned with most tests reported in the literature and consistent with the duration used to develop the current design criteria, it represents a step toward understanding the short- to mid-term behaviour of such protective systems. Subsequent studies should aim to complement this research through extended physical/numerical modelling campaigns (e.g., over 5000 waves) and field observations to assess potential long-term damage mechanisms, including secondary erosion. Moreover, the recoverability capacity, an indicator of dynamic stability, registered during the tests should also be evaluated for long-term durations as well, to determine whether the backfilling reflects a sustainable resilience or merely a temporary delay of failure. Comparative tests using different types of filter layers would be valuable to observe if the phenomenon persists across different configurations or if it may be a signal of progressive failure. Such efforts would help validate whether existing design standards sufficiently tackle these longer-term effects.
The use of a simplified spring-based mechanism over a PTO in the present research allowed for a controlled assessment of the first-order influence of WEC paddle motion on scour. To more accurately determine the direct influence of the converter, future tests should incorporate a fully operational PTO system to consider the damping effects, as it is expected to significantly affect the flap dynamics, alter the flow patterns, and ultimately influence the scour damage around the foundation. Furthermore, a direct quantification of the local flow enhancement induced by the hybrid structure should be assessed via a CFD model. Such a model would enable the determination of the influence of the converter’s paddle motion on the resulting pressure field variations, quantify the enhancement in the bed shear stress acting on the armour layer, and delineate the relative contribution of each flow pattern to the scour damage measured on the scour protection.
Addressing these knowledge gaps will enable the expansion of the existing datasets and raise the current understanding of the key physical mechanisms driving scour in WECs and hybrid systems. This is essential for advancing the comprehension of scour damage processes and ultimately to develop a robust predictive framework. Such efforts are critical to improve or propose new design methodologies and formulations that would be capable of accurately capturing the complex interactions in these intricate marine and offshore environments.
Author Contributions
Writing—original draft preparation, formal analysis, visualisation, J.C.; conceptualisation, J.C., T.F.-F. and P.L.; methodology, J.C., T.F.-F. and M.W.; writing—review and editing, J.C., T.F.-F., M.W., F.T.-P. and P.L.; supervision, T.F.-F., F.T.-P. and P.L.; funding, T.F.-F.; project administration, T.F.-F. and F.T.-P. All authors have read and agreed to the published version of the manuscript.
Funding
J. Chambel acknowledges funding in the form of a Ph.D. scholarship grant awarded to J. Chambel by the Portuguese Foundation for Science and Technology (FCT) and the European Social Fund (ESF) of the European Union (EU), with the reference number 2021.07393.BD (https://doi.org/10.54499/2021.07393.BD). This work was performed in the scope of the POSEIDON project (Project Reference: PTDC-ECI-EGC-5177-2020), which was funded through the FCT.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author, J.C., upon reasonable request.
Acknowledgments
The authors would like to acknowledge Miguel Guerra for the support and expertise during the physical modelling experiments.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADV | Acoustic Doppler Velocimeter |
| Afailure | Area of failure |
| Asub | Area of the overlapping-circle sub-areas |
| a0, a2, a3 | Regression fitting coefficients |
| a1, a4 | Coefficient for hydrodynamic conditions |
| b0 | Regression fitting coefficient |
| CRed | Wave reduction coefficient |
| CTr | Wave transmission coefficient |
| D | Scour protection’s armour layer extent |
| D* | Dimensionless grain size |
| Dcr | Critical stone size |
| Dp | Pile diameter |
| Dn50 | Nominal stone diameter of the scour protection |
| D15 | 15th percentile of scour protection material grading |
| D50 | Mean stone diameter of the scour protection material |
| D67.5 | 67.5th percentile of scour protection material grading |
| D85 | 85th percentile of scour protection material grading |
| DTM | Digital Terrain Model |
| D | Water depth |
| d16 | 16th percentile of sediments |
| d50 | Mean diameter of sediments |
| d84 | 84th percentile of sediments |
| Fr | Froude number |
| FOSWEC | Floating Oscillating Surge Wave Energy Converter |
| GBF | Gravity-based Foundation |
| g | Gravitational acceleration |
| H | Wave height |
| Hm0 | Spectral significant wave height |
| Hs | Significant wave height |
| KC KCc | Keulegan–Carpenter number (wave contribution) Keulegan–Carpenter number (current contribution) |
| KCtot | Total Keulegan–Carpenter number (wave–current contribution) |
| MOB | Mobility parameter |
| MOBtop | Mobility parameter on the top layer of scour protection |
| N | Number of waves |
| ns | Number of rock stone sizes (layers) |
| OSWEC | Oscillating Surge Wave Energy Converter |
| OWT | Offshore Wind Turbine |
| p | Multiplication factor for overlapping-circle sub-area |
| Rcircle | Radius of overlapping-circle sub-area |
| Re | Reynolds number |
| S | Scour depth |
| Spredicted | Predicted scour depth |
| S/Dp | Relative scour depth |
| S/ts | Scour depth relative to the scour protection thickness |
| Spredicted/Dp | Predicted relative scour depth |
| S3D | Damage number |
| S3D,failure | Damage number for failure limit |
| S3D,max | Damage number (maximum) |
| S3D,measured | Damage number (measured) |
| S3D,predicted | Damage number (predicted) |
| S3Dsub,circle | Damage number for overlapping-circle sub-area |
| S3D/ns | Damage number relative to the number of rock stone sizes (layers) |
| s | Specific density (ρs/ρw) |
| stab | Stability parameter |
| T | Wave period |
| T* | Dimensionless time scale |
| Tm | Mean wave period |
| Tm-1,0 | Energy wave period |
| Tp | Wave peak period |
| TEC | Tidal-current Energy Converter |
| ts | Scour protection thickness |
| Uc | Depth-averaged current velocity |
| Ucr | Mean threshold velocity of sediments |
| Ucw | Wave–current velocity ratio |
| Um | Wave orbital bottom velocity |
| Um,top | Wave orbital bottom velocity at the top of the armour layer |
| VA,max | Maximum erosion volume |
| Vcircle | Volume of overlapping-circle sub-area |
| Ve | Eroded volume |
| WEC | Wave Energy Converter |
| ws | Settling velocity |
| α | Amplification factor |
| ΔS3D/ns | Damage increase ratio |
| ηS3D,grid | Grid ratio |
| θ | Shields parameter |
| θcr | Critical Shields parameter |
| θmax | Maximum dimensionless wave–current-induced shear stress |
| ν | Kinematic viscosity of water |
| ρs | Density of rock material |
| ρw | Water mass density |
| σs | Standard deviation of sediments |
| τcr | Critical bed shear stress |
| τm | Mean combined bed shear stress (current and wave-induced) |
| τmax | Maximum combined bed shear stress (current and wave-induced) |
| ϒ | Wave spectrum peak enhancement factor |
Appendix A
Monopile and Hybrid Foundation S3D Results: Overlapping Technique Results (Asub =
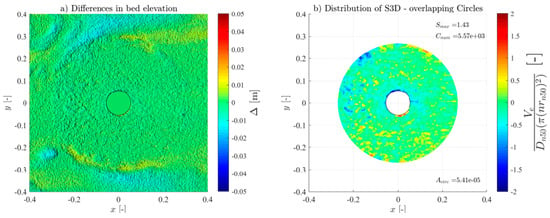
Figure A1.
M_WC_7_1000 test: (a) DTM and (b) S3D distribution—waves and currents from left to right.
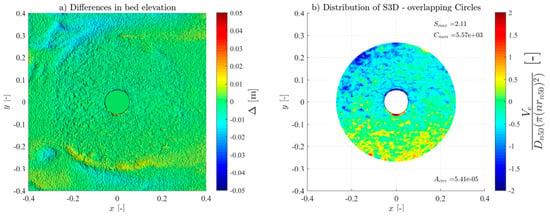
Figure A2.
M_WC_7_2000: (a) DTM and (b) S3D distribution—waves and currents from left to right.
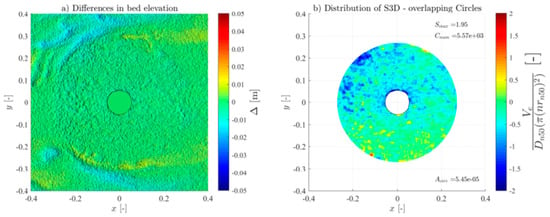
Figure A3.
M_WC_7_3000 test: (a) DTM and (b) S3D distribution—waves and currents from left to right.
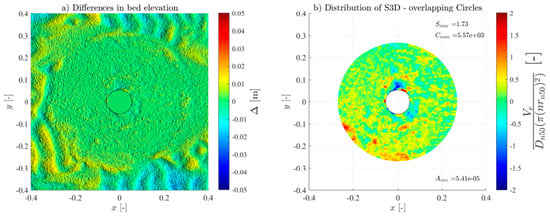
Figure A4.
M_WC_11_1000 test: (a) DTM and (b) S3D distribution—waves and currents from left to right.
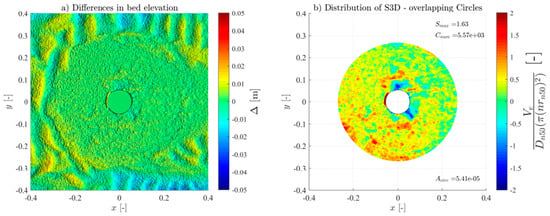
Figure A5.
M_WC_11_2000 test: (a) DTM and (b) S3D distribution—waves and currents from left to right.
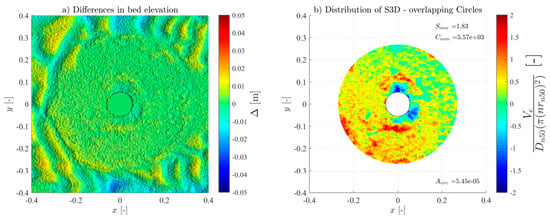
Figure A6.
M_WC_11_3000 test: (a) DTM and (b) S3D distribution—waves and currents from left to right.
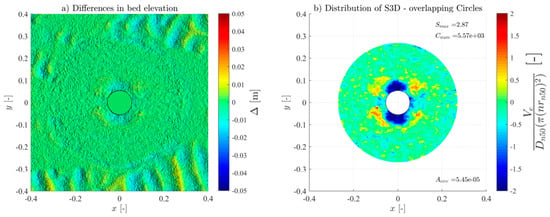
Figure A7.
M_WC_15.5_1000 test: (a) DTM and (b) S3D distribution—waves and currents from left to right.
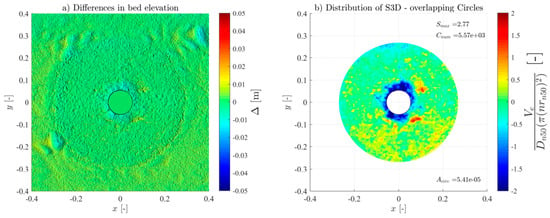
Figure A8.
M_WI_14_1000 test: (a) DTM and (b) S3D distribution—waves from left to right.
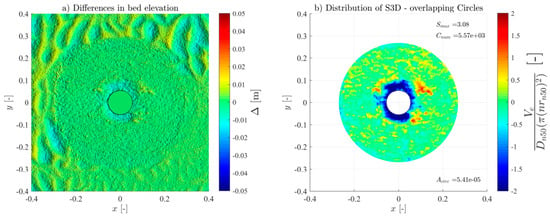
Figure A9.
M_WI_14_2000: (a) DTM and (b) S3D distribution—waves from left to right.
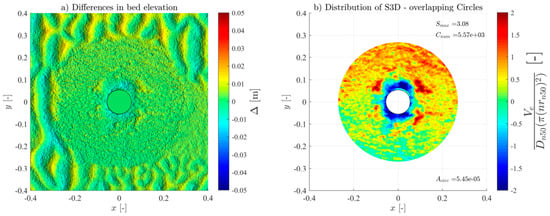
Figure A10.
M_WI_14_3000 test: (a) DTM and (b) S3D distribution—waves from left to right.
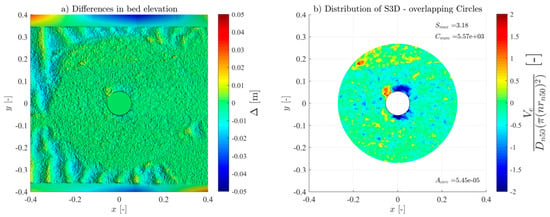
Figure A11.
M_WR_14_1000 test: (a) DTM and (b) S3D Distribution—waves from left to right.
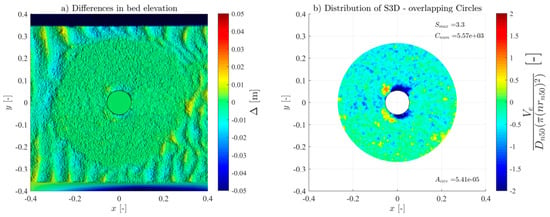
Figure A12.
M_WR_14_2000 test: (a) DTM and (b) S3D distribution—waves from left to right.
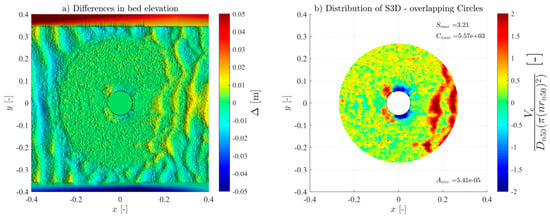
Figure A13.
M_WR_14_3000 test: (a) DTM and (b) S3D distribution—waves from left to right.
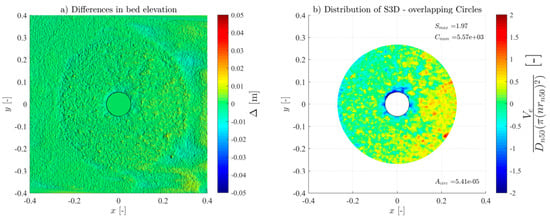
Figure A14.
MH_WC_7_1000 test: (a) DTM and (b) S3D distribution—waves and currents from left to right.
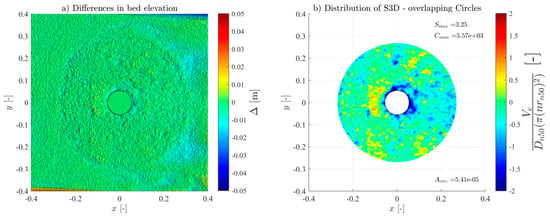
Figure A15.
MH_WC_7_2000 test: (a) DTM and (b) S3D distribution—waves and currents from left to right.
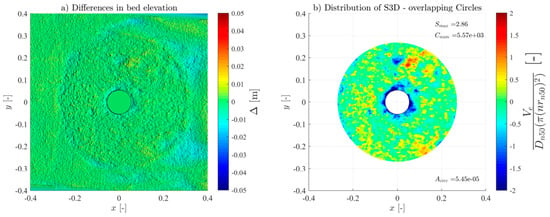
Figure A16.
MH_WC_7_3000 test: (a) DTM and (b) S3D distribution—waves and currents from left to right.
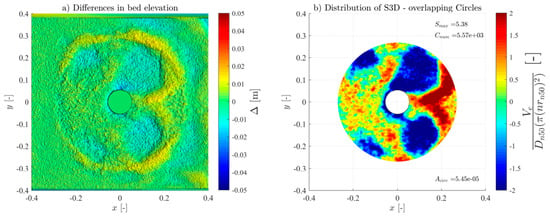
Figure A17.
MH_WC_11_1000 test: (a) DTM and (b) S3D distribution—waves and currents from left to right.
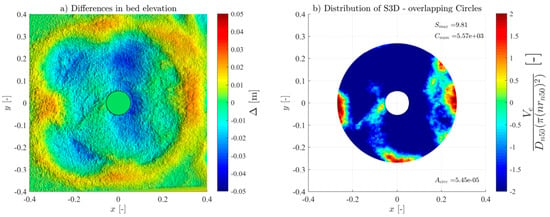
Figure A18.
MH_WC_15.5_1000 test: (a) DTM and (b) S3D distribution—waves and currents from left to right.
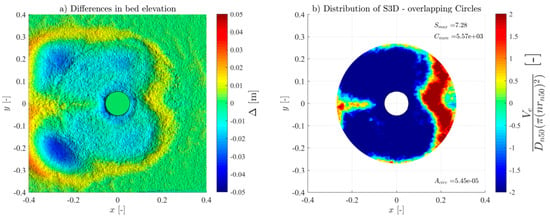
Figure A19.
MH_WI_14_1000 test: (a) DTM and (b) S3D distribution—waves from left to right.
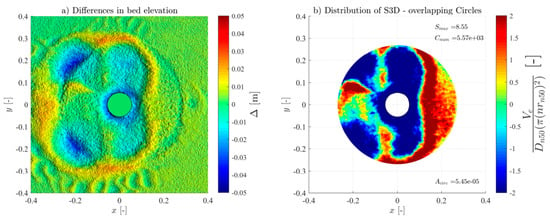
Figure A20.
MH_WR_14_1000 test: (a) DTM and (b) S3D distribution—waves from left to right.
Appendix B
Monopile and Hybrid Foundation S3D Results for Different Grid Ratios

Table A1.
S3D,measured computation for different grid ratios—(A): M_WC_7_3000; (B): M_WC_11_3000; (C): M_WC_15.5_1000; (D): M_WI_3000; (E): M_WR_1000.
Table A1.
S3D,measured computation for different grid ratios—(A): M_WC_7_3000; (B): M_WC_11_3000; (C): M_WC_15.5_1000; (D): M_WI_3000; (E): M_WR_1000.
| Monopile Tests | (A) | (B) | (C) | (D) | (E) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Asub | Value [m2] | ηS3D,grid | p Value | Rcircle [m] | Cnum | S3D,measured | ||||
| 1.000 | 1.1284 | 23,200 | 3.46 | 2.71 | 3.96 | 3.42 | 5.26 | |||
| 0.900 | 1.1894 | 20,700 | 3.12 | 2.21 | 3.71 | 3.39 | 4.75 | |||
| 0.667 | 1.3820 | 15,400 | 3.03 | 2.49 | 3.71 | 3.36 | 4.77 | |||
| 0.500 | 1.5958 | 11,500 | 2.29 | 2.02 | 3.26 | 3.29 | 4.03 | |||
| 0.333 | 1.9544 | 7640 | 2.21 | 1.95 | 3.38 | 3.28 | 3.43 | |||
| 0.250 | 2.2568 | 5570 | 1.95 | 1.83 | 2.87 | 3.08 | 3.18 | |||
| 0.200 | 2.5231 | 4600 | 2.20 | 1.89 | 2.86 | 2.84 | 3.20 | |||
| 0.167 | 2.7640 | 3770 | 1.90 | 1.96 | 2.85 | 2.67 | 2.95 | |||
| 0.143 | 2.9854 | 3250 | 1.94 | 1.78 | 2.79 | 2.63 | 2.59 | |||
| 0.125 | 3.1915 | 2780 | 1.76 | 1.87 | 2.93 | 2.82 | 2.71 | |||
| 0.111 | 3.3851 | 2550 | 1.91 | 1.85 | 2.78 | 2.85 | 2.82 | |||
| 0.100 | 3.5682 | 2150 | 1.70 | 1.64 | 2.69 | 2.70 | 2.49 | |||
| 0.063 | 4.5135 | 1400 | 1.75 | 1.61 | 2.68 | 2.55 | 2.30 | |||
| 0.050 | 5.0463 | 1100 | 1.58 | 1.51 | 2.58 | 2.55 | 2.30 | |||
| 0.040 | 5.6419 | 839 | 1.36 | 1.56 | 2.64 | 2.50 | 1.91 | |||
| 0.020 | 7.9788 | 409 | 1.24 | 1.34 | 2.40 | 2.07 | 1.69 | |||
| 0.010 | 11.2838 | 189 | 1.04 | 1.03 | 2.03 | 1.95 | 1.43 | |||
| Apile | 0.00143 | 29.8103 | 24 | 0.62 | −0.02 | 0.52 | 0.31 | 0.60 | ||

Table A2.
S3D,measured computation for different grid ratios—(A): MH_WC_7_3000; (B): MH_WC_11_1000; (C): MH_WC_15.5_1000; (D): MH_WI_1000; (E): MH_WR_1000.
Table A2.
S3D,measured computation for different grid ratios—(A): MH_WC_7_3000; (B): MH_WC_11_1000; (C): MH_WC_15.5_1000; (D): MH_WI_1000; (E): MH_WR_1000.
| Hybrid Monopile Tests | (A) | (B) | (C) | (D) | (E) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Asub | Value [m2] | ηS3D,grid | p Value | Rcircle [m] | Cnum | S3D,measured | ||||
| 1.000 | 1.1284 | 23,200 | 3.22 | 5.88 | 10.7 | 8.79 | 12.1 | |||
| 0.900 | 1.1894 | 20,700 | 3.54 | 5.72 | 11.2 | 9.4 | 10.4 | |||
| 0.667 | 1.3820 | 15,400 | 3.31 | 5.97 | 11.4 | 8.64 | 10.9 | |||
| 0.500 | 1.5958 | 11,500 | 3.14 | 5.28 | 11.1 | 8.74 | 10.3 | |||
| 0.333 | 1.9544 | 7640 | 3.11 | 5.44 | 10.1 | 8.30 | 9.40 | |||
| 0.250 | 2.2568 | 5570 | 2.86 | 5.38 | 9.81 | 7.28 | 8.55 | |||
| 0.200 | 2.5231 | 4600 | 2.60 | 4.97 | 10.1 | 7.34 | 9.59 | |||
| 0.167 | 2.7640 | 3770 | 2.63 | 5.02 | 9.13 | 6.90 | 8.35 | |||
| 0.143 | 2.9854 | 3250 | 2.60 | 4.80 | 8.88 | 7.11 | 8.49 | |||
| 0.125 | 3.1915 | 2780 | 2.68 | 4.68 | 9.12 | 7.00 | 8.04 | |||
| 0.111 | 3.3851 | 2550 | 2.49 | 4.87 | 8.96 | 6.79 | 8.57 | |||
| 0.100 | 3.5682 | 2150 | 2.32 | 5.03 | 8.97 | 6.59 | 8.21 | |||
| 0.063 | 4.5135 | 1400 | 2.16 | 4.95 | 8.68 | 6.38 | 7.75 | |||
| 0.050 | 5.0463 | 1100 | 1.93 | 4.71 | 8.54 | 6.43 | 7.15 | |||
| 0.040 | 5.6419 | 839 | 1.95 | 4.39 | 8.41 | 6.38 | 7.48 | |||
| 0.020 | 7.9788 | 409 | 1.41 | 4.20 | 8.24 | 6.04 | 6.37 | |||
| 0.010 | 11.2838 | 189 | 1.20 | 3.56 | 8.16 | 5.37 | 5.77 | |||
| Apile | 0.00143 | 29.8103 | 24 | 0.30 | 2.22 | 7.06 | 3.69 | 3.45 | ||
Appendix C
MATLAB Function for Calculating S/Dp, Kctot, and MOBtot—Using Formulas Developed by [21,42]
function [S_over_Dp]=S_over_Dp(temp, rho_s, rho_w, dn50, Hs, Tp, Uc, Um, hw, Dp, ts, L, alpha_deg)
%% Extract input parameters from the structure
% temp = water temperature (°C);
%rho_s = mass density armour layer (kg/m3);
%rho_w = water density (kg/m3);
%dn50 = nominal stone diameter (m);
%Hs = significative wave height (m) measured in the tests;
%Tp = peak period (s) measured in the tests;
%Uc = current velocity (m/s) measured in the tests;
%Um = orbital wave velocity (m/s) measured in the tests;
%hw = water depth (m);
%h_top = water depth at the top of protection (m);
%Dp = pile diameter (m);
%ts = armour layer thickness in units (relative to the Dn50 value)
%L = wavelength (m) calculated using Wiberg and Sherwood (2008);
%alpha_deg = wave–current degree angle (°);
%% A.1: Constants
g = 9.81; % gravity
%% A.2: Kinematic viscosity
nu = (1.14–0.031*(temp–15) + 0.00068*(temp–15)^2) * 1e-6;
%% A.3: Rock properties
d50 = dn50/0.84;
h_top = hw–(ts * dn50);
Delta_s = (rho_s–rho_w)/rho_w; % specific density
d_star = d50 * (((Delta_s * g)/(nu^2))^(1/3)); %dimensionless particle diameter
% Shields critical parameter
theta_cr = 0.055 * (1–exp(-0.02 * d_star)) + 0.3 / (1 + 1.2 * d_star);
% Roughness height
ks = 2.5 * d50;
%% A.4: Current-related parameters
z0 = ks/30; % bed roughness lenght
CD = (0.4/(log(hw/z0)-1))^2; % drag coefficient
u_star_c = sqrt(CD) * Uc; % current-related shear velocity
tau_c = rho_w * u_star_c^2; % current-related shear stress
theta_c = tau_c/((rho_s–rho_w) * g * d50); % current-related Shields parameter
MOBc = theta_c/theta_cr; % current-related relative mobility
KCc = (Uc * Tp)/Dp; % current-related KC number
%% A.5.1: Correction factor K_top for velocity at top of scour
K_top = sinh((2 * pi * hw)/L)/sinh((2 * pi * h_top)/L); % correction factor for orbital velocity on top of scour protection
uw_top = K_top * Um; % wave velocity at top
Aw_top = (uw_top * Tp)/(2 * pi); % wave orbital motion amplitude on top of scour protection
%% A.5.2: Wave friction factor
A_ks = Aw_top/ks;
if A_ks > 0.2 && A_ks < 2.92
fw = 0.32 * A_ks^(−0.8);
elseif A_ks >= 2.92 && A_ks < 727
fw = 0.237 * A_ks^(−0.52);
elseif A_ks >= 727
fw = 0.04 * A_ks^(−0.25);
else
error(‘Awa/ks value must be greater than 0.2 for valid friction factor calculation.’);
end
%% Wave shear velocity and stress
u_star_w = (sqrt(0.5 * fw)) * uw_top; % wave-related shear velocity
tau_w = rho_w * u_star_w^2; % wave-related bed shear stress
theta_w = tau_w/((rho_s–rho_w) * g * d50); % wave-related shields parameter
MOBw = theta_w/theta_cr; % wave-related relative mobility
KCw = (uw_top * Tp)/Dp; % wave-related KC number
%% A.6: Combined shear stress and mobility
tau_m = tau_c + 1.2 * tau_c * ((tau_w/(tau_c + tau_w))^3.2); % Mean combined current- and wave-related bed shear stress
alpha_rad = deg2rad(alpha_deg); % angle between waves and currents
tau_max = sqrt(tau_m^2 + tau_w^2 + 2 * tau_w * tau_m * cos(alpha_rad)); % max combined current- and wave-realted bed shear stress
theta = tau_max/((rho_s–rho_w) * g * d50); % combined current- and wave-related Shields parameter
MOB = theta/theta_cr; % combined current- and wave-related relative mobility
%% Compute KC_tot (Keulegan–Carpenter number)
KC_tot = ((uw_top + Uc) * Tp)/Dp;
%% Compute S/Dp (final equation)
S_over_Dp_value = (1 + (3.93/(1 + exp(−0.74 * KC_tot + 4.75)))) * 0.07 *(MOB^(1.65)); % relative scour depth
%% Display results
fprintf(‘\n’);
fprintf(‘KCtot: %.3f\n’, KC_tot);
fprintf(‘KCc: %.3f\n’, KCc);
fprintf(‘KCw: %.3f\n’, KCw);
fprintf(‘\n’);
fprintf(‘MOB: %.3f\n’, MOB);
fprintf(‘MOBc: %.3f\n’, MOBc);
fprintf(‘MOBw: %.3f\n’, MOBw);
fprintf(‘\n’);
fprintf(‘kinematic viscosity: %.3e\n’, nu);
fprintf(‘delta_s: %.3f\n’, Delta_s);
fprintf(‘D*: %.3f\n’, d_star);
fprintf(‘\n’);
fprintf(‘theta: %.3f\n’, theta);
fprintf(‘theta_cr: %.3f\n’, theta_cr);
fprintf(‘theta_c: %.3f\n’, theta_c);
fprintf(‘theta_w: %.3f\n’, theta_w);
fprintf(‘\n’);
fprintf(‘tau_c: %.3f\n’, tau_c);
fprintf(‘tau_w: %.3f\n’, tau_w);
fprintf(‘tau_medio: %.3f\n’, tau_m);
fprintf(‘tau_maximo: %.3f\n’, tau_max);
fprintf(‘\n’);
fprintf(‘ks: %.3f\n’, ks);
fprintf(‘z0: %.3e\n’, z0);
fprintf(‘CD: %.3f\n’, CD);
fprintf(‘u*c: %.3f\n’, u_star_c);
fprintf(‘u*w: %.3f\n’, u_star_w);
fprintf(‘uw_top: %.3f\n’, uw_top);
fprintf(‘Ktop: %.3f\n’, K_top);
fprintf(‘Awtop: %.3f\n’, Aw_top);
fprintf(‘A/ks: %.3f\n’, A_ks);
fprintf(‘fw: %.3f\n’, fw);
fprintf(‘\n’);
fprintf(‘S/D: %.3f\n’, S_over_Dp_value);
end
References
- WindEurope. Getting Fit for 55 and Set for 2050: Electrifying Europe with Wind Energy; WindEurope: Brussels, Belgium, 2021. [Google Scholar]
- Matutano, C.; Negro, V.; Lopez-Gutierrez, J.S.; Esteban, M.D. Scour prediction and scour protections in offshore wind farms. Renew. Energy 2013, 57, 358–365. [Google Scholar] [CrossRef]
- Bhattacharya, S. Challenges in Design of Foundations for Offshore Wind Turbines. Eng. Technol. Ref. 2014, 2014. [Google Scholar] [CrossRef]
- Sørensen, S.P.H.; Ibsen, L.B. Assessment of foundation design for offshore monopiles unprotected against scour. Ocean Eng. 2013, 63, 17–25. [Google Scholar] [CrossRef]
- Saathoff, J.E.; Goldau, N.; Achmus, M.; Schendel, A.; Welzel, M.; Schlurmann, T. Influence of scour and scour protection on the stiffness of monopile foundations in sand. Appl. Ocean Res. 2024, 144, 103920. [Google Scholar] [CrossRef]
- Fazeres-Ferradosa, T.; Taveira-Pinto, F.; Rosa-Santos, P.; Chambel, J. A review of reliability analysis of offshore scour protections. Proc. Inst. Civ. Eng. Marit. Eng. 2019, 172, 104–117. [Google Scholar] [CrossRef]
- De Vos, L.; De Rouck, J.; Troch, P.; Frigaard, P. Empirical design of scour protections around monopile foundations. Part 2: Dynamic approach. Coast. Eng. 2012, 60, 286–298. [Google Scholar] [CrossRef]
- Chambel, J.; Fazeres Ferradosa, T.; Miranda, F.; Bento, A.; Taveira-Pinto, F.; Lomonaco, P. A Comprehensive Review on Scour and Scour Protections for Complex Bottom-Fixed Offshore and Marine Renewable Energy Foundations. Ocean Eng. 2024, 304, 117829. [Google Scholar] [CrossRef]
- Fazeres-Ferradosa, T.; Chambel, J.; Taveira-Pinto, F.; Rosa-Santos, P.; Taveira-Pinto, F.V.C.; Giannini, G.; Haerens, P. Scour Protections for Offshore Foundations of Marine Energy Harvesting Technologies: A Review. J. Mar. Sci. Eng. 2021, 9, 297. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, X.; Yan, J.; Gao, X. Countermeasures for local scour around offshore wind turbine monopile foundations: A review. Appl. Ocean Res. 2023, 141, 103764. [Google Scholar] [CrossRef]
- Soulsby, R.L. Dynamics of Marine Sands, a Manual for Practical Applications; Thomas Telford Publications: London, UK, 1997; p. 256. [Google Scholar]
- den Boon, J.H.; Sutherland, J.; Whitehouse, R.J.S.; Soulsby, R.L.; Stam, C.J.M.; Verhoeven, K.; Høgedal, M.; Hald, T. Scour behaviour and scour protection for monopile foundations of offshore wind turbines. In Proceedings of the European Wind Energy Conference & Exhibition, London, UK, 22–25 November 2004; p. 14. [Google Scholar]
- Sumer, M.B.; Fredsøe, J. Hydrodynamics Around Cylindrical Structures; World Scientific: Singapore, 1997. [Google Scholar]
- Whitehouse, R.J.S. Scour at Marine Structures: A Manual for Practical Applications; Thomas Telford: London, UK, 1998. [Google Scholar]
- De Vos, L.; De Rouck, J.; Troch, P.; Frigaard, P. Empirical design of scour protections around monopile foundations: Part 1: Static approach. Coast. Eng. 2011, 58, 540–553. [Google Scholar] [CrossRef]
- De Vos, L. Optimisation of Scour Protection Design for Monopiles and Quantification of Waver Run-Up; Faculty of Engineering, Ghent University: Ghent, Belgium, 2008; p. 278. [Google Scholar]
- Van der Meer, J.W. Stability of breakwater armour layers—Design formulae. Coast. Eng. 1987, 11, 219–239. [Google Scholar] [CrossRef]
- De Schoesitter, P.; Audenaert, S.; Baelus, L.; Bolle, A.; Brown, A.; das Neves, L.; Fazeres-Ferradosa, T.; Haerens, P.; Taveira-Pinto, F.; Troch, P. Feasibility of a dynamically stable rock armour layer scour protection for offshore wind farms. In Proceedings of the ASME 2014 33rd International Conference on Ocean, Offshore and Arctic Engineering, American Society of Mechanical Engineers, San Francisco, CA, USA, 8–13 June 2014. V003T10A026. [Google Scholar]
- Whitehouse, R.J.S.; Brown, A.; Audenaert, S.; Bolle, A.; de Schoesitter, P.; Haerens, P.; Baelus, L.; Troch, P.; Das Neves, L.; Fazeres-Ferradosa, T. Optimising scour protection stability at offshore foundations. In Proceedings of the 7th International Conference on Scour and Erosion, Perth, Australia, 2–4 December 2014. [Google Scholar]
- Fazeres-Ferradosa, T.; Taveira-Pinto, F.; Reis, M.T.; das Neves, L. Physical modelling of dynamic scour protections: Analysis of the damage number. Proc. Inst. Civ. Eng. Marit. Eng. 2018, 171, 11–24. [Google Scholar] [CrossRef]
- Fazeres-Ferradosa, T.; Welzel, M.; Schendel, A.; Baelus, L.; Santos, P.R.; Pinto, F.T. Extended characterization of damage in rubble mound scour protections. Coast. Eng. 2020, 158, 103671. [Google Scholar] [CrossRef]
- Broekema, Y.B.; van Steijn, P.W.; Wu, M.; Robijns, T. Predicting loose rock scour protection deformation around monopiles using the relative mobility number and the Keulegan–Carpenter number. Ocean Eng. 2024, 300, 117475. [Google Scholar] [CrossRef]
- van Steijn, P.; Wu, M.; Broekema, Y. Towards a better understanding of loose rock scour protection stability around monopile foundations. In Proceedings of the 11th International Conference on Scour and Erosion (ICSE-11), Copenhagen, Denmark, 17–21 September 2023; Society for Soil Mechanics and Geotechnical Engineering (ISSMGE): London, UK, 2023. [Google Scholar]
- Ruehl, K.M.; Forbush, D.; Lomonaco, P.; Bosma, B.; Simmons, A.; Gunawan, B.; Bacelli, G.; Michelen, C. Experimental Testing of a Floating Oscillating Surge Wave Energy Converter; Sandia National Laboratories: Albuquerque, NM, USA, 2019. [Google Scholar]
- Ruehl, K.M.; Forbush, D.D.; Yu, Y.H.; Tom, N. Experimental and numerical comparisons of a dual-flap floating oscillating surge wave energy converter in regular waves. Ocean Eng. 2020, 196, 106575. [Google Scholar] [CrossRef]
- Coe, R.G.; Bacelli, G.; Forbush, D.; Spencer, S.J.; Dullea, K.J.; Bosma, B.; Lomonaco, P. FOSWEC Dynamics and Controls Test Report; Sandia National Laboratories (SNL-NM): Albuquerque, NM, USA, 2020. [Google Scholar]
- Miranda, F.; Margarida Bento, A.; Chambel, J.; Francisca-Sarmento, M.; Rosa-Santos, P.; Taveira-Pinto, F.; Fazeres-Ferradosa, T. A novel and simple passive absorption system for wave-current flumes. Alex. Eng. J. 2023, 71, 463–477. [Google Scholar] [CrossRef]
- Chambel, J. Analysis of Long-Term Damage of Offshore Wind Turbine Foundations; University of Porto: Porto, Portugal, 2019. [Google Scholar]
- Wiberg, P.L.; Sherwood, C.R. Calculating wave-generated bottom orbital velocities from surface-wave parameters. Comput. Geosci. 2008, 34, 1243–1262. [Google Scholar] [CrossRef]
- CIRIA; CUR; CETMEF. The Rock Manual: The Use of Rock in Hydraulic Engineering, 2nd ed.; CIRIA: London, UK, 2007; Volume 683. [Google Scholar]
- Chen, B.; Li, S. Experimental study of local scour around a vertical cylinder under wave-only and combined wave-current conditions in a large-scale flume. J. Hydraul. Eng. 2018, 144, 04018058. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Experimental study of 2D scour and its protection at a rubble-mound breakwater. Coast. Eng. 2000, 40, 59–87. [Google Scholar] [CrossRef]
- Petersen, T.U.; Sumer, B.M.; Fredsøe, J.; Raaijmakers, T.C.; Schouten, J. Edge scour at scour protections around piles in the marine environment—Laboratory and field investigation. Coast. Eng. 2015, 106, 42–72. [Google Scholar] [CrossRef]
- Schendel, A.; Welzel, M.; Schlurmann, T.; Hsu, T.-W. Scour around a monopile induced by directionally spread irregular Waves in combination with oblique currents. Coast. Eng. 2020, 161, 103751. [Google Scholar] [CrossRef]
- Sumer, B.M.; Fredsøe, J. Scour around a pile in combined waves and currents. J. Hydraul. Eng. 2001, 127, 403–411. [Google Scholar] [CrossRef]
- Rudolph, D.; Bos, J.K. Scour around a monopile under combined wave-current conditions and low KC-numbers. In Proceedings of the 3rd International Conference on Scour and Erosion (ICSE), Amsterdam, The Netherlands, 1–3 November 2006. [Google Scholar]
- Sumer, B.M.; Petersen, T.U.; Locatelli, L.; Fredsøe, J.; Musumeci, R.E.; Foti, E. Backfilling of a scour hole around a pile in waves and currents. J. Waterw. Port Coast. Ocean Eng. 2013, 139, 9–23. [Google Scholar] [CrossRef]
- Qi, W.G.; Gao, F.P. Physical modeling of local scour development around a large-diameter monopile in combined waves and current. Coast. Eng. 2014, 83, 72–81. [Google Scholar] [CrossRef]
- Taheri, O.; Kolahdoozan, M.; Faghihirad, S. Experimental study of bed level changes in the vicinity of flap-type wave energy converters. Ships Offshore Struct. 2022, 18, 450–461. [Google Scholar] [CrossRef]
- Chen, L.; Hashim, R.; Othman, F.; Motamedi, S. Experimental study on scour profile of pile-supported horizontal axis tidal-current turbine. Renew. Energy 2017, 114, 744–754. [Google Scholar] [CrossRef]
- Sun, C.; Lam, W.H.; Cui, Y.; Zhang, T.; Jiang, J.; Guo, J.; Ma, Y.; Wang, S.; Tan, T.H.; Chuah, J.H. Empirical models for Darrieus-type tidal current turbine induced seabed scour. Energy Convers. Manag. 2018, 171, 478–490. [Google Scholar] [CrossRef]
- Deltares. Handbook of Scour and Cable Protection Methods; Report no. Deltares250; Deltares: Delft, The Netherlands, 2024. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).