Comparison of Multi-Physical Coupling Analysis of a Balanced Armature Receiver between the Lumped Parameter Method and the Finite Element/Boundary Element Method

Abstract

The balanced armature receiver (BAR) is a product based on multiphysics that enables coupling between the electromagnetic, mechanical, and acoustic domains. The three domains were modeled using the lumped parameter method (LPM) that takes advantage of an equivalent circuit. In addition, the combined finite element method (FEM) and boundary element method (BEM) was also applied to analyze the BAR. Both simulation results were verified against experimental results. The proposed LPM can predict the sound pressure level (SPL) by making use of the BAR parts dimension and material property. In addition, the previous analysis method, FEM/BEM, took 36 h, while the proposed LPM takes 1 h. So the proposed LPM can be used to check the BAR parts’ dimension and material property influence on the SPL and develop the BAR product efficiently.

1. Introduction

In terms of acoustic transducers, there are the MEMS receiver [1,2], the dynamic receiver [3], the speaker box with passive radiator [4], and the balanced armature receiver [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]. The Balance armature structure was devized by Olsen [5]. Three types of structure are described: the unpolarized armature, the polarized reed, and the polarized balanced armature. A new magnetic circuit balanced armature structure transducer has been developed for use in hearing aids [6,7]. In the balanced armature structure transducer, the coil is moved outside the magnetic structure. Stationary gaps are located at the two side legs. Based on the proposed polarized balanced armature microactuator, an implantable hearing device was developed [8]. The balanced electromagnetic separation transducer used in a bone-anchored hearing aid is presented in ref. [9]. To minimize harmonic distortions, quadratic distortion forces and static forces are counterbalanced. A closed loop armature is proposed in the structure design of BAR [10,11].

Nowadays, the balanced armature receiver (BAR) is widely used in hearing aids and earphones because of its small size and high sensitivity. The BAR is a product that follows the principles of multiphysics. When current is passed through a coil, the flux density in the upper and lower air gap is different, which contributes to the generated force on the armature’s end. With the input force, the armature and pin vibrate. The vibration of the pin contributes to the diaphragm’s vibration, which leads to sound radiation through the spout. The BAR consists of electromagnetic, mechanical, and acoustic physical domains, which are coupled with each other.

To construct the electromagnetic mathematic modeling of the BAR, the lumped parameter method (LPM) was proposed in previous research [12,13] which does not investigate the acoustic domain and cannot predict the SPL result, the key performance criteria of BAR. The multimode of BAR is investigated by using the lumped parameter in refs. [14,15]. The electromagnetic domain and acoustic domain is not involved. To obtain the SPL result, the acoustic domain is considered [16,17,18] while the input electromagnetic parameter (resistance, inductance, force factor) and mechanical parameters (mass, stiffness, force factor) come from experiment, which means the input parameter cannot be obtained in the analysis if there is no sample or experiment.

This paper is organized in the following structure. In the first part, to predict the SPL and develop a new structure BAR product, LPM is proposed to analyze the performance of the BAR by modeling the electromagnetic, mechanical, and acoustic domains along with their coupling effect according to the modeling dimension and material property, which is defined as the proposed method. Second, BAR is analyzed by FEM (electromagnetic, mechanical domain) and BEM (acoustic domain) which is defined as the previous method [19,20]. Consequently, the samples were manufactured according to the analyzed modeling. Based on the samples, the SPL experiment result was obtained. Finally, the result shows that LPM was verified by experiment, as the previous method (FEM and BEM). The difference is that the proposed method (LPM) takes 1 hour, while the previous method (FEM and BEM) took 36 hours. In conclusion, the contribution of the paper is that the proposed LPM method makes use of the BAR modeling dimension and material property to predict the SPL result without parameter identification by experiment and is more efficient than the previous method. The proposed LPM method can be used to design a new structure BAR and shorten the development cycle of the BAR. The method detail is listed in Table 1.

Table 1. Comparison of simulation methods in the paper.

Domain	Proposed Method	Previous Method
Electromagnetic	LPM	FEM
Mechanical	LPM	FEM
Acoustic	LPM	BEM

2. Analysis by LPM

2.1. Electromagnetic Analysis

The electromagnetic modeling can be described by an equivalent circuit, which is demonstrated in Figure 1. By solving Kirchhoff’s voltage and current laws, the flux density in the armature can be expressed as a dimension of the electromagnetic circuit and material property, which includes the B-H curve and coercive force. The B-H curve indicates that the permeability changes with flux density in the armature and magnet house. When the position of the armature end changes, the reluctance of the air gap between armature and permanent magnet is changed, which means the different position contributes to a different flux density and force on the armature. Consequently, the electromagnetic characteristic such as inductance and force factor are nonlinear. Hence, to handle the nonlinear characteristic property of the B-H curve, the under-relaxed Newton–Raphson method is adopted to solve the Kirchhoff’s current and voltage laws [21,22,23].

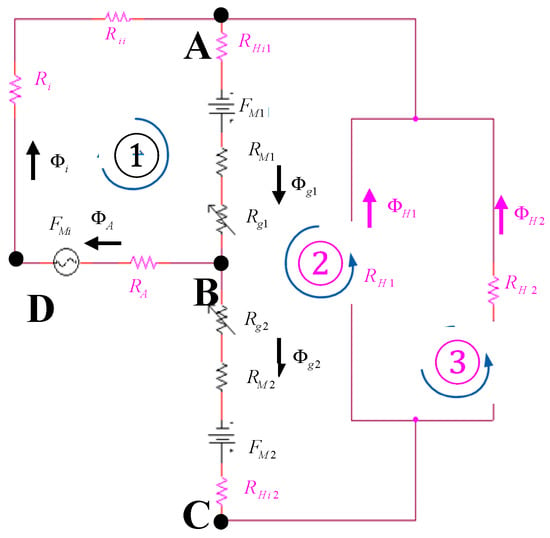
Figure 1. The equivalent circuit of the electromagnetic part.

By post processing flux density, the cogging force, force factor, and inductance can be obtained which are depicted in Figure 2.

Figure 2. Electromagnetic parameters vs displacement.

The cogging force, force factor, and inductance expressions are listed in the following equations:

$$\begin{array}{l}{F}_{cogging}\left(x\right)=2{\mu }_0{A}_g{F}_M^2\frac{\left(D_{eff2}+D_{eff1}+4D_{eff}\right)\left(D_{eff2}-D_{eff1}+2x\right)}{{\left[\left(D_{eff1}-x\right)\left(D_{eff2}+x\right)+D_{eff}\left(D_{eff1}+D_{eff2}\right)\right]}^2}\\ L_E\left(x\right)={\mu }_0{A}_g{N}^2\frac{\left(D_{eff2}+D_{eff1}\right)}{\left(D_{eff1}-x\right)\left(D_{eff2}+x\right)+D_{eff}\left(D_{eff2}+D_{eff1}\right)}\\ Bl\left(x\right)=\frac{{\mu }_0{A}_g}{2}\frac{F_{M}N\left[\left(D_{eff2}+D_{eff1}+4D_{eff}\right)\left(D_{eff2}+D_{eff1}\right)+{\left(D_{eff2}-D_{eff1}+2x\right)}^2\right]}{{\left[\left(D_{eff1}-x\right)\left(D_{eff2}+x\right)+D_{eff}\left(D_{eff2}+D_{eff1}\right)\right]}^2}\end{array}$$

(1)

where

$$\begin{array}{l}{D}_{eff1}={\mu }_0{A}_g\left(R_M+R_{Hi1}\right)+D\\ D_{eff2}={\mu }_0{A}_g\left(R_M+R_{Hi2}+\frac{1}{2}{R}_H\right)+D\\ D_{eff}={\mu }_0{A}_g\left(R_A+R_i+R_{ii}\right)\end{array}$$

where F_cogging, Bl and L_E are cogging force, force factor, and voice coil inductance, respectively, which are expressed by the armature position x. R_A, R_H are the reluctance of the armature and magnet house. F_M, A_g, N and D are the magnetomotive force of the magnet, the area of the magnet, the coil turns, and the air gap width respectively.

The mathematic equation for the electrical part is given in the following equation:

$$Z(s)=R_E+s{L}_E$$

(2)

where R_E is the electrical voice coil resistance at DC and L_E is the voice coil inductance.

2.2. Mechanical Analysis

The modeling of the mechanical simulation is demonstrated in Figure 3. The structure contains the armature, pin, and diaphragm. Magnetic force is generated on the armature end. The diaphragm vibrates through the pin connection. The edge of the diaphragm is fixed.

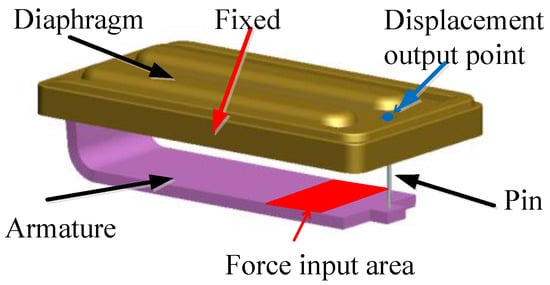
Figure 3. Mechanical simulation modeling.

To describe the mechanical system, one degree-of-freedom of the vibration system’s governing equation is adopted as follows:

$$F=M_{ms}\ddot{x}+R_{ms}\dot{x}+\frac{1}{C_{ms}}x$$

(3)

where M_ms is the mechanical mass of the driver diaphragm, R_ms denotes the mechanical resistance of the total driver losses, and C_ms denotes the mechanical compliance of the driver suspension.

In the modeling, if the input force is 0.01 N, there will be 6.38 × 10⁻³ mm displacement on the output point. If the input force is 0.02 N, the displacement becomes 12.76 × 10⁻³ mm. Hence, the stiffness of the mechanical system is calculated by dividing the difference of the force with the displacement, which is 1570 N/m and defined as original stiffness (K_original). The cogging force stiffness is 720 N/m, which can be treated as negative stiffness. Therefore, the modified stiffness is 850 N/m, which means C_ms is 1.176 m/N. By conducting a modal analysis of the mechanical system, the resonance frequency is obtained, which is 3169.9 Hz. According to the following equation:

$$f_0=\frac{1}{2\pi }\sqrt{\frac{K_{original}}{M_{ms}}}$$

(4)

The mass is calculated as 3.95 × 10⁻⁶ kg.

2.3. Acoustic Analysis

The acoustic domain is modeled as described in the following sections:

There are four tubes in the acoustic modeling which are depicted in Figure 4 and Figure 5. These tubes can be treated as transmission line models which are depicted in Figure 6.

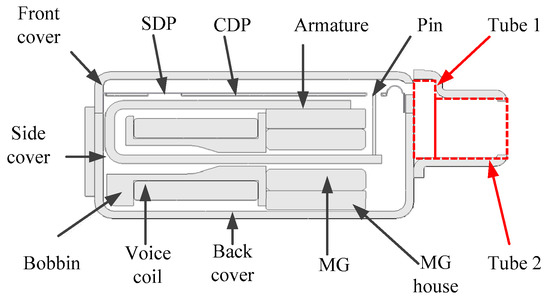
Figure 4. Acoustic modeling in the BAR.

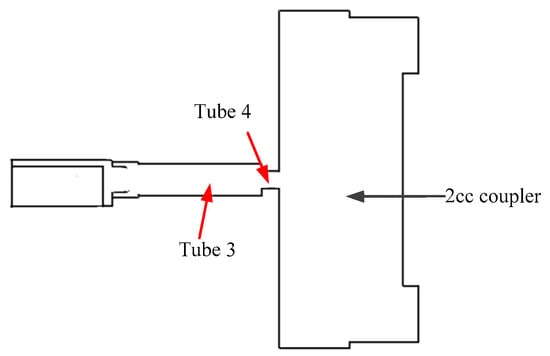
Figure 5. Acoustic modeling in the test jig.

Figure 6. Tube model.

The governing equation is listed below:

$$\left(\begin{array}{c}{p}_1\\ q_1\end{array}\right)=\left[\begin{array}{cc}\cos (kl)& j{Z}_w\sin (kl)\\ (j/Z_w)\sin (kl)& \cos (kl)\end{array}\right]\left(\begin{array}{c}{p}_2\\ q_2\end{array}\right)$$

(5)

and

$$\begin{array}{l}{p}_1=\cos (kl)\times p_2+j{Z}_w\sin (kl)\times q_2\\ q_1=(j/Z_w)\sin (kl)\times p_2+\cos (kl)\times q_2\end{array}$$

(6)

The parameters are k = ω/c, where ω = 2πf; l = tube length; and Z_w = ρc/S, where ρ is the air density and c is the speed of sound propagation.

The 2-cc coupler is modeled as the acoustic capacity, which is shown in Figure 7.

Figure 7. Equivalent circuit of cavity.

The related equation defining the acoustic capacity is given as follows:

$$C_a=\frac{V}{\rho c^2}$$

(7)

The SPL (Sound Pressure Level) can be calculated as below:

$$SPL=20log\left(p/20\times {10}^{-6}\right)$$

(8)

2.4. Electromagnetic-Mechanical–Acoustic Coupling Factors

The force factor is the electromagnetic–mechanical coupling factor and treated as a gyrator which generates a back EMF in the electromagnetic domain and a driving force in the mechanical domain. The effective area is the mechanical–acoustic coupling factor and is treated as the transformer which changes the vibration velocity of the diaphragm into the volume velocity of the air motion. The effective area of the diaphragm is calculated as half of the area of the diaphragm, because it vibrates just like a cantilever beam. The total simulation tool is depicted in Figure 8 which contains the electromagnetic, mechanical, and acoustic domains along with the coupling factor.

Figure 8. Equivalent circuit of BAR.

3. Analysis by FEM and BEM

To check the efficacy of LPM, the BAR is also analyzed by FEM and BEM. In the electromagnetic simulation part, the BAR is modeled with a different deformation, i.e., different displacement. Varying current is then input to the coil. The magnetic vector potential is defined as zero on the surface of the surrounded air box which is shown in Figure 9. Finally, the flux density is solved through FEM simulation. The electromagnetic FEM simulation governing equation is demonstrated by the following equation:

$$\nabla \times \left(\frac{1}{{\mu }_r}\nabla \times A\right)=J{\mu }_0+{\mu }_0\nabla \times H_c$$

(9)

where A is the magnetic vector potential, J is the current density, H_c is the permanent magnetic intensity, µ₀ is the permeability in the vacuum. After solving the governing equation, the flux density of every node in the modeling can be obtained. By post process, the force factor, inductance, and cogging force are obtained, which become the input of the vibro-acoustic simulation.

Figure 9. Modeling of electromagnetic FEM simulation.

The governing equation of the mechanical FEM simulation is listed in equation

$$[M]\ddot{u}+[C]\dot{u}+[K]u=[F_i]$$

(10)

where [M], [C], [K], {F_i}, and u denote the mass matrix, damping matrix, stiffness matrix, vector of current force, and displacement. The surround part of the diaphragm is fixed which means that the displacement is zero. With a given input force, the displacement of every node can be solved.

In the acoustic domain, the velocity of the tube surface is defined as zero, which means a rigid wall and is depicted in Figure 10. The sound pressure on the test point is solved by solving the Helmholtz governing equation.

$${\nabla }^{2}p-k^{2}p=-j{\rho }_{0}wq$$

(11)

where p, k, ρ₀, w, and q are sound pressure, wave number air density, angular frequency, and volume velocity. The volume velocity is from the displacement result obtained in the mechanical FEM simulation. The details are outlined in Table 2 and Table 3.

Figure 10. Modeling of acoustic BEM simulation.

Table 2. Simulation detail by FEM and BEM.

Domain	Package	Elements Order	Number of Nodes
Electromagnetic	ANSYS	3	146817
Mechanical	ANSYS	3	525006
Acoustic	Virtual lab	2	1329

Table 3. Model detail.

Domain	Value	Unit
Total dimension	5 × 3 × 2.6	mm
Coil resistance	23	Ohm
Input voltage	0.115	V

Table 2 shows the simulation detail. ANSYS is taken advantage of in the electromagnetic and mechanical system and Virtual Lab is adopted to simulate the acoustic system. In order to obtain an accurate result, the numbers of nodes in the three systems are 146817, 525006, and 1329. Based on the same computer and the listed node number in Table 2, the computation time by FEM and BEM is 36 h while, the time by the LPM method is 1 hour. So the computation time is improved.

4. Experiment

Furthermore, according to 3D modeling, the balanced armature sample is manufactured and assembled. The sample is shown in Figure 11. The experimental condition is demonstrated in Figure 12. The sweep input source ranges from 100 Hz to 20,000 Hz. The SPL of the BAR is tested using a microphone through the 2-cc coupler jig. In the experimental result, the SPL can maintain 100 dB because the BAR is tested in an enclosed tube and chamber. The first SPL peak is due to resonance of the mechanical structure. The second SPL peak is due to the tube and front chamber. Figure 13 shows the comparison of SPL between the experiment and simulation. The LPM simulation results were verified through experimental results, using FEM and BEM.

Figure 11. Parts of BAR.

Figure 12. Experimental condition.

Figure 13. Comparison of experiment and simulation.

5. Conclusions

The BAR is a product based on multiphysics that considers electromagnetic, mechanical, and acoustic domains. These physical domains are coupled with each other. This study derived LPM simulation, which modeled the multiphysics characteristic and considered the coupling effect. The SPL performance of the BAR was predicted through LPM, which provided the same validation as FEM and BEM. Additionally, it was found that LPM was more efficient and could be used to develop the BAR. In the future, the proposed LPM method will be discussed in relation to the BAR dimension and material property influence on SPL. For example, in the electromagnetic domain, the sensitivity analysis of the magnetomotive force of the magnet will be done to check its influence on SPL. Finally, according to the design target, every dimension can be determined.