Atomic-Scale Understanding of Structure and Properties of Complex Pyrophosphate Crystals by First-Principles Calculations
Abstract
Featured Application
Abstract
1. Introduction
2. Crystal Structures
3. Computational Methods
4. Results and Discussion
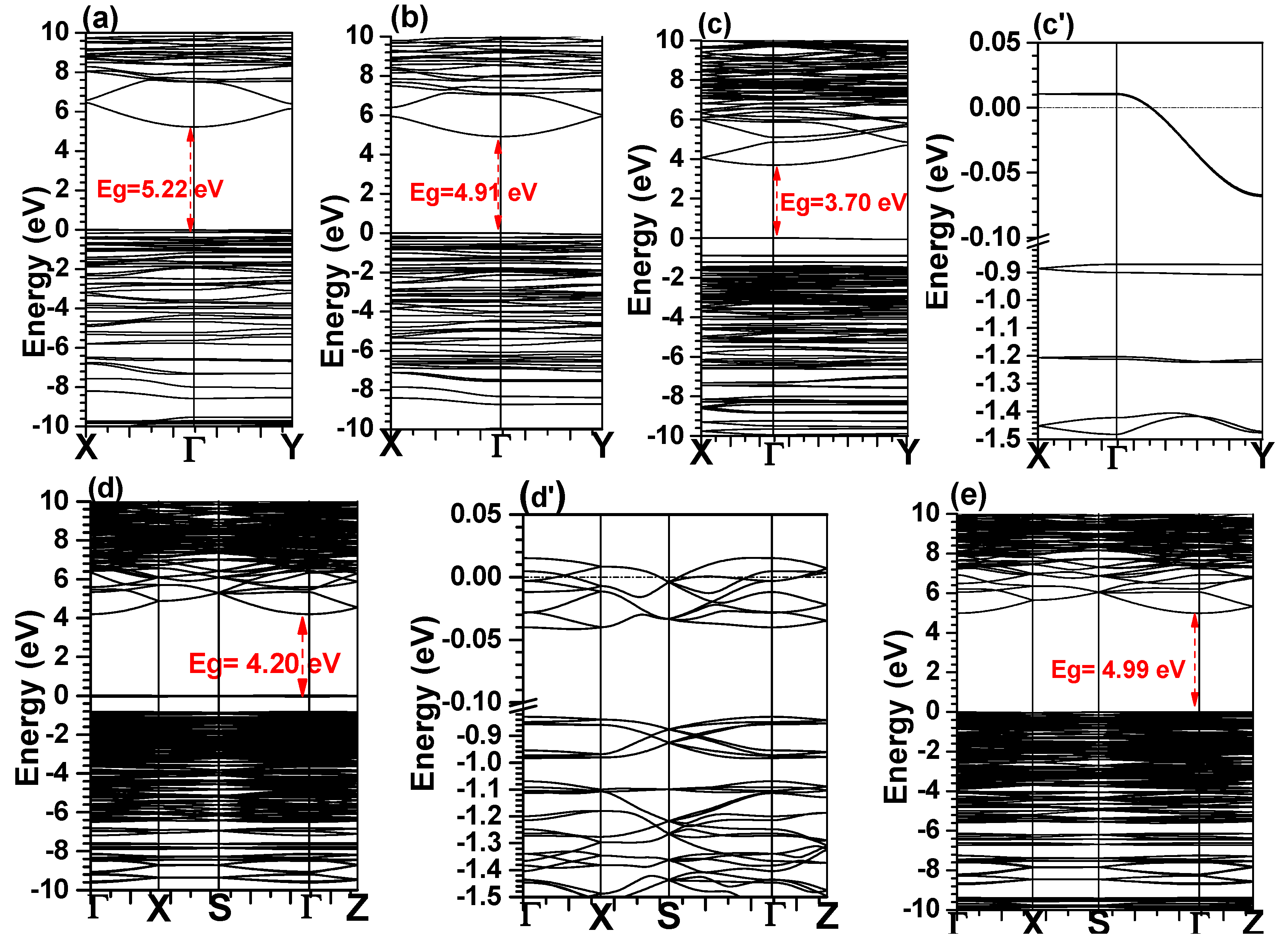
4.1. Electronic Structure
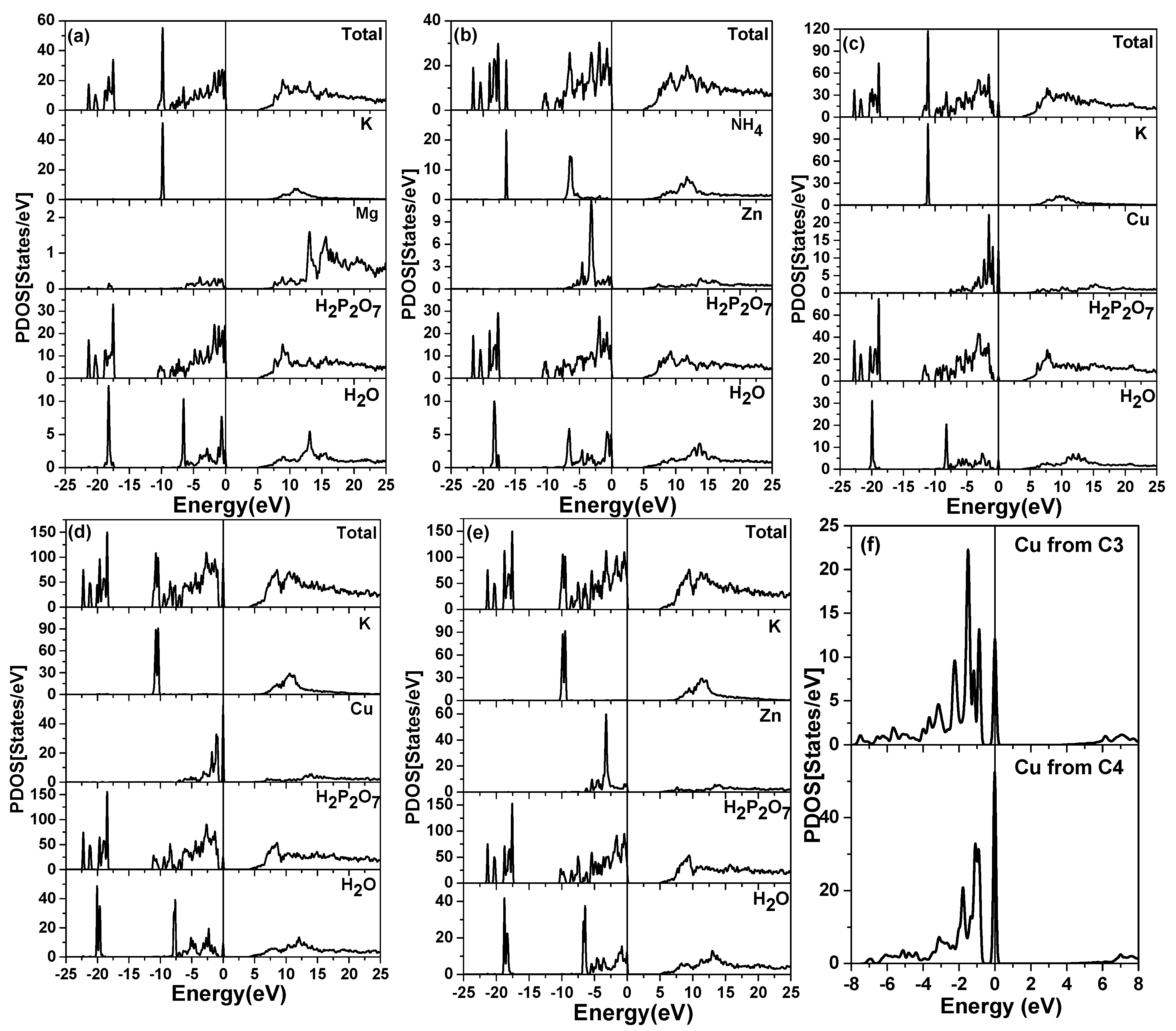
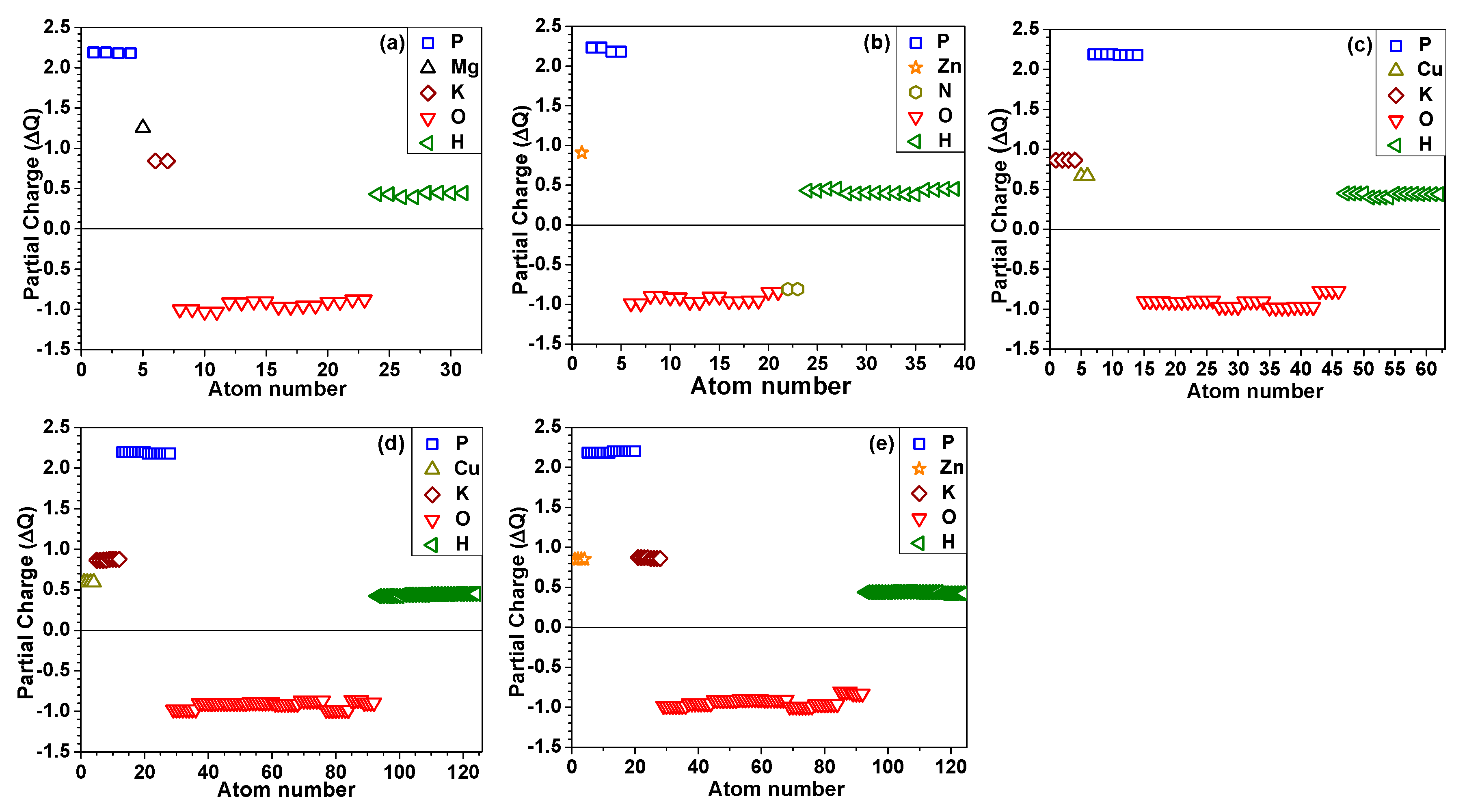
4.2. Partial Charge Distribution
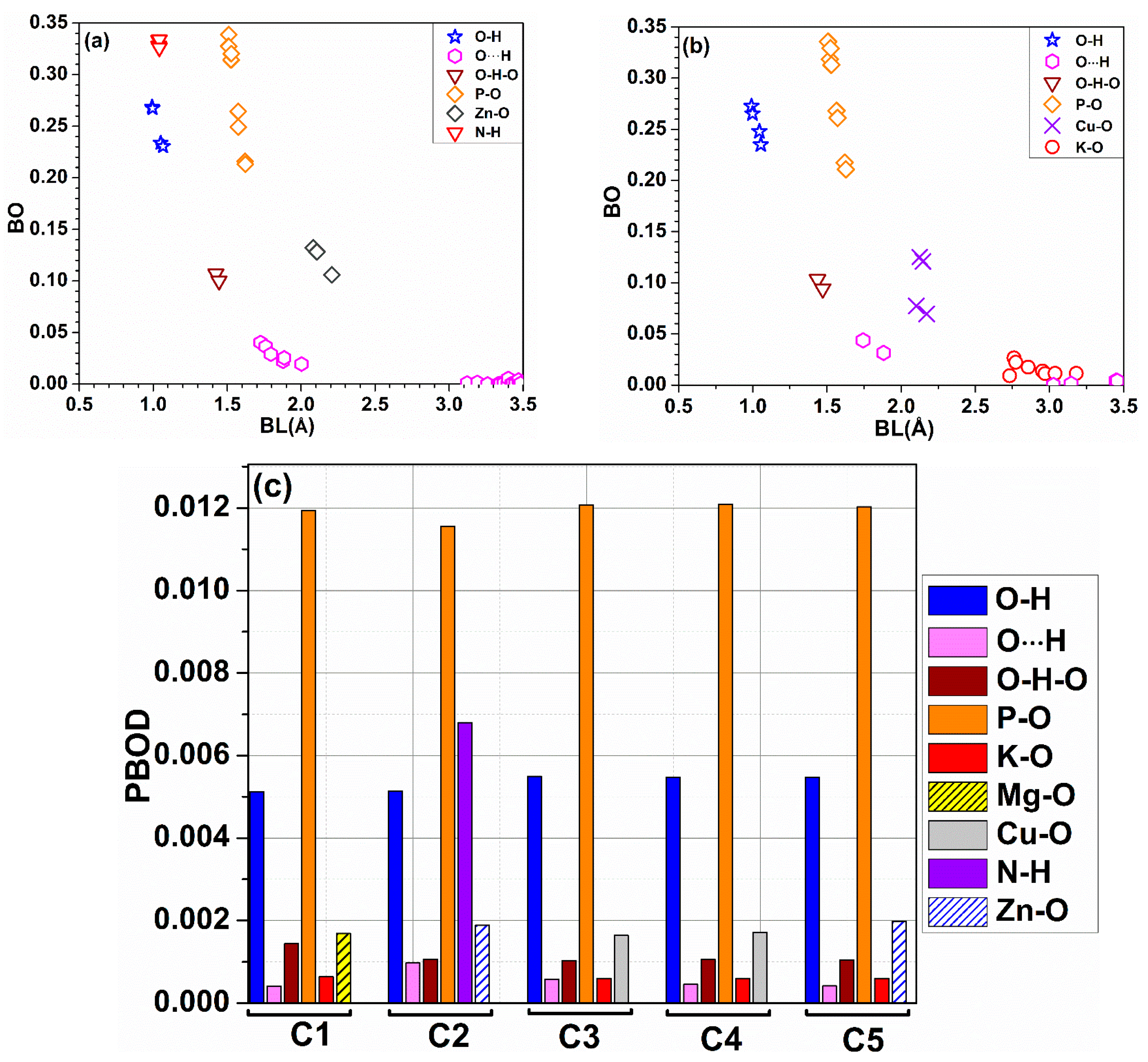
4.3. Interatomic Bonding
4.4. Mechanical Properties
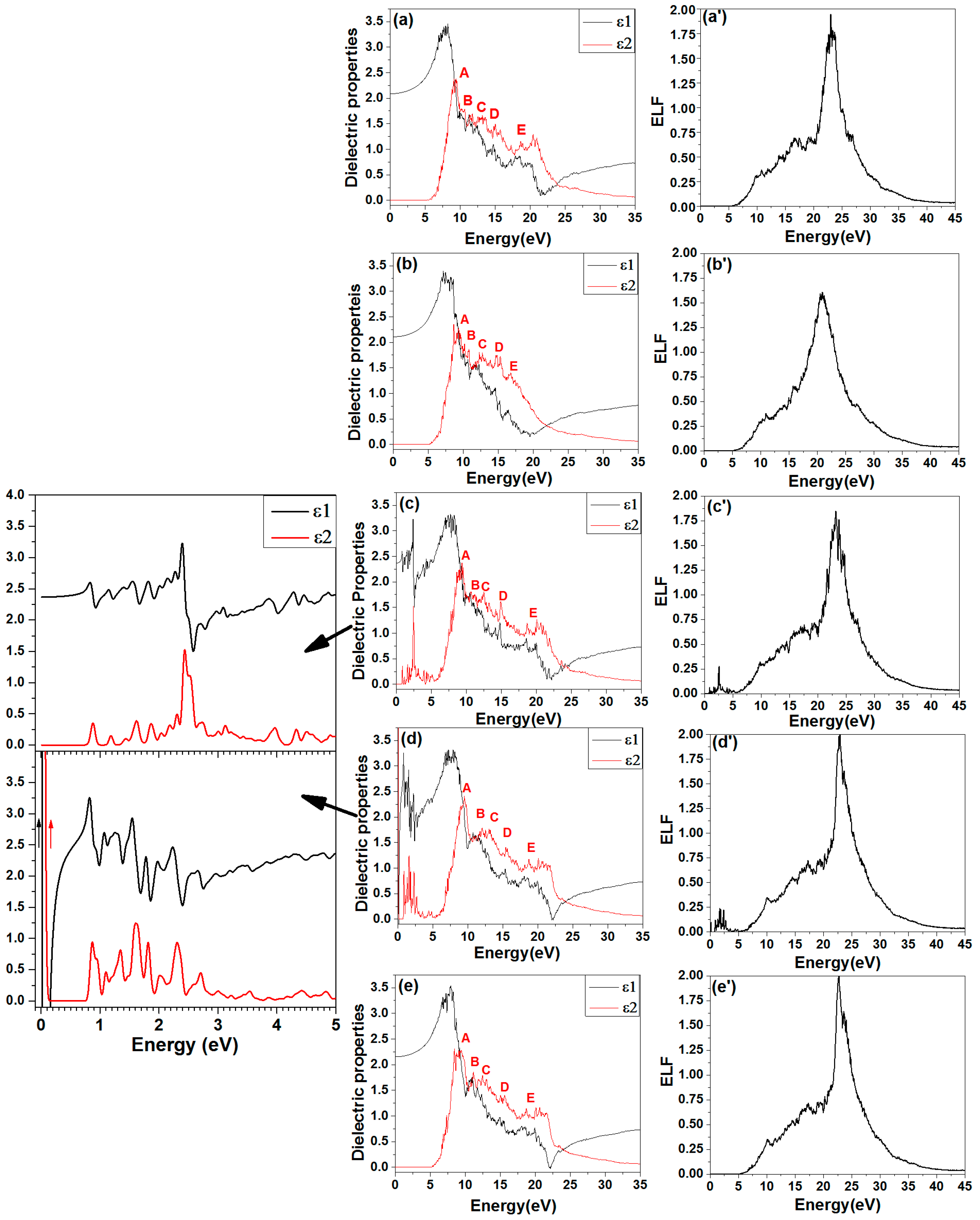
4.5. Optical Properties
5. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Durif, A. Crystal Chemistry of Condensed Phosphates; Springer Science & Business Media: New York, NY, USA, 1995; Volume 408, ISBN 978-1-4757-9896-8. [Google Scholar]
- Brow, R.K. The structure of simple phosphate glasses. J. Non-Crystal. Solids 2000, 263, 1–28. [Google Scholar] [CrossRef]
- Martin, S.W. Ionic conduction in phosphate glasses. J. Am. Ceram. Soc. 1991, 74, 1767–1784. [Google Scholar] [CrossRef]
- Ratnakaram, Y.; Babu, S.; Bharat, L.K.; Nayak, C. Fluorescence characteristics of Nd3+ doped multicomponent fluoro-phosphate glasses for potential solid-state laser applications. J. Lumin. 2016, 175, 57–66. [Google Scholar] [CrossRef]
- Yang, F.; Liu, Y.; Tian, X.; Dong, G.; Yu, Q. Luminescence properties of phosphate phosphor Ba3Y (PO4) 3: Sm3+. J. Solid State Chem. 2015, 225, 19–23. [Google Scholar] [CrossRef]
- Wang, P.; Lu, M.; Gao, F.; Guo, H.; Xu, Y.; Hou, C.; Zhou, Z.; Peng, B. Luminescence in the fluoride-containing phosphate-based glasses: A possible origin of their high resistance to nanosecond pulse laser-induced damage. Sci. Rep. 2015, 5, 8593. [Google Scholar] [CrossRef] [PubMed]
- Krempl, P.; Schleinzer, G.; Wallno, W. Gallium phosphate, GaPO4: A new piezoelectric crystal material for high-temperature sensorics. Sens. Actuators A Phys. 1997, 61, 361–363. [Google Scholar] [CrossRef]
- Westheimer, F.H. Why nature chose phosphates. Science 1987, 235, 1173–1178. [Google Scholar] [CrossRef] [PubMed]
- Andreeva, O.; Efimtseva, E.; Padyukova, N.S.; Kochetkov, S.; Mikhailov, S.; Dixon, H.; Karpeisky, M.Y. Interaction of HIV-1 reverse transcriptase and T7 RNA polymerase with phosphonate analogs of NTP and inorganic pyrophosphate. Mol. Biol. 2001, 35, 717–729. [Google Scholar] [CrossRef]
- Habraken, W.; Habibovic, P.; Epple, M.; Bohner, M. Calcium phosphates in biomedical applications: Materials for the future? Mater. Today 2016, 19, 69–87. [Google Scholar] [CrossRef]
- Knowles, J.C. Phosphate based glasses for biomedical applications. J. Mater. Chem. 2003, 13, 2395–2401. [Google Scholar] [CrossRef]
- Rulis, P.; Ouyang, L.; Ching, W. Electronic structure and bonding in calcium apatite crystals: Hydroxyapatite, fluorapatite, chlorapatite, and bromapatite. Phys. Rev. B 2004, 70, 155104. [Google Scholar] [CrossRef]
- Aryal, S.; Matsunaga, K.; Ching, W.-Y. Ab initio simulation of elastic and mechanical properties of Zn-and Mg-doped hydroxyapatite (HAP). J. Mech. Behav. Biomed. Mater. 2015, 47, 135–146. [Google Scholar] [CrossRef] [PubMed]
- Rulis, P.; Yao, H.; Ouyang, L.; Ching, W. Electronic structure, bonding, charge distribution, and X-ray absorption spectra of the (001) surfaces of fluorapatite and hydroxyapatite from first principles. Phys. Rev. B 2007, 76, 245410. [Google Scholar] [CrossRef]
- Liang, L.; Rulis, P.; Ching, W. Mechanical properties, electronic structure and bonding of α-and β-tricalcium phosphates with surface characterization. Acta Biomate. 2010, 6, 3763–3771. [Google Scholar] [CrossRef] [PubMed]
- Tang, E. Computational Studies of Phosphate Clusters and Bioglasses; UCL (University College London): London, UK, 2011. [Google Scholar]
- Kim, H.; Park, J.; Park, I.; Jin, K.; Jerng, S.E.; Kim, S.H.; Nam, K.T.; Kang, K. Coordination tuning of cobalt phosphates towards efficient water oxidation catalyst. Nat. Commun. 2015, 6, 8253. [Google Scholar] [CrossRef] [PubMed]
- Witko, M.; Tokarz, R.; Haber, J.; Hermann, K. Electronic structure of vanadyl pyrophosphate: Cluster model studies. J. Mol. Catal. A Chem. 2001, 166, 59–72. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, W.; Wu, D.; Zhang, H.; Chen, D.; Gong, Y.; Kan, Z. Crystal and band structures, bonding, and optical properties of solid compounds of alkaline indium (III) pyrophosphates MInP2O7 (M= Na, K, Rb, Cs). Chem. Mater. 2004, 16, 4150–4159. [Google Scholar] [CrossRef]
- Xiang, H.; Feng, Z.; Zhou, Y. Ab initio computations of electronic, mechanical, lattice dynamical and thermal properties of ZrP2O7. J. Eur. Ceram. Soc. 2014, 34, 1809–1818. [Google Scholar] [CrossRef]
- Adhikari, P.; Khaoulaf, R.; Ez-Zahraouy, H.; Ching, W.-Y. Complex interplay of interatomic bonding in a multi-component pyrophosphate crystal: K2Mg (H2P2O7)2·2H2O. R. Soc. Open Sci. 2017, 4, 170982. [Google Scholar] [CrossRef] [PubMed]
- Harcharras, M.; Capitelli, F.; Ennaciri, A.; Brouzi, K.; Moliterni, A.; Mattei, G.; Bertolasi, V. Synthesis, X-ray crystal structure and vibrational spectroscopy of the acidic pyrophosphate KMg0.5H2P2O7·H2O. J. Solid State Chem. 2003, 176, 27–32. [Google Scholar] [CrossRef]
- Capitelli, F.; Khaoulaf, R.; Harcharras, M.; Ennaciri, A.; Habyby, S.H.; Valentini, V.; Mattei, G.; Bertolasi, V. Crystal structure and vibrational spectroscopy of the new acidic diphosphate (NH4)2Zn (H2P2O7)2·2H2O. Z. Kristallogr.-Crystal. Mater. 2005, 220, 25–30. [Google Scholar] [CrossRef]
- Khaoulaf, R.; Ezzaafrani, M.; Ennaciri, A.; Harcharras, M.; Capitelli, F. Vibrational Study of Dipotassium Zinc Bis (Dihydrogendiphosphate) Dihydrate, K2ZN(H2P2O7)2·2H2O. Phosphorus Sulfur Silicon Relat. Elem. 2012, 187, 1367–1376. [Google Scholar] [CrossRef]
- Khaoulaf, R.; Ennaciri, A.; Ezzaafrani, M.; Capitelli, F. Structure and Vibrational Spectra of a New Acidic Diphosphate K2Cu(H2P2O7)2·2H2O. Phosphorus Sulfur Silicon Relat. Elem. 2013, 188, 1038–1052. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Ching, W.-Y.; Rulis, P. Electronic Structure Methods for Complex Materials: The Orthogonalized Linear Combination of Atomic Orbitals; Oxford University Press: Oxford, UK, 2012; ISBN 9780199575800. [Google Scholar]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Nielsen, O.; Martin, R.M. First-principles calculation of stress. Phys. Rev. Lett. 1983, 50, 697. [Google Scholar] [CrossRef]
- Yao, H.; Ouyang, L.; Ching, W.Y. Ab initio calculation of elastic constants of ceramic crystals. J. Am. Ceram. Soc. 2007, 90, 3194–3204. [Google Scholar] [CrossRef]
- Reuss, A. Berechnung der fließgrenze von mischkristallen auf grund der plastizitätsbedingung für einkristalle. ZAMM-J. Appl. Math. Mech./Z. Angew. Math. Mech. 1929, 9, 49–58. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Sect. A 1952, 65, 349. [Google Scholar] [CrossRef]
- Mulliken, R.S. Electronic population analysis on LCAO–MO molecular wave functions. I. J. Chem. Phys. 1955, 23, 1833–1840. [Google Scholar] [CrossRef]
- Mulliken, R. Electronic population analysis on LCAO–MO molecular wave functions. II. Overlap populations, bond orders, and covalent bond energies. J. Chem. Phys. 1955, 23, 1841–1846. [Google Scholar] [CrossRef]
- Poudel, L.; Steinmetz, N.F.; French, R.H.; Parsegian, V.A.; Podgornik, R.; Ching, W.-Y. Implication of the solvent effect, metal ions and topology in the electronic structure and hydrogen bonding of human telomeric G-quadruplex DNA. Phys. Chem. Chem. Phys. 2016, 18, 21573–21585. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, P.; Xiong, M.; Li, N.; Zhao, X.; Rulis, P.; Ching, W.-Y. Structure and electronic properties of a continuous random network model of an amorphous Zeolitic Imidazolate Framework (a-ZIF). J. Phys. Chem. C 2016, 120, 15362–15368. [Google Scholar] [CrossRef]
- Adhikari, P.; Dharmawardhana, C.C.; Ching, W.Y. Structure and properties of hydrogrossular mineral series. J. Am. Ceram. Soc. 2017, 100, 4317–4330. [Google Scholar] [CrossRef]
- Poudel, L.; Twarock, R.; Steinmetz, N.F.; Podgornik, R.; Ching, W.-Y. Impact of Hydrogen Bonding in the Binding Site between Capsid Protein and MS2 Bacteriophage ssRNA. J. Phys. Chem. B 2017, 121, 6321–6330. [Google Scholar] [CrossRef] [PubMed]
- Baral, K.; Li, A.; Ching, W.-Y. Ab Initio Modeling of Structure and Properties of Single and Mixed Alkali Silicate Glasses. J. Phys. Chem. A 2017, 121, 7697–7708. [Google Scholar] [CrossRef] [PubMed]
- Poudel, L.; Tamerler, C.; Misra, A.; Ching, W.-Y. Atomic-Scale Quantification of Interfacial Binding between Peptides and Inorganic Crystals: The Case of Calcium Carbonate Binding Peptide on Aragonite. J. Phys. Chem. C 2017, 121, 28354–28363. [Google Scholar] [CrossRef]
- Ching, W.Y.; Yoshiya, M.; Adhikari, P.; Rulis, P.; Ikuhara, Y.; Tanaka, I. First-principles study in an inter-granular glassy film model of silicon nitride. J. Am. Ceram. Soc. 2018, 101, 2673–2688. [Google Scholar] [CrossRef]
- San, S.; Li, N.; Tao, Y.; Zhang, W.; Ching, W.Y. Understanding the atomic and electronic origin of mechanical property in thaumasite and ettringite mineral crystals. J. Am. Ceram. Soc. 2018, 101, 5177–5187. [Google Scholar] [CrossRef]
- Dharmawardhana, C.; Misra, A.; Ching, W.-Y. Theoretical investigation of C-(A)-SH (I) cement hydrates. Constr. Build. Mater. 2018, 184, 536–548. [Google Scholar] [CrossRef]
- Baral, K.; Li, A.; Ching, W.Y. Understanding the atomistic origin of hydration effects in single and mixed bulk alkali-silicate glasses. J. Am. Ceram. Soc. 2018, 102, 207–221. [Google Scholar] [CrossRef]
- Adhikari, P.; Li, N.; Rulis, P.; Ching, W.-Y. Deformation behavior of amorphous zeolitic imidazolate framework-from supersoft material to complex organometallic alloy. Phys. Chem. Chem. Phys. 2018. [Google Scholar] [CrossRef] [PubMed]
- Martin, P.C. Sum rules, Kramers-Kronig relations, and transport coefficients in charged systems. Phys. Rev. 1967, 161, 143. [Google Scholar] [CrossRef]
- Braunstein, R.; Kane, E. The valence band structure of the III–V compounds. J. Phys. Chem. Solids 1962, 23, 1423–1431. [Google Scholar] [CrossRef]
- Kosicki, B.; Powell, R.; Burgiel, J. Optical Absorption and Vacuum-Ultraviolet Reflectance of GaN Thin Films. Phys. Rev. Lett. 1970, 24, 1421. [Google Scholar] [CrossRef]
- Marple, D. Electron effective mass in ZnSe. J. Appl. Phys. 1964, 35, 1879–1882. [Google Scholar] [CrossRef]
- Riccius, H.; Turner, R. Electroabsorption of zinc telluride films. J. Phys. Chem. Solids 1968, 29, 15–18. [Google Scholar] [CrossRef]
- Hopfield, J.; Thomas, D. Fine structure and magneto-optic effects in the exciton spectrum of cadmium sulfide. Phys. Rev. 1961, 122, 35. [Google Scholar] [CrossRef]
- Wheeler, R.; Dimmock, J. Exciton structure and Zeeman effects in cadmium selenide. Phys. Rev. 1962, 125, 1805. [Google Scholar] [CrossRef]
- Knoll, G.F. Radiation Detection and Measurement; John Wiley & Sons: Hoboken, NJ, USA, 2010; ISBN 978-0470131489. [Google Scholar]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [PubMed]
- Pugh, S. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Sreeram, A.; Varshneya, A.; Swiler, D. Molar volume and elastic properties of multicomponent chalcogenide glasses. J. Non-Crystal. Solids 1991, 128, 294–309. [Google Scholar] [CrossRef]
- Bridge, B.; Patel, N.; Waters, D. On the elastic constants and structure of the pure inorganic oxide glasses. Phys. Status Solidi (a) 1983, 77, 655–668. [Google Scholar] [CrossRef]
- Roberts, R.; Rowe, R.; York, P. The relationship between Young’s modulus of elasticity of organic solids and their molecular structure. Powder Technol. 1991, 65, 139–146. [Google Scholar] [CrossRef]
- Anderson, O.L.; Nafe, J.E. The bulk modulus-volume relationship for oxide compounds and related geophysical problems. J. Geophys. Res. 1965, 70, 3951–3963. [Google Scholar] [CrossRef]
- The Crystran Handbook of Infra-Red and Ultra-Violet Optical Materials; Crystan LTD Broom Road Business Park: Poole, UK, 2014; p. 112.
- CRC Handbook of Physics and Chemistry, 8th ed.; The Chemical Rubber Company: Cleveland, OH, USA, 2001; ISBN 978-0-8493-0482-8.
- Weber, M.J. Handbook of Optical Materials; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
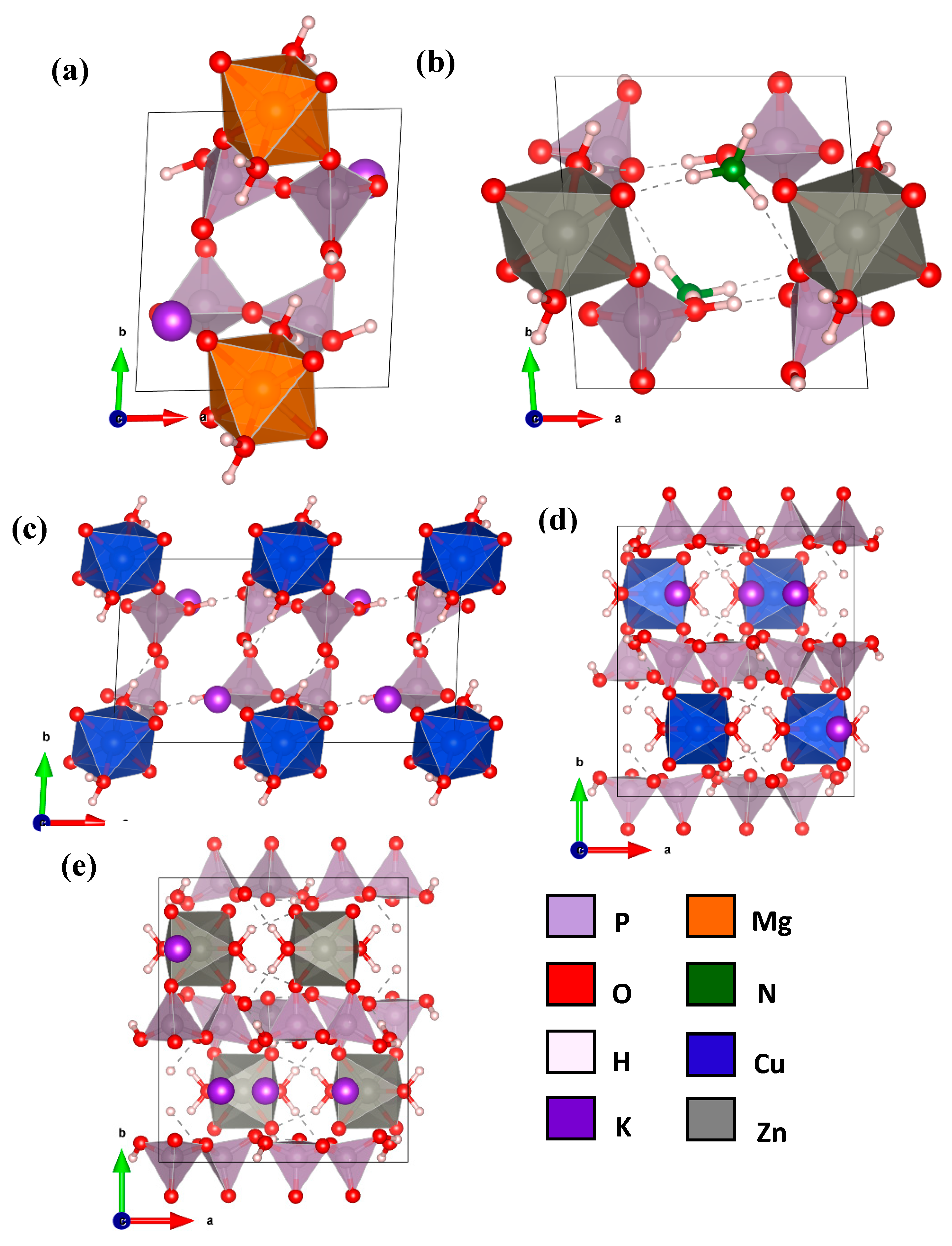

| Space Group | a(Å), b(Å), c(Å), α, β, γ | Volume (Å3) | No. of Atoms | |
|---|---|---|---|---|
| C1 | P-1(Ci) | 6.954, 7.503, 7.589, 81.166°, 75.522°, 84.257° | 378.05 | 31 |
| C2 | P-1(Ci) | 7.178, 7.424, 7.808, 81.007°, 71.428°, 90.952° | 388.58 | 39 |
| C3 | P-1(Ci) | 7.101, 7.430, 7.609, 78.761°, 71.657°, 83.958° | 373.38 | 31 |
| C4 | Pnma(D2h16) | 9.757, 11.134, 13.728, 90.000°, 90.000°, 90.000° | 1491.35 | 124 |
| C5 | Pnma(D2h16) | 9.770, 11.166, 13.746, 90.000°, 90.000°, 90.000° | 1499.60 | 124 |
| K2 | (NH4)2 | Mg | Zn | Cu | (H2P2O7)2 | 2·H2O | |
|---|---|---|---|---|---|---|---|
| C1 | 1.68 | - | 1.26 | - | - | -2.97 | 0.03 |
| C2 | - | 1.55 | - | 0.91 | - | -2.57 | 0.11 |
| C3 | 1.73 | - | - | - | 0.67 | -2.62 | 0.22 |
| C4 | 1.74 | - | - | - | 0.59 | -2.36 | 0.03 |
| C5 | 1.73 | - | - | 0.85 | - | -2.71 | 0.13 |
| Eg (eV) | me* (me) | ɛ1(0) | n | ωp (eV) | TBOD | |
|---|---|---|---|---|---|---|
| C1 | 5.22 | 0.143 | 2.09 | 1.44 | 22.98 | 0.02125 |
| C2 | 4.91 | 0.146 | 2.11 | 1.45 | 20.85 | 0.02743 |
| C3 | 3.70 | 0.146 | 2.37 | 1.53 | 23.14 | 0.02141 |
| C4 | 4.20 | 0.146 | 290.99 | 17.06 | 22.89 | 0.02139 |
| C5 | 4.99 | 0.149 | 2.15 | 1.47 | 22.67 | 0.02155 |
| K(GPa) | G(GPa) | E(GPa) | ƞ | G/K | AU | |
|---|---|---|---|---|---|---|
| C1 | 22.88 | 15.63 | 38.19 | 0.2218 | 0.6831 | 3.6100 |
| C2 | 30.28 | 14.84 | 38.26 | 0.2894 | 0.4899 | 3.1220 |
| C3 | 28.19 | 14.66 | 37.48 | 0.2784 | 0.5199 | 2.7776 |
| C4 | 30.26 | 13.90 | 36.15 | 0.3009 | 0.4591 | 0.7182 |
| C5 | 24.53 | 15.58 | 38.57 | 0.2379 | 0.6351 | 1.9064 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khaoulaf, R.; Adhikari, P.; Harcharras, M.; Brouzi, K.; Ez-Zahraouy, H.; Ching, W.-Y. Atomic-Scale Understanding of Structure and Properties of Complex Pyrophosphate Crystals by First-Principles Calculations. Appl. Sci. 2019, 9, 840. https://doi.org/10.3390/app9050840
Khaoulaf R, Adhikari P, Harcharras M, Brouzi K, Ez-Zahraouy H, Ching W-Y. Atomic-Scale Understanding of Structure and Properties of Complex Pyrophosphate Crystals by First-Principles Calculations. Applied Sciences. 2019; 9(5):840. https://doi.org/10.3390/app9050840
Chicago/Turabian StyleKhaoulaf, Redouane, Puja Adhikari, Mohamed Harcharras, Khalid Brouzi, Hamid Ez-Zahraouy, and Wai-Yim Ching. 2019. "Atomic-Scale Understanding of Structure and Properties of Complex Pyrophosphate Crystals by First-Principles Calculations" Applied Sciences 9, no. 5: 840. https://doi.org/10.3390/app9050840
APA StyleKhaoulaf, R., Adhikari, P., Harcharras, M., Brouzi, K., Ez-Zahraouy, H., & Ching, W.-Y. (2019). Atomic-Scale Understanding of Structure and Properties of Complex Pyrophosphate Crystals by First-Principles Calculations. Applied Sciences, 9(5), 840. https://doi.org/10.3390/app9050840





