Prioritization Assessment for Capability Gaps in Weapon System of Systems Based on the Conditional Evidential Network

Abstract

The prioritization of capability gaps for weapon system of systems is the basis for design and capability planning in the system of systems development process. In order to address input information uncertainties, the prioritization of capability gaps is computed in two steps using the conditional evidential network method. First, we evaluated the belief distribution of degree of required satisfaction for capabilities, and then calculated the reverse conditional belief function between capability hierarchies. We also provided verification for the feasibility and effectiveness of the proposed method through a prioritization of capability gaps calculation using an example of a spatial-navigation-and-positioning system of systems.

1. Introduction

A capability gap is defined by the degree to which a designated action plan of the system of systems cannot be implemented. Such a gap may result from a lack of capability, proficiency in existing capability solutions, and/or the need to replace existing capability solutions to prevent future gaps.

Operational requirements often require more capabilities than equipment developments are able to provide. A capability gap describes the difference between the status of the system of systems’ capabilities and the operational requirements. It is a direct base for maximum capability realization of the system of systems. The purpose of a gap assessment is to identify its size and determine the weaknesses of supported equipment demonstration.

Capability-gap analysis mainly includes two aspects. The first, in response to the functional needs of the capability, is to carry out an assessment of the capabilities in the weapon system of systems. The second aspect consists in comparing the status of the capability needs and the capabilities one by one, according to criteria, such as “be able to support well”, “be able to support under certain conditions”, and “cannot support”, as well as analyzing whether these capabilities support the completion of the task.

1.1. Evidential Network

Knowledge representation and uncertainty reasoning based on the network-based method began with research on early constrained networks, qualitative Markov trees [1], and qualitative Markov networks [2]. In the late 1980s and early 1990s, the Bayesian Network (BN) [3] and the value-based system (VBS) [4] greatly promoted the use of a network model for knowledge representation and uncertainty inference. However, BN and VBS cannot handle knowledge that is described as a belief function. Cano put forward an axiomatic reasoning system in 1993 [5] that extracts an abstract mathematical model so as to represent information by expressing concepts and algorithms that are related to the value, and that provide a general framework for studying knowledge representation and reasoning in causal networks, including probability and belief functions. General information can then be decomposed from a generalized conditional-probability perspective. That same year, Smets, the author of the transitive belief model (TBM), proposed a generalized Bayesian theory (GBT) [6] under the framework of the TBM. By means of the Disjunctive Rule of Combination (DRC), where only one of the two independent evidences is known, the belief of both evidences can be calculated, which is to say that the belief function also has the same conditional belief function as the Bayesian formula. Based on these two basic theoretical achievements, some scholars began to explore the modeling and reasoning of evidence networks. In 1994, Xu and Smets first proposed the concept of evidential networks (EN) [7] and for the first time used the conditional belief function to represent the relationship between network nodes. This paper proposes the concept of using the evidential network with a conditional belief function (ENC) and offers the corresponding reasoning algorithm. By analyzing the characteristics of ENC, this paper also explores reasoning that may simplify the problem.

Attoh-Okine and Bovee et al. proposed an understanding of the evidential network based on the qualitative Markov tree [8,9]. Cobb and Yaghlane et al. by comparing and analyzing the similarities and differences between the evidence network and the VBS, pointed out that the main problem of evidential-network research is how to represent the independence of the belief function through the graph model. Based on the general belief function and the transitive belief function, a model of the directed belief network with the conditional belief function (DEVN) was proposed. The relationship between knowledge and conditions in the network was represented by a directed acyclic graph plus the belief function, and the EN reasoning was realized through DRC and GBT [10,11,12]. Srivastava et al. obtained the causal graph through an explicit causal matching algorithm and then constructed the evidential network by using the basic concepts of the belief function. Expansion and marginalization were used in the reasoning process to solve the problem of job-satisfaction evaluation [13]. Simon and Weber published five consecutive articles from 2007–2009, combining Bayesian networks and evidence theory in order to solve the reliability problems in complex systems, which mainly involve incomplete and inaccurate information. Their reasoning mode is still used in Bayesian theory [14,15,16,17,18]. Trained as a Yaghlane student, Trabelsi developed a BeliefNet tool in 2008 that combines the synthesis, marginalization, expansion, and projection algorithms of the evidential network with inference algorithms such as binary syndication and hash tables [19].

In 2012, Wafa and Yaghlane used a dynamically-directed evidential network with conditional belief functions for a study on system reliability, indicating that the directed evidential network is moving toward a dynamic direction [20]. Later, in 2013, they proposed a new propagation algorithm for a dynamic directed evidence network with conditional belief functions, based on a new computational structure called Mixed Binary Tree [21]. This algorithm is suitable for accurate reasoning. In 2014, Wafa published two consecutive articles, in which Monte Carlo algorithms were used to discuss both the reasoning of single-connected directed evidential networks with conditional belief functions and the approximate reasoning of directed evidential networks with conditional belief functions [22,23]. In terms of evidential-network learning, Hariz and Yaghlane published two articles in 2014 on the parametric learning of conditional-belief evidential networks [24,25], and in an article published in 2015 used an evidence database to discuss the structural learning of evidential networks [26]. In 2015, Wafa and Yaghlane explored the propagation of belief functions in single-connected hybrid directed evidential networks [27]. A hybrid directed evidential network is a promotion of a standard directed evidential network, bringing the development of evidential network one step further.

In addition, initial attempts have also been made to use evidential networks for threat assessment [28], intelligent control [29], medical care [30], convoy detection [31], fault detection [32], virtual-environment training [33], and reliability analysis [34,35].

1.2. Prioritization Assessment of Capability Gaps

There is little research in China that focuses on the priority assessment of capability gaps. Some research in this field exists abroad, but most of it is qualitative. The Technical Cooperation Program (TTCP) joint system and analysis team presents a qualitative analysis method that uses colors to identify the importance of capability gaps [36]. This is a completely subjective and sketchy approach. The US military “Capabilities-Based Assessment Handbook 3.0” introduced the sequencing of biometric information recognition-related capability gaps [37]. This method is based on a comparison of capability gaps among experts, regardless of uncertainty. Linkov, from the research and development center at the US Army Corps of Engineers, examined the issue of capability gaps in the small-arms program for multi-service, using a multi-criteria decision analysis method [38]. The core of this method is an analytic hierarchy process, but its disadvantage is that there is no verification of the consistency of the judgment matrix. Hristov proposed a prioritization method for capability gaps, which was used to solve the problem of how to rank gaps in the combat capability of the Bulgarian armed forces [39]. This method takes into account three factors: the weight of the capability, the expected utility after filling the capability gap, and its urgency. It does not, however, consider the uncertainty. Welch proposed a gap-ranking method based on the utility theory, which is used to solve the capability-gap ranking problem of brigade combat units [40]. This method is part of the United States-based Sandia National Laboratory Modernization assessment process. Most of the work needs to be completed by experts in relevant fields, and the method is subjective.

Langford rethinks the theoretical basis and systematic study of gap analysis, and expands on it while delineating its practicality and limitation. He came up with new ideas on these theoretical foundations by adopting the perspective of systems and value engineering [41]. By qualitatively analyzing the gap in the medium-lift capability of the United States Marine Corps, Harris suggested that a medium-lift platform be added to fill the capability gap between light- and heavy-duty lift planes [42]. By analyzing the capabilities gap, John of the United States Army argued that the quest for high-end capabilities left the Australian Defense Force vulnerable to mission failures, following which he finally obtained the prioritization of defense major capabilities [43]. By combining the soldier’s expertise with a quantifiable analysis, Rubemeyer proposed a gap-assessment method [44]. In this method, combatants on the mission determine the impact of measurable attributes from each capability gap; a mathematical approach is used to incorporate all of the combatants’ responses into a single mission impact for each capability gap. In order to identify Air Force characteristics, the Office of Aerospace Studies of the United States Air Force conducts research on the methods and processes of capability-gap analysis through capability requirement statements, capability gap identification, capability gap statements, gap characterization, risk assessment, and gap prioritization [45]. In order for the Department of Homeland Security’s capability to deal with biochemical threats, the U.S. Government Accountability Office submitted a report to the National Congress that elaborated the need for an analysis of the relevant capability gaps and put forward ways to identify and resolve related capability gaps [46]. These methods are qualitative and do not account for uncertainty.

In this paper, in which we focused on the multiple uncertainties in the priority assessment of capability gaps, we adopted a method based on the conditional evidential network. Using the space-navigation-and-positioning system of systems as an example, we studied the priority assessment of capability gaps in weapon system of systems.

2. Basics of the Conditional Evidential Network

In belief function theory, $\mathsf{\Theta }$ is a set of mutually exclusive and complete finite elements, called the recognition framework. $2^{\mathsf{\Theta }}$ is its power set.

The belief distribution that supports proposition A is called the basic belief assignment (BBA) and is a function that maps from $2^{\mathsf{\Theta }}$ to [0, 1], as shown in the following equation:

$${\displaystyle \sum _{A\in \mathsf{\Theta }}m(A)}=1$$

(1)

If any subset $A\in \mathsf{\Theta }$ basic belief assignment $m\left(A\right)>0$, then A is called a focal element of Θ.

Each basic belief assignment m is associated with a belief function Bel mapped from $2^{\mathsf{\Theta }}$ to [0, 1] and a likelihood function Pl mapped from $2^{\mathsf{\Theta }}$ to [0, 1]. These two functions represent the smallest and largest possible support for A, respectively. These functions are defined as follows:

$$Bel(A)={\displaystyle \sum _{\varnothing \ne B\subseteq A}m(B),Bel(\varnothing )}=0$$

(2)

$$Pl(A)={\displaystyle \sum _{B\cap A\ne \varnothing }m(B),Pl(\varnothing )}=0$$

(3)

A belief function $Bel:2^{\mathsf{\Theta }}\to [0,1]$ is a Bayesian function if and only if there is a unique function $P:\mathsf{\Theta }\to [0,1]$ such that for $\forall X\subset \mathsf{\Theta }$, ${\displaystyle \sum _{\theta \in \mathsf{\Theta }}p(\theta )}=1$ holds, and $bel(X)={\displaystyle \sum _{\theta \in X}p(\theta )}$ holds.

Compared with the Bayesian function, the belief function is a set functions, and the Bayesian function is a point function. The Bayesian function is a special case of the belief function, and the belief function is a generalized Bayesian function.

Conditional basic belief $m(B|A)$, conditional belief function $Bel(B|A)$, and conditional likelihood function $Pl(B|A)$ are defined on the identification framework $\mathsf{\Theta }$ [47].

Generalized Bayesian Theorem (GBT): Let ${\mathsf{\Theta }}_X$ and ${\mathsf{\Theta }}_Y$ be the identification frameworks of X and Y, respectively. Assuming that the identification framework is normalized, that is:

$$Be{l}_X(X|y_i)=1,\forall y_i\in y$$

(4)

For $\forall x_i\in {\mathsf{\Theta }}_x,\forall y_i\in {\mathsf{\Theta }}_x$, the following holds:

$$Be{l}_Y(y|x)=K({\displaystyle \prod _{y_i\in \overline{y}}Be{l}_X(\overline{x}|y_i)}-{\displaystyle \prod _{y_i\in y}Be{l}_X(\overline{x}|y_i)})$$

(5)

$$P{l}_Y(y|x)=K(1-{\displaystyle \prod _{y_i\in y}(1-P{l}_X(x|y_i))})$$

(6)

$$K^{-1}=1-{\displaystyle \prod _{y_i\in y}Be{l}_X(\overline{x}|y_i)}=1-{\displaystyle \prod _{y_i\in y}(1-P{l}_X(x|y_i)})$$

(7)

When y is one dimension, the following holds:

$$m_Y(y|x)=Be{l}_Y(y|x)$$

(8)

The conditional belief function and conditional likelihood function still hold the following relations:

$$Bel(y|x)=1-Pl(\overline{y}|x)$$

(9)

Therefore:

$$m_Y(y|x)=1-P{l}_Y(\overline{y}|x)$$

(10)

The following holds:

$$m_Y(y|x)=1-K(1-{\displaystyle \prod _{y_i\in \overline{y}}(1-P{l}_X(x|y_i))})=1-K(1-{\displaystyle \prod _{y_i\in \overline{y}}{\displaystyle \sum _{x_i\in \overline{x}}{m}_X(x_i|y_i)}})$$

(11)

Forward reasoning: If we know the belief information on each state or subset of Y, denoted as $m_0(y)$, $y\subseteq Y$, then for $\forall x\subseteq X$, the following holds:

$$m_X(x)={\displaystyle \sum _{y\subseteq Y}{m}_0(y)m_X(x|y)}$$

(12)

The above formula is based on the conditional basic belief. By the same token, the above equation, expressed with the conditional belief function and conditional likelihood function, reads:

$$\begin{array}{l}Be{l}_X(x)={\displaystyle \sum _{y\subseteq Y}{m}_0(y)Be{l}_X(x|y)}\\ P{l}_X(x)={\displaystyle \sum _{y\subseteq Y}{m}_0(y)P{l}_X(x|y)}\end{array}$$

(13)

Marginalization: Let the conditional belief function $Be{l}_{XY}^{\downarrow X}$ be the marginal conditional belief function of $Be{l}_{XY}$ on X and $P{l}_{XY}^{\downarrow X}$ be the marginal conditional likelihood function of $P{l}_{XY}$ on X. The following holds:

$$\begin{array}{l}Be{l}_{XY}^{\downarrow X}(x|z)=Be{l}_{XY}((x,Y)|z)\\ P{l}_{XY}^{\downarrow X}(x|z)=P{l}_{XY}((x,Y)|z)\end{array}$$

(14)

3. Capability Gaps Computing Based on the Conditional Evidential Network

This paper specifically sorts the capability-gap priorities of weapon system of systems based on the power product of the inverse conditional belief functions $m(C_1=L|C=L)$ and $m(C_1=L)$. $C=L$ means that the upper-level capability’s requirement satisfaction is low, while $C_1=L$ means that the lower-level capability’s requirement-satisfaction is low. $m(C_1=L)$ represents the belief distribution of the degree of requirement satisfaction of the lower-level capability. $m(C_1=L|C=L)$ represents the belief distribution of the degree of requirement satisfaction of the lower-level capability when that of the upper-level capability is low. $m(C_1=L)$ reflects the gap in capability in an intuitive manner, while $m(C_1=L|C=L)$ reflects the degree of influence of the given gap on the upper-level capability gap. The power product of the two can help with a more comprehensive assessment of capability-gap priorities.

3.1. Calculation of the Belief Distribution of the Requirement-Satisfaction Degree for Capabilities

To calculate the belief distribution of the requirement-satisfaction degree for capabilities, first we need to establish the conditional-evidential-network identification framework and the conditional-belief-parameter table.

We use a causality diagram along with other methods in order to construct the evidential network of weapon system of systems’ capabilities. In order to model it, we use the conditional belief function, based on relevant knowledge and experts’ experience. Following this, we obtain the evidential-network structure-chart and conditional-belief-function table. The conditional belief function in this paper is defined by each node and expressed in $m(C|Pa(C))$, where C represents the state of the capability sub-node and $Pa(C)$ represents the combined state of all of the node’s parent nodes.

Next, we calculate the belief distribution of the requirement-satisfaction degree of the bottom capability.

Let $c_h$ and $c_l$ respectively denote the ideal value and the lowest capability-requirement value. c represents the actual value of the capability, $\epsilon (c)$ represents the credibility of this actual value, and $\phi (c)$ represents the degree to which the actual and ideal values match.

According to the characteristics of the bottom capabilities, the matching degree between the actual and the ideal capabilities can each be calculated according to the indicators of benefit and cost.

(1)

The matching degree of the benefit index and the requirement’s ideal value is:

$$\phi (c)=\{\begin{array}{c}0c\le c_l\\ \frac{c-c_l}{c_h-c_l}{c}_l<c<c_h\\ 1c\ge c_h\end{array}$$

(15)

(2)

The matching degree of the cost index and the requirement’s ideal value is:

$$\phi (c)=\{\begin{array}{c}0c\ge c_l\\ \frac{c_l-c}{c_l-c_h}{c}_h<c<c_l\\ 1c\le c_h\end{array}$$

(16)

According to the matching degree of the bottom index and the ideal value of the demand, the belief distribution of the requirement satisfaction can be calculated as follows:

$$\{\begin{array}{c}{m}_0(c=H)=\phi (c)\epsilon (c)\\ m_0(c=L)=(1-\phi (c))\epsilon (c)\\ m_0(\mathsf{\Theta })=1-\epsilon (c)\end{array}$$

(17)

where $m_0(c=H)$ represents the belief that the degree of requirement satisfaction of the bottom indicators is high, $m_0(c=L)$ represents the belief that it is low, and $m_0(\mathsf{\Theta })$ represents the belief assigned to cognitive uncertainty.

Then we calculate the belief distribution of the requirement-satisfaction degree for the upper layer capability.

According to the conditional-belief-parameter table established using the method in Section 3.1 and the belief distribution of the bottom capability’s requirement satisfaction, the belief distribution of the capability requirement satisfaction for each capability is calculated by the forward reasoning formula:

$$m(C)={\displaystyle \sum m_0(Pa(C))m(C|Pa(C))}$$

(18)

$$m_0(Pa(C))={\displaystyle \prod _{C_i\subseteq Pa(C)}m(C_i})$$

(19)

3.2. Calculation of the Inverse Conditional Belief

The inverse conditional likelihood belief is calculated via the GBT theorem using Equations (9) and (10). The obtained reverse conditional likelihood belief has the joint form $Pl(Pa(C)|C)$ for the lower multiple capabilities and must be marginalized. Marginalization is performed according to Equation (14).

The marginalized inverse likelihood function for the lower-level single capabilities can be used directly in Equation (13) to calculate the basic belief function $m(C_i|C)$ for each capability.

3.3. Prioritization of System of Systems’ Capability Gaps

Based on the product of the belief distribution of the requirement-satisfaction degree for each capability and the reversal basic belief function of each capability obtained through the above steps, the system of systems’ capabilities are prioritized:

$$Pr(C_i)=m^{\alpha }(C_i=L)\cdot m^{\beta }(C_i=L|C=L)$$

(20)

where $Pr(C_i)$ denotes the priority of the lower-level capability gaps, $m(C_i=L)$ denotes the belief that the requirement-satisfaction degree of the lower-level capability is low, and $m(C_i=L|C=L)$ represents the belief that the degree of requirement satisfaction of the lower-level capability is low under the condition that that of the upper-level capability is low. $\alpha ,\beta \in (0,1)$ and $\alpha +\beta =1$.

4. Case Study

This paper applies the above method to assess the prioritization of capability gaps in the space-navigation-and-positioning system of systems, and to verify the above method’s feasibility and effectiveness.

4.1. Construction of the Evidential-Network-Structure Model

Space-navigation-and-positioning system of systems capabilities include navigation and positioning capability, system survivability, system anti-jamming capability, and security and confidentiality. The corresponding evidence network structure was established using the causality-diagram method, as shown in Figure 1.

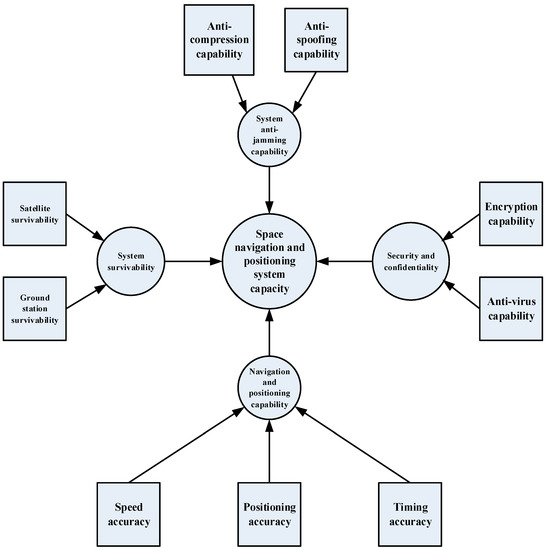
Figure 1. Evidential network structure for the capabilities of the space-navigation-and-positioning system of systems.

4.2. The Construction of the Evidential-Network-Parameter Model

The establishment of the recognition framework, corresponding to the evidence network for the capabilities of the space-navigation-and-positioning system of systems in Figure 1, is shown in Table 1. Among the recognition frames, “high” means that the current capability’s situation is “able to support” the capability requirement or that the capability’s degree of requirement satisfaction is high; “medium” means that the capability’s current situation “can support under certain conditions” the capability requirement or that the capability’s degree of requirement satisfaction is normal; and “low” means that the capability status “cannot support” the capability requirement or that the capability’s degree of requirement satisfaction is low. For convenience’s sake, this article divides the top level into three levels and the remaining levels into two.

Table 1. Identification framework for space navigation and positioning capabilities.

Node	Recognition Frame Θ
Space-navigation-and-positioning system capability (SNP)	{high (H), medium (M), low (L)}
Anti-jamming capability (AJ)	{high, low}
Anti-compression capability (AC)	{high, low}
Anti-spoofing capability (AS)	{high, low}
System survivability (SS)	{high, low}
Satellite survivability (SAS)	{high, low}
Ground station survivability (GSS)	{high, low}
Security and confidentiality (SC)	{high, low}
Encryption capability (EC)	{high, low}
Anti-virus capability (AV)	{high, low}
Navigation and positioning capability (NP)	{high, low}
Positioning accuracy (PA)	{high, low}
Speed accuracy (SA)	{high, low}
Timing accuracy (TA)	{high, low}

We took into consideration the fact that satellite navigation signals are likely to be more compressed in actual combat operations and that satellite survivability is more important than ground-station survivability due to the high launch cost of satellites. Encryption capability is more important than anti-virus capability, and navigation-positioning capability is the core competence in spatial-information-support system of systems. The conditional belief functions are calculated by using the weight coefficient of capabilities [48]. Then, we established the belief-parameter table, shown in Figure 2.

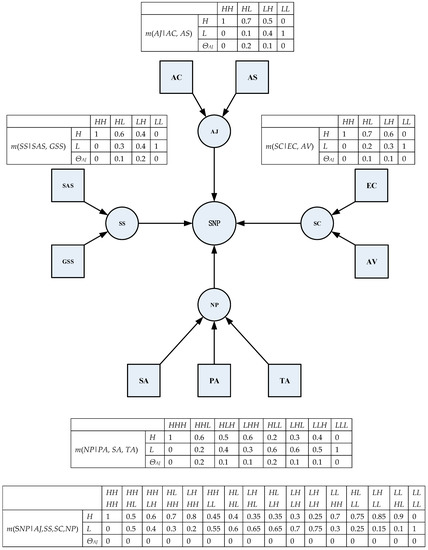
Figure 2. Conditional-belief-parameter table for spatial navigation and positioning capabilities.

In this figure, “m(AJ=H|AC=H, AS=L) = 0.7” indicates that, with the conditional belief of 0.7, the anti-jamming capability of the space-navigation-and-positioning system is “high” when the anti-suppress interference capability is “high” and the anti-spoofing interference capability is “low”. The notation “m(Θ_AJ|AC=H, AS=L) = 0.2” indicates that there is a cognitive uncertainty, that is, a partial ignorance of the subject. At this point, we assigned a portion of the belief to the complete set of recognition frames Θ for node states.

4.3. Capability-Requirement-Satisfaction Assessment

Table 2 shows the capability structure parameters of a satellite-navigation-and-positioning system of systems, including sub-capability names, bottom indicators, weights, capability requirements, actual levels, and the credibility of the actual levels.

Table 2. Capability parameters.

Capability	Sub-Capabilities and Indicators	Weight	Ideal Value	Minimum Value	Actual Value	Credibility
Anti-jamming capability (0.15)	Anti-compression capability (dBc)	0.6	120	50	90	1
	Anti-spoofing capability (dBc)	0.4	100	40	90	1
System survivability (0.1)	Satellite survivability	0.7	100	60	90	0.9
	Ground-station survivability	0.3	100	60	80	0.9
Security and confidentiality (0.1)	Encryption capability	0.5	100	50	70	0.9
	Anti-virus capability	0.5	100	50	80	0.9
Navigation and positioning capability (0.65)	Positioning accuracy (m)	0.4	5	20	10	0.95
	Speed accuracy (m/s)	0.3	0.1	0.5	0.2	0.95
	Timing accuracy (ns)	0.3	10	100	50	0.95

For example, a positioning accuracy with a confidence level of 0.95 means that the horizontal positioning accuracy is less than or equal to 10 m at a confidence level of 0.95.

Table 3 shows the prior belief distribution of the requirement-satisfaction degree for each index.

Table 3. The belief distribution of the degree of demand-satisfaction for bottom-capability indicators.

Bottom-Capability Indicators	m0 (c=H)	m0 (c=L)	m0 (Θ)
Anti-compression capability	0.571	0.429	0
Anti-spoofing capability	0.833	0.167	0
Satellite survivability	0.675	0.225	0.1
Ground station survivability	0.45	0.45	0.1
Encryption capability	0.36	0.54	0.1
Anti-virus capability	0.54	0.36	0.1
Speed accuracy	0.7125	0.2375	0.05
Timing accuracy	0.528	0.422	0.05

We calculated the belief distribution of the requirement-satisfaction degrees of second-layer capabilities using the method described in Section 3.3.

Table 4 and Figure 3 show the belief distributions of the requirement-satisfaction degrees for second-layer capabilities.

Table 4. The belief distribution of the requirement-satisfaction degree for each upper-layer capability.

Capability	m (c=H)	m (c=M)	m (c=L)	m(Θ)
Anti-jamming capability	0.7211	-	0.2241	0.0548
System survivability	0.6588	-	0.1816	0.1596
Security and confidentiality	0.5008	-	0.3460	0.1533
Navigation and positioning capability	0.5647	-	0.2714	0.1639
Space-navigation-and-positioning system capability	0.3567	0.1656	0.1699	0.3077

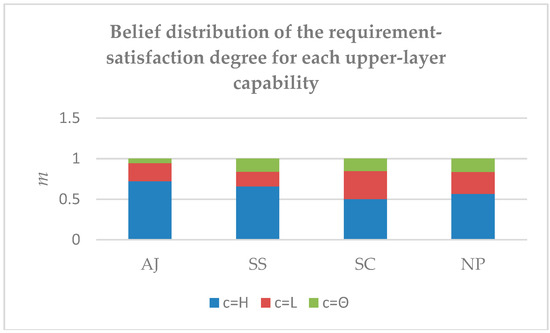
Figure 3. The belief distribution of the requirement-satisfaction degree of each upper-layer capability.

Figure 3 shows that the system anti-jamming capability has the highest requirement-satisfaction degree, followed by both system survivability and the navigation-and-positioning capability; the security and confidentiality capability has the lowest requirement-satisfaction degree. In addition, the cognitive uncertainty of the anti-jamming capability is the lowest, and the cognitive uncertainty of the other three capabilities is similar.

4.4. Comparison with the Bayesian Network Method

In order to make a comparison, we created a model using the Bayesian network-based method: we used the same structural model and identification framework employed for the evidential network to establish the conditional-probability-parameter table for capabilities in the space-navigation-and-positioning system of systems.

Figure 4 shows the conditional-probability table for capability indicators defined in the capability-requirement-satisfaction model of the Bayesian network-based space-navigation-and-positioning system of systems.

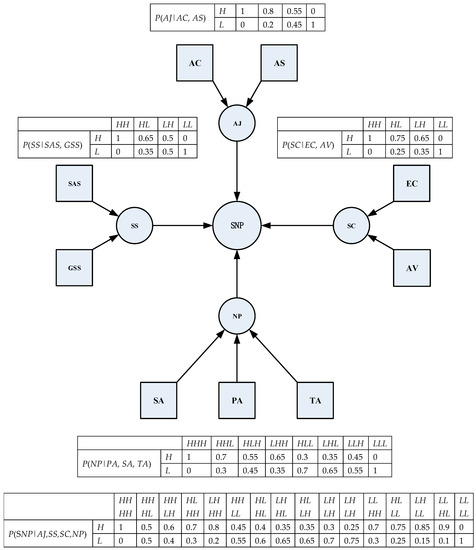
Figure 4. Conditional probability distribution (CPD) of spatial navigation and positioning capabilities.

The difference between Figure 2 and Figure 4 is that, in the event of cognitive uncertainty, the Bayesian network divides cognitive uncertainty into definite states. This is because Bayesian networks cannot handle cognitive uncertainties, so accurate probabilistic judgments are required before reasoning. This will inevitably lead to the loss of uncertain information.

Similarly, the determination of the prior probability of the underlying ability index also requires an accurate probability judgment. Cognitive uncertainty, should it occur, must be assigned to the definite states, as shown in Table 5.

Table 5. The prior probability of bottom capability indicators.

Bottom Capability Indicators	P0 (c=H)	P0 (c=L)
Satellite survivability	0.725	0.275
Ground station survivability	0.5	0.5
Anti-compression capability	0.571	0.429
Anti-spoofing capability	0.833	0.167
Positioning accuracy	0.658	0.342
Speed accuracy	0.7375	0.2625
Timing accuracy	0.543	0.447
Encryption capability	0.41	0.59
Anti-virus capability	0.59	0.41

We used the Matlab BNT 1.0.7 toolbox in order to establish, via Figure 1, the structure of the Bayesian network. We then entered the conditional probability distribution (CPD) parameters and the prior probability of the underlying capability index, and obtained the marginal probability of each capability, as shown in Table 6.

Table 6. The probability distribution of the requirement-satisfaction degree for each upper-layer capability.

Capability	P (c=H)	P (c=M)	P (c=L)
Anti-jamming capability	0.6875	-	0.3125
System survivability	0.7485	-	0.2515
Security and confidentiality	0.5942	-	0.4053
Navigation and positioning capability	0.6404	-	0.3596
Space-navigation-and-positioning system capability	0.4482	0.2745	0.2773

We compared Table 4 and Table 6 to the data shown in Figure 5. We obtained AJ, SS, SC, NP through the evidence-based method and AJ’, SS’, SC’, NP’ through the Bayesian-based method. The requirement-satisfaction degree with the highest value corresponds to the anti-jamming capability in the results obtained via the evidential network, while it corresponds to system survivability for results obtained through the Bayesian network.

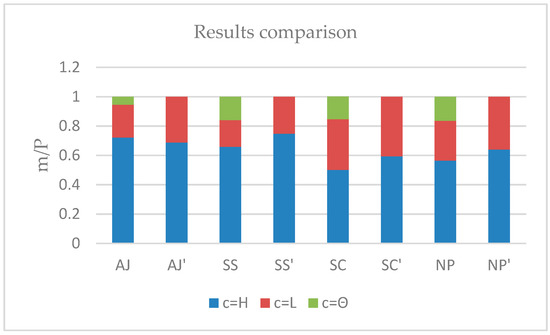
Figure 5. A comparison of the results obtained through the two methods (Bayesian and evidential).

The methods—Bayesian and evidential—used to assess the degree of capability requirement satisfaction differed in mainly two aspects: parameter modeling and reasoning methods.

The difference between parameter modeling in Bayesian networks and evidential networks is that the former requires an accurate probability judgment, while the latter does not. Moreover, the latter can both model cognitive uncertainty and handle the aspects that involve the researcher’s ignorance on the subject.

The difference between reasoning methods in Bayesian and evidential networks is that the former must make a fuzzy estimation of prior knowledge before initiating the reasoning process. However, fuzzy estimations often yield invalid results that can be used for reasoning when the individual state probabilities of the variables are similar. Even if the results are valid, some uncertain information will be lost. The reasoning method based on evidential networks does not need a fuzzy estimation of the evidence of uncertainty, thus avoiding the loss of uncertain information to an optimal degree. It is able to obtain more accurate results while avoiding misjudgment.

In addition, evidential network-based reasoning methods can combine multiple uncertain evidences that are passed to a node directly through Dempster’s combination rules. A combined evidence of information is then formed and transferred to the adjacent node. This avoids double-counting multiple pieces of evidence in the same path; it can be said that this model is an efficient parallel-computing model. In the Bayesian network, the reasoning method’s mechanism-of-combination rule is unable to fuse uncertain evidences due to the fact that the use of probability is the basis of the uncertainty reasoning: every piece of evidence information is required to travel through the entire network. After updating all of the nodes’ probability values as one new prior probability, the same operations can be performed on other nodes’ evidences in order to update the multi-evidence information. For the complex network, the computational complexity of the Bayesian network makes it difficult to complete the reasoning task. Conversely, the evidential network-based reasoning method greatly improves and accelerates the efficiency of the reasoning.

4.5. Calculation of the Inverse Conditional Belief Functions

Following the method described in Section 3.2, GBT was used to calculate the inverse conditional belief. We first calculated the inverse conditional likelihood function. After marginalization, we obtained the inverse conditional basic belief function. The reverse conditional likelihood function calculation process is as follows:

$$\begin{array}{l}Pl((AJ=H, SS=H, SC=H, NP=H)|SNP=L)\\ =\mathrm{K}(1-(1-Pl((SNP=L | AJ=H, SS=H, SC=H, NP=H)))\\ =\mathrm{K}(1-(1-(1-\mathrm{m}(SNP=H | AJ=H, SS=H, SC=H, NP=H)-\mathrm{m}(SNP=M | AJ=H, SS=H, SC=H, NP=H))))\\ =0\end{array}$$

Similarly, we can obtain other reverse conditional likelihood functions, as shown in Table 7.

Table 7. The reverse conditional likelihood functions.

(AJ, SS, SC, NP)	HHHH	HHHL	HHLH	HLHH	LHHH	HHLL	HLHL	LHHL
Pl((AJ,SS,SC,NP)|SNP=L)	0	0	0	0	0	0.55K	0.6K	0.65K
(AJ, SS, SC, NP)	HLLH	LHLH	LLHH	HLLL	LHLL	LLHL	LLLH	LLLL
Pl((AJ,SS,SC,NP)|SNP=L)	0.65K	0.7K	0.75K	0.7K	0.75K	0.85K	0.9K	K

For which:

$$K=1-{\displaystyle \prod _{\begin{array}{l}{X}_{AJ}=HorL\\ X_{SS}=HorL\\ X_{SC}=HorL\\ X_{NP}=HorL\end{array}}(1-Pl(SNP=L | AJ=X_{AJ},SS=X_{SS},SC=X_{SC},NP=X_{NP}))}=1$$

The calculation of the inverse conditional basic belief function after marginalization is as follows:

$$\begin{gathered} Pl\left(AJ=H | SNP=L\right)=\underset{\begin{array}{l}{X}_{SS}=HorL\\ X_{SC}=HorL\\ X_{NP}=HorL\end{array}}{{\displaystyle MAX}}(Pl((AJ=H,SS=X_{SS},SC=X_{SC},NP=X_{NP})|AJ=L)=0.7 \\ m(AJ=L|SNP=L)=1-Pl(AJ=H|SNP=L)=0.3 \end{gathered}$$

Similarly, we can obtain other reverse conditional basic belief functions as follows:

$$\begin{array}{l}m(SS=L|SNP=L)=0.25\\ m(SC=L|SNP=L)=0.15\\ m(NP=L|SNP=L)=0.1\end{array}$$

4.6. Prioritization of Capability Gaps

Finally, we calculated the priority of capability gaps in layer 2, as described in Section 3.3., where $\alpha$ and $\beta$ are both 0.5.

The priority of system of systems’ capability gaps was calculated as follows:

$$\begin{array}{l}Pr(AJ)=m^{0.5}(AJ=L)*m^{0.5}(AJ=L|SNP=L)=0.2593\\ Pr(SS)=m^{0.5}(SS=L)*m^{0.5}(SS=L|SNP=L)=0.2131\\ Pr(SC)=m^{0.5}(SC=L)*m^{0.5}(SC=L|SNP=L)=0.2278\\ Pr(NP)=m^{0.5}(NP=L)*m^{0.5}(NP=L|SNP=L)=0.1647\end{array}$$

The priority ranking result of capability gaps is as follows:

AJ >> SC >> SS >>NP

4.7. Results and Analysis

Figure 6 shows that the system’s anti-jamming capability gap has the highest priority, followed by both the security-and-confidentiality capability and the system survivability, with the navigation-and-positioning capability gap having the lowest priority. In order to improve the degree of requirement satisfaction in the entire space-navigation-and-positioning system of systems, measures must focus on improving the system’s anti-jamming capability.

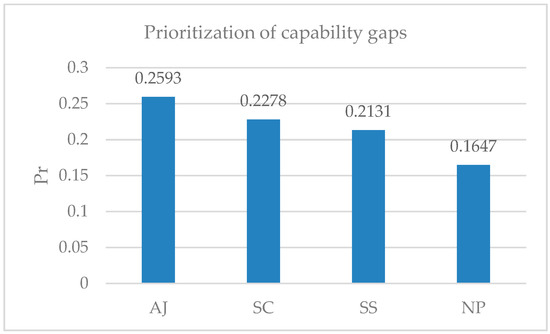
Figure 6. Prioritization of capability gaps.

In Figure 7, “Gap Priority” indicates the capability-gap priority, “IBF−” indicates the inverse belief function value, and “RSD+” indicates the belief with a high degree of requirement satisfaction, calculated using the method in Section 3.1.

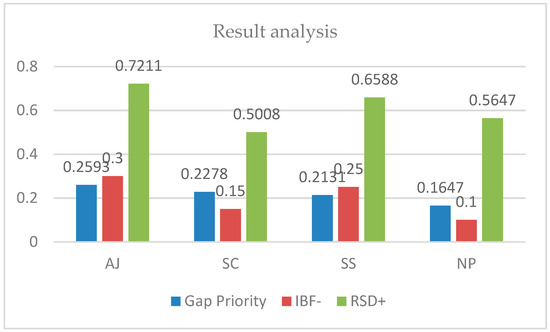
Figure 7. Result analysis.

While, as shown in Figure 6, the degree of requirement satisfaction of the anti-jamming capability has the highest value, it also remains the top final gap priority as it has the largest inverse-belief-function value.

We used a conditional evidential network in order to assess the prioritization of capability gaps in space-navigation-and-positioning system of systems. This network is able to efficiently handle the experience of relevant experts while making full use of the input of uncertain knowledge. This all helps to improve the credibility of capability assessment in space-navigation-and-positioning system of systems.

5. Conclusions

The assessment of capability-gap priority in weapon system of systems is the basis for equipment and non-equipment solutions for solving capability gaps. Based on the conditional evidential network, this paper evaluates the priority of capability gaps for weapon system of systems from a purely quantitative perspective. Compared with qualitative methods, this method enhances the credibility of the assessment work. In addition, this method integrates many different forms of input data and various uncertain information into a unified belief expression framework, thus facilitating the assessment of a large-scale weapon system of systems. Unlike the Bayesian network-based approach, the evidential network-based approach does not require accurate probabilistic judgments and fuzzy estimates, minimizing the loss of uncertain information. In addition, it can handle cognitive uncertainty. It is therefore able to obtain results in evidence reasoning that are more accurate, while avoiding misjudgment. Having conducted a case analysis, we consider this method to be both feasible and effective.