Abstract
The latest model for light scattering by pure seawater was used to investigate the anomalous behavior of pure water. The results showed that water exhibits a minimum scattering at 24.6 °C, as compared to the previously reported values of minimum scattering at 22 °C or maximum scattering at 15 °C. The temperature corresponding to the minimum scattering also increases with the salinity, reaching 27.5 °C for S = 40 psu.
1. Introduction
Light scattering by pure water or pure seawater is a fundamental quantity in aquatic optics. Because of hydrogen bonding, many bulk properties of water exhibit anomalous behavior with temperature that is unlike any other liquids [1,2]. For example, liquid water has a maximum density near 4 °C [3], a minimum isothermal compressibility near 46 °C [4] and a maximum refractive index near 0 °C [5]. The scattering seems to behave “anomalously” too [6]. Cohen and Eisenberg [6] measured the scattering at 436 and 546 nm by pure water at temperatures from 5 to 65 °C, and found a scattering minimum at approximately 22 °C that is consistent with their theoretical estimate using the Einstein–Smoluchowski equation and the temperature variation of the isothermal compressibility. Using the same Einstein-Smoluchowski equation, with inputs re-evaluated using newer experimental results, Buiteveld et al. [7] improved the estimate of light scattering by pure water, which showed a better agreement with the spectral values measured by Morel [8]. However, their model predicts a maximum scattering at 15 °C, which differs from Cohen and Eisenberg [6] not only in value but in the behavior as well. To the best of our knowledge, few other studies have explored the temperature behavior of scattering by water. In addition, it is still unknown whether and how this temperature dependence of scattering by water would vary in the presence of sea salts.
2. Methods
Recently, Zhang and coworkers refined the models for light scattering by pure water [9], by pure seawater [10,11], and by simple sea salt solutions [12] using the improved measurements of the key thermodynamic parameters, and their models agree with the spectral scattering measurements [13,14] for both pure water and seawater within the experimental errors (2%). Localized fluctuation in density for pure water, as well as additional fluctuations in the mixing ratio of salt ions and water for pure seawater, lead to microscopic inhomogeneities in the refractive index (n) [15], which in turn cause scattering of light. Since the fluctuations in density and mixing ratio are independent, the scattering coefficient of seawater, b (m−1) can be expressed as
where bd represents the scattering due to density fluctuation, and bc the scattering due to fluctuation of mixing ratio (concentration). Following Zhang and Hu [9],
and following Zhang et al. [11]
where, respectively, λ, k (=1.38064852 × 10−23 m2·kg·s−2·K−1), and NA (=6.022 × 1023 mol−1) are the wavelength of light, the Boltzmann constant, and Avogadro’s number; ρ, n, T, βT, S, and δ are the density, the absolute refractive index, the absolute temperature, the isothermal compressibility, the mass concentration of salts, and the depolarization ratio of the seawater; and aw and Mw (=18.01528 g mol−1) are the activity and molecular weight of pure water. Also,
In Equation (1), bc vanishes for pure water, and the scattering of light is due entirely to density fluctuation. Replacing the density derivative in Equation (2) with pressure derivative, i.e., , Equation (2) becomes the Einstein–Smoluchowski equation
which was used by Cohen and Eisenberg [6] and Buiteveld et al. [7] in evaluating the temperature dependence of scattering by pure water. Historically, Equation (4) was often used because the isothermal piezo-optic coefficient was relatively easier to measure, even though the uncertainty was high as compared to n(T), n(λ), or n(S) [16]. However, recent theoretical development [17] has greatly improved our knowledge in . This, together with the development of Equation (3) to explicitly account for the effect of salinity on scattering [11], has advanced our capability for modeling scattering by seawater [9,10,11], and our confidence in using Equations (1)–(3) to evaluate its temperature effect. The formulae used in the equations to estimate n, ρ, βT, and aw can be found in Zhang and Hu [9] and Zhang et al. [11], and the Matlab code for the model can be accessed at https://goo.gl/jKAZgT. Light scattering by seawater is a function of salinity, temperature, and pressure. In this study, we focus on the temperature and salinity ranges of 0–60 °C and 0–40 psu under one atmospheric pressure, which cover the majority of natural inland, coastal, and oceanic surface water bodies. The presence of sea salts is expected to modify the value of δ through two contrasting effects: isotropic ions would decrease δ; whereas their electrostatic field would increase anisotropy, and hence the value of δ [18,19]. Both effects have been observed in pure salt solutions: δ for KNO3 solution increases and δ for KCl solution decreases, with their respective concentrations [20]. To the best of our knowledge, however, no studies have been reported on how the δ of seawater would vary with salinity. For this study, we assumed a constant value of 0.039 for the depolarization ratio δ for pure water [21] and for seawater [8,9,22,23].
3. Results and Discussion
Light scattering by pure water at 436 and 546 nm was estimated using Equation (2) for temperatures 0–60 °C, and the values normalized to the scattering at 25 °C were compared with the measurements by Cohen and Eisenberg [6] in Figure 1. Between the two wavelengths, the temperature variations of the scattering are almost identical, showing a minimum scattering at 24.7 °C ± 0.2%. The scattering increases by 4.3% towards 0 °C and increases by 4.7% towards 60 °C at both wavelengths. The root mean square difference between our model and the measurements by Cohen and Eisenberg [6] is approximately 1.3% at both wavelengths. The refractive index model [24] used in Equations (2) and (3) were developed using the Austin and Halikas [16] measurements, which had a temperature precision of 0.1 °C. Also, the Cohen and Eisenberg [6] data we used for comparison in Figure 1 had a temperature precision of 0.1 °C as well. Therefore, we report the temperature in this study at a precision of 0.1 °C. We denote the temperature at which the scattering reaches the minimum as Tmin hereafter. The predicted values of Tmin are close to the value of 22 °C measured by Cohen and Eidenberg [6], but differ significantly in both value and trend from the Buiteveld, et al. [7] model, which predicts a maximum near 15 °C. We believe the difference is largely due to the uncertainty in modeling in Equation (4) that was used by Buiteveld, et al. [7]. Austin and Halikas [16] pointed out that the measurements of the refractive index of water as a function of the pressure, i.e., n(P), were of worse quality when compared to those of n(T), n(λ), or n(S). Also, it is well-known that to numerically approximate a derivative, such as , as a ratio of measured values is very sensitive to the uncertainties in the measurements of n(P). In addition, Buiteveld, et al. [7] derived the temperature dependency of by fitting the measurements [25] between 5 and 35 °C, which also explains the relatively large deviation as shown in Figure 1 when extrapolating their model beyond 35 °C.
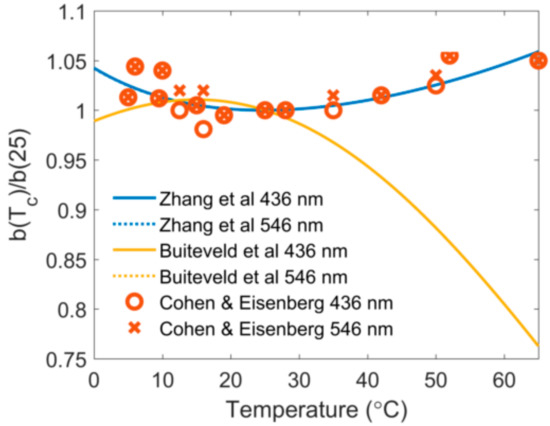
Figure 1.
The temperature variations of light scattering by pure water, calculated using the Zhang and Hu [9] model (i.e., Equation (2)) at 436 and 546 nm and normalized by their respective values at 25 °C, are compared with the estimates using the Buiteveld, et al. [7] model and with the measurements by Cohen and Eisenberg [6]. Note that the normalized variations estimated by the Zhang and Hu model overlap with each other at the two wavelengths.
Several bulk properties of pure water needed to estimate the scattering coefficient behave “anomalously”: density has the maximum near 4 °C [3]; isothermal compressibility has the minimum near 46 °C [4]; and the refractive index has the maximum near 0 °C [5]. Also, less apparent but indirectly relevant is that , as in Equation (4), has its minimum near 50 °C [5]. Clearly, anomalous light scattering by pure water results from the combination of all of these anomalous properties, as well as its direct proportionality with the temperature (Equation (2) or (4)). Even though scattering by pure water varies strongly with wavelength, with a spectral slope of −4.28 [9], the anomalous temperature behavior of scattering varies little with wavelength (Figure 1).
The scattering coefficient at 546 nm as a function of temperature for different salinities is shown in Figure 2a for bd (due to density fluctuation) and Figure 2b for bc (due to concentration fluctuation). Both bd and bc vary with temperature in the same anomalous way, all exhibiting a minimum. Also, both Tmin for bd and Tmin for bc change with salinity—however, with differing patterns. Tmin for bd decreases about 20% from 24.6 °C to 19.1 °C for salinity varying from 0 to 40 psu, whereas over the same salinity range Tmin for bc increases slightly by ~3%, from 32.2 °C to 33.2 °C. In terms of absolute magnitude, bd is about 2–10 times greater than bc (Figure 2a), but in terms of change with respect to salinity, bc is about 10 times greater than bd (Figure 2b). As a result, the change of Tmin for the total scattering coefficient, b is dominated by bc, and increases from 24.6 °C to 27.5 °C for S from 0–40 psu (Figure 3). It is well known that Tmax for density [26] and Tmin for isothermal compressibility [27] decrease with the salinity. Here, we show for the first time that Tmin for light scattering increases with salinity, which is largely due to the temperature variation of scattering introduced by sea salts. Table 1 lists the variations of Tmin for bd, bc, and b at different salinities.
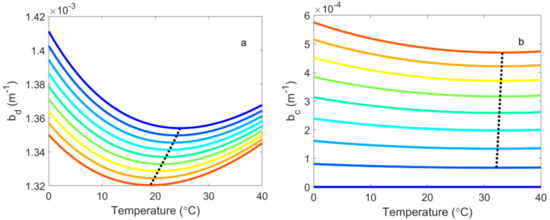
Figure 2.
Light scattering by pure seawater at 546 nm as a function of temperature and salinity. (a) bd, the scattering due to density fluctuation; and (b) bc, the scattering due to concentration fluctuation. Lines of progressive colors from blue to red correspond to different salinities from 0 to 40 psu, at 5 psu increments. The dotted line in each plot connects Tmin at different salinities.
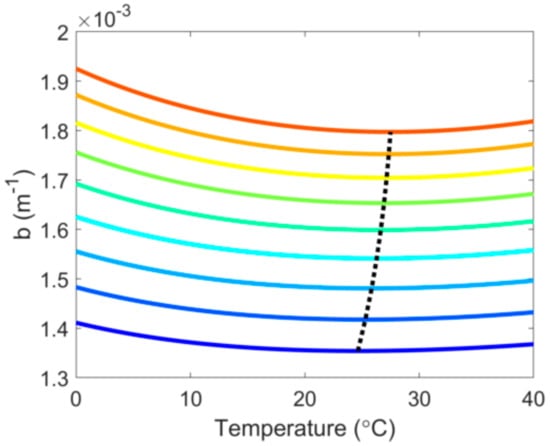
Figure 3.
Total scattering coefficient by pure seawater at 546 nm as a function of temperature and salinity. Lines of progressive colors from blue to red correspond to different salinities from 0 to 40 psu at 5 psu increments. The dotted line connects Tmin at different salinities.

Table 1.
Temperatures (Tmin in °C) at which the scattering of light at 546 nm by pure seawater due to density fluctuations (bd), concentration fluctuations (bc), and their total (b) reach the minimum for various salinities (S).
In conclusion, using the latest scattering models for water and seawater, we find that water exhibits an anomalous light scattering behavior, with a minimum occurring at 24.6 °C for pure water, and that this minimum increases with the salinity, reaching 27.5 °C at 40 psu. This temperature behavior changes little spectrally. Caution should be exercised when using the Buiteveld, et al. [7] model, which predicts a temperature behavior of scattering that is inconsistent with the measurements [6] or the results of this study.
Author Contributions
X.Z. and L.H. conceived and designed the experiments; X.Z. wrote the paper.
Funding
National Aeronautics and Space Administration (NASA) (NNX13AN72G, NNX15AC85G) and National Science Foundation (NSF) (1355466, 1459168).
Acknowledgments
We thank three anonymous reviewers and Dariusz Stramski for their comments, which have improved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; and in the decision to publish the results.
References
- Brovchenko, I.; Oleinikova, A. Multiple Phases of Liquid Water. ChemPhysChem 2008, 9, 2660–2675. [Google Scholar] [CrossRef] [PubMed]
- Ball, P. Water—An enduring mystery. Nature 2008, 452, 291. [Google Scholar] [CrossRef] [PubMed]
- Vedamuthu, M.; Singh, S.; Robinson, G.W. Properties of Liquid Water: Origin of the Density Anomalies. J. Phys. Chem. 1994, 98, 2222–2230. [Google Scholar] [CrossRef]
- Vedamuthu, M.; Singh, S.; Robinson, G.W. Properties of Liquid Water. 4. The Isothermal Compressibility Minimum near 50 °C. J. Phys. Chem. 1995, 99, 9263–9267. [Google Scholar] [CrossRef]
- Cho, C.H.; Urquidi, J.; Gellene, G.I.; Robinson, G.W. Mixture model description of the T-, P dependence of the refractive index of water. J. Chem. Phys. 2001, 114, 3157–3162. [Google Scholar] [CrossRef]
- Cohen, G.; Eisenberg, H. Light Scattering of Water, Deuterium Oxide, and Other Pure Liquids. J. Chem. Phys. 1965, 43, 3881–3887. [Google Scholar] [CrossRef]
- Buiteveld, H.; Hakvoort, J.H.M.; Donze, M. The optical properties of pure water. SPIE 1994, 2258, 174–183. [Google Scholar]
- Twardowski, M.S.; Claustre, H.; Freeman, S.A.; Stramski, D.; Huot, Y. Optical backscattering properties of the “clearest” natural waters. Biogeosciences 2007, 4, 1041–1058. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, L. Estimating scattering of pure water from density fluctuation of the refractive index. Opt. Express 2009, 17, 1671–1678. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Hu, L. Scattering by pure seawater at high salinity. Opt. Express 2009, 17, 12685–12691. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Hu, L.; He, M.-X. Scattering by pure seawater: Effect of salinity. Opt. Express 2009, 17, 5698–5710. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Hu, L.; Twardowski, M.S.; Sullivan, J.M. Scattering by solutions of major sea salts. Opt. Express 2009, 17, 19580–19585. [Google Scholar] [CrossRef] [PubMed]
- Morel, A. Etude Experimentale de la diffusion de la lumiere par l’eau, les solutions de chlorure de sodium et l’eau de mer optiquement pures. J. Chim. Phys. 1966, 10, 1359–1366. [Google Scholar] [CrossRef]
- Morel, A. Note au sujet des constantes de diffusion de la lumiere pour l’eau et l’eau de mer optiquement pures. Cahiers Oceanogr. 1968, 20, 157–162. [Google Scholar]
- Einstein, A. Theorie der Opaleszenz von homogenen Flüssigkeiten und Flüssigkeitsgemischen in der Nähe des kritischen Zustandes. Annalen der Physik 1910, 338, 1275–1298. [Google Scholar] [CrossRef]
- Austin, R.W.; Halikas, G. The Index of Refraction of Seawater; SIO Ref. No. 76-1; Scripps Institute of Oceanography: La Jolla, CA, USA, 1976; p. 121. [Google Scholar]
- Proutiere, A.; Megnassan, E.; Hucteau, H. Refractive index and density variations in pure liquids: A new theoretical relation. J. Phys. Chem. 1992, 96, 3485–3489. [Google Scholar] [CrossRef]
- Morel, A. Optical Properties of Pure Water and Pure Sea Water. In Optical Aspects of Oceanography; Jerlov, N.G., Nielsen, E.S., Eds.; Academic Press: New York, NY, USA, 1974; pp. 1–24. [Google Scholar]
- Shifrin, K.S. Physical Optics of Ocean Water; American Institute of Physics: New York, NY, USA, 1988; p. 285. [Google Scholar]
- Pethica, B.A.; Smart, C. Light scattering of electrolyte solutions. Trans. Faraday Soc. 1966, 62, 1890–1899. [Google Scholar] [CrossRef]
- Farinato, R.S.; Rowell, R.L. New values of the light scattering depolarization and anisotropy of water. J. Chem. Phys. 1976, 65, 593–595. [Google Scholar] [CrossRef]
- Zhang, X. Molecular Light Scattering by Pure Seawater. In Light Scattering Reviews 7; Kokhanovsky, A., Ed.; Springer: Heidelberg, Germany, 2013; pp. 225–243. [Google Scholar]
- Werdell, P.J.; McKinna, L.I.; Boss, E.; Ackleson, S.G.; Craig, S.E.; Gregg, W.W.; Lee, Z.; Maritorena, S.; Roesler, C.S.; Rousseaux, C.S.; et al. An overview of approaches and challenges for retrieving marine inherent optical properties from ocean color remote sensing. Prog. Oceanogr. 2018, 160, 186–212. [Google Scholar] [CrossRef]
- Quan, X.; Fry, E.S. Empirical equation for the index of refraction of seawater. Appl. Opt. 1995, 34, 3477–3480. [Google Scholar] [CrossRef] [PubMed]
- O’Connor, C.L.; Schlupf, J.P. Brillouin Scattering in Water: The Landau—Placzek Ratio. J. Chem. Phys. 1967, 47, 31–38. [Google Scholar] [CrossRef]
- Millero, F.J.; Chen, C.-T.; Bradshaw, A.; Schleicher, K. A new high pressure equation of state for seawater. Deep-Sea Res. 1980, 27, 255–264. [Google Scholar] [CrossRef]
- Lepple, F.K.; Millero, F.J. The isothermal compressibility of seawater near one atmosphere. Deep-Sea Res. 1971, 18, 1233–1254. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).