Multi-Objective Resource Allocation Scheme for D2D Multicast with QoS Guarantees in Cellular Networks

Abstract

Device-to-device (D2D) multicast communication can greatly improve the spectrum utilization in a content delivery scenario. However, the co-channel interference and power consumption brought by D2D bring new challenges. All the D2D multicast groups expect to achieve a higher system capacity with less extra energy cost. In this paper, we investigate the uplink resource allocation issue when D2D multicast groups share the resources with other cellular uses (CUs), while guaranteeing a certain level of quality of service (QoS) to CUs and D2D users. Firstly we address a flexible tradeoff framework in which the system power consumption and the system capacity (i.e., the number of admitted D2D links) are assigned with different weight factors so that these two objectives are jointly considered. Then we propose an efficient resource optimization scheme, which comprises sub-channel allocation and signal-to-interference- plus-noise ratio (SINR) assignment. Numerical results validate the effectiveness of the proposed framework, and demonstrate the advantages in dealing with the proposed multi-objective optimization problem.

1. Introduction

In recent years, the popularity of mobile multimedia services has led to an explosive growth of mobile data traffic. To meet various requirements for local wireless services, such as mobile TV, teleconferencing, multiplayer games, the Third Generation Partnership Project (3GPP) is focusing on Device-to-Device (D2D) communication as a goal in Long Term Evolution-Advanced (LTE-A) [1]. With the support of evolved node base stations (eNBs) in a cellular network, D2D communication provides direct data transmission among user equipments (UEs). The proximity of D2D communication brings many benefits for conventional cellular networks, such as high transmission rates, low delays, extended cell coverage and so on [2,3].

As a promising technique of future cellular network, D2D communication is being intensively mined for its potentials of wireless application by worldwide researchers. The authors in [4] propose a social-aware D2D MAC protocol that exploits social network properties of community to reduce the energy consumption through D2D collaboration and D2D relaying. Depending on how the cellular spectrum used by UEs, different resource sharing modes of D2D communication have been investigated, including non-orthogonal mode (i.e., underlay D2D communication) [5,6,7], orthogonal mode (overlay D2D communication) [8] and outband mode D2D communication [9]. Among these, underlay D2D communication can improve the spectrum efficiency by allocating the same resources to D2D users and cellular users (CUs), however, co-channel interference is introduced in this case, and thus careful resource allocation is required for coexistence of CUs and D2D users. Most of the existing research on D2D resource allocation concerns more about D2D unicast communication scenario [10,11,12,13]. In [10], an alternative greedy heuristic algorithm is proposed to solve the mixed integer non-linear programing (MINLP) resource allocation problem, which can lessen interference to the primary cellular network utilizing channel gain information. To improve the performance of D2D UE, a proportional fair scheduling algorithm is proposed in [11] for D2D users sharing resources with CUs. In [12], a low complexity power control algorithm is proposed to avoid the interference issue in the case of one D2D pair sharing sub-channel with one CU. The joint subchannel assignment and power control design using dynamic spectrum sharing is conducted in [13], where the target is maximizing the sum-rate while guaranteeing minimum individual cellular link data rates. The method of game theory has also been investigated and introduced into resource allocation for D2D communication in several existing works [14,15,16]. In [14], a coalition game approach is employed to address the D2D resource sharing that aim at maximizing the energy efficiency of overall system. Both works [15] and [16] employ the non-cooperative game for D2D content dissemination scenarios to achieve transmission delay reducing as well as energy efficiency increasing.

Only a limited amount of the previous work take into consideration the resource management for D2D multicast communication. Because of the difference of data rate among multiple D2D links in multicast communication, the capacity of multicast group is restricted to the worst channel condition. An interference coordination scheme for D2D multicast is proposed in [17], which proposes an efficient power control scheme to obtain an upper bound on D2D transmit power and based on that power level, a suboptimal resource block allocation scheme is proposed. However, this scheme focus on only a single D2D multicast group sharing resources with multiple CUs. The authors of [18,19] consider the content delivery scenario of D2D multicast. In [18], a model where UEs cooperate on the short range by forming coalitions is proposed to improve energy efficiency, while the QoS of UE is not considered. A practical multicast clustering and power controlling strategy with theoretical analysis using game theory is proposed in [19] for the target of decreasing the data distribution time and achieving the QoS requirement of requested uses. However, cellular channel allocation is ignored in this scheme. The authors in [20] present a joint power and channel allocation algorithm to maximize the overall throughput while preserving certain level of QoS for both CUs and D2D groups. However, in this research, each D2D group can reuse the spectrum resource of at most one CU.

This paper focus on the radio resource allocation problem for D2D multicast communications in cellular networks, where one multicast group can reuse multiple cellular spectrum resources. In this case of content dissemination application, the data requests from all UE should be satisfied as much as possible. Nevertheless, with the increase in the number of admitted D2D links, the power consumption of D2D transmitter becomes higher and cannot be ignored. Therefore, optimizing multiple objectives at the same time has a more practical significance in the resource allocation problem. As an important tool, multi-objective optimization has been studied in several recent works. The authors in [21] propose a robust resource allocation strategy to maximize energy harvesting efficiency while minimizing total transmit power in a cognitive network. Similarly, A. multiobjective framework is proposed in [22] to simultaneously improve the network energy efficiency and system throughput. Inspired by these studies, we employ a new multiple-objective optimization framework with the aim to jointly minimize the power consumption of D2D communication and maximize the system capacity of D2D groups. In particular, the main contributions of our work are as follows: (1) We formulate a simple but flexible multi-objective optimization framework via introducing weighted factors for power consumption and system capacity. In addition, we consider a certain level of SINR to guarantee the QoS requirements for both CUs and D2D groups. The framework allows network operators to adjust the tradeoff between the two objectives with various preferences; (2) We use the way of one D2D group sharing sub-channels with multiple CUs to allocate cellular resources, which further enhances the performance of our optimization; (3) We develop an efficient resource allocation scheme to achieve the desired tradeoff for given preferences (i.e., coefficients for power consumption and system capacity).

The remaining of the paper is organized as follows. In Section 2, we describe the system model and problem optimization. In Section 3, we derive and propose the resource allocation algorithm for D2D multicast communication. Simulation results are shown and discussed in Section 4. Finally, conclusion is drawn in Section 5.

2. System Model and Problem Formulation

2.1. System Model

We consider a single cellular system supporting D2D communication where M D2D multicast groups coexist with K CUs, as depicted in Figure 1. Let $\mathcal{K}=\{1,2,\mathrm{...},K\}$ and $ℳ=\{1,2,\mathrm{...},M\}$ denote the index sets of CUs and D2D groups respectively. The available spectrum is divided into K orthogonal sub-channels, and each of them has been pre-assigned to a CU. Besides, M D2D groups are trying to access into the cellular system in non-orthogonal spectrum sharing model. We adopt uplink resource sharing of cellular network, which is more effective than downlink resource sharing in a fully loaded cellular network, as demonstrated in [23]. We assume in this paper a single multicast group can share spectrum resources with multiple CUs and each CU’s spectrum resource can only be reused by at most one D2D group in order to avoid cross-interference between different D2D groups. Additionally, we assume the eNB can obtain the perfect channel state information (CSI) of all the links, based on which, the available spectrum resources are allocated effectively to the CUs and the D2D groups.

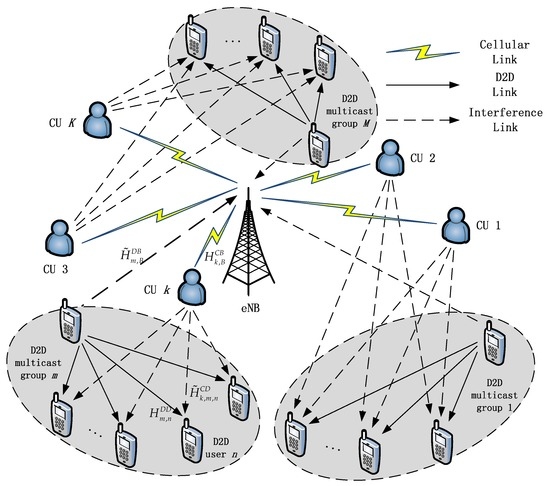
Figure 1. System model of Device-to-device (D2D) multicast groups and cellular uses (CUs).

Define a set of binary variables ${\omega }_{m,k}$ with ${\omega }_{m,k}=1$ if the m-th D2D group reuses channel k and ${\omega }_{m,k}=0$ otherwise. For CU $k\in \mathcal{K}$, the maximum transmission power is limited to $p_k^C$. The signal to interference plus noise ratio (SINR) of eNB on the sub-channel k can be expressed as

$${\gamma }_k^C=\frac{p_k^C{H}_{k,B}^{CB}}{{\displaystyle {\sum }_{m\in ℳ}{\mathsf{\omega }}_{m,k}{p}_{m,k}^D{\tilde{H}}_{m,B}^{DB}}+{\mathsf{\sigma }}_0^2},$$

(1)

where $H_{k,B}^{CB}$ and ${\tilde{H}}_{m,B}^{DB}$ represent channel gain of the cellular communication link from CU k to the eNB and the interference link from D2D transmitter m to the eNB, respectively. $p_k^C$ and $p_{m,k}^D$ represent the transmission powers of the CU k and the m-th D2D group transmitter on sub-channel k, respectively. ${\mathsf{\sigma }}_0^2$ represents the noise power on the sub-channel k. For simplicity, we assume that the noise power is the same for the CUs and the D2D links on each sub-channel.

Let ${\mathcal{D}}_m$ represent the set of D2D receivers in the m-th multicast group. Then, $\left|{\mathcal{D}}_m\right|$ is the total number of receivers in the group, where $\left|\cdot \right|$ is to derive the cardinality of the corresponding set. The SINR of D2D receiver $n\in {\mathcal{D}}_m$ in the m-th multicast group on sub-channel k can be expressed as

$${\gamma }_{n,m,k}^D=\frac{p_{m,k}^D{H}_{m,n}^{DD}}{p_k^C{\tilde{H}}_{k,m,n}^{CD}+{\mathsf{\sigma }}_0^2},$$

(2)

where $H_{m,n}^{DD}$ and ${\tilde{H}}_{k,m,n}^{CD}$ represent channel gain of the cellular communication link from the m-th D2D group transmitter to its desired D2D receiver n and the interference link from CU k to D2D receiver n in group m.

For the D2D link between multicast transmitter m and receiver $n\in {\mathcal{D}}_m$, we define its channel quality on the sub-channel k by

$$q_{n,m,k}^D=\frac{H_{m,n}^{DD}}{p_k^C{\tilde{H}}_{k,m,n}^{CD}+{\mathsf{\sigma }}_0^2}.$$

(3)

In order to minimize the D2D link’s power consumption, there is no need to transmit data in minimum rate to ensure all D2D users receive data correctly. Let $q_{n,m,k}^D$ represent the lowest channel quality of D2D links in m-th group on sub-channel k, the set of admitted D2D receivers in m-th multicast group on sub-channel k whose channel quality is higher than user n can be expressed as

(4)

Furthermore, $X_{n,m,k}=\left|A_{n,m,k}\right|$ shows the number of D2D links that are admitted to transmit data correctly in m-th D2D group on sub-channel k.

2.2. Problem Formulation

In this paper, our goal is to gain minimal D2D power consumption with maximal system capacity while satisfying the QoS requirement of CUs and D2D users. Hence, we introduce weighted coefficients for power and capacity to strike and regulate the balance between D2D links’ aggregated power consumption minimization and system capacity maximization. For simplicity, we denote the SINR thresholds of cellular links and D2D links as ${\mathsf{\Gamma }}_k^C$ and ${\mathsf{\Gamma }}_m^D$, which must be attained to meet the individual QoS requirement. In addition, we use ${\mathcal{S}}_m=\{k\in \mathcal{K}|{\mathsf{\omega }}_{m,k}=1\}$ to denote the set of the sub-channels which are assigned to the m-th multicast group. Then, by using the linear weighted aggregative method, we formulate the multi-objective optimization problem as

$$\underset{\left\{p_k^C,p_{m,k}^D,{\omega }_{m,k}\right\}}{\min }{\displaystyle \sum _{m\in ℳ}{\displaystyle \sum _{k\in \mathcal{K}}{\mathsf{\omega }}_{m,k}}}\left\{\frac{\mathsf{\eta }\cdot p_{m,k}^D}{P_{m,k,\max }^D}-\frac{(1-\mathsf{\eta })\cdot X_{n,m,k}}{\left|{\mathcal{D}}_m\right|}\right\},$$

(5)

$$\begin{array}{lll}s.t.& \mathrm{C}1:& {\displaystyle \sum _{k\in \mathcal{K}}{\mathsf{\omega }}_{m,k}{\log }_2(1+{\mathsf{\gamma }}_{n,m,k}^D)}\ge {\log }_2(1+{\mathsf{\Gamma }}_m^D),\\ & & \hfill \forall m\in ℳ,n\in {\mathcal{D}}_m,\\ & \mathrm{C}2:& {\mathsf{\gamma }}_k^C\ge {\mathsf{\Gamma }}_k^C,\forall k\in \mathcal{K},\\ & \mathrm{C}3:& 0\le {\displaystyle \sum _{k\in \mathcal{K}}{\mathsf{\omega }}_{m,k}{p}_{m,k}^D}\le P_{thr}^D,\forall m\in ℳ,\\ & \mathrm{C}4:& 0\le p_k^C\le P_{thr}^C,\forall k\in \mathcal{K},\\ & \mathrm{C}5:& {\omega }_{m,k}\in \left\{0,1\right\},\forall k\in \mathcal{K},m\in ℳ,\\ & \mathrm{C}6:& {\displaystyle \sum _{k\in \mathcal{K}}{\mathsf{\omega }}_{m,k}}=\left|{\mathcal{S}}_m\right|,\forall m\in ℳ.\\ & \mathrm{C}7:& {\displaystyle \sum _{m\in ℳ}{\mathsf{\omega }}_{m,k}}\le 1,\forall k\in \mathcal{K}.\end{array}$$

where $P_{m,k,\max }^D$ represents the maximum expected power of D2D group m. The positive coefficients $\mathsf{\eta }$ and $1-\mathsf{\eta }$ regulate the tradeoff between power consumption and system capacity, where $\mathsf{\eta }\in \left(0,1\right)$. C1 and C2 stand for the QoS guarantees for the D2D links and cellular links. C3 and C4 are the transmission power constraints for D2D groups and CUs. C5 and C6 indicate each channel can be reused by at most one D2D group.

3. The Proposed Resource Allocation for D2D Communication

Obviously, the optimization problem (5) in an MINLP problem which is a NP-hard problem and hard to get an optimal and satisfactory solution, as the complexity may increase exponentially with the problem size. Next, we propose an effective source allocation algorithm to address this problem.

3.1. Problem Equivalence

Consider CU $k\in \mathcal{K}$, D2D multicast group $m\in ℳ$ and D2D receiver $n\in {\mathcal{D}}_m$. If the frequency resource of CU k is reused by D2D multicast group m, i.e., ${\mathsf{\omega }}_{m,k}=1$, Equation (1) can be rewritten as

$${\mathsf{\gamma }}_{k,m}^C=\frac{p_k^C{H}_{k,B}^{CB}}{p_{m,k}^D{\tilde{H}}_{m,B}^{DB}+{\mathsf{\sigma }}_0^2}.$$

(6)

According to Equation (6) and constraint C2 and C4 in Equation (5), $P_{m,k}^D$ reaches a maximum value when ${\mathsf{\gamma }}_k^C={\mathsf{\Gamma }}_k^C$ and $p_k^C=P_{thr}^C$ are both satisfied. Substituting ${\mathsf{\gamma }}_k^C={\mathsf{\Gamma }}_k^C$ and $p_k^C=P_{thr}^C$ into Equation (6), we can get

$$P_{m,k,\max }^D=\min \left\{\frac{P_{thr}^C{H}_{k,B}^{CB}}{{\tilde{H}}_{m,B}^{DB}{\mathsf{\Gamma }}_k^C}-\frac{{\mathsf{\sigma }}_0^2}{{\tilde{H}}_{m,B}^{DB}},P_{thr}^D\right\}.$$

(7)

In addition, by combining Equations (2) and (6), the transmission power of D2D multicast transmitter m and CU k can be obtained as follows:

$$\{\begin{array}{l}{p}_{m,k}^D\left({\mathsf{\gamma }}_{k,m}^C,{\mathsf{\gamma }}_{n,m,k}^D\right)=\frac{\left(H_{k,B}^{CB}+{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\gamma }}_{k,m}^C\right){\mathsf{\gamma }}_{n,m,k}^D{\sigma }_0^2}{H_{k,B}^{CB}{H}_{m,n}^{DD}-{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\gamma }}_{k,m}^C{\mathsf{\gamma }}_{n,m,k}^D}\\ p_k^C\left({\mathsf{\gamma }}_{k,m}^C,{\mathsf{\gamma }}_{n,m,k}^D\right)=\frac{\left(H_{m,n}^{DD}+{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\gamma }}_{n,m,k}^D\right){\mathsf{\gamma }}_{k,m}^C{\sigma }_0^2}{H_{k,B}^{CB}{H}_{m,n}^{DD}-{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\gamma }}_{k,m}^C{\mathsf{\gamma }}_{n,m,k}^D}\end{array}.$$

(8)

From Equation (8), we can observe that $P_{m,k}^D$ and $p_k^C$ are monotonically increasing in ${\mathsf{\gamma }}_{k,m}^C$ for fixed ${\mathsf{\gamma }}_{n,m,k}^D$. In order to minimize the power consumption of D2D group, we need to keep the minimum QoS guarantees of cellular link, i.e., ${\mathsf{\gamma }}_{k,m}^{C*}={\mathsf{\Gamma }}_k^C$. Substituting ${\mathsf{\gamma }}_{k,m}^{C*}={\mathsf{\Gamma }}_k^C$ into Equation (8) leads to

$$\{\begin{array}{l}{p}_{m,k}^D({\mathsf{\gamma }}_{k,m}^{C*},{\mathsf{\gamma }}_{n,m,k}^D)=\frac{\left(H_{k,B}^{CB}+{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C\right){\mathsf{\gamma }}_{n,m,k}^D{\mathsf{\sigma }}_0^2}{H_{k,B}^{CB}{H}_{m,n}^{DD}-{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C{\mathsf{\gamma }}_{n,m,k}^D}\\ p_k^C({\mathsf{\gamma }}_{k,m}^{C*},{\mathsf{\gamma }}_{n,m,k}^D)=\frac{\left(H_{m,n}^{DD}+{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\gamma }}_{n,m,k}^D\right){\mathsf{\Gamma }}_k^C{\mathsf{\sigma }}_0^2}{H_{k,B}^{CB}{H}_{m,n}^{DD}-{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C{\mathsf{\gamma }}_{n,m,k}^D}\end{array}.$$

(9)

Then, we substitute $p_{m,k}^D({\mathsf{\gamma }}_{k,m}^{C*},{\mathsf{\gamma }}_{n,m,k}^D)$ into Equation (5), and the optimization problem can be rewritten as

$$\underset{\left\{{\mathsf{\gamma }}_{n,m,k}^D,{\mathsf{\omega }}_{m,k}\right\}}{\min }{\displaystyle \sum _{m\in ℳ}{\displaystyle \sum _{k\in \mathcal{K}}{\omega }_{m,k}\left\{\eta \frac{p_{m,k}^D({\mathsf{\gamma }}_{k,m}^{C*},{\mathsf{\gamma }}_{n,m,k}^D)}{P_{m,k,\max }^D}-(1-\mathsf{\eta })\frac{X_{n,m,k}}{\left|{\mathcal{D}}_m\right|}\right\}}}.$$

(10)

Define

$$\mathsf{\Phi }\left({\mathsf{\gamma }}_{k,m}^{C*},{\mathsf{\gamma }}_{n,m,k}^D\right)=\mathsf{\eta }\frac{p_{m,k}^D({\mathsf{\gamma }}_{k,m}^{C*},{\mathsf{\gamma }}_{n,m,k}^D)}{P_{m,k,\max }^D}-(1-\mathsf{\eta })\frac{X_{n,m,k}}{\left|{\mathcal{D}}_m\right|}.$$

(11)

Then Eqaution (10) can be expressed as

$$\underset{\left\{{\mathsf{\gamma }}_{n,m,k}^D,{\mathsf{\omega }}_{m,k}\right\}}{\min }{\displaystyle \sum _{m\in ℳ}{\displaystyle \sum _{k\in \mathcal{K}}{\mathsf{\omega }}_{m,k}\mathsf{\Phi }\left({\mathsf{\gamma }}_{k,m}^{C*},{\mathsf{\gamma }}_{n,m,k}^D\right)}}.$$

(12)

As explained above, if the resource of CU k is reused by D2D group m, the constraints C5, C6 and C7 should be satisfied. Then, we introduce the following Proposition.

Proposition 1. 

The optimal solutions of the power values $p_{m,k}^D$ of the optimization problem in Equation (12) must be the optimal solutions of the optimization problem $\underset{\left\{{\mathsf{\gamma }}_{n,m,k}^D\right\}}{\min }{\displaystyle \sum _{k\in {\mathcal{S}}_m}\mathsf{\Phi }\left({\mathsf{\gamma }}_{k,m}^{C*},{\mathsf{\gamma }}_{n,m,k}^D\right)}$.

Proof. 

The proof is presented in Appendix A.

It can be seen from Proposition 1 that the original dimensional non-convex optimization problem can be transformed into two separate optimization sub-problems. In the first sub-problem, for single D2D group with a given multiple sub-channels reusing, we find the optimal SINR value on each sub-channel to achieve the multi-objective optimization. In the second sub-problem, for multiple D2D groups sharing the resources with multiple CUs, we propose a practice algorithm to allocate each sub-channel to the D2D multicast groups.

3.2. SINR Assignment for One D2D Multicast Group

Without loss of generality, we consider the m-th D2D group, which reuses spectrum resources with the CUs specified in ${\mathcal{S}}_m$. According to constraint C4 in Equation (5), if the spectrum resource of CU k is reused by D2D group m, $0\le p_k^C\le P_{thr}^C$ should be satisfied. By substituting Equation (9) into constraint C4, we have

$$0\le \frac{H_{m,n}^{DD}+{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\gamma }}_{n,m,k}^D}{H_{k,B}^{CB}{H}_{m,n}^{DD}-{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C{\mathsf{\gamma }}_{n,m,k}^D}{\mathsf{\Gamma }}_k^C{\mathsf{\sigma }}_0^2\le P_{thr}^D.$$

(13)

Form above inequality, we can get

$$\{\begin{array}{l}{\mathsf{\gamma }}_{n,m,k}^D<\frac{H_{k,B}^{CB}{H}_{m,n}^{DD}}{{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C},\\ {\mathsf{\gamma }}_{n,m,k}^D\le \frac{P_{thr}^D{H}_{k,B}^{CB}{H}_{m,n}^{DD}-H_{m,n}^{DD}{\mathsf{\Gamma }}_k^C{\mathsf{\sigma }}_0^2}{{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C\left({\mathsf{\sigma }}_0^2+P_{thr}^D{\tilde{H}}_{m,B}^{DB}\right)}.\end{array}$$

(14)

Define

(15)

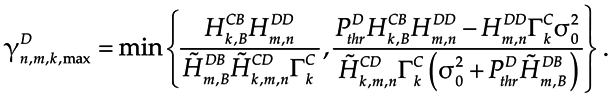
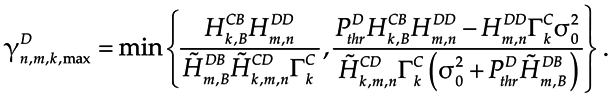
According to Proposition 1, the multi-objective optimization model for D2D group m can be simplified to the following problem:

$$\begin{array}{cc}& \underset{\left\{{\gamma }_{n,m,k}^D\right\}}{\min }{\displaystyle \sum _{k\in {\mathcal{S}}_m}\mathsf{\Phi }\left({\mathsf{\gamma }}_{k,m}^{C*},{\mathsf{\gamma }}_{n,m,k}^D\right)}\\ s.t.& \mathrm{C}1:{\displaystyle \sum _{k\in {\mathcal{S}}_m}{\log }_2(1+{\mathsf{\gamma }}_{n,m,k}^D)}\ge {\log }_2(1+{\mathsf{\Gamma }}_m^D),\\ & \mathrm{C}2:0\le {\mathsf{\gamma }}_{n,m,k}^D\le {\mathsf{\gamma }}_{n,m,k,\max }^D,\forall k\in {\mathcal{S}}_m.\end{array}$$

(16)

By taking the second order derivative of the $\mathsf{\Phi }$ versus ${\mathsf{\gamma }}_{n,m,k}^D$, we can get

$$\begin{array}{ll}\frac{{\partial }^2\mathsf{\Phi }}{\partial {{\mathsf{\gamma }}_{n,m,k}^D}^2}& =\frac{2{\mathsf{\eta }\mathsf{\sigma }}_0^2{H}_{k,B}^{CB}{H}_{m,n}^{DD}{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C}{P_{m,k,\max }^D}\cdot \frac{H_{k,B}^{CB}+{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C}{H_{k,B}^{CB}{H}_{m,n}^{DD}-{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C{\mathsf{\gamma }}_{n,m,k}^D}\\ & >0\end{array},$$

(17)

indicating that $\mathsf{\Phi }$ is a convex function. Then, it is obvious that the optimization problem in Equation (16) is a convex optimization problem about ${\mathsf{\gamma }}_{n,m,k}^D$ [24].

In order to solve Equation (16), we introduce the non-negative Lagrangian multipliers $\mathsf{\lambda }\ge 0$, associating with the constraint C1 in Equation (5). Then, we write its Lagrangian function as

$$L\left(\left\{{\mathsf{\gamma }}_{n,m,k}^D\right\},\mathsf{\lambda }\right)={\displaystyle \sum _{k\in {\mathcal{S}}_m}\mathsf{\Phi }\left({\mathsf{\gamma }}_{k,m}^{C*},{\mathsf{\gamma }}_{n,m,k}^D\right)}+\mathsf{\lambda }\left[{\log }_2(1+{\mathsf{\Gamma }}_m^D)-{\displaystyle \sum _{k\in {\mathcal{S}}_m}{\log }_2(1+{\mathsf{\gamma }}_{n,m,k}^D)}\right].$$

(18)

By applying Karush–Kuhn–Tucker (KKT) conditions [14], the first order optimality conditions and the equation constraint are given as follows,

$$\begin{array}{ll}\frac{\partial L\left(\left\{{\mathsf{\gamma }}_{n,m,k}^D\right\},\mathsf{\lambda }\right)}{\partial {\mathsf{\gamma }}_{n,m,k}^D}=& \frac{{\mathsf{\eta }\mathsf{\sigma }}_0^2{H}_{k,B}^{CB}{H}_{m,n}^{DD}\left(H_{k,B}^{CB}+{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C\right)}{P_{m,k,\max }^D{\left(H_{k,B}^{CB}{H}_{m,n}^{DD}-{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C{\mathsf{\gamma }}_{n,m,k}^D\right)}^2}-\frac{\lambda }{\ln 2\left(1+{\mathsf{\gamma }}_{n,m,k}^D\right)}\\ & =0,\forall k\in {\mathcal{S}}_m\end{array},$$

(19)

$$\mathsf{\lambda }\left[{\log }_2(1+{\mathsf{\Gamma }}_m^D)-{\displaystyle \sum _{k\in {\mathcal{S}}_m}{\log }_2(1+{\mathsf{\gamma }}_{n,m,k}^D)}\right]=0.$$

(20)

From Equation (19), it can be easily found that the optimal $\mathsf{\lambda }$ must be positive, since $\mathsf{\lambda }=0$ implies that the equation ${\mathsf{\eta }\mathsf{\sigma }}_0^2{H}_{k,B}^{CB}{H}_{m,n}^{DD}\left(H_{k,B}^{CB}+{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C\right)=0$ is satisfied for all $k\in {\mathcal{S}}_m$, which is impossible in practice. With simple mathematical operations, Equation (19) can be rewritten into following quadratic equation:

$$A_k\left(\mathsf{\lambda }\right){{\gamma }_{n,m,k}^D}^2+B_k\left(\mathsf{\lambda }\right){\mathsf{\gamma }}_{n,m,k}^D+C_k\left(\mathsf{\lambda }\right)=0,$$

(21)

where

$$\begin{array}{l}{A}_k\left(\mathsf{\lambda }\right)={\left({\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C\right)}^2\mathsf{\lambda }\\ B_k\left(\mathsf{\lambda }\right)=-2\mathsf{\lambda }{H}_{k,B}^{CB}{H}_{m,n}^{DD}{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C-D_k\\ C_k\left(\mathsf{\lambda }\right)={\left(H_{k,B}^{CB}{H}_{m,n}^{DD}\right)}^2\mathsf{\lambda }-D_k\\ D_k=\ln 2\cdot \frac{\mathsf{\eta }{\sigma }_0^2{H}_{k,B}^{CB}{H}_{m,n}^{DD}\left(H_{k,B}^{CB}+{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C\right)}{P_{m,k,\max }^D}\end{array}.$$

(22)

Then we can easily get

$$\begin{array}{ll}{B}_k{\left(\mathsf{\lambda }\right)}^2-4A_k\left(\mathsf{\lambda }\right)C_k\left(\mathsf{\lambda }\right)=& {D_k}^2+4\mathsf{\lambda }{D}_k{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C\left({\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C+H_{k,B}^{CB}{H}_{m,n}^{DD}\right)\\ & >0\end{array}.$$

(23)

Therefore, the available solution to Equation (21) can be obtained as follows:

$${\mathsf{\gamma }}_{n,m,k}^D{\left(\mathsf{\lambda }\right)}_{1,2}=\frac{-B_k\left(\mathsf{\lambda }\right)\pm \sqrt{B_k{\left(\mathsf{\lambda }\right)}^2-4A_k\left(\mathsf{\lambda }\right)C_k\left(\mathsf{\lambda }\right)}}{2A_k\left(\mathsf{\lambda }\right)}.$$

(24)

From the above equation, we find

$$\begin{array}{ll}{\mathsf{\gamma }}_{n,m,k}^D{\left(\mathsf{\lambda }\right)}_1& =\frac{-B_k\left(\lambda \right)+\sqrt{B_k{\left(\mathsf{\lambda }\right)}^2-4A_k\left(\mathsf{\lambda }\right)C_k\left(\mathsf{\lambda }\right)}}{2A_k\left(\mathsf{\lambda }\right)}\\ & >\frac{-B_k\left(\mathsf{\lambda }\right)}{2A_k\left(\mathsf{\lambda }\right)}=\frac{2\mathsf{\lambda }{H}_{k,B}^{CB}{H}_{m,n}^{DD}{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C+D_k}{2{\left({\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C\right)}^2\mathsf{\lambda }}\\ & >\frac{H_{k,B}^{CB}{H}_{m,n}^{DD}}{{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C},\end{array},$$

(25)

which contradicts Equation (14). Consequently, the optimal solution to Equation (21) is given by

$$\begin{array}{ll}{{\mathsf{\gamma }}_{n,m,k}^D}^{*}& ={\mathsf{\gamma }}_{n,m,k}^D{\left(\mathsf{\lambda }\right)}_2\\ & ={\left[\frac{-B_k\left(\mathsf{\lambda }\right)-\sqrt{B_k{\left(\mathsf{\lambda }\right)}^2-4A_k\left(\mathsf{\lambda }\right)C_k\left(\mathsf{\lambda }\right)}}{2A_k\left(\mathsf{\lambda }\right)}\right]}_0^{{\gamma }_{n,m,k,\max }^D}\end{array},$$

(26)

where ${\left[x\right]}_0^{{\mathsf{\gamma }}_{n,m,k,\max }^D}$ represents the projection onto the interval $\left[0,{\mathsf{\gamma }}_{n,m,k,\max }^D\right]$. Furthermore, according to Equation (20), the optimal ${{\mathsf{\gamma }}_{n,m,k}^D}^{*}$ must satisfy

$${\displaystyle \sum _{k\in {\mathcal{S}}_m}{\log }_2(1+{{\mathsf{\gamma }}_{n,m,k}^D}^{*})}={\log }_2(1+{\mathsf{\Gamma }}_m^D).$$

(27)

Given that ${{\mathsf{\gamma }}_{n,m,k}^D}^{*}$ in Equation (27) depends on $\mathsf{\lambda }$ in a highly nonlinear way, directly computing the optimal $\mathsf{\lambda }$ is difficult. Nevertheless, the optimal $\mathsf{\lambda }$ can be efficiently found via bisection, for which one needs to know an interval containing the optimal $\mathsf{\lambda }$. The following result provides such an interval.

Lemma 1. 

The optimal $\mathsf{\lambda }$ satisfying ${\displaystyle \sum _{k\in {\mathcal{S}}_m}{\log }_2(1+{{\mathsf{\gamma }}_{n,m,k}^D}^{*})}={\log }_2(1+{\mathsf{\Gamma }}_m^D)$ is within $\left[{\mathsf{\lambda }}_{\min },{\mathsf{\lambda }}_{\max }\right]$ where ${\mathsf{\lambda }}_{\max }\triangleq {\max }_{{\mathcal{S}}_m}\left\{D_k\cdot \frac{1+{\mathsf{\gamma }}_{n,m,k,\max }^D}{{\left(H_{k,B}^{CB}{H}_{m,n}^{DD}-{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C{\mathsf{\gamma }}_{n,m,k,\max }^D\right)}^2}\right\}$ and ${\mathsf{\lambda }}_{\min }\triangleq {\min }_{{\mathcal{S}}_m}\left\{\frac{D_k}{{\left(H_{k,B}^{CB}{H}_{m,n}^{DD}\right)}^2}\right\}$.

Proof. 

The proof is presented in Appendix B.

3.3. Sub-Channel Allocation for Multiple D2D Multicast Groups

Before the SINR allocation, the set ${\mathcal{S}}_m$ of CUs sharing resources with the m-th D2D group must be determined through sub-channel allocation for the matching between multiple D2D groups and CUs’ sub-channels. In this subsection, the details of the sub-channel allocation are introduced.

At the beginning of the allocation, the eNB collects the location information of all the D2D groups. Then, in order to remove coupling of the sub-channel allocation and the SINR assignment, it is assumed that the D2D group transmitters allocate the same SINR ${\widehat{\mathsf{\gamma }}}_{n,m,k}^D$ on each sub-channel, i.e., the transmission rate of D2D group m on the sub-channel k is ${\widehat{R}}_{m,k}^D={\log }_2(1+{\mathsf{\Gamma }}_m^D)/\left[K/M\right]$, where $\left[\cdot \right]$ is to take the integer portion of the output. Based on Proposition 1, in order to achieve the multi-objective optimization goal while guaranteeing the QoS of D2D groups and CUs, the sub-channel allocation problem can be expressed as

$$\begin{array}{}{\displaystyle \underset{\left\{{\mathsf{\omega }}_{m,k}\right\}}{\min }}{\displaystyle \sum _{m\in ℳ}{\displaystyle \sum _{k\in \mathcal{K}}{\omega }_{m,k}\mathsf{\Phi }\left({\mathsf{\gamma }}_{k,m}^{C*},{\widehat{\mathsf{\gamma }}}_{n,m,k}^D\right)}}\\ s.t.& {\log }_2(1+{\widehat{\mathsf{\gamma }}}_{n,m,k}^D)\ge R_{m,k}^D\\ & C5~C7\mathrm{in}\left(5\right)\end{array},$$

(28)

where the SINR of D2D group m on the sub-channel k can be calculated by ${\widehat{\mathsf{\gamma }}}_{n,m,k}^D=2^{{\widehat{R}}_{m,k}^D}-1$. By substituting ${\widehat{\mathsf{\gamma }}}_{n,m,k}^D$ into Equation (9), we can get

$$\{\begin{array}{l}{p}_{m,k}^D({\mathsf{\gamma }}_{k,m}^{C*},{\widehat{\mathsf{\gamma }}}_{n,m,k}^D)=\frac{\left(H_{k,B}^{CB}+{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C\right){\widehat{\mathsf{\gamma }}}_{n,m,k}^D{\mathsf{\sigma }}_0^2}{H_{k,B}^{CB}{H}_{m,n}^{DD}-{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C{\widehat{\mathsf{\gamma }}}_{n,m,k}^D}\\ p_k^C({\mathsf{\gamma }}_{k,m}^{C*},{\widehat{\mathsf{\gamma }}}_{n,m,k}^D)=\frac{\left(H_{m,n}^{DD}+{\tilde{H}}_{k,m,n}^{CD}{\widehat{\mathsf{\gamma }}}_{n,m,k}^D\right){\mathsf{\Gamma }}_k^C{\mathsf{\sigma }}_0^2}{H_{k,B}^{CB}{H}_{m,n}^{DD}-{\tilde{H}}_{m,B}^{DB}{\tilde{H}}_{k,m,n}^{CD}{\mathsf{\Gamma }}_k^C{\widehat{\mathsf{\gamma }}}_{n,m,k}^D}\end{array},$$

(29)

and the lowest channel quality of D2D links in m-th multicast on sub-channel k is

$${\widehat{q}}_{n,m,k}^D=\frac{{\widehat{\mathsf{\gamma }}}_{n,m,k}^D}{p_{m,k}^D({\mathsf{\gamma }}_{k,m}^{C*},{\widehat{\mathsf{\gamma }}}_{n,m,k}^D)}.$$

(30)

Then, the value of $\mathsf{\Phi }\left({\mathsf{\gamma }}_{k,m}^{C*},{\widehat{\mathsf{\gamma }}}_{n,m,k}^D\right)$ is given by

$$\mathsf{\Phi }\left({\mathsf{\gamma }}_{k,m}^{C*},{\widehat{\mathsf{\gamma }}}_{n,m,k}^D\right)=\eta \frac{p_{m,k}^D({\mathsf{\gamma }}_{k,m}^{C*},{\widehat{\mathsf{\gamma }}}_{n,m,k}^D)}{P_{m,k,\max }^D}-(1-\mathsf{\eta })\frac{{\widehat{X}}_{n,m,k}}{\left|{\mathcal{D}}_m\right|},$$

(31)

where ${\widehat{X}}_{n,m,k}$ can be calculated by the following formula

(32)

Note that the multi-objective optimization value brought by any D2D multicast group reusing any sub-channel can be roughly measured by $\mathsf{\Phi }\left({\mathsf{\gamma }}_{k,m}^{C*},{\widehat{\mathsf{\gamma }}}_{n,m,k}^D\right)$. Therefore, the D2D pair that has the minimum $\mathsf{\Phi }\left({\mathsf{\gamma }}_{k,m}^{C*},{\widehat{\mathsf{\gamma }}}_{n,m,k}^D\right)$ has the priority to reuse the k-th sub-channel. When the k-th sub-channel is allocated to the D2D group m, it will be recorded into set ${\mathcal{S}}_m,m=1,2,\mathrm{...},M$ and not be used by other D2D groups. For purpose of fairness among D2D multicast groups, the sub-channels are firstly assigned to D2D groups who meet $\left|{\mathcal{S}}_m\right|\le \frac{K}{M}-1$. The sub-channel allocation procedure ends up until all sub-channels have been assigned.

3.4. Overall Mechanism

The overall mechanism includes the above two phases to jointly allocate sub-channel and SINR. The first phase described in Section 3.3 is to match multiple sub-channels to D2D multicast groups. After the sub-channel allocation in phase 1 is finished, the SINR assignment method in Section 3.2 is performed to determine the optimal SINR of all D2D links for multi-objective optimization on any given sub-channel from phase 1, the pseudo code of overall algorithm is shown in Algorithm 1.

Algorithm 1. Resource Allocation For D2D Multicast.

* Initialization: The eNB collects the location information of all D2D multicast groups. The initial valid sub-channel set ${\mathcal{S}}_m=\varnothing ,\forall m$, the initial feasible sub-channel set ${ℱ}_m=\mathcal{K},\forall m$, the initial available sub-channel set $\mathcal{A}=\mathcal{K}$, and the initial binary variable ${\omega }_{m,k}=0,\forall m,k$ are set up. The multi-objective optimization value brought by any D2D multicast group reusing any sub-channel is $\mathsf{\Phi }\left({\mathsf{\gamma }}_{k,m}^{C*},{\widehat{\mathsf{\gamma }}}_{n,m,k}^D\right)$, which is given (31).

* Phase 1. Sub-channel Allocation: 1. If $\exists m\in ℳ,{ℱ}_m\ne \varnothing$, find the optimal matching $\left(m^{\ast },k^{\ast }\right)$ which satisfies $\left(m^{\ast },k^{\ast }\right)=\arg {\min }_{\left(m,k\right):m\in ℳ,k\in \mathcal{C}}\mathsf{\Phi }\left({\mathsf{\gamma }}_{k,m}^{C*},{\widehat{\mathsf{\gamma }}}_{n,m,k}^D\right)$; Otherwise, go to step 4. 2. If the number of sub-channels allocated to m* satisfies $\left|{\mathcal{S}}_{m*}\right|\le \frac{K}{M}-1$, set ${\omega }_{m*,k*}=1$, ${\mathcal{S}}_m={\mathcal{S}}_m\cup \left\{k^{*}\right\}$, ${ℱ}_m={ℱ}_m\backslash \left\{k^{*}\right\}$, $\mathcal{A}=\mathcal{A}\backslash \left\{k^{*}\right\}$. Return to step 1. 3. Otherwise, ${ℱ}_{m*}={ℱ}_{m*}\backslash \left\{k^{*}\right\}$, return to step 1. 4. If the available sub-channel set $\mathcal{A}=\varnothing ,$ go to step 5. Otherwise, for every $k^{\prime }\in \mathcal{A}$, find optimal $m^{opt}\in ℳ$ which satisfies $\left(m^{opt},k^{\prime }\right)=\arg {\min }_{\left(m,k\right):m\in ℳ,k^{\prime }\in \mathcal{A}}\mathsf{\Phi }\left({\mathsf{\gamma }}_{k^{\prime },m}^{C*},{\widehat{\mathsf{\gamma }}}_{n,m,k^{\prime }}^D\right)$, then set ${\mathsf{\omega }}_{m^{opt},k^{\prime }}=1$, ${\mathcal{S}}_{m^{opt}}={\mathcal{S}}_{m^{opt}}\cup \left\{k^{\prime }\right\}$, $\mathcal{A}=\mathcal{A}\backslash \left\{k^{\prime }\right\}$. 5. The sub-channel allocation can be determined by repeating the above steps. Phase 1 continues until all available sub-channels are allocated to the D2D groups.

* Phase 2. SINR Assignment: 1. For the D2D group $m\in ℳ$, obtain all SINR ${{\mathsf{\gamma }}_{n,m,k}^D}^{*}$ on the sub-channels by solving the problem (16). 2. According Equations (3), (4) and (9), calculate all $p_{m,k}^D({{\mathsf{\gamma }}_{k,m}^C}^{*},{{\mathsf{\gamma }}_{n,m,k}^D}^{*})$ and $A_{n,m,k}$. 3. The power consumption and system capacity of D2D group m are respectively given by $p_m^D={\displaystyle {\sum }_{k\in {\mathcal{S}}_m}{p}_{m,k}^D({{\gamma }_{k,m}^C}^{*},{{\gamma }_{n,m,k}^D}^{*})}$, $X_{n,m}=\left|{\displaystyle {\cup }_{k\in {\mathcal{S}}_m}{A}_{n,m,k}}\right|$. Repeat the above steps until the power consumptions and system capacities of all D2D groups are calculated ultimately.

We analyze the complexity of our proposed algorithm in this subsection. In phase 1, we search for the optimal matching of sub-channel resources between all D2D groups and CUs, and then all available sub-channels are allocated to the D2D groups. Hence the complexity of the sub-channel allocation is $\mathcal{O}(MK)$. In phase 2, with $\mathsf{\tau }$ as a small acceptable tolerance for bisection algorithm, the complexity of the SINR assignment is $\mathcal{O}(K{\log }_2(1/\mathsf{\tau }))$. Therefore the complexity of multi-object optimization resource allocation is $\mathcal{O}(MK)+\mathcal{O}(K{\log }_2(1/\mathsf{\tau }))$. Obviously, our algorithm has polynomial complexity which has a linear relation with the scale of $M$ and $K$.

4. Numerical Results

In this section, we provide several simulation results to evaluate the performance of our proposed resource allocation scheme. The simulated network is contained in a single cell with a radius of 500 m where CUs and D2D multicast groups are uniformly and randomly distributed. We follow the clustered distribution model in [25], where D2D multicast groups of radius r are randomly located in a cell and the D2D users in each group are randomly distributed in the corresponding cluster. Simulation parameters such as path loss models, maximum transmission power, etc. are the same as those proposed in [26], and the main simulation parameters are listed in Table 1.

Table 1. Main Simulation Parameters.

Parameter	Value
Cellular layout	one isolated cellular cell
Cell radius, R	300 m~700 m
Uplink bandwidth	180 kHz
Noise spectral density	−174 dBm/Hz
Path loss for cellular links	128.1 + 37.6log10 (d (km))
Path loss for D2D links	148 + 40log10 (d (km))
Shadowing standard deviation	10 dB for cellular links
	12 dB for D2D links
Noise spectral density	−174 dBm/Hz
Maximum transmission power of CU	20 dBm
Maximum transmission power of D2D	20 dBm
SINR threshold of CU	0 dB~10 dB
SINR threshold of CU link	10 dB~35 dB
Number of CUs, K	20
Number of D2D groups, M	3~10
Number of D2D receivers in each group	10
D2D group size, r	20 m~60 m

We evaluate the performance of the proposed scheme by comparing it with four benchmarks: (1) power minimization (“MinP”); (2) capacity maximization (“MaxC”); (3) multi-objective optimization with each D2D group reusing one single sub-channel (“Single”); and (4) sum rate Maximization scheme in [12]. The first three can be regarded as the special cases of the proposed scheme by setting ($\mathsf{\eta }=1$), ($\mathsf{\eta }=0$) and ($\left|{\mathcal{S}}_m\right|=1$) for “MinP”, “MaxC” and “Single”. The fourth one is a pure throughput optimization scheme, which assumes each D2D group can reuse the sub-channel of at most one CU.

Figure 2 presents the power consumption and system capacity performance with the varying of the weighted factor $\mathsf{\eta }$, where $K=20$, $M=10$, $\left|{\mathcal{D}}_m\right|=10$, $R=500$m, $r=50$m, ${\mathsf{\Gamma }}_k^C=5$ dB and ${\mathsf{\Gamma }}_m^D=35$ dB. For the proposed scheme, the power consumption preference is enhanced with larger $\mathsf{\eta }$, while, from Figure 2b, the system capacity preference requires smaller $\mathsf{\eta }$ with upper bound identical to the performance of the benchmark “MaxC”. Hence, using the proposed scheme, the operator can flexibly configure the network with different preferences to satisfy specific system or user requirements simply by varying the weighted factors. Furthermore, it can be seen from Figure 2 that for the proposed scheme, increasing $\mathsf{\eta }$ decreases its power consumption value from 150 to 82, and its number of admitted D2D links from 87.3 to 76.4; while the power consumption and the number of admitted D2D links for “MaxR” are about 461.8 and 43.5, respectively. This implies that compared to the “MaxR” scheme, the proposed scheme seems to achieve more admitted D2D links in the network by consuming less power. This is because adopting the single sub-channel reusing for the “MaxR” scheme makes the power on the sub-channel fixed while the proposed scheme enables one D2D group to reuse multiple sub-channels and fully explore the spatial gain among different sub-channels, and be able to adjust power level on each sub-channel so as to perform power consumption minimization as well as admitting the maximum number of D2D links into the system. Moreover, we observe that the performance of the “Single” scheme is close to “MaxR” when weighted factor $\mathsf{\eta }\le 0.2$, while the consumed power in the “Single” scheme is less than in “MaxR” at the cost of removing more D2D links from the system.

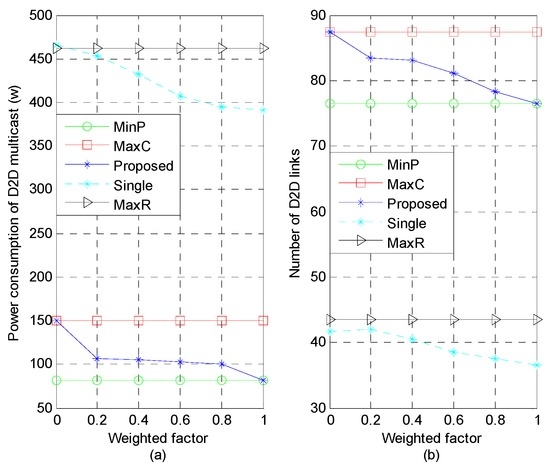
Figure 2. Power consumption and number of D2D links versus weighted factor: (a) Impact of weighted factor on power consumption; (b) Impact of weighted factor on system capacity.

Figure 3 shows the power consumption and system capacity with different D2D group size, where $K=20$, $M=10$, $\left|{\mathcal{D}}_m\right|=10$, $R=500$ m, ${\mathsf{\Gamma }}_k^C=5$ dB, ${\mathsf{\Gamma }}_m^D=35$ dB and $\mathsf{\eta }=0.5$. As shown in Figure 3b, the number of admitted D2D links decreases with increasing of the D2D group size. Especially, the “MaxR” and “Single” schemes fall faster than the proposed scheme. Since the channel gain of D2D link decreases when the multicast radius increases, more D2D links are likely to be removed to benefit the QoS maintenance of the remaining system, with bigger influence on the single sub-channel reusing scheme (“MaxR” and “Single”). However, the change in power consumption is not monotonic and depends on the following two factors: (i) more transmission power is required for the D2D groups to satisfy the SINR threshold constraint; and (ii) the worst channel condition of D2D multicast becomes relatively better along with the removed D2D links, thus the required transmission power decreases. It is seen from Figure 3a that the power consumption of “MaxR” shows a trend of earlier increase and later decrease. The decrement of proposed scheme in the number of admitted D2D links is much less than that of the “MaxR” scheme, thus power consumption of the proposed scheme keeps growing.

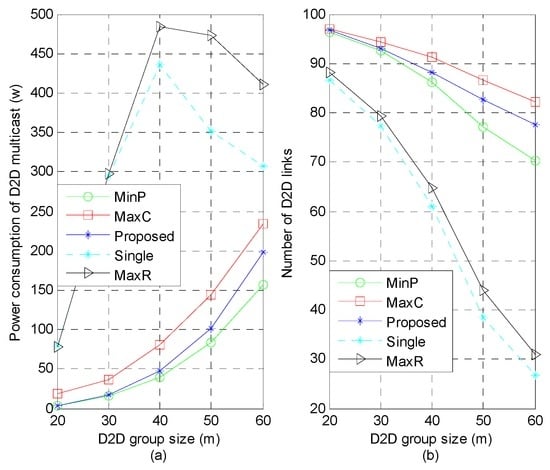
Figure 3. Power consumption and number of D2D links versus D2D group size: (a) Impact of D2D group size on power consumption; (b) Impact of D2D group size on system capacity.

The power consumption and system capacity with different cell radius is depicted in Figure 4, where $K=20$, $M=10$, $\left|{\mathcal{D}}_m\right|=10$, $r=50$ m, ${\mathsf{\Gamma }}_k^C=5$ dB, ${\mathsf{\Gamma }}_m^D=35$ dB and $\mathsf{\eta }=0.5$. Intuitively, the larger the cell radius, the greater the distance between the CUs and D2D receivers in groups, hence the smaller the interference from CUs to the D2D receivers. Thus the number of admitted D2D links increases with the cell radius as shown in Figure 4b. Similarly, the change in power consumption depends on the following two factors: (i) transmission power decreases along with the lower interference between CUs and the D2D receivers; and (ii) the worst channel condition of D2D multicast becomes relatively worse with the increment of the number of admitted D2D links, thus the required transmission power increases. From Figure 4a, compared to the scheme of reusing single sub-channel (“MaxR” and “Single”), the proposed scheme further utilizes the gain that is brought by the decrement of interference between CUs and the D2D receivers on multiple sub-channels.

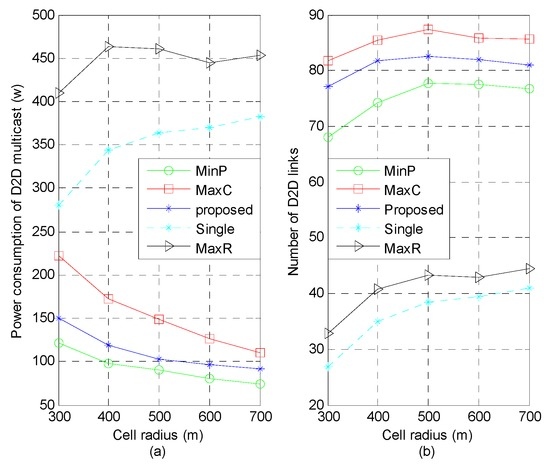
Figure 4. Power consumption and number of D2D links versus cell radius: (a) Impact of cell radius on power consumption; (b) Impact of cell radius on system capacity.

In Figure 5 and Figure 6, the power consumption and system capacity performance with different SINR thresholds of CUs and D2D links are illustrated, where $K=20$, $M=10$, $\left|{\mathcal{D}}_m\right|=10$, $R=500$ m, $r=50$ m and $\mathsf{\eta }=0.5$. It is seen that increasing the SINR threshold leads to decreasing the number of admitted D2D links since it tightens the SINR threshold constraints of both CUs and D2D links and limits the chances for a D2D group to find a CU partner. From Figure 5a, the increase in the SINR threshold of CUs, which has a greater impact on reusing single sub-channel scheme (“MaxR” and “Single”), is helpful to reduce D2D transmission power. As shown in Figure 6a, as the SINR threshold of D2D links increases, the power consumption rises gradually. Furthermore, the power consumption in “MaxR” and “Single” scheme begins a downward trend when the SINR threshold 30 dB. This due to the fact that the dramatic reduction in the number of admitted D2D links reduces the power consumption efficiently.

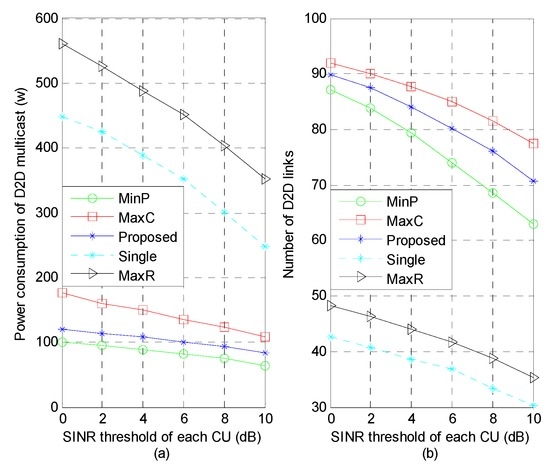
Figure 5. Power consumption and number of D2D links versus signal-to-interference- plus-noise ratio (SINR) threshold of each CU: (a) Impact of SINR requirement of CUs on power consumption; (b) Impact of SINR requirement of CUs on system capacity.

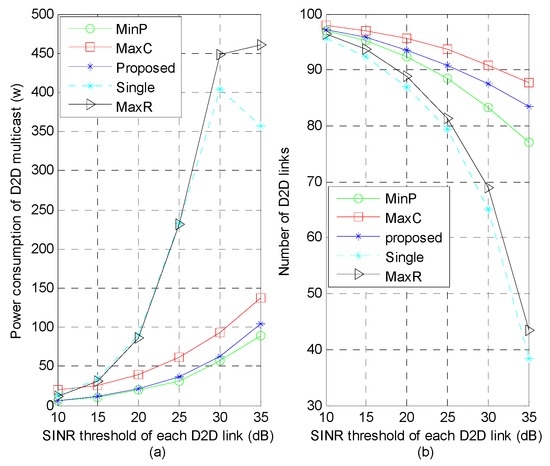
Figure 6. Power consumption and number of D2D links versus SINR threshold of each D2D link: (a) Impact of SINR requirement of D2D links on power consumption; (b) Impact of SINR requirement of D2D links on system capacity.

In Figure 7, the fairness of the proposed scheme is compared with the “MaxR” scheme. The Jain’s fairness index is used to evaluate the fairness of the algorithms. The Jain’s fairness index is defined as: $f(x_1,x_2,\mathrm{...},x_M)=\frac{{\left({\displaystyle {\sum }_{i=1}^M{x}_i}\right)}^2}{M\cdot {\displaystyle {\sum }_{i=1}^M{x}_i^2}}$ [27], where x_i is the resource allocated to D2D groups i, and M is the number of D2D groups. In Figure 7, fairness index of two schemes decreases with the increasing number of D2D groups in the network. Nevertheless, the fairness index of the proposed scheme always has higher fairness than referenced scheme since it considers a constrained multi-objective optimization problem.

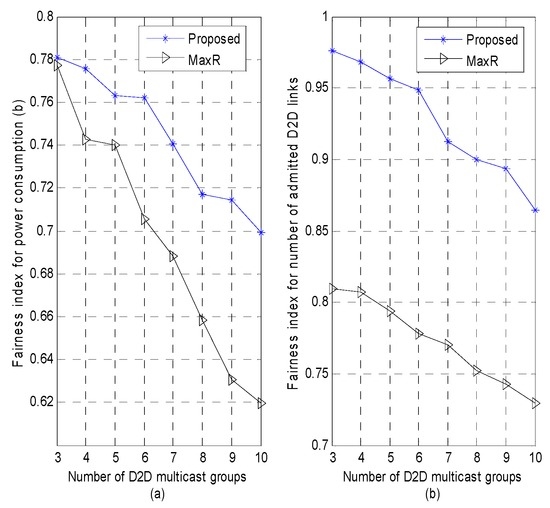
Figure 7. Fairness index versus number of D2D multicast groups: (a) Impact of the number of D2D multicast groups on fairness index for power consumption; (b) Impact of the number of D2D multicast groups on fairness index for system capacity.

5. Conclusions

In this paper, a multi-objective resource allocation is studied with QoS guarantees for multiple D2D multicast groups and multiple CUs. Using the linear weighted approach, we formulate a simple but flexible optimization framework in which system power consumption and system capacity are jointly considered. Then, we propose a novel resource allocation scheme that consists of sub-channel allocation and SINR assignment to solve a MINLP problem effectively. Simulation results demonstrate the flexibility and availability of the proposed framework in terms of multi-objective optimization. The results also reveal that the proposed scheme can enhance the performance of power consumption as well as system capacity significantly, and can maintain better fairness for different D2D multicast groups.