Multi-Objective Optimization of Meat Sheep Feed Formulation Based on an Improved Non-Dominated Sorting Genetic Algorithm

Abstract

Feed formulation is a typical multi-objective optimization problem that aims to minimize cost while satisfying multiple nutritional constraints. However, existing methods often suffer from limitations in handling nonlinear constraints, high-dimensional decision spaces, and solution feasibility. To address these challenges, this study proposes a multi-objective feed formulation method based on an improved Non-dominated Sorting Genetic Algorithm II (NSGA-II). A hybrid Dirichlet–Latin Hypercube Sampling (Dirichlet-LHS) strategy is introduced to generate an initial population with high feasibility and diversity, together with an iterative normalization-based dynamic repair operator to efficiently handle ingredient proportion and nutritional constraints. In addition, an adaptive termination mechanism based on the hypervolume improvement rate (Hypervolume Termination, HVT) is designed to avoid redundant computation while ensuring effective convergence of the Pareto front. Experimental results demonstrate that the Dirichlet–LHS strategy outperforms random sampling, Dirichlet sampling, and Latin hypercube sampling in terms of hypervolume and solution diversity. Under identical nutritional constraints, the improved NSGA-II reduces formulation cost by 1.52% compared with multi-objective Bayesian optimization and by 2.17% relative to conventional feed formulation methods. In a practical application to meat sheep diet formulation, the optimized feed cost is reduced to 1162.23 CNY per ton, achieving a 4.83% cost reduction with only a 1.09 s increase in computation time. These results indicate that the proposed method effectively addresses strongly constrained multi-objective feed formulation problems and provides reliable technical support for precision feeding in intelligent livestock production.

1. Introduction

In recent years, heuristic optimization algorithms, including particle swarm optimization (PSO) [1] and the Non-dominated Sorting Genetic Algorithm II (NSGA-II) [2], have been widely applied to complex control, modeling, and optimization problems. These methods have demonstrated strong capabilities in handling nonlinear, multi-objective, and constrained problems, and have been successfully employed in robust system identification [3], robot path planning [4], industrial scheduling [5], and evolutionary multi-objective optimization research [6]. Their population-based search mechanisms and flexibility make them particularly suitable for problems characterized by conflicting objectives and complex constraint structures.

In parallel, probabilistic model-based sequential optimization approaches, especially Bayesian optimization, have attracted increasing attention due to their ability to efficiently explore expensive or black-box objective functions [7]. Such methods have been progressively introduced into decision-support systems for animal production [8], including applications in animal nutrition optimization, breeding strategy design, and farm-level management decision-making [9]. These developments have contributed to the broader advancement of intelligent animal husbandry by enabling data-driven optimization under uncertainty and limited experimental budgets.

Feed formulation design and feed processing strategies constitute a fundamental component of modern livestock production systems. Rational ration formulation directly affects nutrient availability, animal growth performance, feed efficiency, and economic sustainability [10]. The primary objective of feed formulation is to satisfy animal nutritional requirements while minimizing production costs and ensuring feed quality and consistency [11]. However, this task has become increasingly challenging under the combined influence of climate change [12], intensified environmental pressures on agricultural systems [13], and the growing diversification of feed resources driven by alternative protein sources and agro-industrial by-products [14]. These factors have led to instability in feed ingredient supply [15] and variability in nutritional composition, thereby increasing formulation uncertainty and economic risk [16]. Moreover, climate-induced heat stress has been shown to reduce feed intake efficiency and animal growth performance [17], further complicating ration optimization [18].

From a methodological perspective, feed formulation problems are commonly formulated as constrained optimization problems, involving either single or multiple objectives such as cost minimization, nutrient balance, and environmental impact reduction [19]. Traditional feed formulation approaches are predominantly based on linear programming (LP). Early studies demonstrated that LP-based models can effectively improve production efficiency and reduce feed costs under simplified nutritional constraints [20]. Subsequent research extended these approaches to pasture-based beef cattle and sheep systems [21], as well as dairy ration formulation using nonlinear or mixed-integer programming frameworks [21]. However, while these models are effective for least-cost ration design, they exhibit limited flexibility in addressing multiple conflicting objectives and complex constraint interactions [22]. To enhance practical applicability, LP-based decision-support tools have been developed to incorporate local feed availability and market prices, improving cost efficiency in real-world feeding management [23]. Moreover, recent work has applied mathematical optimization frameworks to precision-fed dairy cattle diet formulation [24], demonstrating that optimized ration design can reduce feed cost and increase income over feed cost compared with conventional ration strategies [25].

Nevertheless, with the increasing diversity of feed ingredients, the growing number of nutritional indicators, and the emergence of nonlinear and many-objective constraint relationships, the limitations of traditional LP-based methods have become increasingly evident. These limitations have motivated the introduction of intelligent optimization algorithms into feed formulation research. For example, Altun and Şahman [26] applied particle swarm optimization to mixed feed cost optimization and reported superior performance compared with conventional optimization methods in nonlinear problem settings. Akintan et al. [27] systematically reviewed data-driven and AI-enabled decision-support approaches for animal feed formulation, highlighting their potential to enhance feed efficiency, animal performance, and system resilience. From a methodological perspective, Liang et al. provided a comprehensive survey of evolutionary constrained multi-objective optimization methods, systematically summarizing key techniques for handling complex constraint structures and conflicting objectives [28]. Peña et al. [29] investigated multi-objective stochastic programming for feed formulation, focusing on balancing feed cost with lysine and metabolizable energy requirements under uncertainty. Related studies have further shown that evolutionary and genetic algorithm-based approaches can outperform traditional linear programming methods in poultry and livestock feed cost optimization [30]. Moreover, recent research has increasingly integrated data-driven, machine learning [31], and advanced optimization frameworks into livestock feed formulation and decision-making processes, demonstrating improvements in production efficiency and economic performance compared with conventional methods [32].

In summary, heuristic and intelligent algorithms show broad application prospects in solving multi-objective optimization problems under complex constraints [33]. However, current feed formulation optimization still faces several challenges, including difficulties in cost control caused by large fluctuations in feed ingredient prices and the high computational cost associated with optimization under complex and high-dimensional constraint spaces. For example, Bayesian optimization often requires the construction and repeated updating of surrogate models when addressing complex nonlinear optimization problems [34], which demands substantial computational resources and leads to high computational cost in multi-objective settings [35]. Motivated by these challenges, this study develops an improved optimization approach based on the heuristic algorithm NSGA-II, aiming to achieve a balanced trade-off between optimization efficiency and convergence performance in feed formulation problems.

2. Materials and Methods

2.1. Problem Description

Feed formulation is inherently a trade-off problem between economic efficiency and nutritional adequacy. In practical livestock production systems, minimizing feed cost is essential for improving economic profitability, while ensuring adequate intake of key nutritional components is critical for supporting animal growth performance and feed utilization efficiency. Among various nutritional indicators, lysine is widely recognized as a limiting amino acid in ruminant and monogastric diets, and metabolizable energy is a core determinant of growth and production performance. However, improving nutritional quality often leads to increased feed cost, resulting in inherently conflicting objectives. This naturally motivates the formulation of feed formulation as a multi-objective optimization problem.

From an engineering and decision-support perspective, feed formulation should not be optimized with respect to a single criterion, but rather through a balanced consideration of multiple conflicting objectives. Following this principle, and in line with commonly adopted practices in feed formulation optimization studies, this work considers three objectives: minimizing total feed cost while maximizing lysine content and metabolizable energy. This objective configuration has been widely used in the literature to represent the fundamental trade-off between economic efficiency and nutritional performance, and allows a systematic exploration of Pareto-optimal solutions for decision-making.

Formally, the feed formulation problem is expressed as a constrained multi-objective optimization model:

$$\left\{\begin{array}{c}{min f}_c\left(\mathbf{x}\right)={\mathbf{c}}^T \mathbf{x}\\ {max f}_l\left(\mathbf{x}\right)={\mathbf{l}}^T \mathbf{x}\\ {max f}_e\left(\mathbf{x}\right)={\mathbf{e}}^T \mathbf{x}\end{array}\right.$$

(1)

$$s.t.\left\{\begin{array}{c}{\mathbf{l}}^T \mathbf{x}=1\\ {\mathbf{b}}_l\le {\mathbf{A}}^T\mathbf{x}\le {\mathbf{b}}_u \\ 0\le \mathbf{x}\le \mathbf{s}\end{array}\right.$$

(2)

where $\mathbf{x}={\left(x_1,x_2,\cdots ,x_d\right)}^{\mathrm{T}}$ denotes the decision variable vector, and each element $x_i$ represents the proportion of the i-th feed ingredient in the formulation on a mass basis. The dimension d corresponds to the total number of candidate feed ingredients included in the formulation, and all decision variables are continuous.

In Equation (1), $\mathbf{c}$, $\mathbf{l}$, and $\mathbf{e}$ denote the unit cost vector, lysine content vector, and metabolizable energy vector of the candidate feed ingredients, respectively. These vectors do not represent fixed scalar values, but ingredient-specific parameter vectors whose elements characterize the economic and nutritional properties of each ingredient. The objective values are determined by the weighted linear combination of these ingredient-specific coefficients with the decision vector $\mathbf{x}$, reflecting the system-level cost and nutritional outcomes of a given formulation.

The constraint set in Equation (2) ensures the practical feasibility of the formulation. The proportion normalization constraint enforces that the ingredient proportions sum to one. The nutritional constraint ${\mathbf{b}}_l\le {\mathbf{A}}^{\mathrm{T}}\mathbf{x}\le {\mathbf{b}}_u$ guarantees that essential nutrient requirements are satisfied within predefined bounds, where $\mathbf{A}$ is the nutrient composition matrix and ${\mathbf{b}}_l$ and ${\mathbf{b}}_u$ denote the lower and upper requirement limits, respectively. The bound constraint $0\le \mathbf{x}\le \mathbf{s}$ restricts the inclusion level of each ingredient according to practical feeding considerations.

It should be emphasized that both the set of design variables (i.e., candidate feed ingredients) and the associated coefficient vectors are instance-dependent and can be constructed based on different nutritional standards or databases. In this study, the same general formulation in Equations (1) and (2) is instantiated under different data settings. For benchmark experiments and methodological comparisons with existing studies, ingredient composition and cost data consistent with commonly used literature sources are adopted to ensure comparability. For the practical meat sheep diet formulation case, the coefficient vectors and nutrient matrix are constructed using China-specific ingredient composition data and nutritional standards. Therefore, the proposed optimization model is not restricted to a specific feed composition standard and can be generalized to different production contexts.

Although the objective functions in Equation (1) are linear with respect to the decision variables, the overall optimization problem remains highly nontrivial due to the high-dimensional continuous decision space, strong coupling among nutritional constraints, strict proportion normalization, and upper bounds on ingredient inclusion levels. Moreover, lysine and metabolizable energy appear in the model as ingredient attributes and are aggregated through formulation proportions to form system-level nutritional objectives, rather than being redundantly or independently optimized. The inherent heterogeneity among ingredient-specific economic and nutritional coefficients leads to conflicting objectives and a generally non-convex feasible region. Consequently, the problem gives rise to a Pareto-optimal solution set rather than a single optimal solution, motivating the use of population-based evolutionary multi-objective optimization methods.

While the objective structure of the feed formulation problem considered in this study is aligned with commonly adopted cost–nutrition trade-off formulations, the novelty of this work does not lie in redefining the objective functions themselves. Instead, it lies in addressing the challenges arising from their integration with strong proportion constraints, heterogeneous ingredient standards, and high-dimensional continuous decision spaces. These characteristics substantially increase the difficulty of obtaining feasible and well-distributed Pareto-optimal solutions using conventional approaches, thereby providing a clear motivation for the improved optimization framework proposed in this study.

2.2. NSGA-II Algorithm

NSGA-II is a multi-objective optimization algorithm proposed by Deb et al. [36]. It is primarily designed to solve multi-objective optimization problems in which multiple objectives are mutually conflicting and has become one of the most widely used multi-objective evolutionary algorithms. Compared with standard genetic algorithms, NSGA-II exhibits clear advantages in maintaining solution diversity and computational efficiency [37].

The NSGA-II algorithm begins by generating an initial population and evaluating the fitness of each individual based on the selected objective functions. Subsequently, a non-dominated sorting procedure is applied to rank the population into different fronts according to dominance relationships among individuals with respect to multiple objectives. To preserve diversity within each non-dominated front, NSGA-II introduces a crowding distance mechanism, which measures the density of individuals in the objective space. Individuals with larger crowding distances are located in less crowded regions and are therefore assigned higher selection priority.

During the selection stage, NSGA-II employs a tournament selection strategy based on both dominance rank and crowding distance to select individuals from the parent population for reproduction. The selected individuals generate offspring through crossover and mutation operations. The parent and offspring populations are then combined, and non-dominated sorting is performed again. Based on dominance rank and crowding distance, the best N individuals are selected to form the new population.

As the number of iterations increases, the solutions in the population gradually approach the true Pareto-optimal front while maintaining a relatively uniform distribution in the objective space [38]. Owing to the incorporation of elitism and crowding distance control mechanisms, NSGA-II not only improves the efficiency of solving multi-objective optimization problems but also helps reduce the risk of premature convergence to local optima.

3. Improved NSGA-II Algorithm

3.1. Initial Sampling

To address the issues of low feasibility of initial solutions, severe constraint violations, insufficient processing efficiency, and unstable convergence encountered by the standard NSGA-II when dealing with high-dimensional and strongly constrained diet formulation problems, this study introduces a series of key improvements aimed at enhancing the quality of the initial population and strengthening the search capability of the algorithm under complex constraints.

A hybrid Dirichlet–Latin Hypercube Sampling (Dirichlet-LHS) strategy is proposed to generate the initial population. This strategy combines the advantages of the Dirichlet distribution [39] in modeling proportion constraints with the strengths of Latin Hypercube Sampling (LHS) [40] in space-filling design, thereby ensuring both feasibility of initial solutions and population diversity. Unlike conventional random sampling methods, the proposed initialization strategy consists of three main steps: (1) a uniform Dirichlet distribution is constructed based on the dimensionality of ingredient proportions to generate initial solution vectors that satisfy proportion constraints (i.e., ${\displaystyle {\sum }_{i=1}^d{x}_i=1}$), and upper bounds on ingredient usage are imposed while preserving the proportional structure to ensure the rationality of the basic formulation; (2) LHS is introduced in the vicinity of the feasible solutions obtained above or within the remaining solution space, where the high-dimensional space is partitioned into equiprobable intervals and sampled randomly to enhance the uniformity of space coverage; (3) the samples generated by Dirichlet and LHS are merged and subjected to final normalization to form the initial population.

By integrating the structural constraint enforcement provided by the Dirichlet distribution with the space coverage capability of LHS, the proposed hybrid sampling strategy is able to generate an initial population with high feasibility, strong diversity, and broad coverage, thus providing a high-quality starting point for subsequent optimization. Moreover, by embedding constraints directly into the sampling stage, this strategy effectively avoids the generation of a large number of infeasible solutions under complex constraints, which commonly occurs in traditional Dirichlet sampling and leads to reduced computational efficiency due to extensive post hoc repair operations.

3.2. Dynamic Repair Operator Mechanism

In feed formulation optimization problems, due to the stochastic nature of genetic operators such as crossover and mutation, the generated offspring individuals often violate formulation constraints, for example, exceeding the upper limit of a single ingredient or having ingredient proportions that do not sum to one. This results in an increased number of infeasible solutions and a reduction in overall algorithmic efficiency. To address this issue, this study designs an iterative normalization-based dynamic repair operator to perform real-time correction of individual solutions during the evolutionary process.

Assuming that a feed formulation consists of d ingredients, an individual solution is denoted as $\mathbf{x}=\left[x_1,x_2,\cdots x_d\right]$ where $x_i$ denotes the proportion of the i-th ingredient. The dynamic repair operator is implemented in two sequential steps.

Boundary constraint repair is first applied to each decision variable:

$${\mathrm{x}}_i^{\prime }=clip(x_i,0,u_i)=\left\{\begin{array}{cc}0& if\hspace{0.33em}{x}_i<0\\ u_i& if\hspace{0.33em}{x}_i>u_i\\ x_i& otherwise\end{array}\right.$$

(3)

where $u_i$ denotes the upper bound of the i-th ingredient, and clip ($x_i,0,u_i$) represents an element-wise truncation operator.

Proportion normalization is then performed to ensure that the sum of all ingredient proportions equals one:

$${\widehat{x}}_i={\displaystyle \frac{x_i^{\prime }}{{\displaystyle {\sum }_{j=1}^d{x}_j^{\prime }}}}$$

(4)

To prevent division-by-zero errors, when ${\displaystyle {\sum }_{\mathrm{j}=1}^d{x}_j^{\prime }}=0$, all decision variables are reset to $x_i={\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$d$}\right.}$.

3.3. Adaptive Stopping Mechanism

To address the limitation of traditional genetic algorithms that rely on a fixed number of iterations as the stopping criterion, this study proposes an adaptive termination criterion based on hypervolume (HV). The core idea is to establish a dynamic evaluation window mechanism. The termination condition is defined as:

$$\psi \left(\mathrm{t}\right)=\left\{\begin{array}{cc}True,& \hspace{1em}\hspace{1em}if{\displaystyle \frac{\Delta HT\left(t\right)}{HT\left(t-1\right)}}<\epsilon \hspace{0.33em}for\hspace{0.33em}k\hspace{0.33em}consecutive\hspace{0.33em}generations\\ False,& \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}otherwise\end{array}\right.$$

(5)

where $\Delta HT\left(t\right)=HT\left(t\right)-HT\left(t-1\right)$ denotes the hypervolume increment at generation $t$, $\epsilon$ is the predefined improvement threshold, and $k$ represents the upper limit of consecutive stagnation generations. A maximum stagnation generation limit is also specified, and the algorithm terminates when either the above stagnation condition is satisfied or the maximum stagnation limit is exceeded. This mechanism ensures that a high-quality solution set is obtained while effectively avoiding overfitting or unnecessary long-term computation. The improved algorithmic framework is illustrated in Figure 1.

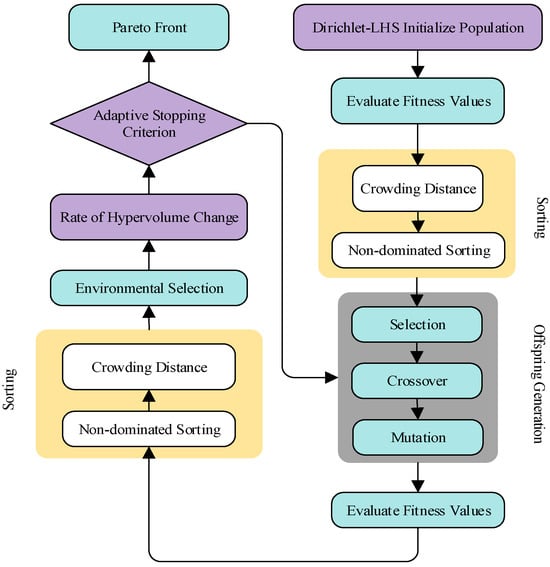
Figure 1. Workflow diagram for improving the NSGA-II algorithm.

4. Experiments and Results

4.1. Experimental Setup

To comprehensively evaluate the performance of the proposed improved NSGA-II algorithm and to verify its effectiveness in practical meat sheep diet formulation problems, a systematic experimental framework was designed in this study. The experiments were conducted in three stages: (i) optimization of algorithm hyperparameter configurations; (ii) performance comparison of the improved NSGA-II under different initial sampling strategies, with results further compared against the methods proposed by Peña et al. [29] and Uribe-Guerra et al. [30]; and (iii) application of the improved NSGA-II algorithm to meat sheep diet formulation optimization to validate its generalization ability and practical applicability.

The first stage focused on determining the optimal parameter combination for the improved NSGA-II algorithm to ensure performance stability and result reliability in subsequent comparative experiments. This stage involved three categories of key parameters: (1) core NSGA-II parameters, including population size, crossover probability, and mutation probability, which directly affect the algorithm’s search capability, convergence speed, and solution diversity; (2) parameters related to the adaptive stopping mechanism, including the evaluation window size and hypervolume improvement threshold, which are used to control the termination timing and avoid unnecessary computation; and (3) parameters of the elite solution selection mechanism, with the diversity weight coefficient as the core factor, used to balance cost optimality and diversity of the Pareto solution distribution [41]. To ensure fairness in the comparative experiments, these parameters were kept consistent across different experimental settings.

4.2. Results and Analysis

4.2.1. Ablation Study of the Dynamic Repair Operator

An ablation experimental scheme was designed to evaluate the effectiveness of the dynamic repair operator in terms of algorithmic efficiency and solution quality. The initial population was generated using random sampling to ensure that all comparative experiments started from identical and representative conditions, thereby eliminating the influence of hybrid sampling on the convergence process. The population size was fixed at 200, with a crossover probability of 0.9 and a mutation probability of 0.3. These parameter settings follow common practice in NSGA-II-based optimization. A relatively high crossover probability facilitates effective information exchange among candidate solutions, while a moderate mutation probability helps maintain population diversity and prevents premature convergence, thus achieving a balanced trade-off between convergence speed and solution diversity. Based on the experimental datasets used by Peña [30] and Uribe-Guerra [31], the performance of the algorithm with and without the dynamic repair operator was compared to comprehensively analyze its impact on convergence speed, convergence stability, and search performance. The results are presented in Table 1.

Table 1. Comparison of results whether dynamic repair operator is enabled or not.

Evaluation Dimension	Key Metric	Dynamic Repair Operator (Experimental Group)	Original Repair Operator (Control Group)	Comparative Advantage
Convergence Speed	Generation of first feasible solution	Generation 27	Generation 29	400 fewer evaluations
	Full convergence point	Generation 38	Generation 43	1000 fewer evaluations
Convergence Stability	Mean ε value in late stage	0.019	0.037	Fluctuation reduced by 48.6%
	Proportion of iterations with ε > 0.05	12%	24%	High-fluctuation iterations reduced by 50%
Search Efficiency	Generation of high-quality solutions	Generation 37	Generation 42	1000 fewer evaluations
	Final cost (€/MT)	150.59	152.70	Cost reduced by 1.38%

The core advantage of the dynamic repair operator lies in its real-time constraint satisfaction capability. After offspring individuals are generated, the operator immediately performs iterative normalization to simultaneously correct ingredient proportion constraints and boundary constraints on ingredient usage. This immediate repair mechanism significantly reduces the computational overhead associated with evaluating infeasible solutions, improves search efficiency, and avoids degradation of feasible solution quality caused by delayed repair or traditional penalty-based mechanisms. As shown in Table 1, the dynamic repair operator markedly accelerates the convergence process and improves the feasibility and stability of the final solutions, achieving a cost reduction of 1.38% under identical nutritional constraints.

4.2.2. Evaluation of the Hypervolume-Based Adaptive Termination Mechanism

To verify the effectiveness of the adaptive stopping mechanism based on the hypervolume improvement rate (Hypervolume Termination, HVT), its performance in avoiding redundant computation while maintaining the quality of the Pareto front was evaluated. The experiments focused on whether the HVT mechanism could significantly reduce computational cost without degrading, or even while improving, solution quality when replacing a fixed maximum number of iterations.

The experimental parameter settings were kept consistent with those used in the ablation study of the dynamic repair operator, and the dynamic repair operator was enabled to ensure that the HVT experiments were conducted under optimal constraint-handling conditions. All experiments were carried out on the same datasets and application scenarios. The experimental group adopted the HVT-based adaptive stopping mechanism, and the improvement threshold and the upper limit of consecutive stagnation generations were determined through multiple trials. The control group employed a fixed maximum iteration strategy, which was set to 500 generations based on preliminary experiments, slightly exceeding the number of iterations required by the adaptive stopping mechanism to obtain optimal solutions.

The experimental results are summarized in Table 2. When the parameter was set to k = 7, the algorithm converged within only 390 generations, reducing computational cost by approximately 22% compared with the fixed 500-generation strategy. When k < 7, premature termination occurred due to parameter sensitivity, resulting in a significant decline in solution quality, with hypervolume values decreasing by 6.5–6.8% and costs increasing by 4.0–4.1%, confirming the necessity of k ≥ 6. When k > 7, the number of iterations increased substantially (by approximately 255%), while the formulation cost increased by 0.18–1.72%, indicating that excessively extending the search process does not further improve economic performance and may instead lead to overfitting. The hypervolume variation further demonstrates that, in the later stages of optimization, improvements of the Pareto front become saturated, and additional computation yields only marginal gains. In contrast, the HVT mechanism effectively avoids unnecessary long-term computation while ensuring solution quality.

Table 2. Adaptive stopping mechanism ablation experimental results.

Configuration	Termination Generation	Final HV	Optimal Cost (€/MT)	Nutritional Indicators
Experimental group (k = 4)	192	857.26	152.76	Lysine: 0.969%, Energy: 14.13 MJ/kg
Experimental group (k = 5)	193	855.26	148.99	Lysine: 0.975%, Energy: 14.08 MJ/kg
Experimental group (k = 6)	389	921.84	147.13	Lysine: 0.961%, Energy: 14.21 MJ/kg
Experimental group (k = 7)	390	919.97	146.87	Lysine: 0.955%, Energy: 14.07 MJ/kg
Experimental group (k = 8)	1382	964.74	147.14	Lysine: 0.955%, Energy: 14.05 MJ/kg
Experimental group (k = 9)	1383	964.05	149.40	Lysine: 1.037%, Energy: 14.26 MJ/kg
Control group	500	945.18	148.18	Lysine: 0.955%, Energy: 14.19 MJ/kg

4.2.3. Comparison with Existing Feed Formulation Methods

By comparing the results of the proposed improved NSGA-II algorithm with those reported in previous studies, as summarized in Table 3, the experimental results demonstrate that under the same nutritional constraints adopted in the MFP [29] and MOBO [30] studies, the proposed algorithm achieves lower formulation cost by prioritizing cost as the primary optimization objective and effectively eliminating infeasible solutions through the dynamic repair operator. Specifically, the formulation cost is reduced by 1.52% compared with the MOBO method and by 2.17% compared with the MFP method. In addition, the Pareto solution set obtained by the improved NSGA-II exhibits a wider coverage range, providing decision-makers with more alternative solutions under identical constraint conditions.

Table 3. Comparison of the optimal solution and corresponding feed composition.

Ingredients	MFP	MOBO	NSGA-II
	[151.4, 1.02, 14.31]	[150.4, 1.15, 14.35]	[146.16, 0.96, 14.06]	[149.21, 1.05, 14.01]
Barley	13.53	40.00	10.95	21.30
Wheat	22.25	0.00	40.00	14.08
Corn	0.00	0.00	0.33	8.15
Alfalfa	0.00	0.00	3.12	1.79
Cassava Meal	0.00	0.00	0.09	1.24
Soybean meal	15.08	9.09	21.49	23.46
Fish meal	0.00	0.11	4.00	3.86
Gluten feed	3.74	8.00	0.61	0.40
Calcium Carbonate	0.94	1.25	0.14	0.64
Lysine 78%	0.00	0.39	0.08	0.02
Sunflower meal	0.00	3.00	0.82	0.84
Animal fat	0.00	0.00	0.77	2.32
Beet pulp	0.00	0.00	0.02	1.40
Lupin	10.00	10.00	0.20	0.11
Peas	14.06	8.15	0.13	8.68
Rye	20.00	20.00	16.03	9.35
Dicalcium	0.4	0.00	1.23	2.36

Note: The bracketed values denote [Cost (€/MT), Lysine (%), Energy (MJ/kg)].

From the perspective of feed composition, the improved NSGA-II algorithm enables more flexible adjustment of ingredient proportions while satisfying key nutritional constraints such as lysine and energy. As a result, certain low-cost ingredients with relatively high utilization efficiency are more effectively incorporated, leading to a further reduction in the overall formulation cost.

Overall, the comparative results indicate that under identical nutritional constraints, the proposed improved NSGA-II algorithm not only achieves superior economic performance but also maintains good solution diversity, demonstrating strong overall advantages in multi-objective feed formulation optimization problems.

4.2.4. Application to Meat Sheep Diet Formulation

In this application case, the coefficient vectors and nutrient composition matrix in Equations (1) and (2) are instantiated using China-specific ingredient composition data and nutritional standards, while the optimization model itself remains identical to the general formulation described in Section 2.1. Table 4 provides the ingredient composition and nutrient profiles used in this application case. To further verify the applicability and effectiveness of the proposed improved NSGA-II algorithm in practical feed formulation design, it was applied to a meat sheep diet formulation optimization problem. This application case is based on the nutritional requirements of meat sheep with a body weight of 40 kg and a daily weight gain of 100 g/d, as specified in the NY/T 816–2021 [42]. Nutrient Requirements of Meat Sheep. The basic feed composition and corresponding nutrient levels are listed in Table 4. Feed cost data were obtained from market surveys and publicly available online sources, with costs expressed in CNY per ton.

Table 4. Basic feed composition and nutrient levels.

Ingredients	Cost (CNY/ton)	DM (%)	Ca (%)	CP (%)	P (%)	NDF (%)	ME (MJ/kg)	MP (%)
Barley bran	2080	87.00	0.09	11.00	0.33	18.40	12.12	4.41
Wheat bran	1950	92.50	0.24	17.90	1.04	30.10	10.83	8.08
Corn	1780	88.80	0.07	8.53	0.23	3.74	13.04	3.10
Sorghum	1900	88.60	0.13	9.00	0.36	17.40	12.23	3.35
Soybean meal	2200	91.63	0.27	45.27	0.54	15.59	12.43	22.64
Cottonseed meal	2950	90.45	0.23	43.09	0.93	30.68	10.76	21.48
Peanut meal	5400	88.00	0.27	47.80	0.56	15.50	12.44	23.99
Sheepgrass	680	91.00	0.49	12.26	0.07	73.50	6.02	5.08
Alfalfa silage	3300	37.60	-	20.81	-	48.30	8.81	9.63
Corn straw	200	92.40	0.64	4.25	0.08	76.20	5.72	0.96
Soybean straw	550	90.50	0.99	5.22	0.15	77.40	5.59	1.34
Corn straw silage	260	31.03	-	6.60	-	74.70	5.89	2.07
Dicalcium phosphate	2200	99.40	29.60	-	22.86	-	-	-

Under the constraints of meeting the minimum requirements for key nutritional indicators such as crude protein (CP) and metabolizable energy (ME), the improved NSGA-II algorithm was employed to perform multi-objective optimization of the meat sheep diet formulation. The optimization results show that the optimal formulation achieved a cost of 1162.23 CNY per ton, while all nutritional indicators met or exceeded the required industry standards.

4.2.5. Effect of Different Initial Sampling Strategies

Table 5 compares the economic and performance outcomes of different initial sampling strategies in meat sheep diet formulation optimization. The results indicate that, compared with random sampling, the hybrid Dirichlet–LHS strategy achieves a 4.83% reduction in formulation cost with an increase in computation time of only 1.09 s. Compared with using Dirichlet sampling or LHS alone, the Dirichlet–LHS strategy demonstrates superior overall performance in terms of cost control and solution quality.

Table 5. Comparison of economic and performance indicators of different sampling methods.

Sampling Method	Cost (CNY/ton)	CP (%)	ME (MJ/kg)	Time (s)
Random	1221.16	15.65	8.77	8.64
Dirichlet	1257.87	16.37	8.92	6.47
LHS	1283.06	15.52	8.68	15.13
Dirichlet-LHS	1162.23	15.52	8.75	9.73

4.2.6. Convergence Behavior and Population Diversity Analysis

Figure 2 presents a comparative analysis of different initial sampling strategies during the optimization process under the meat sheep nutritional requirements. For each strategy, the left panel illustrates the hypervolume (HV) convergence behavior, while the right panel shows the distribution of solutions in the decision space, enabling a joint evaluation of convergence efficiency and population diversity.

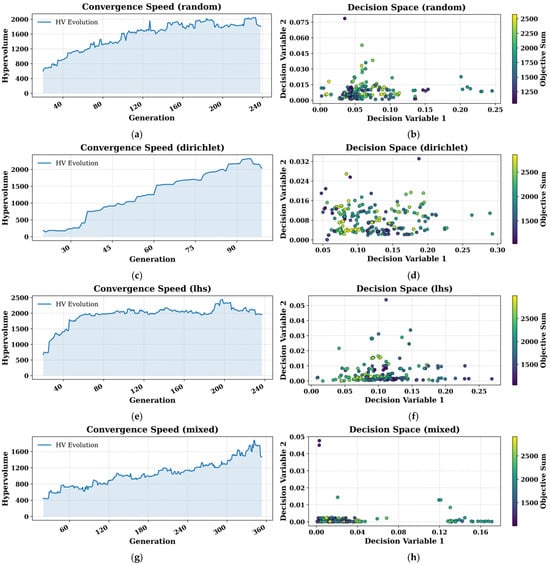
Figure 2. Comparison of different initial sampling strategies in terms of hypervolume convergence and decision space distribution (a) Random sampling HV curve (b) Random sampling decision space (c) Dirichlet sampling HV curve (d) Dirichlet sampling decision space (e) LHS sampling HV curve (f) LHS sampling decision space (g) Hybrid Dirichlet–LHS HV curve (h) Hybrid Dirichlet–LHS decision space.

For random sampling (Figure 2a,b), the HV curve increases steadily but with noticeable fluctuations, indicating a moderate and relatively unstable convergence process. The corresponding decision space distribution is widely scattered, reflecting good exploration capability but limited guidance toward high-quality feasible regions, which explains the moderate convergence performance.

In the case of Dirichlet sampling (Figure 2c,d), a high initial HV value is achieved due to the strict enforcement of proportion constraints, allowing many solutions to be feasible from the early generations. However, the HV curve exhibits an evident plateau after approximately 100 generations, suggesting premature convergence. This behavior is consistent with the decision space results, where solutions are highly concentrated in a narrow region, indicating insufficient diversity and a tendency to fall into local optima.

For Latin Hypercube Sampling (LHS) (Figure 2e,f), the HV evolution shows a delayed but continuous increase. The first several generations contribute little to HV improvement, mainly because a considerable number of individuals violate constraints and require repair. Once feasibility is gradually achieved, the HV grows more rapidly. The decision space distribution demonstrates improved coverage compared with Dirichlet sampling, confirming the advantage of stratified sampling in enhancing diversity.

The hybrid Dirichlet–LHS strategy (Figure 2g,h) exhibits the most balanced performance. Although its initial HV growth is slower than that of pure Dirichlet sampling, it shows a sustained and stable improvement throughout the optimization process. The decision space distribution is the most widely spread among all strategies, indicating strong exploration ability while maintaining feasibility. This combination effectively alleviates premature convergence and supports the construction of a high-quality initial population. Overall, the results demonstrate that the Dirichlet–LHS hybrid sampling strategy achieves superior performance by jointly considering feasibility, diversity, and convergence stability, making it more suitable for multi-objective optimization problems with strict nutritional proportion constraints.

Figure 3 illustrates the convergence behavior of hypervolume (HV) and formulation cost with respect to the number of generations under different sampling strategies. The HV curve obtained with random sampling exhibits pronounced zigzag fluctuations, reflecting instability in the search process. For Dirichlet sampling, the HV value increases rapidly in the early stages but reaches saturation at an early point, corresponding to premature convergence of formulation cost. Due to low initial feasibility, LHS shows large fluctuations in the HV curve and pronounced oscillations in the cost curve, indicating high repair overhead and relatively low overall optimization efficiency.

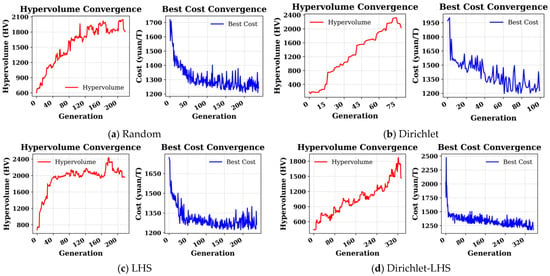
Figure 3. Convergence behavior of hypervolume and formulation cost under different initial sampling strategies.

In contrast, the Dirichlet–LHS strategy presents a steadily increasing HV curve, with formulation cost decreasing progressively without obvious stagnation. Approximately 80% of the optimization process is completed within about 150 generations, demonstrating favorable convergence speed and stability. These results indicate that by jointly improving initial feasibility and space coverage, the Dirichlet–LHS sampling strategy effectively enhances long-term convergence performance and provides an efficient search pathway for meat sheep diet formulation optimization.

4.2.7. Analysis of the Optimized Diet Composition

To further analyze the details of the optimal formulation obtained by the improved NSGA-II algorithm, Table 6 presents the specific proportion of each ingredient in the optimized diet. The results indicate that the ingredient composition achieves a good balance between economic efficiency and synergistic utilization. Low-cost ingredients rich in structural fiber, such as soybean straw, are effectively utilized to support the basal diet structure. Soybean meal, as a high-quality protein source, accounts for a relatively large proportion to meet protein requirements. Energy is mainly supplied by sorghum and corn, whose relatively stable market prices contribute to overall cost control. In addition, dicalcium phosphate is used to precisely regulate calcium and phosphorus levels. Overall, the formulation achieves an optimized cost structure while satisfying nutritional requirements.

Table 6. Ingredient Proportions of the Optimized Diet.

Ingredients	Proportion (%)
Barley bran	1.69
Wheat bran	1.12
Corn	10.42
Sorghum	15.66
Soybean meal	21.30
Cottonseed meal	0.79
Peanut meal	2.82
Sheepgrass	1.33
Alfalfa silage	7.78
Corn straw	4.32
Soybean straw	30.60
Corn straw silage	0.49
Dicalcium phosphate	1.68

Table 7 summarizes the key economic and nutritional indicators of the feed formulation obtained using the improved NSGA-II multi-objective optimization algorithm.

Table 7. Nutritional and cost indicators of the feed formulation.

Indicator	Value
cost (CNY/ton)	1162.23
DM (%)	82.01
Ca (%)	0.95
CP (%)	15.52
P (%)	0.68
NDF (%)	45.58
ME (MJ/kg)	8.75
MP (%)	6.87

Under the condition that all predefined nutritional constraints are satisfied, cost is treated as the primary optimization objective while key nutritional indicators, such as crude protein (CP) and metabolizable energy (ME), are simultaneously considered, achieving coordinated optimization of economic performance and nutritional adequacy. The resulting formulation is suitable for meat sheep with a body weight of 40 kg and a daily weight gain of 100 g/d.

4.2.8. Robustness and Sensitivity Discussion

In practical feed formulation scenarios, moderate variations in ingredient costs and nutritional requirement bounds are inevitable due to market fluctuations and management uncertainty. To evaluate the robustness of the proposed multi-objective optimization framework, the sensitivity of the optimized solutions was analyzed from a practical perspective. The results indicate that moderate parameter variations do not significantly affect the feasibility of the optimized formulations or the overall trade-off structure among the three objectives. The optimized solutions remain nutritionally feasible, and the corresponding cost variations are limited, demonstrating that the proposed formulation model and optimization approach are robust under realistic parameter uncertainty.

5. Conclusions

This study addresses the multi-objective optimization problem in meat sheep diet formulation, which requires balancing economic cost and multiple nutritional components, and proposes an improved NSGA-II algorithm. The proposed algorithm aims to overcome the limitations of traditional linear programming methods in handling nonlinear, strongly constrained, and multi-objective problems, as well as the challenges faced by existing heuristic algorithms in feed formulation optimization, such as low-quality initial solutions, inefficient constraint handling, and high computational cost.

The main contributions and innovations of this study can be summarized as follows:

(1)

A hybrid Dirichlet–Latin Hypercube initial sampling strategy is proposed, which combines the proportional constraint modeling capability of the Dirichlet distribution with the space-filling advantage of Latin Hypercube Sampling. This strategy effectively improves the feasibility and diversity of the initial population under high-dimensional and strongly constrained conditions. Experimental results demonstrate that the proposed strategy significantly enhances initial population quality and improves the coverage and convergence quality of the Pareto front.

(2)

To address ingredient usage constraints and complex nutritional constraints in feed formulation, an iterative normalization-based dynamic repair operator is designed and combined with a penalty mechanism to eliminate infeasible solutions that cannot be repaired, thereby ensuring efficient population evolution within the feasible region. Experimental results show that under identical nutritional constraints, the improved NSGA-II algorithm reduces formulation cost by 1.52% compared with the MOBO method and by 2.17% compared with the MFP method.

(3)

An adaptive termination mechanism based on the hypervolume improvement rate is proposed. By dynamically monitoring the convergence status of the Pareto front, this mechanism effectively avoids redundant computation while maintaining solution quality, thereby improving the overall computational efficiency of the algorithm.

(4)

The proposed improved NSGA-II algorithm is applied to a practical meat sheep diet formulation optimization problem. The optimization results show that the formulation cost is significantly reduced to 1162.23 CNY per ton, while key nutritional indicators such as crude protein and metabolizable energy meet or exceed industry standards. A substantial improvement in economic performance is achieved with only a slight increase in computation time.

In summary, the improved NSGA-II algorithm integrating Dirichlet–LHS initial sampling, dynamic repair and penalty mechanisms, and the HVT-based adaptive termination strategy provides an efficient and reliable multi-objective optimization solution for meat sheep diet formulation. While ensuring feasibility under high-dimensional and complex constraints, the proposed method effectively balances multiple objectives such as cost minimization and nutritional adequacy, demonstrating strong application potential and practical value.