User-Aware Trust Evaluation of Web Services: A Fuzzy-Based MCDM Approach

Abstract

With the development of service-based and cloud-based architectures, the number of web services is rapidly increasing, and when users use these services, they expect reliability, security, and performance. However, existing trust evaluation approaches are predominantly based on QoS characteristics (e.g., availability, throughput, and compliance) and do not fully reflect user satisfaction and expectations. This research addresses this gap by posing the following research question: How can a fuzzy-based multi-criteria decision-making (MCDM) approach incorporate user experience to enhance web service trust score evaluation under uncertainty? To address this, we propose a trust score–weighted model and an evaluation approach that extends traditional methods by integrating a fuzzy-based MCDM approach, such as fuzzy TOPSIS, fuzzy VIKOR, and fuzzy WASPAS, thereby allowing both objective service metrics and subjective user expectations to be jointly considered when evaluating service trust. The results of the proposed approach demonstrate the evaluation of trust scores through a fuzzy-based MCDM approach, allowing for the ranking of WSs. Our case study validates the model’s ability to incorporate predictive quality-of-service performance and its relevance to real-world, user-centric service selection scenarios.

1. Introduction

With the continuously growing number of web service-based systems, assessing their reliability becomes a crucial task for their users. Web services (WS), which are made available over the internet via standardised access protocols, play an important role in applications such as online shopping [1,2], social media interaction [3], and service-orientated architecture (SOA) [1]. In such environments, services often function as independent components, contributing to the overall functionality of the system. As a result, evaluating trust in these services is essential to maintaining system performance [4], response time and performance [5], security [6], and availability [7]. Of the quality characteristics mentioned, some researchers suggest approaches that are based on technical QoS characteristics and do not explicitly relate to user satisfaction or standards-based quality characteristics. Other researchers suggest trust models that depend on user ratings or feedback, which are often sparse, noisy, and influence the trust score, leading to uncertainty and unreliability [8,9,10]. These leave a gap between objective service performance and the perceived trustworthiness of WSs [11]. The subjective user experience is based on assigned weights for objective QoS characteristics, which are mapped according to the ISO/IEC 25010 [12] product quality standards. The trust value of cloud service providers is evaluated using a fuzzy inference-based analytical process.

The goal of this research is to propose a fuzzy-based multi-criteria decision-making approach for evaluating the trust score of web services. The proposed trust score–weighted model addresses uncertainty and subjective judgment in trust evaluation, allowing for more comprehensive assessments of web services. Therefore, the main scientific contributions of this paper are as follows:

• A novel theoretical trust score–weighted model that includes both objective quality-of-service and subjective user-oriented quality aspects that seamlessly integrates fuzzy logic with multi-criteria decision-making (MCDM) techniques by combining ISO/IEC 25010:2023 [13] product quality characteristics with quality-of-service measured characteristics.
• The proposed fuzzy decision-making approach enables the ranking and recommendation of trusted web services under uncertainty. The application of the suggested approach ensures the effective management of the imprecision and uncertainty inherent in both the service quality data and user perceptions.

As WSs become more complex and interconnected, there is a pressing need for trust evaluation models that not only rely on objective WS quality metrics but also consider user experience and satisfaction. Incorporating fuzzy logic into the evaluation process enables the handling of uncertainty in subjective assessments, making the proposed methodology highly relevant for practical applications.

The rest of this paper is structured as follows. Section 2 presents the related work on the evaluation of trust in WS trust. Section 3 presents the background of the theoretical trust score model and fuzzy-based models used for evaluating trust scores. Section 4 presents our proposed fuzzy-based MCDM approach. Section 5 demonstrates the use case of the newly proposed approach and the results obtained. Section 6 presents discussions and outlines future work. Finally, Section 7 provides conclusions.

2. Related Works

To support our proposed trust score evaluation, we conducted a review of related works to identify methods for trust assessment, highlight suggested solutions, and uncover gaps—particularly those related to user experience-based evaluations. Various trust evaluation techniques have been analysed, including fuzzy inference systems (FISs), MCDM methods, and machine learning (ML) classifiers. The scientific studies that best reflect the research area are presented in Table 1. These studies vary in focus from technical reliability and QoS classification to subjective user-based evaluation models. We analysed only research that very closely explored various fuzzy ways of establishing service trust. In our analysis, we excluded research that focused on studies of clustering or exploring the trustworthiness of ML or neural network services.

Table 1. Analysis of studies on WSs trust evaluation (WS—web service, psigmf—sigmoidal membership function, FIS—fuzzy inference system).

Source	Main Question	Method Used	Research Area	Non-Functional Criteria	Evaluation/ Verification	Result
[14]	WS failure reduction	Mamdani fuzzy inference	Fault tolerance	Reliability, failure rate, updating speed	Tested with various logic systems	More reliable and faster than alternatives
[15]	Trust evaluation of autonomous services	Neuro-fuzzy clustering	WS reliability	QoS, reliability, security	Neuro-fuzzy tests	Lowest RMSE using psigmf
[16]	Classification of QoS characteristics for ranking	Binary classification, cross-validation	QoS evaluation	Throughput, latency, performance	Confusion matrix-based accuracy	Custom method for user-oriented service ranking
[11]	Subjective trust evaluation	Fuzzy sets and user expectation modelling	Composite services	QoS, trust	Subjective fuzzy-based assessment	Effective for both simple and composite services
[17]	Lack of QoE-focused models	Blockchain + Fuzzy TOPSIS	QoE trust evaluation	Accessibility, availability, latency	Accuracy comparison with AHP and fuzzy TOPSIS	More accurate than AHP and F-TOPSIS
[18]	Trust via ML for time/throughput metrics	REPTree, J48, Logistic	ML-based trust ranking	Sensitivity, specificity, precision	ML classifiers were tested using Kappa statistics	WS1 has the highest trust, whereas WS2 has the lowest trust
[19]	Selection of the best service through MCDM	AHP, ANP, MCDM	Cloud computing	Availability, reliability, and response time	Comparative analysis of MCDM schemes	The best results with AHP in service filtering
[20]	Evaluation and ranking of cloud services	Fuzzy sets, Naïve Bayes, MARCOS, and random forest	Cloud service	QoS	MCDM and ML	Higher accuracy and robustness in trust-based cloud services
[10]	Fuzzy trust evaluation model	Rule-based FIS	Cloud service	Security, privacy, integrity, performance	Rule-based FIS with triangular membership functions	Increased efficiency in the evaluation of cloud services trust

These studies, briefly discussed in Table 1, explored a variety of approaches, such as fuzzy logic-based inference systems like Mamdani, TOPSIS, AHP, and ML; algorithms such as REPTree, and J48; and hybrid models combining multiple decision-making criteria. Several studies emphasised technical trust characteristics, such as latency, availability, and throughput, while others incorporated user-centred dimensions.

A noticeable trend in the literature is the growing use of the fuzzy-based MCDM approach. For instance, [14] employed a Mamdani FIS to reduce service failure rates, achieving higher performance compared to traditional models. Ref. [15] explored neuro-fuzzy clustering for trust modelling and obtained a low root mean square error (RMSE = 0.085) using MATLAB R2025a sigmoidal membership function psigmf, indicating high prediction precision.

Other studies focused on ML classifiers for trust prediction. Ref. [16] used binary classification and confusion matrices to evaluate services based on QoS metrics, while [18] expanded this by comparing REPTree, J48, and BayesNet classifiers on the WS-Dream dataset. These studies show the effectiveness of ML models in handling large-scale structured QoS data.

Studies provide a different perspective on subjective trust modelling. The authors of [11] proposed a trust evaluation method based on fuzzy set theory and user expectations, enabling a more personalised trust assessment. Similarly, [17] introduced a hybrid model based on blockchain and fuzzy TOPSIS, reporting accuracy improvements of up to 19.25% over traditional AHP.

In summary, fuzzy logic and MCDM-based approaches dominate the landscape of trust evaluation research, particularly in environments where uncertainty or subjective judgment plays a significant role. Although these methods demonstrate promising accuracy and flexibility, integrating QoE alongside QoS—a still underexplored area—is a valuable direction to extend trust evaluation models. Several studies [17,21] on QoE-aware cloud monitoring and QoS/QoE prediction demonstrate the importance of incorporating user-oriented quality, yet these models are not integrated into a hierarchical, ISO/IEC 25010-based trust score framework and typically employ a single fuzzy decision-making technique. In contrast, our research aims to bridge these gaps by conducting a trust search comparison between different fuzzy methods and testing them on a dataset that differs from those studied in the literature.

According to these observations, we propose a new approach to evaluate trust scores that relates objective QoS characteristics to ISO/IEC 25010:20203 [12] product quality characteristics, derives the weights from the QoE performance score related to QoS, and integrates multiple fuzzy MCDM methods

3. Background

3.1. Theoretical Trust Score Model

According to [5,6,11,22,23,24,25], the trust score evaluation model consists of objective QoS and subjective QoE characteristics. In SOAs where multiple services may offer similar functionalities, non-functional characteristics become the principal criteria for service selection and ranking.

The suggested trust score structure is designed by aligning the measurable web service QoS metrics with the product quality characteristics from ISO/IEC 25010 and drawing on empirical studies [26] that aggregate these indicators into a single trust/reputation value. The ISO/IEC 25010 describes the fundamental characteristics of quality, such as performance efficiency, reliability, and compatibility, which are assessed by measuring operationalised metrics, such as response time, latency, throughput, and availability (see leaves in Figure 1). The metrics included in the QWS dataset are essential for evaluating the quality of WS selection and ranking, which are often used in similar research [27,28,29].

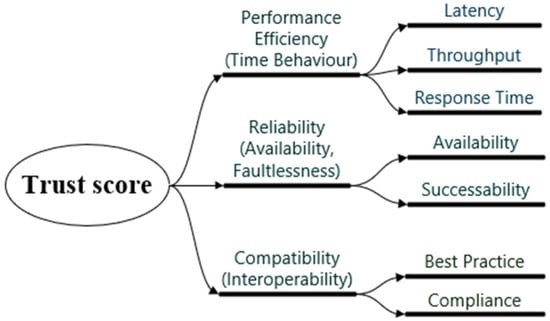
Figure 1. The theoretical trust score tree.

The trust models for cloud and web services compute one trustworthiness value by normalising and weighting these QoS dimensions—via fuzzy logic or multi-criteria aggregation—for provider evaluation, composition, and recommendation; we follow the same evidence-driven aggregation pattern in our trust score evaluation.

The multiple trust models in services and/or cloud computing [10,30] compute a single trust value by aggregating QoS characteristics (e.g., availability, response time, throughput, and related reliability indicators) using probabilistic, fuzzy, or multi-criteria aggregation—precisely the aggregation we perform using branch scores to determine a unified trust score for provider evaluation, composition, and recommendation. In our research, we follow the same evidence-based aggregation pattern in our trust score.

Quality of service refers to service-level operational metrics that are observable by end users or clients at runtime and can be measured. The ISO/IEC 25010 describes the quality of the product service at the highest level. Quality of service metrics are related and indicate the operationalisation of the specific ISO/IEC 25010 quality characteristics (performance efficiency, compatibility, and reliability), sub-characteristics (time behaviour, availability, faultlessness, and interoperability), which are measured using QoS metrics such as latency, throughput, response time, availability, successability, best practices, and compliance. These relations are presented in Figure 1.

The trust score value tree may vary depending on the application domain and the usage context of the WS.

The proposed trust score model is user-aware because the effects of QoS characteristics are derived from their empirically measured impact on the QoE. As a result, it constructs a hierarchical trust score–weighted tree, which uses implication rules and fuzzy inference from bottom to top. The values of QoS characteristics directly influence user satisfaction, thereby shaping the weight of each branch in the trust score tree.

3.2. Fuzzy-Based Models for Trust Evaluation

According to [31], trust is based on subjective judgments. Subjective judgments, in turn, are derived from user experience, and often this experience is taken for granted as being correct. The following prerequisites are necessary for the evaluation of trust: (1) trust evaluation is based on a set of observations, including user experience and evidence; (2) different experiences and evidence have different effects on trust; (3) trust has scales, meaning that trust is comparable; (4) the more reliable the available evidence, the more reliable the trust score.

The authors of [31] state that there are two types of trust derived from user experience: direct trust (based on the user’s experience) and recommendation trust (based on the experiences of others). For direct trust, trust builds up over time due to repeated interactions between the trustor and trustee. Reputation can be defined as a measure of an individual’s trustworthiness based on recommendations or ratings from other community members.

4. Fuzzy-Based MCDM Approach

In this section, we describe the fuzzy-based MCDM approach for predicting the trust score of WSs under uncertainty as a composite methodological pipeline that relates ISO/IEC 25010 quality characteristics with measurable QoS metrics extracted from the QWS dataset and subjective user perceptions. The general conceptual workflow is summarised in the principal scheme presented in Figure 2.

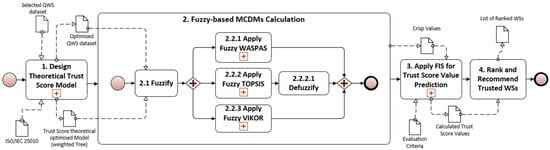
Figure 2. The principal scheme of the fuzzy-based MCDM approach for predicting trust scores.

The suggested fuzzy-based MCDM approach (see Figure 1) consists of the following steps:

1. Design the Theoretical Trust Score Model. The detailed explanation of the expanded sub-process is presented in Figure 3.

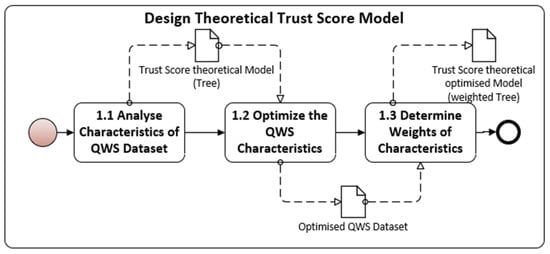
Figure 3. Expanded sub-process used in the fuzzy-based MCDM approach.

A more detailed description is presented as follows:

1.1. Analyse the characteristics of the QWS dataset.

The research starts with dataset selection and pre-processing, where raw QoS characteristics are cleaned, normalised, and transformed to ensure comparability across services. The first process of the proposed approach involves designing a theoretical trust score model (see Section 3.1) that relates the ISO/IEC 25010:2023 product quality characteristics to the measurable characteristics available in the QWS dataset.

1.2. Optimise the QWS characteristics. The QWS characteristics are first analysed and mapped to the relevant product quality characteristics. Optimisation is based on Spearman’s correlation coefficient; comparison of the QWS characteristics is performed to identify a strong, weak, or negative correlation. Optimisation indicates the removal of one of the characteristics with a strong positive correlation. The trust score values obtained by applying fuzzy WASPAS, fuzzy TOPSIS, and fuzzy VIKOR are analysed using Spearman’s (Equation (1)) correlation coefficients, which measure non-linear relationships.

$$R_{xy}^{Spearman}={\displaystyle \frac{{\sum }_{i=1}^n\left(R\left(x_i\right)-{\overline{R}}_x\right)\left(R\left(y_i\right)-{\overline{R}}_y\right)}{\sqrt{{\sum }_{i=1}^n{\left(R\left(x_i\right)-{\overline{R}}_x\right)}^2}\sqrt{{\sum }_{i=1}^n{\left(R\left(y_i\right)-{\overline{R}}_y\right)}^2}}},$$

(1)

where $R\left(x_i\right)$ and $R\left(y_i\right)$ are the ranks of $x_i$ and $y_i$, respectively; ${\overline{R}}_x$ and ${\overline{R}}_y$ are the mean ranks of X and Y; and n denotes the sample size.

1.3. Determine the weights of the characteristics.

The determination of characteristic weights is based on values derived from the QoE performance values, which were modelled in our previous research [21]. The QoS characteristics are evaluated using the Pearson correlation coefficient with the corresponding QoE performance values obtained through the fuzzy control system. The absolute values of these correlation coefficients are then normalised so that they sum up to one, resulting in a weight vector that reflects the relative influence of each value of QoS performance on QoE performance. Our suggested modelling approach yields a weighted trust score model, where the importance of each characteristic is explicitly based on its measured contribution to the resulting QoE.

2. Fuzzy-based MCDM Calculation. The main idea of fuzzy WASPAS (weighted aggregated sum product assessment under fuzzy environment), fuzzy TOPSIS (technique for order of preference by similarity to ideal solution under fuzzy environment), and fuzzy VIKOR (VlseKriterijumska Optimizacija I Kompromisno Resenje under fuzzy environment) is to extend the traditional WASPAS, TOPSIS, and VIKOR methods by incorporating fuzzy logic to handle uncertainty and vagueness in decision-making [32]. It is especially useful when the decision-making criteria or ratings are not crisp but rather uncertain or imprecise.

2.1. Fuzzify. In this step, each linguistic term (High, Moderate, Low) of each QoS characteristic, such as Throughput or Latency, can be represented by a triangular fuzzy number $\tilde{A}=(l,m,u)$, where l is the lower bound, m is the modal value, and u is the upper bound. The triangular membership function $\mu \left(x\right)$ for $\tilde{A}$ of crisp value x is defined as follows (Equation (2)):

$${\mu }_{\tilde{A}}\left(\mathrm{x}\right)=\left\{\begin{array}{c}\begin{array}{cc}0,& x\le l,\\ {\displaystyle \frac{x-1}{m-l}},& l<x\le m,\end{array}\\ {\displaystyle \frac{u-x}{u-v}},m<x<u,\\ \begin{array}{cc}0,& x\ge u.\end{array}\end{array}\right.$$

(2)

2.2.1. Apply fuzzy WASPAS. After fuzzification, the first fuzzy-based MCDM method, fuzzy WASPAS, is applied to calculate crisp values, which will be further used to determine the trust score value of the WSs. According to [32], fuzzy WASPAS can be represented by the following steps:

Define a decision matrix (DM) X of size $i\times j$ consisting of triangular fuzzy numbers

$x_{ij}$ (Equation (3)):

$$X=\left[\begin{array}{ccc}\left[\begin{array}{c}{x}_{11}^{lb},x_{11}^{mv},x_{11}^{ub}\\ x_{21}^{lb},x_{21}^{mv},x_{21}^{ub}\end{array}\right]& \dots & \left[\begin{array}{c}{x}_{1n}^{lb},x_{1n}^{mv},x_{1n}^{ub}\\ x_{2n}^{lb},x_{2n}^{mv},x_{2n}^{ub}\end{array}\right]\\ ⋮& \ddots & ⋮\\ \left[x_{m1}^{lb},x_{m1}^{mv},x_{m1}^{ub}\right]& \dots & \left[x_{mn}^{lb},x_{mn}^{mv},x_{mn}^{ub}\right]\end{array}\right],$$

(3)

where i is the number of alternatives being evaluated and j is the number of evaluation criteria in fuzzy DM, and where lb represents the lower bound, mv—the modal or most likely value, and ub—the upper bound value of $x_{ij}$.

Normalise the fuzzy DM by $max{\tilde{x}}_{ij}$ (Equation (4)) or $min{\tilde{x}}_{ij}$ (Equation (5)):

$${\tilde{\overline{x}}}_{ij}={\displaystyle \frac{{\tilde{x}}_{ij}}{max{\tilde{x}}_{ij}}},$$

(4)

$${\tilde{\overline{x}}}_{ij}={\displaystyle \frac{min{\tilde{x}}_{ij}}{{\tilde{x}}_{ij}}},$$

(5)

where $i=\overline{1,m}$ and $j=\overline{1,n}$ define row and column indexes, respectively, of fuzzy number ${\tilde{x}}_{ij}$ in fuzzy DM at position (i, j). ${\tilde{\overline{x}}}_{ij}$ is the normalised fuzzy value corresponding to ${\tilde{x}}_{ij}$.

Calculate the fuzzy matrix for the weighted sum model (WSM) (Equation (6)) and the weighted product model (WPM) (Equation (7)):

$${{\tilde{\widehat{x}}}_{ij}}^{WSM}={\tilde{\overline{x}}}_{ij}{\tilde{w}}_{j,}i=\overline{1,m},j=\overline{1,n},$$

(6)

$${{\tilde{\widehat{x}}}_{ij}}^{WPM}={{\tilde{\overline{x}}}_{ij}}^{{\tilde{w}}_j},i=\overline{1,m},j=\overline{1,n},$$

(7)

$${\tilde{Q}}_i={\sum }_{j=1}^n{{\tilde{\widehat{x}}}_{ij}}^{WSM},i=\overline{1,m},$$

(8)

$${\tilde{R}}_i={\prod }_{j=1}^n{{\tilde{\widehat{x}}}_{ij}}^{WPM},i=\overline{1,m},$$

(9)

where ${\tilde{Q}}_i$ and ${\tilde{R}}_i$ are the fuzzy numbers and where the middle areas $Q_i$ (Equation (10)) and $R_i$ (Equation (11)) in defuzzification are calculated as follows:

$$Q_i={\displaystyle \frac{1}{3}}\left(Q_{i\alpha }+Q_{i\beta }+Q_{i\gamma }\right).$$

(10)

$$R_i={\displaystyle \frac{1}{3}}\left(R_{i\alpha }+R_{i\beta }+R_{i\gamma }\right).$$

(11)

Calculate the value of integrated utility $K_i$ of each alternative i (Equation (12)):

$$K_i=\lambda \sum _{j=1}^m{Q}_1+\left(1-\lambda \right)\sum _{j=1}^m{R}_i,\lambda =0,\dots ,\mathrm{1,0}\le K_i\le 1$$

(12)

where $Q_i$ is the WSM-based (additive) and $R_i$ is the WPM-based (multiplicative) score of alternative i. $\mathsf{\lambda }$ is the balancing coefficient that controls the relative influence of WSM vs. WPM in the final score (Equation (13)):

$$\lambda ={\displaystyle \frac{{\sum }_{i=1}^m{R}_i}{{\sum }_{i=1}^m{Q}_i+{\sum }_{i=1}^m{R}_i}}$$

(13)

For defuzzification of the obtained integrated utility function ${\tilde{K}}_i=\left(K_i^{lb},K_i^{mv},K_i^{ub}\right)$, use Equation (14):

$$Crisp\left({\tilde{K}}_i\right)={\displaystyle \frac{2K_i^{mv}+K_i^{lb}+K_i^{ub}}{4}}.$$

(14)

2.2.2. Apply fuzzy TOPSIS. The second fuzzy-based MCDM method is applied for crisp value calculation. According to [32], fuzzy TOPSIS can be represented by the following steps:

Define DM, which consists of the membership function ${\mu }_A\left(x\right)$ of fuzzy set $A$ on a universe of discourse X (Equation (15)). The entry ${\widehat{x}}_{ij}$ of the fuzzy DM consists of triangular fuzzy numbers (Equation (16)).

$$A=\left\{x,{\mu }_A\left(x\right):x\in X,{\mu }_A\left(x\right)\in ⟨\mathrm{0,1}⟩\right\},$$

(15)

$${\widehat{x}}_{ij}=\left(a_{ij},b_{ij},c_{ij}\right),$$

(16)

where $a_{ij}$, $b_{ij}$, and $c_{ij}$ are the pessimistic (lower bound), the most likely (modal), and the optimistic (upper bound) fuzzy numbers, respectively.

Normalise the DM using the benefit criterion ${\widehat{z}}_{ij}$ (Equation (17)) and cost-type criterion (Equation (18)) and assign the weights (Equation (19)).

$${\widehat{z}}_{ij}=\left({\displaystyle \frac{a_{ij}}{{max}_i{c}_{ij}}},{\displaystyle \frac{b_{ij}}{{max}_i{c}_{ij}}},{\displaystyle \frac{c_{ij}}{{max}_i{c}_{ij}}}\right),i\in I,j=1,\dots ,n,$$

(17)

$${\widehat{z}}_{ij}=\left({\displaystyle \frac{{min}_i{a}_{ij}}{c_{ij}}},{\displaystyle \frac{{min}_i{a}_{ij}}{b_{ij}}},{\displaystyle \frac{{min}_i{a}_{ij}}{a_{ij}}}\right),i\in J,j=1,\dots ,n,$$

(18)

$${\widehat{r}}_{ij}=w_j\otimes {\widehat{z}}_{ij},i=1,\dots ,m;j=1,\dots ,n,$$

(19)

where ${\widehat{z}}_{ij}$ is the normalised triangular fuzzy rating by ${max}_i{c}_{ij}$ (maximum optimistic value over all alternatives for criterion j) or ${min}_i{a}_{ij}$ (minimum pessimistic value over all alternatives for criterion j). ${\widehat{r}}_{ij}$ is the weighted normalised triangular fuzzy rating.

Determine the ideal $A^{+}$ (Equation (20)) and anti-ideal $A^{-}$ (Equation (21)) solutions:

$$A^{+}=\left({\widehat{v}}_1^{+},{\widehat{v}}_2^{+},\dots ,{\widehat{v}}_n^{+}\right)=\left({max}_i{\widehat{r}}_{i1},{max}_i{\widehat{r}}_{i2},\dots ,{max}_i{\widehat{r}}_{in}\right),$$

(20)

$$A^{-}=\left({\widehat{v}}_1^{-},{\widehat{v}}_2^{-},\dots ,{\widehat{v}}_n^{-}\right)=\left({min}_i{\widehat{r}}_{i1},{min}_i{\widehat{r}}_{i2},\dots ,{min}_i{\widehat{r}}_{in}\right),$$

(21)

where ${\widehat{v}}_{\mathrm{j}}^{+}$ is the ideal (best) fuzzy value and ${\widehat{v}}_{\mathrm{j}}^{-}$ is the anti-ideal (worst) fuzzy value obtained as the fuzzy maximum or minimum over all ${\widehat{r}}_{i\mathrm{j}}$ for fixed j, respectively.

Calculate the distance of the alternative from the ideal $dp\left(\widehat{A},{\widehat{A}}^{+}\right)$ (Equation (22)) and anti-ideal $dp\left(\widehat{A},{\widehat{A}}^{-}\right)$ (Equation (23)) solution:

$$dp\left(\widehat{A},{\widehat{A}}^{+}\right)=\sqrt{{\displaystyle \frac{1}{3}}\left({\left(a_1-a_2^{+}\right)}^2+{\left(b_1-b_2^{+}\right)}^2+{\left(c_1-c_2^{+}\right)}^2\right)},$$

(22)

$$dp\left(\widehat{A},{\widehat{A}}^{-}\right)=\sqrt{{\displaystyle \frac{1}{3}}\left({\left(a_1-a_2^{-}\right)}^2+{\left(b_1-b_2^{-}\right)}^2+{\left(c_1-c_2^{-}\right)}^2\right)},$$

(23)

where $\widehat{A}$ is the aggregated fuzzy value by triangular fuzzy numbers ($a_1,b_1,c_1)$, ${\widehat{A}}^{+}$ is the fuzzy ideal value obtained by the pessimistic, most likely, and optimistic components $(a_2^{+},b_2^{+},c_2^{+})$ of the ideal fuzzy value $A^{+}$. ${\widehat{A}}^{-}$ is the triangular fuzzy anti-ideal value defined by pessimistic, most likely, and optimistic components $\left(a_2^{-},b_2^{-},c_2^{-}\right)$ of the anti-ideal fuzzy value $A^{-}$.

Calculate a closeness coefficient, $C_i$, for each alternative i (Equation (24)):

$$C_i={\displaystyle \frac{dp({\widehat{A}}_i,{\widehat{A}}^{-})}{dp\left({\widehat{A}}_i,{\widehat{A}}^{+}\right)+dp({\widehat{A}}_i,{\widehat{A}}^{-})}},0\le C_i\le 1.$$

(24)

Define the triangular fuzzy closeness index ${\tilde{N}}_i$ for each alternative i as presented in Equation (25):

$${\tilde{N}}_i=\left(l_i,m_i,r_i\right),$$

(25)

where $l_i$ is a pessimistic closeness value, $m_i$ is the most representative closeness value, and $r_i$ is an optimistic closeness value of fuzzy closeness index ${\tilde{N}}_i$.

2.2.2.1. Defuzzify. The defuzzification step is introduced for consistency with other fuzzy MCDM approaches such as fuzzy VIKOR and fuzzy WASPAS. The defuzzified (crisp) score $Crisp\left({\tilde{N}}_i\right)$ for alternative i is calculated using Equation (26):

$$Crisp\left({\tilde{N}}_i\right)=(2m_i+l_i+r_i)/4.$$

(26)

2.2.3. Apply fuzzy VIKOR. According to [32], fuzzy VIKOR can be represented by the following steps:

Define a fuzzy DM X of size $m\times n$ which consists of the triangular fuzzy numbers (Equation (27)):

$$X=\left[\begin{array}{c}{\tilde{f}}_{11}{\tilde{f}}_{12}\dots {\tilde{f}}_{1n}\\ {\tilde{f}}_{21}{\tilde{f}}_{22}\dots {\tilde{f}}_{2n}\\ \dots \dots \dots \dots \\ {\tilde{f}}_{m1}{\tilde{f}}_{m2}\dots {\tilde{f}}_{mn}\end{array}\right],$$

(27)

where ${\tilde{f}}_{\mathrm{i}\mathrm{j}}$ is the triangular fuzzy rating of alternative i under criterion j $(i=1,\dots ,m,j=1,\dots ,n)$.

Calculate the positively ideal ${\tilde{f}}_i^{\ast }$ and negatively ideal ${\tilde{f}}_i^{\circ }$ values for all criterion values (see Equations (28) and (29)):

$${\tilde{f}}_i^{\ast }={max}_j{\tilde{f}}_{ij,}{\tilde{f}}_i^{\circ }={min}_j{\tilde{f}}_{ij},fori\in I^b,$$

(28)

$${\tilde{f}}_i^{\ast }={min}_j{\tilde{f}}_{ij,}{\tilde{f}}_i^{\circ }={max}_j{\tilde{f}}_{ij},fori\in I^c,$$

(29)

where ${\tilde{f}}_{ij}$ is the triangular fuzzy value of alternative j under criterion I, $I^b$ is a set of benefit-type criteria (larger is better), and $I^c$ is a set of cost-type criteria (smaller is better).

Compute the normalised fuzzy difference ${\tilde{d}}_{ij}$ (Equation (30)):

$${\tilde{d}}_{ij}={\displaystyle \frac{\left({\tilde{f}}_i^{\ast }\ominus {\tilde{f}}_{ij}\right)}{\left(r_i^{\ast }-l_i^{\circ }\right)}}fori\in I^b;{\tilde{d}}_{ij}={\displaystyle \frac{\left({\tilde{f}}_{ij}\ominus {\tilde{f}}_i^{\ast }\right)}{\left(r_i^{\circ }-l_i^{\ast }\right)}}fori\in I^c,$$

(30)

where ${\tilde{f}}_{ij}$ is the triangular fuzzy performance value; $\ominus$ means fuzzy substraction between triangular fuzzy numbers; $l_i^{\circ }$ and $r_i^{\circ }$ are the left and right endpoints of the ideal fuzzy value ${\tilde{f}}_i^{\circ }$; and $l_i^{\ast }$ and $r_i^{\ast }$ are the left and right endpoints of the ideal fuzzy value ${\tilde{f}}_i^{\ast }$.

Calculate the fuzzy weighted sum $\tilde{S}$ (Equation (31)) and the fuzzy weighted max $\tilde{R}$ (Equation (32)):

$${\tilde{S}}_j={\sum }_{i=1\oplus }^n\left({\tilde{w}}_i\otimes {\tilde{d}}_{ij}\right),$$

(31)

$${\tilde{R}}_j={max}_i\left({\tilde{w}}_i\otimes {\tilde{d}}_{ij}\right),$$

(32)

where ⊗ is fuzzy multiplication between a fuzzy weight ${\tilde{w}}_i$ and normalised fuzzy difference ${\tilde{d}}_{ij}$.

Calculate the fuzzy VIKOR index value $\tilde{Q}$ of alternative j (overall compromise measure) (Equation (33)):

$${\tilde{Q}}_j={\displaystyle \frac{v\left({\tilde{S}}_j^o⊝{\tilde{S}}^{\ast }\right)}{\left(S^{or}-S^{\ast l}\right)}}\oplus {\displaystyle \frac{\left(1-v\right)\left({\tilde{R}}_j^o⊝{\tilde{R}}^{\ast }\right)}{\left(R^{or}-R^{\ast l}\right)}},$$

(33)

where $v\in [0,1]$ is the strategy weight (closer to 1 means more emphasis on group utility (${\tilde{S}}_j$) and closer to 0 means more emphasis on individual regret (${\tilde{R}}_j$). $S^{or}$ is the right endpoint of the worst ${\tilde{S}}^o$ (fuzzy worst (anti-ideal) value of S), and $S^{\ast l}$ is the left endpoint of the best ${\tilde{S}}^{\ast }$ (fuzzy best (ideal) value of S over all alternatives). $R^{\ast l}$ and $R^{or}$ are the left and right endpoints of ${\tilde{R}}^{\ast }$ (fuzzy best (ideal) value of R) and ${\tilde{R}}^o$ (fuzzy worst (anti-ideal) value of R).

In descending order, rank the alternatives according to the base values $Q_j^m,j=\mathrm{1,2},\dots ,J$.

Create the fuzzy ranking of the j-th $A_{Q^m}$ alternative $A^{\left(j\right)};j=1,\dots ,J$ is confirmed if ${min}_{k\in J^j}{\tilde{Q}}^k={\tilde{Q}}^j$, where $J^j=j,j+1,\dots ,J$ and ${\tilde{Q}}^{\left(k\right)}$ is the fuzzy metric for the alternative $A^{\left(k\right)}$ located at the k-th position in the set $A_{Q^m}$.

Deffuzify ${\tilde{S}}_j$, ${\tilde{R}}_j$, ${\tilde{Q}}_j,j=\mathrm{1,2},\dots ,J$ (Equation (34)):

$$Crisp\left({\tilde{N}}_i\right)=(2m_i+l_i+r_i)/4,$$

(34)

where $\tilde{N}$ is the fuzzy closeness coefficient standing for ${\tilde{S}}_j$, ${\tilde{R}}_j$, or ${\tilde{Q}}_j$ for alternative j and defined by $l,m,andr$, which are the left (pessimistic) value of triangular fuzzy number, middle (most likely) value, and right (optimistic) value, respectively.

3. Apply FIS for Trust Score Value Prediction. The crisp values achieved from thefuzzy-based MCDMs are inferred using the fuzzy inference system (FIS) to predict the trust score values of WSs. According to [33], a classical FIS is used to evaluate the trust score values (see Figure 4).

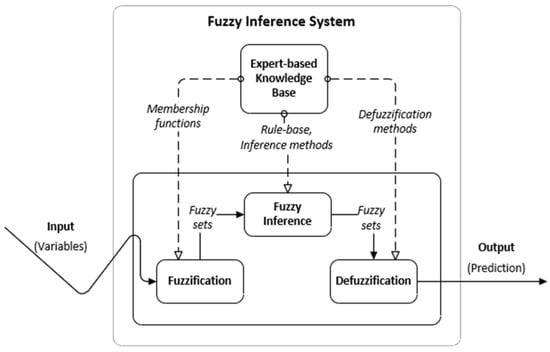
Figure 4. The general schema of a fuzzy inference system (FIS).

This FIS consists of the following parts: Fuzzification—crisp input values conversion into fuzzy values using a particular fuzzification method. Fuzzy Inference—fuzzy “if-then” rules are applied from the Knowledge Base to simulate human thinking. Defuzzification—fuzzy values conversion to crisp values using a particular defuzzification method. Expert-Based Knowledge Base—the storage of fuzzification methods, fuzzy rules for inferencing, and defuzzification methods.

4. Rank and Recommend Trusted WSs. Applying a fuzzy-based MCDM approach for trust evaluation of WSs, the deffuzified values are ranked to obtain a list of the best-ranked and recommended WSs by linguistic terms.

5. Case Study and Results

In this case study, we used the QWS dataset (https://qwsdata.github.io/ (accessed on 12 October 2024) [34], which consists of nine characteristic values for 2507 different WSs. Since the dataset itself is quite old and is likely no longer maintained, to determine the actual WSs that might be considered trustworthy, we excluded those services that had missing or incomplete values before searching for reliable WSs. After applying the data cleaner module of the practical application, more than 300 WS were removed from the original dataset.

A pairwise correlation analysis between the main non-functional (QoS) characteristics in the QWS dataset, using Spearman’s (rank-based) correlation method, was applied to the selected WSs.

Spearman’s correlation was chosen because of its ability to measure monotonic, not just linear, relationships between different values. Also, as this is a rank-based approach, it is often used to compare the effectiveness of each fuzzy method. Calculation results are given in the table below (see Table 2). The intensity of the grey colour of the cell indicates the strength of the correlation: the more intense the grey colour, the stronger the Spearman’s correlation results. The white colour of the cell demonstrates a very weak correlation.

Table 2. Spearman’s correlation results of the QWS dataset.

	Resp. Time	Availability	Throughput	Successability	Reliability	Compliance	Best Practices	Latency
Resp. Time	1	0.0962	0.9791	0.0221	0.2712	0.0103	−0.083	0.0552
Availability	0.096	1	0.1071	0.2558	−0.008	0.1666	−0.284	−0.025
Throughput	0.979	0.1071	1	0.0221	0.2903	0.0221	−0.11	0.0706
Successability	0.022	0.2558	0.0221	1	−0.035	0.734	−0.211	0.0414
Reliability	0.271	−0.008	0.2903	−0.035	1	0.0268	−0.019	−0.028
Compliance	0.01	0.1666	0.0221	0.734	0.0268	1	−0.218	−0.024
Best Practices	−0.08	−0.284	−0.11	−0.211	−0.019	−0.218	1	−0.102
Latency	0.055	−0.025	0.0706	0.0414	−0.028	−0.024	−0.102	1

As can be seen from the results, most characteristics have a weak or a negative correlation. Response time vs. throughput (0.9791) characteristics have a quite strong positive correlation. As it makes no sense to compare those characteristics that correlate strongly, one of the characteristics was removed from the research. To sum up, Spearman’s correlation results indicate that QoS values can be compared so that the best-performing and most trusted WSs that exist in a provided dataset can be located.

Determined by the ISO/IEC 25010 [26] and the correlation calculation (see Table 2), the trust score tree used for this case study is presented in Figure 5.

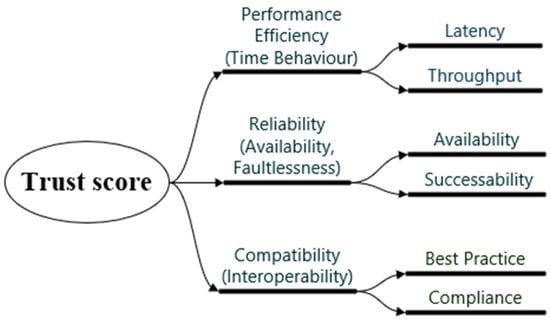
Figure 5. The theoretical trust score tree used for the case study.

The FIS model, modelled in MATLAB Simulink, for trust score valuation is presented in Figure 6.

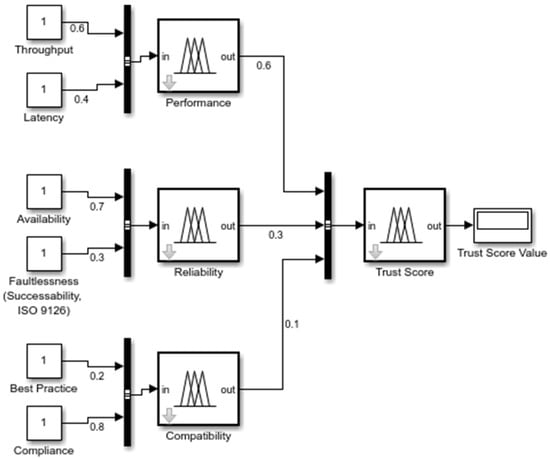
Figure 6. The scheme of the trust score tree, which was applied in FIS for simulation [35].

In this study, based on the results in Table 2, we utilised only the characteristics highlighted in Figure 2. Fuzzy weights were calculated for each criterion to rank the alternatives when applying fuzzy methods to determine the actual trust score. Since not all criteria are equally important, we used fuzzy weights in the calculation process to assign importance to each criterion.

The results provide insight into how different QoS metrics are interrelated, as shown in the table below (see Table 3).

Table 3. QoS characteristics for calculating the trust score.

QoS Characteristics	Description	Units	Weights	Linguistic Term	Centroid Value	Crisp Value Range
Availability	Number of successful invocations/total invocations	%	0.7	High	83.33	67–100
				Low	16.67	0–33
				Medium	50.0	34–66
Best Practices	The extent to which a WS follows the WS-I Basic Profile	%	0.2	High	83.33	67–100
				Low	16.67	0–33
				Medium	50.0	34–66
Latency	Time taken for the server to process a given request	ms	0.4	Fast	333.33	0–1000
				Medium	2166.67	1001–3000
				Slow	4333.33	3001–5000
Compliance	The extent to which a WSDL document follows the WSDL specification	%	0.8	High	83.33	67–100
				Low	16.67	0–33
				Medium	50.0	34–66
Throughput	Total number of invocations in the given period	invokes/s	0.6	Fast	1667	1334–2000
				Medium	1000.5	668–1333
				Slow	333.33	0–667
Successability	Number of responses/number of request messages	%	0.3	High	83.33	67–100
				Low	16.67	0–33
				Medium	50.0	34–66

In Table 4, we present some intermediate calculations based on the trust score value for WSs in the dataset when aggregating QoS attribute values [28]. When the trust score is known for each WS, it is normalised based on fuzzy techniques by applying the WASPAS, TOPSIS, and VIKOR methods to determine the trust level of each WS.

Table 4. Trust score values calculation.

Performance	Successability	Dependability	Trust Score Value
0.687948	0.669154	0.755053	0.721501
0.759912	0.877778	0.810258	0.785085
0.455502	0.669154	0.755053	0.605278
0.751100	0.691376	0.759005	0.755052
0.671233	0.551244	0.708582	0.689907
0.672874	0.691376	0.694489	0.683681
0.658032	0.855556	0.813731	0.735881

After trust score value normalisation, the WS trust score values were calculated using the fuzzy-based MCDM approach (see Table 5) [36].

Table 5. Part of the calculated trust score values using fuzzy WASPAS, fuzzy VIKOR, and fuzzy TOPSIS.

Trust Score Values
Fuzzy WASPAS	Fuzzy TOPSIS	Fuzzy VIKOR
0.759912	0.602752	0.296738
0.788744	0.768492	0.208536
0.592328	0.548365	0.509682
0.756788	0.730958	0.244604
0.682472	0.661639	0.322376
0.689944	0.650937	0.337846
0.736098	0.739709	0.296540

From Table 4, we can observe that fuzzy WASPAS (mean ≈ 0.72) and fuzzy TOPSIS (mean ≈ 0.67) yield relatively high trust scores, whereas fuzzy VIKOR has lower values (mean ≈ 0.32). In summary, all three methods capture a similar underlying trust pattern but express it on different scales.

As a final step in evaluating the WS trust score, we needed to rank the most trusted WSs. A few trusted services were predicted using FIS after the application of a fuzzy-based MCDM approach for trust score evaluation and are presented in Table 6.

Table 6. The ranked WSs example by trust score values (fragment).

Service Name “URLs (accessed on 12 October 2024)”	Trust Score Value			Decision of Trustiness
	Fuzzy WASPAS	Fuzzy TOPSIS	Fuzzy VIKOR
espcolour.co.uk (http://web1.espcolour.co.uk/sbswebservicetest/sbswebservice.asmx?wsdl)	Medium (0.382245)	High (0.848835)	High (0.667785)	Strongly trusted
SOAPCLIENT.COM (http://soapclient.com/interop/doclitparam.wsdl)	Medium (0.554546)	High (0.833278)	Medium (0.501580)	Medium trusted
services.edneeis.com (http://services.edneeis.com/ErrorReporting.asmx?wsdl)	Low (0.265273)	Medium (0.619798)	Medium (0.619798)	Medium trusted

Finally, after all WSs were ranked by their level of trust, system users could generate a comprehensive service recommendation label. Using FIS, the trust score decision regarding WS trustworthiness was determined by partitioning the fuzzy-based MCDM approaches into three terms: “High”, “Medium”, and “Low”. The labels describe what kind of WS is achieved—“Strongly trusted”, “Medium trusted” or “Low trusted”. WS ranked lists with labels may be used in practice; for instance, they can be shared with WS developers, which can lead to improved WS quality characteristics, user trust, and user satisfaction.

6. Discussions and Future Works

This empirical experiment relied on the publicly available QWS dataset, which was collected on 1 November 2019 and contains data on 2507 real web services. The amount of data and QoS characteristics were sufficient to validate our proposed approach. However, a limitation of our experiment was that the data on the characteristics could be newer and better reflect today’s WS data instances. To obtain the most recent data on web service quality, we begin gathering a new dataset. To date, our collected dataset comprises over 1200 WSs. The results of applying our collected dataset to validate our proposed approach would not have been reliable because there is not enough data. Lack of data can distort the theoretical optimisation model construction of the trust score. This was the primary reason we utilised the oldest QWS dataset, ensuring that our proposed trust score model would be reliable and robust.

Another limitation of our trust score optimisation model (weighted model) is that it infers user expectations indirectly from QoS and QoE performance scores using our proposed modelling methodology [21]. The proposed approach is methodologically reproducible, but it may not fully capture domain-specific preferences, different contexts, or evolving user behaviours.

Future work will involve completing the collection of our new dataset and publishing it with the hope that it will be extended by other interested scientists in the future.

7. Conclusions

Through a comprehensive review of related works, it was observed that while numerous studies focus on trust evaluation using traditional technical metrics, few address the challenge of incorporating subjective user experience into the trust evaluation framework. This gap motivated us to develop a fuzzy-based MCDM approach for WS trust score evaluation that integrates QoS characteristics related to ISO/IEC 25010:2023 product quality characteristics and considers user expectations. To address the mentioned gap, the proposed approach utilizes fuzzy set theory combined with multi-criteria decision-making (MCDM) techniques—namely fuzzy TOPSIS, fuzzy WASPAS, and fuzzy VIKOR—to model trust under conditions of uncertainty and incomplete information. These methods enable the translation of linguistic and imprecise judgments into quantifiable trust scores, supporting more user-aware decision-making. The proposed approach’s case study results confirm that the fuzzy-based MCDMs approach effectively supports the ranking and recommendation of web services using our suggested trust score optimisation model in the presence of imprecision and uncertainty in both service quality data and user perception.

In the future, we plan to explore the integration of machine learning techniques for dynamic weight adjustment, real-time trust evaluation, and the extension of the newly constructed dataset to include more working WSs.