A Multi-Objective Formulation for the Internet Shopping Optimization Problem with Multiple Item Units

Abstract

The Internet Shopping Optimization Problem with multiple item Units looks for the best selection of stores where to buy various or individual units in a required list of items to minimize the final purchase cost. The problem belongs to the most challenging complexity class of optimization problems (NP-Hard). This paper adds to the already complex problem a more difficult situation with a second objective conflicting with the purchase cost minimization. As far as we know, this is the first state-of-the-art proposal with conflicting objectives for the Internet Shopping Optimization Problem or its variants. The objective in conflict with the minimization of the purchase final cost is the cash-back or reward points on personal or corporate credit cards, the most common payment method for online purchases. Due to the nature of the conflicting objectives, this paper proposes using evolutionary multi-objective optimization algorithms. We perform an experimental comparison using eight algorithms from the literature. The experimental results show that NSGA-II achieves the best overall performance for the studied instances from the state of the art.

1. Introduction

Currently, in the state of the art, a multi-objective formulation has not been developed to address the recently proposed problem of online purchasing with multiple units per product, known as the Internet Shopping Optimization Problem with multiple item Units (ISHOP-U). An obvious scenario is presented where the objective of minimizing the cost of purchases is faced with another objective in conflict, which consists of maximizing the benefits by total spending. Credit cards and companies usually offer points or cash bonuses in proportion to the cost of purchases made. This paper proposes to formulate the problem so that the total cost of purchases is minimized while maximizing the benefits in points per purchase. The problem of optimizing online purchases with multiple units per item proves to be an NP-Hard problem [1]. Therefore, no computationally efficient algorithms can solve it classically in polynomial time in a deterministic way. The online shopping optimization challenge with multiple units of items, called ISHOP-U, seeks to find the best stores to purchase a required list of items, either in multiple units or individually, to minimize the total purchase cost. This problem, classified as NP-Hard [1,2,3], represents one of the most complex categories in terms of optimization; adding a second objective that conflicts with minimizing purchasing costs is another challenge. This pioneering proposal is the first to introduce contradictory objectives into the Internet Shopping Optimization Problem or its variations. The objectives in conflict are minimizing the purchase cost and maximizing the cash-back or reward points on personal or corporate credit cards, the most common payment method for online purchases. Given these conflicting objectives, a set of eight algorithms specialized in multi-objective optimization are used (AGEMOEA, AGEMOEA2, GWASFGA, MOCell, MOMBI, MOMBI2, NSGA-II [4,5,6], SMS-EMOA). The experimental results illustrate that NSGA-II generates the best Pareto front approximations with uniform linear dispersion for ISHOP-U instances in the current state of the art, which supports addressing it as a multi-objective optimization problem.

Although some bi-objective formulations appear in the literature [7,8,9], as far as we know, this proposal is unique in the state-of-the-art because of the consideration of conflicting objectives for the online shopping optimization problem. To be more clear, the purpose of this work is to demonstrate that it is possible to formulate the ISHOP-U as a real multi-objective optimization problem where the objectives conflict and do not treat objectives as merely secondary goals or preferences as in many proposals in the literature, which claim to be multi-objective optimization proposals and by definition if the objectives do not conflict they are not multi-objective optimization problems. Problems that do not conflict with their objectives do not produce a Pareto front where the optimal solutions are nondominated between them. In a Pareto front, every solution is mathematically as good as the others. This proposal’s final solutions are mathematically equivalent (nondominated between them), producing a Pareto front. The remainder of this paper is as follows: Section 1 is the introduction. Section 2 presents the mathematical formulation of the multi-objective ISHOP-U. Section 3 shows the NSGA-II implementation for the Multi-Objective ISHOP-U. Section 4 provides the experimental configuration. Section 5 gives numerical results of the experimentation. Section 6 presntes the graphical results of the experimentation. Finally, Section 7 gives our research conclusions.

2. Proposed Multi-Objective Formulation

This section presents our proposed multi-objective mathematical formulation for the ISHOP-U. Equation (1) ($f_1$) computes the ISHOP-U final purchase cost objective function from their original publication in [1]. In $f_1$, given a total of n products and m stores, the components $s_{i,j}$ represent the quantity to be bought in the store i for the j-th product and the components $c_{i,j}$ represent the price of the j-th product in the store i-th. The delivery price of every i-th store is represented by $d_i$, and the binary variable $y_i$ guarantees that the delivery price is summed up once, i.e., $y_i=1$ if one product or more are bought in the store i. The $s_{i,j}$ are constrained by product availability in stores and the number of item units required.

$$\begin{array}{c}\hfill f_1=\sum _{i=1}^m\left(\left(\sum _{j=1}^n{s}_{i,j}{c}_{i,j}\right)+y_i{d}_i\right)\end{array}$$

(1)

$$\begin{array}{c}\hfill f_2=f_1·\alpha \end{array}$$

(2)

Equation (2) ($f_2$) is our second proposed new objective function. In $f_2$, $\alpha \in [0,1]$ represents the percentage of cash-back or reward points on the final purchase. From the above formulation, maximizing $f_2$ increases the final purchase cost, which is undesirable, and minimizing the final purchase cost decreases $f_2$, which is also undesirable. Therefore, being a multi-objective optimization problem, the objectives are in evident conflict. This work uses a 5% cash-back return for the final purchase, i.e., $\alpha =0.05$.

3. Algorithms for the Experimental Comparison

This section briefly presents the eight algorithms in our experimental comparison. The eight algorithms implement the same evolutionary operators for the crossover, mutation, and repair methods described in the original ISHOP-U publication [1]. We use the same selection of evolutionary algorithms as in [10] due to the convenience in adapting them to our discrete optimization problem.

3.1. AGEMOEA

The main loop of the Adaptive Geometry Estimation-based Multi-Objective Evolutionary Algorithm (AGEMOEA) is similar to that of NSGA-II, with the key difference being the use of a survival score in place of the crowding distance density estimator. AGEMOEA estimates the geometry of the Pareto front by identifying the value of p in its associated $L_p$ norm (distance). Once p is defined, the proximity of a solution is measured using the $L_p$ norm to the ideal point, while the diversity of solutions is determined by the minimum distance between them. The survival score for the solutions is calculated as the ratio between diversity and proximity.

3.2. AGEMOEA2

Adaptive Geometry Estimation Based Multi-Objective Evolutionary Algorithm 2 (AGEMOEA2) enhances the original AGEMOEA. AGEMOEA2 utilizes the Newton-Raphson method to determine the value of p in the $L_p$ norm; when $p=2$, it corresponds to the Euclidean distance. Additionally, the diversity between solutions is assessed using geodesic distance.

3.3. GWASFGA

Global Weighting Achievement Scalarizing Function Genetic Algorithm (GWASFGA [11]) enhances the original WASFGA [12]. It uses a set of weights whose inverses are uniform, using as environmental selection a scalarizing function, similar to [13]. In their evaluation, GWASFGA uses an augmented weighted Tchebycheff as a scalarizing function and uses two reference points, an ideal point and a nadir point, slightly improved and worsened, respectively.

3.4. MOCell

Multi-objective Cellular (MOCell [14]) adapts the cellular genetic algorithm for multi-objective optimization. MOCell uses an external archive to keep track of the best nondominated solutions found. When the archive is full, the crowding distance density estimator discriminates solutions. Random individuals from the archive update the population.

3.5. MOMBI

Many-Objective Metaheuristic Based on the $R2$ Indicator (MOMBI [15]) is a many-objective optimization evolutionary algorithm. MOMBI environmental selection is based on the $R2$ indicator, and the weighted Tchebycheff scalarizing function using a set of weights as in decomposition [13]. The population of individuals is ranked according to the R2 indicator for environmental selection.

3.6. MOMBI2

Many-Objective Metaheuristic Based on the $R2$ Indicator 2 (MOMBI2 [16]) improves MOMBI’s loss of diversity for high-dimensionality problems. The enhancements are as follows: (i) An achievement scalarizing function instead of weighted Tchebycheff. (ii) An adaptative nadir point. (iii) The use of Euclidean distance to discriminate individuals with a tie in the R2 indicator.

3.7. NSGA2

Nondominated Sorting Genetic Algorithm 2 (NSGA2 [4]) is the most well-known algorithm in the literature of evolutionary multi-objective optimization with two key components: (i) The nondominated sort, which ranks the individuals into sets of nondominated solutions. (ii) The diversity measure of crowding distance. Their environmental selection is elitist based on the individuals’ first ranks and crowding distance.

3.8. SMS-EMOA

The S Metric Selection EMOA (SMS-EMOA [17]) is a steady-state evolutionary algorithm using hypervolume contributions as a solution discriminant. The solution in the last rank with the least contribution to the hypervolume is the one removed from the population.

4. Experimental Setup

This section details the parameters needed to reproduce our experiments. To evaluate our proposed multi-objective problem formulation and the performance of the selection of algorithms from Section 3, we use the same initial proposed benchmark in [1] of five small instances (10 products with 25 stores), five medium instances (25 products with 50 stores), and five large instances (50 products with 100 stores). Instances are available at https://github.com/AASantiago/ISHOP-U-Instances (accesed on 21 April 2025). The experimentation parameters for the eight algorithms studied are the ones recommended in their original publications and appear in Table 1, except for a crossover probability $p_r=1.0$, a mutation probability $p_m=0.05$, a population size of 100, and 25,000 objective function evaluations as stop criterion, the above are parameters and evolutionary operators that have been already fine-tuned in [1] for the ISHOP-U.

Table 1. Parameters for the eight state-of-the-art algorithms in comparison. Parameters tuned as in the original ISHOP-U publication.

Parameter	AGEMOEA	AGEMOEA2
Population size:	100	100
Selection:	Binary Tournament	Binary Tournament
Recombination:	$p_r=1.0$	$p_r=1.0$
Mutation:	$p_m=0.05$	$p_m=0.05$
	MOMBI	MOMBI2
Population size:	101	101
Selection:	Binary Tournament	Binary Tournament
Recombination:	$p_r=1.0$	$p_r=1.0$
Mutation:	$p_m=0.05$	$p_m=0.05$
	SMS-EMOA	MOCell
Archive size:	-	100
Population size:	100	100
Selection:	Binary Tournament	Binary Tournament
Recombination:	$p_r=1.0$	$p_r=1.0$
Mutation:	$p_m=0.05$	$p_m=0.05$
	GWASFGA	NSGA2
Population size:	100	100
Selection:	Binary Tournament	Binary Tournament
Recombination:	$p_r=1.0$	$p_r=1.0$
Mutation:	$p_m=0.05$	$p_m=0.05$

Following the recommendations in [18], to achieve statistical confidence, we performed 30 independent executions per problem instance; the numerical results are summarized in the result tables as the median and interquartile range (${\mathrm{MEDIAN}}_{IQR}$) as measures of central tendency and dispersion, respectively. To quickly identify the best and second-best algorithms, the best and second-best results appear in gray and light gray, respectively. Due to the multi-objective nature of the problem studied, we use the same multi-objective quality indicators as in [19], the hypervolume [20] as a measure of the dominated region, the additive epsilon [21] as a measure of the necessary distance to weakly dominance the reference Pareto front, the inverted generational distance plus [22] as a measure of the solutions distance to their nearest point in the reference Pareto front. Since the real true Pareto front is unknown for this newly proposed multi-objective problem, we use the added nondominated solutions after the complete experimentation as reference fronts.

5. Numerical Results

This section outlines the numerical results of the experimentation. For the numerical results that appear in Table 2, Table 3 and Table 4 for the multi-objective quality indicators of hypervolume, additive epsilon, and inverted generational plus, respectively. In the column problem for the nomenclature used in the name of the instances, the first character indicates their size: S for small, M for medium, and L for large.

Table 2. Hypervolume numerical results in terms of ${\mathrm{MEDIAN}}_{IQR}$. The best and second-best results are highlighted in gray and light gray, respectively.

Problem	AGEMOEA	AGEMOEA2	GWASGFA	MOCell	MOMBI	MOMBI2	NSGA2	SMS-EMOA
S1	$3.7\times {10}_{8.6\times {10}^{-3}}^{-1}$	$3.7\times {10}_{1.3\times {10}^{-2}}^{-1}$	$4.8\times {10}_{1.8\times {10}^{-4}}^{-1}$	$4.9\times {10}_{1.5\times {10}^{-3}}^{-1}$	$3.8\times {10}_{1.8\times {10}^{-2}}^{-1}$	$3.7\times {10}_{1.3\times {10}^{-2}}^{-1}$	$4.9\times {10}_{8.4\times {10}^{-4}}^{-1}$	$4.9\times {10}_{2.1\times {10}^{-3}}^{-1}$
S2	$3.6\times {10}_{1.0\times {10}^{-2}}^{-1}$	$3.6\times {10}_{1.2\times {10}^{-2}}^{-1}$	$4.8\times {10}_{2.1\times {10}^{-4}}^{-1}$	$4.9\times {10}_{2.0\times {10}^{-3}}^{-1}$	$3.7\times {10}_{1.2\times {10}^{-2}}^{-1}$	$3.7\times {10}_{1.2\times {10}^{-2}}^{-1}$	$4.9\times {10}_{9.7\times {10}^{-4}}^{-1}$	$4.9\times {10}_{2.4\times {10}^{-3}}^{-1}$
S3	$3.5\times {10}_{1.2\times {10}^{-2}}^{-1}$	$3.5\times {10}_{7.7\times {10}^{-3}}^{-1}$	$4.8\times {10}_{2.2\times {10}^{-4}}^{-1}$	$4.9\times {10}_{2.7\times {10}^{-3}}^{-1}$	$3.6\times {10}_{1.1\times {10}^{-2}}^{-1}$	$3.7\times {10}_{1.3\times {10}^{-2}}^{-1}$	$4.9\times {10}_{8.0\times {10}^{-4}}^{-1}$	$4.9\times {10}_{1.9\times {10}^{-3}}^{-1}$
S4	$3.6\times {10}_{1.1\times {10}^{-2}}^{-1}$	$3.6\times {10}_{9.7\times {10}^{-3}}^{-1}$	$4.8\times {10}_{2.1\times {10}^{-4}}^{-1}$	$4.9\times {10}_{1.7\times {10}^{-3}}^{-1}$	$3.7\times {10}_{1.3\times {10}^{-2}}^{-1}$	$3.7\times {10}_{1.3\times {10}^{-2}}^{-1}$	$4.9\times {10}_{9.5\times {10}^{-4}}^{-1}$	$4.9\times {10}_{1.8\times {10}^{-3}}^{-1}$
S5	$3.5\times {10}_{8.2\times {10}^{-3}}^{-1}$	$3.5\times {10}_{1.1\times {10}^{-2}}^{-1}$	$4.8\times {10}_{2.2\times {10}^{-4}}^{-1}$	$4.9\times {10}_{1.9\times {10}^{-3}}^{-1}$	$3.6\times {10}_{1.1\times {10}^{-2}}^{-1}$	$3.7\times {10}_{1.5\times {10}^{-2}}^{-1}$	$4.9\times {10}_{1.0\times {10}^{-3}}^{-1}$	$4.9\times {10}_{1.6\times {10}^{-3}}^{-1}$
M1	$3.2\times {10}_{9.0\times {10}^{-3}}^{-1}$	$3.2\times {10}_{6.3\times {10}^{-3}}^{-1}$	$4.8\times {10}_{3.9\times {10}^{-4}}^{-1}$	$4.7\times {10}_{3.6\times {10}^{-3}}^{-1}$	$3.3\times {10}_{1.3\times {10}^{-2}}^{-1}$	$3.2\times {10}_{8.9\times {10}^{-3}}^{-1}$	$4.9\times {10}_{2.5\times {10}^{-3}}^{-1}$	$4.8\times {10}_{2.9\times {10}^{-3}}^{-1}$
M2	$3.1\times {10}_{6.1\times {10}^{-3}}^{-1}$	$3.1\times {10}_{5.2\times {10}^{-3}}^{-1}$	$4.8\times {10}_{4.6\times {10}^{-4}}^{-1}$	$4.7\times {10}_{3.8\times {10}^{-3}}^{-1}$	$3.2\times {10}_{1.0\times {10}^{-2}}^{-1}$	$3.3\times {10}_{8.2\times {10}^{-3}}^{-1}$	$4.9\times {10}_{2.1\times {10}^{-3}}^{-1}$	$4.8\times {10}_{4.0\times {10}^{-3}}^{-1}$
M3	$3.1\times {10}_{5.6\times {10}^{-3}}^{-1}$	$3.1\times {10}_{7.5\times {10}^{-3}}^{-1}$	$4.8\times {10}_{4.4\times {10}^{-4}}^{-1}$	$4.7\times {10}_{3.8\times {10}^{-3}}^{-1}$	$3.2\times {10}_{7.8\times {10}^{-3}}^{-1}$	$3.2\times {10}_{1.2\times {10}^{-2}}^{-1}$	$4.8\times {10}_{2.6\times {10}^{-3}}^{-1}$	$4.8\times {10}_{3.9\times {10}^{-3}}^{-1}$
M4	$3.1\times {10}_{6.0\times {10}^{-3}}^{-1}$	$3.1\times {10}_{8.7\times {10}^{-3}}^{-1}$	$4.8\times {10}_{4.7\times {10}^{-4}}^{-1}$	$4.7\times {10}_{3.2\times {10}^{-3}}^{-1}$	$3.2\times {10}_{1.1\times {10}^{-2}}^{-1}$	$3.3\times {10}_{9.5\times {10}^{-3}}^{-1}$	$4.9\times {10}_{2.5\times {10}^{-3}}^{-1}$	$4.8\times {10}_{3.8\times {10}^{-3}}^{-1}$
M5	$3.1\times {10}_{7.1\times {10}^{-3}}^{-1}$	$3.1\times {10}_{6.6\times {10}^{-3}}^{-1}$	$4.8\times {10}_{3.2\times {10}^{-4}}^{-1}$	$4.7\times {10}_{3.8\times {10}^{-3}}^{-1}$	$3.2\times {10}_{1.1\times {10}^{-2}}^{-1}$	$3.3\times {10}_{1.2\times {10}^{-2}}^{-1}$	$4.9\times {10}_{2.5\times {10}^{-3}}^{-1}$	$4.8\times {10}_{3.8\times {10}^{-3}}^{-1}$
L1	$3.0\times {10}_{4.6\times {10}^{-3}}^{-1}$	$3.0\times {10}_{4.9\times {10}^{-3}}^{-1}$	$4.8\times {10}_{6.7\times {10}^{-4}}^{-1}$	$4.7\times {10}_{4.8\times {10}^{-3}}^{-1}$	$3.0\times {10}_{5.6\times {10}^{-3}}^{-1}$	$3.0\times {10}_{1.5\times {10}^{-2}}^{-1}$	$4.9\times {10}_{2.2\times {10}^{-3}}^{-1}$	$4.8\times {10}_{4.4\times {10}^{-3}}^{-1}$
L2	$3.0\times {10}_{5.4\times {10}^{-3}}^{-1}$	$3.0\times {10}_{4.9\times {10}^{-3}}^{-1}$	$4.8\times {10}_{8.3\times {10}^{-4}}^{-1}$	$4.7\times {10}_{4.0\times {10}^{-3}}^{-1}$	$3.1\times {10}_{8.0\times {10}^{-3}}^{-1}$	$3.0\times {10}_{5.5\times {10}^{-3}}^{-1}$	$4.9\times {10}_{2.3\times {10}^{-3}}^{-1}$	$4.8\times {10}_{3.7\times {10}^{-3}}^{-1}$
L3	$3.0\times {10}_{5.5\times {10}^{-3}}^{-1}$	$3.0\times {10}_{8.4\times {10}^{-3}}^{-1}$	$4.8\times {10}_{4.3\times {10}^{-4}}^{-1}$	$4.8\times {10}_{3.6\times {10}^{-3}}^{-1}$	$3.1\times {10}_{8.2\times {10}^{-3}}^{-1}$	$3.0\times {10}_{8.3\times {10}^{-3}}^{-1}$	$4.9\times {10}_{2.0\times {10}^{-3}}^{-1}$	$4.8\times {10}_{3.1\times {10}^{-3}}^{-1}$
L4	$3.0\times {10}_{4.3\times {10}^{-3}}^{-1}$	$3.0\times {10}_{4.7\times {10}^{-3}}^{-1}$	$4.8\times {10}_{1.1\times {10}^{-3}}^{-1}$	$4.7\times {10}_{4.6\times {10}^{-3}}^{-1}$	$3.0\times {10}_{6.6\times {10}^{-3}}^{-1}$	$3.0\times {10}_{1.1\times {10}^{-2}}^{-1}$	$4.8\times {10}_{3.0\times {10}^{-3}}^{-1}$	$4.7\times {10}_{4.2\times {10}^{-3}}^{-1}$
L5	$3.0\times {10}_{4.2\times {10}^{-3}}^{-1}$	$3.0\times {10}_{6.4\times {10}^{-3}}^{-1}$	$4.8\times {10}_{1.0\times {10}^{-3}}^{-1}$	$4.7\times {10}_{4.4\times {10}^{-3}}^{-1}$	$3.0\times {10}_{6.8\times {10}^{-3}}^{-1}$	$3.0\times {10}_{1.3\times {10}^{-2}}^{-1}$	$4.8\times {10}_{2.9\times {10}^{-3}}^{-1}$	$4.8\times {10}_{3.7\times {10}^{-3}}^{-1}$

Table 3. Additive Epsilon numerical results in terms of ${\mathrm{MEDIAN}}_{IQR}$. The best and second-best results are highlighted in gray and light gray, respectively.

Problem	AGEMOEA	AGEMOEA2	GWASGFA	MOCell	MOMBI	MOMBI2	NSGA2	SMS-EMOA
S1	$4.0\times {10}_{1.7\times {10}^{-2}}^{-1}$	$4.1\times {10}_{2.8\times {10}^{-2}}^{-1}$	$3.8\times {10}_{6.0\times {10}^{-4}}^{-2}$	$8.2\times {10}_{1.7\times {10}^{-2}}^{-2}$	$3.9\times {10}_{4.0\times {10}^{-2}}^{-1}$	$4.0\times {10}_{2.6\times {10}^{-2}}^{-1}$	$5.3\times {10}_{1.5\times {10}^{-2}}^{-2}$	$8.9\times {10}_{2.1\times {10}^{-2}}^{-2}$
S2	$4.0\times {10}_{2.5\times {10}^{-2}}^{-1}$	$4.0\times {10}_{2.4\times {10}^{-2}}^{-1}$	$3.8\times {10}_{1.0\times {10}^{-3}}^{-2}$	$1.0\times {10}_{1.5\times {10}^{-2}}^{-1}$	$3.8\times {10}_{2.5\times {10}^{-2}}^{-1}$	$4.0\times {10}_{2.4\times {10}^{-2}}^{-1}$	$6.4\times {10}_{1.1\times {10}^{-2}}^{-2}$	$1.0\times {10}_{1.7\times {10}^{-2}}^{-1}$
S3	$4.3\times {10}_{2.2\times {10}^{-2}}^{-1}$	$4.3\times {10}_{1.7\times {10}^{-2}}^{-1}$	$3.8\times {10}_{8.5\times {10}^{-4}}^{-2}$	$1.1\times {10}_{2.0\times {10}^{-2}}^{-1}$	$4.0\times {10}_{2.5\times {10}^{-2}}^{-1}$	$4.2\times {10}_{2.7\times {10}^{-2}}^{-1}$	$6.1\times {10}_{1.0\times {10}^{-2}}^{-2}$	$9.6\times {10}_{1.5\times {10}^{-2}}^{-2}$
S4	$3.8\times {10}_{1.5\times {10}^{-2}}^{-1}$	$3.8\times {10}_{1.4\times {10}^{-2}}^{-1}$	$3.9\times {10}_{2.1\times {10}^{-3}}^{-2}$	$1.0\times {10}_{1.5\times {10}^{-2}}^{-1}$	$3.7\times {10}_{2.4\times {10}^{-2}}^{-1}$	$3.7\times {10}_{1.7\times {10}^{-2}}^{-1}$	$6.4\times {10}_{1.3\times {10}^{-2}}^{-2}$	$9.9\times {10}_{1.4\times {10}^{-2}}^{-2}$
S5	$4.1\times {10}_{2.2\times {10}^{-2}}^{-1}$	$4.2\times {10}_{2.2\times {10}^{-2}}^{-1}$	$3.8\times {10}_{7.0\times {10}^{-4}}^{-2}$	$1.0\times {10}_{1.4\times {10}^{-2}}^{-1}$	$4.1\times {10}_{2.2\times {10}^{-2}}^{-1}$	$4.1\times {10}_{2.2\times {10}^{-2}}^{-1}$	$6.5\times {10}_{1.3\times {10}^{-2}}^{-2}$	$1.0\times {10}_{1.3\times {10}^{-2}}^{-1}$
M1	$4.5\times {10}_{1.6\times {10}^{-2}}^{-1}$	$4.5\times {10}_{1.0\times {10}^{-2}}^{-1}$	$4.8\times {10}_{9.3\times {10}^{-3}}^{-2}$	$1.6\times {10}_{1.2\times {10}^{-2}}^{-1}$	$4.4\times {10}_{1.8\times {10}^{-2}}^{-1}$	$4.5\times {10}_{1.4\times {10}^{-2}}^{-1}$	$1.1\times {10}_{1.9\times {10}^{-2}}^{-1}$	$1.4\times {10}_{1.7\times {10}^{-2}}^{-1}$
M2	$4.5\times {10}_{7.7\times {10}^{-3}}^{-1}$	$4.4\times {10}_{8.9\times {10}^{-3}}^{-1}$	$5.2\times {10}_{1.2\times {10}^{-2}}^{-2}$	$1.8\times {10}_{1.9\times {10}^{-2}}^{-1}$	$4.3\times {10}_{9.4\times {10}^{-3}}^{-1}$	$4.4\times {10}_{1.1\times {10}^{-2}}^{-1}$	$1.1\times {10}_{1.7\times {10}^{-2}}^{-1}$	$1.4\times {10}_{1.9\times {10}^{-2}}^{-1}$
M3	$4.4\times {10}_{9.9\times {10}^{-3}}^{-1}$	$4.5\times {10}_{1.0\times {10}^{-2}}^{-1}$	$5.9\times {10}_{1.1\times {10}^{-2}}^{-2}$	$1.8\times {10}_{1.5\times {10}^{-2}}^{-1}$	$4.4\times {10}_{1.3\times {10}^{-2}}^{-1}$	$4.3\times {10}_{1.5\times {10}^{-2}}^{-1}$	$1.2\times {10}_{1.7\times {10}^{-2}}^{-1}$	$1.5\times {10}_{1.8\times {10}^{-2}}^{-1}$
M4	$4.5\times {10}_{1.1\times {10}^{-2}}^{-1}$	$4.5\times {10}_{1.3\times {10}^{-2}}^{-1}$	$4.8\times {10}_{9.2\times {10}^{-3}}^{-2}$	$1.7\times {10}_{1.4\times {10}^{-2}}^{-1}$	$4.3\times {10}_{1.7\times {10}^{-2}}^{-1}$	$4.2\times {10}_{1.0\times {10}^{-2}}^{-1}$	$1.1\times {10}_{2.0\times {10}^{-2}}^{-1}$	$1.5\times {10}_{2.3\times {10}^{-2}}^{-1}$
M5	$4.4\times {10}_{7.3\times {10}^{-3}}^{-1}$	$4.4\times {10}_{7.2\times {10}^{-3}}^{-1}$	$4.7\times {10}_{1.1\times {10}^{-2}}^{-2}$	$1.7\times {10}_{1.5\times {10}^{-2}}^{-1}$	$4.3\times {10}_{1.2\times {10}^{-2}}^{-1}$	$4.3\times {10}_{1.2\times {10}^{-2}}^{-1}$	$1.0\times {10}_{1.7\times {10}^{-2}}^{-1}$	$1.4\times {10}_{2.2\times {10}^{-2}}^{-1}$
L1	$4.7\times {10}_{7.6\times {10}^{-3}}^{-1}$	$4.7\times {10}_{9.8\times {10}^{-3}}^{-1}$	$7.0\times {10}_{1.5\times {10}^{-2}}^{-2}$	$1.6\times {10}_{2.2\times {10}^{-2}}^{-1}$	$4.6\times {10}_{1.2\times {10}^{-2}}^{-1}$	$4.7\times {10}_{2.4\times {10}^{-2}}^{-1}$	$1.0\times {10}_{1.9\times {10}^{-2}}^{-1}$	$1.4\times {10}_{1.9\times {10}^{-2}}^{-1}$
L2	$4.7\times {10}_{7.4\times {10}^{-3}}^{-1}$	$4.7\times {10}_{8.5\times {10}^{-3}}^{-1}$	$6.1\times {10}_{1.7\times {10}^{-2}}^{-2}$	$1.6\times {10}_{1.8\times {10}^{-2}}^{-1}$	$4.6\times {10}_{1.1\times {10}^{-2}}^{-1}$	$4.7\times {10}_{1.1\times {10}^{-2}}^{-1}$	$1.0\times {10}_{2.1\times {10}^{-2}}^{-1}$	$1.4\times {10}_{1.9\times {10}^{-2}}^{-1}$
L3	$4.6\times {10}_{8.9\times {10}^{-3}}^{-1}$	$4.6\times {10}_{1.1\times {10}^{-2}}^{-1}$	$5.0\times {10}_{1.2\times {10}^{-2}}^{-2}$	$1.6\times {10}_{1.9\times {10}^{-2}}^{-1}$	$4.6\times {10}_{1.4\times {10}^{-2}}^{-1}$	$4.7\times {10}_{1.4\times {10}^{-2}}^{-1}$	$9.2\times {10}_{1.9\times {10}^{-2}}^{-2}$	$1.3\times {10}_{1.4\times {10}^{-2}}^{-1}$
L4	$4.6\times {10}_{6.6\times {10}^{-3}}^{-1}$	$4.6\times {10}_{7.1\times {10}^{-3}}^{-1}$	$8.0\times {10}_{1.6\times {10}^{-2}}^{-2}$	$1.8\times {10}_{1.5\times {10}^{-2}}^{-1}$	$4.6\times {10}_{1.0\times {10}^{-2}}^{-1}$	$4.7\times {10}_{1.8\times {10}^{-2}}^{-1}$	$1.2\times {10}_{1.4\times {10}^{-2}}^{-1}$	$1.6\times {10}_{1.7\times {10}^{-2}}^{-1}$
L5	$4.5\times {10}_{5.0\times {10}^{-3}}^{-1}$	$4.5\times {10}_{7.3\times {10}^{-3}}^{-1}$	$8.8\times {10}_{1.3\times {10}^{-2}}^{-2}$	$1.9\times {10}_{1.6\times {10}^{-2}}^{-1}$	$4.5\times {10}_{8.4\times {10}^{-3}}^{-1}$	$4.6\times {10}_{1.3\times {10}^{-2}}^{-1}$	$1.3\times {10}_{1.9\times {10}^{-2}}^{-1}$	$1.6\times {10}_{1.6\times {10}^{-2}}^{-1}$

Table 4. Inverted generational distance plus numerical results in terms of ${\mathrm{MEDIAN}}_{IQR}$. The best and second-best results are highlighted in gray and light gray, respectively.

Problem	AGEMOEA	AGEMOEA2	GWASGFA	MOCell	MOMBI	MOMBI2	NSGA2	SMS-EMOA
S1	$8.8\times {10}_{4.6\times {10}^{-5}}^{-4}$	$8.9\times {10}_{7.1\times {10}^{-5}}^{-4}$	$9.1\times {10}_{1.1\times {10}^{-6}}^{-5}$	$7.2\times {10}_{2.1\times {10}^{-5}}^{-5}$	$8.2\times {10}_{1.0\times {10}^{-4}}^{-4}$	$8.6\times {10}_{6.6\times {10}^{-5}}^{-4}$	$4.4\times {10}_{1.1\times {10}^{-5}}^{-5}$	$8.0\times {10}_{2.7\times {10}^{-5}}^{-5}$
S2	$8.8\times {10}_{5.6\times {10}^{-5}}^{-4}$	$8.8\times {10}_{6.2\times {10}^{-5}}^{-4}$	$9.4\times {10}_{1.6\times {10}^{-6}}^{-5}$	$1.0\times {10}_{2.2\times {10}^{-5}}^{-4}$	$8.3\times {10}_{6.2\times {10}^{-5}}^{-4}$	$8.3\times {10}_{6.2\times {10}^{-5}}^{-4}$	$5.4\times {10}_{1.2\times {10}^{-5}}^{-5}$	$1.0\times {10}_{2.5\times {10}^{-5}}^{-4}$
S3	$9.6\times {10}_{5.9\times {10}^{-5}}^{-4}$	$9.5\times {10}_{3.9\times {10}^{-5}}^{-4}$	$9.3\times {10}_{1.7\times {10}^{-6}}^{-5}$	$1.1\times {10}_{2.9\times {10}^{-5}}^{-4}$	$8.7\times {10}_{5.6\times {10}^{-5}}^{-4}$	$8.7\times {10}_{6.9\times {10}^{-5}}^{-4}$	$5.5\times {10}_{1.1\times {10}^{-5}}^{-5}$	$1.0\times {10}_{2.1\times {10}^{-5}}^{-4}$
S4	$8.9\times {10}_{5.7\times {10}^{-5}}^{-4}$	$8.9\times {10}_{5.0\times {10}^{-5}}^{-4}$	$9.2\times {10}_{1.1\times {10}^{-6}}^{-5}$	$1.0\times {10}_{2.0\times {10}^{-5}}^{-4}$	$8.4\times {10}_{7.1\times {10}^{-5}}^{-4}$	$8.2\times {10}_{6.3\times {10}^{-5}}^{-4}$	$5.1\times {10}_{1.2\times {10}^{-5}}^{-5}$	$9.8\times {10}_{2.0\times {10}^{-5}}^{-5}$
S5	$9.3\times {10}_{4.4\times {10}^{-5}}^{-4}$	$9.3\times {10}_{5.5\times {10}^{-5}}^{-4}$	$9.5\times {10}_{1.5\times {10}^{-6}}^{-5}$	$1.1\times {10}_{2.1\times {10}^{-5}}^{-4}$	$8.9\times {10}_{5.5\times {10}^{-5}}^{-4}$	$8.8\times {10}_{7.3\times {10}^{-5}}^{-4}$	$5.6\times {10}_{1.4\times {10}^{-5}}^{-5}$	$1.1\times {10}_{1.8\times {10}^{-5}}^{-4}$
M1	$9.6\times {10}_{4.1\times {10}^{-5}}^{-4}$	$9.5\times {10}_{2.8\times {10}^{-5}}^{-4}$	$9.4\times {10}_{2.9\times {10}^{-6}}^{-5}$	$1.6\times {10}_{2.5\times {10}^{-5}}^{-4}$	$9.2\times {10}_{6.0\times {10}^{-5}}^{-4}$	$9.4\times {10}_{3.8\times {10}^{-5}}^{-4}$	$6.7\times {10}_{1.9\times {10}^{-5}}^{-5}$	$1.1\times {10}_{2.4\times {10}^{-5}}^{-4}$
M2	$9.8\times {10}_{2.6\times {10}^{-5}}^{-4}$	$9.7\times {10}_{2.3\times {10}^{-5}}^{-4}$	$9.4\times {10}_{3.7\times {10}^{-6}}^{-5}$	$1.7\times {10}_{2.7\times {10}^{-5}}^{-4}$	$9.3\times {10}_{4.4\times {10}^{-5}}^{-4}$	$8.9\times {10}_{3.5\times {10}^{-5}}^{-4}$	$6.5\times {10}_{1.7\times {10}^{-5}}^{-5}$	$1.2\times {10}_{3.0\times {10}^{-5}}^{-4}$
M3	$9.3\times {10}_{2.5\times {10}^{-5}}^{-4}$	$9.4\times {10}_{3.2\times {10}^{-5}}^{-4}$	$8.9\times {10}_{3.4\times {10}^{-6}}^{-5}$	$1.7\times {10}_{2.5\times {10}^{-5}}^{-4}$	$9.1\times {10}_{3.5\times {10}^{-5}}^{-4}$	$8.8\times {10}_{5.1\times {10}^{-5}}^{-4}$	$6.9\times {10}_{1.8\times {10}^{-5}}^{-5}$	$1.1\times {10}_{2.7\times {10}^{-5}}^{-4}$
M4	$9.7\times {10}_{2.6\times {10}^{-5}}^{-4}$	$9.7\times {10}_{3.9\times {10}^{-5}}^{-4}$	$9.3\times {10}_{3.6\times {10}^{-6}}^{-5}$	$1.7\times {10}_{2.3\times {10}^{-5}}^{-4}$	$9.3\times {10}_{4.8\times {10}^{-5}}^{-4}$	$8.8\times {10}_{4.0\times {10}^{-5}}^{-4}$	$7.0\times {10}_{2.1\times {10}^{-5}}^{-5}$	$1.3\times {10}_{3.1\times {10}^{-5}}^{-4}$
M5	$9.8\times {10}_{3.1\times {10}^{-5}}^{-4}$	$9.8\times {10}_{2.9\times {10}^{-5}}^{-4}$	$9.4\times {10}_{3.3\times {10}^{-6}}^{-5}$	$1.7\times {10}_{2.5\times {10}^{-5}}^{-4}$	$9.5\times {10}_{4.8\times {10}^{-5}}^{-4}$	$9.0\times {10}_{4.9\times {10}^{-5}}^{-4}$	$6.7\times {10}_{2.0\times {10}^{-5}}^{-5}$	$1.2\times {10}_{3.1\times {10}^{-5}}^{-4}$
L1	$9.8\times {10}_{2.0\times {10}^{-5}}^{-4}$	$9.8\times {10}_{2.1\times {10}^{-5}}^{-4}$	$8.9\times {10}_{3.3\times {10}^{-6}}^{-5}$	$1.0\times {10}_{3.4\times {10}^{-5}}^{-4}$	$9.5\times {10}_{2.5\times {10}^{-5}}^{-4}$	$9.9\times {10}_{6.6\times {10}^{-5}}^{-4}$	$4.2\times {10}_{1.4\times {10}^{-5}}^{-5}$	$7.2\times {10}_{2.7\times {10}^{-5}}^{-5}$
L2	$9.8\times {10}_{2.3\times {10}^{-5}}^{-4}$	$9.8\times {10}_{2.1\times {10}^{-5}}^{-4}$	$9.1\times {10}_{4.4\times {10}^{-6}}^{-5}$	$1.1\times {10}_{2.7\times {10}^{-5}}^{-4}$	$9.6\times {10}_{3.5\times {10}^{-5}}^{-4}$	$9.9\times {10}_{2.4\times {10}^{-5}}^{-4}$	$4.4\times {10}_{8.7\times {10}^{-6}}^{-5}$	$7.3\times {10}_{2.4\times {10}^{-5}}^{-5}$
L3	$1.0\times {10}_{2.4\times {10}^{-5}}^{-3}$	$1.0\times {10}_{3.8\times {10}^{-5}}^{-3}$	$9.4\times {10}_{4.4\times {10}^{-6}}^{-5}$	$1.2\times {10}_{2.8\times {10}^{-5}}^{-4}$	$9.9\times {10}_{3.5\times {10}^{-5}}^{-4}$	$1.0\times {10}_{3.6\times {10}^{-5}}^{-3}$	$4.5\times {10}_{1.0\times {10}^{-5}}^{-5}$	$7.8\times {10}_{2.1\times {10}^{-5}}^{-5}$
L4	$9.4\times {10}_{1.8\times {10}^{-5}}^{-4}$	$9.3\times {10}_{2.0\times {10}^{-5}}^{-4}$	$8.8\times {10}_{4.5\times {10}^{-6}}^{-5}$	$1.1\times {10}_{2.7\times {10}^{-5}}^{-4}$	$9.2\times {10}_{2.8\times {10}^{-5}}^{-4}$	$9.4\times {10}_{4.7\times {10}^{-5}}^{-4}$	$4.3\times {10}_{1.4\times {10}^{-5}}^{-5}$	$8.2\times {10}_{2.3\times {10}^{-5}}^{-5}$
L5	$9.3\times {10}_{1.8\times {10}^{-5}}^{-4}$	$9.3\times {10}_{2.7\times {10}^{-5}}^{-4}$	$8.8\times {10}_{5.6\times {10}^{-6}}^{-5}$	$1.1\times {10}_{2.5\times {10}^{-5}}^{-4}$	$9.0\times {10}_{2.9\times {10}^{-5}}^{-4}$	$9.2\times {10}_{5.4\times {10}^{-5}}^{-4}$	$4.3\times {10}_{1.2\times {10}^{-5}}^{-5}$	$6.7\times {10}_{2.2\times {10}^{-5}}^{-5}$

For the hypervolume computation, the extreme points from the reference set of nondominated solutions are used as the reference point to compute the hypervolume as follows. Normalization of the objectives is applied using the extreme points, and the minimization objectives are inverted to compute the hypervolume. Table 2 and Figure 1 present the Friedman average rankings numerically and graphically, respectively, achieved by the algorithms in experimental comparison. As Table 2 shows, NSGA2 achieves outstanding performance, near 0.5 for the entire set of instances studied. NSGA2 achieves the best hypervolume median value in the 15 instances studied, followed by SMS-EMOA with seven, MOCell with five, and GWASFGA with the three best median values. The above results are over $0.48$, close to the optimal hypervolume for Pareto fronts with linear shapes, since it should be approximately 0.5, half the total unit square area for a normalized two-objective space. Considering the Friedman average rankings in Table 5 best-ranked algorithm is NSGA2 with an average rank of 1.25, followed by GWASFGA, SMS-EMOA, MOCell, MOMBI, MOMBI2, AGEMOEA2, and AGEMOEA with average rankings of 2.63, 2.72, 3.40, 6.11, 6.18, 6.83, and 6.88, respectively.

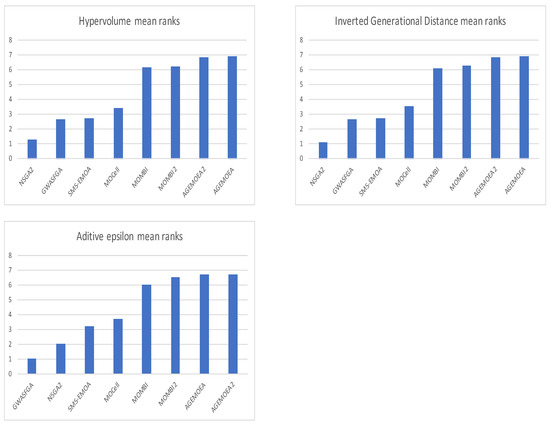
Figure 1. This is a graphic representation of the Friedman average rankings for hypervolume, inverted generational distance plus, and additive epsilon; the lower the value, the better.

Table 5. Friedman average rankings of the algorithms for the studied instances, presenting the numeric mean of the ranks (places) achieved in every independent execution; the lower, the better.

Hypervolume		IGD Plus		Additive Epsilon
Algorithm	Ranking	Algorithm	Ranking	Algorithm	Ranking
NSGA2	1.25	NSGA2	1.12	GWASFGA	1.03
GWASFGA	2.63	GWASFGA	2.64	NSGA2	2.05
SMS-EMOA	2.72	SMS-EMOA	2.72	SMS-EMOA	3.21
MOCell	3.40	MOCell	3.53	MOCell	3.71
MOMBI	6.11	MOMBI	6.05	MOMBI	6.03
MOMBI2	6.18	MOMBI2	6.24	MOMBI2	6.53
AGEMOEA2	6.83	AGEMOEA2	6.82	AGEMOEA	6.72
AGEMOEA	6.88	AGEMOEA	6.89	AGEMOEA2	6.72

Regarding the additive epsilon multi-objective quality indicator, GWASGFA achieves the best median values on the 15 studied problem instances, followed by NSGA2 with 15 second-best median values achieved. The differences between the NSGA2 and GWASFGA diversity preservation mechanisms could explain the result. NSGA2 environmental selection always keeps the extreme points of the Pareto approximation, i.e., the best-found solutions in every objective, the minimum purchase cost, and the maximum cash-back/reward points. Meanwhile, GWASFGA points half of its population toward the same extreme points by referencing the slightly improved ideal point and the other half towards the opposite of the extreme points (the worst in every objective) by referencing the worsened nadir point. Moreover, as an auxiliary diversity mechanism, the direction of the GWASFGA population depends on the set of weights. Therefore, the two diversity mechanisms in GWASFGA produce Pareto approximations that require less distance to weakly dominate the reference front. Contrary to the crowding distance (NSGA2), which strongly depends on the current extreme points (ideal point), neglecting the direction of the nadir point. The above result coincides with the Friedman average rankings from Table 5, where the best-ranked algorithm is GWASFGA, with an average rank of 1.03, followed by NSGA2, SMS-EMOA, MOCell, MOMBI, MOMBI2, AGEMOEA, and AGEMOEA2 with average rankings of 2.05, 3.21, 3.71, 6.03, 6.53, 6.72, and 6.72, respectively.

According to the inverted generational distance plus compute results, NSGA2 is the best-performing algorithm with 15 best median values. NSGA2 Pareto front approximations are notably close to the Pareto reference front; for all instances, the computed value is lower than $0.00007$ (the minimum possible value is zero). The second-best performer algorithm is GWASFGA, with nine second-best median values. The Friedman average rankings confirm the above result in Table 5, where the ranked algorithm is NSGA2 with an average rank of 1.12, followed by GWASFGA, SMS-EMOA, MOCell, MOMBI, MOMBI2, AGEMOEA2, and AGEMOA with average rankings of 2.64, 2.72, 3.53, 6.05, 6.24, 6.82, and 6.89, respectively.

6. Graphical Results

To have a graphical insight into the Multi-objective ISHOP-U formulation and the outputs produced by the two best performer algorithms NSGA-II and GWASFGA, we graph their Pareto front approximations with the best additive epsilon indicator from the 30 independent executions for two instances, Small 1 (S1), and Large 5 (L5) (see Figure 2). The x and y axes in Figure 2 graphs denote the final purchase cost and cash-back or reward, respectively. The decision to graph according to the additive Epsilon indicator is because it is the only studied quality indicator in which a studied algorithm, GWASFGA, outperforms NSGA2. As Figure 2 shows, GWASFGA struggles to uniformly cover the linear Pareto front shape in our proposed multi-objective problem formulation. The above is a known problem in multi-objective decomposition approaches [23,24,25], which works well with simple convex Pareto front shapes but struggles with complex ones. Since GWASFGA uses vector weights, the drawback still applies. However, GWASFGA, using vector weights in synergy with the ideal and nadir points, outperforms NSGA2 in finding solutions in the extremes of the Pareto front. The graphical results are consistent with the computed average Friedman rankings in Table 5. It is important to highlight that the real Pareto front is unknown because of the combinatorial nature of the problem.

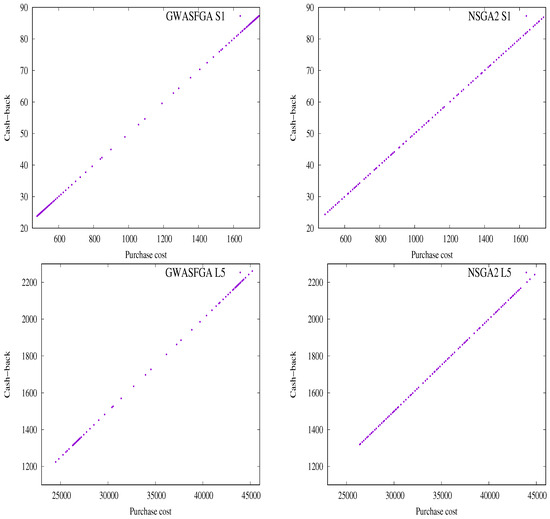
Figure 2. Best Pareto fronts provided by the two best-performing algorithms (NSGA2 and GWASFGA) according to additive Epsilon for the problem instances S1 and L5. For every independent execution, hypervolume is computed, and the Pareto front approximation with greater hypervolume is plotted.

7. Conclusions and Future Research

This paper introduces a novel multi-objective optimization problem, the Multi-Objective Internet Shopping Optimization Problem with multiple item Units (MO ISHOP-U). Formulating a multi-objective optimization problem is not as trivial as proposing to use two or more objectives/goals simultaneously; it is mandatory for every objective to conflict (improving one objective worsens the others). The above condition produces solutions that can not outperform each other, namely Pareto nondominated solutions, which produce a Pareto front when plotted by their objective values. In the case of nonconflicting objectives, one solution can outperform others, producing a single optimal point in the search space instead of a set.

We visually demonstrate the conflict among the objectives, resulting in linear Pareto front shapes. It is important to note that while the problem formulation may appear straightforward, it is far from trivial. There is no theoretical property to determine the real Pareto front. Furthermore, the real Pareto fronts for the problem are discrete and not continuous, with the potential for multiple disconnected (far away) regions in the real Pareto fronts. The limitation of using a multi-objective decomposition-based approach is evident in the proposed problem formulation, as seen in the GWASFGA results, which fail to produce an even, uniform spread Pareto front approximation due to the linear shape of the Pareto front. We recommend NSGA2 for our proposed problem because it consistently delivers the best results and performs well in linear Pareto front shapes. Moreover, NSGA2 obtains the best results according to hypervolume, which is a quality indicator that considers convergence and diversity of the Pareto front approximations. Hypervolume is the only quality indicator in the literature, i.e., Pareto-compliant [19], meaning approximations with higher hypervolume dominate the ones with lesser hypervolume. In future research, we want to try an exact combinatorial approach [26] to discover the real Pareto fronts of the studied instance problems, consequently improving the accuracy of the studied quality indicators. However, exact combinatorial approaches are exponential, and computational times may be unfeasible. Another interesting future research line is using a linear representation of the individuals (candidate solutions) as in [27,28] to improve the evolutionary algorithm results.