Product Demand Forecasting Method Based on Spatiotemporal Hypergraph Attention Network

Abstract

Traditional product demand forecasting has typically been modeled as a single time series problem relying exclusively on temporal information. However, temporal features alone are insufficient to capture complex demand dynamics in modern, interconnected markets. To address this limitation, we propose a product demand forecasting method based on a Spatiotemporal Hypergraph Attention Network (STHA), which jointly models temporal dependencies and higher-order spatial interactions among multiple market entities to enhance forecasting accuracy and robustness. STHA integrates a Long Short-Term Memory (LSTM) network with a Hawkes attention mechanism to capture temporal patterns and constructs a hypergraph to represent multi-entity relationships. It further incorporates hypergraph convolution and a hypergraph attention mechanism to dynamically aggregate higher-order spatial information and weight relational importance. Experiments on the Corporación Favorita sales dataset demonstrate that STHA substantially outperforms single time series benchmarks (ARIMA, LSTM, TCN, Transformer, and PatchTST), achieving notable reductions in MAE, RMSE, and MAPE—with improvements in MAPE exceeding 15 percentage points for certain stores. Compared with the graph-based STGCN model, STHA also exhibits superior robustness. These results demonstrate the effectiveness of STHA for complex multi-market-entity demand forecasting and highlight its potential as a reliable framework for improving inventory management and supply chain decision-making.

1. Introduction

Against the backdrop of increasingly competitive markets and progressively shorter product life cycles, product demand forecasting has become a critical capability for enterprises to optimize production planning, inventory management, and supply chain coordination. Accurate demand forecasting greatly enhances decision-making efficiency and resource allocation for a wide range of market entities, including manufacturers and retailers.

Product demand forecasting is intrinsically complex and challenging. Market demand is influenced by multiple factors, such as seasonal fluctuations and economic cycles, leading to significant volatility and unpredictability. Moreover, consumer purchasing behavior is often affected by external factors such as advertising campaigns, promotional activities, and social trends, making demand patterns more complex and difficult to capture. Current forecasting approaches primarily rely on time series analysis, which identifies patterns from historical data to construct mathematical models for predicting future trends [1]. These methods can be broadly classified into statistical, machine learning, deep learning, and graph-based techniques [2,3]. Subsequently, hybrid models have emerged to combine the strengths of different approaches. For example, Ou-Yang et al. incorporated online sentiment data into a CNN-LSTM hybrid model to forecast automotive sales trends [4]. Chen et al. introduced a method integrating GRU and LightGBM to effectively predict sales of short-shelf-life products [5]. Nevertheless, despite substantial progress in diversity and accuracy, existing forecasting paradigms still face two fundamental limitations.

First, most studies model the demand fluctuations of individual products as independent processes, overlooking the widespread higher-order nonlinear correlations among market entities. This simplification reduces a complex systemic problem to a set of isolated single time series forecasting tasks. In reality, the sales volume of a product is influenced not only by the operational characteristics of its own market entity but also by synergistic, competitive, or complementary effects from other entities in the region, driven by factors such as geographical proximity or similarities in business format and product category composition. For instance, geographically adjacent market entities often exhibit synchronized demand fluctuations due to overlapping customer bases or supply chain coordination, reflecting evident spatial aggregation effects. Similarly, entities with comparable business formats (e.g., flagship stores, convenience stores, membership stores) or product category structures (e.g., fresh food-oriented, daily necessities-oriented) tend to share similar customer attributes and consumption scenarios, resulting in similar temporal response patterns. Such high-order interactions beyond pairwise relationships are pervasive in real-world systems, yet they remain largely overlooked in most forecasting models.

Second, studies that incorporate graph structures to model inter-entity associations remain limited, and those that exist are constrained by the representational capacity of simple graphs. Simple graphs are restricted to pairwise relationships, which fundamentally limits their ability to model higher-order interactions. As a result, they cannot naturally represent group-level associations—such as those arising when multiple market entities fall within the same regional industrial cluster or exhibit similar business formats and product category structures. Although hypergraphs have been initially applied in other fields to model such multi-node relationships, existing hypergraph-based approaches tend to inadequately address structural noise. They generally lack the ability to differentiate the importance of different hyperedges with respect to the forecasting target, resulting in suboptimal model performance.

Taken together, these methodological gaps lead to significant practical deficiencies. By overlooking the interdependent mechanisms embedded within industrial cluster economies, existing models fail to capture the complex, system-wide sales dynamics that arise from multi-market-entity interactions. Consequently, they struggle to sense or adapt to high-volatility shocks induced by sudden events such as localized promotions, supply chain disruptions, or shifts in social trends. This limitation directly results in reduced forecasting accuracy and insufficient robustness in multi-market-entity product demand prediction tasks. In practical applications, these shortcomings can cascade into inefficient inventory allocation, missed sales opportunities during demand surges, and delayed responses to market disturbances. Ultimately, such constraints weaken the competitiveness and operational resilience of market entities operating in complex and rapidly evolving market environments.

To address these issues, this paper proposes a product demand forecasting method based on a Spatiotemporal Hypergraph Attention Network (STHA). The primary objective of this study is to leverage the constructed STHA model to transform product demand forecasting from independent single time series problems into interconnected multi-time-series problems. Through this approach, the model is intended to more accurately characterize real-world market environments in which multiple market entities interact dynamically, thereby improving forecasting accuracy and robustness and providing enterprises with more reliable and scientifically grounded decision support.

The principal contribution of this work lies in the development of a unified framework that offers a hierarchical solution integrating temporal dependency modeling and spatial correlation learning:

• At the temporal modeling level, we move beyond traditional temporal attention mechanisms by introducing a Hawkes attention mechanism, which more effectively reflects real-world market dynamics. By modeling the self-exciting effects present in historical demand event sequences, this approach captures inherent temporal dependencies more accurately, generating more refined and informative temporal features for subsequent spatial correlation analysis.
• At the spatial association level, we extend the hypergraph structure—widely used in financial applications—to the product demand forecasting task. By constructing a hypergraph that incorporates multi-dimensional attributes such as geographical location, business format, and product category, we overcome the limitation of conventional simple graphs that only capture binary relationships. This enables more flexible and precise modeling of complex higher-order nonlinear correlations among market entities.
• At the information aggregation level, we introduce a dynamic hypergraph attention mechanism that adaptively learns the importance scores of different market entities and their multi-dimensional associations with respect to the forecasting target. This mechanism suppresses irrelevant connections and noise effects, thereby significantly enhancing the model’s feature selection ability and robustness.

Experimental results demonstrate that the proposed STHA method effectively integrates spatiotemporal information. In scenarios involving multiple market entities, it achieves higher accuracy and greater robustness compared with current baseline models. This study presents a novel framework that integrates multi-dimensional data and multi-time-series modeling into product demand forecasting, offering considerable theoretical value and practical implications.

2. Related Works

2.1. Traditional Product Demand Forecasting Methods

Historically, product demand forecasting methods were primarily based on statistical models. The Autoregressive Integrated Moving Average (ARIMA) model, proposed by Box and Jenkins [6], established a systematic framework for time series forecasting and has since served as a foundational model in this domain. For instance, Wang et al. developed an ARIMA-based method for customer demand prediction and applied it in a supply chain context [7]. This led to the development of numerous ARIMA variants designed for diverse industrial forecasting needs. Olsson and Soder, recognizing the significant impact of seasonal variations on power demand, employed a Seasonal Autoregressive Integrated Moving Average (SARIMA) model for electricity market price prediction [8]. Although these statistical methods often perform well in short-term forecasting, they typically assume linear data patterns, limiting their capacity to capture nonlinear characteristics and long-range dependencies present in complex market environments.

With advancements in computational power and data processing techniques, machine learning and deep learning approaches have gained prominence. Models such as Support Vector Machines (SVM) [9], Long Short-Term Memory (LSTM) networks [10], Convolutional Neural Networks (CNN) [11], Gated Recurrent Units (GRU) [12], and Light Gradient Boosting Machines (LightGBM) [13] significantly enhance the ability to model nonlinear relationships and have demonstrated superior performance with high-dimensional data. For example, Sun constructed a hybrid forecasting model using LightGBM and LSTM for product sales prediction, achieving promising performance [14]. However, most of these models assume that the demand fluctuations of individual products are independent, overlooking potential spatial correlations and thus limiting their ability to exploit latent interactions among different demands. Following the introduction of the Transformer model [15], which is based on the attention mechanism, temporal attention [16] has received considerable research interest. This mechanism dynamically allocates importance weights to different time steps, thereby enhancing the model’s ability to capture critical temporal features. Temporal attention mechanisms have been widely applied in product demand forecasting tasks. For example, Huang et al. proposed a transfer learning approach named TransTLA, based on the attention mechanism, to address household appliance sales forecasting in small towns [17].

2.2. Graph-Structured Methods

In recent years, with the development of Graph Neural Networks (GNNs), researchers have begun to incorporate graph structures into time series forecasting, extending the task from a purely temporal dimension to a spatiotemporal one. Feng et al. introduced temporal convolutions into Graph Convolutional Networks (GCNs), demonstrating the feasibility of leveraging stock relationships to improve forecasting performance [18]. Li et al. utilized spatial graph neural networks for product demand prediction, with experimental results confirming the superiority of graph-based methods over non-graph methods in this task [19]. Kim et al. proposed a graph attention network for stock movement prediction, noting that constructing an extensive set of pairwise relationships can introduce noise, thereby degrading predictive performance [20]. While these studies confirm that incorporating structural relationships enhances performance, the simple graph structures they rely on, along with their corresponding attention mechanisms, have inherent limitations. Since each edge in a simple graph can only connect two nodes, it struggles to represent the higher-order relationships common in real-world scenarios. For instance, in product demand forecasting, a single promotional event affecting five market entities would require a simple graph to construct ten distinct edges to represent all pairwise relationships. This not only introduces substantial noise but also prevents the model from representing the promotional event as a holistic entity, thus limiting its representation capacity. Furthermore, the attention mechanism in simple graphs can only capture importance differences within pairwise relationships and cannot accommodate the importance variations between hyperedges and nodes in many-to-many relationships.

Consequently, hypergraphs—a generalized graph structure—have been introduced into spatiotemporal forecasting. Hypergraphs can connect multiple nodes simultaneously via a single hyperedge, making them naturally suited for modeling group interactions [21]. Wang et al. applied hypergraph structures to metro passenger flow prediction [22], while Su et al. employed hypergraph convolutional networks for MOOC course recommendation [23]. Although these studies have shown potential, research applying hypergraph structures to the field of product demand forecasting remains largely unexplored. In exploring methods for modeling complex correlations in multiple time series, the hypergraph-based spatiotemporal attention architecture proposed by Sawhney et al. for stock selection via a learning-to-rank approach offers a promising direction [24]. Although their ranking task differs significantly from the numerical regression forecasting problem addressed in this paper, both in objectives and evaluation metrics, their architecture offers valuable insights for tackling multi-time-series product demand forecasting.

3. Methodology

3.1. Spatiotemporal Hypergraph Attention Network

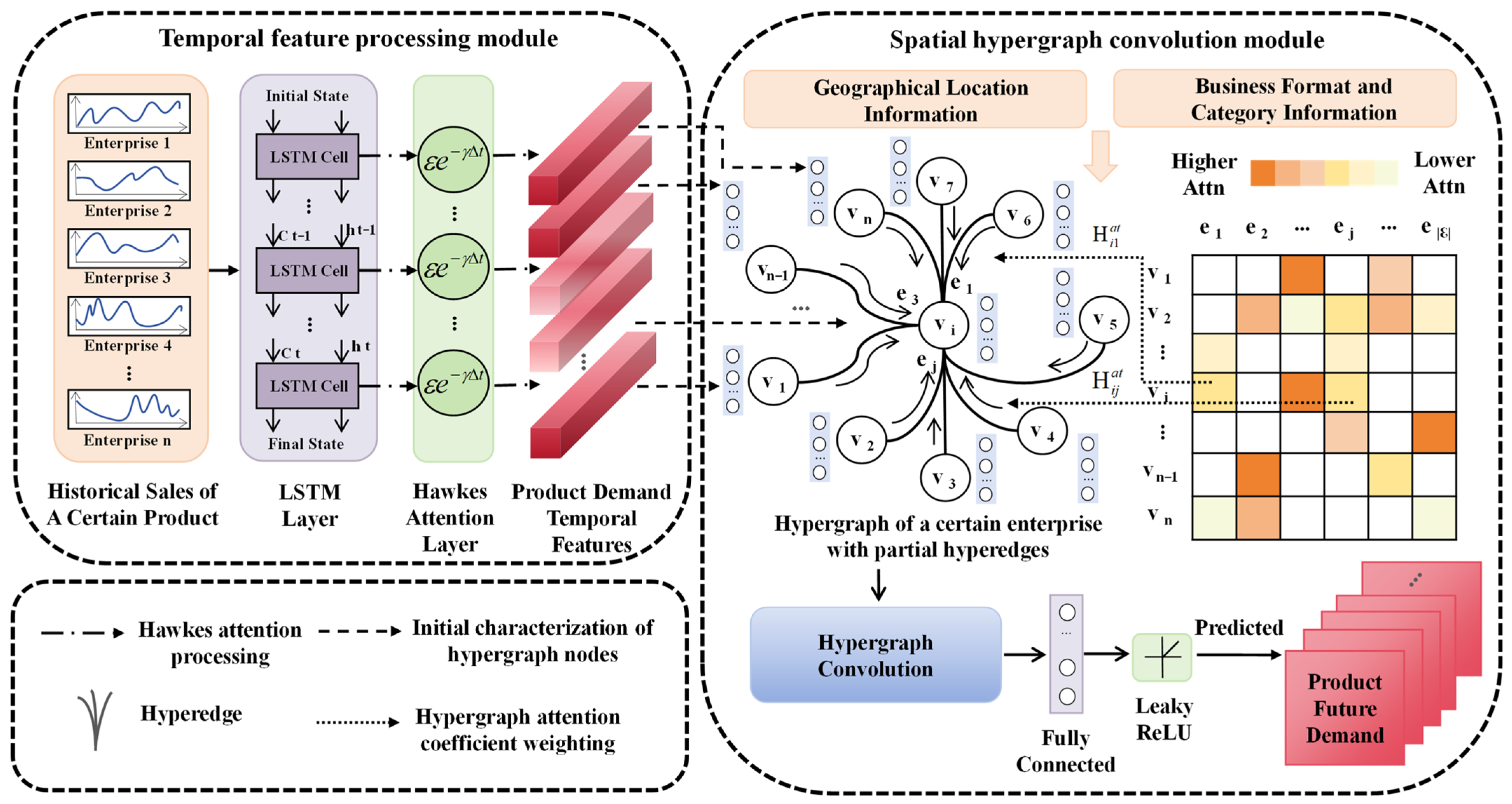
The proposed Spatiotemporal Hypergraph Attention Network (STHA) comprisestwo main components: a temporal feature processing module and a spatial hypergraph convolution module (Figure 1). The model takes as input the historical sales data from all market entities over the past t days. First, in the temporal dimension, the temporal feature processing module employs a Long Short-Term Memory (LSTM) network to extract temporal dependency information from the sales data of each market entity. It incorporates a Hawkes process-based temporal attention mechanism to dynamically evaluate the importance of different historical time points for future predictions. This module outputs a temporal feature representation for each market entity. Subsequently, in the spatial dimension, a hypergraph is constructed based on spatial relationships—such as geographical proximity and groupings based on business format and product category—to represent complex higher-order correlations among multiple market entities. The spatial hypergraph convolution module takes the output from the temporal feature processing module as the initial node features of the hypergraph. It enables higher-order message passing and feature aggregation through hypergraph convolution layers and incorporates a hypergraph attention mechanism to adaptively learn the contribution scores of different spatial relationships to the prediction outcome. This enables the effective adjustment of external market influences on an entity’s own demand during joint multi-time-series forecasting tasks. The module outputs node representations enhanced by spatial relationships, integrating both the entity’s own historical patterns and influences from related market entities. Finally, the output of the spatial hypergraph convolution module is passed through a fully connected output layer followed by a nonlinear activation function to generate the final product demand predictions for all market entities. Through the coordinated design of its spatiotemporal modules, the framework enables unified modeling of temporal dynamics and spatial dependencies, thereby significantly improving the model’s ability to capture multi-dimensional interaction patterns in complex market environments.

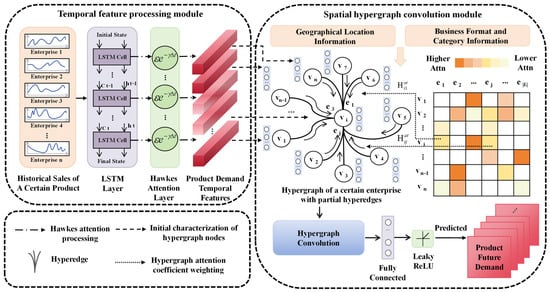
Figure 1. Product demand forecasting process based on spatiotemporal hypergraph attention network.

3.2. Temporal Feature Processing Module

To better capture the temporal characteristics within the historical sales data of various market entities, this section presents a specialized temporal feature processing module for modeling long-range dependencies in time series. This module primarily consists of an LSTM network and a Hawkes Attention (HA) mechanism.

First, the primary advantage of the LSTM lies in its gated mechanisms and cell state update strategy. These components enable the selective retention of historical information, making the LSTM particularly suitable for processing sequential data with long-term dependencies. Owing to these properties, LSTM is widely adopted in product demand forecasting, as it enables the extraction of key features from historical sales data and supports more accurate forecasting of future demand trends based on past sales patterns. The computations for the forget gate (f_t), input gate (i_t), candidate cell state (g_t), updated cell state (c_t), output gate (o_t), and hidden state (h_t) are defined as follows:

$$f_t=\sigma ({\mathit{W}}_{xf}{x}_t+{\mathit{W}}_{hf}{h}_{t-1}+b_f)$$

(1)

$$i_t=\sigma ({\mathit{W}}_{xi}{x}_t+{\mathit{W}}_{hi}{h}_{t-1}+b_i)$$

(2)

$$g_t=\tanh ({\mathit{W}}_{xg}{x}_t+{\mathit{W}}_{hg}{h}_{t-1}+b_g)$$

(3)

$$c_t=f_t{c}_{t-1}+i_t{g}_t$$

(4)

$$o_t=\sigma ({\mathit{W}}_{xo}{x}_t+{\mathit{W}}_{ho}{h}_{t-1}+b_o)$$

(5)

$$h_t=o_t\tanh \left(c_t\right)$$

(6)

Here, W_xf, W_hf, W_xi, W_hi, W_xg, W_hg, W_xo, W_ho are weight matrices; b_f, b_i, b_g, b_o are bias vectors; x_t denotes the input at the current time step; c_t−1 represents the cell state from the previous time step; h_t−1 represents the hidden state from the previous time step; σ is the Sigmoid function, and tanh is the hyperbolic tangent function.

In addition, for product demand forecasting tasks, demand events for market entities (e.g., social media trends, product promotions) often exhibit a significant self-exciting effect. This means that one event can substantially increase the probability of subsequent related demand events occurring in the short term, with this influence decaying over time. For instance, the popularity of a product can trigger a surge in purchases of the same or complementary products within the same region, leading to a clustered surge of regional demand. However, as time passes and the hype subsides while demand becomes saturated, demand for the product gradually declines. Therefore, to better capture this phenomenon in product demand forecasting, this paper proposes a temporal attention mechanism based on the Hawkes process.

The temporal attention mechanism assigns distinct weights to different time steps, enabling the model to automatically focus on historical sales information that is more critical for future demand prediction, thereby enhancing forecasting accuracy and model flexibility. The calculation process for the basic attention weights is as follows:

$${\beta }_{\tau }={\displaystyle \frac{exp\left(h_{\tau }^T\mathit{Q}{h}_t\right)}{{\displaystyle \sum _{\tau }exp\left(h_{\tau }^T\mathit{Q}{h}_t\right)}}}$$

(7)

$${\lambda }_{\tau }={\beta }_{\tau }{h}_{\tau }$$

(8)

Here, h_τ represents the demand hidden state for historical date τ, h_t represents the demand hidden state for the current date t, Q is a learnable weight matrix, and λ_τ denotes the output after aggregating historical temporal features weighted by the basic attention weights.

The Hawkes process [25] is a point process characterized by a self-exciting property. Its core idea is to quantify the residual impact of historical events on the current instantaneous intensity through a decay kernel function, thereby capturing the time-varying principle that recent events exert greater influence than distant ones. This paper explicitly incorporates the decay and excitation effects of the Hawkes process into the basic attention representation, generating an enhanced modulated temporal feature z_t, as detailed below:

$$z_t={\displaystyle \sum _{\tau =0,\Delta t>0}({\lambda }_{\tau }+\epsilon max({\lambda }_{\tau },0\left)e^{-\gamma \Delta t}\right)}$$

(9)

Here, Δt denotes the time interval between the current date t and the historical date τ, ε is a learnable excitation parameter, γ is a learnable decay parameter, and e^−γΔt is termed the exponential decay kernel.

The Hawkes attention mechanism retains the flexibility of the standard temporal attention mechanism in capturing complex patterns while incorporating temporal dynamics aligned with business intuition (namely, that recent events are generally more important than distant ones). This design enhances both the predictive performance and the interpretability of the model.

For the historical sales sequence of each market entity, this module first feeds it into the LSTM to generate a sequence of hidden states containing long-term dependency information. Subsequently, these hidden states are fed into the Hawkes attention mechanism, which dynamically aggregates all historical information by computing time-decay-weighted attention scores. The final output is an enhanced feature representation that incorporates the self-exciting effect. This representation will serve as the initial node feature for the corresponding market entity in the subsequent hypergraph structure.

3.3. Spatial Hypergraph Convolution Module

3.3.1. Hypergraph

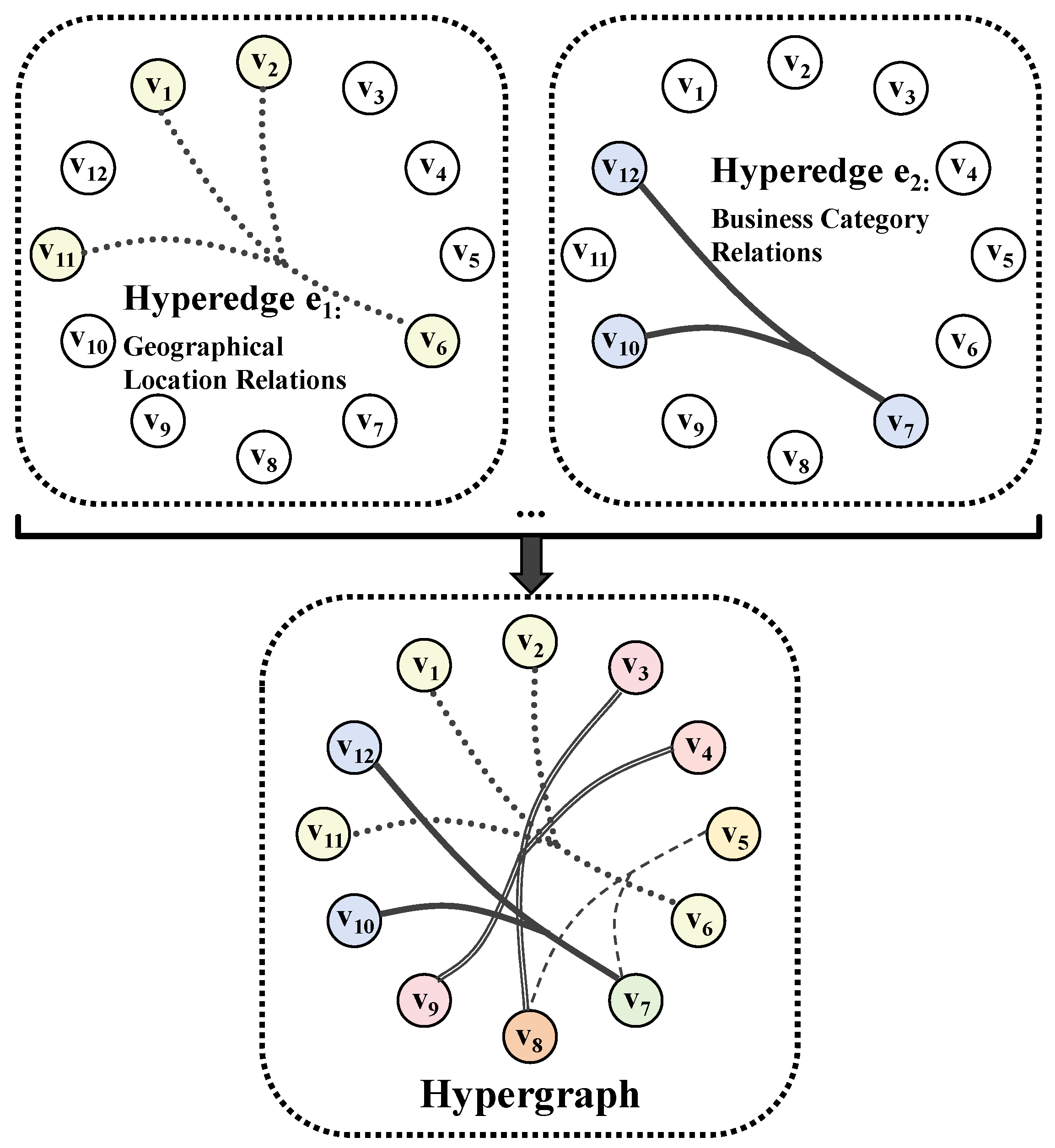
This section models interdependencies among market entities by constructing a hypergraph G = (V,ε,D), where hyperedges represent higher-order relationships among market entities. A hypergraph is a generalization of a simple graph. In a simple graph, each edge can connect only two vertices, whereas in a hypergraph, each hyperedge can connect two or more vertices. If all hyperedges connect only two nodes, the hypergraph degenerates into a simple graph [26].

In the hypergraph, each vertex v ∈ V represents a market entity within the region, and each hyperedge e ∈ ε connects a set of related market entities {v₁, v₂,…, v_n} ∈ V. Each hyperedge e is assigned a positive weight d(e), and all weights are stored in a diagonal matrix D ∈ R^|ε|×|ε|. Initially, D is set to the identity matrix, indicating that all hyperedges are assigned equal weights. A schematic diagram of the market entity hypergraph is shown in Figure 2.

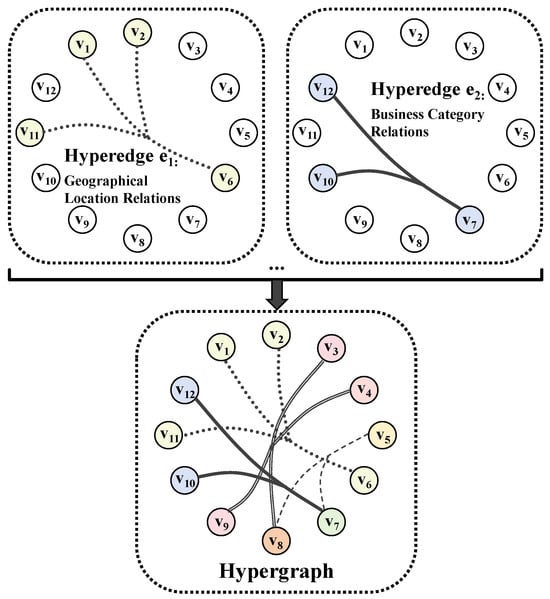
Figure 2. A hypergraph of market entities constructed based on geographical location and business format and product category groupings.

In this paper, hyperedges in the market entity hypergraph are constructed based on the following two types of relationships:

• Geographical Location Hyperedges: These hyperedges are formed according to the geographical proximity of market entities. Specifically, this category includes two geographical scales: (a) market entities located within the same province/state and the same city, capturing spatial aggregation effects at the intra-city level; and (b) market entities located within the same province/state but distributed across different cities, characterizing macro-level spatial correlations across cities within a region.
• Business Format and Product Category Hyperedges: Market entities are grouped into categories according to their business format and product category structure, such as full-category flagship stores, fresh food standard supermarkets, daily necessities standard supermarkets, food-oriented community stores, and convenience stores. Each category corresponds to one business format and product category hyperedge, and all market entities belonging to the same category form the vertex set of that hyperedge.

The hypergraph G can be equivalently represented by an incidence matrix H ∈ R^|V|×|ε|, formally defined as

$$h (v,e)=\left\{\begin{array}{c}1,v\in e\hfill \\ 0,v\notin e\hfill \end{array}\right.$$

(10)

The degree of each vertex v, denoted by β(v) and encoded in the vertex degree diagonal matrix D_v ∈ R^|V|×|V|, is calculated as

$$\beta (v)={\displaystyle \sum _{e\in \epsilon }d\left(e\right)h(v,e)}$$

(11)

The degree of each hyperedge e, denoted by δ(e) and encoded in the hyperedge degree diagonal matrix D_e ∈ R^|ε|×|ε|, is calculated as

$$\delta (e)={\displaystyle \sum _{v\in V}d\left(e\right)h(v,e)}$$

(12)

3.3.2. Hypergraph Attention Mechanism

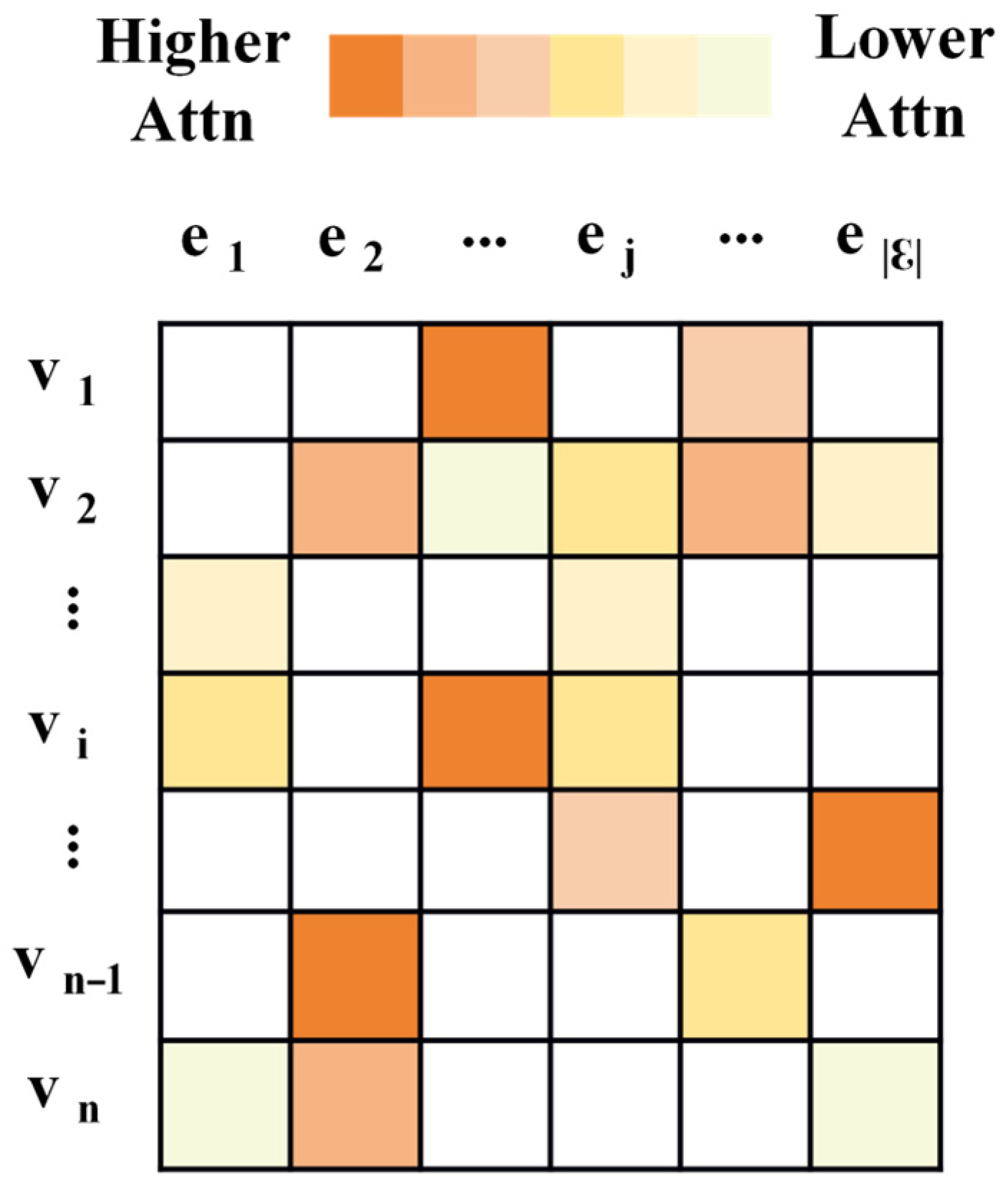
To capture the differential influence of market entity relationships on product demand fluctuations, this paper introduces a hypergraph attention mechanism built upon the incidence matrix H. The mechanism adaptively learns the importance weights of individual hyperedges by leveraging the temporal features of product sales together with hyperedge features derived from geographical location information and business-format/product-category groupings. This process yields an attention-weighted, enhanced incidence matrix H^at, as illustrated in Figure 3. This operation effectively bridges the Hawkes attention mechanism with spatial hypergraph convolution, thereby enhancing the model’s ability to achieve joint spatiotemporal representation.

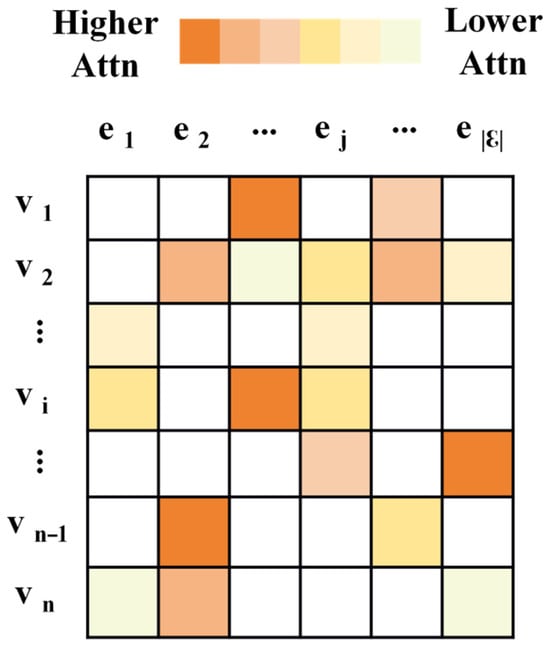
Figure 3. Reinforcement association matrix based on hypergraph attention.

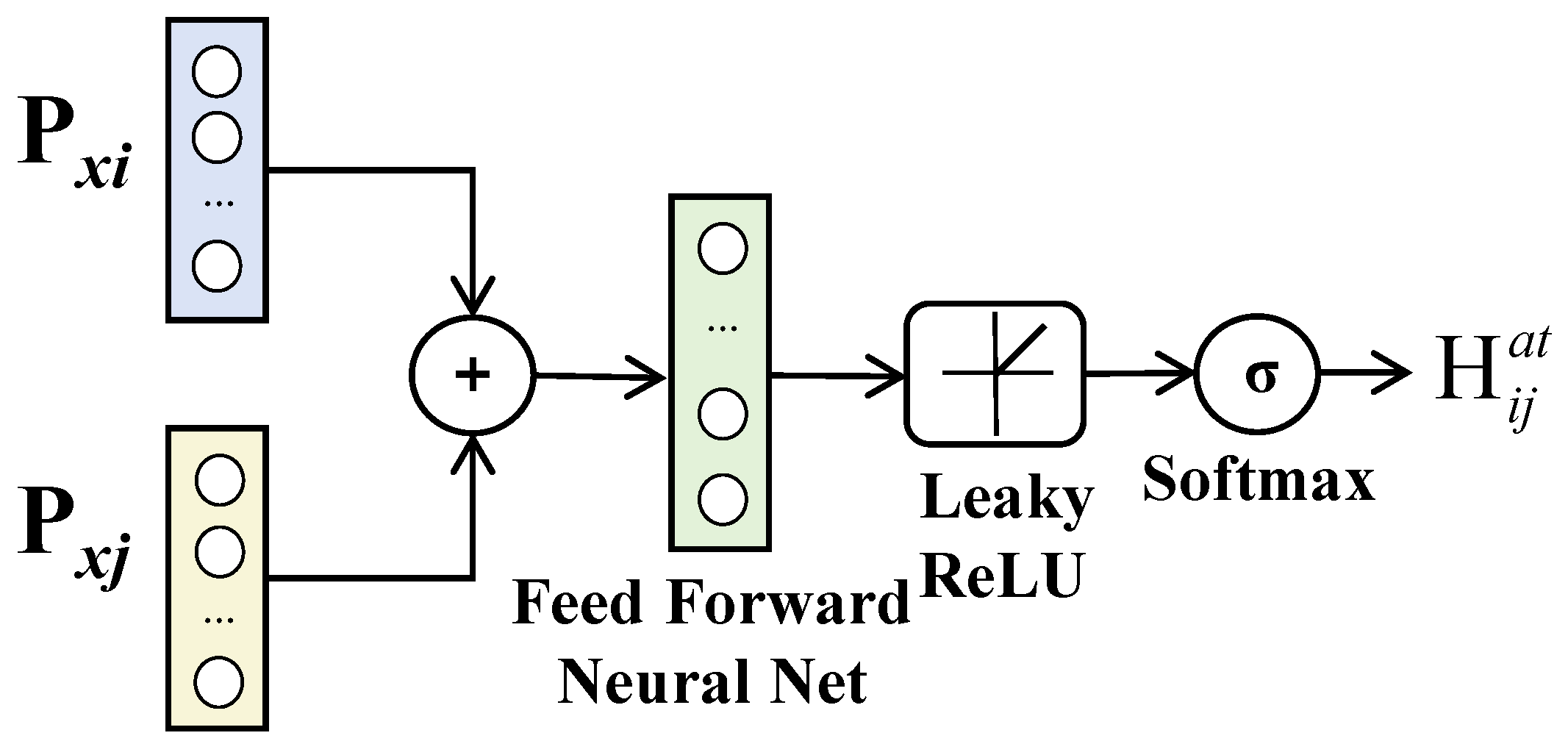
Formally, for each node v_i ∈ V and its associated hyperedge e_j ∈ ε, an attention coefficient is computed using the temporal feature x_i of product sales and the corresponding hyperedge-level feature x_j. This coefficient quantifies the importance of the corresponding relationship e_j for modeling product sales dynamics. The specific calculation formula is as follows:

$$H_{ij}^{at}={\displaystyle \frac{exp(LeakyReLU({\overrightarrow{a}}^T[{\mathit{P}}_{x_i}\oplus {\mathit{P}}_{x_j}]) )}{{\displaystyle \sum _{n\in Ni}exp(LeakyReLU({\overrightarrow{a}}^T[{\mathit{P}}_{x_i}\oplus {\mathit{P}}_{x_n}]) )}}}$$

(13)

Here, P is a learnable weight matrix applied to linearly transform the temporal and hyperedge features, ⊕ denotes the concatenation operation, $\overrightarrow{a}$ is a learnable attention vector used to compute the similarity between the transformed temporal and hyperedge features, LeakyReLU is the activation function, and N_i represents the neighborhood of node x_i. The computational process is depicted in Figure 4.

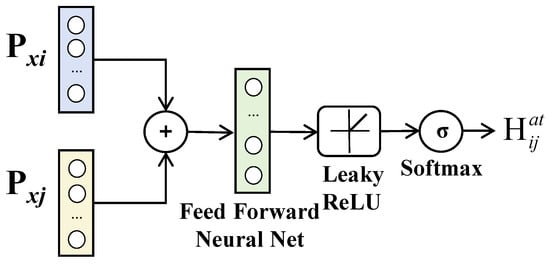
Figure 4. Calculation process of the attention coefficient in the hypergraph attention mechanism.

3.3.3. Hypergraph Convolution

To aggregate higher-order relational information among different market entities regarding product sales fluctuations, this paper introduces a hypergraph convolution method [27] over the hypergraph structure. First, a hypergraph convolutional layer H_conv is constructed. Its input is a temporal feature matrix X^l ∈ R^|V|×F(l), where F(l) denotes the dimensionality of the original temporal features. This convolution operation models the higher-order relationships of the hypergraph G, mapping the original features X^l to new node features X^l+1 ∈ R^|V|×F(l+1) with dimensionality F(l + 1). The specific computation is given by

$${\mathit{X}}^{(l+1)}=HConv({\mathit{X}}^{\left(l\right)},{\mathit{H}}^{at},\mathit{P})=ELU({\mathit{D}}_v^{-{\displaystyle \frac{1}{2}}}{\mathit{H}}^{at}\mathit{W}{\mathit{D}}_e^{-1}{\mathit{H}}^{{at}^T}{\mathit{D}}_v^{-{\displaystyle \frac{1}{2}}}{\mathit{X}}^{\left(l\right)}\mathit{P})$$

(14)

Here, H^at is the enhanced incidence matrix, P is a learnable weight matrix, D_v is the vertex degree diagonal matrix, D_e is the hyperedge degree diagonal matrix, and ELU is the Exponential Linear Unit activation function.

Following the construction of the hypergraph convolutional layer and the hypergraph attention mechanism, a multi-head architecture is employed to stabilize the training process. Formally, K independent heads perform hypergraph convolution based on the enhanced incidence matrix, and their outputs are concatenated, expressed as follows:

$${\mathit{X}}^{(l+1)}=\underset{k=1}{\overset{K}{\oplus }}ELU({\mathit{D}}_v^{-{\displaystyle \frac{1}{2}}}{\mathit{H}}_k^{at}\mathit{W}{\mathit{D}}_e^{-1}{\mathit{H}}_k^{{at}^T}{\mathit{D}}_v^{-{\displaystyle \frac{1}{2}}}{\mathit{X}}^{(l)}{\mathit{P}}_k)$$

(15)

Here, ${\mathit{H}}_k^{at}$ and P_k are the enhanced incidence matrix and weight matrix for the k-th head, respectively, and ⊕ denotes the concatenation operation.

This module first feeds the initial node representations of each market entity into the hypergraph convolutional layer. Leveraging the hypergraph structure and hypergraph attention mechanism, it models information propagation under higher-order associations. During this process, nodes interact and aggregate features with other nodes through their incident hyperedges, generating spatially enhanced node representations. Finally, the enhanced representations of all market entities are fed into a fully connected output layer to obtain the final demand predictions.

3.4. Notation Summary and Algorithmic Overview

The STHA model jointly captures the complex dependencies among multiple market entities through the coordinated operation of its temporal feature processing module and spatial hypergraph convolution module. The mathematical formulation of these components involves numerous symbols, matrix operations, and iterative procedures. To improve clarity and ensure reproducibility, we first provide a comprehensive notation table (Table 1), which systematically summarizes all key symbols, their meanings, dimensionality, and the specific stages of the model in which they are utilized.

Table 1. Comprehensive notation table for the STHA model.

Symbol	Description	Shape/Dimension	Stage/Usage
General Symbols
t	Current time step index	Scalar	Temporal Module
τ	Historical time step index	Scalar	Temporal Module
V	Set of market entities	|V|	Hypergraph Construction
|V|	Number of market entities	Scalar	Hypergraph Construction
ε	Set of hyperedges	|ε|	Hypergraph Construction
|ε|	Number of hyperedges	Scalar	Hypergraph Construction
Temporal Module
xt	Input at current time step	Rd_in	LSTM Input
ht	Hidden state at time t	Rd_hidden	LSTM Output, Hawkes Attention
hτ	Hidden state at historical time step τ	Rd_hidden	Hawkes Attention
ft	Forget gate at time t	Rd_hidden	LSTM
it	Input gate at time t	Rd_hidden	LSTM
gt	Candidate cell state at time t	Rd_hidden	LSTM
ct	Updated cell state at time t	Rd_hidden	LSTM
ot	Output gate at time t	Rd_hidden	LSTM
Wxf, Whf	Weight matrices for forget gate	Rd_hidden×d_in, Rd_hidden×d_hidden	LSTM
Wxi, Whi	Weight matrices for input gate	Rd_hidden×d_in, Rd_hidden×d_hidden	LSTM
Wxg, Whg	Weight matrices for candidate cell state	Rd_hidden×d_in, Rd_hidden×d_hidden	LSTM
Wxo, Who	Weight matrices for output gate	Rd_hidden×d_in, Rd_hidden×d_hidden	LSTM
bf, bi, bg, bo	Bias vectors for LSTM gates	Rd_hidden	LSTM
βτ	Basic attention weight for historical step τ	Scalar	Hawkes Attention
λτ	Weighted historical feature	Rd_hidden	Hawkes Attention
Q	Learnable weight matrix for attention	Rd_hidden×d_hidden	Hawkes Attention
Δt	Time interval between current time t and historical time τ	Scalar	Hawkes Attention
γ	Learnable decay parameter	Scalar	Hawkes Attention
zt	Hawkes-modulated temporal feature	Rd_hidden	Hawkes Attention
Hypergraph Construction
G	Hypergraph	(V,ε,D)	Hypergraph Representation
v	Vertex (market entity)	v ∈ V	Hypergraph
e	Hyperedge	e ∈ ε	Hypergraph
D	Diagonal matrix of hyperedge weights	R|ε|×|ε|	Hypergraph
H	Incidence matrix of hypergraph	R|V|×|ε|	Hypergraph Representation
β(v)	Degree of vertex v	Scalar	Hypergraph
δ(e)	Degree of hyperedge e	Scalar	Hypergraph
Dv	Diagonal matrix of vertex degrees	R|V|×|V|	Hypergraph Convolution
De	Diagonal matrix of hyperedge degrees	R|ε|×|ε|	Hypergraph Convolution
Hypergraph Attention and Convolution
xi	Temporal feature of node i	RF(0)	Hypergraph Attention
xj	Feature of hyperedge ej	RF(l)	Hypergraph Attention
P	Learnable weight matrix for linear transformation	RF(l)×F(l+1)	Hypergraph Attention and Convolution
Ni	Neighborhood of node i	Set of hyperedges	Hypergraph Attention
Hat	Attention-enhanced incidence matrix	R|V|×|ε|	Output of Hypergraph Attention, Input to Convolution
Xl	Node feature matrix at layer l	R|V|×F(l)	Input/Output of Hypergraph Convolution
F(l)	Feature dimension at layer l	Scalar	Hypergraph Convolution
K	Number of attention heads	Scalar	Hypergraph Convolution
L	Number of hypergraph convolution layers	Scalar	Hypergraph Convolution
Algorithm Pseudocode
X0	Initial spatial hypergraph node features	R|V|×F(0)	Input to Hypergraph Convolution
Y	Predicted sales matrix	R|V|×1	Algorithm output

In addition, to present a concise overview of the complete computational workflow, we introduce the pseudocode of STHA in Algorithm 1. This pseudocode integrates the two core modules into a unified end-to-end prediction pipeline. It clearly delineates each step—from processing historical sales data and extracting temporal representations, to constructing the hypergraph, performing attention-weighted hypergraph convolutions, and ultimately generating the final demand predictions. This algorithmic description is intended to assist readers in understanding the overall implementation logic of the proposed method.

Algorithm 1: Pseudocode for product demand prediction method based on spatiotemporal hypergraph attention network.

Input: historical sales matrix X ∈ R|V|×t, hyperedge definitions (geography location, business format and product category) Output: predicted sales matrix Y ∈ R|V|×1 1.# Temporal Feature Processing Module for each store i in V do:   # Step 1.1: LSTM for temporal feature extraction   {hi,1,…,hi,t} = LSTM(xi)  # xi: sales sequence of store i   # Step 1.2: Hawkes attention mechanism   for each historical time step τ = 1 to t do:   Compute basic attention weight βτ  # Equation (7)   Compute weighted historical feature λi,τ = βτhi,τ  # Equation (8)   # After processing all historical steps, compute the Hawkes-modulated feature   zi = HawkesModulation(λi,1,…,λi,t)  # Equation (9) 2. # Construct Hypergraph G = (V,ε,D) V = {v1, v2,…, v|V|} # nodes: stores ε = {e1, e2,…, e|ε|} # hyperedges H = construct incidence matrix H ∈ {0,1}|V|×|ε|  # Equation (10) Dv,De= compute vertex and hyperedge degree matrices  # Equations (11) and (12) 3. # Initial Spatial Hypergraph Node Features X0 = [z1, z2,…, z|V|]T # shape: |V| × F(0) 4. # Hypergraph Attention Mechanism and Multi-layer Hypergraph Convolution for l = 0 to L − 1 do:  # L: hypergraph convolution layers   for each hyperedge ej in ε do:     # Step 4.1: Compute hyperedge features xj for the current layer     $x_j^l$ = MEAN({Xl[i,:]|vi ∈ ej})     # Step 4.2: Compute hypergraph attention matrix Hat     for each node vi in ej do:       # Here xi is the node feature at layer l (updated through hypergraph       # convolution), not the initial sales sequence of store i       Scoreij = LeakyReLU($\overrightarrow{a}$T[Pxi⊕Pxj])  # Equation (13)       $H_{ij}^{at}$ = exp(Scoreij)/∑n ∈Niexp(Scorein)  Equation (13)   # Step 4.3: Multi-Head Hypergraph Convolution   for each head k = 1 to K do: # K: heads     $X_k^{l+1}$$= \mathrm{HConv}({\mathit{X}}^l, H_k^{at}$, Pk)  # Equation (14)   ${\mathit{X}}^{l+1} = \mathrm{Concatenate}(X_1^{l+1}$$, X_2^{l+1}$$, \dots , X_k^{l+1}$)  # Equation (15) 5. # Prediction Y = FullyConnectedLayer(XL) return Y

3.5. Dataset and Experimental Setup

3.5.1. Dataset Description and Data Processing

The experimental dataset used in this study was obtained from Kaggle [28] and consists of real sales records from the multiple stores of Corporación Favorita, a large grocery retailer in Ecuador. The dataset covers sales information and store-related details from 54 stores across various states in Ecuador. The historical sales data spans from 1 January 2013 to 15 August 2017, covering more than one thousand days, with daily records capturing the daily sales performance of various products across the stores. The key fields include date, product ID, store ID, and unit sales, with unit sales serving as the target variable for prediction. Additionally, the dataset provides several auxiliary tables to facilitate feature construction, including

• Store Information Table: which contains basic store attributes such as store ID, city, state, store class, and business format and product category group.
• Product Information Table: which includes product properties such as product ID, product family, product class, and the perishable status of the product.

The stores’ geographical locations and business format and product category groups are leveraged to model the spatial relationships among the stores.

Given the large scale of the original dataset, a subset was selected for further analysis. Following preliminary experiments involving multiple stores and products, we randomly selected 12 stores as the study focus. For these stores, historical sales data for product #502331 between 1 January 2017, and 15 August 2017, was extracted to form a multi-time-series dataset for detailed experimental evaluation. The selection of this specific period was guided by four criteria: (i) Data Completeness—the period provides continuous, high-quality daily sales records without systemic anomalies; (ii) Representative Dynamics—it captures seasonal variations, weekends, and regional holidays, reflecting typical demand patterns; (iii) Event Stability—no major nationwide disruptions occurred during this interval, minimizing outlier bias; and (iv) Training Sufficiency—its length and continuity enable effective learning of temporal and spatial dependencies under a chronological train-test split. The selected stores exhibit diverse geographical distributions across Ecuador, including scenarios where stores are located within the same city and state, within the same state but different cities, and across different states. Simultaneously, these stores belong to multiple distinct business format and product category groups, thus ensuring representativeness. The detailed information of the 12 selected stores is presented in Table 2.

Table 2. Store Information Table.

Store ID	City	State	Business Format and Product Category Group
3	Quito	Pichincha	8
9	Quito	Pichincha	6
21	Santo Domingo	Santo Domingo de los Tsachilas	6
27	Daule	Guayas	1
28	Guayaquil	Guayas	10
38	Loja	Loja	4
41	Machala	El Oro	4
44	Quito	Pichincha	5
45	Quito	Pichincha	11
47	Quito	Pichincha	14
48	Quito	Pichincha	14
50	Ambato	Tungurahua	14

Based on the above store information, hyperedges are generated and subsequently used to construct the hypergraph, as shown in Table 3.

Table 3. Generated hyperedge information.

Hyperedge Information	Associated Store ID
Same City-Same State Hyperedges (Quito, Pichincha)	3, 9, 44, 45, 47, 48
Different Cities-Same State Hyperedges (Daule, Guayaquil, Guayas)	27, 28
Business Format and Product Category Hyperedges (4)	38, 41
Business Format and Product Category Hyperedges (6)	9, 21
Business Format and Product Category Hyperedges (14)	47, 48, 50

3.5.2. Experimental Setup

The algorithm was implemented in Python 3.8 using the PyTorch 2 framework, and was executed on the Windows 10 operating system. The hardware configuration comprised an AMD Ryzen 5 5600G with Radeon Graphics processor (3.90 GHz), 24 GB RAM, an AMD Radeon RX 550X graphics card (4 GB VRAM), in addition to the integrated AMD Radeon Graphics.

Prior to model training, a unified set of hyperparameters was configured for the prediction model. The dataset was chronologically split into training and testing sets in a 4:1 ratio. The model’s historical lookback window was set to 10, with a forecasting horizon of 1. Thus, in each prediction step, sales data from the past 10 days served as input to generate a single-step forecast, thus defining the demand forecasting task. During training, the batch size was set to 16, the maximum number of training epochs was set to 200, and an early stopping mechanism with a patience of 20 was employed. The Adam optimizer was employed with an initial learning rate of 0.0001. The LSTM featured a single-layer structure with a hidden dimension of 128, the TCN utilized 128 filters, the hypergraph convolution consisted of 2 layers with an output dimension of 128, and the multi-head attention mechanism employed 4 heads.

Three widely used evaluation metrics were employed to assess model performance: Mean Absolute Error (MAE), Root Mean Square Error (RMSE), and Mean Absolute Percentage Error (MAPE). Lower values of these metrics corresponded to better forecasting performance. Their calculation formulas are as follows:

$$E_{\mathrm{MA}}={\displaystyle \frac{1}{n}}\sum _{i=1}^n|y_i-{\widehat{y}}_i|$$

(16)

$$E_{\mathrm{RMS}}=\sqrt{\frac{1}{n}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

(17)

$$E_{\mathrm{MAP}}={\displaystyle \frac{1}{n}}\sum _{i=1}^n|{\displaystyle \frac{y_i-{\widehat{y}}_i}{y_i}}|\times 100\%$$

(18)

Here, y_i represents the actual product demand value, ${\widehat{y}}_i$ represented the predicted product demand value, and n is the total number of samples involved in the prediction.

4. Experimental Results and Analysis

4.1. Comparison of Prediction Results from Different Models

To systematically validate the effectiveness of the Spatiotemporal Hypergraph Attention Network (STHA) in product demand forecasting, STHA was compared against six representative baseline models. The selection of baseline models is based on the following considerations:

• ARIMA: Served as a representative statistical forecasting model, capturing the stationarity and trend of time series through autoregressive, integrated, and moving average components.
• LSTM: A widely used deep learning method for temporal modeling, serving as both a fundamental model in product demand forecasting and the baseline for our temporal feature processing.
• TCN (Temporal Convolutional Network) [29]: Utilized causal and dilated convolutional structures to process temporal data, forming a key component of spatiotemporal graph convolutional networks.
• Transformer: This self-attention-based model captured global dependencies among different time steps, providing a contrast to the Hawkes and hypergraph attention mechanisms used in this study.
• PatchTST [30]: Incorporated an innovative patching strategy that segments long sequences into localized semantic units, enhancing computational efficiency while preserving global dependency modeling. Its inclusion as a benchmark enabled rigorous evaluation of the proposed method against state-of-the-art time seriesforecasting techniques.
• STGCN (Spatio-Temporal Graph Convolutional Network) [31]: Integrated Graph Convolutional Networks (GCN) [32] with temporal convolutional networks to form spatiotemporal convolutional blocks. This model simplified complex market entity relationships into numerous pairwise interactions, contrasting with the spatiotemporal hypergraph architecture.

The experimental comparison was conducted systematically from three perspectives. First, at the methodology type level, comparing ARIMA against deep learning models demonstrated the limitations of traditional statistical methods in handling the complexities of modern product demand forecasting. Second, at the forecasting paradigm level, LSTM, TCN, Transformer, and PatchTST models were employed to model and predict the product demand for each store independently, which demonstrated the performance of single time series forecasting methods. Conversely, the STHA model performed joint modeling of the multi-store time series to fully leverage potential spatial correlations and temporal dependencies, enabling information complementarity and demonstrating the superiority of joint multi-time-series forecasting. Finally, at the graph structure design level, comparison against STGCN—which simplifies complex inter-store relationships as pairwise interactions—highlighted the limitations of simple graph structures compared to hypergraph structures in representing complex spatial dependencies. Both the STHA model and the six baseline models were executed under three random seeds. Table 4 reports the average experimental results for all models.

Table 4. Comparison of evaluation metrics for different prediction models.

Prediction Model	Evaluation Metrics	Store ID
		3	9	21	27	28	38	41	44	45	47	48	50
ARIMA	MAE	16.319	11.778	17.034	14.179	18.943	20.508	13.461	25.770	16.826	24.183	23.992	17.587
	RMSE	20.447	15.109	22.449	17.713	25.495	24.912	17.293	31.732	20.284	30.266	29.486	21.973
	MAPE/%	24.814	36.682	38.070	30.591	48.232	43.077	32.231	33.214	35.627	31.705	35.422	36.266
LSTM	MAE	12.959	8.628	14.406	15.154	12.842	15.041	11.055	19.335	14.297	18.912	20.839	14.228
	RMSE	17.343	11.622	18.352	19.077	16.113	19.289	15.235	25.614	18.315	22.792	26.247	16.844
	MAPE/%	20.541	31.482	34.126	33.862	44.223	23.864	25.062	22.569	25.093	25.437	32.263	28.191
TCN	MAE	11.930	8.569	13.751	14.765	12.909	14.328	9.962	20.273	12.304	18.225	19.331	13.883
	RMSE	14.994	11.142	17.414	18.496	16.734	18.164	13.641	26.947	15.548	22.536	24.482	16.633
	MAPE/%	18.717	31.048	32.099	32.671	43.313	22.115	22.576	23.263	20.824	24.143	29.827	26.624
Transformer	MAE	12.249	9.099	14.606	15.955	13.312	14.776	9.413	22.261	12.628	19.408	20.571	14.316
	RMSE	15.857	12.379	18.188	19.562	16.655	18.688	12.867	28.567	15.688	23.484	25.745	17.631
	MAPE/%	19.232	34.316	33.586	34.464	45.641	23.801	21.925	26.046	21.681	26.184	31.680	28.475
PatchTST	MAE	12.835	8.605	11.729	11.211	12.640	15.874	8.033	17.556	15.941	16.942	17.994	12.959
	RMSE	17.313	12.105	16.720	13.746	16.199	19.595	10.715	23.561	19.762	22.203	24.586	16.453
	MAPE/%	18.859	31.383	29.864	25.787	33.405	25.882	21.003	21.977	25.588	21.643	29.483	26.207
STGCN	MAE	12.498	8.421	15.185	19.196	20.211	13.210	17.371	26.305	12.019	16.976	16.131	12.668
	RMSE	15.746	10.836	19.547	23.046	22.246	16.343	20.326	34.272	14.836	22.905	20.952	16.241
	MAPE/%	18.850	24.834	33.993	45.492	53.905	22.397	42.040	27.408	21.277	21.239	24.742	24.958
STHA	MAE	9.978	8.103	10.492	9.434	12.312	8.439	6.556	10.787	8.830	12.329	10.767	11.827
	RMSE	13.185	10.298	13.525	12.657	16.035	10.275	9.426	14.190	9.967	15.153	15.301	15.801
	MAPE/%	15.362	22.762	19.347	19.734	31.549	14.383	14.345	11.839	16.258	16.922	17.594	24.863

The bolded figures represent the optimal results.

The experimental results demonstrated that ARIMA, as a representative traditional statistical model, achieved markedly inferior accuracy, with forecasting accuracy rates below 70% for most stores, highlighting the limitations of traditional methods in handling modern market data characterized by high volatility and significant nonlinearity. In contrast, deep learning models based on single time series (e.g., LSTM, TCN, Transformer, PatchTST) exhibited substantial performance improvements. However, comparison of evaluation metrics across models revealed that, despite distinct architectural mechanisms—TCN’s convolutional operations, Transformer’s self-attention, and PatchTST’s patching strategy—the performance differences remained marginal. This finding suggested that relying solely on the temporal feature extraction capabilities of individual time series was insufficient for achieving further breakthroughs in complex product demand forecasting.

On the other hand, the results for STGCN showed that while the simple graph structure yielded modest accuracy gains for a limited number of stores, it led to considerably higher prediction errors in most instances. This indicated that although leveraging spatial correlations held potential, the oversimplification of complex multivariate relationships into numerous pairwise interactions could introduce redundant information and noise, ultimately impairing model performance.

The proposed STHA model seamlessly integrated information from both spatial and temporal dimensions via a hypergraph structure, thereby incorporating a more comprehensive set of influencing factors. By leveraging information complementarity across multiple time series, the STHA model significantly enhanced forecasting accuracy in multi-market-entity environments. Furthermore, the incorporated hypergraph attention mechanisms effectively mitigated performance degradation caused by variations in hyperedge importance and structural noise. In our experiments, STHA achieved a maximum improvement in accuracy of 15 percentage points over traditional single time series models, validating the effectiveness of joint multi-time-series forecasting. In contrast to the simple graph-based model, STHA maintained consistently low prediction errors, demonstrating superior robustness and forecasting stability, thereby fully underscoring its advantages and potential in modeling complex relationships.

4.2. Ablation Experiment

To validate the effectiveness of individual components of the Spatiotemporal Hypergraph Attention Network (STHA), this study performed a systematic ablation study. Four variant models were constructed by sequentially removing: the Hawkes attention mechanism from the temporal feature processing module; the spatial hypergraph convolution module in its entirety; the hypergraph attention mechanism within the spatial convolution module; and all attention mechanisms from the model. These variants are denoted as STHA-w/o-HA, STHA-w/o-HG, STHA-w/o-HGA, and STHA-w/o-ATT, respectively. Under identical experimental conditions and using the Mean Absolute Percentage Error (MAPE) as the evaluation metric, a comparison of these models is presented in Table 5. The results indicate that all four variant models yield higher MAPE values than the complete STHA model, reflecting a substantial decline in prediction accuracy. This confirms that the Hawkes attention mechanism, the hypergraph structure, and the hypergraph attention mechanism constitute essential components of the model.

Table 5. Ablation experiment results of the STHA model.

Model Variant	Store ID
	3	9	21	27	28	38	41	44	45	47	48	50
STHA-w/o-HA	15.739	32.715	21.736	19.851	35.506	17.987	18.021	12.253	22.354	17.742	18.747	27.402
STHA-w/o-HG	24.092	27.213	26.477	24.027	35.341	16.642	19.760	13.157	23.819	17.684	20.342	35.648
STHA-w/o-HGA	27.488	32.376	31.267	22.363	36.573	19.860	24.589	18.687	28.590	17.780	18.289	30.221
STHA-w/o-ATT	21.509	60.347	24.742	24.510	36.654	14.477	29.373	18.273	25.106	17.416	18.238	42.861
STHA-Full	15.362	22.762	19.357	19.734	31.549	14.383	14.345	11.839	16.258	16.922	17.594	24.863

The bolded figures represent the optimal results.

A detailed analysis reveals that, compared with STHA-w/o-HA, the variants lacking components of the spatial hypergraph convolution module (STHA-w/o-HG and STHA-w/o-HGA) exhibit greater performance deterioration for certain stores, with declines exceeding 10 percentage points in some cases. This pronounced decline can be attributed to the intrinsic characteristics of both the dataset and the forecasting task. The demand patterns of the selected stores exhibit strong and dynamically evolving spatial dependencies. Consequently, when the hypergraph structure responsible for capturing these dependencies is removed (STHA-w/o-HG) or replaced by a static, non-adaptive version (STHA-w/o-HGA), the model fails to leverage key spatial dependency signals that enhance the prediction of individual stores, resulting in marked degradation in accuracy. This observation highlights the dominant role of spatial correlation information in multi-market-entity product demand forecasting.

Furthermore, STHA-w/o-HGA yields higher MAPE values than STHA-w/o-HG in most store experiments, indicating that incorporating only spatial information without the hypergraph attention mechanism may introduce noise and diminish performance. This occurs because the constructed hyperedges represent a static prior assumption that may contain irrelevant or weakly informative connections for specific forecasting targets. Without the hypergraph attention mechanism, the model cannot distinguish informative hyperedges from noisy ones, leading to suboptimal feature aggregation. This comparative result demonstrates that the hypergraph attention mechanism substantially enhances the effectiveness of the spatial hypergraph convolution module and underscores the critical importance of adaptive model design.

Additionally, the STHA-w/o-ATT variant, in which all attention mechanisms are removed, is conceptually similar to hypergraph convolutional neural networks applied in other domains, as it focuses solely on temporal feature extraction and employs hypergraphs to model higher-order relationships. Experimental results show that although STHA-w/o-ATT demonstrates satisfactory prediction performance in certain instances, it frequently exhibits substantially higher prediction errors, resulting in considerable performance volatility. This finding further illustrates that combining temporal features with a static hypergraph is insufficient for capturing the evolving dependency patterns that characterize real-world demand dynamics. The instability of STHA-w/o-ATT validates the necessity of the integrated dual-attention design (HA + HGA), which enables dynamic, context-aware spatiotemporal information fusion. This result further corroborates the limitations of existing hypergraph convolutional neural networks for product demand forecasting tasks.

4.3. Correlation Verification

Based on the aforementioned experimental results, we hypothesize that stores in close geographical proximity or belonging to the same business format and product category group exhibit historical sales time series with substantial similarity in both data distribution and temporal variation patterns. Consequently, during joint multi-time-series forecasting, statistical interdependencies among these series may enhance prediction accuracy. To validate this correlation hypothesis, the Pearson Correlation Coefficient (PCC) is calculated using synchronous sales data of the same product category across the participating stores. The Pearson Correlation Coefficient measures the degree of linear correlation between two variables, with values ranging from −1 to 1. A coefficient close to 1 indicates a positive correlation, meaning the two series exhibit concordant upward or downward trends. A strong correlation is generally considered when |PCC| ≥ 0.7, suggesting that the influence of one variable should be considered when forecasting the other.

For the selected 12 stores, Table 6 reports the top 20 pairwise correlations with the highest Pearson Correlation Coefficients, as detailed below.

Table 6. Pearson correlation coefficient of sales data for the same product in different stores.

Store ID Combination	PCC
44–48	0.8497
44–47	0.8352
44–45	0.8352
45–48	0.8317
03–47	0.8315
48–50	0.8240
47–48	0.8178
44–50	0.8060
45–47	0.8052
38–44	0.8026
45–50	0.8014
38–48	0.7989
03–48	0.7940
03–45	0.7916
09–48	0.7748
38–47	0.7712
21–48	0.7623
47–50	0.7569
27–48	0.7468
38–41	0.7308

The results confirm that geographically adjacent stores or those belonging to the same business format and product category group exhibit strong correlations in the sales patterns of identical products. This finding further validates the effectiveness of the proposed Spatiotemporal Hypergraph Attention Network (STHA) model. The model leverages real historical sales data to explicitly incorporate the interrelationships among multiple market entities and their spatiotemporal dependencies. Consequently, it aligns more closely with real-world business scenarios and fundamental economic principles, leading to notable improvements in demand forecasting accuracy. Thus, this innovative forecasting approach provides a sound scientific basis and robust decision support for enterprises operating in complex and volatile market environments.

5. Conclusions

5.1. Summary of Findings and Contributions

This paper proposes a product demand forecasting method based on a Spatiotemporal Hypergraph Attention Network. The framework advances the forecasting task by shifting from isolated single time series modeling to joint prediction across interconnected multiple time series through the integration of temporal dynamics and higher-order spatial dependencies. Experimental results on the Corporación Favorita dataset confirm the efficacy of the proposed approach. Quantitatively, STHA achieves substantial improvements over the statistical benchmark ARIMA, with the maximum reduction in MAPE exceeding 25 percentage points for individual stores and most stores showing improvements of over 15 percentage points. Relative to the strongest deep learning baseline, PatchTST, STHA further reduces MAPE by 2–10 percentage points across most stores. In contrast to the graph-based model STGCN—which exhibits pronounced volatility, with MAPE for some stores exceeding 40%—STHA maintains consistently low error rates, demonstrating superior robustness in modeling complex spatial interactions.

The contributions of this work are threefold, spanning conceptual, methodological, and practical dimensions. Conceptually, we reframe product demand forecasting as a spatiotemporal joint modeling problem. Methodologically, we introduce an integrated framework that combines (i) a Hawkes process–based temporal attention mechanism for modeling demand self-excitation; (ii) a hypergraph structure to represent higher-order spatial relationships; and (iii) a dynamic hypergraph attention mechanism that adaptively weights multi-dimensional spatial dependencies. This unified design overcomes limitations in models that treat time series independently or rely on static relational assumptions. Empirical evidence from extensive model comparisons and ablation studies provides strong support for these methodological innovations. Practically, STHA enables more precise inventory allocation, reduced safety stock requirements, and enhanced supply chain coordination—offering tangible operational benefits for real-world sales management.

5.2. Limitations and Future Directions

Despite its promising results, this study has several limitations that point to fruitful directions for future work. Correlation analyses suggest the existence of latent relational mechanisms beyond those represented in the manually constructed hyperedges. Future work will explore data-driven and dynamically evolving hypergraph construction strategies and incorporate additional external factors (e.g., weather conditions, macroeconomic indicators) to further enhance predictive generalizability. In addition to the above methodological and data-driven enhancements, several important avenues for future research emerge to further validate and extend the proposed framework:

First, the empirical analysis relies on data from a single country (Ecuador). Because market structures, economic environments, and consumer behaviors vary widely across regions, evaluating STHA on datasets from other countries is essential for assessing its cross-context robustness and enabling broader comparative research.

Second, although the selected time period (January–August 2017) is representative, its limited duration restricts the ability to analyze long-term structural changes in demand. Future work should extend the temporal horizon to multi-year datasets. More importantly, evaluating the model on periods characterized by major disruptive events—such as the COVID-19 pandemic or macroeconomic shocks—would provide a stringent benchmark for assessing the model’s resilience under highly volatile and non-stationary conditions.

Third, given its capacity to model complex multi-entity dependencies, the STHA framework holds substantial potential for broader scientific applications, including epidemiology, logistics, energy demand forecasting, and financial risk analysis. Exploring its applicability in these areas represents a promising direction for interdisciplinary extensions.

Finally, an important avenue for enhancing practical utility is integrating STHA into automated decision-support systems. Embedding the model within operational platforms would enable real-time, actionable recommendations for inventory management, logistics optimization, dynamic pricing, and resource allocation—closing the loop between prediction and decision-making and maximizing the framework’s practical value.